An Assessment of Anthropogenic CO2 Emissions by Satellite-Based Observations in China
Abstract
1. Introduction
2. Data and Methodology
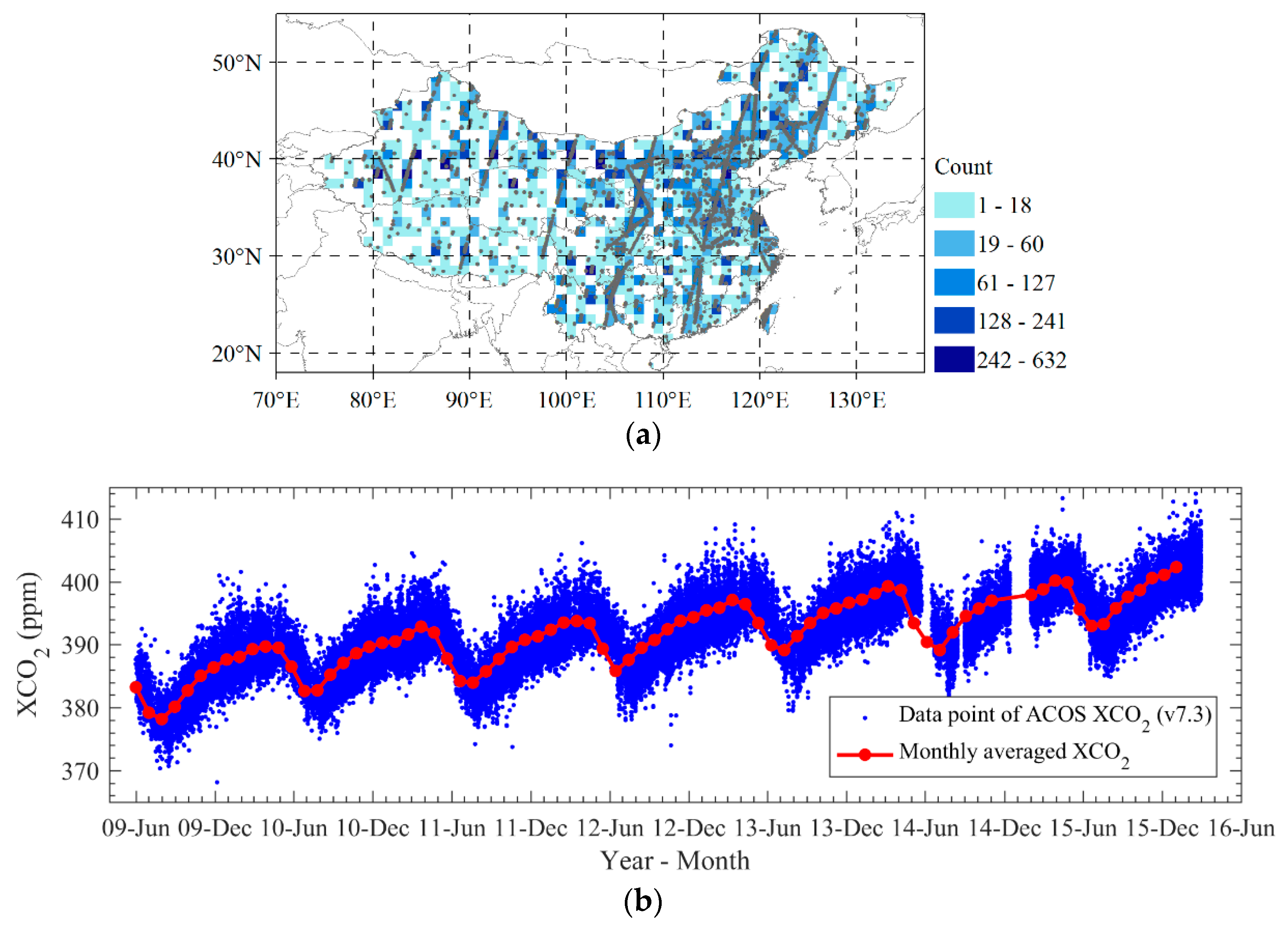
2.1. XCO2 Retrievals and Mapping XCO2 Dataset
2.2. Anthropogenic Emission Data
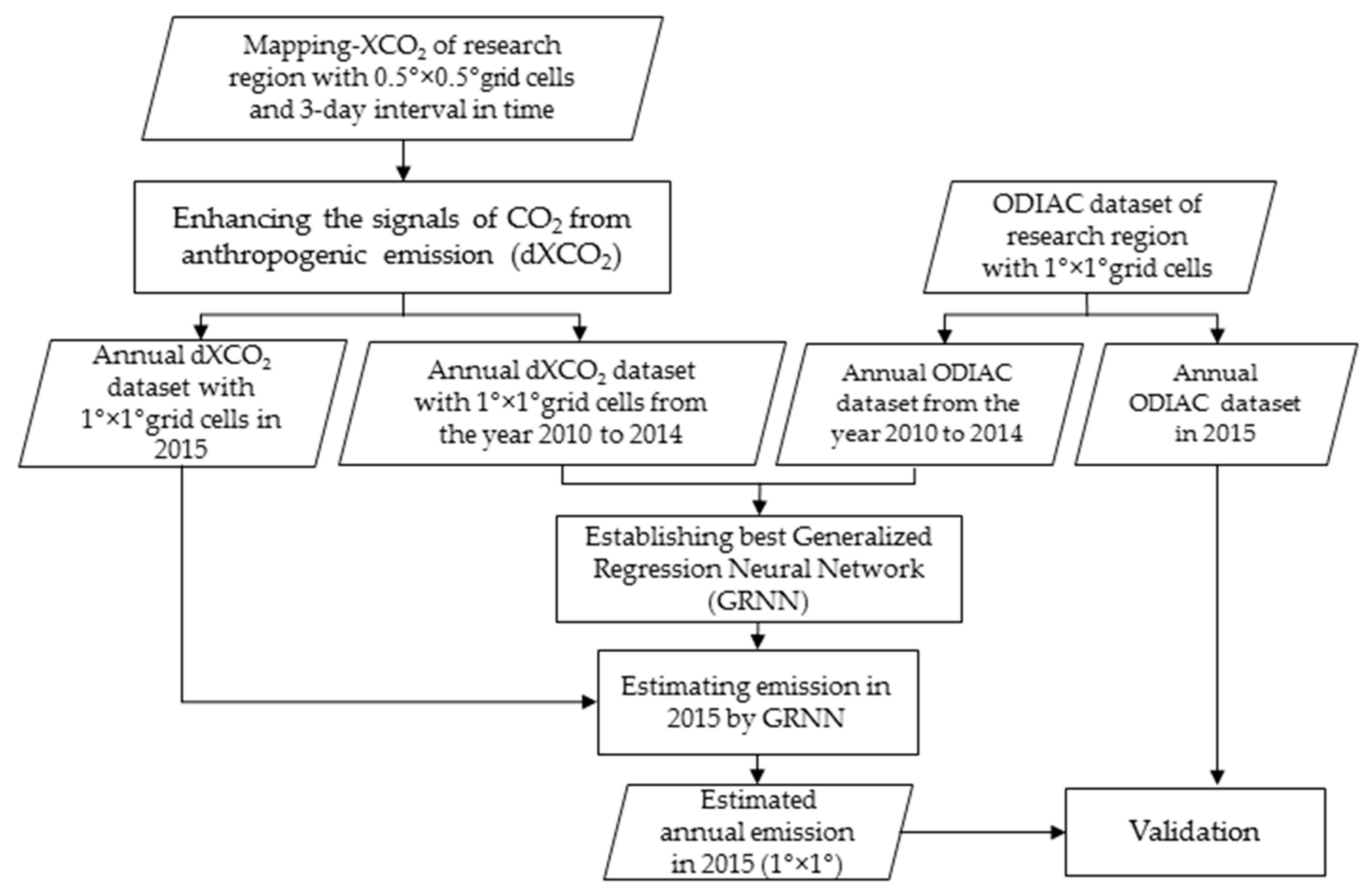
2.3. Methodology
2.3.1. Variable of XCO2 Used for Estimation of Anthropogenic Emission
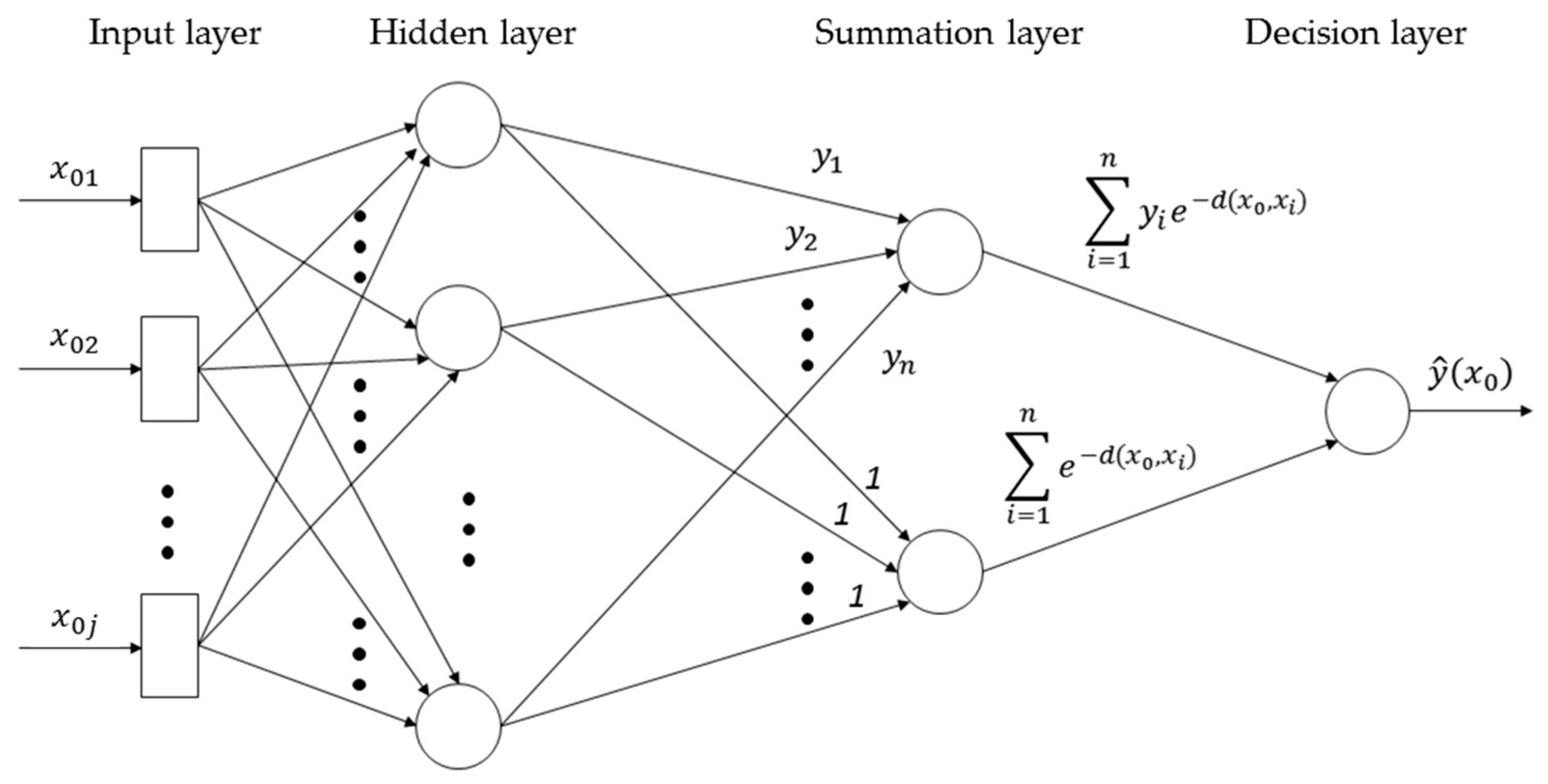
2.3.2. Estimation of Anthropogenic CO2 Emission by Neural Network Development
3. Results and Discussion
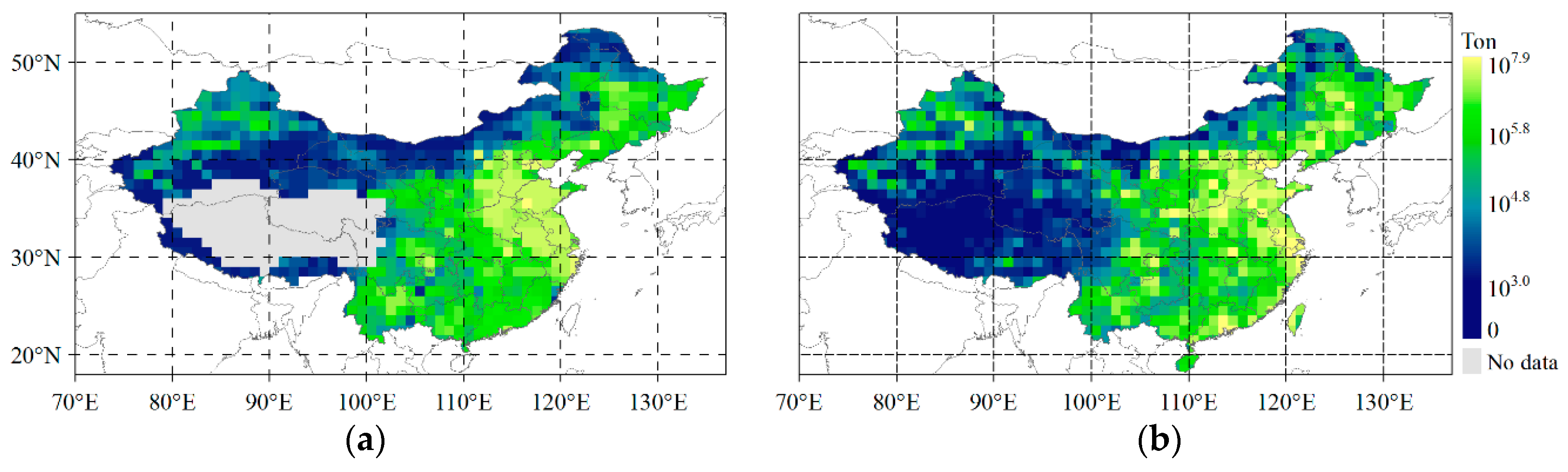
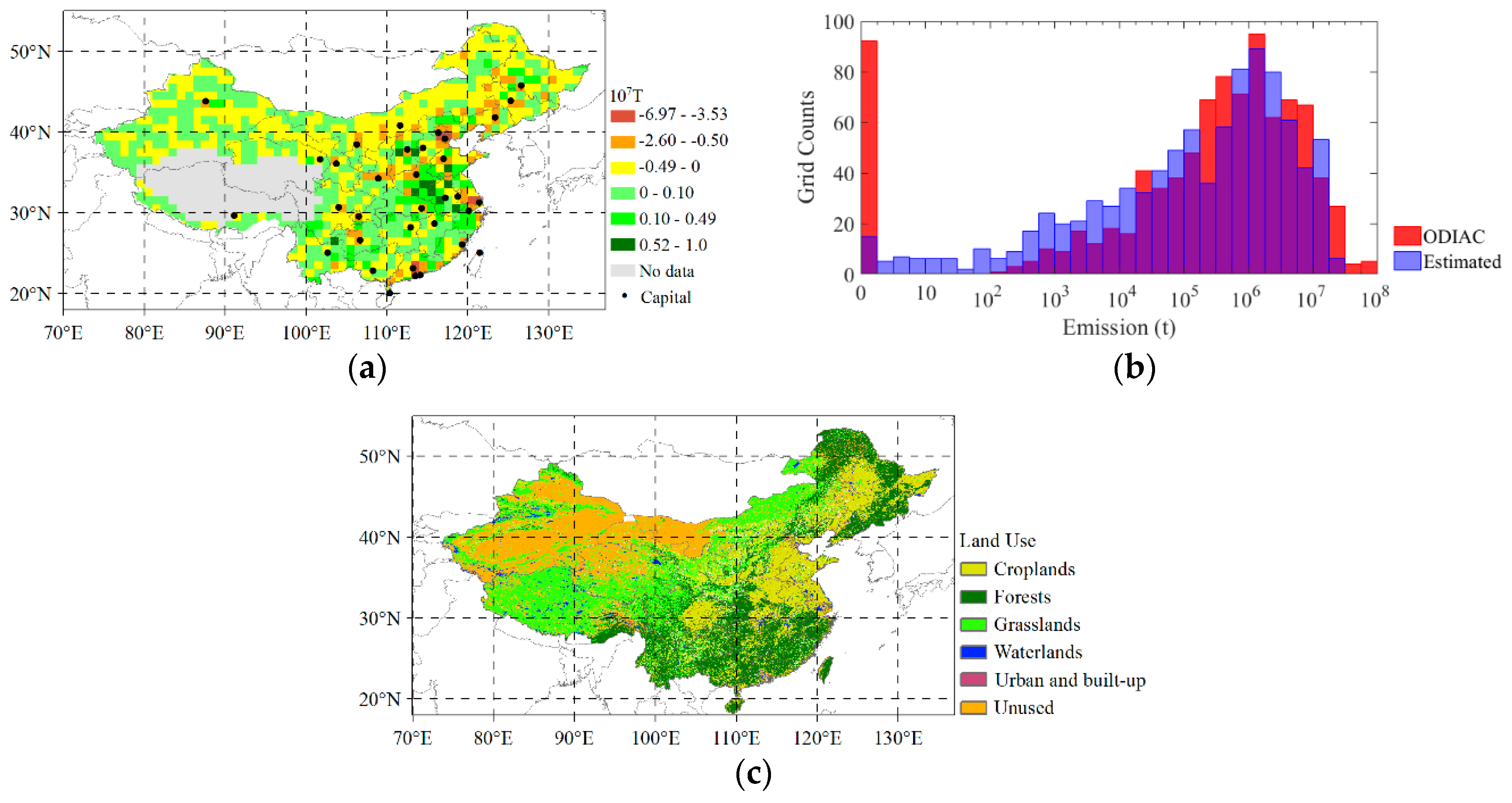
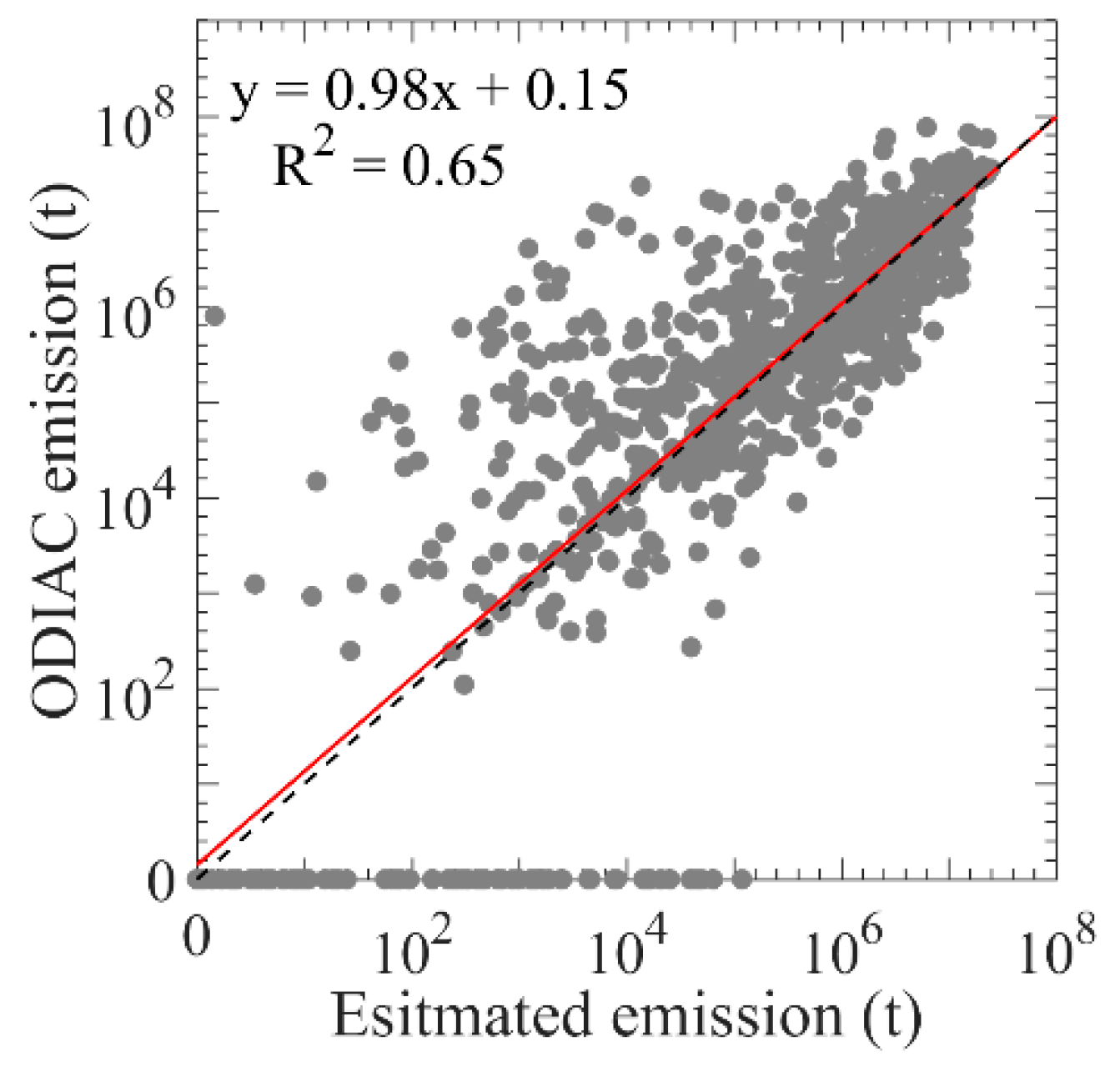
3.1. Estimated Anthropogenic Emissions by GRNN
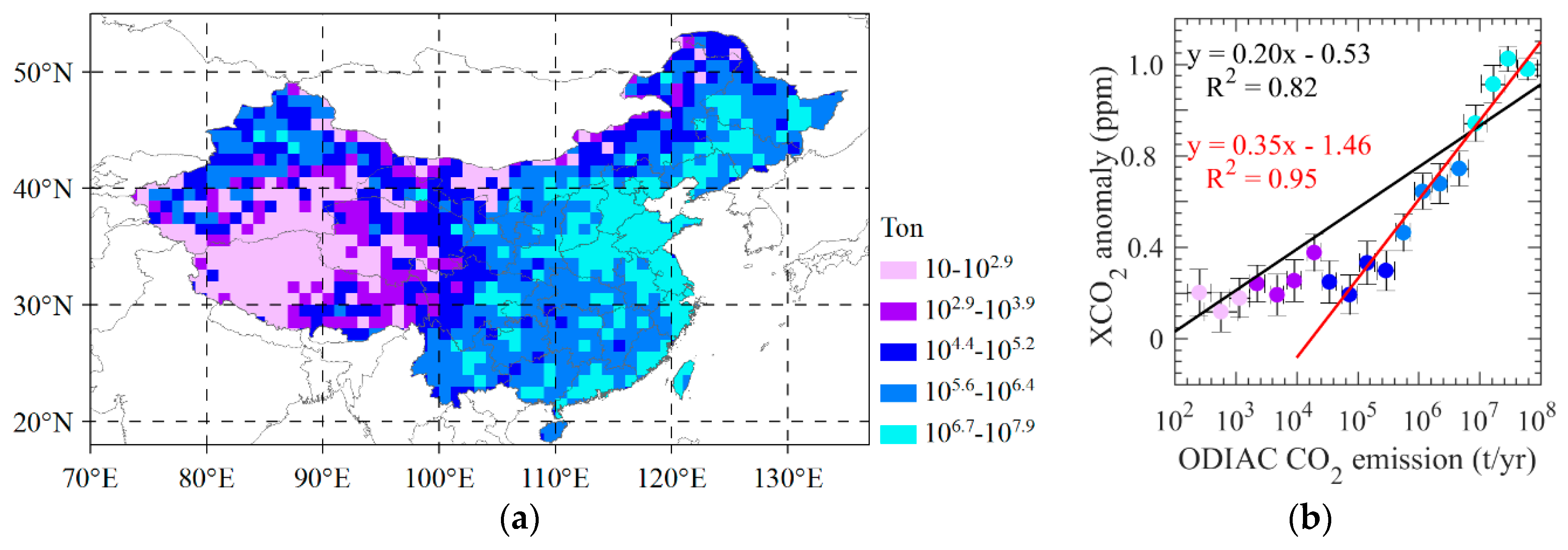
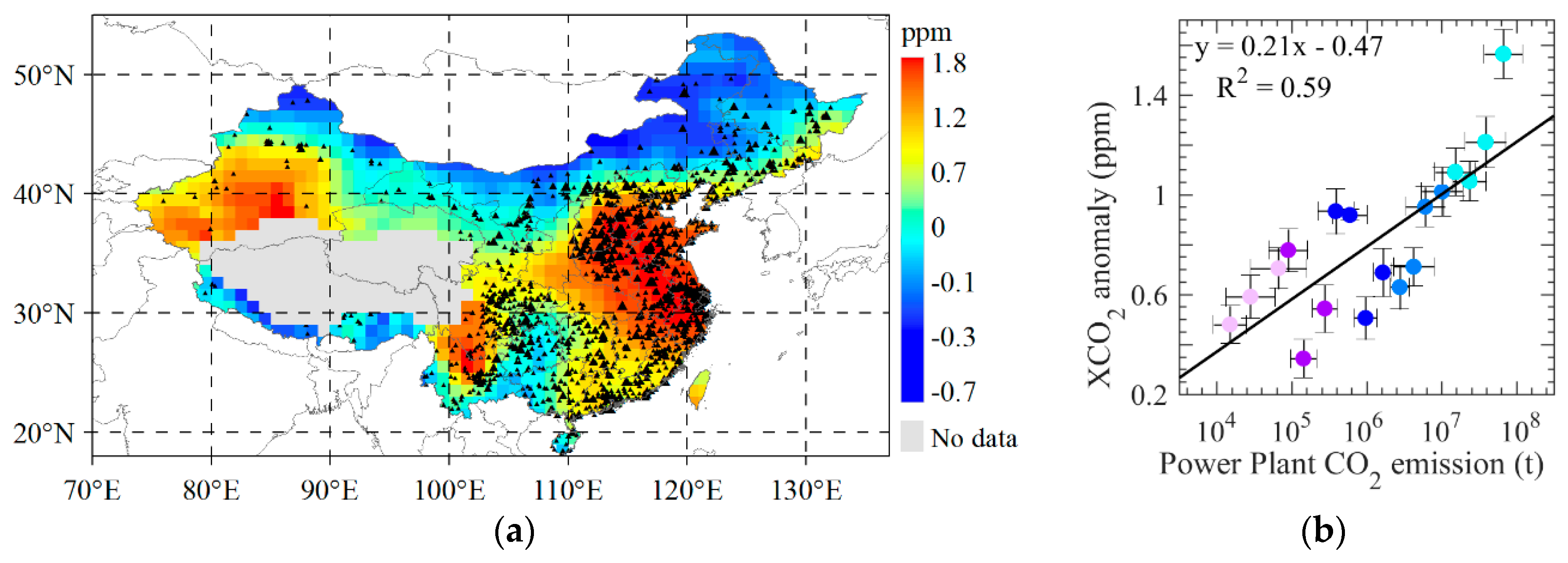
3.2. Discussion of Correlation between Retrieved XCO2 and Anthropogenic Emissons
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Meteorological Organization (WMO). Greenhouse Gas Bulletin, No. 13. Available online: https://public.wmo.int/en/media/press-release/greenhouse-gas-concentrations-surge-new-record (accessed on 2 January 2019).
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; Volume 3, pp. 3–29. [Google Scholar]
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C; An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; pp. 6–13. [Google Scholar]
- Yoshida, Y.; Ota, Y.; Eguchi, N.; Kikuchi, N.; Nobuta, K.; Tran, H.; Morino, I.; Yokota, T. Retrieval algorithm for CO2 and CH4 column abundances from short-wavelength infrared spectral observations by the greenhouse gases observing satellite. Atmos. Meas. Tech. 2011, 4, 717–734. [Google Scholar] [CrossRef]
- Crisp, D.; Miller, C.; Team, O.S. Contributions of the Orbiting Carbon Observatory (OCO) to the detection of anthropogenic CO2 emissions. ADS Abstr. Serv. 2015, 19, 73–86. [Google Scholar]
- Lei, L.P.; Guan, X.H.; Zeng, Z.Z.; Zhang, B.; Ru, F.; Bu, R. A comparison of atmospheric CO2 concentration GOSAT-based observations and model simulations. Sci. China Earth Sci. 2014, 57, 1393–1402. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schnesing, O.; Boesch, H.; Guerlet, S.; Dils, B.; Aben, I.; Armante, R.; Bergamaschi, P.; Bovensmann, H.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparison and quality assessment of near-surface-sensitive satellite-derived CO2 and CH4 global data sets. Remote Sens. Environ. 2015, 162, 344–362. [Google Scholar] [CrossRef]
- Crisp, D.; Miller, C.E.; DeCola, P.L. NASA Orbiting Carbon Observatory: Measuring the column averaged carbon dioxide mole fraction from space. J. Appl. Remote Sens. 2008, 2, 142–154. [Google Scholar] [CrossRef]
- Yoshida, T.; Yoshida, Y.; Eguchi, N.; Ota, Y.; Tanaka, T.; Watanabe, H.; Maksyutov, S. Global concentrations of CO2 and CH4 retrieved from GOSAT: First preliminary results. Sci. Online Lett. Atmos. Sola 2009, 5, 160–163. [Google Scholar]
- Liu, Y.; Yang, D.X.; Cai, Z.N. A retrieval algorithm for TanSat XCO2 observation: Retrieval experiments using GOSAT data. Chin. Sci. Bull. 2013, 58, 1520–1523. [Google Scholar] [CrossRef]
- Bovensmann, H.; Buchwitz, M.; Burrows, J.P.; Reuter, M.; Krings, T.; Gerilowski, K.; Schneising, O.; Heymann, J.; Tretner, A.; Erzinger, J. A remote sensing technique for global monitoring of power plant CO2 emissions from space and related applications. Atmos. Meas. Tech. 2010, 3, 781–811. [Google Scholar] [CrossRef]
- Schneising, O.; Heymann, J.; Buchwitz, M.; Reuter, M.; Bovensmann, H.; Burrows, J. Anthropogenic carbon dioxide source areas observed from space: Assessment of regional enhancements and trends. Atmos. Chem. Phys. 2013, 13, 2445–2454. [Google Scholar] [CrossRef]
- Keppel-Aleks, G.; Wennberg, P.O.; O’Dell, C.W.; Wunch, D. Towards constraints on fossil fuel emissions from total column carbon dioxide. Atmos. Chem. Phys. 2013, 13, 4349–4357. [Google Scholar] [CrossRef]
- Kort, E.A.; Frankenberg, C.; Miller, C.; Oda, T. Space-based observations of megacity carbon dioxide. Geophys. Res. Lett. 2012, 39, L17806. [Google Scholar] [CrossRef]
- Janardanan, R.; Maksyutov, S.; Oda, T.; Saito, M.; Kaiser, J.W.; Ganshin, A.; Stohl, A.; Matsunaga, T.; Yoshida, Y.; Yokota, T. Comparing GOSAT observations of localized CO2 enhancements by large emitters with inventory-based estimates. Geophys. Res. Lett. 2016, 43, 3486–3493. [Google Scholar] [CrossRef]
- Lei, L.P.; Zhong, H.; He, Z.H.; Cai, B.F.; Yang, S.Y.; Wu, C.J.; Zeng, Z.C.; Liu, L.Y.; Zhang, B. Assessment of atmospheric CO2 concentration enhancement from anthropogenic emissions based on satellite observations. Chin. Sci. Bull. 2017, 25, 2941–2950. [Google Scholar] [CrossRef]
- Hakkarainen, J.; Ialongo, I.; Tamminen, J. Direct space-based observations of anthropogenic CO2 emission areas from OCO-2. Geophys. Res. Lett. 2016, 43, 400–411. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). CO2 Emissions from Fuel Combustion Overview (2018 Edition). Available online: https://webstore.iea.org/co2-emissions-from-fuel-combustion-2018 (accessed on 2 January 2019).
- O’Dell, C.W.; Connor, B.; Bösch, H.; Brien, D.; Frankenberg, C.; Castano, R.; Christi, M.; Eldering, D.; Fisher, B.; Gunson, M.; et al. The ACOS CO2 retrieval algorithm—Part 1: Description and validation against synthetic observations. Atmos. Meas. Tech. 2012, 5, 99–121. [Google Scholar]
- Osterman, G.; Eldering, A.; Cheng, C.; O’Dell, C.W.; Crisp, D. Christian Frankenberg. Brendan Fisher. ACOS Level 2 Standard Product and Lite Data Product Data User’s Guide, v7.3; NASA GES DISC: Pasadena, CA, USA, 2017.
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The total carbon column observing network. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.C.; Lei, L.P.; Guo, L.J.; Zhang, L.; Zhang, B. Incorporating temporal variability to improve geostatistical analysis of satellite-observed CO2 in China. Chin. Sci. Bull. 2013, 58, 1948–1954. [Google Scholar] [CrossRef]
- Zeng, Z.C.; Lei, L.P.; Hou, S.S.; Ru, F.; Guan, X.X.; Zhang, B. A Regional Gap-Filling Method Based on Spatiotemporal Variogram Model of CO2 Columns. IEEE Transaftions Geosci. Remote Sens. 2014, 52, 3594–3603. [Google Scholar] [CrossRef]
- Guo, L.J.; Lei, L.P.; Zeng, Z.C.; Zou, P.F.; Liu, D.; Zhang, B. Evaluation of Spatio-Temporal Variogram Models for Mapping XCO2 Using Satellite Observations: A Case Study in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 376–385. [Google Scholar] [CrossRef]
- Oda, T.; Maksyutov, S.; Andres, R.J. The Open-source Data Inventory for Anthropogenic Carbon dioxide (CO2), version 2016 (ODIAC2016): A global, monthly fossil-fuel CO2 gridded emission data product for tracer transport simulations and surface flux inversions. Earth Syst. Sci. Data 2018, 10, 87–107. [Google Scholar] [CrossRef]
- Wheelwer, D.; Ummel, K. Calculating CARMA: Global Estimation of CO2 Emissions from the Power Sector; Working Papers; Center for Global Development: Washington, DC, USA, 2008. [Google Scholar]
- Suntharalingam, P.; Jacob, D.J.; Palmer, P.I.; Logan, J.A.; Yantosca, R.M.; Xiao, Y.P.; Evans, M.J. Improved quantification of Chinese carbon fluxes using CO2/CO correlations in Asian outflow. J. Geophys. Res. 2004, 109, D18S18. [Google Scholar] [CrossRef]
- Keppel-Aleks, G.; Wennberg, P.O.; Schneider, T. Sources of variations in total column carbon dioxide. Atmos. Chem. Phys. 2011, 11, 3581–3593. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 569–576. [Google Scholar] [CrossRef] [PubMed]
- Cigizoglu, H.K.; Alp, M. Generalized regression neural network in modelling river sediment yield. Adv. Eng. Softw. 2006, 37, 63–68. [Google Scholar] [CrossRef]
- Delon, C.; SerçA, D.; Boissard, C.; Dupont, R.; Dutot, A.; Laville, P.; De Rosnay, P.; Delmas, R. Soil NO emissions modelling using artificial neural network. Tellus B: Chem. Phys. Meteorol. 2007, 59, 502–513. [Google Scholar] [CrossRef]
- Disorntetiwat, P.; Dagli, C.H. Simple Ensemble-averaging model based on Generalized Regression Neural Network in Finacial Forecasing Problems. In Proceedings of the Adaptive Systems for Signal Processing Communications, and Control Symposium, Lake Louise, AB, Canada, 1–4 October 2000; pp. 204–218. [Google Scholar]
- Liu, D.; Lei, L.P.; Guo, L.J.; Zeng, Z.C. A Cluster of CO2 Change Characteristics with GOSAT Observations for Viewing the Spatial Pattern of CO2 Emission and Absorption. Atmosphere 2015, 6, 1695–1713. [Google Scholar] [CrossRef]
- Bie, N.; Lei, L.P.; Zeng, Z.C.; Cai, B.F.; Yang, S.Y.; He, Z.H.; Wu, C.J.; Nassar, R. Regional uncertainty of GOSAT XCO2 retrievals in China: Quantification and attribution. Atmos. Meas. Tech. Discuss. 2018, 11, 1251–1272. [Google Scholar] [CrossRef]
| ODIAC | CARMA | |
|---|---|---|
| Grid, timely unit/period | 1° × 1°, Month/2010–2015 | Points/2009 |
| Unit | Ton | Ton |
| Statistical sectors | Point sources non-point sources | - |
| Cement production | ||
| Gas flaring | ||
| International aviation and marine bunker | ||
| Used data sources | Fuel statistic data published as united nation energy statistics database BP statistical review of world energy 2017 | The environmental protection agency and department of energy International atomic energy agency |
| Producer | Center for global environment research, national institute for environment studies | Center for Global Development |
| Oda, T et al. [25] | Wheeler, D et al. [26] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Lei, L.; Zeng, Z.; He, Z.; Zhong, H. An Assessment of Anthropogenic CO2 Emissions by Satellite-Based Observations in China. Sensors 2019, 19, 1118. https://doi.org/10.3390/s19051118
Yang S, Lei L, Zeng Z, He Z, Zhong H. An Assessment of Anthropogenic CO2 Emissions by Satellite-Based Observations in China. Sensors. 2019; 19(5):1118. https://doi.org/10.3390/s19051118
Chicago/Turabian StyleYang, Shaoyuan, Liping Lei, Zhaocheng Zeng, Zhonghua He, and Hui Zhong. 2019. "An Assessment of Anthropogenic CO2 Emissions by Satellite-Based Observations in China" Sensors 19, no. 5: 1118. https://doi.org/10.3390/s19051118
APA StyleYang, S., Lei, L., Zeng, Z., He, Z., & Zhong, H. (2019). An Assessment of Anthropogenic CO2 Emissions by Satellite-Based Observations in China. Sensors, 19(5), 1118. https://doi.org/10.3390/s19051118





