Design and Calibration of a Force/Tactile Sensor for Dexterous Manipulation
Abstract
:1. Introduction
2. Design of the Force/Tactile Sensor
2.1. Requirements for Dexterous Manipulation
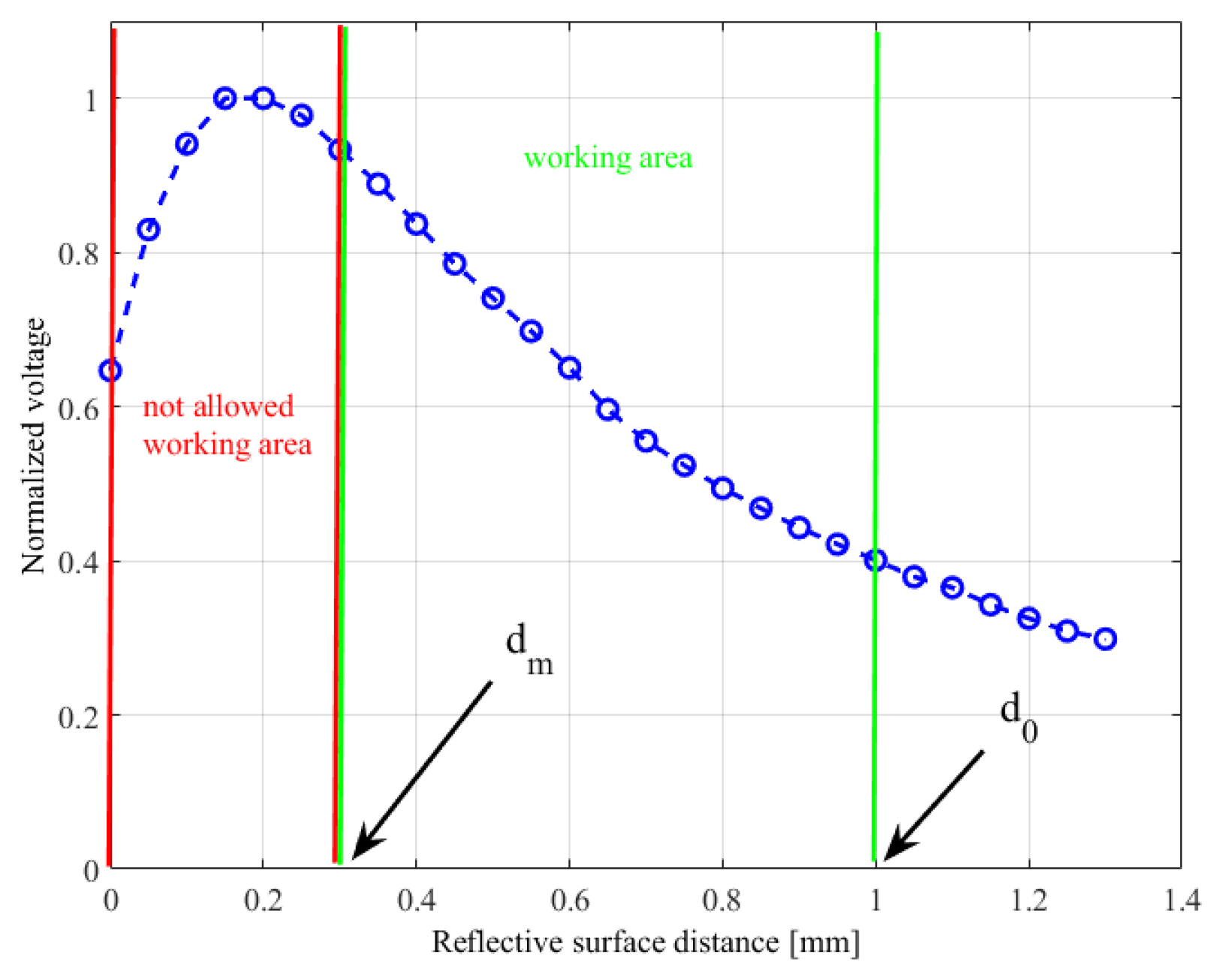
2.2. The Working Principle and the Technology
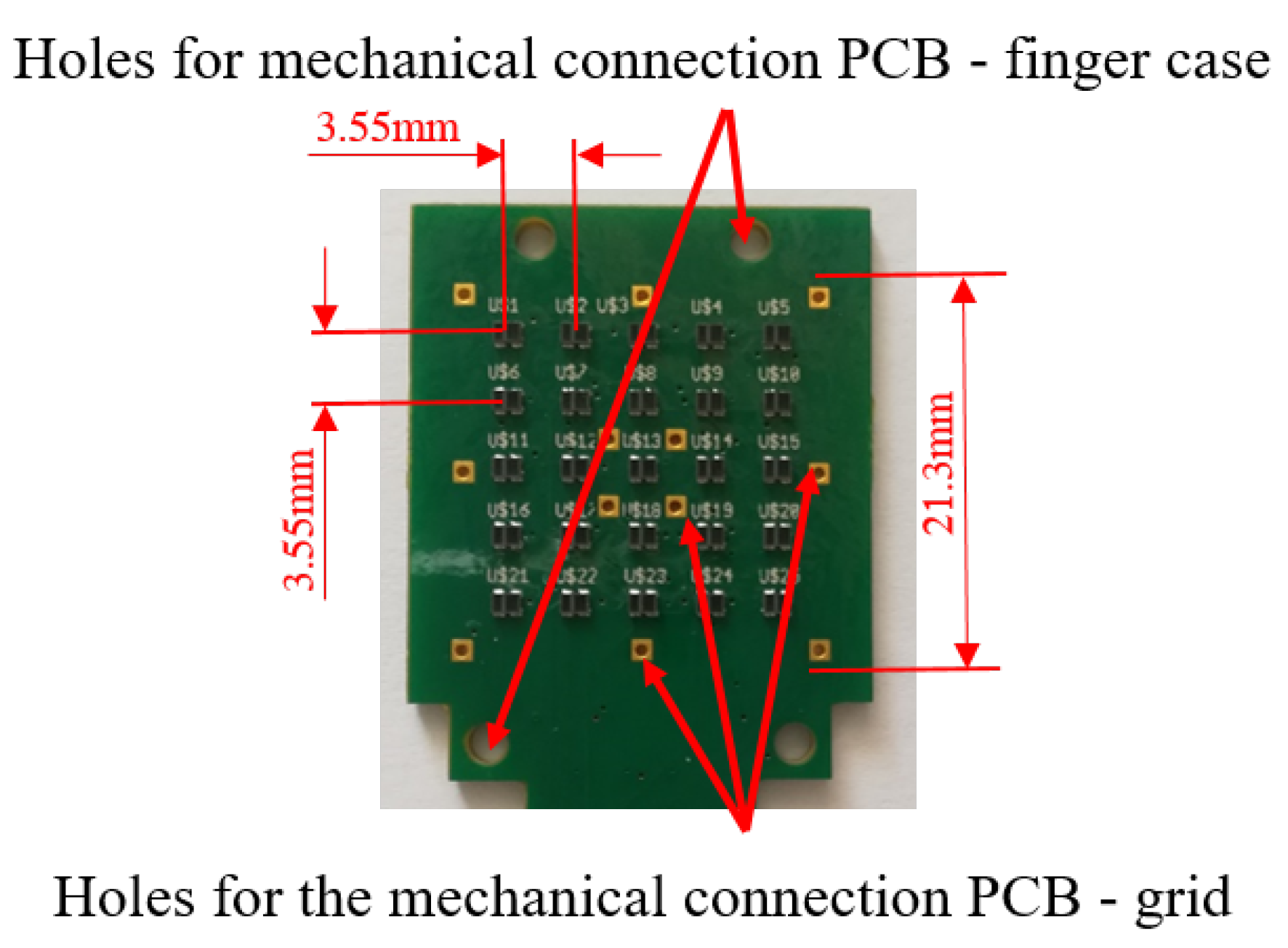
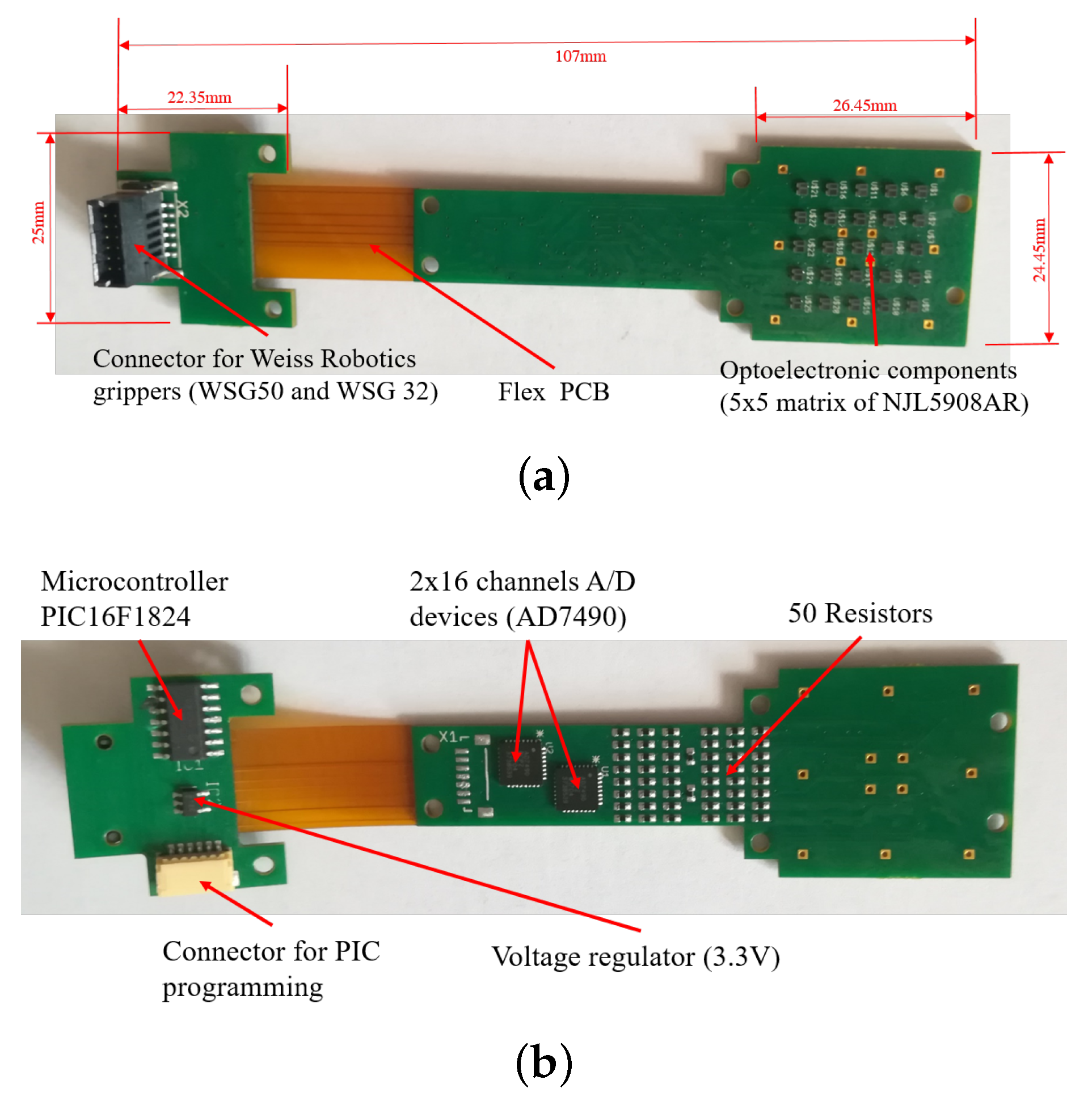
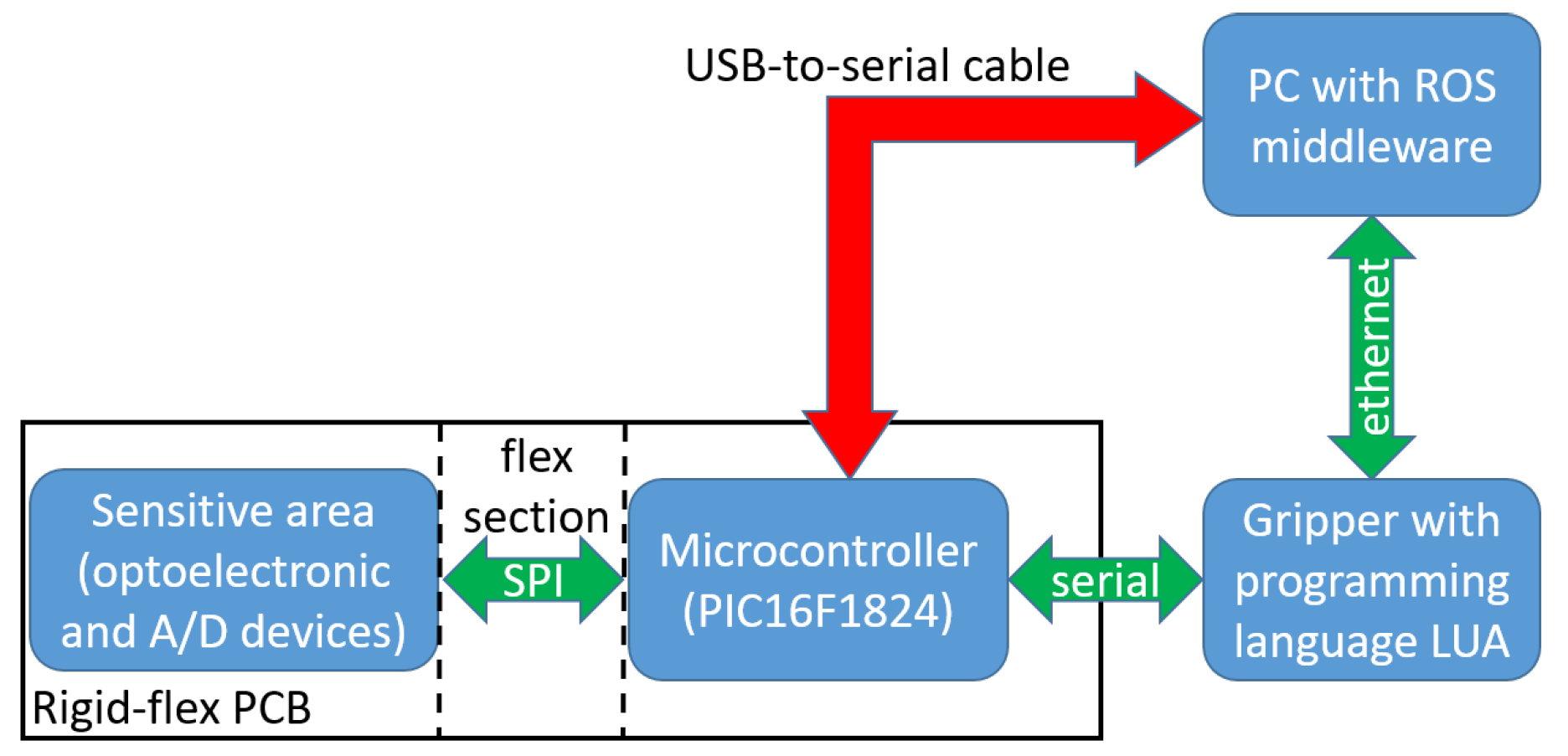
2.3. Detailed Design of the Rigid-Flex PCB
2.4. Detailed Design of the Deformable Pad
2.5. Integration of the Sensor into a Commercial Gripper
3. Sensor Calibration
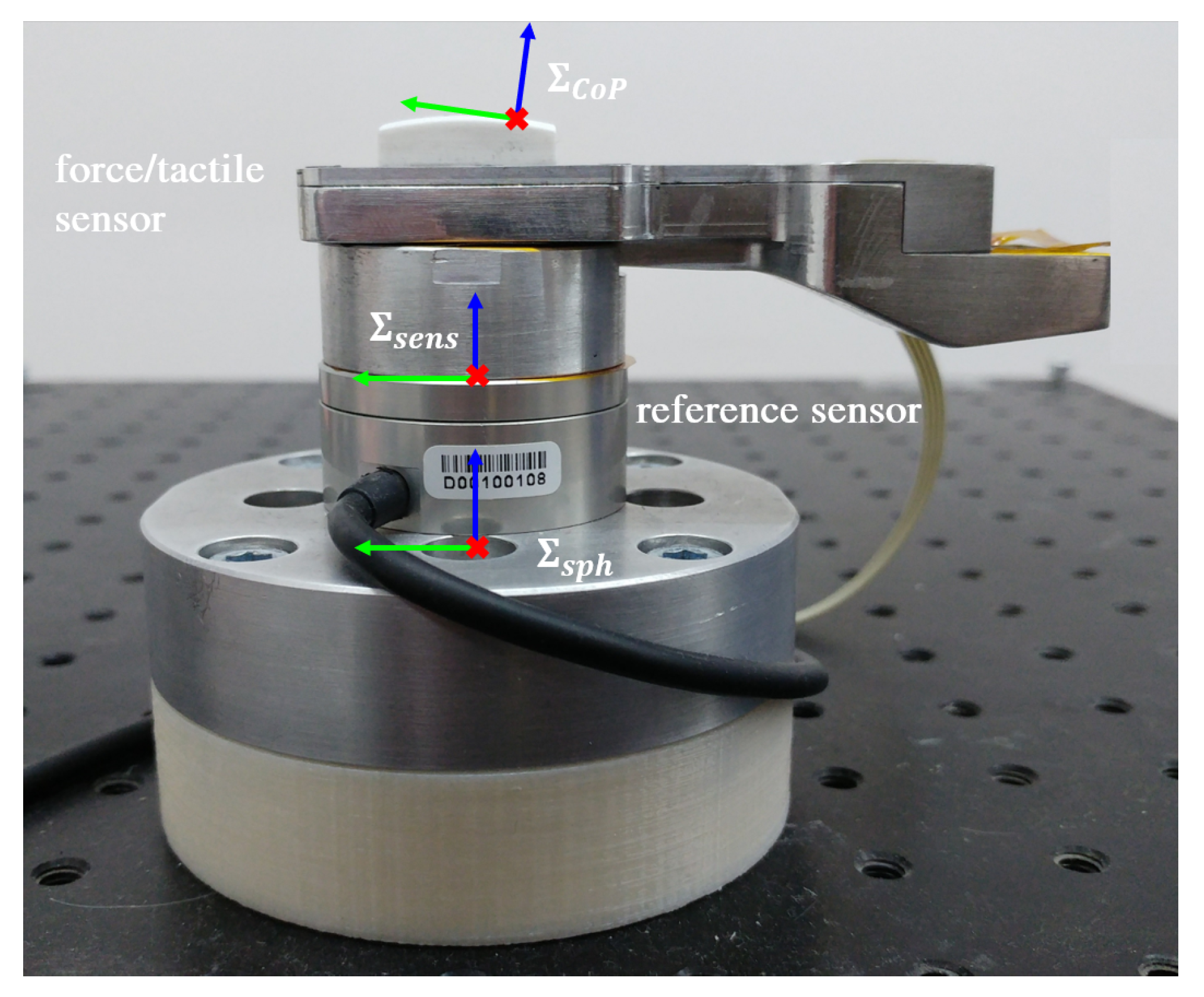
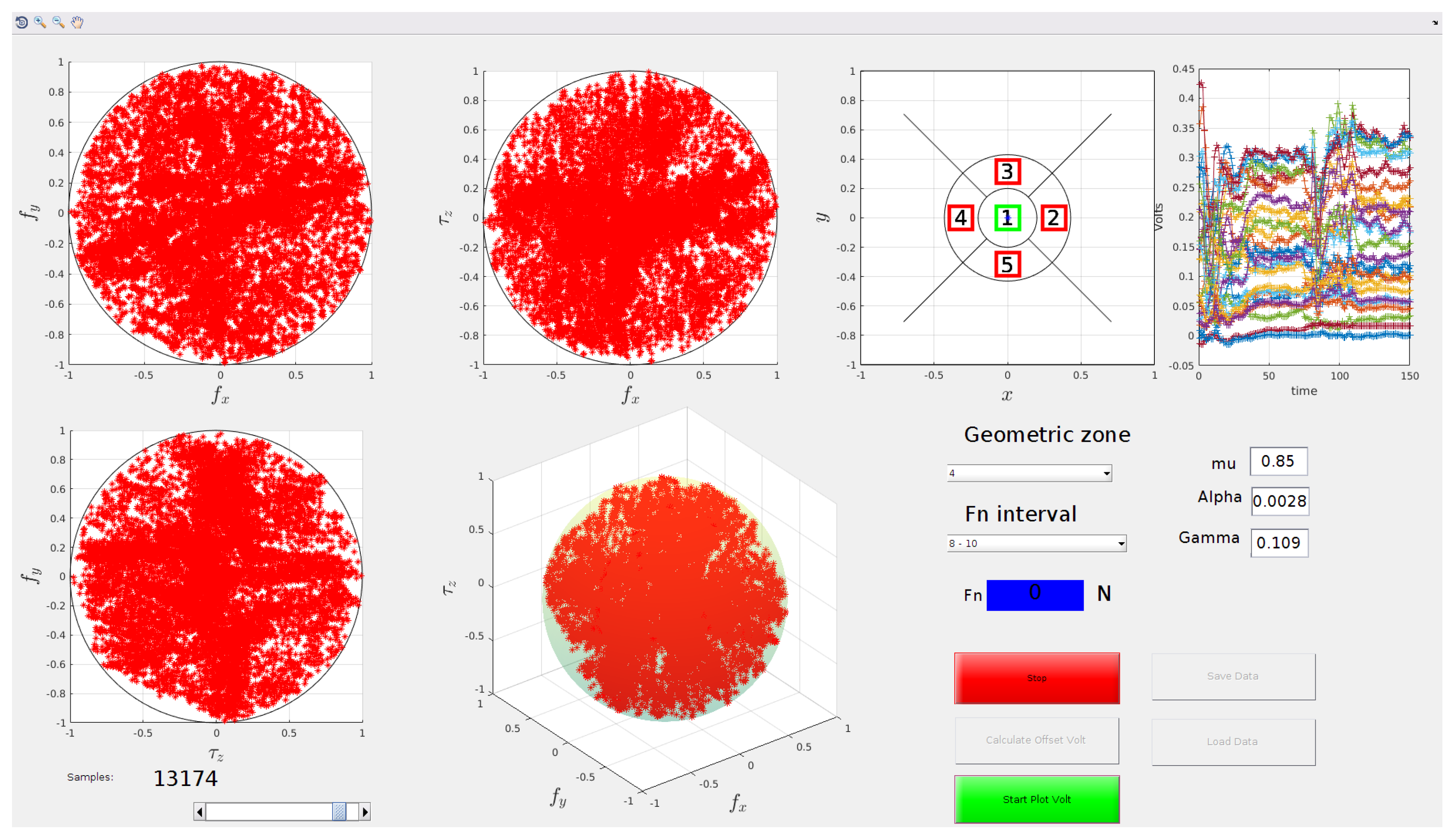
3.1. Construction of the Training Set
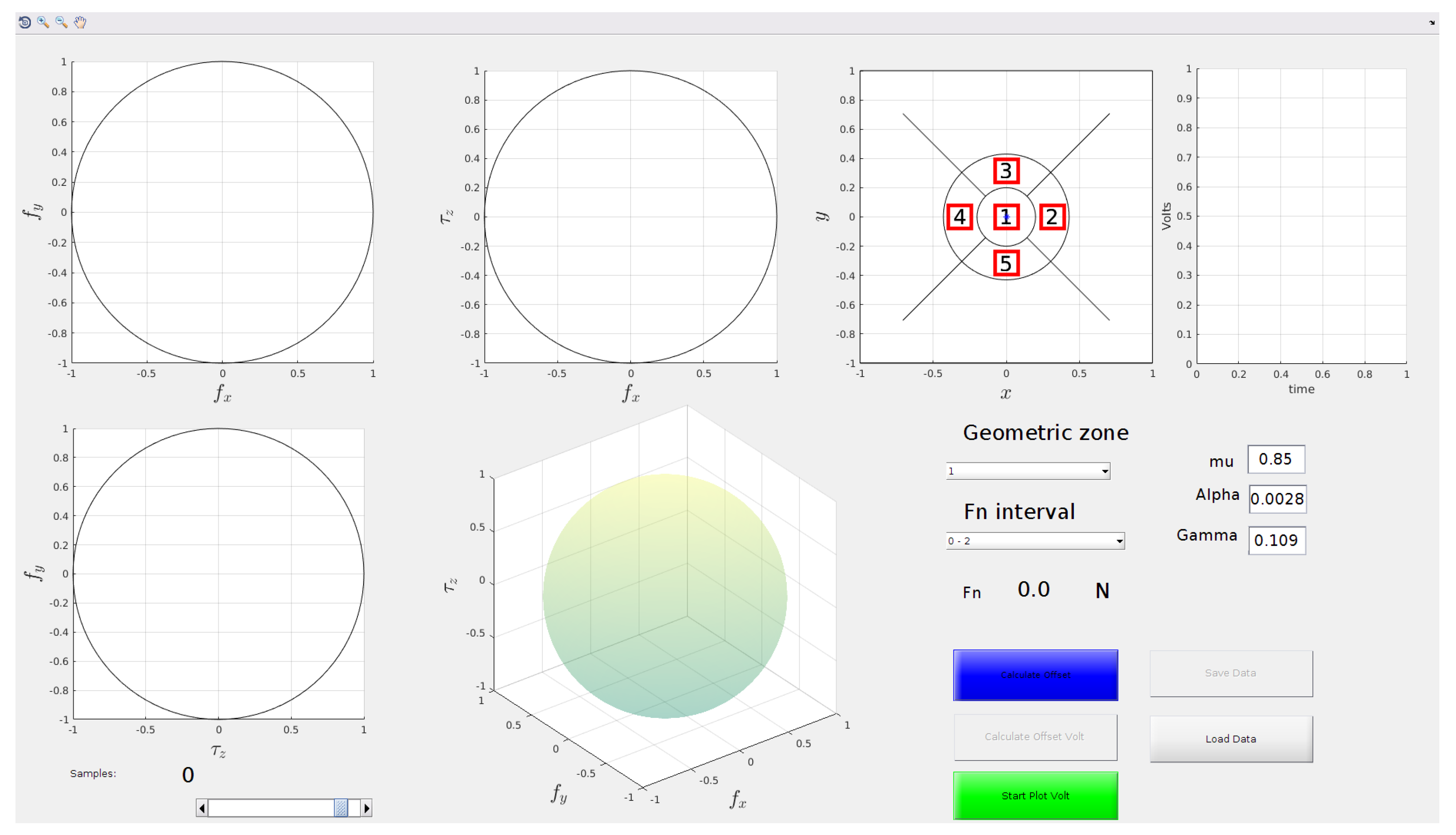
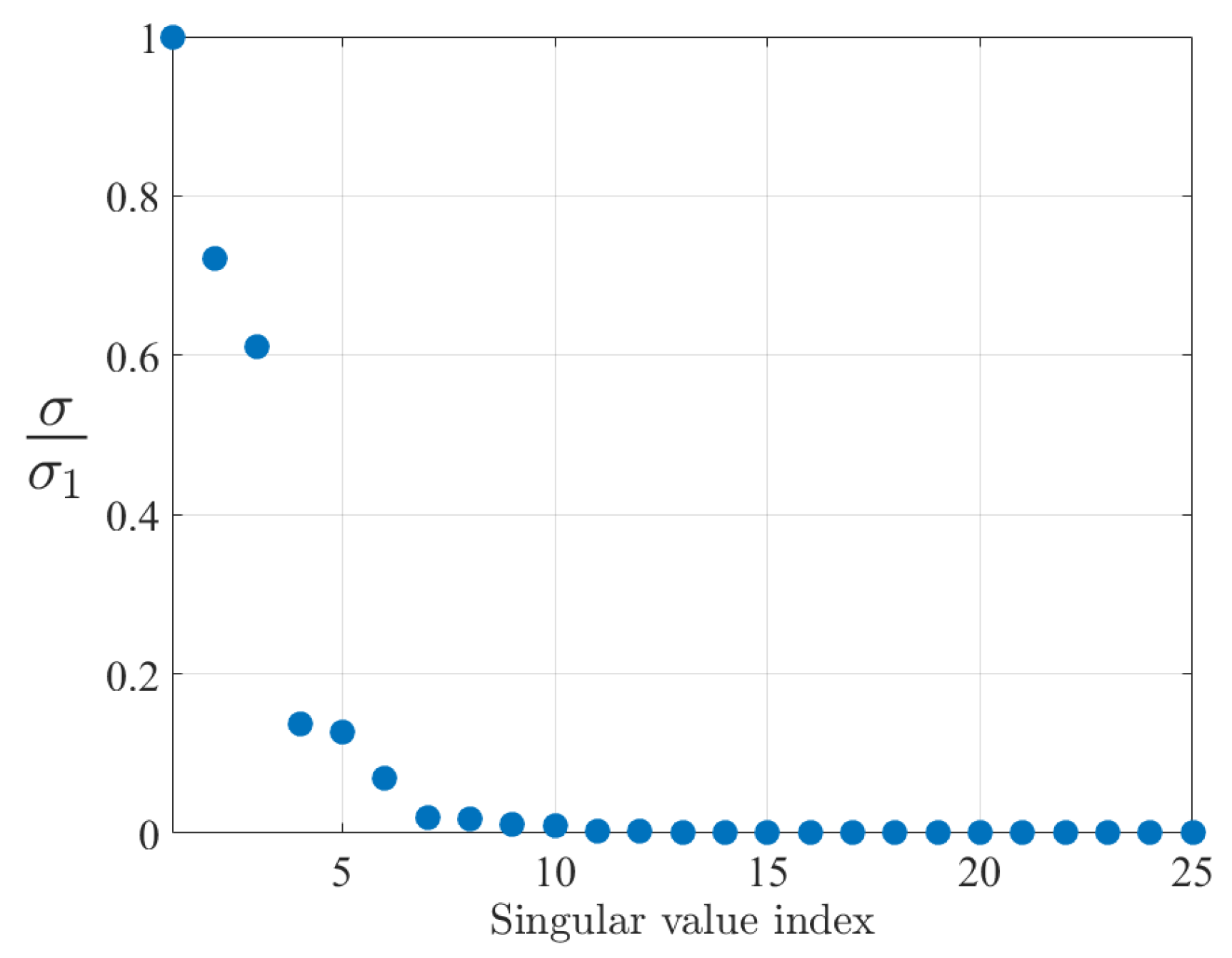
3.2. Training Set Pre-Processing
function [ inputs , targets ,mask_keep ] . . . = decimation( inputs , targets , radius ) % Bubble-based decimation function , % Ts = {( inputs _ i , targets _ i ) } %Initialization radius_square = radius ^2; mask_keep = false ( 1 , size ( inputs , 2 ) ) ; mask_not_computed = ~mask_keep ; %Repeat until process all samples while any (mask_not_computed ) actual_index = find (mask_not_computed , 1 ) ; mask_keep ( actual_index ) = true ; mask_not_computed ( actual_index ) = false ; mask_not_computed (mask_not_computed ) = . . . sum( ( inputs ( : , mask_not_computed ) . . . − inputs ( : , actual_index ) ) .^2 . . . ) > radius_square ; end %select only good samples inputs = inputs ( : , mask_keep ) ; targets = targets ( : , mask_keep ) ; end
3.3. FF-NN Training
4. Experimental Validation
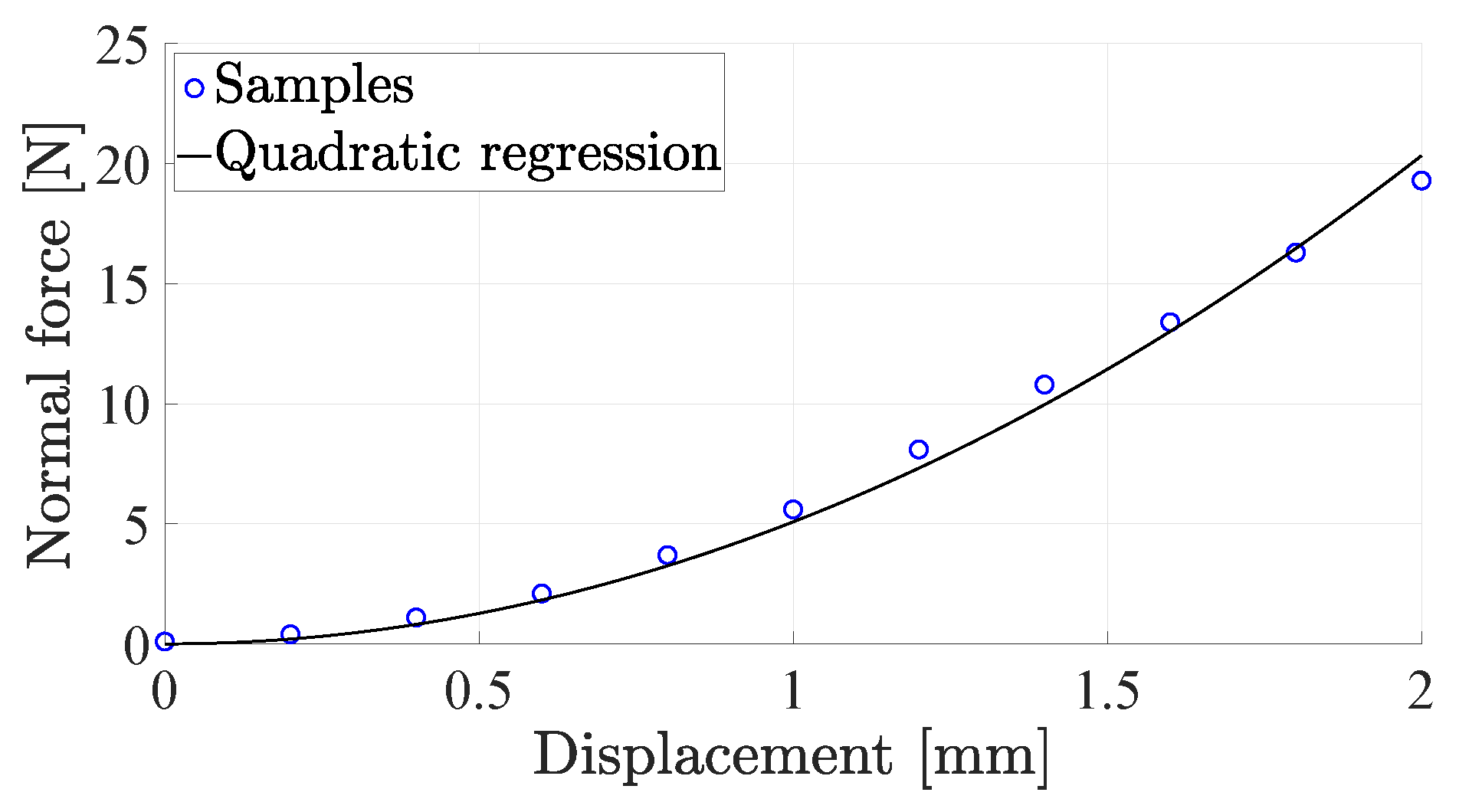
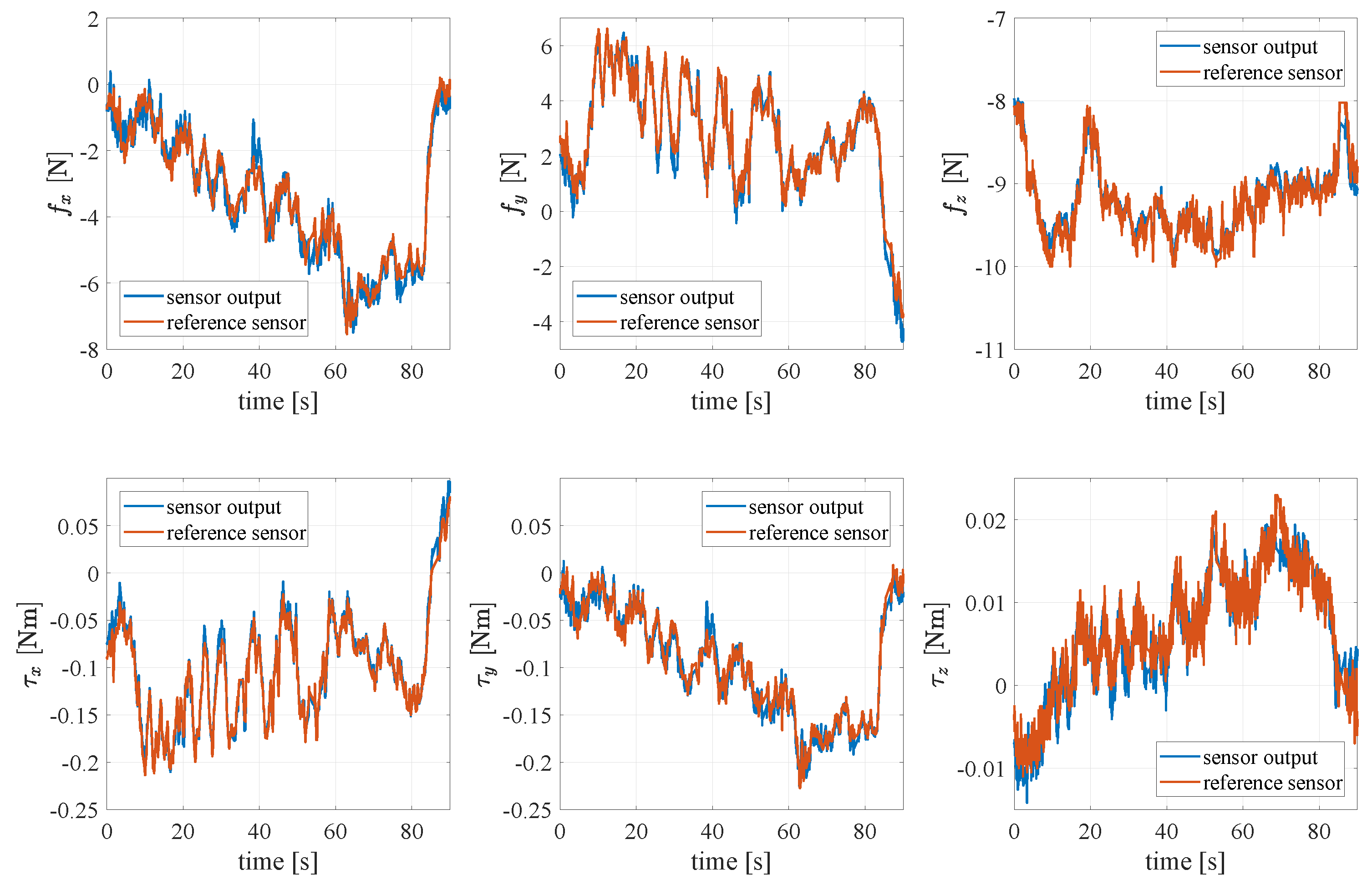
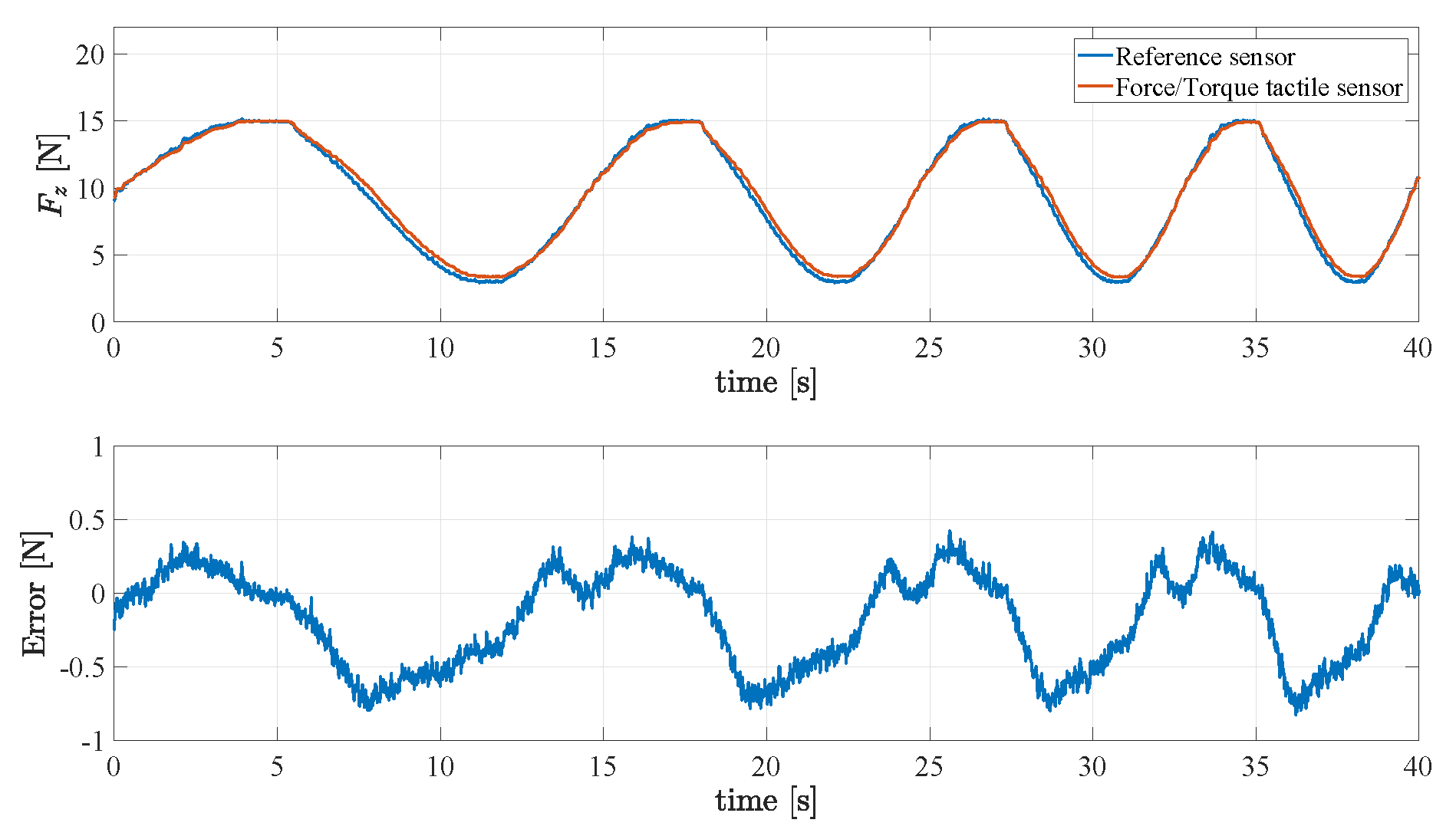
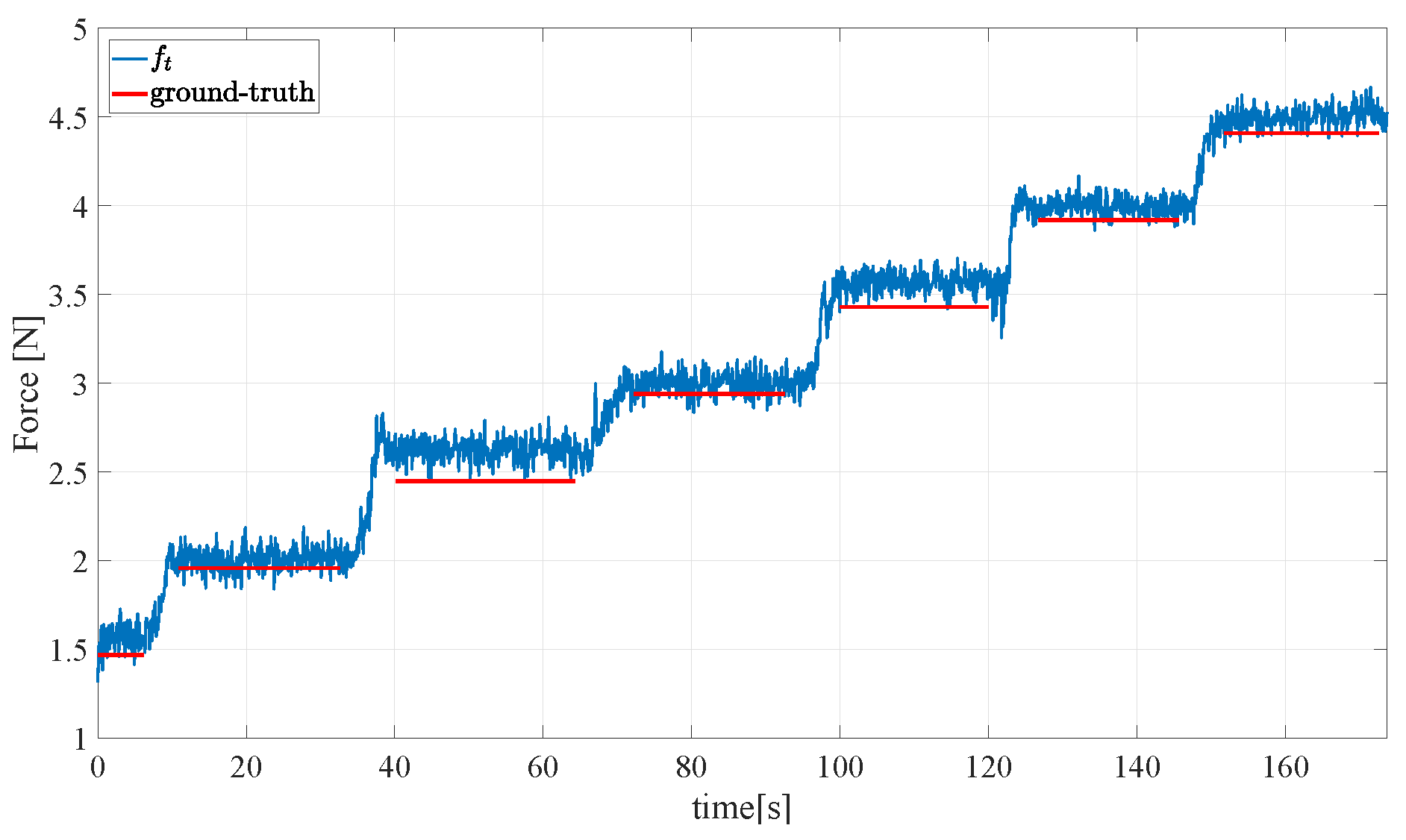
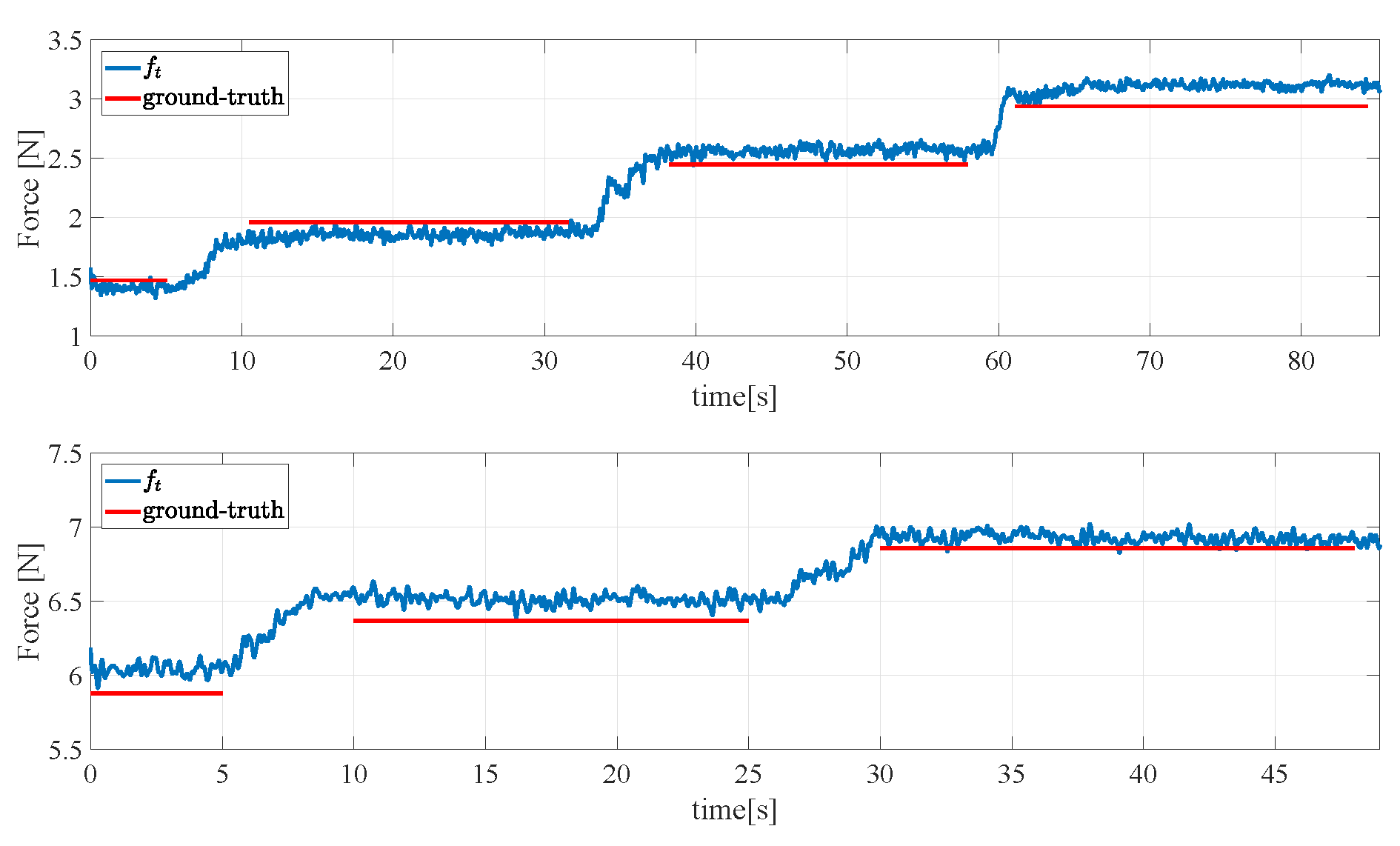
4.1. Reconstruction of the Normal Force Component
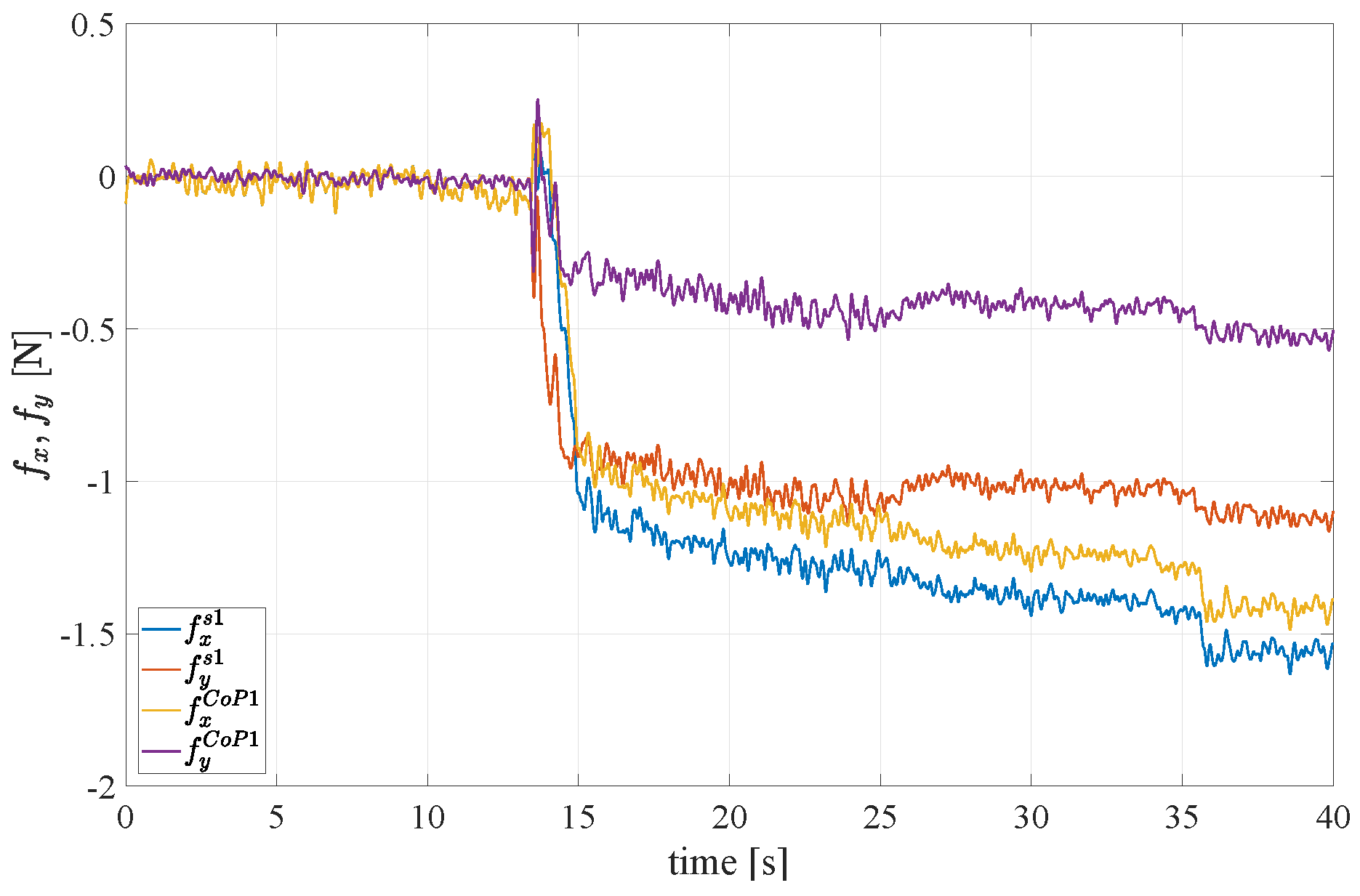
4.2. Reconstruction of the Tangential Force Components
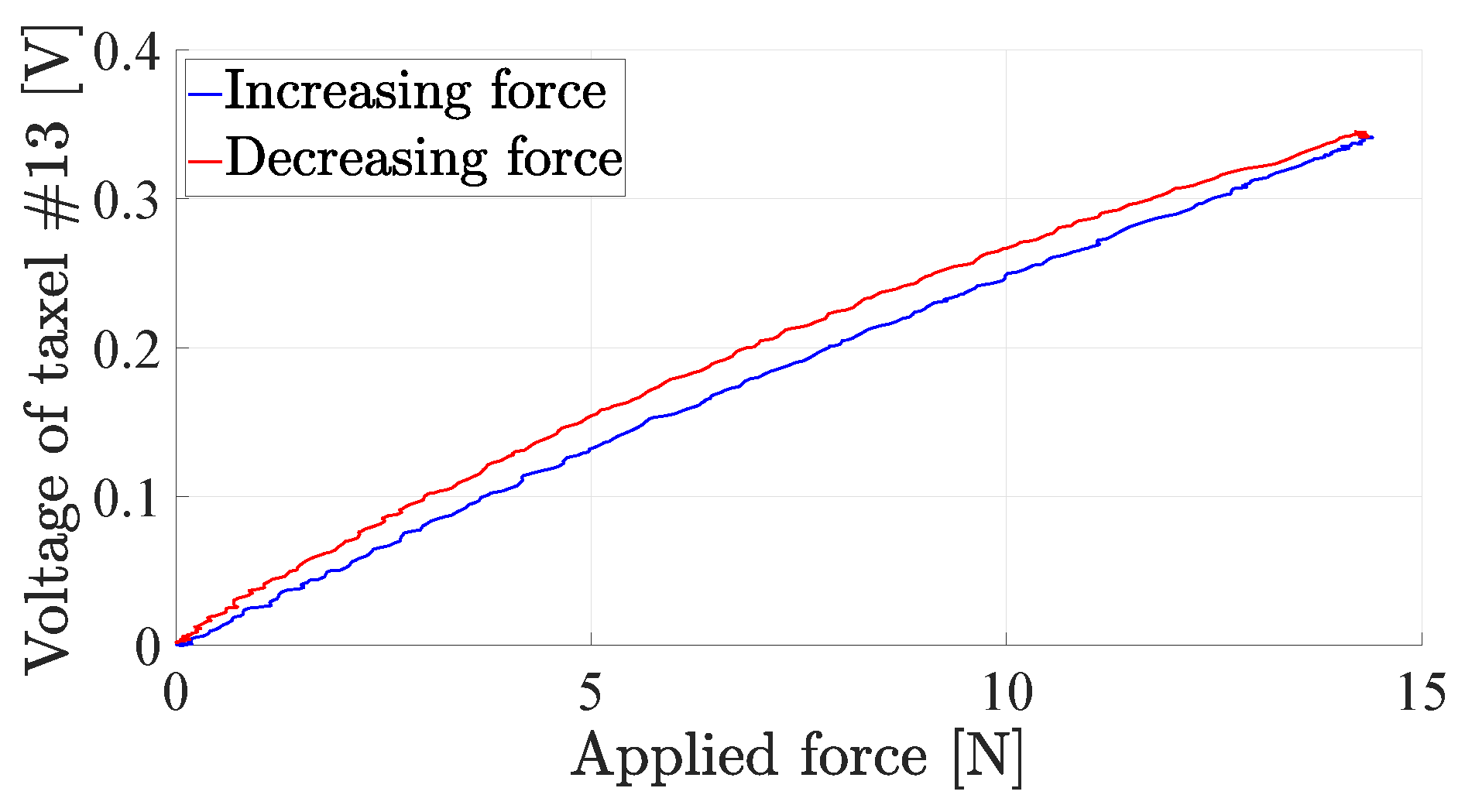
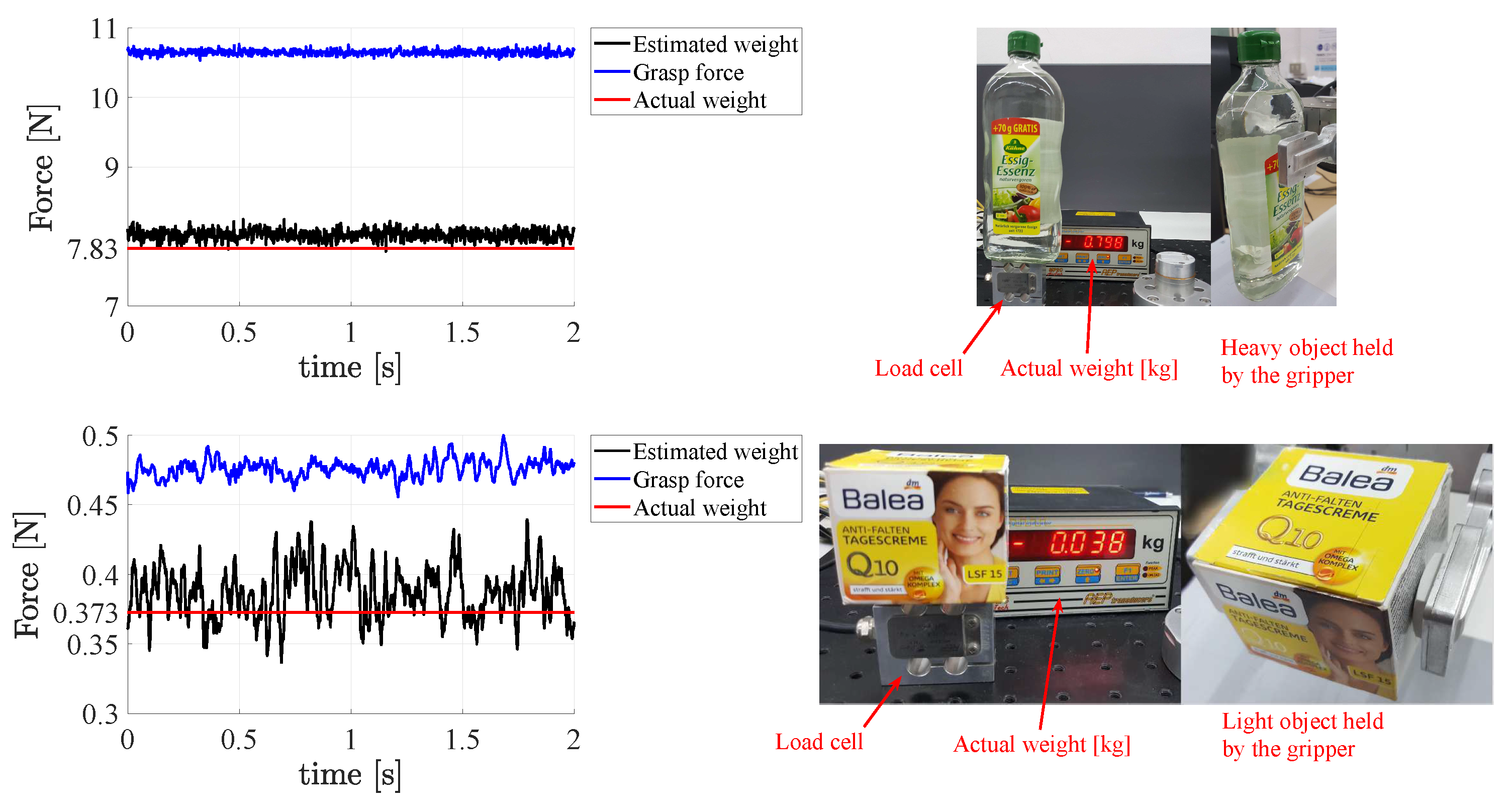
4.3. Assessment of Sensor Sensitivity and Dynamic Range
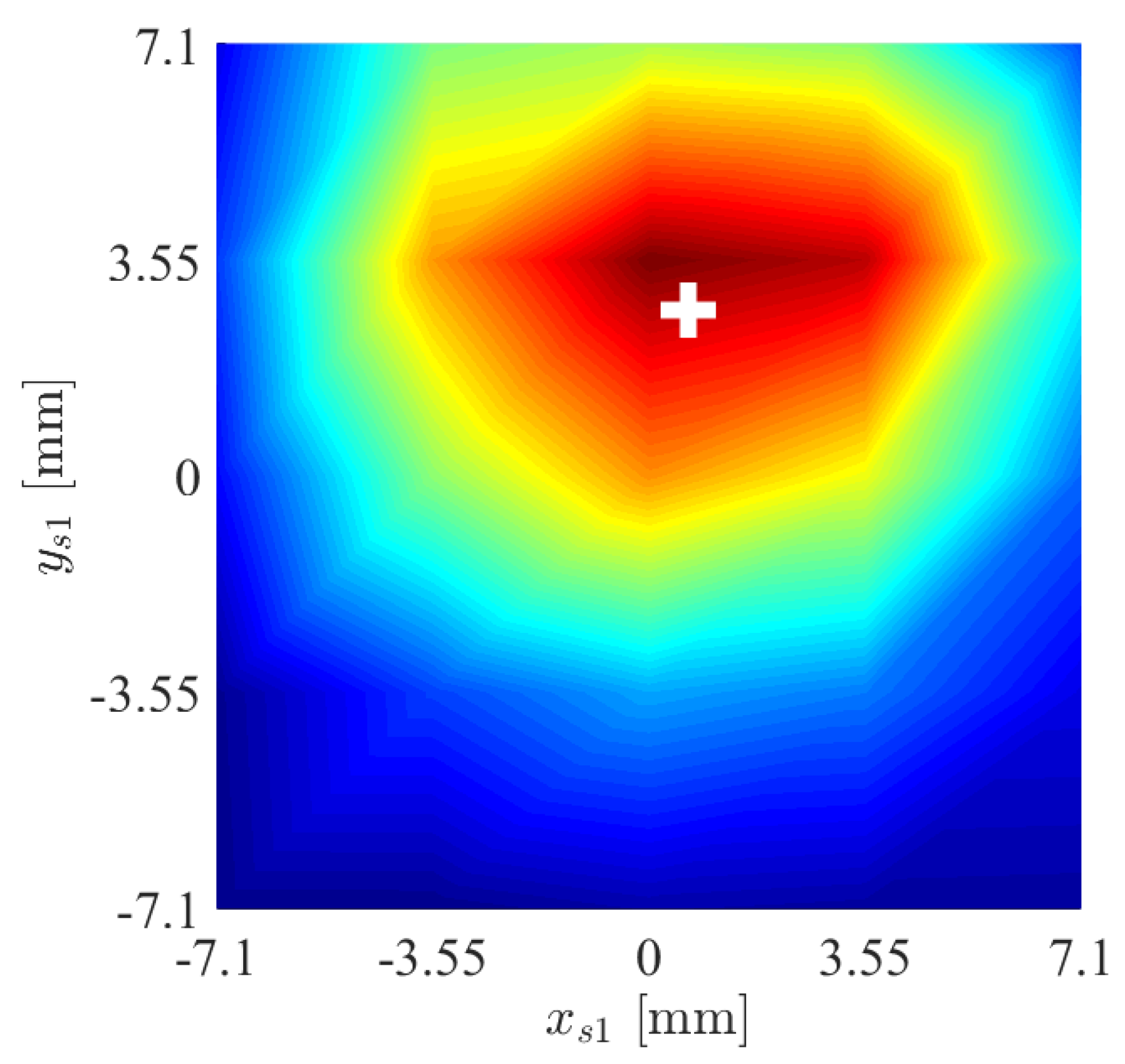
4.4. Reconstruction of the Contact Plane Orientation
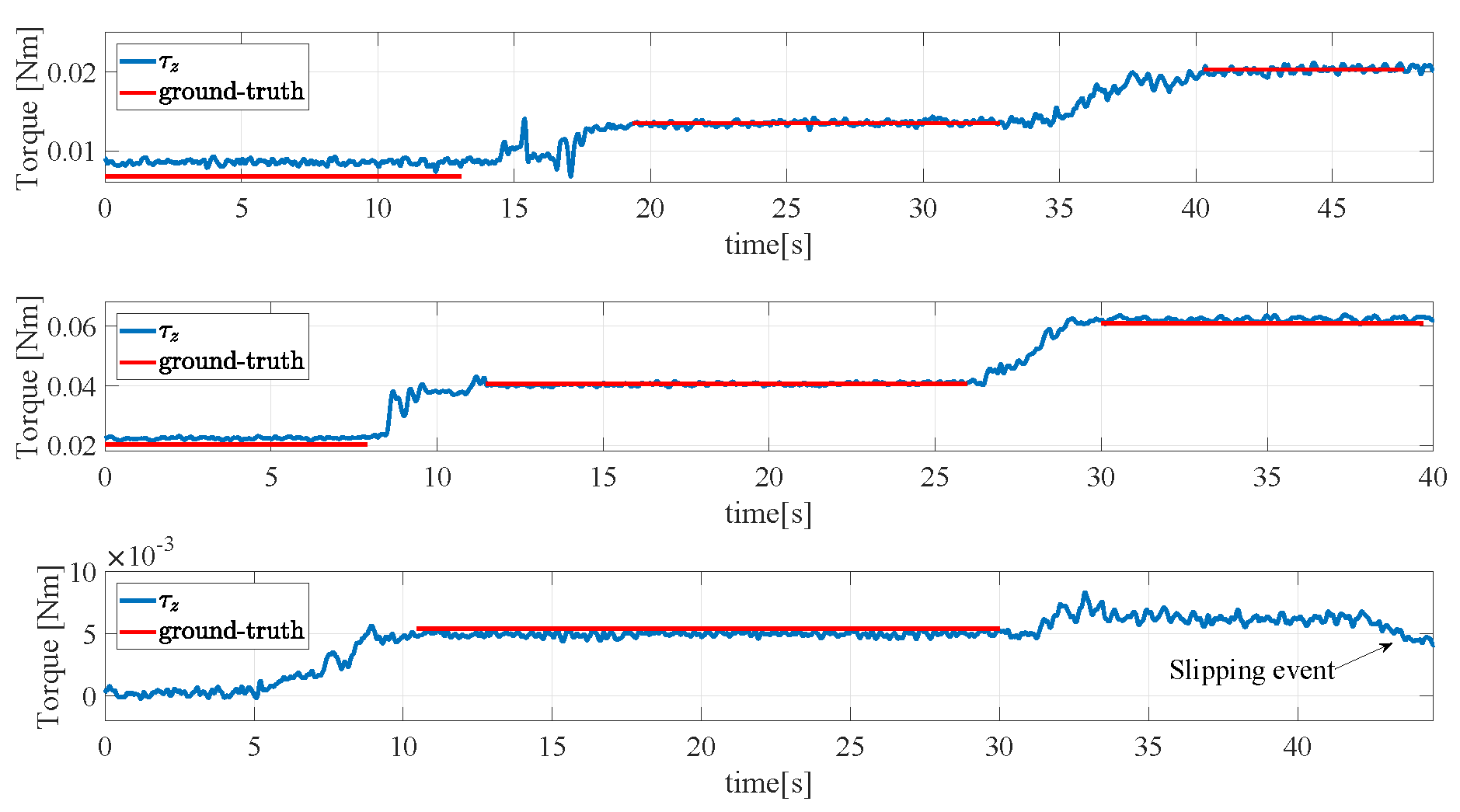
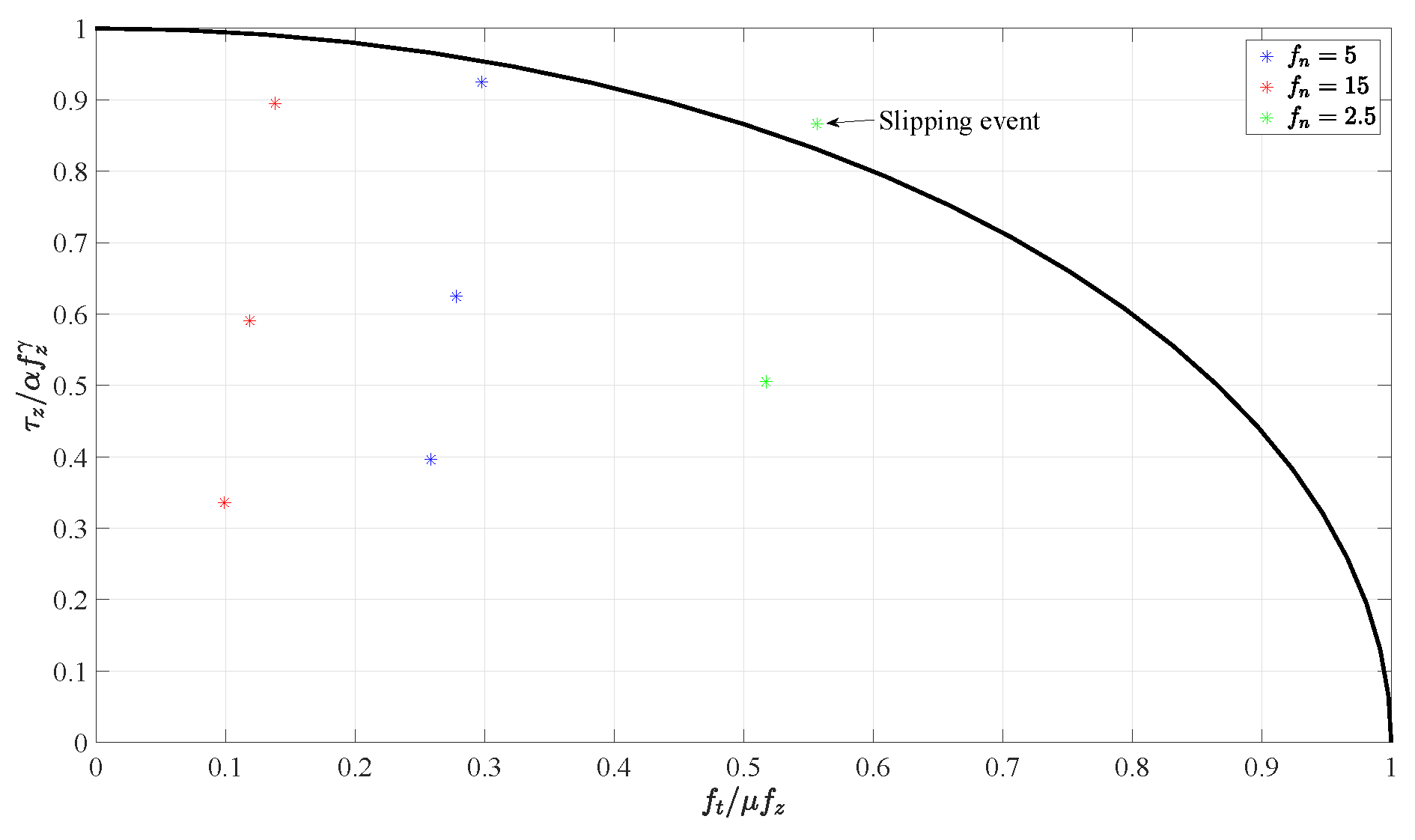
4.5. Reconstruction of the Torsional Moment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Palli, G.; Melchiorri, C.; Vassura, G.; Scarcia, U.; Moriello, L.; Berselli, G.; Cavallo, A.; De Maria, G.; Natale, C.; Pirozzi, S.; et al. The DEXMART hand: Mechatronic design and experimental evaluation of synergy-based control for human-like grasping. Int. J. Robot. Res. 2014, 33, 799–824. [Google Scholar] [CrossRef]
- Grebenstein, M.; Chalon, M.; Friedl, W.; Haddadin, S.; Wimböck, T.; Hirzinger, G.; Siegwart, R. The hand of the DLR Hand Arm System: Designed for interaction. Int. J. Robot. Res. 2012, 31, 1531–1555. [Google Scholar] [CrossRef]
- Kawasaki, H.; Komatsu, T.; Uchiyama, K. Dexterous anthropomorphic robot hand with distributed tactile sensor: Gifu hand II. IEEE/ASME Trans. Mech. 2002, 7, 296–303. [Google Scholar] [CrossRef]
- Shadow Robot Company. Design of a Dexterous Hand for Advanced CLAWAR Applications. In Proceedings of the International Conference on Climbing and Walking Robots, Catania, Italy, 17–19 September 2003. [Google Scholar]
- Controzzi, M.; Cipriani, C.; Carrozza, M.C. Design of Artificial Hands: A Review. In The Human Hand as an Inspiration for Robot Hand Development; Balasubramanian, R., Santos, V.J., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 219–246. [Google Scholar]
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Tactile Sensing in Dexterous Robot Hands—Review. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Mittendorfer, P.; Valle, M.; Cheng, G.; Lumelsky, V.J. Directions Toward Effective Utilization of Tactile Skin: A Review. IEEE Sens. J. 2013, 13, 4121–4138. [Google Scholar] [CrossRef]
- D’Amore, A.; De Maria, G.; Grassia, L.; Natale, C.; Pirozzi, S. Silicone rubber based tactile sensor for measurement of normal and tangential components of the contact force. J. Appl. Polym. Sci. 2011, 122, 3758–3770. [Google Scholar] [CrossRef]
- De Maria, G.; Natale, C.; Pirozzi, S. Force/Tactile Sensor for Robotic Applications. Sens. Actuators A Phys. 2012, 175, 60–72. [Google Scholar] [CrossRef]
- Cirillo, A.; Cirillo, P.; Maria, G.D.; Natale, C.; Pirozzi, S. Control of linear and rotational slippage based on six-axis force/tactile sensor. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1587–1594. [Google Scholar]
- Deimel, R.; Brock, O. A novel type of compliant and underactuated robotic hand for dexterous grasping. Int. J. Robot. Res. 2016, 35, 161–185. [Google Scholar] [CrossRef]
- Della Santina, C.; Piazza, C.; Grioli, G.; Catalano, G.M.; Bicchi, A. Towards Dexterous Manipulation with Augmented Adaptive Synergies: The Pisa/IIT SoftHand 2. IEEE Trans. Robot. 2018, 34, 1141–1156. [Google Scholar] [CrossRef]
- Dafle, N.C.; Rodriguez, A.; Paolini, R.; Tang, B.; Srinivasa, S.S.; Erdmann, M.; Mason, M.T.; Lundberg, I.; Staab, H.; Fuhlbrigge, T. Extrinsic dexterity: In-hand manipulation with external forces. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1578–1585. [Google Scholar]
- Dafle, N.; Rodriguez, A. Prehensile pushing: In-hand manipulation with push-primitives. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and System, Hamburg, Germany, 28 September–2 October 2015; pp. 6215–6222. [Google Scholar]
- Viña, F.E.; Karayiannidis, Y.; Smith, C.; Kragic, D. Adaptive Control for Pivoting with Visual and Tactile Feedback. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 399–406. [Google Scholar]
- Costanzo, M.; Maria, G.D.; Natale, C. Slipping Control Algorithms for Object Manipulation with Sensorized Parallel Grippers. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 7455–7461. [Google Scholar]
- Maria, G.D.; Natale, C.; Pirozzi, S. Tactile data modelling and interpretation for stable grasping and manipulation. Robot. Auton. Syst. 2013, 61, 1008–1020. [Google Scholar] [CrossRef]
- Cirillo, A.; Cirillo, P.; Maria, G.D.; Natale, C.; Pirozzi, S. Modeling and Calibration of a Tactile Sensor for Robust Grasping. In Proceedings of the 20th World Congress of the IFAC, Toulouse, France, 9–14 July 2017; pp. 7037–7044. [Google Scholar]
- Qian, S.; Bao, K.; Zi, B.; Wang, N. Kinematic calibration of a cable-driven parallel robot for 3D printing. Sensors 2018, 18, 2898. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Zhao, D.; Yin, F.; Tian, W.; Chetwynd, D.G. Kinematic calibration of a 6-DOF hybrid robot by considering multicollinearity in the identification Jacobian. Mech. Mach. Theory 2019, 131, 371–384. [Google Scholar] [CrossRef]
- Howe, R.; Cutkosky, M. TPractical force-motion models for sliding manipulation. Int. J. Robot. Res. 1996, 15, 557–572. [Google Scholar] [CrossRef]
- Cirillo, A.; De Maria, G.; Natale, C.; Pirozzi, S. Design and Evaluation of Tactile Sensors for the Estimation of Grasped Wire Shape. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM2017), Munich, Germany, 3–7 July 2017; pp. 490–496. [Google Scholar]
- Timoshenko, S.; Goodier, J. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Cirillo, A.; Cirillo, P.; De Maria, G.; Natale, C.; Pirozzi, S. An Artificial Skin Based on Optoelectronic Technology. Sens. Actuators A Phys. 2014, 212, 110–122. [Google Scholar] [CrossRef]
- Xydas, N.; Kao, I. Modelling of contact mechanics and friction limit surfaces for soft fingers in robotics, with experimental results. Int. J. Robot. Res. 1999, 18, 941–950. [Google Scholar] [CrossRef]
- Uchiyama, M.; Dauchez, P. Symmetric kinematic formulation and non-master/slave coordinated control of two-arm robots. Adv. Robot. 1992, 7, 361–383. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costanzo, M.; De Maria, G.; Natale, C.; Pirozzi, S. Design and Calibration of a Force/Tactile Sensor for Dexterous Manipulation. Sensors 2019, 19, 966. https://doi.org/10.3390/s19040966
Costanzo M, De Maria G, Natale C, Pirozzi S. Design and Calibration of a Force/Tactile Sensor for Dexterous Manipulation. Sensors. 2019; 19(4):966. https://doi.org/10.3390/s19040966
Chicago/Turabian StyleCostanzo, Marco, Giuseppe De Maria, Ciro Natale, and Salvatore Pirozzi. 2019. "Design and Calibration of a Force/Tactile Sensor for Dexterous Manipulation" Sensors 19, no. 4: 966. https://doi.org/10.3390/s19040966
APA StyleCostanzo, M., De Maria, G., Natale, C., & Pirozzi, S. (2019). Design and Calibration of a Force/Tactile Sensor for Dexterous Manipulation. Sensors, 19(4), 966. https://doi.org/10.3390/s19040966




