An Unsupervised Learning Technique to Optimize Radio Maps for Indoor Localization
Abstract
1. Introduction
2. Related Work
3. Methodology
3.1. Experimental Configuration
3.2. Radio Map
- Free-space model [19]: the free-space path loss (FSPL) is the attenuation of radio energy between a sender and receiver antenna in idealized conditions, i.e., the antenna polarizations are perfectly matched, the environment is unobstructed free-space and the antennas are in each others far-field. The FSPL is calculated as follows:[dB] denotes the free-space path loss, d [m] is the distance between the sender and receiver antenna and f [MHz] is the operating frequency, if this is set to 2400 MHz, then the model reduces to:
- IEEE 802.11 TGn model [20]: the IEEE 802.11 TGn model is a two-slope path loss model, which is suitable for path-loss predictions in office environments. The TGn is calculated as follows:[dB] denotes the path loss predicted by the TGn model, [dB] is the reference path loss and is equal to 40.05 dB, and are the path loss exponents for the first and second part of the two-slope model and are equal to 2 and 5.2, and [m] is the breakpoint distance and is equal to 10 m. For , the TGn model equals to the free-space model.
- WHIPP model [21]: the WHIPP model is a theoretical model for indoor environments that includes wall and interaction losses. This model does not use a ray tracing algorithm, but is based on a heuristic algorithm where the dominant path is searched, i.e., the path along which the path loss is the lowest. Here, the path loss values are modeled as:[dB] denotes the path loss predicted by the WHIPP path loss model, [dB] is the path loss at a reference distance [m], [-] is the path loss exponent, d [m] is the distance along the path between transmitter and receiver. These two terms represent the path loss due to the traveled distance. The cumulated wall loss represents the sum of all wall losses when a signal propagates through a wall . The interaction loss represents the cumulated losses caused by all propagation direction changes along the path between sender and receiver, and [dB] is a log-normally distributed variable with zero mean and standard deviation , corresponding to the large-scale shadow fading.
3.3. Self-Calibration
4. Unsupervised Learning
4.1. Motivation
- overall deviation: the overall deviation represents the variation for the whole building and is used as an indication of radio map quality. A value of zero would mean that the measured path losses are exactly equal to the theoretically predicted values at all locations, for all access points.is the difference between the self-calibrated measurement and the reference value for access point i, grid point j, and path loss model . The average difference for access point i is denoted by , the total number of grid points by , the overall deviation by , and the total number of access points by .
- room deviation: the room deviation models the difference between the radio map and the measurements, averaged over a whole room.is the average difference for access point i and room k, these values are visualized for one access point in Figure 4. are the grid points within room k, is defined in Equation (7), is the average room difference for access point i, are the number of rooms in the building, is the room deviation, and the number of access points.
- local deviation: the local deviation represents the variation within a room on top of the room deviation, i.e., the differences between measured path loss values and the theoretical path loss values from the radio map are similar within a room but not exactly the same for all locations in this room.represents the local difference for access point i and grid point j, is the room difference for access point i and room , i.e., the room of grid point j (Equation (10)), is the average local difference for access point i, is the number of grid points, is the local deviation, and is the number of access points.
4.2. Route Mapping Filter
4.3. Radio Map Update Step
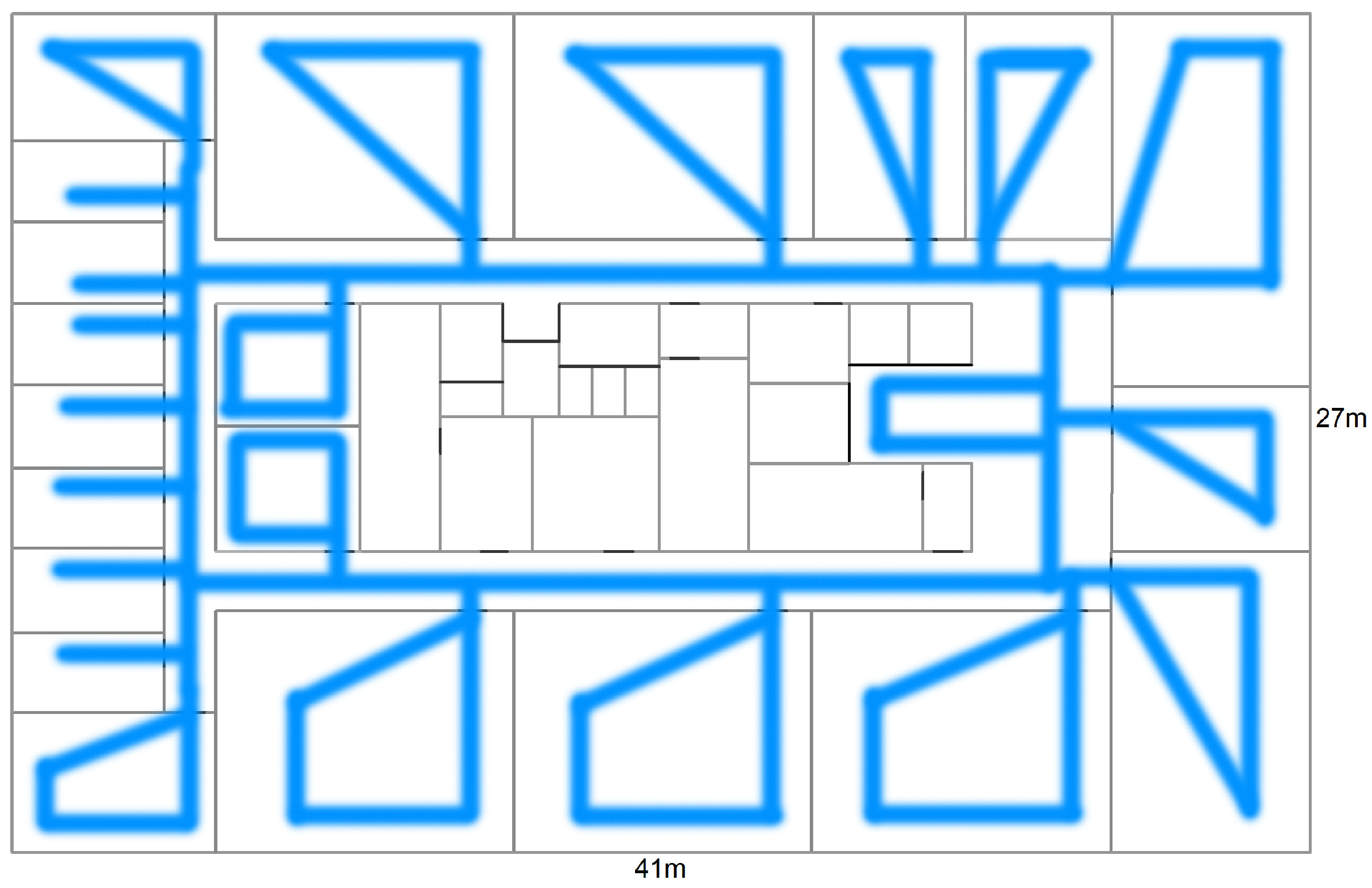
5. Simulation
5.1. Settings
5.2. Results
5.2.1. Influence of Room and Local Deviation
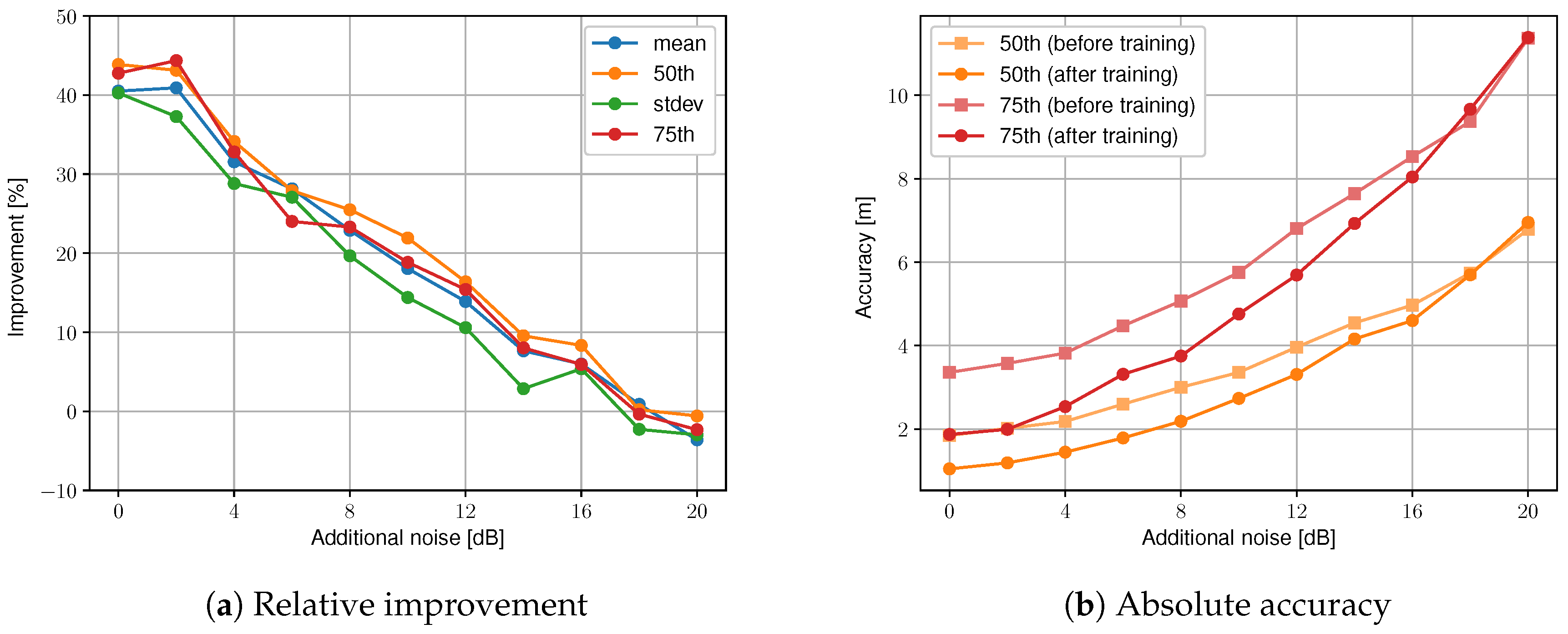
5.2.2. Influence of Additional Noise
6. Experimental Validation
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thomas, F.; Ros, L. Revisiting trilateration for robot localization. IEEE Trans. Robot. 2005, 21, 93–101. [Google Scholar] [CrossRef]
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM 2000), Tel Aviv, Israel, 26–30 March 2000; Volume 2, pp. 775–784. [Google Scholar]
- Bahl, P.; Padmanabhan, V.N.; Balachandran, A. Enhancements to the RADAR user location and tracking system. Microsoft Res. 2000, 2, 775–784. [Google Scholar]
- Constandache, I.; Gaonkar, S.; Sayler, M.; Choudhury, R.R.; Cox, L. Enloc: Energy-efficient localization for mobile phones. In Proceedings of the INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 2716–2720. [Google Scholar]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed]
- Ni, L.M.; Zhang, D.; Souryal, M.R. RFID-based localization and tracking technologies. IEEE Wirel. Commun. 2011, 18, 45–51. [Google Scholar] [CrossRef]
- Merhi, Z.; Elgamel, M.; Bayoumi, M. A lightweight collaborative fault tolerant target localization system for wireless sensor networks. IEEE Trans. Mob. Comput. 2009, 8, 1690–1704. [Google Scholar] [CrossRef]
- Jimenez, A.R.; Seco, F.; Prieto, C.; Guevara, J. A comparison of pedestrian dead-reckoning algorithms using a low-cost MEMS IMU. In Proceedings of the IEEE International Symposium on Intelligent Signal Processing (WISP 2009), Budapest, Hungary, 26–28 August 2009; pp. 37–42. [Google Scholar]
- Chintalapudi, K.; Padmanabha Iyer, A.; Padmanabhan, V.N. Indoor localization without the pain. In Proceedings of the Sixteenth Annual International Conference on Mobile Computing and Networking, Chicago, IL, USA, 20–24 September 2010; pp. 173–184. [Google Scholar]
- Wang, H.; Sen, S.; Elgohary, A.; Farid, M.; Youssef, M.; Choudhury, R.R. No need to war-drive: Unsupervised indoor localization. In Proceedings of the 10th International Conference on Mobile Systems, Applications, and Services, Low Wood Bay, UK, 25–29 June 2012; pp. 197–210. [Google Scholar]
- Rai, A.; Chintalapudi, K.K.; Padmanabhan, V.N.; Sen, R. Zee: Zero-effort crowdsourcing for indoor localization. In Proceedings of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, 22–26 August 2012; pp. 293–304. [Google Scholar]
- Sorour, S.; Lostanlen, Y.; Valaee, S.; Majeed, K. Joint indoor localization and radio map construction with limited deployment load. IEEE Trans. Mob. Comput. 2015, 14, 1031–1043. [Google Scholar] [CrossRef]
- Jiang, Q.; Ma, Y.; Liu, K.; Dou, Z. A probabilistic radio map construction scheme for crowdsourcing-based fingerprinting localization. IEEE Sens. J. 2016, 16, 3764–3774. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Zhou, B.; Li, Q.; Mao, Q.; Tu, W. A robust crowdsourcing-based indoor localization system. Sensors 2017, 17, 864. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wei, D.; Lai, Q.; Li, X.; Yuan, H. Geomagnetism-Aided Indoor Wi-Fi Radio-Map Construction via Smartphone Crowdsourcing. Sensors 2018, 18, 1462. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Fan, X.; Wang, S.; Ren, Y. Optimization-Based Wi-Fi Radio Map Construction for Indoor Positioning Using Only Smart Phones. Sensors 2018, 18, 3095. [Google Scholar] [CrossRef] [PubMed]
- Zolertia Online Resources and Documentation. 2018. Available online: https://github.com/Zolertia/Resources/wiki (accessed on 10 December 2018).
- Free-Space Path Loss. 2018. Available online: https://en.wikipedia.org/wiki/Free-space_path_loss (accessed on 10 December 2018).
- Erceg, V.; Schumacher, L.; Kyritsi, P. IEEE 802.11 Document 03/940r4 (TGn Channel Models). Available online: https://www.iitk.ac.in/mwn/papers/11-03-0940-01-000n-tgn-channel-models.pdf (accessed on 10 December 2018).
- Plets, D.; Joseph, W.; Vanhecke, K.; Tanghe, E.; Martens, L. Coverage prediction and optimization algorithms for indoor environments. EURASIP J. Wirel. Commun. Netw. 2012, 2012, 1–23. [Google Scholar] [CrossRef]
- Laoudias, C.; Piché, R.; Panayiotou, C.G. Device self-calibration in location systems using signal strength histograms. J. Location Based Serv. 2013, 7, 165–181. [Google Scholar] [CrossRef]
- Trogh, J.; Plets, D.; Thielens, A.; Martens, L.; Joseph, W. Enhanced indoor location tracking through body shadowing compensation. IEEE Sens. J. 2016, 16, 2105–2114. [Google Scholar] [CrossRef]
- Schmitt, S.; Adler, S.; Kyas, M. The effects of human body shadowing in RF-based indoor localization. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; pp. 307–313. [Google Scholar]
- Honkavirta, V.; Perala, T.; Ali-Loytty, S.; Piché, R. A comparative survey of WLAN location fingerprinting methods. In Proceedings of the 6th Workshop on Positioning, Navigation and Communication (WPNC 2009), Hannover, Germany, 19 March 2009; pp. 243–251. [Google Scholar]
- Fet, N.; Handte, M.; Marrón, P.J. A model for WLAN signal attenuation of the human body. In Proceedings of the 2013 ACM International Joint Conference On Pervasive and Ubiquitous Computing, Zurich, Switzerland, 8–12 September 2013; pp. 499–508. [Google Scholar]
- Trogh, J.; Plets, D.; Martens, L.; Joseph, W. Advanced Real-Time Indoor Tracking Based on the Viterbi Algorithm and Semantic Data. Int. J. Distrib. Sens. Netw. 2015, 501, 271818. [Google Scholar] [CrossRef]
- Chen, Z.; Zou, H.; Jiang, H.; Zhu, Q.; Soh, Y.C.; Xie, L. Fusion of WiFi, smartphone sensors and landmarks using the Kalman filter for indoor localization. Sensors 2015, 15, 715–732. [Google Scholar] [CrossRef] [PubMed]
- Evennou, F.; Marx, F.; Novakov, E. Map-aided indoor mobile positioning system using particle filter. In Proceedings of the 2005 IEEE Wireless Communications and Networking Conference, New Orleans, LA, USA, 13–17 March 2005; Volume 4, pp. 2490–2494. [Google Scholar]






| Path Loss Model | Difference [dB] | Deviation [dB] | ||||
|---|---|---|---|---|---|---|
| min | max | avg | Overall | Room | Local | |
| Free-space | −30.3 | 19.7 | −0.4 | 10.9 | 9.7 | 3.5 |
| IEEE 802.11 TGn | −37.5 | 19.1 | −0.7 | 9.6 | 8.8 | 3.5 |
| WHIPP | −22.0 | 24.0 | 0.8 | 7.6 | 5.7 | 3.7 |
| #APs | PL Model | Accuracy [m] | |||
|---|---|---|---|---|---|
| μ | σ | 50th | 75th | ||
| 9 (sparse configuration) | Free-space | 5.04 → 5.11 (−1.3%) | 3.93 → 3.98 (−1.3%) | 4.12 → 3.93 (4.8%) | 6.50 → 6.35 (2.2%) |
| TGn | 4.35 → 4.23 (2.9%) | 3.73 → 3.72 (0.3%) | 3.14 → 3.07 (2.1%) | 5.72 → 5.13 (10.4%) | |
| WHIPP | 4.66 → 3.77 (19.0%) | 3.24 → 2.49 (23.3%) | 3.94 → 3.03 (23.3%) | 5.97 → 4.83 (19.1%) | |
| 15 (normal configuration) | Free-space | 4.28 → 3.97 (7.4%) | 3.43 → 2.88 (16.1%) | 3.49 → 3.40 (2.4%) | 5.03 → 4.99 (0.8%) |
| TGn | 4.22 → 3.96 (6.0%) | 3.48 → 3.18 (8.7%) | 3.42 → 3.31 (3.2%) | 5.42 → 4.71 (13.0%) | |
| WHIPP | 4.33 → 3.50 (19.1%) | 2.98 → 2.38 (20.0%) | 3.50 → 3.02 (13.7%) | 6.03 → 4.44 (26.4%) | |
| 35 (dense configuration) | Free-space | 3.13 → 3.22 (−2.9%) | 3.09 → 2.62 (15.5%) | 2.40 → 2.30 (4.1%) | 3.61 → 3.98 (−10.4%) |
| TGn | 3.65 → 2.92 (20.1%) | 3.18 → 2.10 (33.9%) | 2.75 → 2.43 (11.7%) | 4.51 → 3.65 (19.1%) | |
| WHIPP | 3.23 → 2.66 (17.6%) | 2.14 → 1.74 (18.7%) | 2.90 → 2.07 (28.6%) | 4.31 → 3.52 (18.4%) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trogh, J.; Joseph, W.; Martens, L.; Plets, D. An Unsupervised Learning Technique to Optimize Radio Maps for Indoor Localization. Sensors 2019, 19, 752. https://doi.org/10.3390/s19040752
Trogh J, Joseph W, Martens L, Plets D. An Unsupervised Learning Technique to Optimize Radio Maps for Indoor Localization. Sensors. 2019; 19(4):752. https://doi.org/10.3390/s19040752
Chicago/Turabian StyleTrogh, Jens, Wout Joseph, Luc Martens, and David Plets. 2019. "An Unsupervised Learning Technique to Optimize Radio Maps for Indoor Localization" Sensors 19, no. 4: 752. https://doi.org/10.3390/s19040752
APA StyleTrogh, J., Joseph, W., Martens, L., & Plets, D. (2019). An Unsupervised Learning Technique to Optimize Radio Maps for Indoor Localization. Sensors, 19(4), 752. https://doi.org/10.3390/s19040752






