Joint Optimization for Task Offloading in Edge Computing: An Evolutionary Game Approach
Abstract
:1. Introduction
- We jointly formulate the problem of task offloading and resource allocation for mobile users in the MEC cloud platform as an evolutionary game, by taking account both resource procurement cost and users’ QoS. The populations of mobile users are modeled as players in the evolutionary game. The competition among players is to share the limited amount of resources in heterogeneous edge clouds and central clouds. By utilizing the process of replicator dynamics [8], we model the strategy adaption among different players.
- We design a decentralized strategy based on the evolutionary game theory to solve the problem of task offloading and resource allocation, following constraints of resource limitation in edge clouds and quality of experience (QoE) requirements of different tasks. Our strategy can ensure stability and can achieve an evolutionary equilibrium. We prove the stability and fairness of our strategy by mathematical analysis. The convergence rate is also analyzed in our work.
- We develop a discrete-event simulator based on OMNeT++ and conduct several trace-driven experiments. We compare the performance of our proposed strategy with other alternative methods and show that our method can not only satisfy the QoE requirement for players among different populations, but can also minimize the resource procurement cost.
2. Related Work
3. Modeling and Formulation
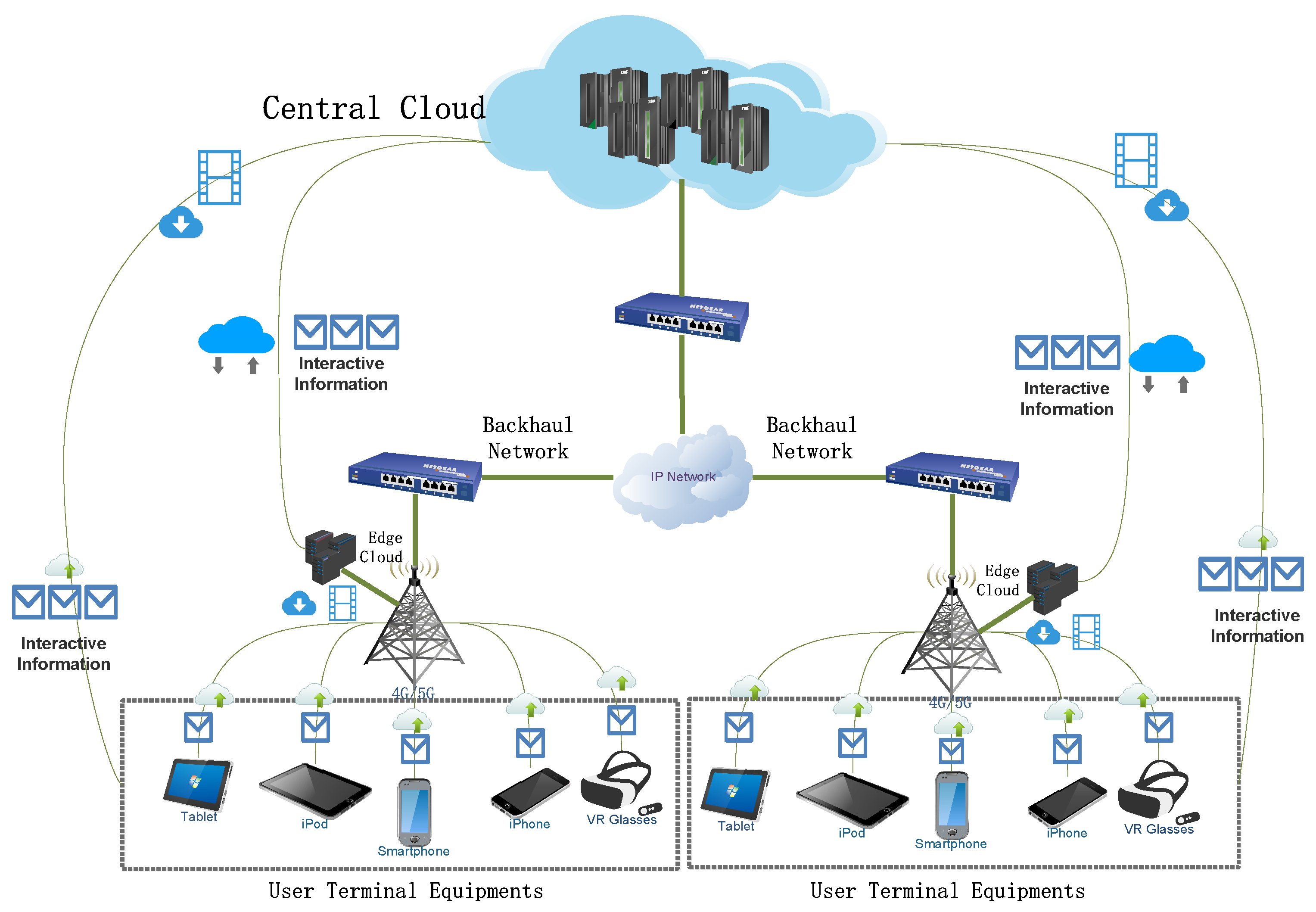
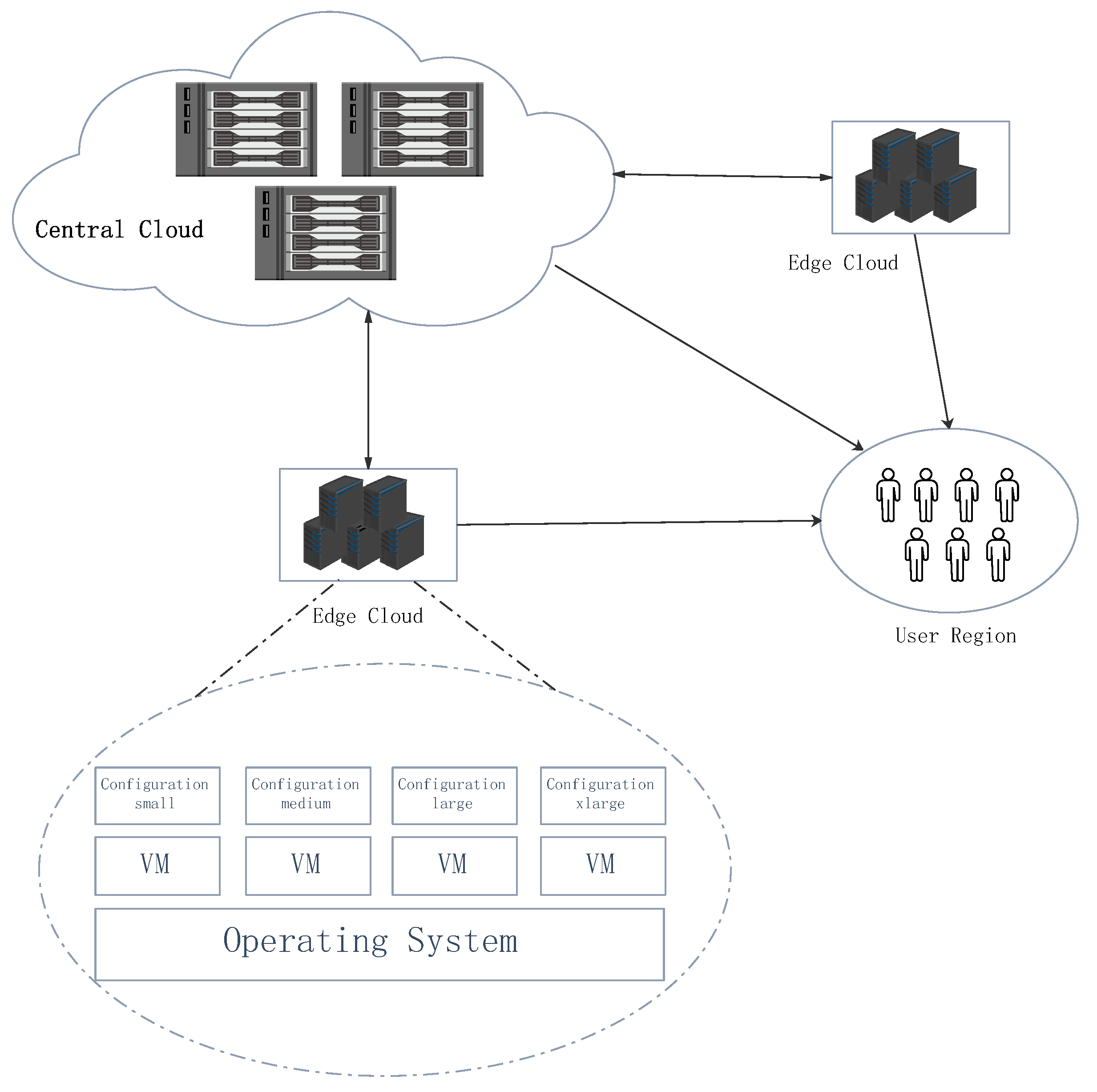
3.1. System Model
3.2. Service Utility Model
3.3. Cost Model
3.4. Joint Optimization Problem
4. Evolutionary Game Theoretic Strategy
4.1. Evolutionary Game Formulation
4.2. Evolutionary Stable Strategy
- 1.
- .
- 2.
- if , .
4.3. Replicator Dynamics
4.4. Delay in Replicator Dynamics
5. Iterative Algorithm Design and Analysis
5.1. Online Algorithm Implement
| Algorithm 1 Iterative Algorithm on Cloud Selection and VM Configuration Assignment (IASVA) |
|
5.2. Performance Analysis
6. Illustrative Studies
6.1. Experiment Setting
6.2. Methodology
6.3. Experiment Results and Analysis
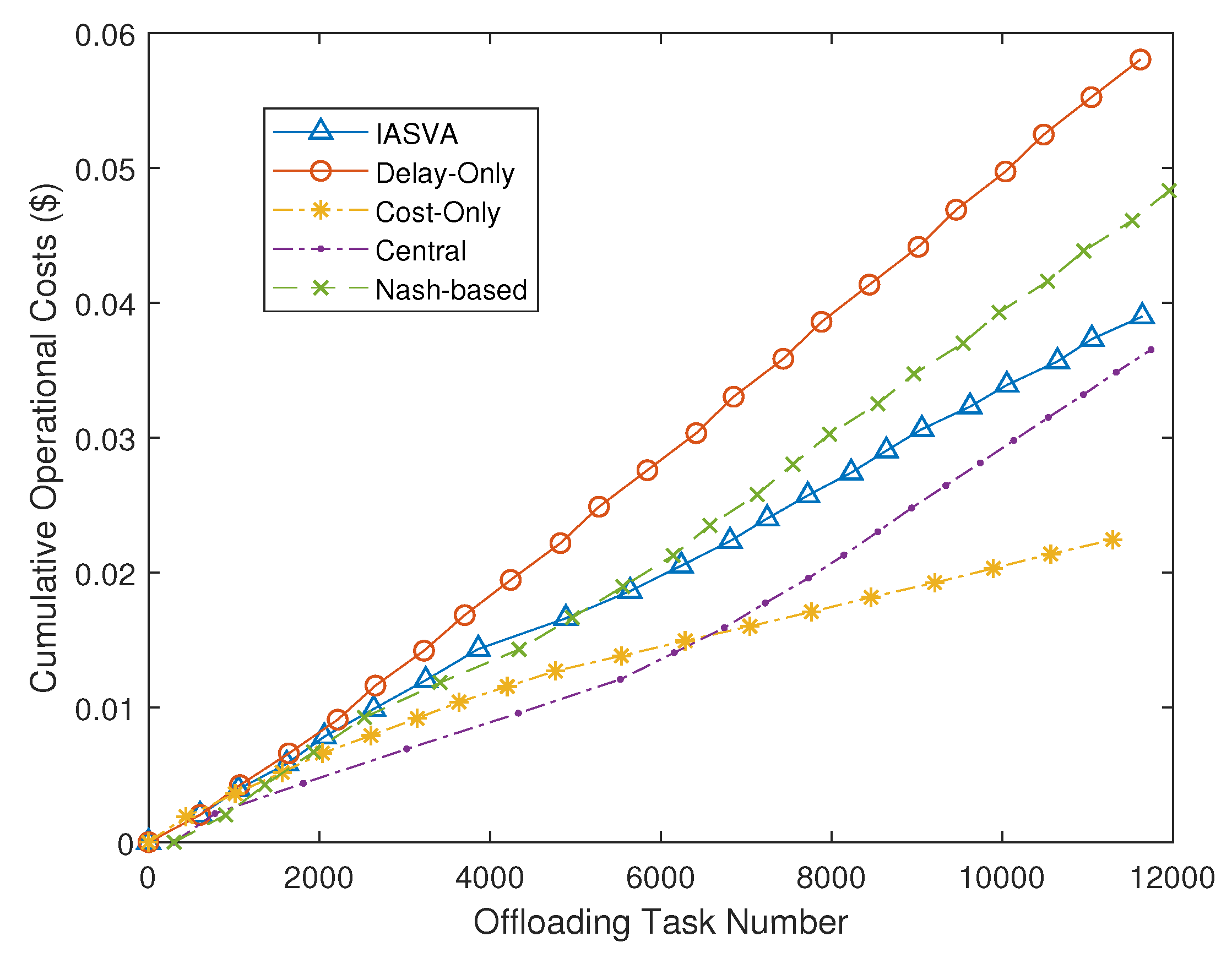
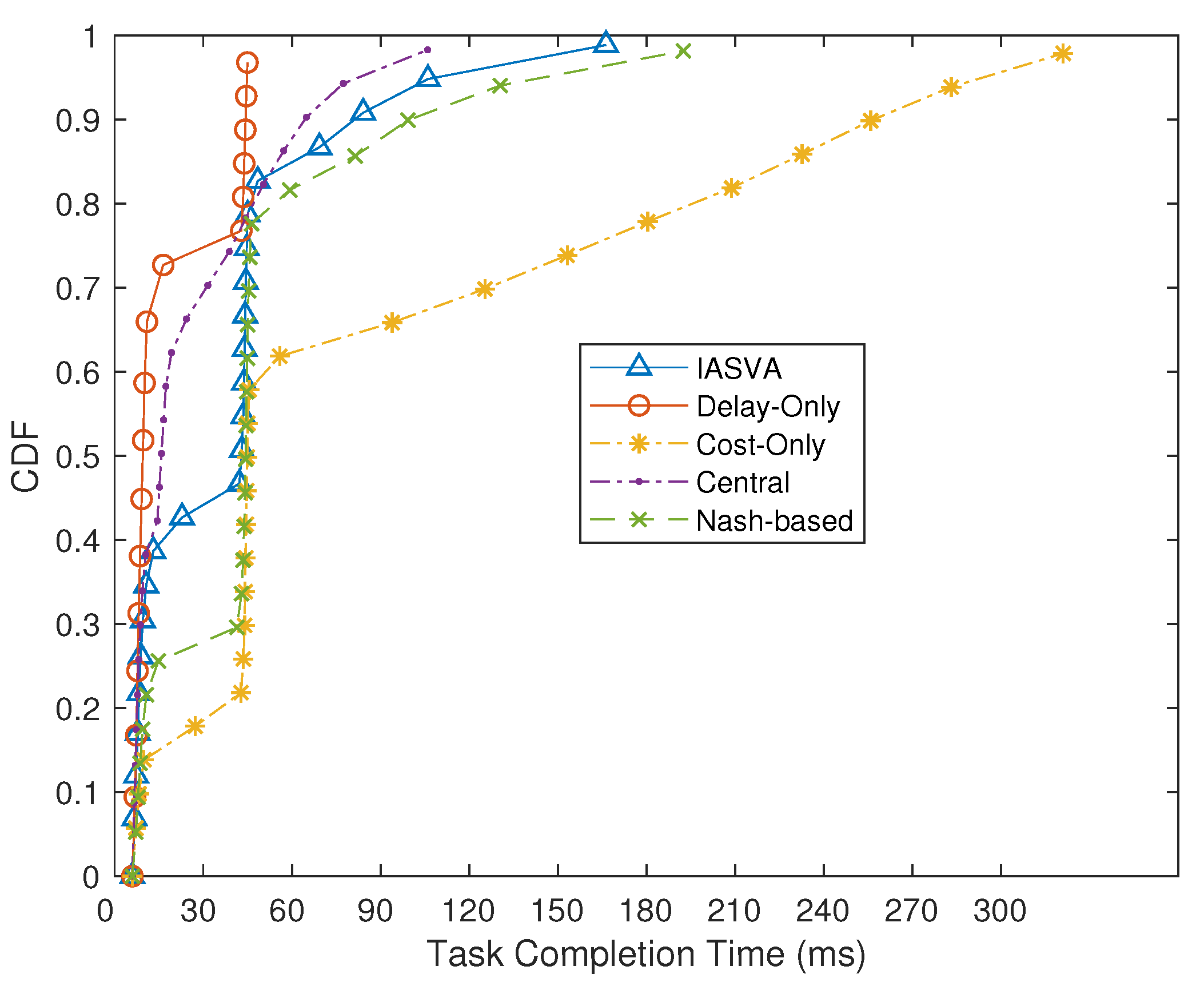
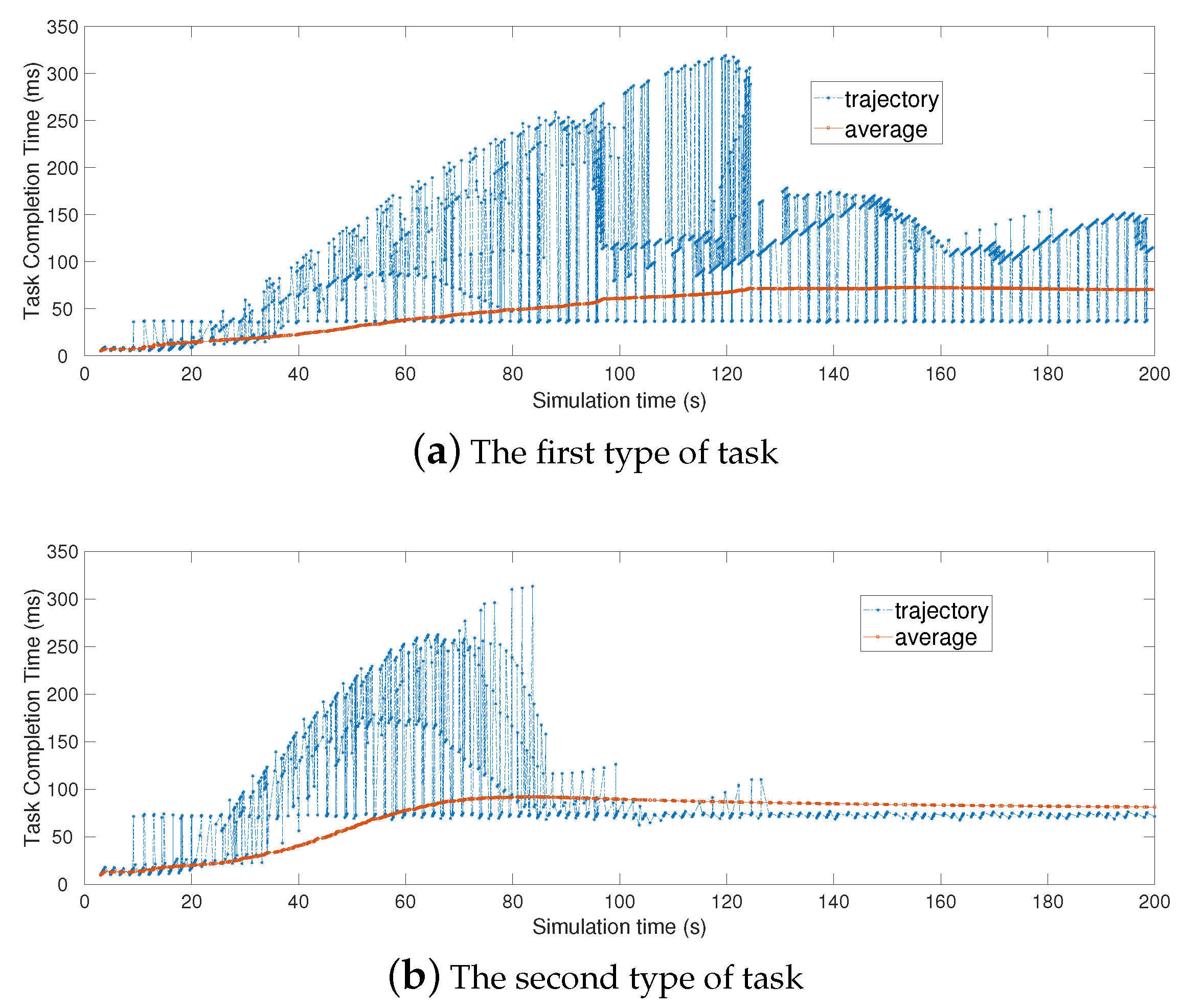
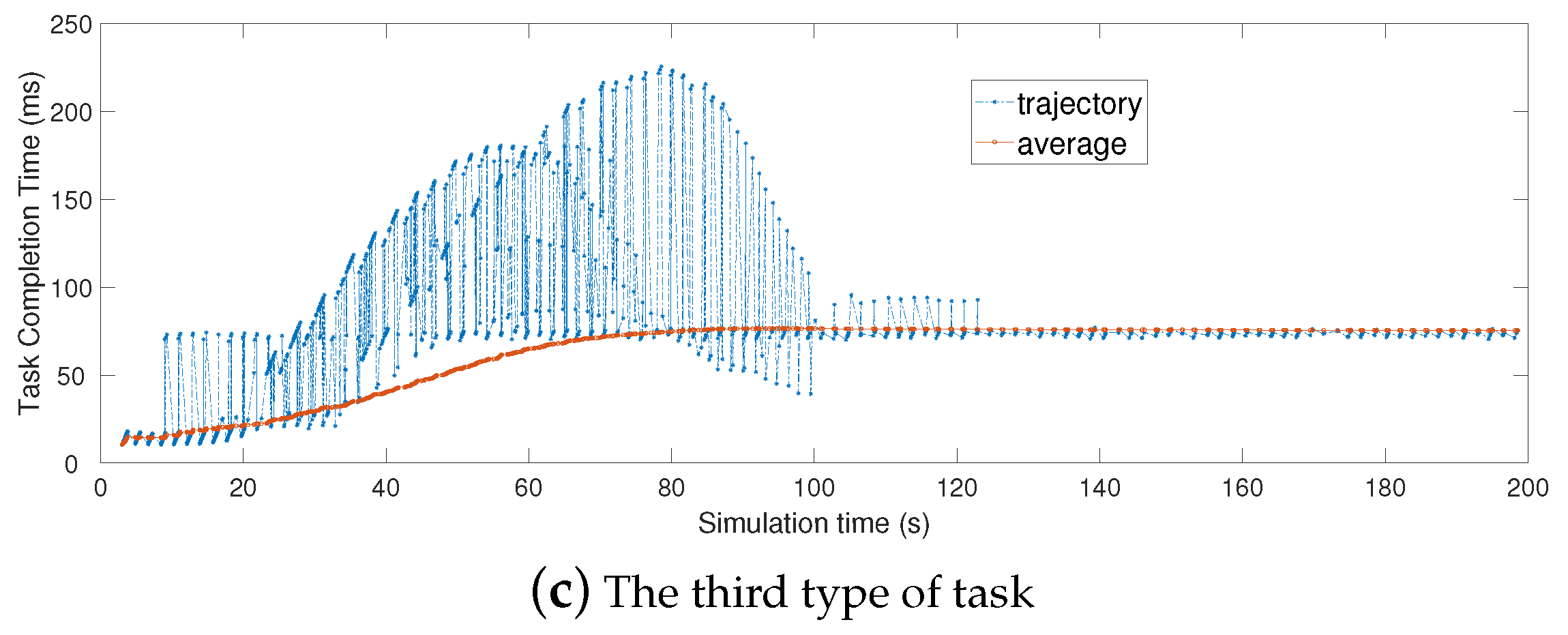
6.3.1. Performance Comparison
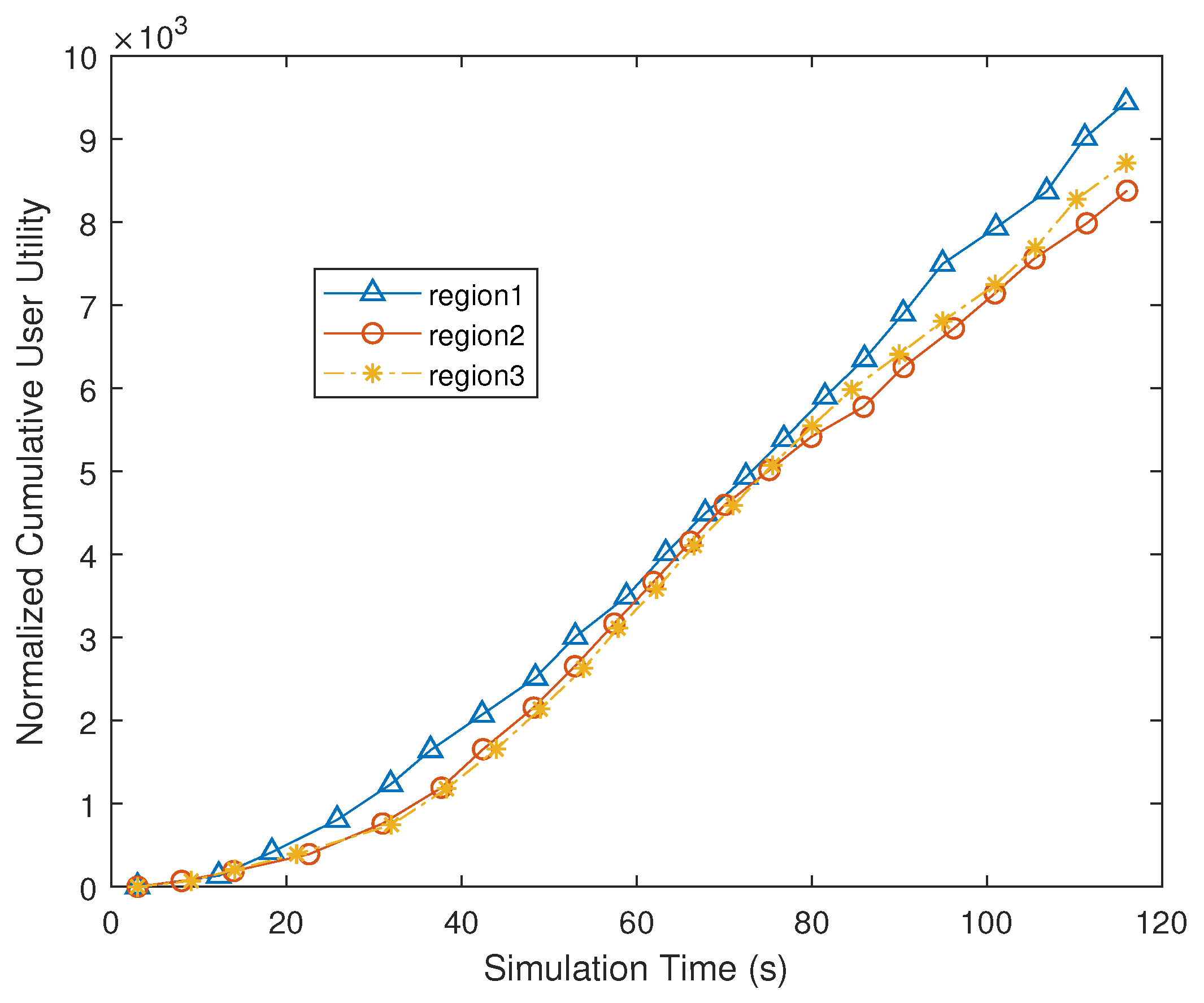
6.3.2. Fairness Evaluation
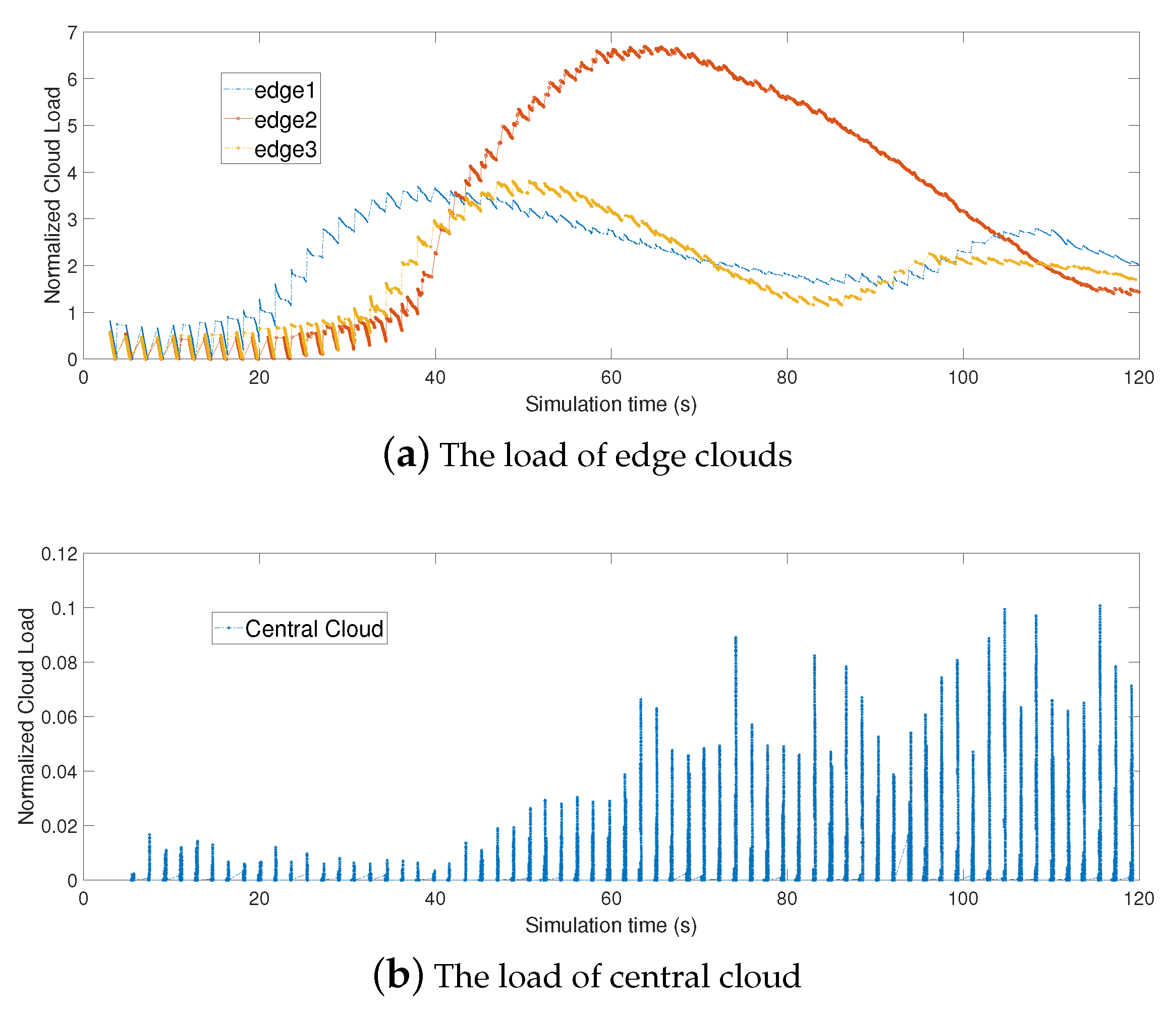
6.3.3. Stability of Our Proposed Strategy
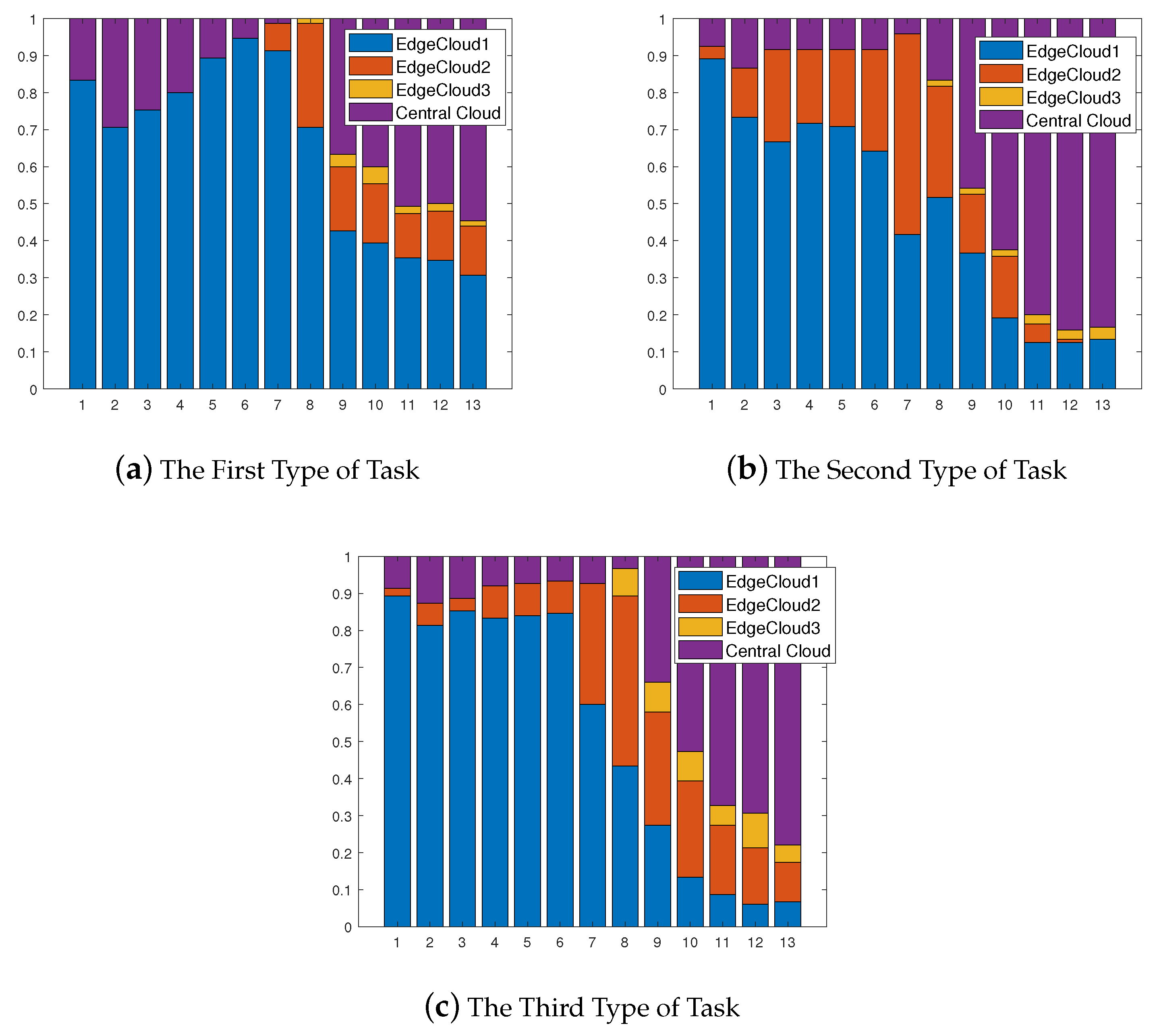
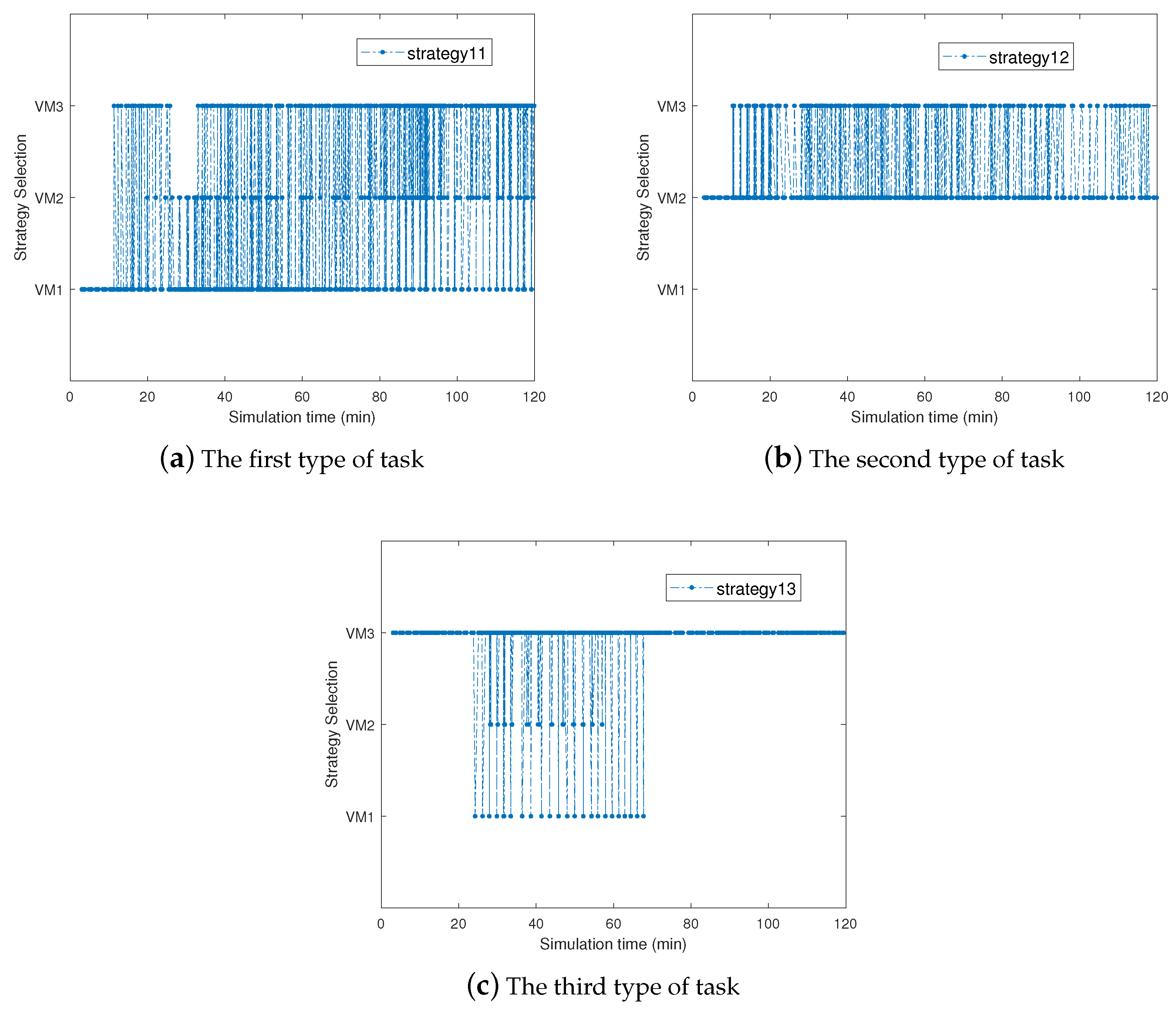
6.3.4. Adaptiveness of Our Proposed Strategy
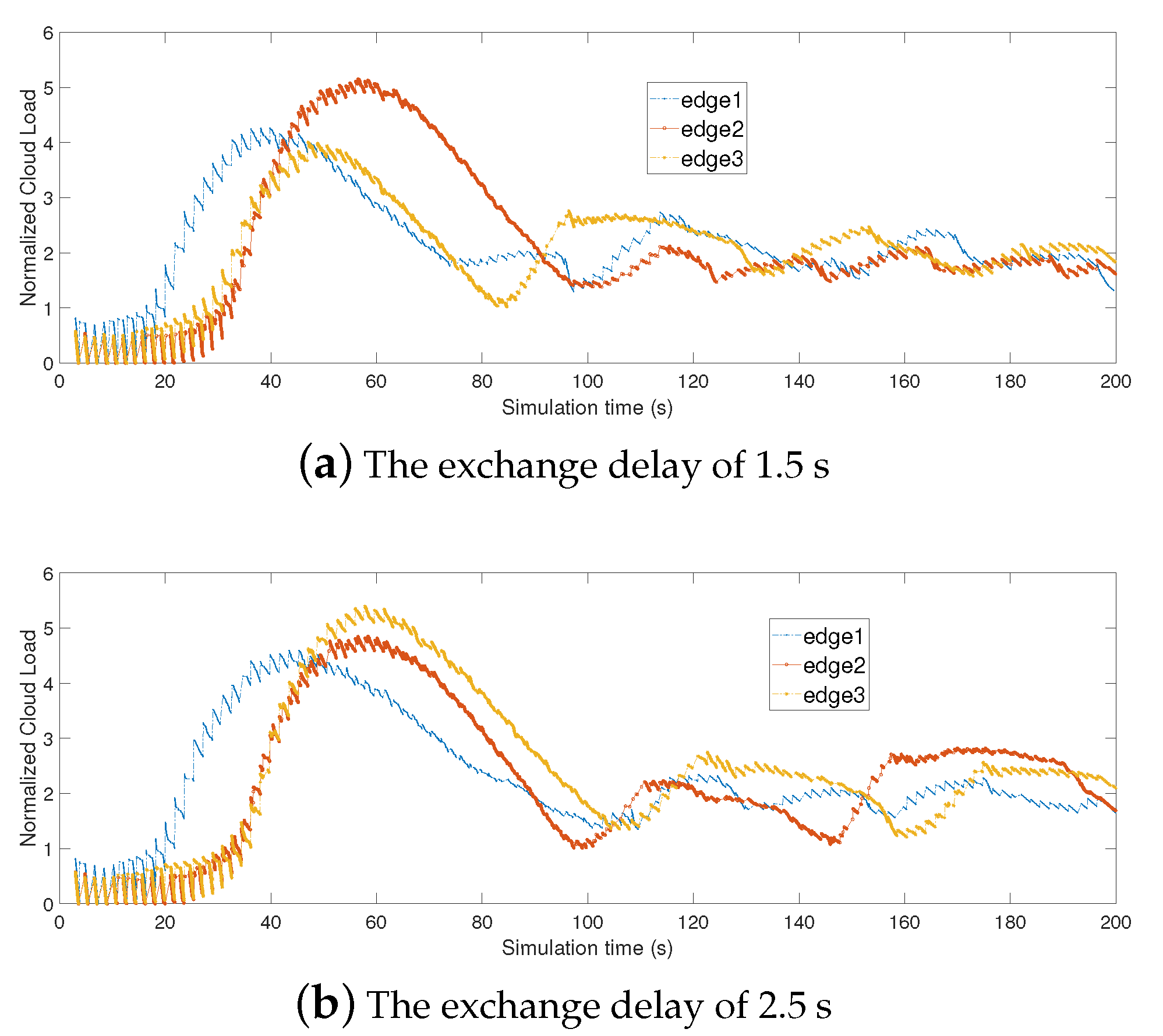
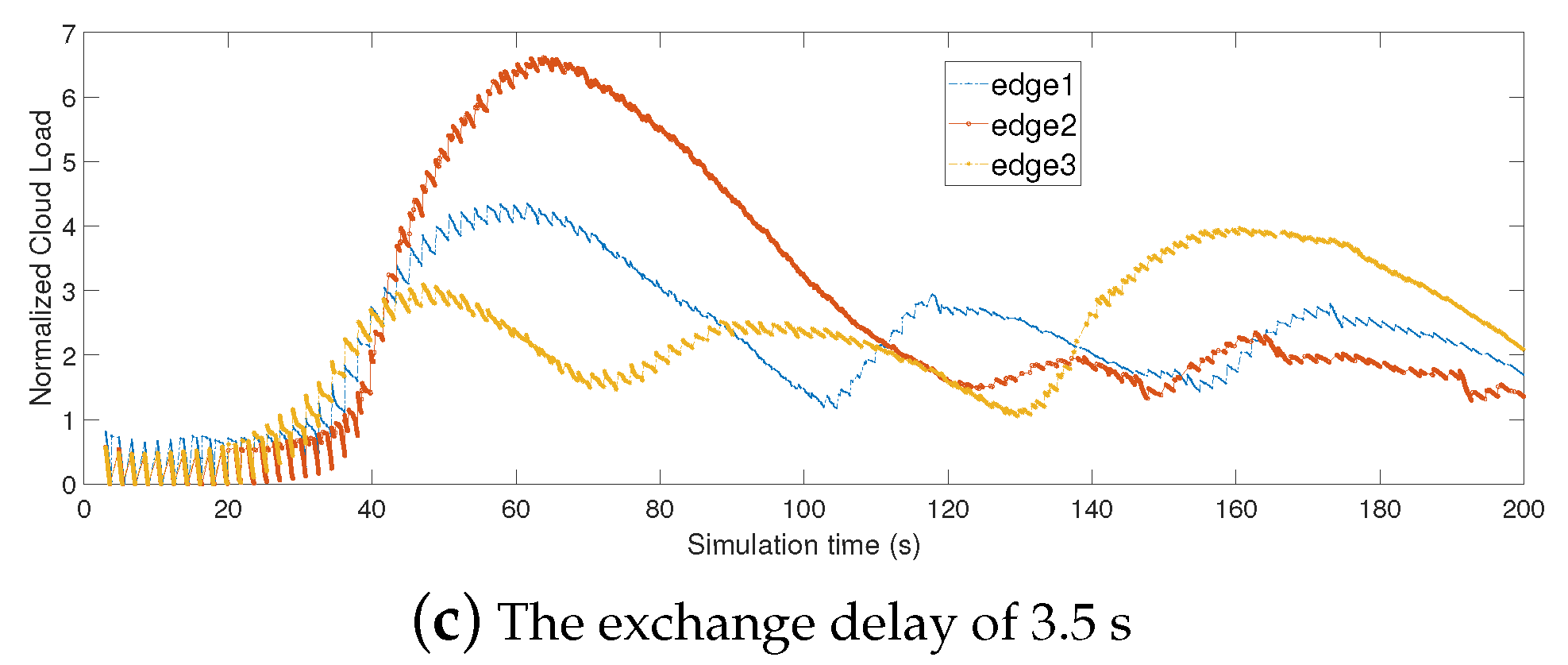
6.3.5. Impact of Delay in Information Exchange
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Billinghurst, M.; Clark, A.; Lee, G. A survey of augmented reality. Found. Trends Hum.–Comput. Interact. 2015, 8, 73–272. [Google Scholar] [CrossRef]
- Shea, R.; Fu, D.; Sun, A.; Cai, C.; Ma, X.; Fan, X.; Gong, W.; Liu, J. Location-Based Augmented Reality with Pervasive Smartphone Sensors: Inside and Beyond Pokemon Go! IEEE Access 2017, 5, 9619–9631. [Google Scholar] [CrossRef]
- Mach, P.; Becvar, Z. Mobile Edge Computing: A Survey on Architecture and Computation Offloading. IEEE Commun. Surv. Tutor. 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog Computing and Its Role in the Internet of Things. In Proceedings of the MCC Workshop on Mobile Cloud Computing, Helsinki, Finland, 17 August 2012; pp. 13–16. [Google Scholar]
- Satyanarayanan, M.; Bahl, P.; Caceres, R.; Davies, N. The Case for VM-Based Cloudlets in Mobile Computing. IEEE Pervasive Comput. 2009, 8, 14–23. [Google Scholar] [CrossRef]
- Lobillo, F.; Becvar, Z.; Puente, M.A.; Mach, P.; Presti, F.L.; Gambetti, F.; Goldhamer, M.; Vidal, J.; Widiawan, A.K.; Calvanesse, E. An architecture for mobile computation offloading on cloud-enabled LTE small cells. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Istanbul, Turkey, 6–9 April 2014; pp. 1–6. [Google Scholar]
- Taleb, T.; Ksentini, A.; Frangoudis, P. Follow-Me Cloud: When Cloud Services Follow Mobile Users. IEEE Trans. Cloud Comput. 2017. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Zhou, Z.; Liao, H.; Gu, B.; Huq, K.M.S.; Mumtaz, S.; Rodriguez, J. Robust Mobile Crowd Sensing: When Deep Learning Meets Edge Computing. IEEE Netw. 2018, 32, 54–60. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Lai, Z.; Hu, Y.C.; Cui, Y.; Sun, L.; Dai, N. Furion: Engineering High-Quality Immersive Virtual Reality on Today’s Mobile Devices. In Proceedings of the 23rd Annual International Conference on Mobile Computing and Networking (MobiCom ’17), Snowbird, UT, USA, 16–20 October 2017; pp. 409–421. [Google Scholar]
- Eeckhout, L. Is Moore’s Law Slowing Down? What’s Next? IEEE MICRO 2017, 37, 4–5. [Google Scholar] [CrossRef]
- Wang, S.; Urgaonkar, R.; He, T.; Chan, K.; Zafer, M.; Leung, K.K. Dynamic Service Placement for Mobile Micro-Clouds with Predicted Future Costs. IEEE Trans. Parallel Distrib. Syst. 2017, 28, 1002–1016. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, L.; Li, W.; Fu, X. Efficient Multi-User Computation Offloading for Mobile-Edge Cloud Computing. IEEE/ACM Trans. Netw. 2016, 24, 2795–2808. [Google Scholar] [CrossRef]
- Cho, J.; Sundaresan, K.; Mahindra, R.; Van der Merwe, J.; Rangarajan, S. ACACIA: Context-Aware Edge Computing for Continuous Interactive Applications over Mobile Networks. In Proceedings of the 12th International on Conference on Emerging Networking EXperiments and Technologies (CoNEXT ’16), Irvine, CA, USA, 12–15 December 2016; pp. 375–389. [Google Scholar]
- Chen, X.; Shi, Q.; Yang, L.; Xu, J. ThriftyEdge: Resource-Efficient Edge Computing for Intelligent IoT Applications. IEEE Netw. 2018, 32, 61–65. [Google Scholar] [CrossRef]
- Wang, H.; Li, T.; Shea, R.; Ma, X.; Wang, F.; Liu, J.; Xu, K. Toward Cloud-Based Distributed Interactive Applications: Measurement, Modeling, and Analysis. IEEE/ACM Trans. Netw. 2018, 26, 3–16. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, S.; Li, W.; Zhang, P.; Lin, C.; Shen, X. Cost-efficient workload scheduling in Cloud Assisted Mobile Edge Computing. In Proceedings of the 2017 IEEE/ACM 25th International Symposium on Quality of Service (IWQoS), Vilanova i la Geltru, Spain, 14–16 June 2017; pp. 1–10. [Google Scholar]
- Plachy, J.; Becvar, Z.; Mach, P. Path selection enabling user mobility and efficient distribution of data for computation at the edge of mobile network. Comput. Netw. 2016, 108, 357–370. [Google Scholar] [CrossRef]
- Zhang, Y.; Niyato, D.; Wang, P. Offloading in Mobile Cloudlet Systems with Intermittent Connectivity. IEEE Trans. Mob. Comput. 2015, 14, 2516–2529. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, F.; Ji, H.; Zhu, C. Combinational auction-based service provider selection in mobile edge computing networks. IEEE Access 2017, 5, 13455–13464. [Google Scholar] [CrossRef]
- Samimi, P.; Teimouri, Y.; Mukhtar, M. A combinatorial double auction resource allocation model in cloud computing. Inf. Sci. 2016, 357, 201–216. [Google Scholar] [CrossRef]
- Hou, L.; Zheng, K.; Chatzimisios, P.; Feng, Y. A Continuous-Time Markov decision process-based resource allocation scheme in vehicular cloud for mobile video services. Comput. Commun. 2018, 118, 140–147. [Google Scholar] [CrossRef]
- Xu, J.; Chen, L.; Ren, S. Online Learning for Offloading and Autoscaling in Energy Harvesting Mobile Edge Computing. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 361–373. [Google Scholar] [CrossRef]
- Wang, L.; Jiao, L.; He, T.; Li, J.; Mühlhäuser, M. Service Entity Placement for Social Virtual Reality Applications in Edge Computing. In Proceedings of the IEEE Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018. [Google Scholar]
- Urgaonkar, R.; Wang, S.; He, T.; Zafer, M.; Chan, K.; Leung, K.K. Dynamic Service Migration and Workload Scheduling in Edge-clouds. Perform. Eval. 2015, 91, 205–228. [Google Scholar] [CrossRef]
- Aryal, R.G.; Altmann, J. Dynamic application deployment in federations of clouds and edge resources using a multiobjective optimization AI algorithm. In Proceedings of the 2018 Third International Conference on Fog and Mobile Edge Computing (FMEC), Barcelona, Spain, 23–26 April 2018; pp. 147–154. [Google Scholar]
- Kuang, Z.; Guo, S.; Liu, J.; Yang, Y. A quick-response framework for multi-user computation offloading in mobile cloud computing. Future Gener. Comput. Syst. 2018, 81, 166–176. [Google Scholar] [CrossRef]
- Gu, B.; Chen., Y.; Liao, H.; Zhou, Z.; Zhang, D. A Distributed and Context-Aware Task Assignment Mechanism for Collaborative Mobile Edge Computing. Sensors 2018, 18, 2423. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T. Data Offloading in Mobile Edge Computing: A Coalition and Pricing Based Approach. IEEE Access 2018, 6, 2760–2767. [Google Scholar] [CrossRef]
- Jošilo, S.; Dan, G. Selfish Decentralized Computation Offloading for Mobile Cloud Computing in Dense Wireless Networks. IEEE Trans. Mob. Comput. 2019, 18, 207–220. [Google Scholar] [CrossRef]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Chen, X. Decentralized Computation Offloading Game for Mobile Cloud Computing. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 974–983. [Google Scholar] [CrossRef]
- Dong, C.; Jia, Y.; Peng, H.; Yang, X.; Wen, W. A Novel Distribution Service Policy for Crowdsourced Live Streaming in Cloud Platform. IEEE Trans. Netw. Serv. Manag. 2018, 15, 679–692. [Google Scholar] [CrossRef]
- Semasinghe, P.; Hossain, E.; Zhu, K. An evolutionary game for distributed resource allocation in self-organizing small cells. IEEE Trans. Mob. Comput. 2015, 14, 274–287. [Google Scholar] [CrossRef]
- Merkin, D.R. Introduction to the Theory of Stability; Springer Science & Business Media: New York, NY, USA, 2012; Volume 24. [Google Scholar]
- Mazenc, F.; Niculescu, S.I. Lyapunov stability analysis for nonlinear delay systems. Syst. Control Lett. 2001, 42, 245–251. [Google Scholar] [CrossRef]
- Hu, H.; Wen, Y.; Niyato, D. Public cloud storage-assisted mobile social video sharing: A supermodular game approach. IEEE J. Sel. Areas Commun. 2017, 35, 545–556. [Google Scholar] [CrossRef]
- Cressman, R. Evolutionary Dynamics and Extensive Form Games; MIT Press: Cambridge, MA, USA, 2003; Volume 5. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; McGraw-Hill Higher Education: Boston, MA, USA, 2010. [Google Scholar]
- Varga, A.; Hornig, R. An overview of the OMNeT++ simulation environment. In Proceedings of the 1st International Conference on Simulation Tools and Techniques for Communications, Networks and Systems & Workshops, Marseille, France, 3–7 March 2008; p. 60. [Google Scholar]
- Oueis, J.; Calvanese-Strinati, E.; Domenico, A.D.; Barbarossa, S. On the impact of backhaul network on distributed cloud computing. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Istanbul, Turkey, 6–9 April 2014; pp. 12–17. [Google Scholar]
- Ghosh, A.; Ratasuk, R.; Mondal, B.; Mangalvedhe, N.; Thomas, T. LTE-advanced: Next-generation wireless broadband technology. IEEE Wirel. Commun. 2010, 17, 10–22. [Google Scholar] [CrossRef]
- Soyata, T.; Muraleedharan, R.; Funai, C.; Kwon, M.; Heinzelman, W. Cloud-vision: Real-time face recognition using a mobile-cloudlet-cloud acceleration architecture. In Proceedings of the 2012 IEEE Symposium on Computers and Communications (ISCC), Cappadocia, Turkey, 1–4 July 2012; pp. 000059–000066. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, C.; Wen, W. Joint Optimization for Task Offloading in Edge Computing: An Evolutionary Game Approach. Sensors 2019, 19, 740. https://doi.org/10.3390/s19030740
Dong C, Wen W. Joint Optimization for Task Offloading in Edge Computing: An Evolutionary Game Approach. Sensors. 2019; 19(3):740. https://doi.org/10.3390/s19030740
Chicago/Turabian StyleDong, Chongwu, and Wushao Wen. 2019. "Joint Optimization for Task Offloading in Edge Computing: An Evolutionary Game Approach" Sensors 19, no. 3: 740. https://doi.org/10.3390/s19030740
APA StyleDong, C., & Wen, W. (2019). Joint Optimization for Task Offloading in Edge Computing: An Evolutionary Game Approach. Sensors, 19(3), 740. https://doi.org/10.3390/s19030740




