Improvement of 3D Power Line Extraction from Multiple Low-Cost UAV Imagery Using Wavelet Analysis
Abstract
:1. Introduction
Research Problem
2. Materials and Methods
Description of Data Sets
3. Methods
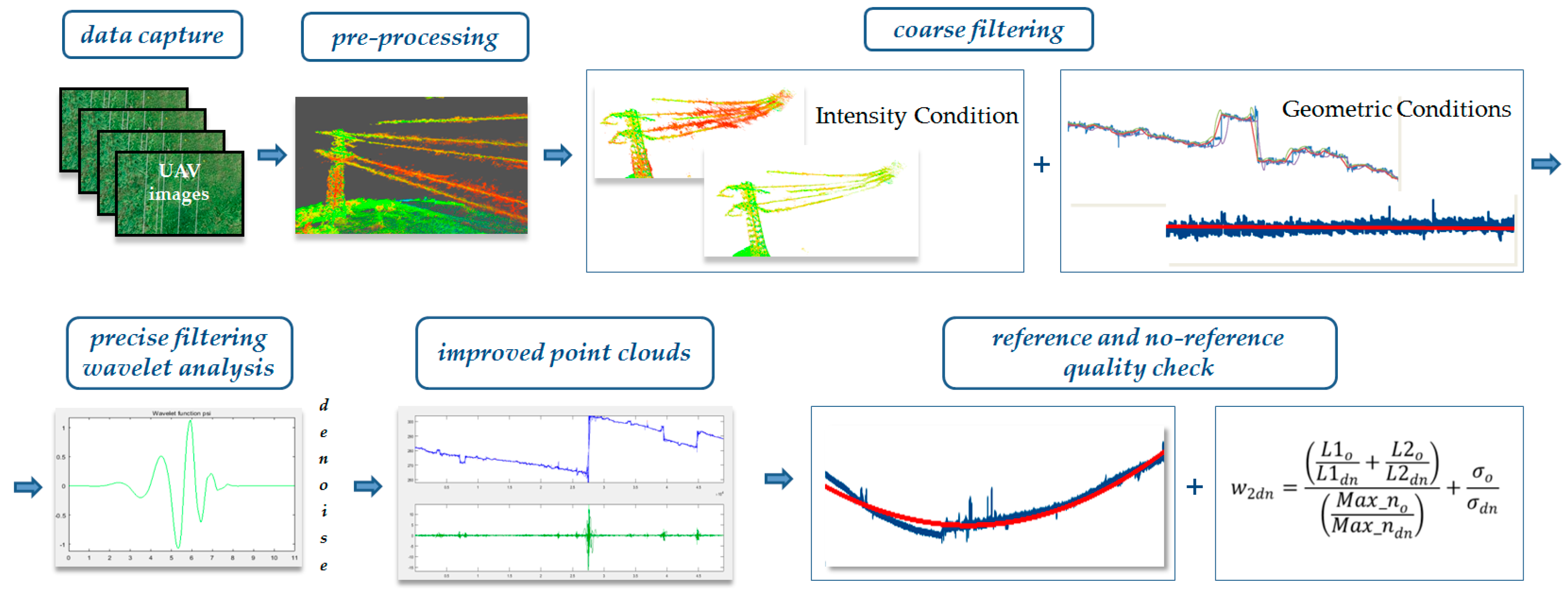
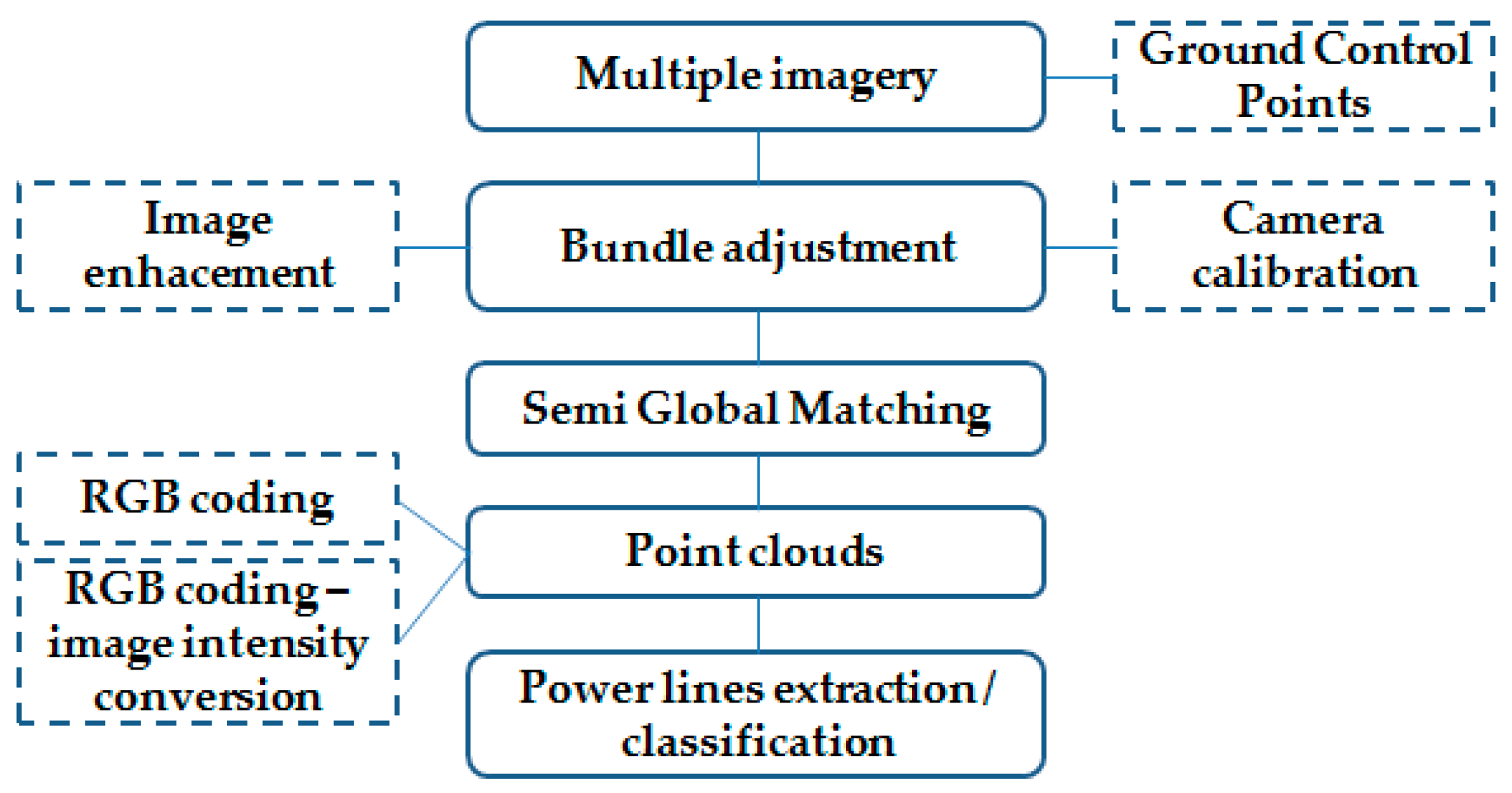
3.1. Data Capture
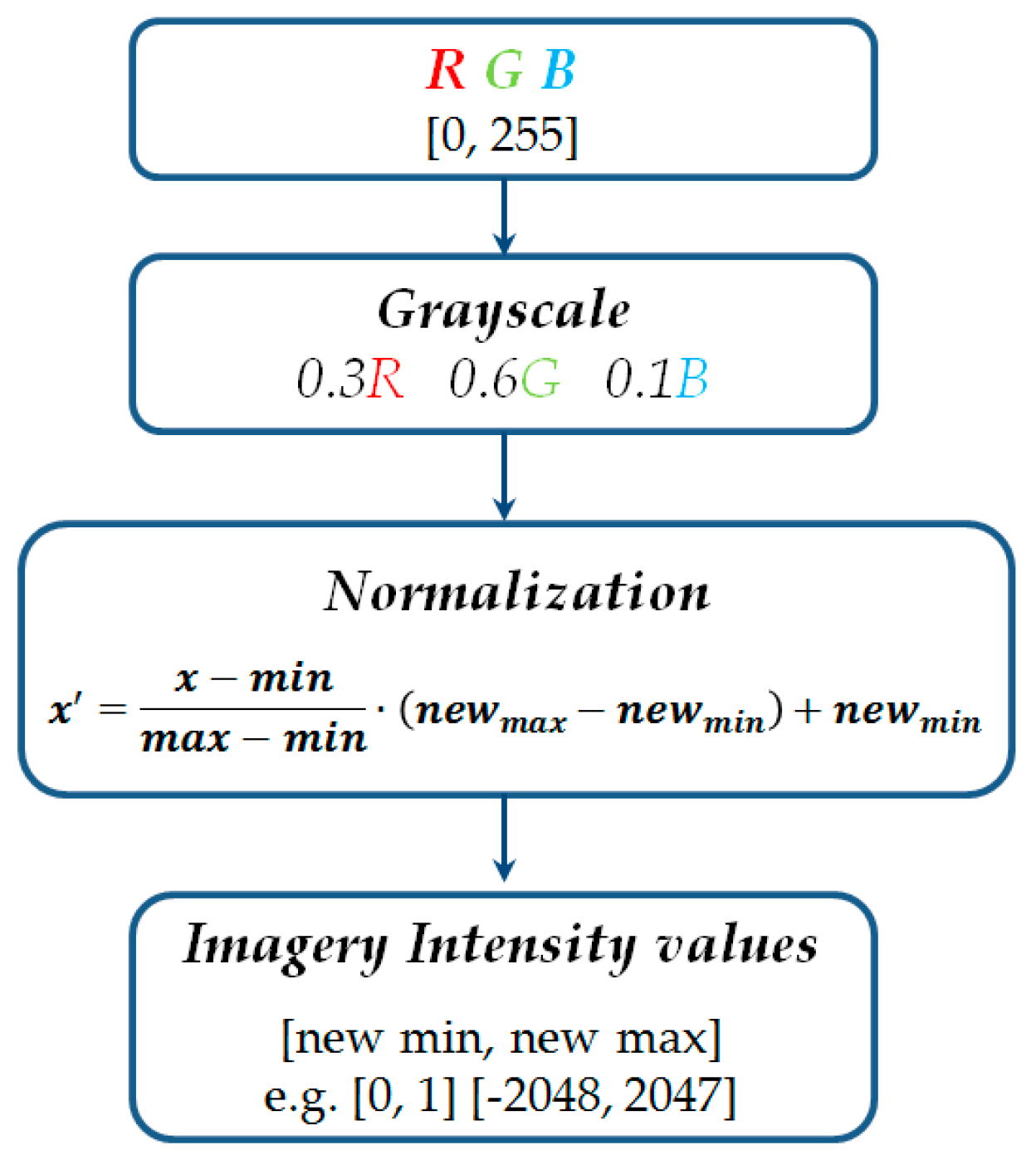
3.2. Imagery Pre-Processing
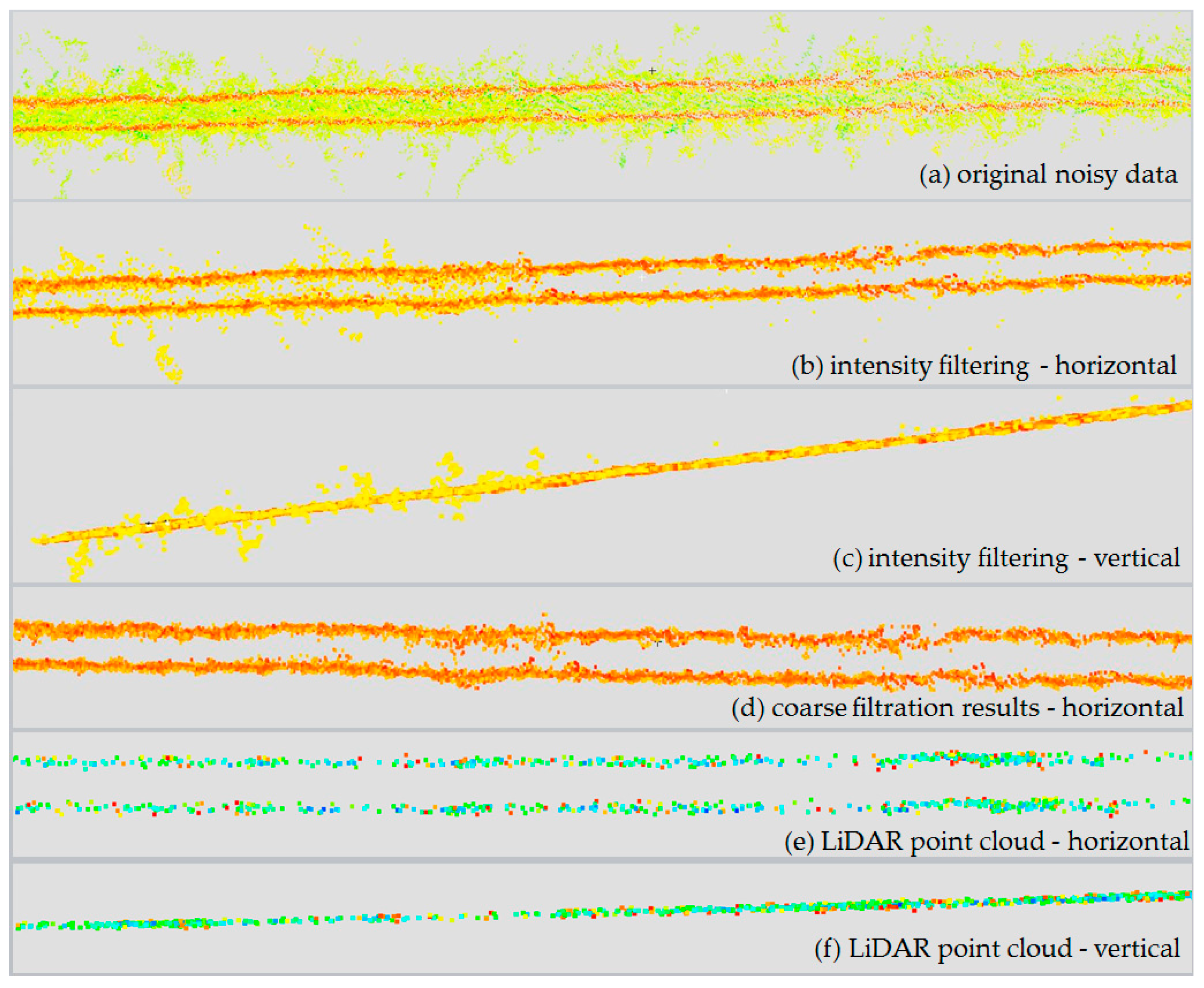
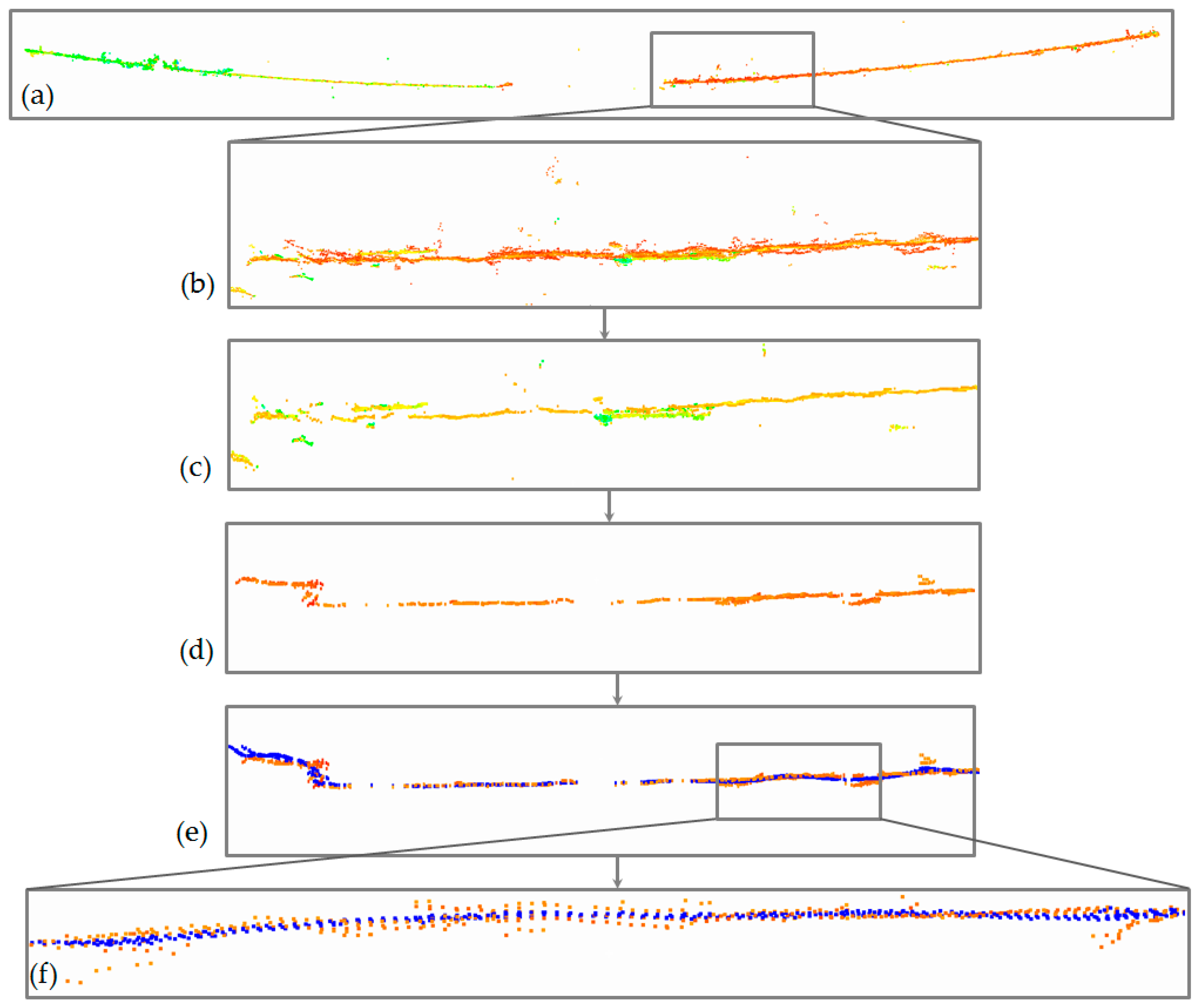
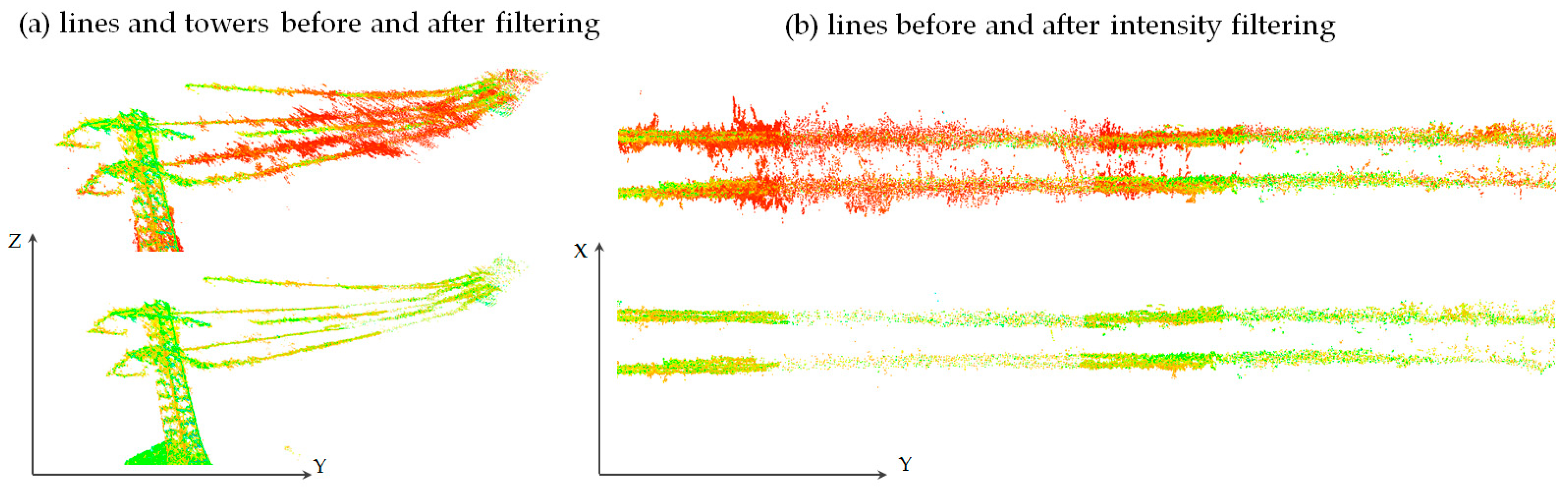
3.3. Classifying and Filtering Power Lines
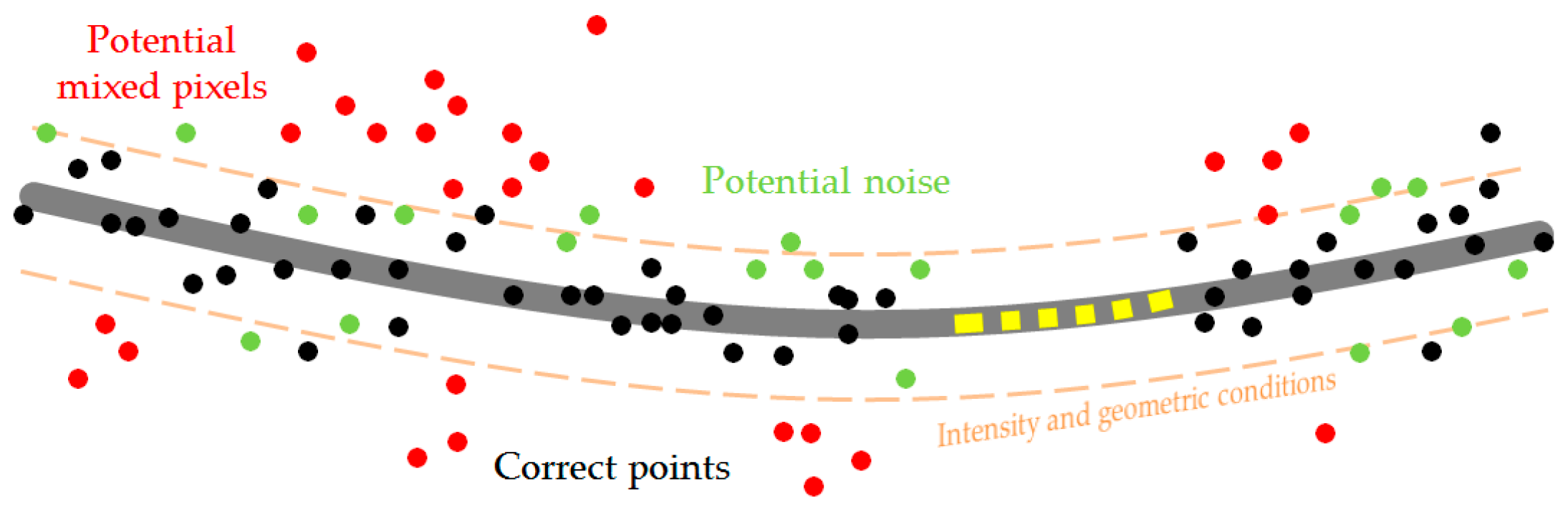
3.3.1. Two-Stage Coarse Filtration
Intensity Condition
Geometric Conditions
| Algorithm 1. Filtering points horizontally | |
| Initial: points from data set after coarse filtration Determining an approximated line based on power line’s points | |
| 1: | Look for a linear model for a straight line: Y_t = α + βt, (t,y_t) for t = 1, …, n |
| 2: | Solve the optimisation problem: |
| where ( realisation of variable Yt), (theoretical value of variable) | |
| 3: | Determine the coefficients defining the straight line: |
 straight line is constructed straight line is constructed | |
| 4: | Calculate the distance of each point P(Py, Px) from the line d’(P,L) |
| 5: | Reject the points whose distance exceeds the set d value constituting 65% of the theoretical radius of the cable |
d ≤ 0.65 ⋅ ϕT  output: correct points output: correct points | |
| Algorithm 2. Filtering points vertically | |
| Initial: points from data set after coarse filtration Determining Bollinger Bands for power line approximation | |
| 1: | Divide the points of the line with the length dL into a set number of intervals n = 0.1 dL |
| 2: | Determine the moving average: |
| for y—the variable Z, and t—the current points interval, n—the number of intervals in the average | |
| Determine the side trends—upper (UT) and lower (LT): | |
| 3: | UT = MA + σ |
| LT = MA − σ | |
| 4: | Reject the points outside side trends.  output: correct points output: correct points |
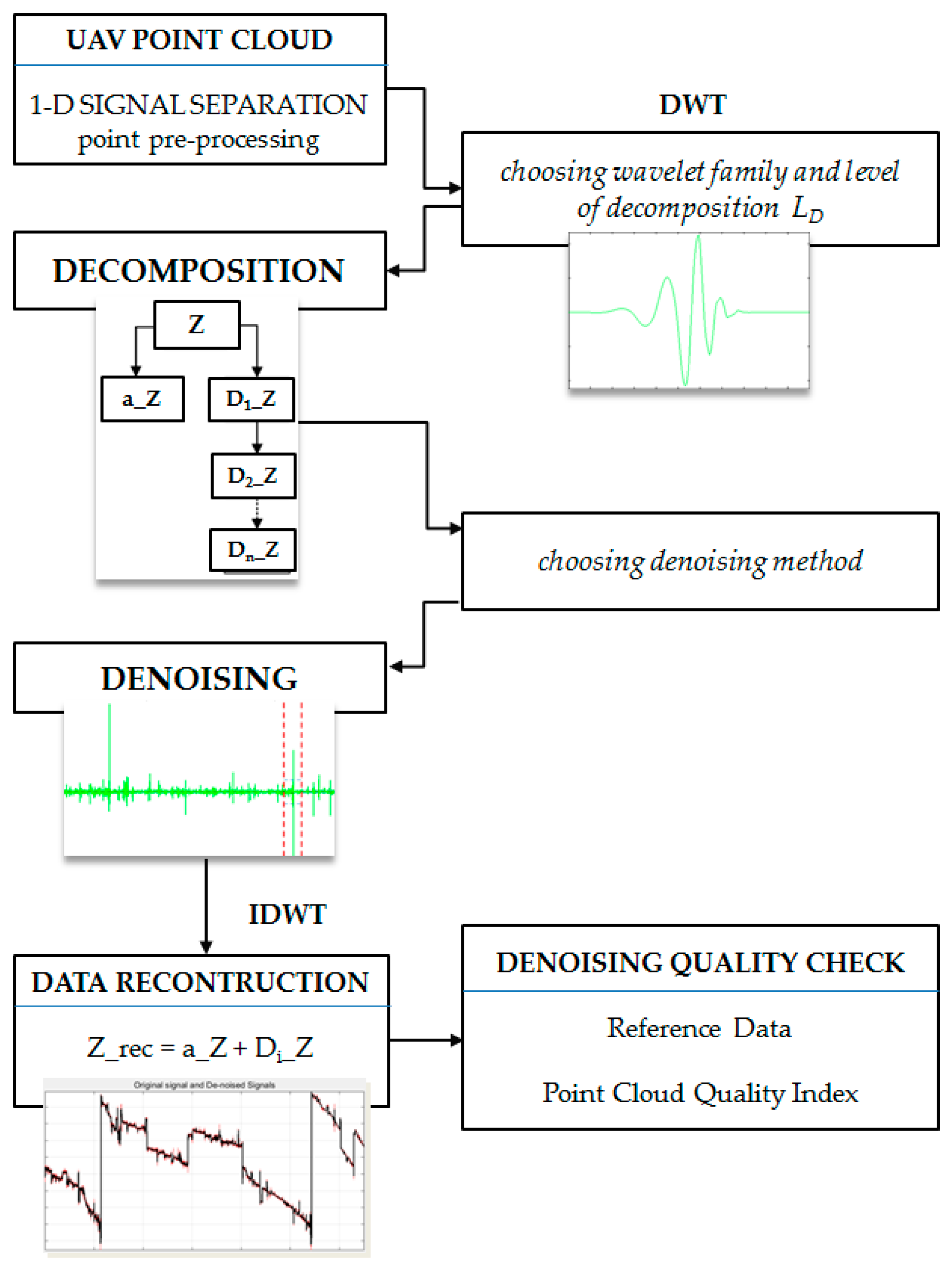
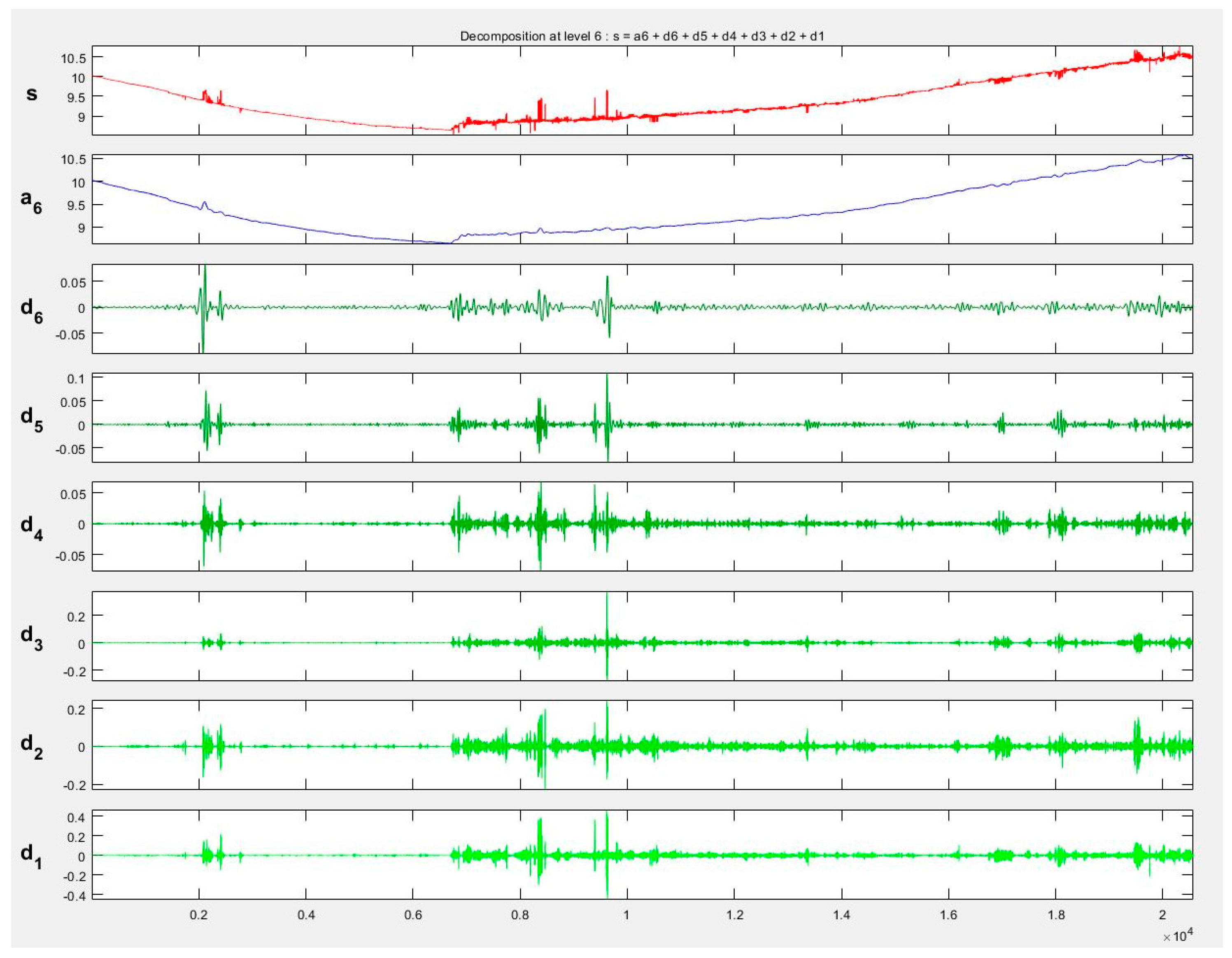
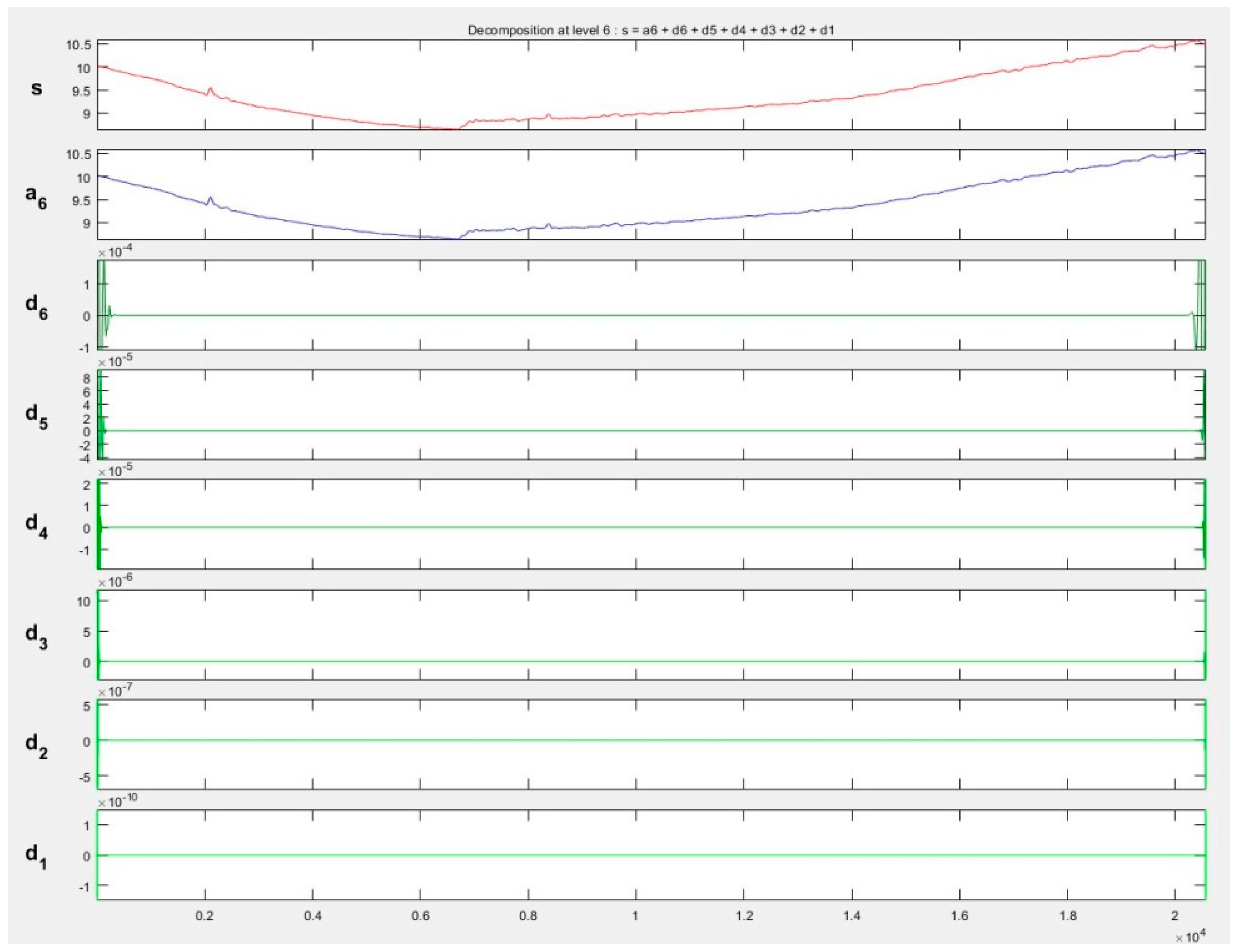
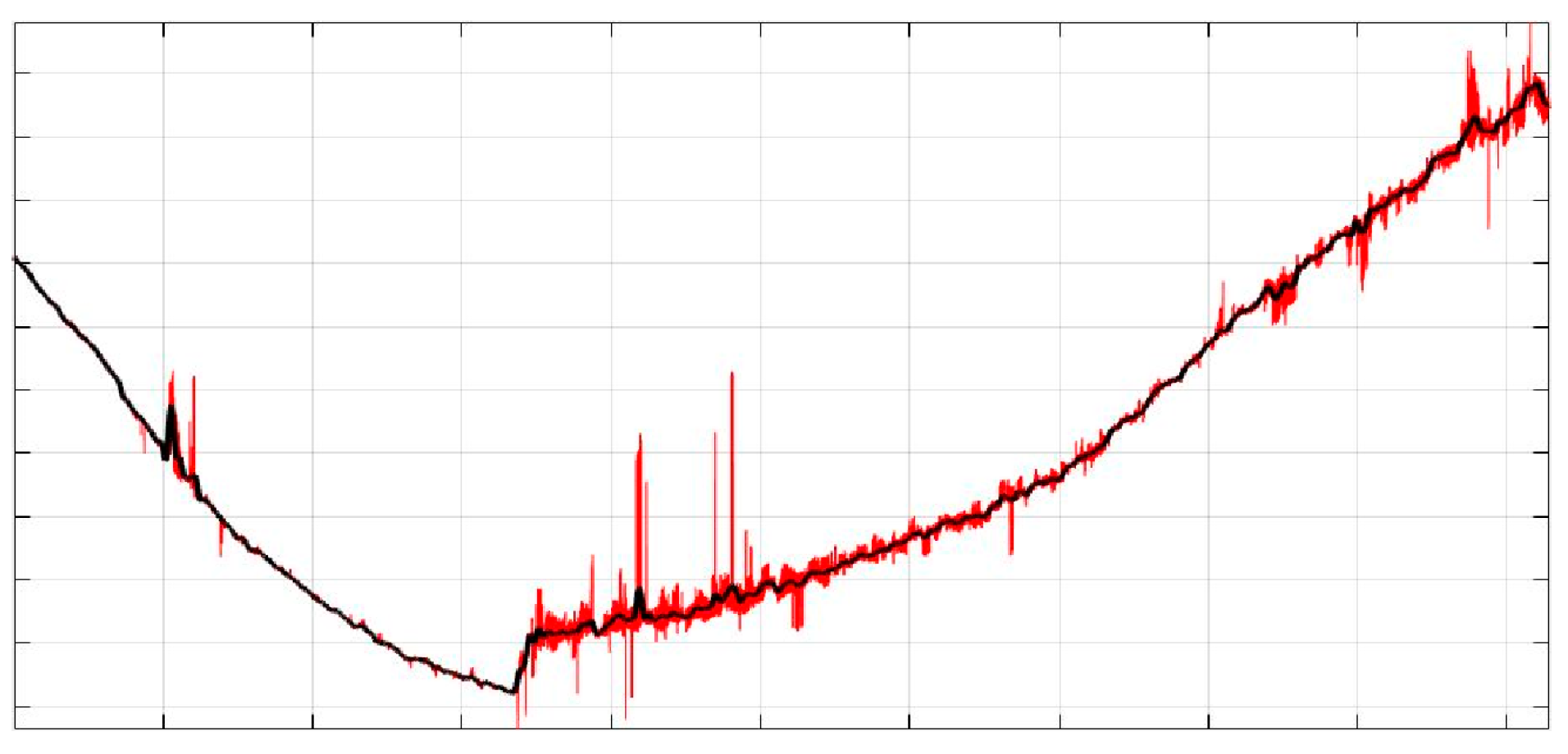
3.4. Denoising Using Wavelet Analysis
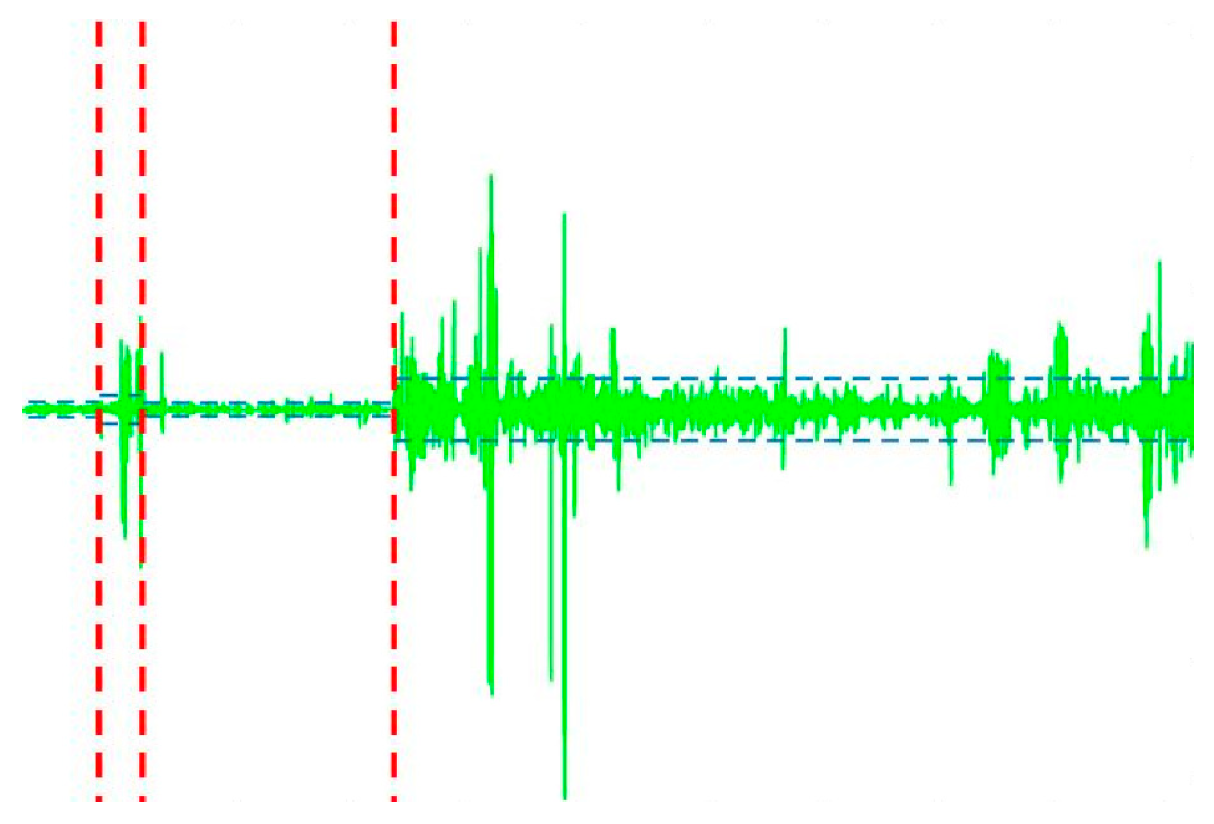
3.4.1. Data Preparation
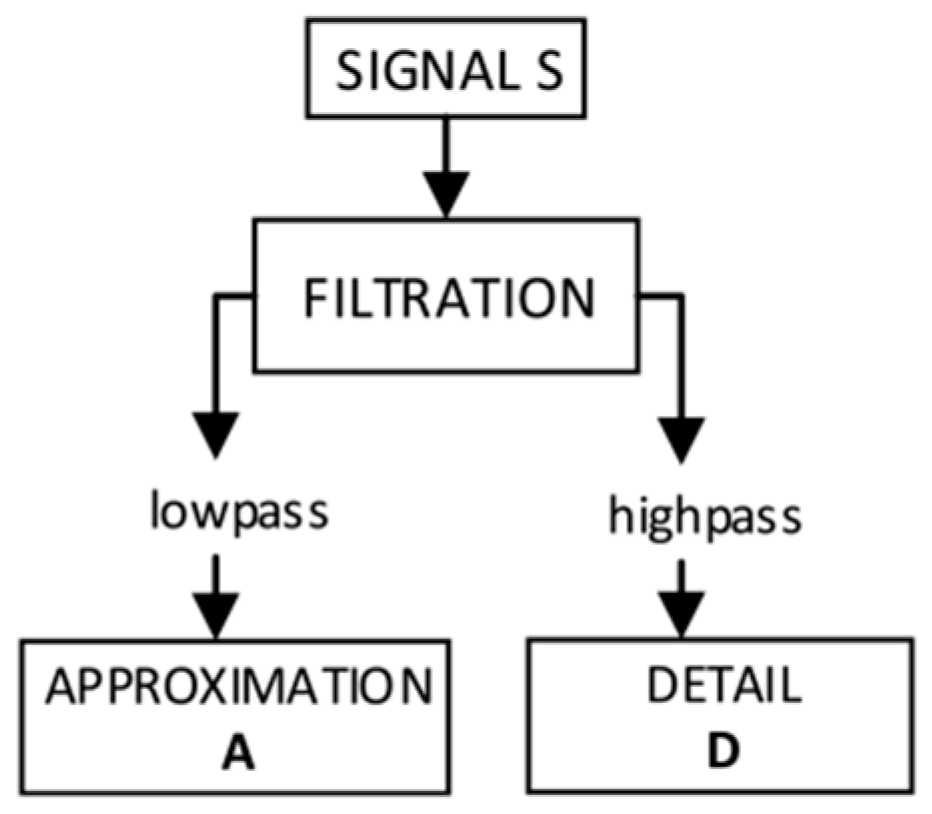
3.4.2. Wavelet Analysis
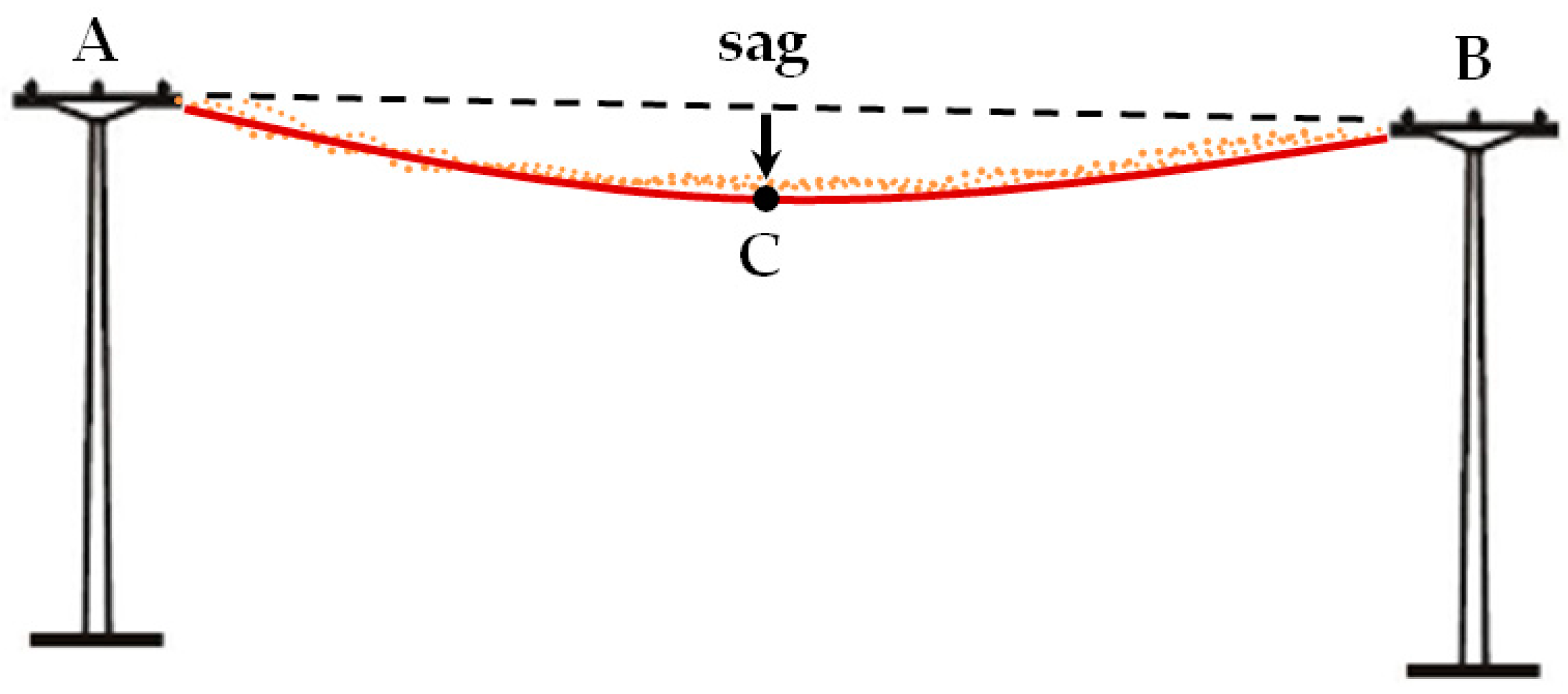
3.5. Quality Check—Point Cloud Quality Index
Validation—Comparative Study
4. Experiment and Results
4.1. Point Cloud Filtering of Power Lines
4.2. Denoising with Wavelet Transform
5. Discussion and Conclusions
Funding
Conflicts of Interest
References
- Ahokas, E.; Hyyppa, J.; Karjalainen, M.; Jaakkola, A.; Kukko, A.; Heinonen, T. Remote sensing methods for power line corridor surveys. ISPRS J. Photogramm. Remote Sens. 2016, 119, 10–31. [Google Scholar]
- Lubczonek, J. Location Determination of Radar Sensors by Using LIDAR data. In Proceedings of the 17th International Radar Symposium (IRS), Krakow, Poland, 20–12 May 2016. [Google Scholar] [CrossRef]
- Moussa, W.; Abdel-Wahab, M.; Fritsch, D. An automatic procedure for combining digital images and laser scanner data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012. [Google Scholar] [CrossRef]
- Zhu, L.; Hyyppä, J. Fully-Automated Power Line Extraction from Airborne Laser Scanning Point Clouds in Forest Areas. Remote Sens. 2014, 6, 11267–11282. [Google Scholar] [CrossRef]
- Guo, B.; Li, Q.; Huang, X.; Wang, C. An Improved Method for Power-Line Reconstruction from Point Cloud Data. Remote Sens. 2016, 8, 36. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Liu, L.; Li, X.; Sangaiah, A.K.; Li, K. Systematic Comparison of Power Line Classification Methods from ALS and MLS Point Cloud Data. Remote Sens. 2018, 10, 1222. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Z.; Hu, Q. A Model-Driven Approach for 3D Modeling of Pylon from Airborne LiDAR Data. Remote Sens. 2015, 7, 11501–11524. [Google Scholar] [CrossRef]
- Zhou, R.; Jiang, W.; Huang, W.; Xu, B.; Jiang, S. A Heuristic Method for Power Pylon Reconstruction from Airborne LiDAR Data. Remote Sens. 2017, 9, 1172. [Google Scholar] [CrossRef]
- Zhou, R.; Jiang, W.; Jiang, S. A Novel Method for High-Voltage Bundle Conductor Reconstruction from Airborne LiDAR Data. Remote Sens. 2018, 10, 2051. [Google Scholar] [CrossRef]
- Yan, G.; Li, C.; Zhou, G.; Zhang, W.; Li, X. Automatic extraction of power lines from aerial images. IEEE Geosci. Remote Sens. Lett. 2007, 4, 387–391. [Google Scholar] [CrossRef]
- Oh, J.; Lee, C. 3D Power Line Extraction from Multiple Aerial Images. Sensors 2017, 17, 2244. [Google Scholar] [CrossRef]
- Ax, M.; Thamke, S.; Kuhnert, L.; Kuhnert, K.-D. UAV based laser measurement for vegetation control at high-voltage transmission lines. Adv. Mater. Res. 2013, 614–615, 1147–1152. [Google Scholar] [CrossRef]
- Teng, G.E.; Zhou, M.; Li, C.R.; Wu, H.H.; Li, W.; Meng, F.R.; Zhou, C.C.; Ma, L. Mini-UAV LiDAR for power line inspection. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 297–300. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Li, W.; Chen, S. Automatic Power Line Inspection Using UAV Images. Remote Sens. 2017, 9, 824. [Google Scholar] [CrossRef]
- Jozkow, B.; Vander Jagt, C.T. Experiments with UAS Imagery for Automatic Modeling of Power Line 3D Geometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-1/W4. [Google Scholar] [CrossRef]
- Orych, A.; Walczykowski, P.; Jenerowicz, A.; Zdunek, Z. Impact of the cameras radiometric resolution on the accuracy of determining spectral reflectance coefficients. Int. Arch. Photogrmm. IEEE Geosci. Remote Sens. Lett. 2014, 40, 347–349. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, X.; Fang, Y.; Chen, S. UAV Low Altitude Photogrammetry for Power Line Inspection. ISPRS Int. J. Geo-Inf. 2017, 6, 14. [Google Scholar] [CrossRef]
- Shao, Z.; Yang, N.; Xiao, X.; Zhang, L.; Peng, Z. A Multi-View Dense Point Cloud Generation Algorithm Based on Low-Altitude Remote Sensing Images. Remote Sens. 2016, 8, 381. [Google Scholar] [CrossRef]
- Hirschmüller, H. Stereo Processing by Semi-Global Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Kedzierski, M.; Fryskowska, A.; Wierzbicki, D. Chosen Aspects of The Production of The Basic Map Using UAV Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 873–877. [Google Scholar] [CrossRef]
- Kedzierski, M.; Delis, P. Fast Orientation of Video Images of Buildings Acquired from a UAV without Stabilization. Sensors 2016, 16, 951. [Google Scholar] [CrossRef] [PubMed]
- Wawrzyniak, N.; Stateczny, A. Automatic Watercraft Recognition and Identification On Water Areas Covered By Video Monitoring As Extension For Sea And River Traffic Supervision Systems. Polish Marit. Res. 2018, 25, 5–13. [Google Scholar] [CrossRef]
- Pepe, M. Two Approaches for Dense DSM Generation from Aerial Digital Oblique Camera System. In Proceedings of the 2nd International Conference on Geographical Information Systems Theory, Applications and Management, Rome, Italy, 26–27 April 2016. [Google Scholar] [CrossRef]
- Wu, B.; Xie, L.; Zhu, H.H.Q.; Yau, E. Integration of aerial oblique imagery and terrestrial imagery for optimized 3D modeling in urban areas. ISPRS J. Photogramm. Remote Sens. 2018, 139, 119–132. [Google Scholar] [CrossRef]
- Hirschmüller, H. Semi Global Matching Motivation, Developments and Applications. Photogramm. Week 2011, 53, 173–181. [Google Scholar]
- Balaguer-Puig, M.; Molada-Tebar, A.; Marqués-Mateu, A.; Lerma, J.L. Characterisation Of Intensity Values on Terrestrial Laser Scanning For Recording Enhancement. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W5. [Google Scholar] [CrossRef]
- Haala, N.; Cramer, M.; Rothermel, M. Quality of 3D Point clouds from Highly overlapping UAV Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W2, 183–188. [Google Scholar] [CrossRef]
- Fryskowska, A. A novel approach of laser scanning point cloud quality assessment using wavelet analysis. In Proceedings of the Baltic Geodetic Congress (Geomatics) Gdansk University of Technology, Gdansk, Poland, 22–25 June 2017. [Google Scholar] [CrossRef]
- Kedzierski, M.; Fryskowska, A. Methods of laser scanning point clouds integration in precise 3D building modeling. Measurement 2015, 74, 221–232. [Google Scholar] [CrossRef]
- RIEGL Laser Measurement Systems GmbH, Riedenburgstraße 48, A-3580 Horn, Austria. Available online: http://www.riegl.com/products/unmanned-scanning/ricopter/ (accessed on 5 February 2019).
- Leica Geosystems AG—Part of Hexagon. Available online: https://leica-geosystems.com/products/laser-scanners/scanners/leica-scanstation-p40--p30 (accessed on 5 February 2019).
- Orych, A.; Walczykowski, P. Wyznaczanie Terenowej Zdolności Rozdzielczej Sensorów Cyfrowych W Oparciu O Cele Kalibracyjne Determining the Ground Resolved Distance For Digital Sensors Using Calibration Targets. Archiwum Fotogrametrii Kartografii i Teledetekcji 2010, 21, 291–300. [Google Scholar]
- Wierzbicki, D.; Fryśkowska, A.; Kędzierski, M.; Wojtkowska, M.; Deliś, P. Method of radiometric quality assessment of NIR images acquired with a custom sensor mounted on an unmanned aerial vehicle. J. Appl. Remote Sens. 2018, 12, 015008. [Google Scholar] [CrossRef]
- Fryskowska, A.; Kedzierski, M.; Grochala, A.; Braula, A. Calibration of Low Cost RGB And NIR UAV Cameras. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B1, 817–821. [Google Scholar] [CrossRef]
- Wierzbicki, D. Multi-Camera Imaging System for UAV Photogrammetry. Sensors 2018, 18, 2433. [Google Scholar] [CrossRef] [PubMed]
- Mikrut, S. Classical Photogrammetry and Uav—Selected Ascpects. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B1, 947–952. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Liu, L.; Zheng, D.; Li, C.; Li, K. Supervised Classification of Power Lines from Airborne LiDAR Data in Urban Areas. Remote Sens. 2017, 9, 771. [Google Scholar] [CrossRef]
- Lech, X.; Desai, M. Binarization of document images using the modified local-global Otsu and Kapur algorithms. IEEE Signal Process. Lett. 1998, 5, 265–267. [Google Scholar] [CrossRef]
- Almeida, M.; Lins, R.D.; Bernardino, R.; Jesus, D.; Lima, B. A New Binarization Algorithm for Historical Documents. J. Imaging 2018, 4, 27. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE. Trans. Syst. Man Cybern. C 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Sauvola, J.; Pietikakinen, M. Adaptive document image binarization. Pattern Recogit. 2000, 33, 225–236. [Google Scholar] [CrossRef]
- Jakovljevic, Z.; Puzovic, R.; Pajic, M. Recognition of Planar Segments in Point Cloud Based on Wavelet Transform. IEEE Trans. Ind. Inform. 2015, 11, 342–352. [Google Scholar] [CrossRef]
- Pyka, K. Wavelet-Based Local Contrast Enhancement for Satellite, Aerial and Close Range Images. Remote Sens. 2017, 9, 25. [Google Scholar] [CrossRef]
- Kedzierski, M.; Fryskowska, A. Terrestrial and aerial laser scanning data integration using wavelet analysis for the purpose of 3D building modeling. Sensors 2014, 14, 12070–12092. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, D.; Wu, J.C. Entropy-based method of choosing the decomposition level in wavelet threshold de-noising. Entropy 2010, 12, 1499–1513. [Google Scholar] [CrossRef]
- Madhur Srivastava, C.; Anderson, L.; Freed, J.H. A New Wavelet Denoising Method for Selecting Decomposition Levels and Noise Thresholds. IEEE Access 2016, 4, 3862–3877. [Google Scholar] [CrossRef] [PubMed]
- Md Yusof, M.R.; Arin, A.K. Using Stein’s Unbiased Risk Estimate (SURE) to Optimize Level of Decomposition in Stationary Wavelet Transform Denoising. Available online: https://arxiv.org/pdf/1701.03594.pdf (accessed on 5 February 2019).
- Donoho, D. De-noising by soft-tresholding. IEEE Trams. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Zhang, X.P.; Desai, M. Adaptive Denoising Based On SURE Risk. IEEE Signal Process. Lett. 1998, 5, 265–267. [Google Scholar] [CrossRef]
- Vidakovicand, B.; Mueller, P. Wavelets for Kids A Tutorial Introduction, Institute of Statistics and Decision Sciences; Duke University: Durham, NC, USA, 1994. [Google Scholar]
- Nason, G. Choice of the Threshold Parameter in Wavelet Function Estimation; Department of Mathematics University of Bristol: Bristol, UK, 2002. [Google Scholar]
- Mallat, S. A theory for miltiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, II, 674–693. [Google Scholar] [CrossRef]
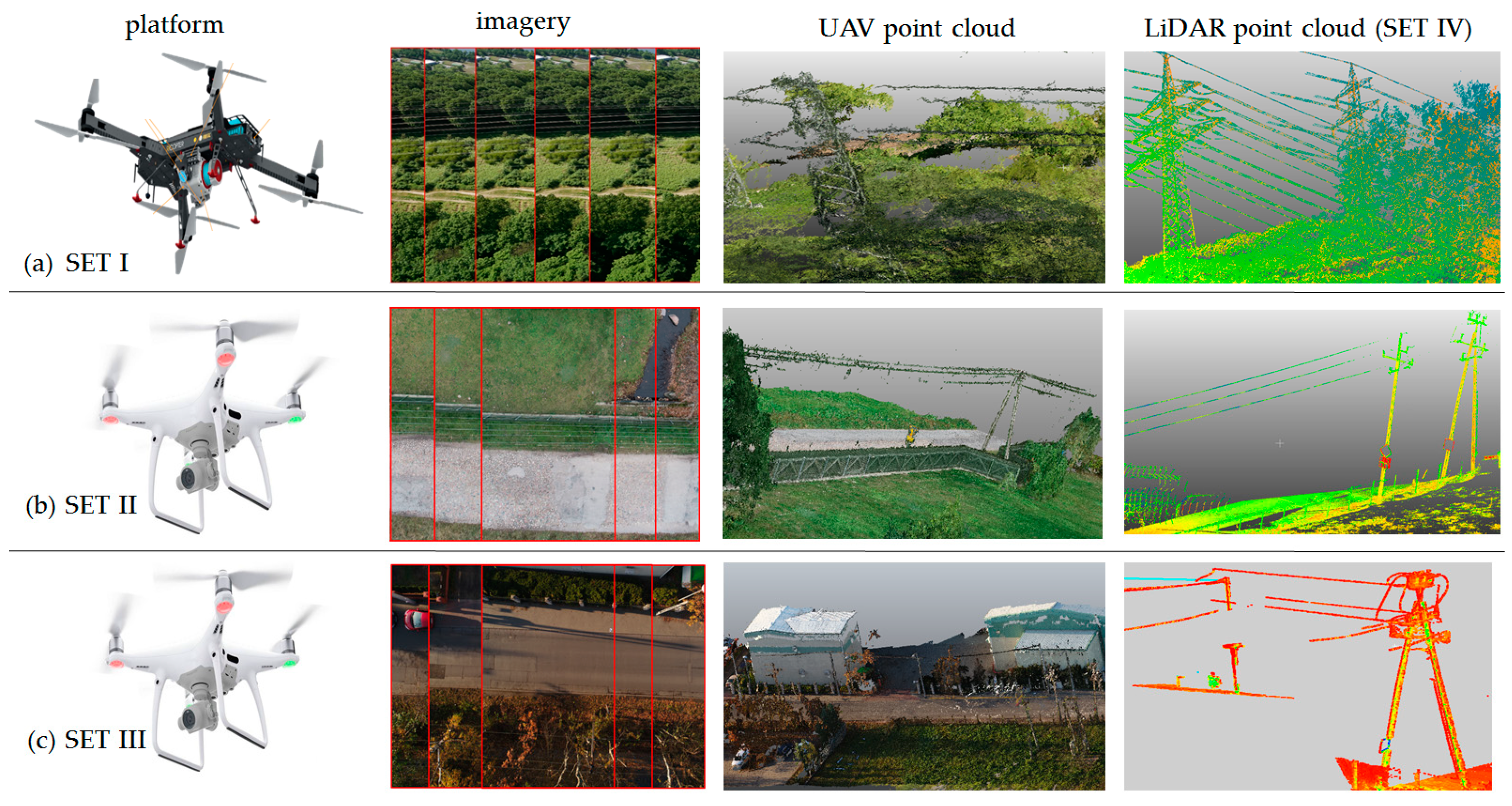


| Feature | Set I | Set II | Set III | |
|---|---|---|---|---|
| Objects and area | Power line type Cable diameter (cm) Scene type | High-voltage (ϕT = 30 mm) Open and forest area | Low-voltage (ϕT = 6 mm) Rural area | Low-voltage (ϕT = 28 mm) Urban area |
| Image and point clouds | Camera model GSD (cm) Flight height (m) Point cloud resolution (cm) | Sony Alpha 6000 4 cm 90 AGL 4 | Sony RX100 0.3 23 m, 30 m 0.5–1.0 | Sony RX100 0.5 28 m 0.6–1.2 |
| Set IV Reference data type | Laser scanning model and type | Riegl VUX-1UAV (UAV-ALS) | Leica P40 (TLS) | Leica P40 (TLS) |
| SET I (Summer) | SET II (Summer) | SET II (Winter) | SET III (Autumn) | |
|---|---|---|---|---|
| Minimum | 0.499 | 0.499 | 0.499 | 0.499 |
| Maximum | 0.560 | 0.560 | 0.560 | 0.560 |
| Mean | 0.509 | 0.523 | 0.529 | 0.512 |
| SD | 0.019 | 0.013 | 0.015 | 0.009 |
| Max. SD | 0.031 | 0.031 | 0.031 | 0.031 |
| K coefficient | 0.20 | 0.15 | 0.20 | 0.07 |
| Threshold value t | 0.522 | 0.523 | 0.525 | 0.513 |
| Filtration | 68% | 67% | 75% | 84% |
| Original Data | Fixed from Threshold | RSURE | HSURE | |||||
|---|---|---|---|---|---|---|---|---|
| Coeff. | Rec. | Coeff. | Rec. | Coeff. | Rec. | Coeff. | Rec. | |
| SD | 0.024 | 0.020 | 0.018 | 0.012 | 4.769 × 10−07 | 1.972 × 10−07 | 0.018 | 0.013 |
| MAD | 0.005 | 0.009 | 0.002 | 0.002 | 1.045 × 10−08 | 6.24 × 10−09 | 0.002 | 0.002 |
| L1 norm | 129.4 | 182.6 | 19.55 | 33.93 | 0.0001 | 0.0001 | 22.09 | 38.16 |
| L2 norm | 2.879 | 2.879 | 1.808 | 1.808 | 4.837 × 10−05 | 0.0001 | 1.877 | 1.877 |
| Max norm | 0.624 | 0.459 | 0.567 | 0.389 | 3.645 × 10−05 | 0.0001 | 0.574 | 0.398 |
| w1dn | 6.0 | 4.6 | 82.7 | 105.2 | 5.4 | 4.2 | ||
| w2dn | 8.8 | 7.5 | 50,201 | 101,935 | 8.1 | 7.0 | ||
| Original Data | Fixed from Threshold | RSURE | HSURE | |||||
|---|---|---|---|---|---|---|---|---|
| Coeff. | Rec. | Coeff. | Rec. | Coeff. | Rec. | Coeff. | Rec. | |
| SD | 0.004 | 0.003 | 0.002 | 0.001566 | 0.001991 | 0.0014 | 0.0022 | 0.0015 |
| MAD | 0.002 | 0.002 | 0.0003 | 0.000225 | 0.0002494 | 0.0002 | 0.0003 | 0.0002 |
| L1 norm | 25.3 | 35.3 | 2.77 | 4.69 | 2.44 | 4.21 | 2.77 | 4.69 |
| L2 norm | 0.447 | 0.447 | 0.226 | 0.226 | 0.203 | 0.203 | 0.226 | 0.226 |
| Max norm | 0.086 | 0.077 | 0.078 | 0.066 | 0.077 | 0.066 | 0.077 | 0.066 |
| w1dn | 5.8 | 5.6 | 6.6 | 6.3 | 5.8 | 5.6 | ||
| w2dn | 18.2 | 20.3 | 20.4 | 22.6 | 18.2 | 20.3 | ||
| Line | Point Cloud Resolution (mm) | Span (m) | Theor. Cable Diameter ϕT (mm) | Cable Diameter ϕUAVo (mm) | Cable Diameter Corrected ϕUAVc (mm) | Sag SUAVo (m) | Sag Corrected SUAVc (m) | |
|---|---|---|---|---|---|---|---|---|
| SET I | S1_L1_ALS | 38 | 292.69 | 30 | 46 | - | 5.52 | - |
| S1_L1_UAV | 43 | 291.88 | 96 | 64 | 5.71 | 5.61 | ||
| S1_L2_ALS | 38 | 291.19 | 65 | - | 8.10 | - | ||
| S1_L2_UAV | 43 | 291.25 | 88 | 58 | 8.24 | 8.31 | ||
| SET II | S2_L3_TLS | 6 | 48.94 | 6 | 10 | - | 0.26 | - |
| S2_L3_UAV | 4 | 48.41 | 10 | 8 | 0.22 | 0.25 | ||
| S2_L1_TLS (winter) | 4 | 44.52 | 13 | - | 0.47 | - | ||
| S2_L1_UAV (summer) | 10 | 44.86 | 26 | 15 | 0.76 | 0.69 | ||
| S2_L1_UAV (winter) | 5 | 43.78 | 12 | 10 | 0.51 | 0.46 | ||
| SET III | S3_L1_TLS | 7 | 40.62 | 28 | 30 | - | 1.61 | - |
| S3_L1_UAV | 11 | 40.62 | 42 | 29 | 1.58 | 1.63 |
| SET I | SET II | SET III | ||||
|---|---|---|---|---|---|---|
| Sag Delta [m] | S1_L1 | S1_L2 | S2_L3 | S2_L1 (Winter) | S2_L1 (Summer) | S3_L1 |
| SUAVo–SLS | 0.19 | 0.14 | 0.03 | 0.04 | 0.03 | |
| SUAVc–SLS | 0.09 | 0.20 | 0.01 | 0.01 | 0.02 | |
| SUAVo–SUAVc | 0.09 | 0.07 | 0.02 | 0.04 | 0.07 | 0.05 |
| Correction level | 2% | 1% | 10% | 10% | 9% | 3% |
| Diameter Delta (mm) | S1_L1 | S1_L2 | S2_L3 | S2_L1 (Winter) | S2_L1 (Summer) | S3_L1 |
|---|---|---|---|---|---|---|
| ϕUAVo–ϕT | 66 | 58 | 4 | 6 | 20 | 14 |
| ϕUAVc–ϕT | 34 | 28 | 2 | 4 | 9 | 1 |
| ϕLS–ϕT | 16 | 35 | 4 | 7 | 7 | 2 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fryskowska, A. Improvement of 3D Power Line Extraction from Multiple Low-Cost UAV Imagery Using Wavelet Analysis. Sensors 2019, 19, 700. https://doi.org/10.3390/s19030700
Fryskowska A. Improvement of 3D Power Line Extraction from Multiple Low-Cost UAV Imagery Using Wavelet Analysis. Sensors. 2019; 19(3):700. https://doi.org/10.3390/s19030700
Chicago/Turabian StyleFryskowska, Anna. 2019. "Improvement of 3D Power Line Extraction from Multiple Low-Cost UAV Imagery Using Wavelet Analysis" Sensors 19, no. 3: 700. https://doi.org/10.3390/s19030700
APA StyleFryskowska, A. (2019). Improvement of 3D Power Line Extraction from Multiple Low-Cost UAV Imagery Using Wavelet Analysis. Sensors, 19(3), 700. https://doi.org/10.3390/s19030700





