A Common Assessment Space for Different Sensor Structures
Abstract
:1. Introduction
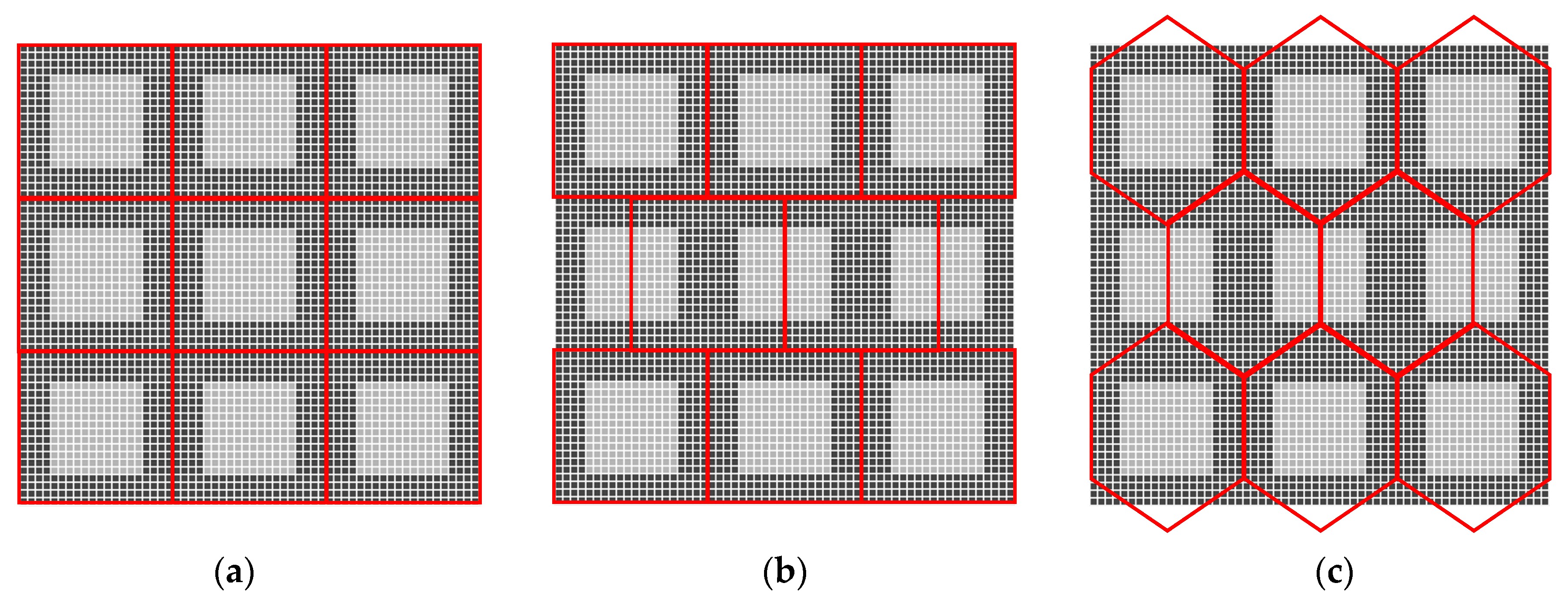
2. Arrangement Addressing
3. Image Generation
3.1. Generation of the Virtual Hexagonal Enriched Image (Hex_E)
3.2. Generation of the Virtual Half-Pixel Shift Enriched Image (HS_E)
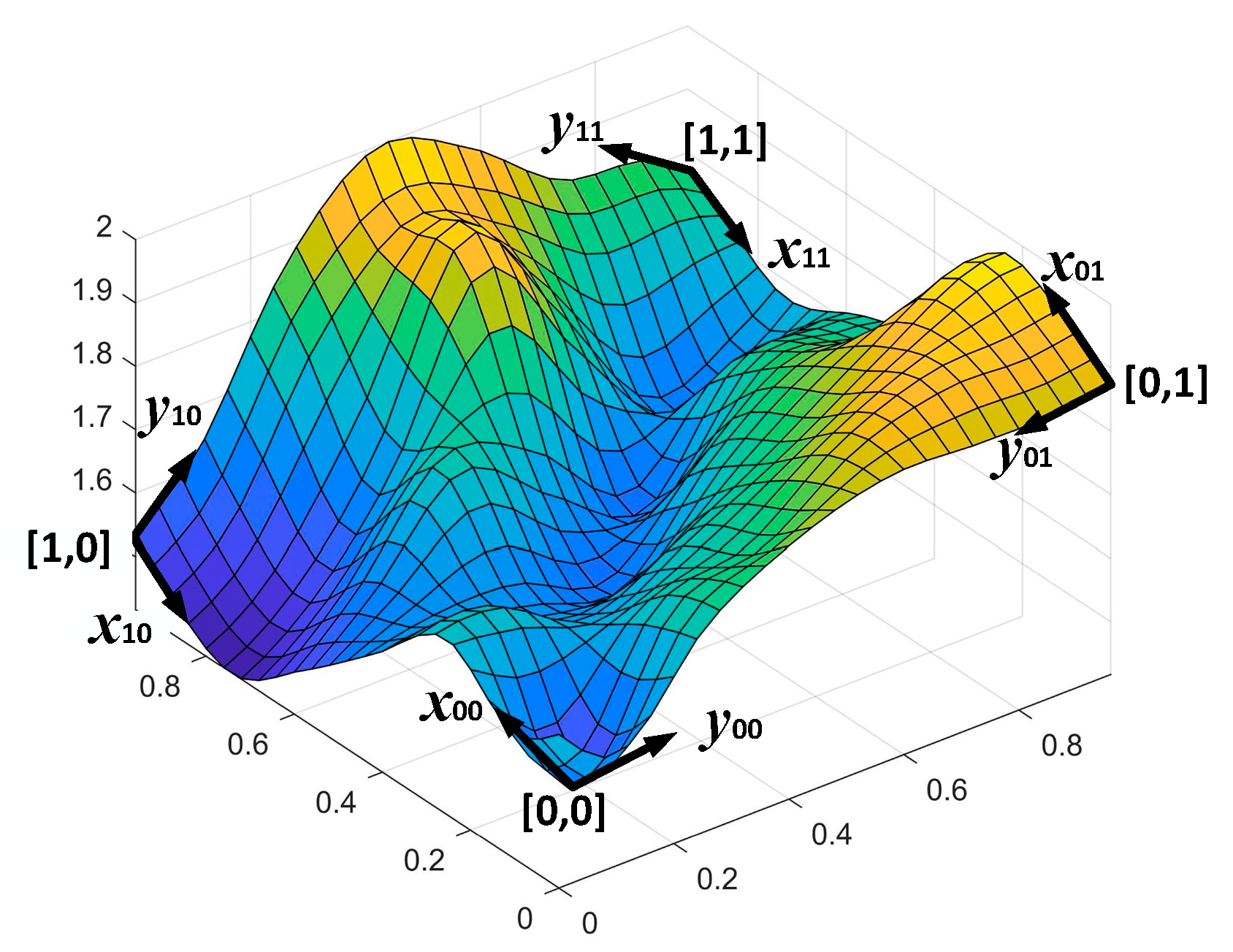
4. Common Space Based on Continuous Extension
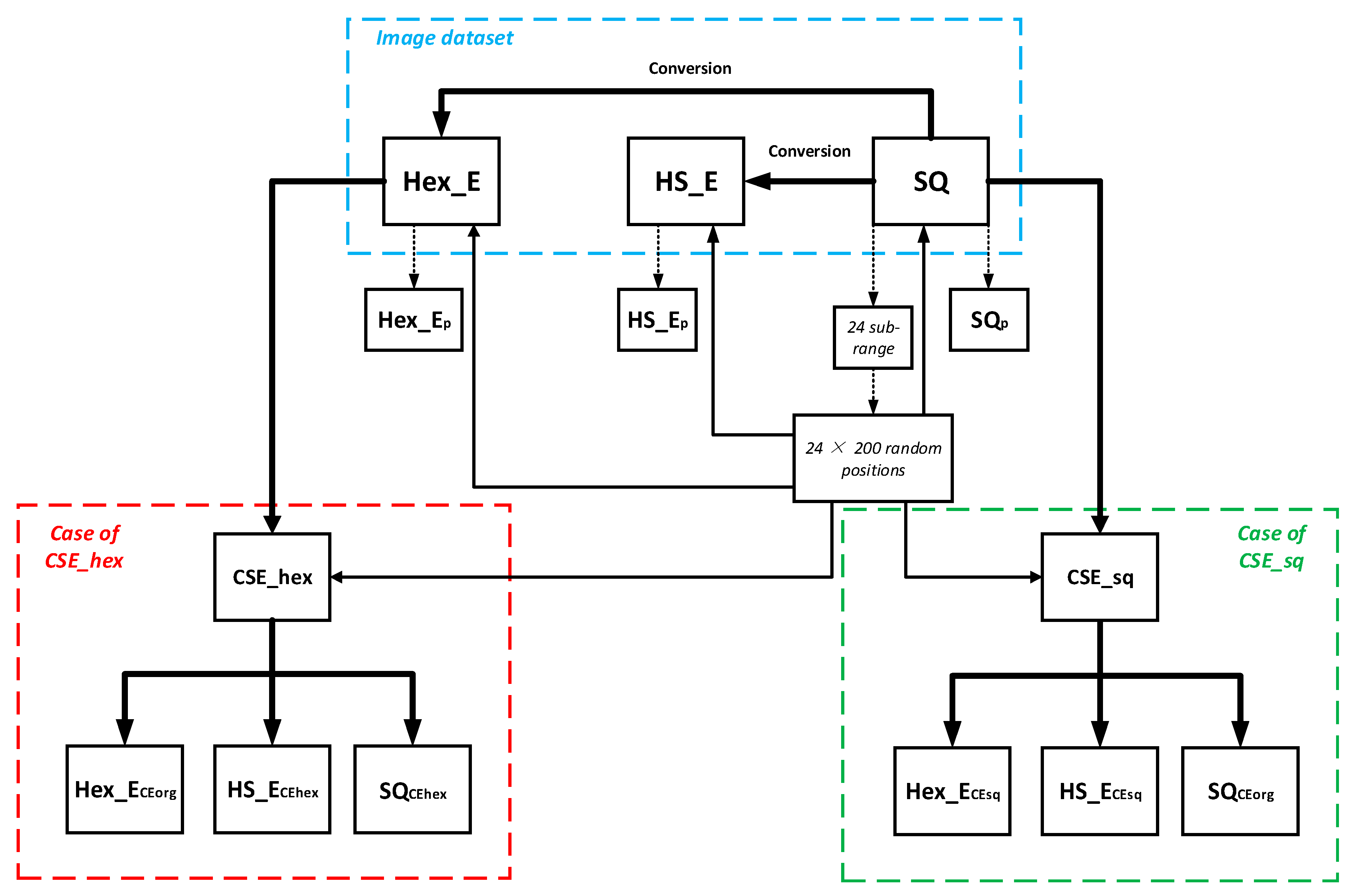
5. Experimental Setup
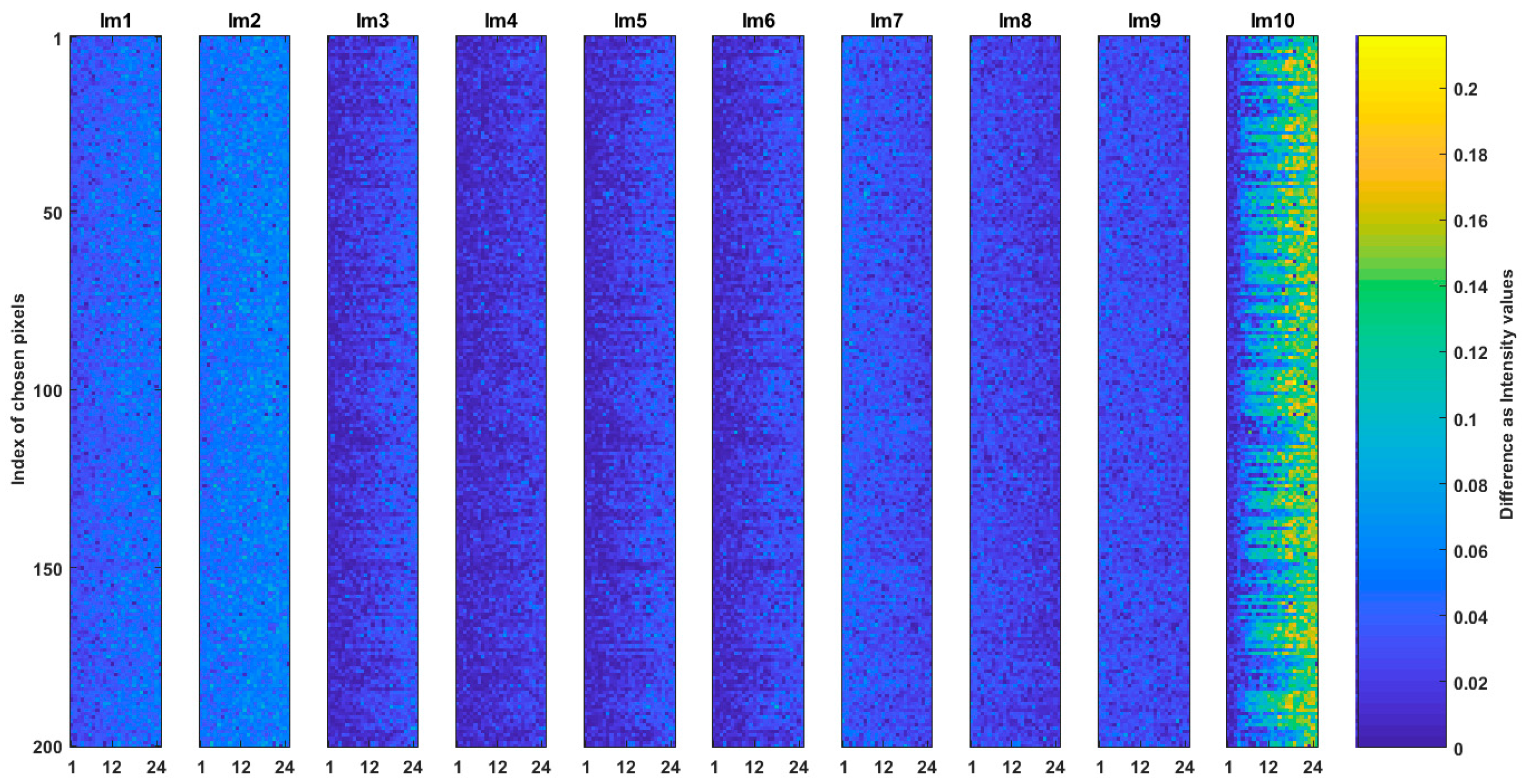
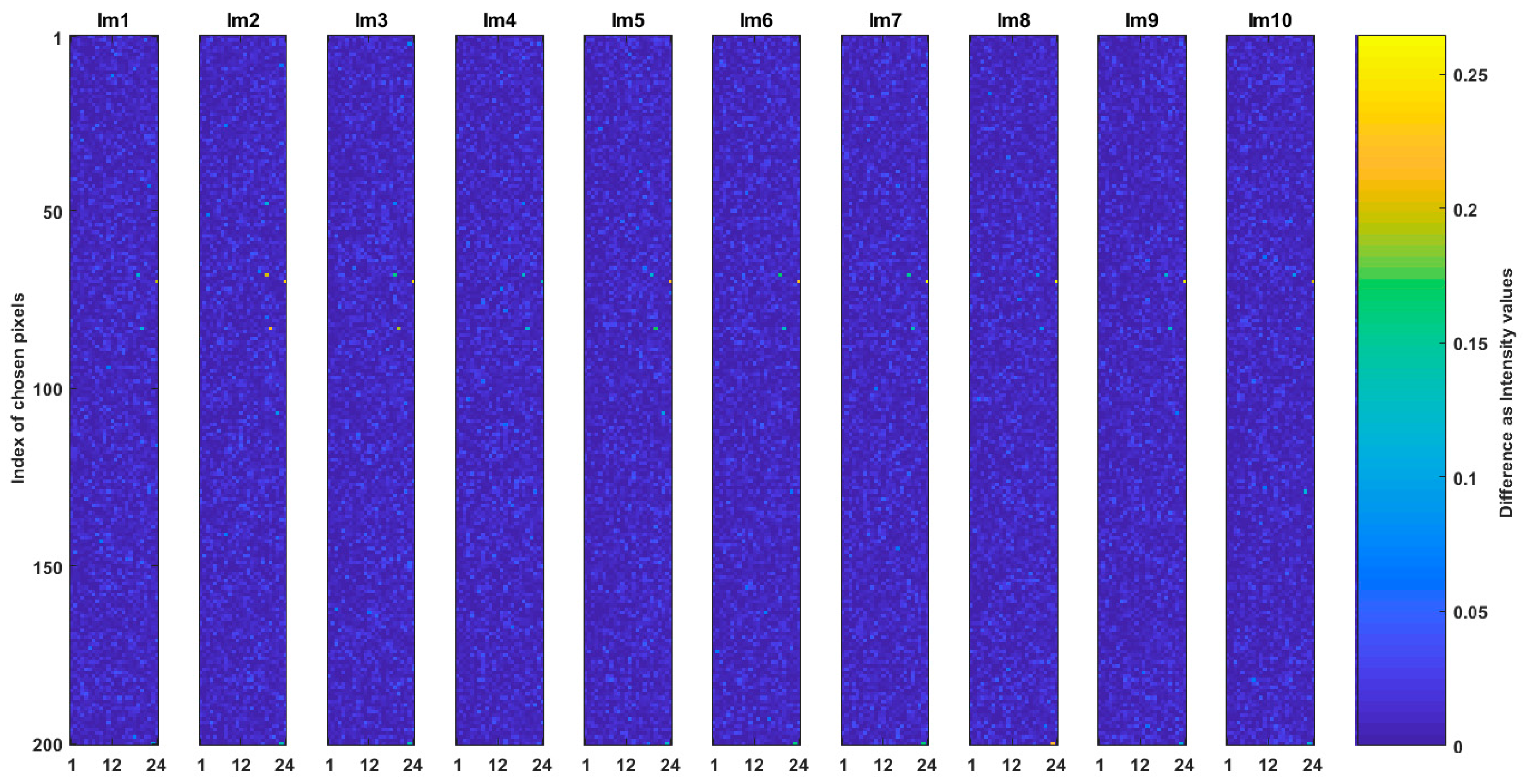
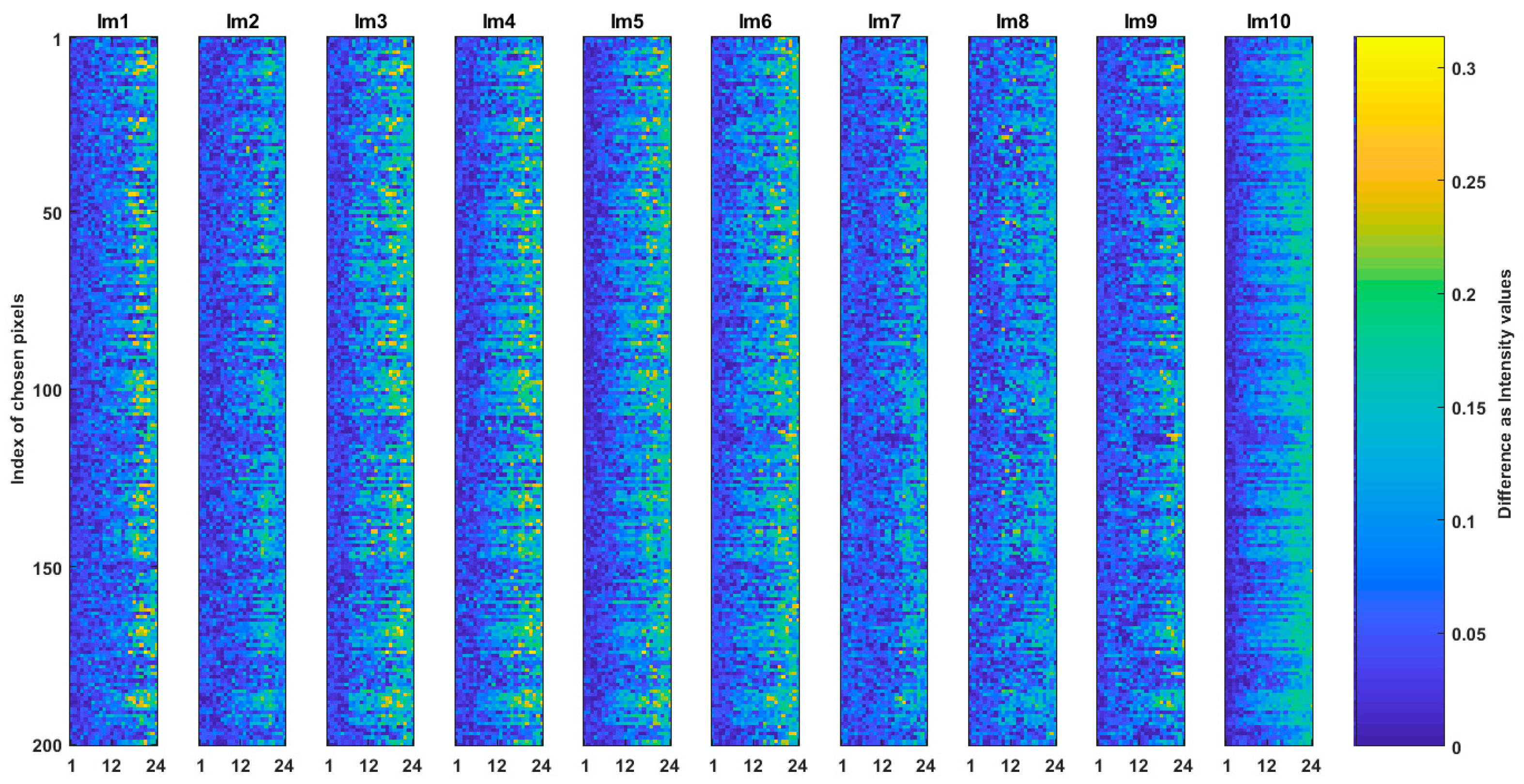
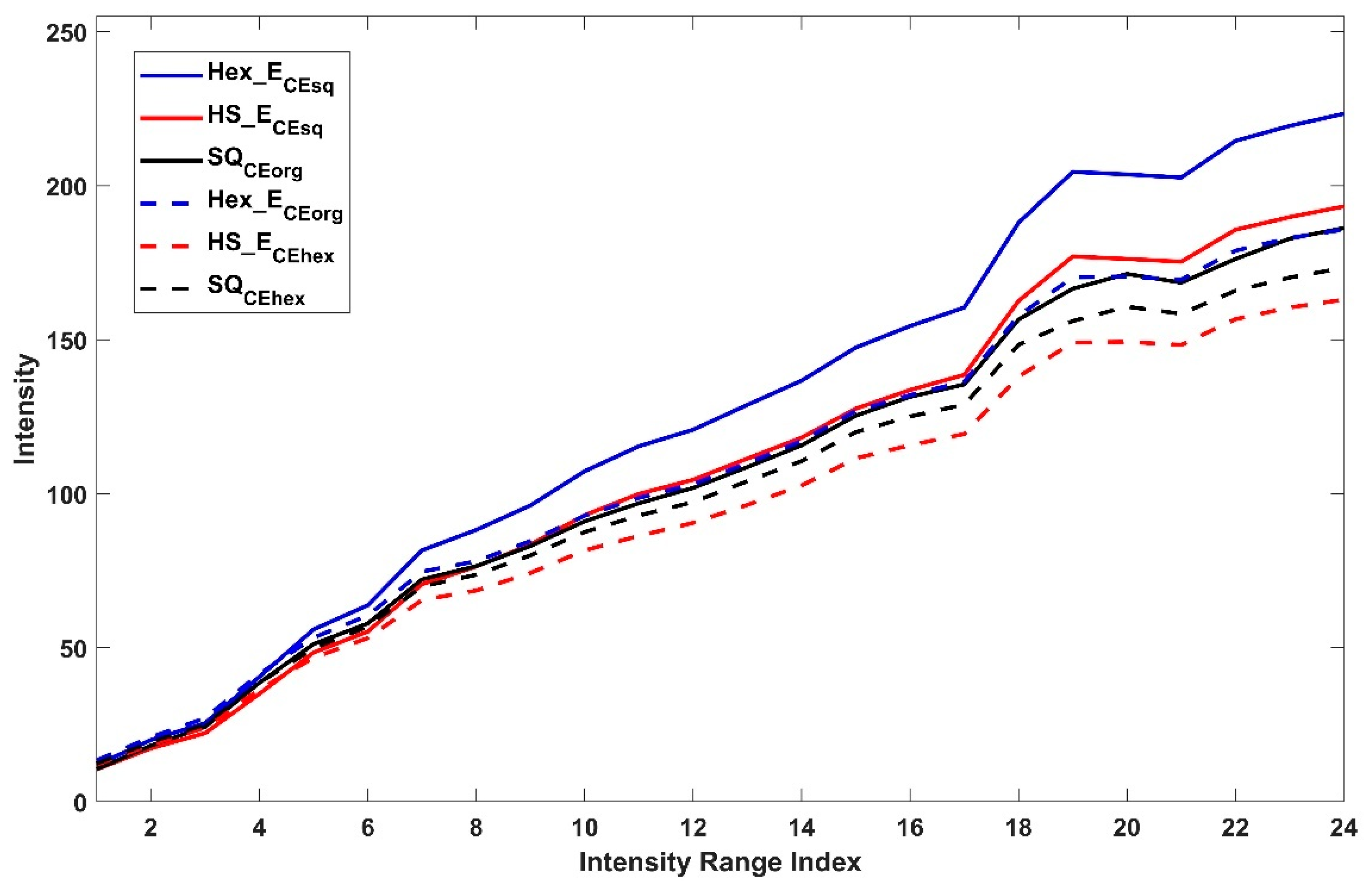
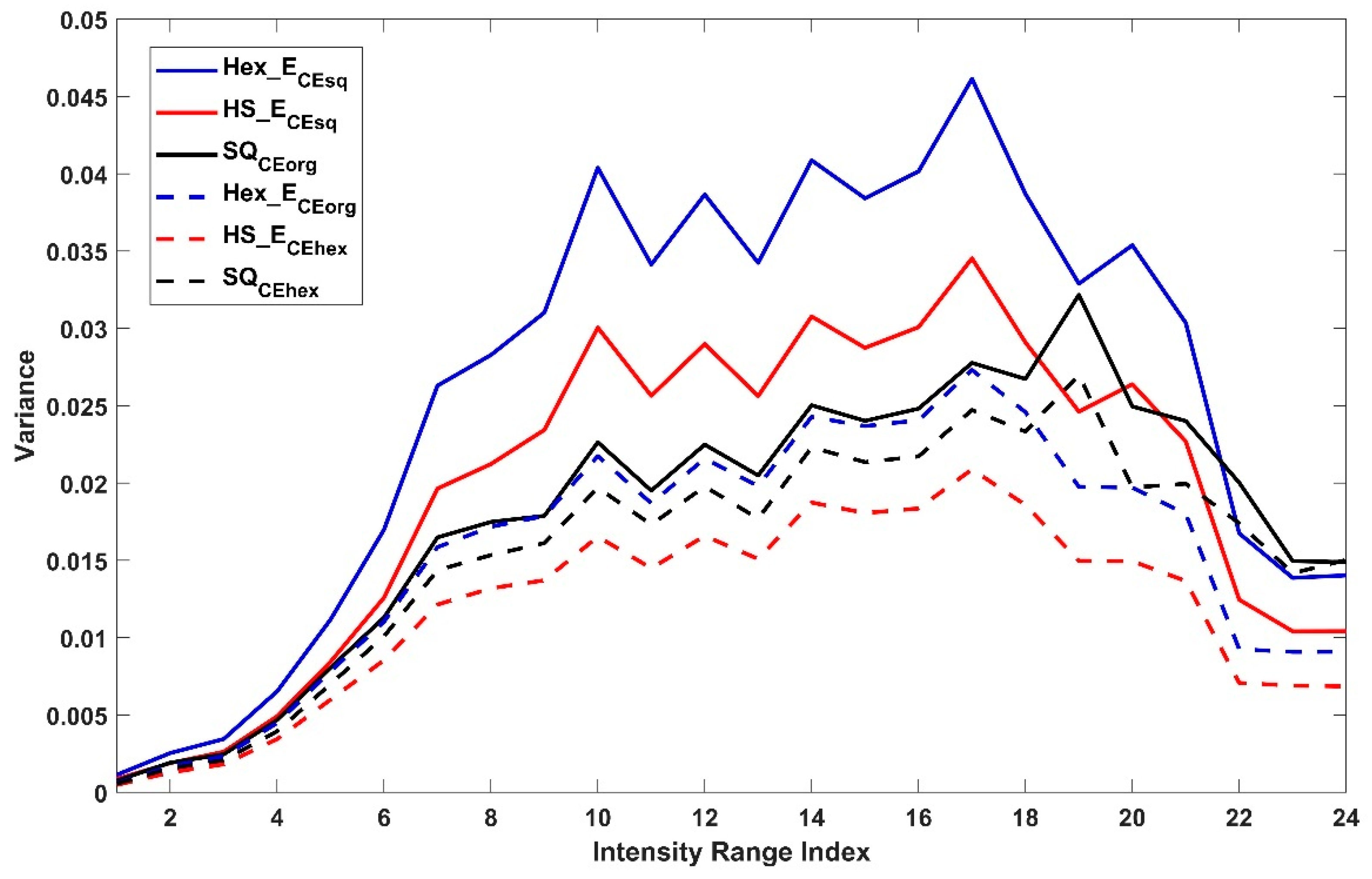
6. Results and Analysis
6.1. General Preparation
6.2. In Case of CSE_sq
6.3. In Case of CSE_hex
6.4. Analysis of the Two Cases
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
A.1. Root System
- Roots
- If , then : every root system contains only two scalar multiples of each root: the root itself and its reflection,
- : root system is closed under reflection with respect to hyperplanes orthogonal to roots. denotes reflection of root with respect to hyperplane orthogonal to root .
- all simple roots are linearly independent,
- every root , can be expressed as a linear combination of simple roots, such that all coefficients of this linear combinations are either all non-negative (such root is called positive root), or are all non-positive (negative root).
A.2. Weyl Groups
A.3. Orbit Functions and Orbit Transforms
A.4. Continuous Extension
References
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef] [Green Version]
- Lamb, T.D. Evolution of phototransduction, vertebrate photoreceptors and retina. Prog. Retinal Eye Res. 2013, 36, 52–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, W.; Khatibi, S. Back to basics: Towards novel computation and arrangement of spatial sensory in images. Acta Polytech. 2016, 56, 409–416. [Google Scholar] [CrossRef]
- Luczak, E.; Rosenfeld, A. Distance on a hexagonal grid. IEEE Trans. Comput. 1976, 25, 532–533. [Google Scholar] [CrossRef]
- Wüthrich, C.A.; Stucki, P. An algorithmic comparison between square- and hexagonal-based grids. CVGIP Graph. Models Image Process. 1991, 53, 324–339. [Google Scholar] [CrossRef]
- Snyder, W.E.; Qi, H.; Sander, W.A. Coordinate system for hexagonal pixels. In Proceedings of the Medical Imaging 1999: Image Processing, San Diego, CA, USA, 20–26 February 1999; Volume 3661, pp. 716–728. [Google Scholar]
- Her, I. A symmetrical coordinate frame on the hexagonal grid for computer graphics and vision. J. Mech. Des. 1993, 115, 447–449. [Google Scholar] [CrossRef]
- Her, I.; Yuan, C.-T. Resampling on a pseudohexagonal grid. CVGIP Graph. Models Image Process. 1994, 56, 336–347. [Google Scholar] [CrossRef]
- Her, I. Geometric transformations on the hexagonal grid. IEEE Trans. Image Process. 1995, 4, 1213–1222. [Google Scholar] [CrossRef] [PubMed]
- Nagy, B. Finding shortest path with neighbourhood sequences in triangular grids. In Proceedings of the 2nd International Symposium on Image and Signal Processing and Analysis (ISPA 2001), Pula, Croatia, 19–21 June 2001; pp. 55–60. [Google Scholar]
- Sheridan, P. Spiral Architecture for Machine Vision. Ph.D. Thesis, University of Technology Sydney, Sydney, Australia, 1996. [Google Scholar]
- He, X. 2D-Object Recognition with Spiral Architecture. Ph.D. Thesis, University of Technology Sydney, Sydney, Australia, 1999. [Google Scholar]
- Middleton, L.; Sivaswamy, J. Edge detection in a hexagonal-image processing framework. Image Vis. Comput. 2001, 19, 1071–1081. [Google Scholar] [CrossRef]
- Middleton, L.; Sivaswamy, J. Framework for practical hexagonal-image processing. J. Electron. Imaging 2002, 11, 104–115. [Google Scholar]
- Wu, Q.; He, S.; Hintz, T. Virtual Spiral Architecture. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications, Las Vegas, NV, USA, 21–24 June 2004. [Google Scholar]
- He, S.; Hintz, T.; Wu, Q.; Wang, H.; Jia, W. A new simulation of Spiral Architecture. In Proceedings of the International Conference on Image Processing, Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26–29 June 2006. [Google Scholar]
- Wen, W.; Khatibi, S. Novel Software-Based Method to Widen Dynamic Range of CCD Sensor Images. In Proceedings of the International Conference on Image and Graphics, Tianjin, China, 13–16 August 2015; pp. 572–583. [Google Scholar]
- Wen, W.; Khatibi, S. The Impact of Curviness on Four Different Image Sensor Forms and Structures. Sensors 2018, 18, 429. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Jia, W. Hexagonal Structure for Intelligent Vision. In Proceedings of the 2005 International Conference on Information and Communication Technologies, Karachi, Pakistan, 27–28 August 2005; pp. 52–64. [Google Scholar]
- Horn, B. Robot Vision; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Perlin, K. An image synthesizer. ACM SIGGRAPH Comput. Graph. 1985, 19, 287–296. [Google Scholar] [CrossRef]
- Parberry, I. Amortized noise. J. Comput. Graph. Tech. 2014, 3, 31–47. [Google Scholar]
- Asharindavida, F.; Hundewale, N.; Aljahdali, S. Study on hexagonal grid in image processing. In Proceedings of the 2012 International Conference on Information and Knowledge Management, Kuala Lumpur, Malaysia, 24–26 July 2012. [Google Scholar]






| 0. | Input |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | ) |
| 6. | |
| 7. | |
| 8. | ) |
| 9. | Output ) |
| Symbol | Full Name and Size | Sensor Arrangement | Originated from | Method |
|---|---|---|---|---|
| SQ | Square image 4096 × 2160 | square | - | - |
| Hex_E | Hexagonal enriched image 4096 × 2160 | hexagonal | SQ | Conversion |
| HS_E | Half-pixel shift image 4096 × 2160 | square | SQ | Conversion |
| Square matrix image 200 × 24 | square | SQ | Pixel selection on SQ | |
| Hexagonal enriched matrix image 200 × 24 | hexagonal | Hex_E | Pixel selection on Hex_E | |
| Half-pixel shift matrix image 200 × 24 | square | HS_E image | Pixel selection on HS_E | |
| CSE_sq | Common Space surface | continuous extension | SQ image | New method, see Section 4 |
| CSE_hex | Common Space surface | continuous extension | Hex_E image | New method, see Section 4 |
| Estimated Square matrix image 200 × 24 | square | CSE_sq | Pixel selection on the CSE_sq | |
| Estimated Hexagonal matrix image 200 × 24 | hexagonal | CSE_sq | Pixel selection on the CSE_sq | |
| Estimated Half-pixel shift matrix image 200 × 24 | square | CSE_sq | Pixel selection on the CSE_sq | |
| Estimated Square matrix image 200 × 24 | square | CSE_hex | Pixel selection on the CSE_hex | |
| Estimated Hexagonal matrix image 200 × 24 | hexagonal | CSE_hex | Pixel selection on the CSE_hex | |
| Estimated Half-pixel shift matrix image 200 × 24 | square | CSE_hex | Pixel selection on the CSE_hex |
| Image Index | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pair of Pixel Sets | No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | No.9 | No.10 | |
| Corre-lation | 99.63% | 99.63% | 99.62% | 99.61% | 99.66% | 99.64% | 99.63% | 99.63% | 99.61% | 99.63% | |
| 98.25% | 98.45% | 98.28% | 98.39% | 98.79% | 98.32% | 98.41% | 97.76% | 98.49% | 99.79% | ||
| 98.23% | 98.44% | 98.26% | 98.39% | 98.78% | 98.32% | 98.41% | 97.77% | 98.49% | 99.78% | ||
| MSE | 0.0024 | 0.0021 | 0.0038 | 0.0046 | 0.0040 | 0.0038 | 0.0038 | 0.0044 | 0.0039 | 0.0005 | |
| 0.0070 | 0.0054 | 0.0092 | 0.0085 | 0.0080 | 0.0091 | 0.0055 | 0.0065 | 0.0060 | 0.0080 | ||
| 0.0104 | 0.0080 | 0.0136 | 0.0125 | 0.0119 | 0.0135 | 0.0081 | 0.0095 | 0.0088 | 0.01193 | ||
| Image Index | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pair of Pixel Sets | No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | No.9 | No.10 | |
| Corre-lation | 98.19% | 98.17% | 98.00% | 98.00% | 97.96% | 97.89% | 98.02% | 97.96% | 97.99% | 98.07% | |
| 98.23% | 98.16% | 98.01% | 97.94% | 97.95% | 97.88% | 98.04% | 97.98% | 97.97% | 98.07% | ||
| 95.99% | 96.19% | 96.12% | 96.20% | 96.67% | 96.16% | 96.03% | 95.49% | 96.08% | 97.76% | ||
| 98.22% | 98.42% | 98.22% | 98.37% | 98.77% | 98.28% | 98.39% | 97.72% | 98.47% | 99.75% | ||
| 95.98% | 96.19% | 96.13% | 96.20% | 96.66% | 96.18% | 96.02% | 95.52% | 96.07% | 97.76% | ||
| 98.24% | 98.46% | 98.30% | 98.40% | 98.79% | 98.35% | 98.41% | 97.79% | 98.49% | 99.79% | ||
| 96.43% | 96.78% | 96.55% | 96.51% | 96.93% | 96.59% | 96.55% | 96.20% | 96.51% | 98.05% | ||
| 96.42% | 96.78% | 96.56% | 96.51% | 96.91% | 96.59% | 96.54% | 96.22% | 96.50% | 98.04% | ||
| 97.93% | 97.84% | 97.88% | 97.86% | 97.87% | 97.77% | 97.68% | 97.70% | 97.70% | 97.99% | ||
| 97.98% | 97.84% | 97.90% | 97.80% | 97.86% | 97.76% | 97.72% | 97.72% | 97.68% | 97.99% | ||
| 99.98% | 99.98% | 99.98% | 99.98% | 99.98% | 99.98% | 99.98% | 99.98% | 99.98% | 99.98% | ||
| 99.90% | 99.90% | 99.89% | 99.90% | 99.90% | 99.89% | 99.90% | 99.90% | 99.89% | 99.91% | ||
| MSE | 0.0044 | 0.0037 | 0.0072 | 0.0071 | 0.0075 | 0.0068 | 0.0039 | 0.0047 | 0.0043 | 0.0069 | |
| 0.9823 | 0.9816 | 0.9801 | 0.9794 | 0.9795 | 0.9788 | 0.9804 | 0.9798 | 0.9797 | 0.9807 | ||
| 0.0089 | 0.0080 | 0.0096 | 0.0100 | 0.0086 | 0.0100 | 0.0100 | 0.0107 | 0.0099 | 0.0032 | ||
| 0.0031 | 0.0027 | 0.0032 | 0.0029 | 0.0022 | 0.0031 | 0.0034 | 0.0036 | 0.0034 | 0.0012 | ||
| 0.0255 | 0.0236 | 0.0274 | 0.0283 | 0.0259 | 0.0283 | 0.0278 | 0.0288 | 0.0274 | 0.0120 | ||
| 0.0238 | 0.0204 | 0.0288 | 0.0274 | 0.0270 | 0.0287 | 0.0201 | 0.0220 | 0.0212 | 0.0279 | ||
| 0.0051 | 0.0048 | 0.0049 | 0.0050 | 0.0043 | 0.0049 | 0.0048 | 0.0052 | 0.0050 | 0.0030 | ||
| 0.0148 | 0.0148 | 0.0136 | 0.0131 | 0.0123 | 0.0141 | 0.0138 | 0.0137 | 0.0135 | 0.01257 | ||
| 0.0018 | 0.0020 | 0.0021 | 0.0019 | 0.0022 | 0.0021 | 0.0023 | 0.0023 | 0.0021 | 0.0078 | ||
| 0.0053 | 0.0064 | 0.0042 | 0.0051 | 0.0044 | 0.0046 | 0.0089 | 0.0083 | 0.0079 | 0.0029 | ||
| 0.0061 | 0.0061 | 0.0061 | 0.0061 | 0.0061 | 0.0061 | 0.0061 | 0.0061 | 0.0061 | 0.0061 | ||
| 0.0039 | 0.0040 | 0.0036 | 0.0036 | 0.0036 | 0.0036 | 0.0041 | 0.0040 | 0.0041 | 0.0035 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, W.; Kajínek, O.; Khatibi, S.; Chadzitaskos, G. A Common Assessment Space for Different Sensor Structures. Sensors 2019, 19, 568. https://doi.org/10.3390/s19030568
Wen W, Kajínek O, Khatibi S, Chadzitaskos G. A Common Assessment Space for Different Sensor Structures. Sensors. 2019; 19(3):568. https://doi.org/10.3390/s19030568
Chicago/Turabian StyleWen, Wei, Ondřej Kajínek, Siamak Khatibi, and Goce Chadzitaskos. 2019. "A Common Assessment Space for Different Sensor Structures" Sensors 19, no. 3: 568. https://doi.org/10.3390/s19030568
APA StyleWen, W., Kajínek, O., Khatibi, S., & Chadzitaskos, G. (2019). A Common Assessment Space for Different Sensor Structures. Sensors, 19(3), 568. https://doi.org/10.3390/s19030568





