A Two-Dimensional Adaptive Target Detection Algorithm in the Compressive Domain
Abstract
1. Introduction
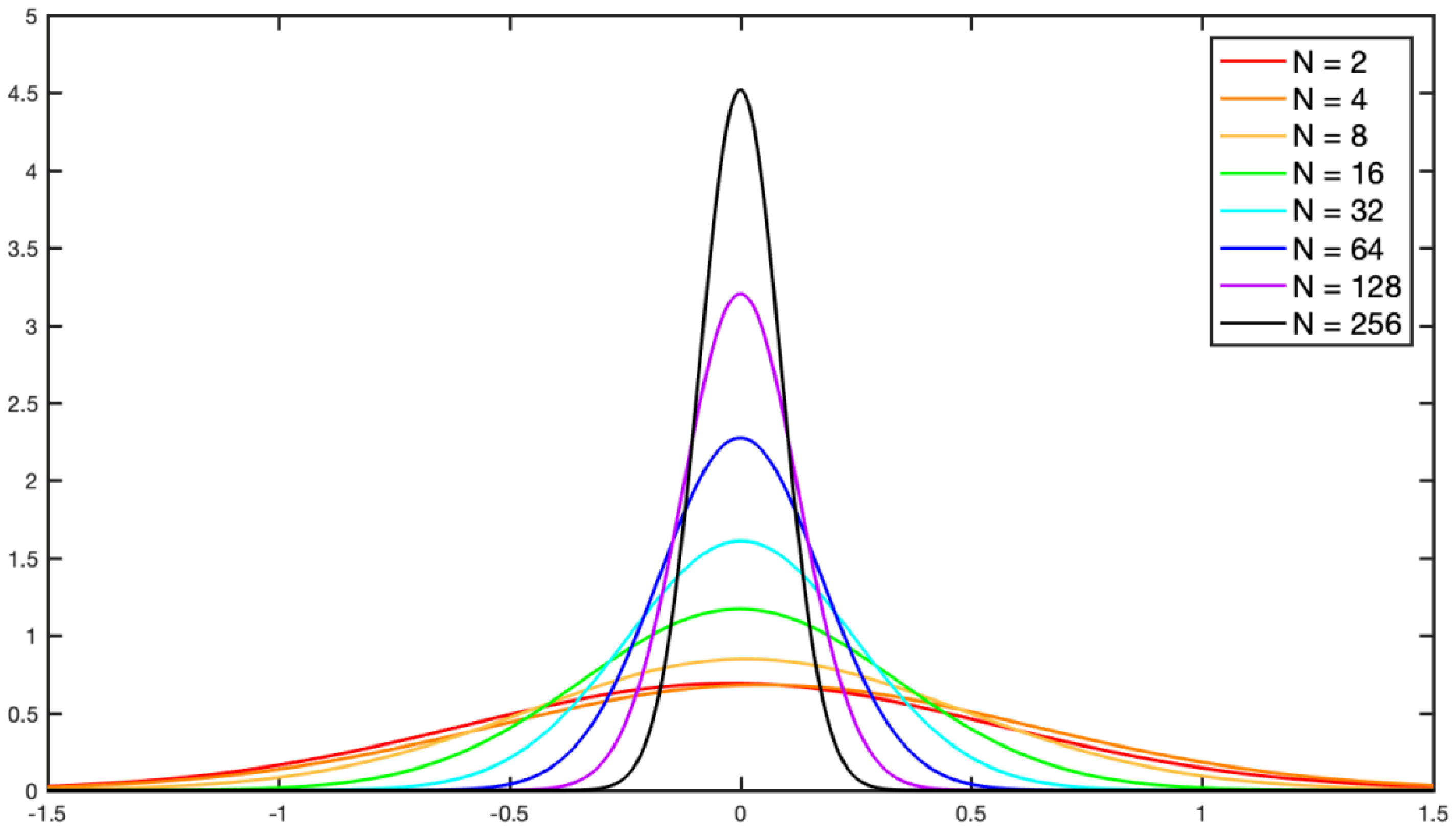
2. Compressive Sensing—The Basics
3. The 2D CDAT Target Detection Algorithm
3.1. Background Subtraction Method
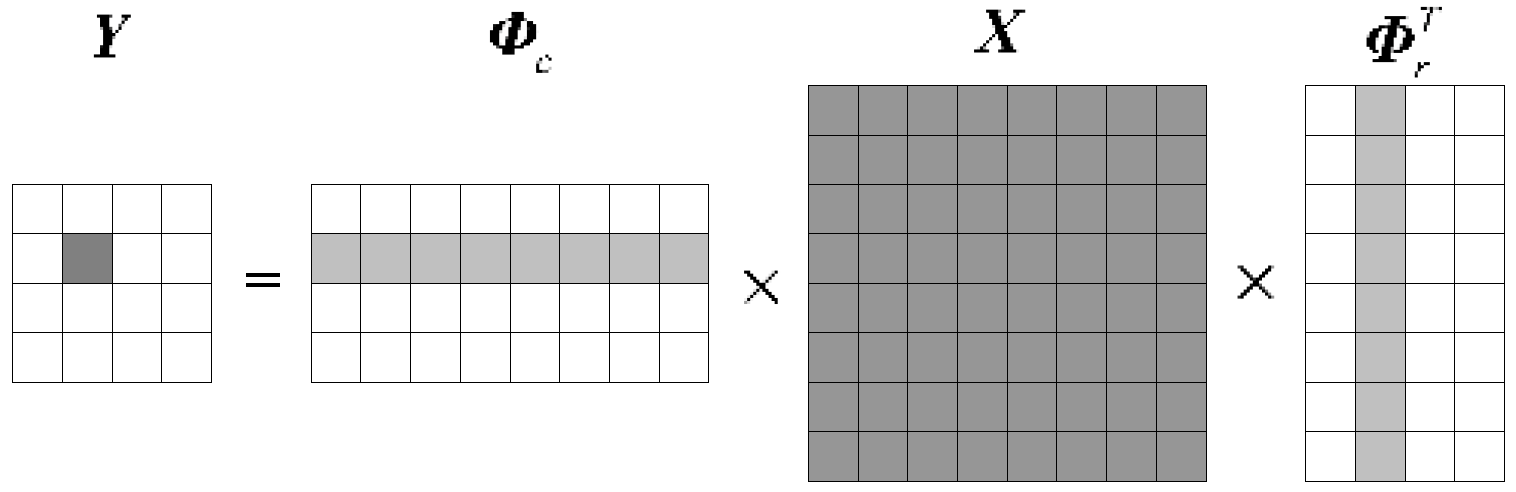
3.2. Mapping from the Compressive Domain to the Spatial Domain
3.3. Adaptive Threshold Partition
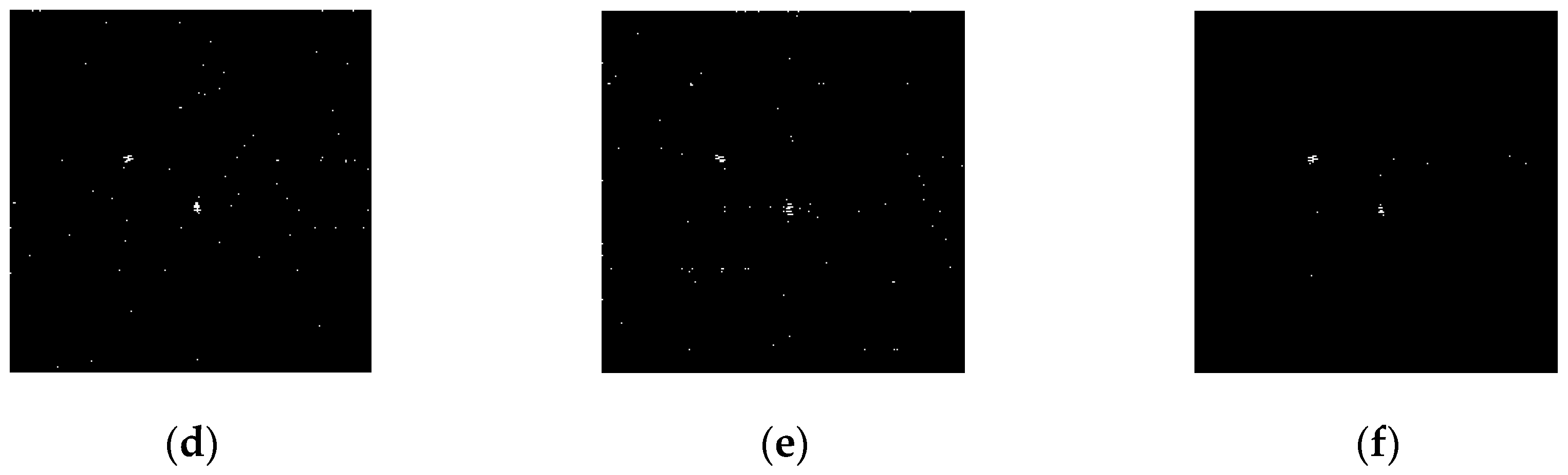
4. Simulation and Analysis
5. Conclusions
- (1)
- 2D CDAT was proposed to detect a target without reconstruction. Aiming at a 2D measurement model, the signal was mapped from the compressive domain to the spatial domain by directly using the characteristics of the Gram matrix, and the advanced adaptive threshold partition method was used to detect the target.
- (2)
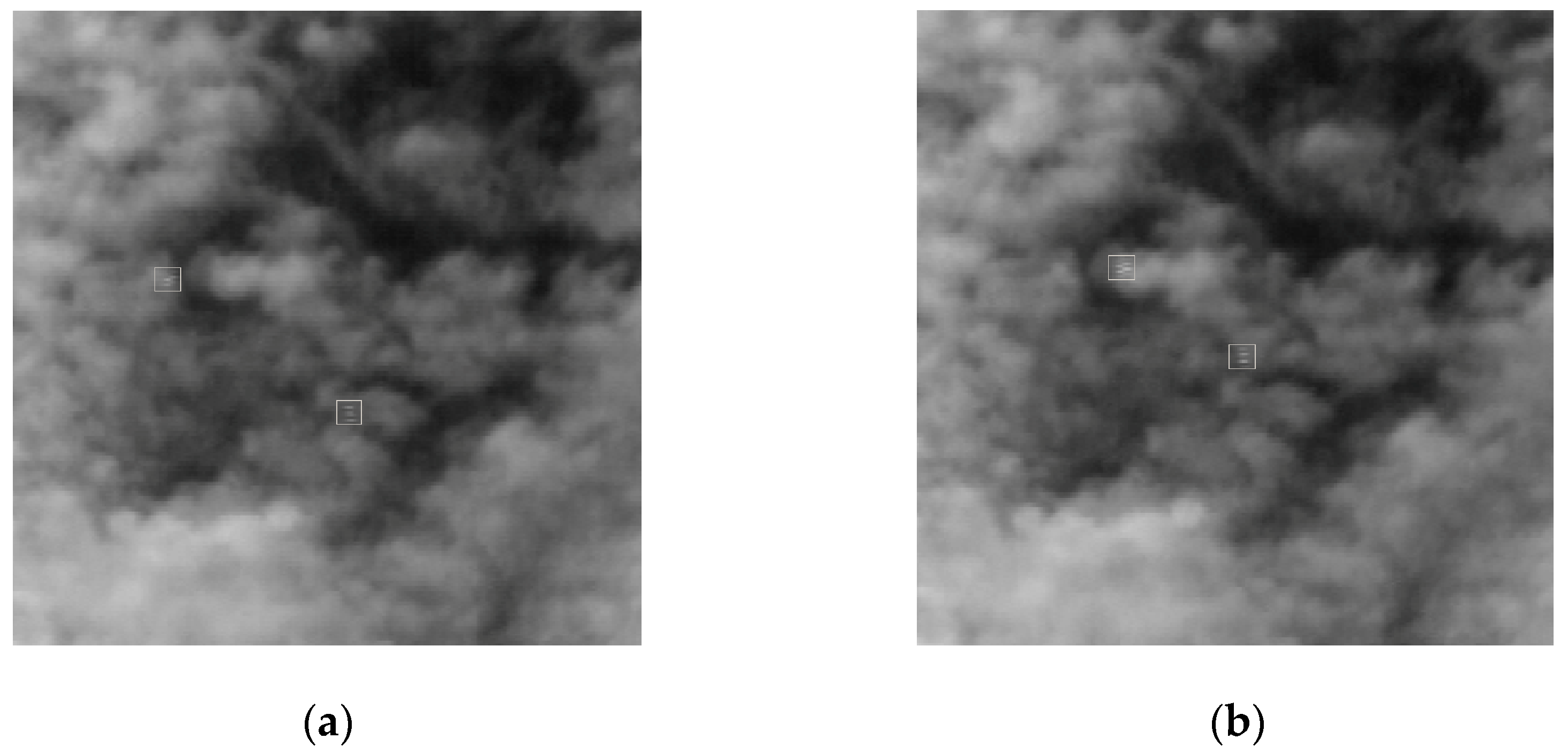
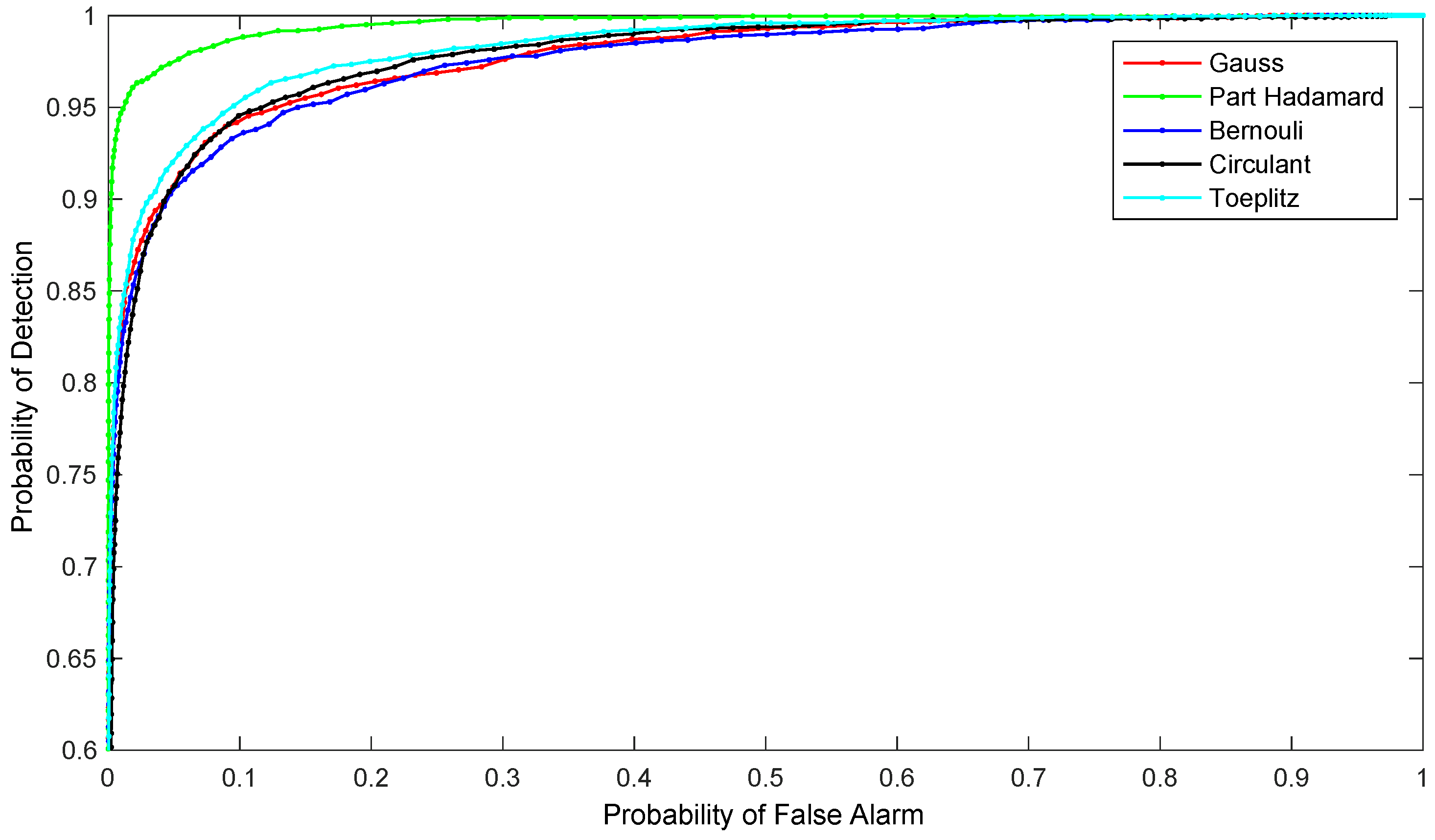
- Using real infrared images as the experimental data, the compressive subtracted images were mapped to the spatial domain using different measurement matrixes. Experiments showed that the decoded subtraction images produced higher SNR and SCR than the original images. The comparison of the mapping effect of the observation matrixes indicated that the subtraction images mapped by the Part Hadamard matrix achieved higher SNR, SCR, BSF, and AUC values, and better detection performance.
- (3)
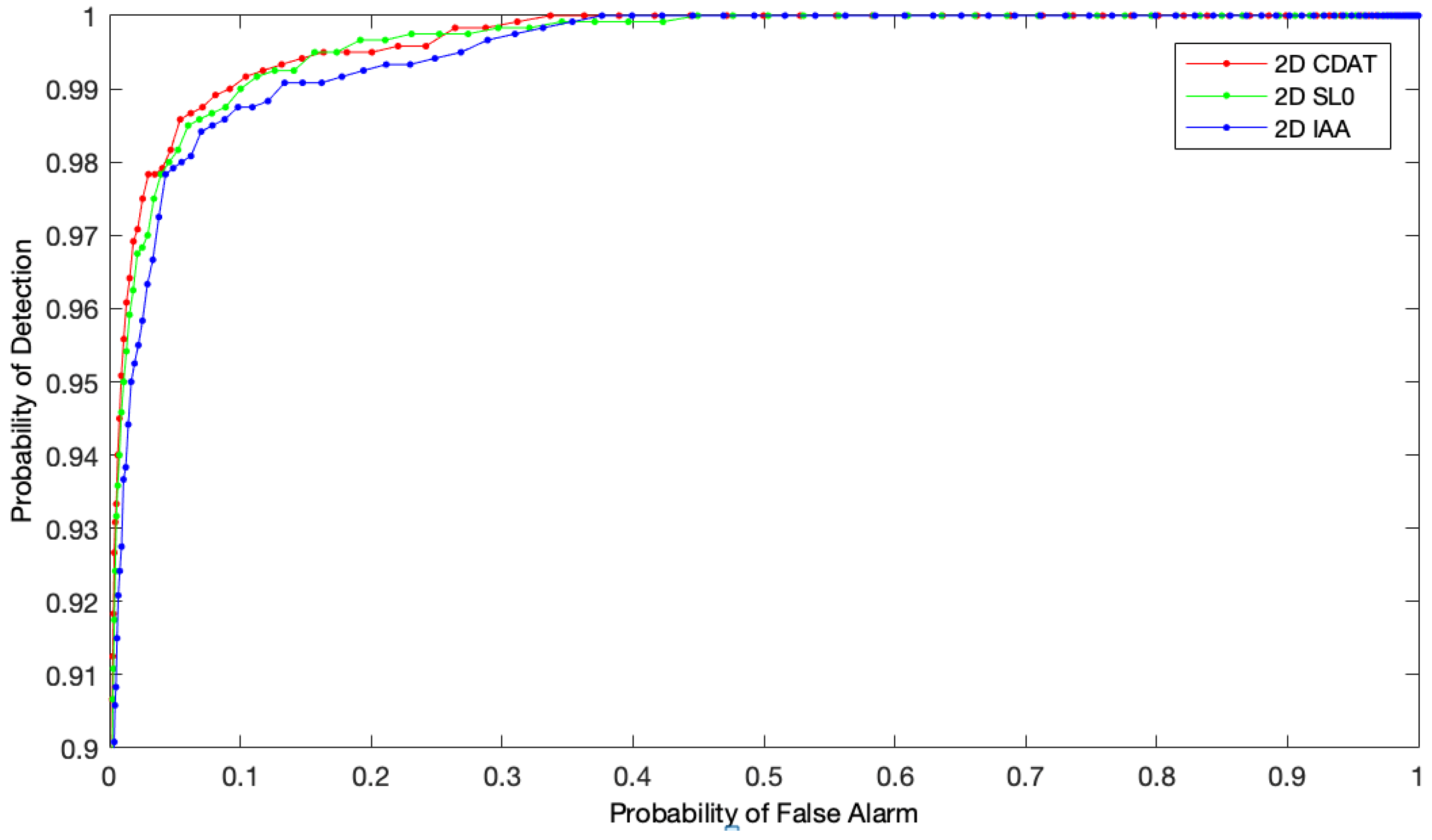
- Comparing the 2D CDAT algorithm with the traditional reconfiguration detection algorithms, three algorithms—2D CDAT, 2D IAA, and 2D SL0—were used to detect the target. The results showed that the 2D CDAT algorithm was superior to the other two algorithms in terms of operation time, AUC, SNR, and SCR, and that it could achieve more efficient target detection.
- (4)
- The proposed 2D CDAT algorithm can be used in remote sensing field to achieve a more efficient target detection. In the next step, we consider to apply the 2D CDAT algorithm to the target tracking issues.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jarvis, H.; Nowak, R. Compressive Sampling for Signal Detection. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing-ICASSP ‘07 IEEE, Honolulu, HI, USA, 15–20 April 2007. [Google Scholar]
- Haupt, J.; Castro, R.; Nowak, R.; Fudge, G.; Yeh, A. Compressive Sampling for Signal Classification. In Proceedings of the 2006 Fortieth Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 29 October–1 November 2006; 2007; pp. 1430–1434. [Google Scholar]
- Shujuan, G.; Insuk, K.; Seong, T.J. Sparse representation based target detection infrared image. Int. J. Energy Inf. Commun. 2013, 4, 21–28. [Google Scholar]
- Jahromi, M.J.; Kahaei, M.H. Two-Dimensional Iterative Adaptive Approach for Sparse Matrix Solution. Electron. Lett. 2014, 50, 45–47. [Google Scholar] [CrossRef]
- Ghafari, A.; Babaiezadeh, M.; Jutten, C. Sparse Decomposition of Two Dimensional Signals. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009. [Google Scholar]
- Van Den Berg, E.; Friedlander, M.P. “SPGL1: A Solver for Large-Scale Sparse Reconstruction”. June 2007. Available online: http://www.cs.ubc.ca/mpf/spgl1 (accessed on 14 April 2013).
- Rivenson, Y.; Wu, Y.; Wang, H.; Zhang, Y.; Feizi, A.; Ozcan, A. Sparsity-based multi-height phase recovery in holographic microscopy. Sci. Rep. 2016, 6, 37862. [Google Scholar] [CrossRef] [PubMed]
- Fournier, C.; Jolivet, F.; Denis, L.; Verrier, N.; Thiebaut, E.; Allier, C.; Fournel, T. Pixel super-resolution in digital holography by regularized reconstruction. Appl. Opt. 2017, 56, 69–77. [Google Scholar] [CrossRef]
- Xiong, Z.; Melzer, J.E.; Garan, J.; McLeod, E. Optimized sensing of sparse and small targets using lens-free holographic microscopy. Opt. Express 2018, 26, 25676–25692. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Xu, P.; Gao, Y. Optimization of the Measurement Matrix Used for CS-based Non-Reconstruction Detection Method in Cognitive Radio. In Proceedings of the 2014 Fourth International Conference on Instrumentation & Measurement, Computer, Communication and Control, Harbin, China, 18–20 September 2014; pp. 484–488. [Google Scholar]
- Xu, W.; Yan, Z.; Tian, Y.; Cui, Y.; Lin, J. Detection with Compressive Measurements Corrupted by Sparse Errors. In Proceedings of the 2017 9th International Conference on Wireles Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017. [Google Scholar]
- Li, S.; Liang, S.; Zhang, K.; Dong, M.; Yan, J. Research of Infrared Compressive Imaging Based Point Target Tracking Method. J. Electron. Inf. Technol. 2015, 37, 1639–1645. [Google Scholar]
- Candes, E.J. Compressive sampling. In Proceedings of the International Congress of Mathematicians, Madrid, Spain, 22–30 August 2006; pp. 1433–1452. [Google Scholar]
- Tian, W.; Rui, G.; Zhang, H.; Wang, L. A 2-Dimensional Measurement Model-Oriented Compressed Sensing Reconfiguration Algorithm. J. Astronaut. 2014, 35, 1072–1077. [Google Scholar]
- Mahalanobis, A.; Muise, R.; Roy, S. Efficient Target Detection Using an Adaptive Compressive Imager. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2528–2540. [Google Scholar] [CrossRef]
- Zhang, B.; Fadili, J.M.; Starck, J.L. Wavelets, ridgelets and curvelets for Poisson noise removal. IEEE Trans. Image Process. 2008, 17, 1093–1108. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Krolak, P.; Steele, C. The generalized Gabor transform. IEEE Trans. Image Process. 1995, 4, 978–988. [Google Scholar] [PubMed]
- Granai, L.; Vandergheynst, P. Sparse decomposition over multi-component redundant dictionaries. In Proceedings of the IEEE 6th Workshop on Multimedia Signal Processing, Siena, Italy, 29 September–1 October 2004; pp. 494–497. [Google Scholar]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Yang, J.; Liu, L.; Qu, X. Compressive Sensing and Its Applications; National Defence Industry Press: Beijing, China, 2015; Volume 10, pp. 6–70. [Google Scholar]
- Zhong, Y.; Wu, X.; Huang, S.; Li, C. Sensitivity analysis of SNR model for satellite-based infrared detector. Infrared Technol. 2014, 36, 582–587. [Google Scholar]



| Parameter | Details | Parameter | Details |
|---|---|---|---|
| Wide field of view | 13.75 × 11° | Charge-coupled device (CCD) | 480 × 640 |
| Narrow field of view | 2.29 × 1.83° | Frame frequency | 50 Hz |
| Pixel size | 30 × 30 μm | Power | 28 W |
| Focal length | 40–240 mm | Noise equivalent temperature difference (NETD) | ≤35 mK |
| Working waveband | 3–5 μm | Minimum resolvable temperature difference (MRTD) | ≤0.3 K |
| Image | Signal-to-Noise Ratio (SNR) | Signal Clutter Ratio (SCR) | Background Suppression Factor (BSF) | Area Under the Curve (AUC) |
|---|---|---|---|---|
| 2980th frame image | 1.038 | 0.169 | — | — |
| Gauss | 4.888 | 1.016 | 46.18 | 0.9779 |
| Part Hadamard | 8.307 | 1.064 | 103.25 | 0.9966 |
| Bernouli | 4.415 | 1.021 | 45.62 | 0.9757 |
| Circulant | 7.027 | 1.015 | 40.58 | 0.9781 |
| Toeplitz | 4.483 | 1.035 | 57.13 | 0.9827 |
| Algorithms | Operation Time (s) | AUC | SNR | SCR | BSF |
|---|---|---|---|---|---|
| 2D CDAT | 0.26 | 0.9966 | 8.307 | 1.064 | 103.25 |
| 2D SL0 | 8.24 | 0.9962 | 7.641 | 1.009 | 1.54 × 103 |
| 2D IAA | 13.93 | 0.9950 | 6.619 | 1.007 | 780.66 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Huang, S. A Two-Dimensional Adaptive Target Detection Algorithm in the Compressive Domain. Sensors 2019, 19, 567. https://doi.org/10.3390/s19030567
Cao W, Huang S. A Two-Dimensional Adaptive Target Detection Algorithm in the Compressive Domain. Sensors. 2019; 19(3):567. https://doi.org/10.3390/s19030567
Chicago/Turabian StyleCao, Wenhuan, and Shucai Huang. 2019. "A Two-Dimensional Adaptive Target Detection Algorithm in the Compressive Domain" Sensors 19, no. 3: 567. https://doi.org/10.3390/s19030567
APA StyleCao, W., & Huang, S. (2019). A Two-Dimensional Adaptive Target Detection Algorithm in the Compressive Domain. Sensors, 19(3), 567. https://doi.org/10.3390/s19030567





