A Clutter-Analysis-Based STAP for Moving FOD Detection on Runways
Abstract
1. Introduction
2. Scattering Cells
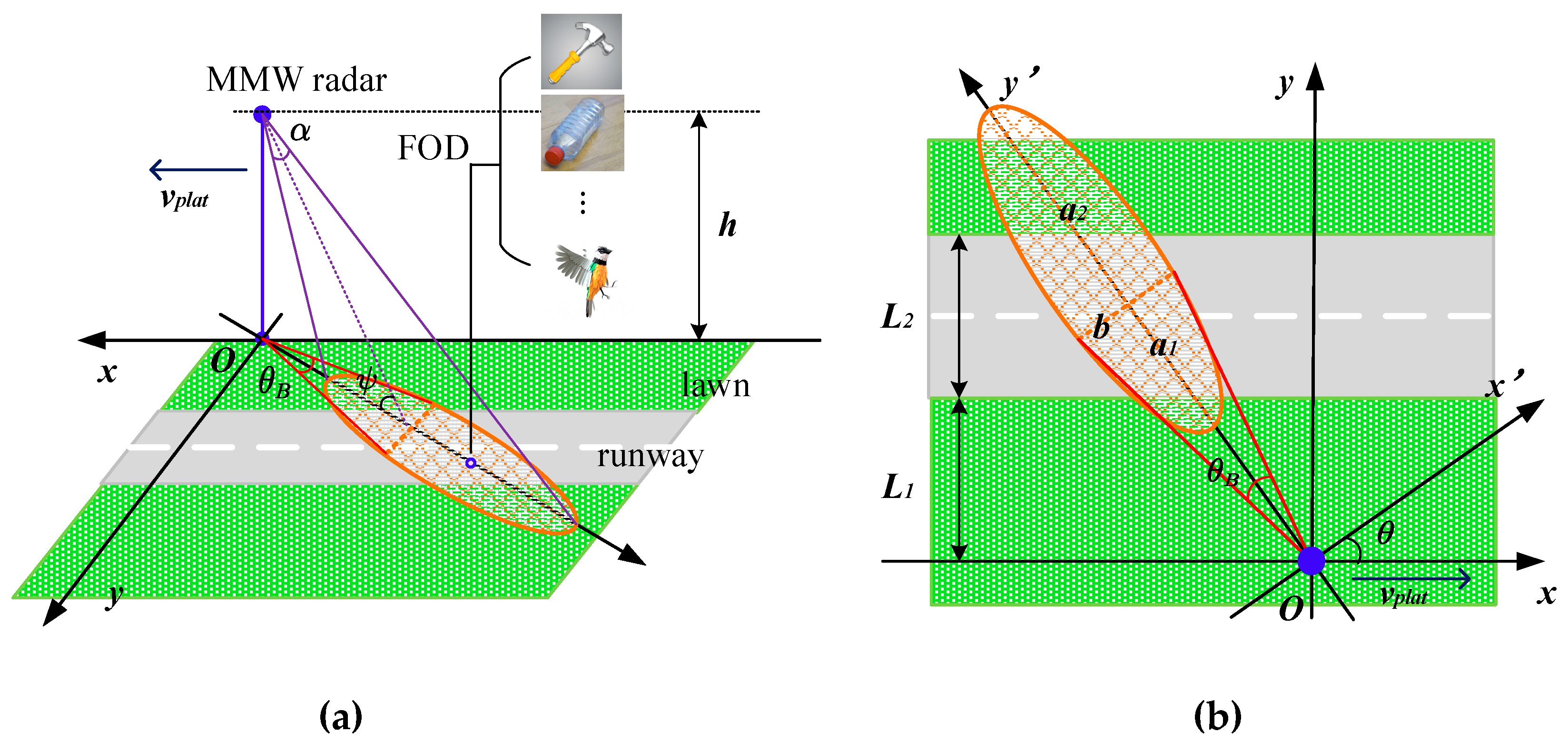
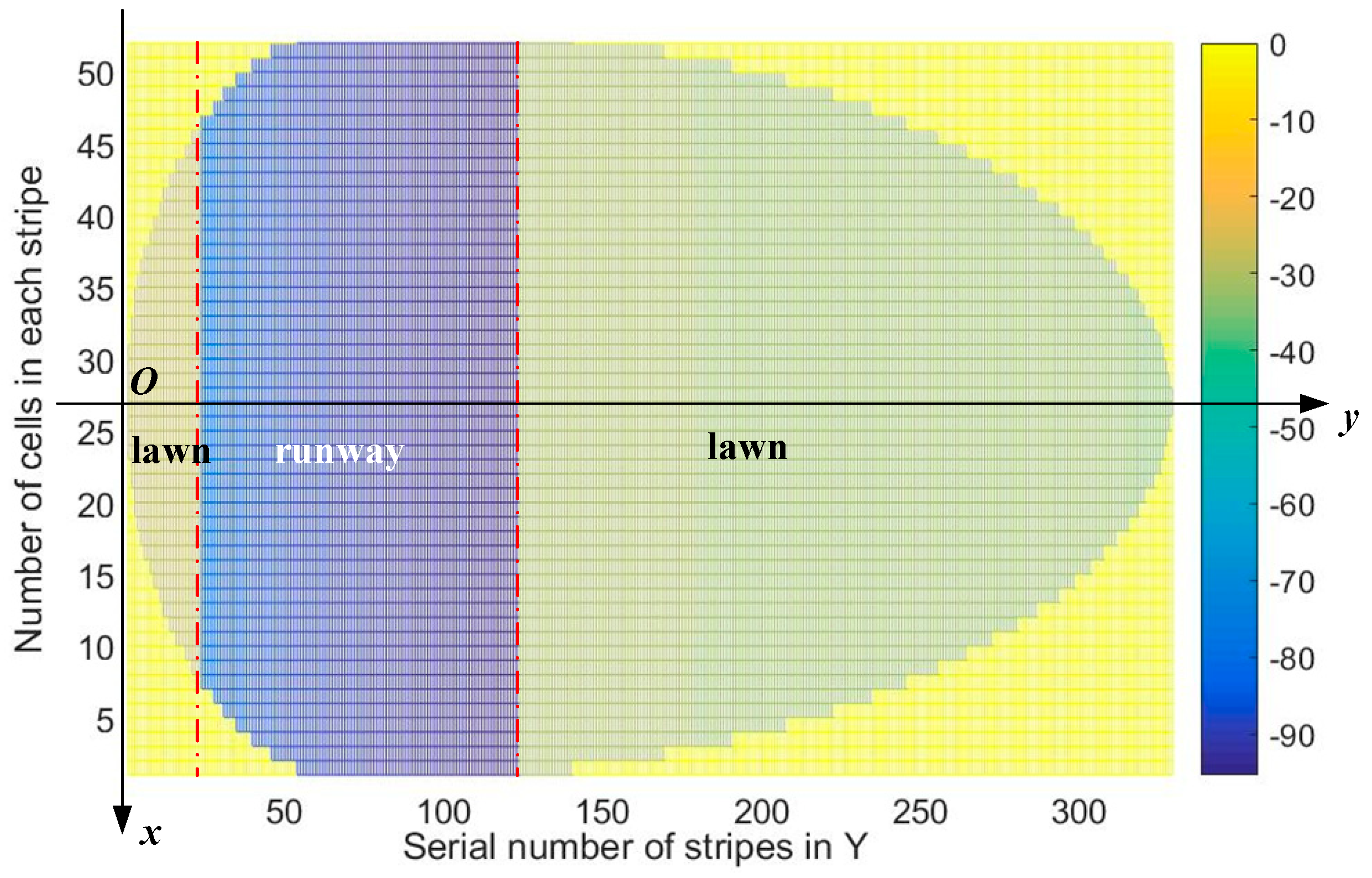
2.1. Geometric Model of Scene
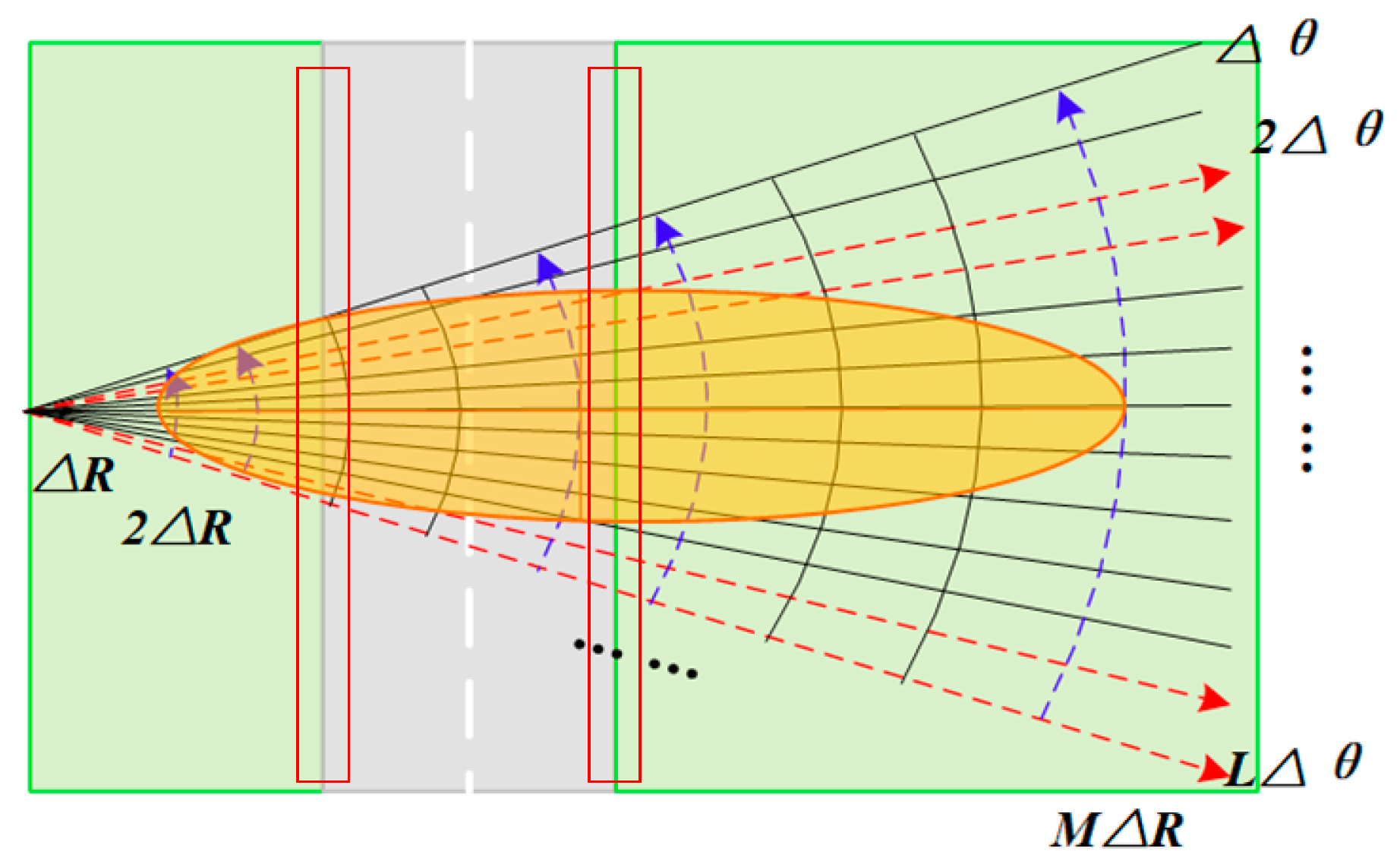
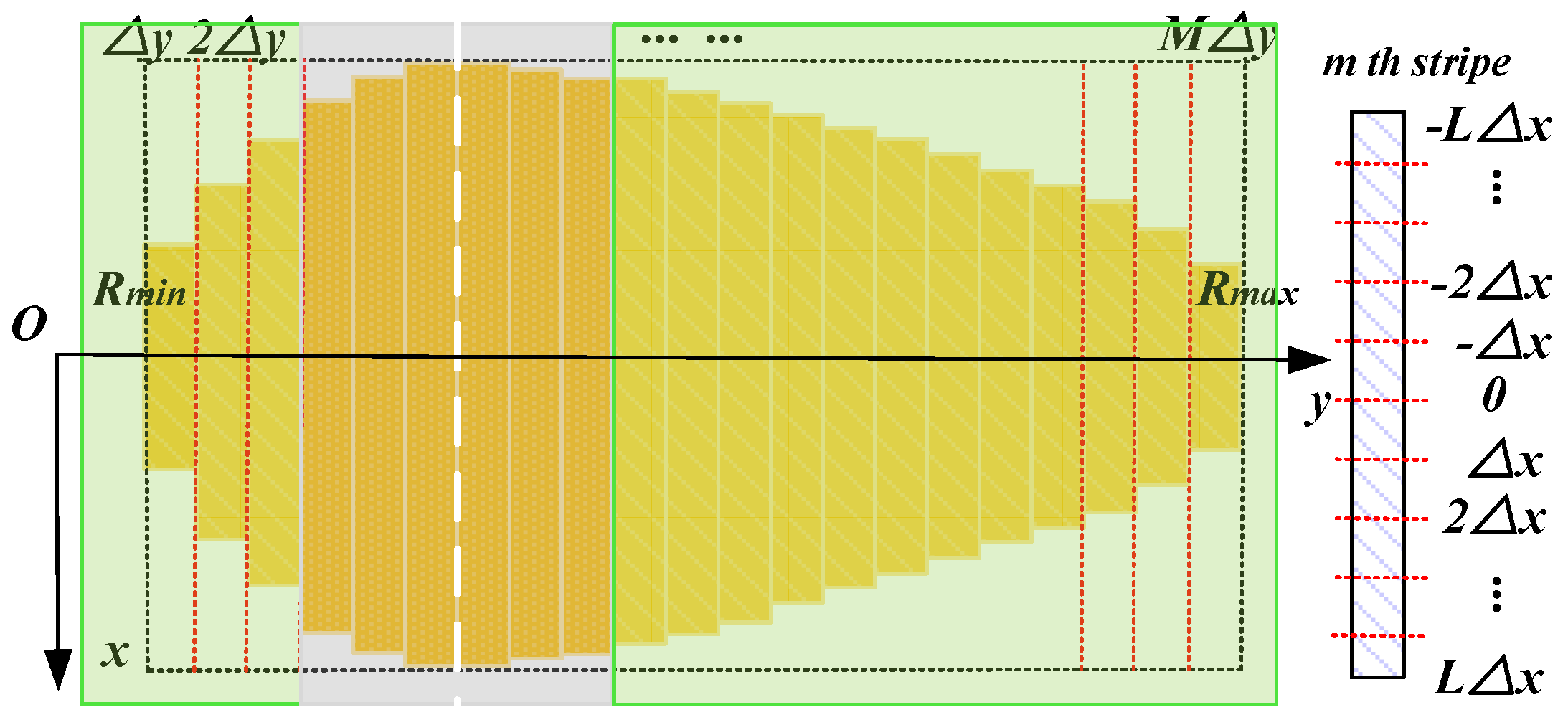
2.2. Scattering Cell Dividing
3. Ground Clutter Deduction
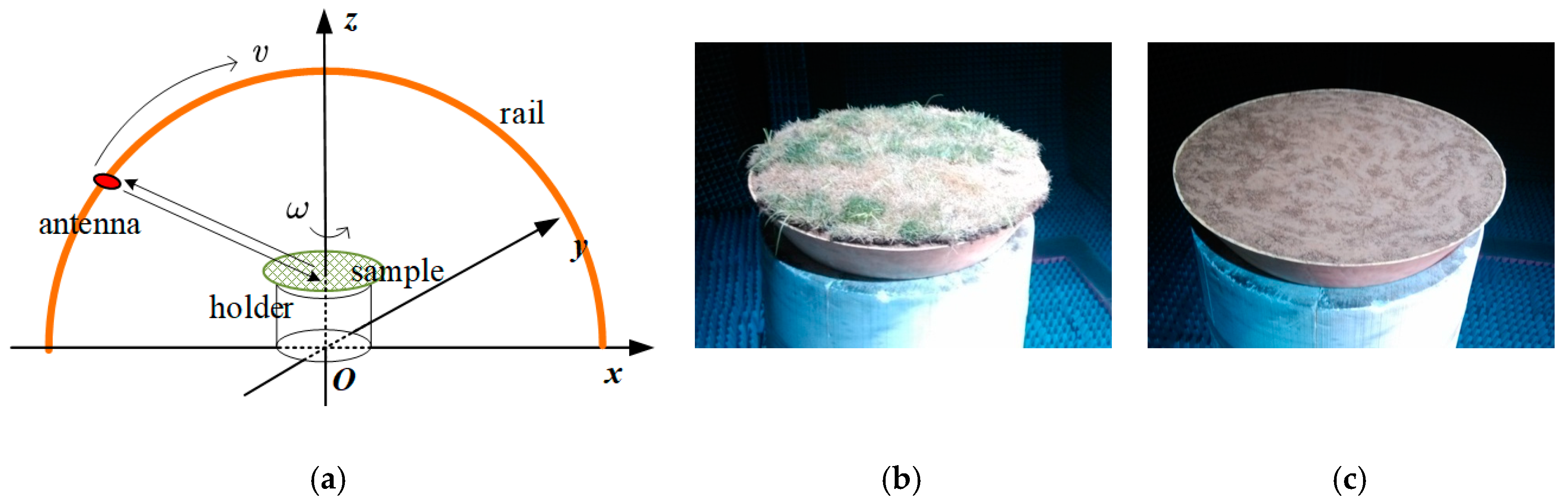
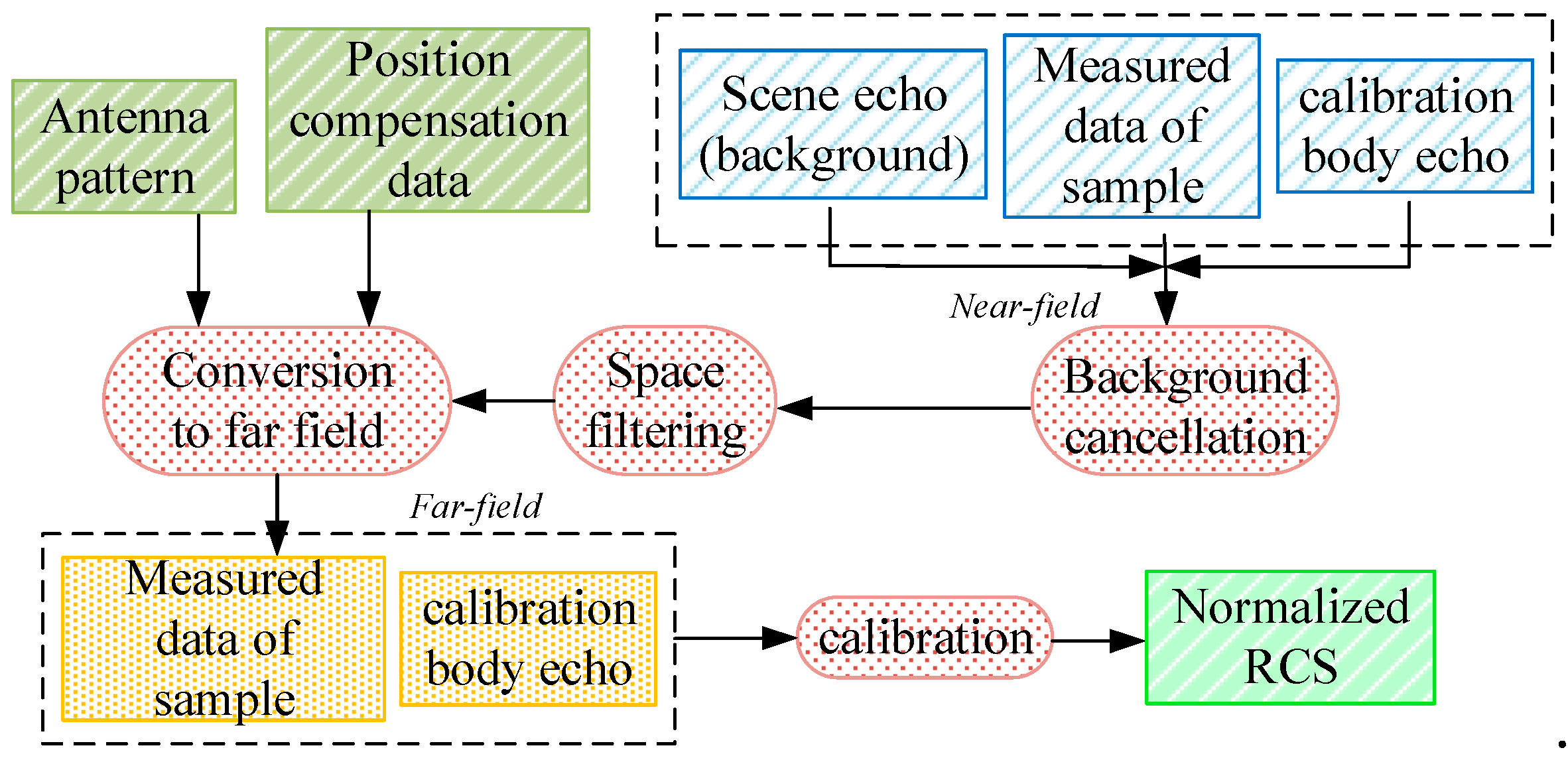
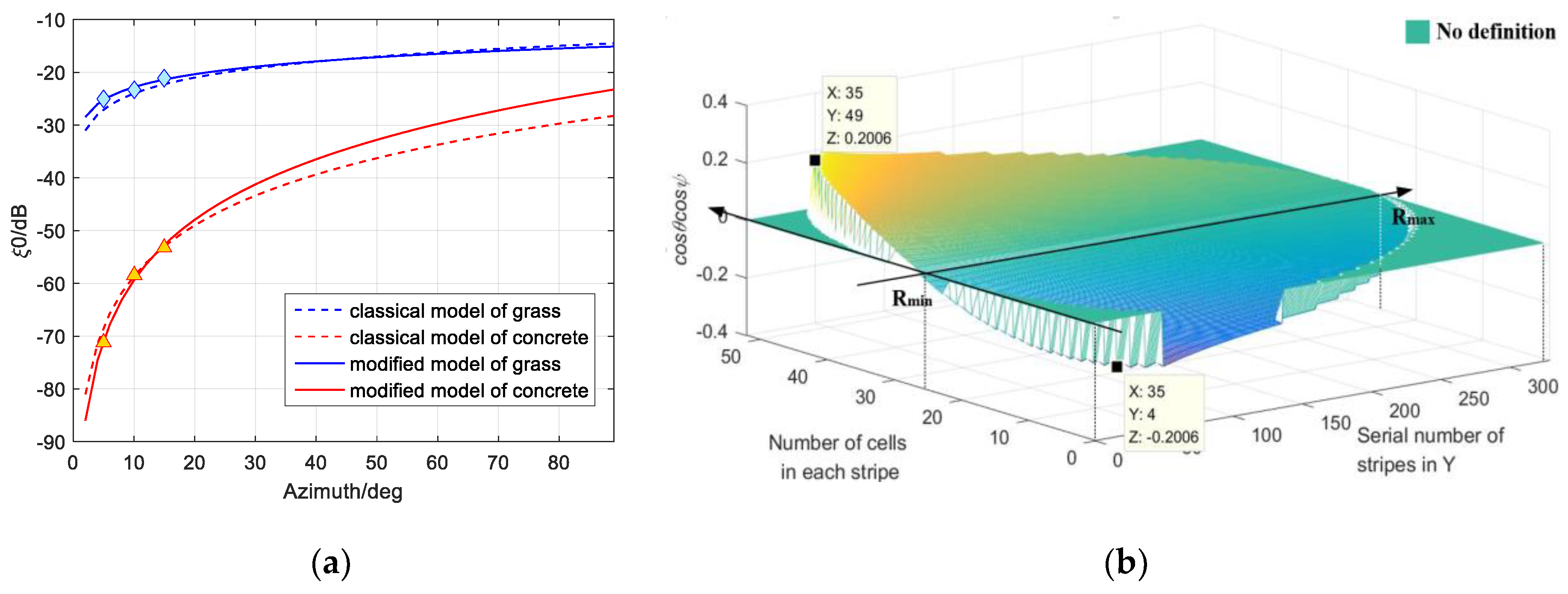
3.1. Test-based Kulemin Model
3.2. Space-time Coupled Clutter
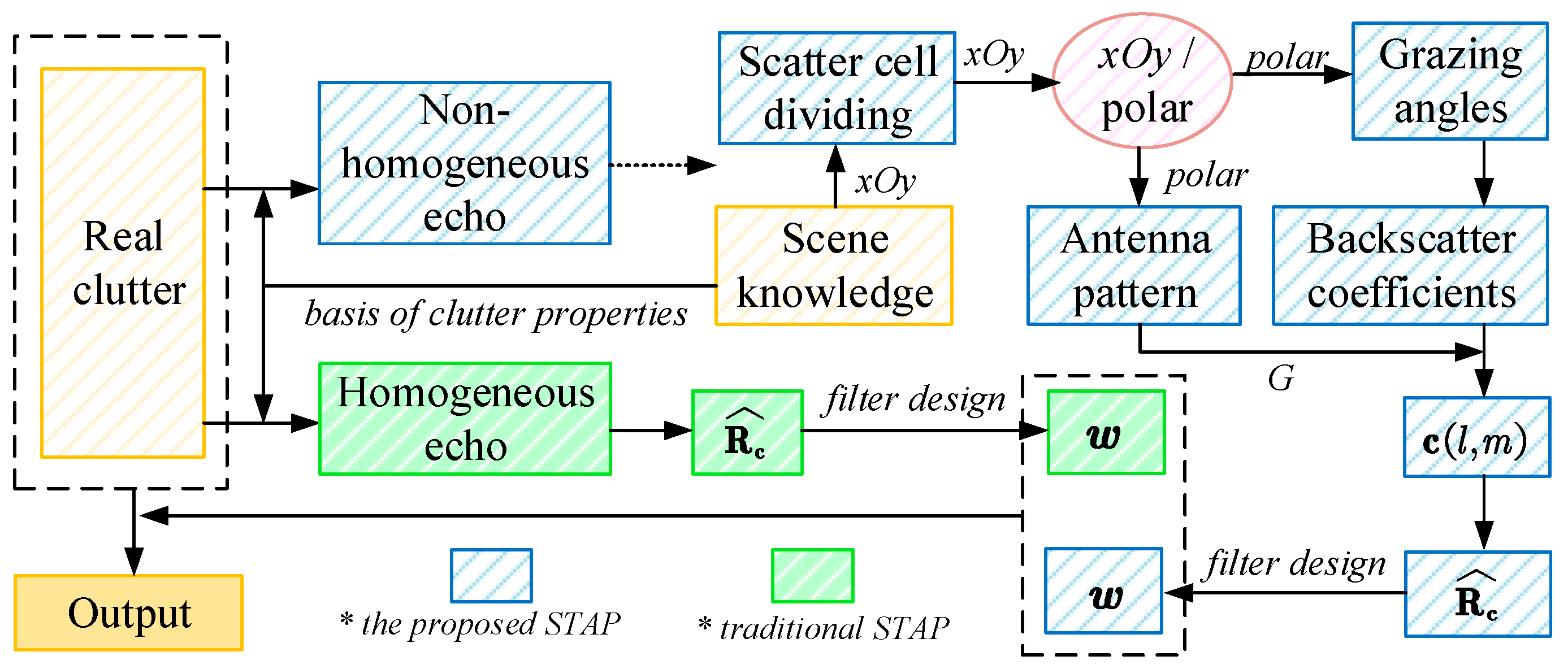
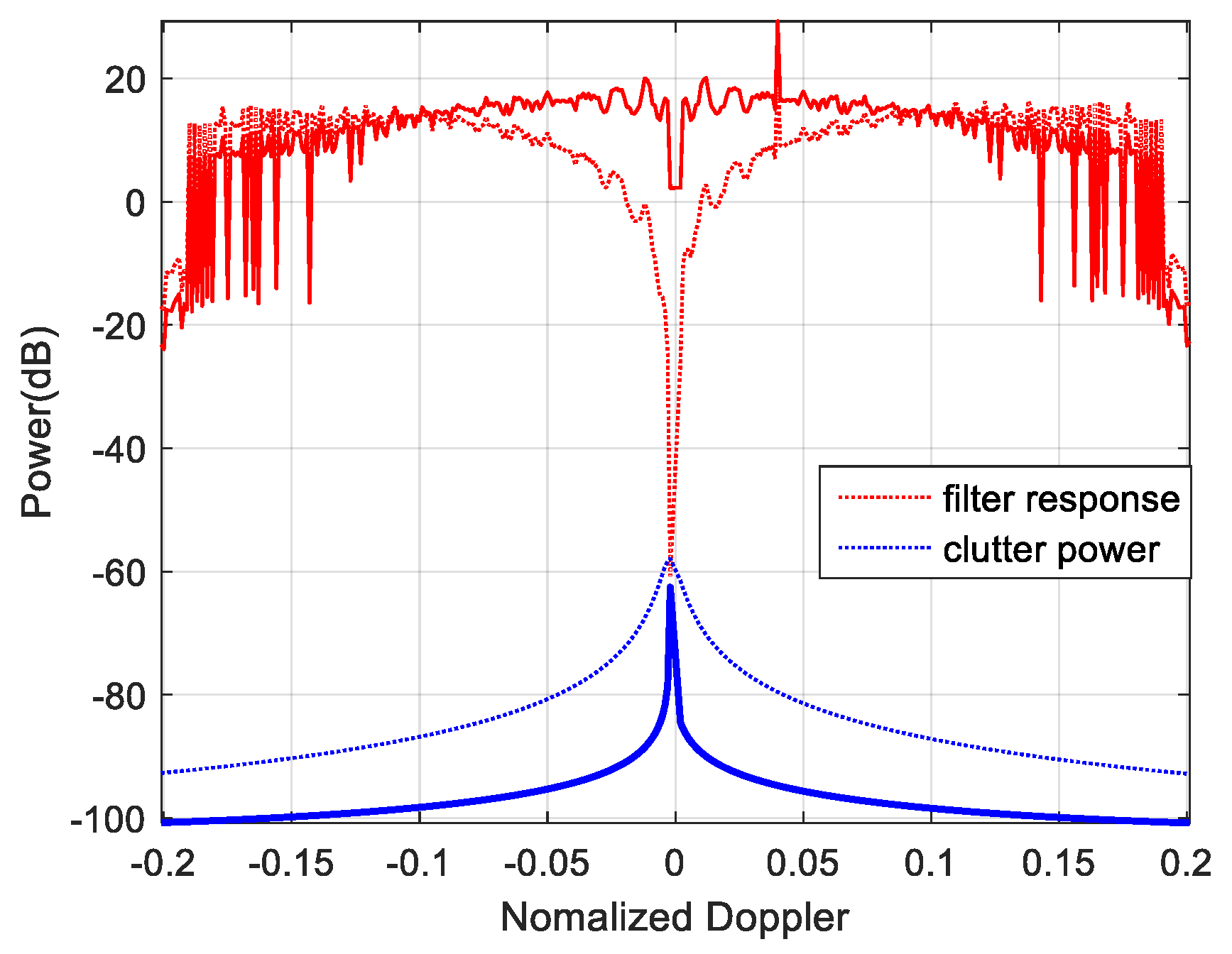
4. Clutter-Analysis-Based STAP
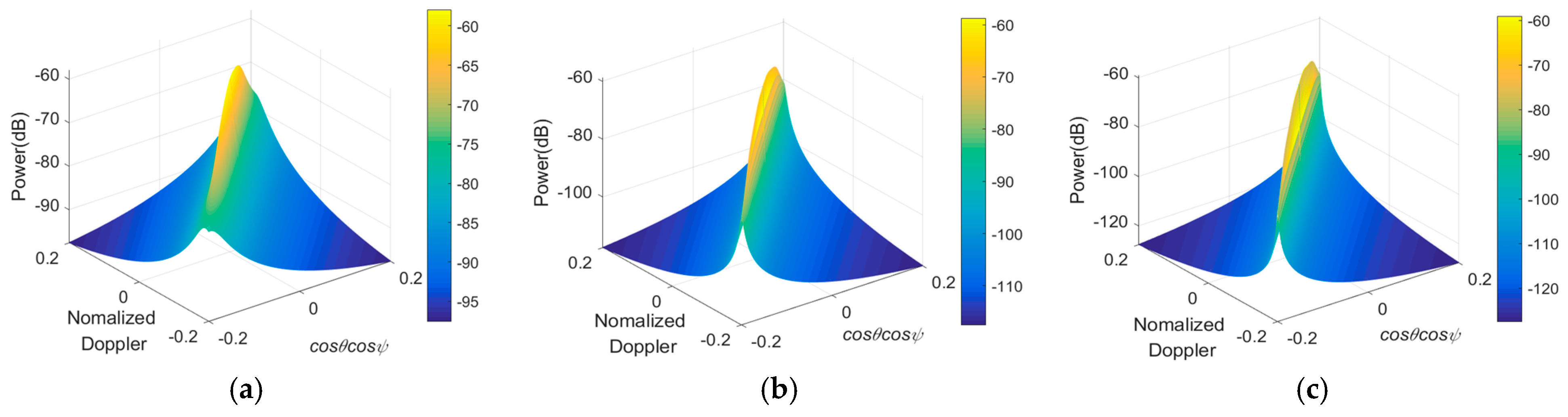
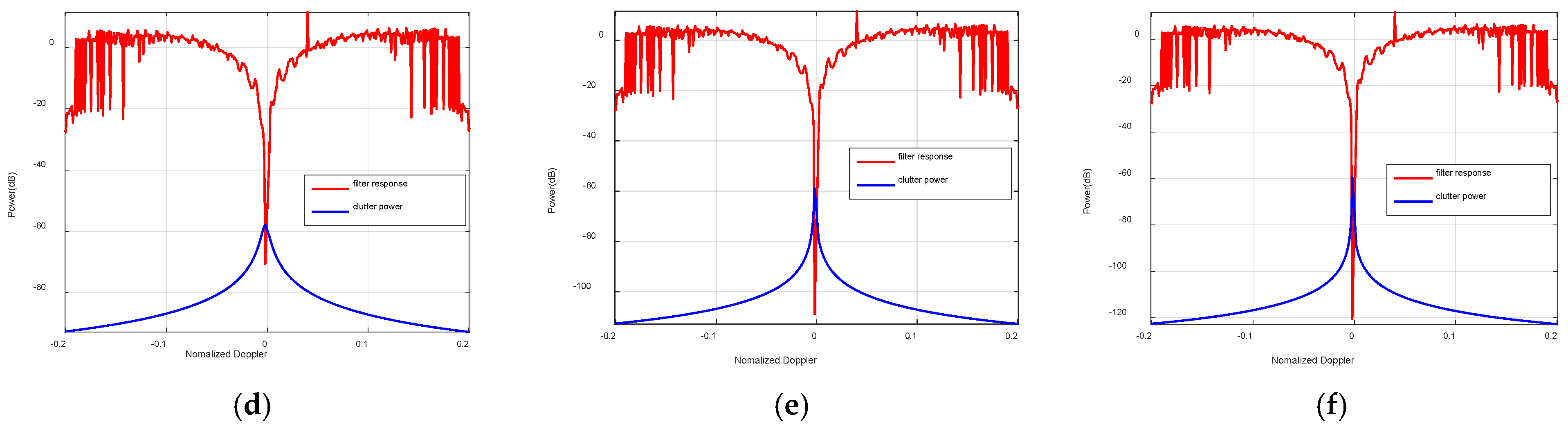
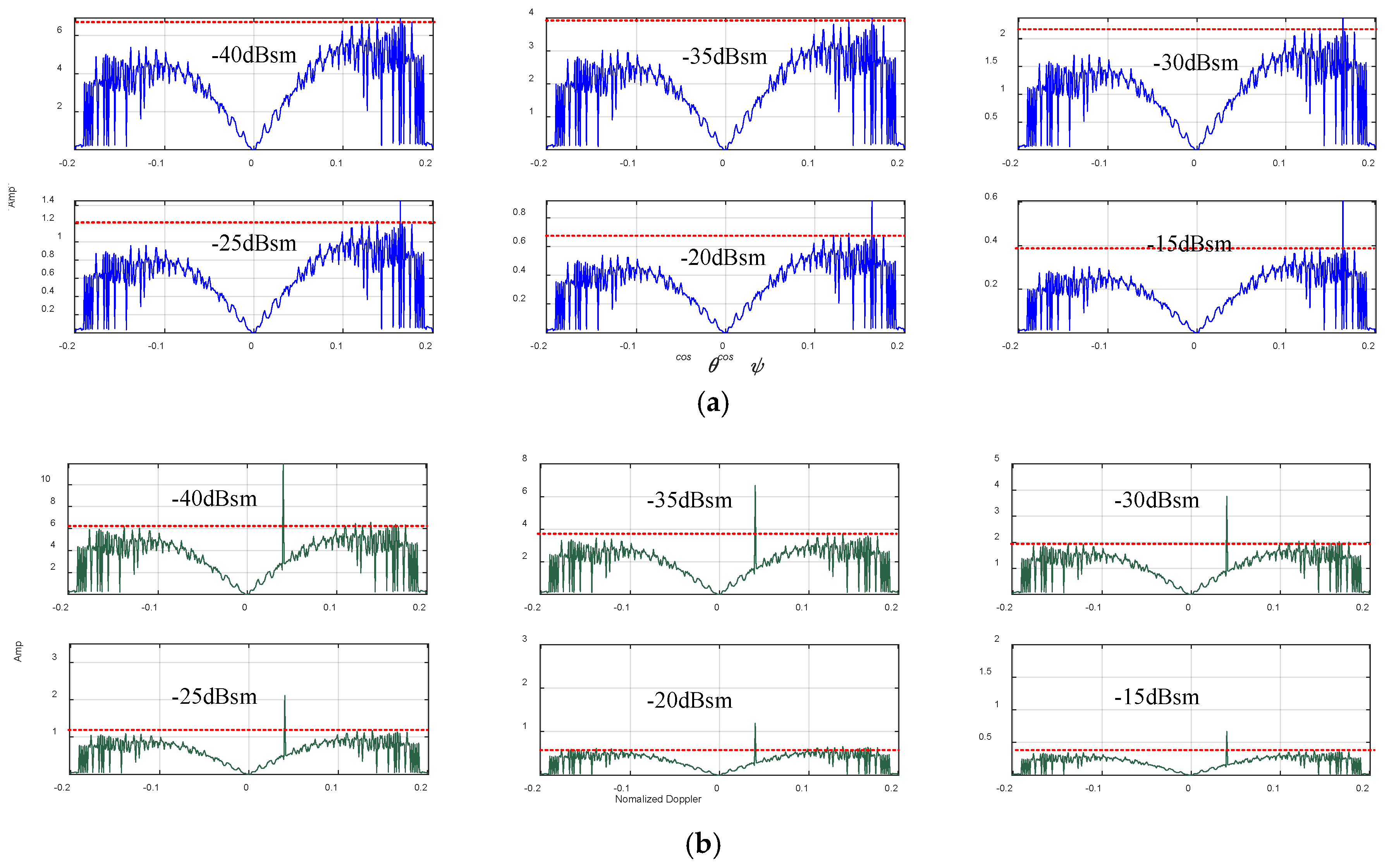
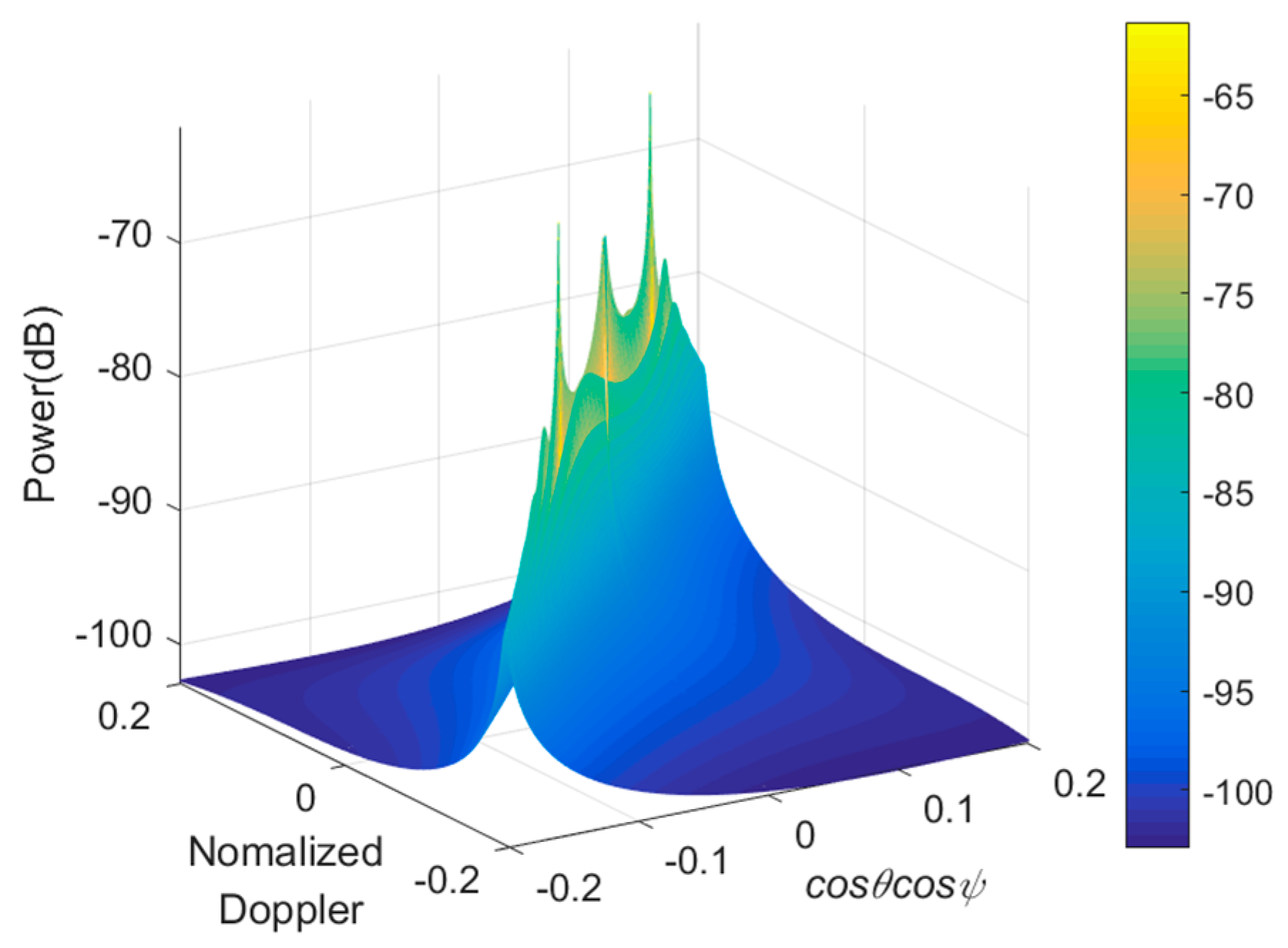
5. Experiments and Discussion
5.1. Dataset
5.2. Simulations and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- CAAC. Manual on Preventing Foreign Object Debris (FOD); National Civil Aviation Administration of China: Beijing, China, 2009; pp. 1–2.
- Zhou, Y.; Xiong, J. Study on typical case analysis and preventive measures of runway invasion during take-off stage. J. Civ. Aviat. Flight Univ. Chin. 2010, 21, 32–35. [Google Scholar] [CrossRef]
- Patterson, J., Jr. Foreign Object Debris (FOD) Detection Research. Int. Airpt. Rev. 2008, 12, 22–27. [Google Scholar]
- iFerret on Scratch. Available online: https://www.sourcesecurity.com/news/stratech-iferret-assess-ground-surveillance-systems-co-7811-ga.19664.html/ (accessed on 24 January 2019).
- Tarsier®: Automatic Runway FOD Detection System. Available online: https://www.tarsierfod.com/ (accessed on 19 December 2018).
- FOD Finder™. Available online: https://www.xsightsys.com/index.php/fodetect/ (accessed on 4 January 2016).
- What Is FODetect? Available online: http://www.xsightsys.com/fodetect.html (accessed on 24 January 2018).
- CCTV Introduces the Foreign Object Debris System of Airport Runway in the Second Airport of Civil Aviation. Available online: http://news.carnoc.com/list/403/403257.html (accessed on 16 May 2017).
- Zeitler, A.; Lanteri, J.; Pichot, C. Folded reflect arrays with shaped beam pattern for foreign object debris detection on runways. IEEE Trans. Antennas Propag. 2010, 58, 3065–3068. [Google Scholar] [CrossRef]
- He, Y. Millimeter-Wave Radar FOD Detection Technology. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2014. [Google Scholar]
- Kang, Z.; Long, T. A New SAR Imaging Scheme in Foreign Object Debris Detection. In Proceedings of the International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012; pp. 952–956. [Google Scholar] [CrossRef]
- Fan, M. Research on Foreign Object Debris Detection. Master’s Thesis, Beijing Jiaotong University, Beijing, China, June 2011. [Google Scholar]
- Mollo, G.; Napoli, R.D.; Naviglio, G. Multifrequency Experimental Analysis (10 to 77 GHz) on the Asphalt Reflectivity and RCS of FOD Targets. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1441–1443. [Google Scholar] [CrossRef]
- Mazouni, K.; Zeitler, A.; Lanteri, J. 76.5 GHz millimeter-wave radar for foreign objects debris detection on airport runways. In Proceedings of the 8th European Radar Conference, Manchester, UK, 12–14 October 2011; pp. 317–326. [Google Scholar] [CrossRef]
- Mazouni, K.; Pichot, C.; Lantéri, J. 77 GHz offset reflectarray for FOD detection on airport runways. Int. J. Microw. Wirel. Technol. 2012, 4, 37–43. [Google Scholar] [CrossRef]
- Feil, P.; Menzel, W.; Nguyen, T.P. Foreign objects debris detection (FOD) on airport runways using a broadband 78 GHz sensor. In Proceedings of the European Radar Conference, Amsterdam, The Netherlands, 30–31 October 2008; pp. 451–454. [Google Scholar] [CrossRef]
- Futatsumori, S.; Morioka, K.; Kohmura, A. Design and Field Feasibility Evaluation of Distributed-Type 96 GHz FMCW Millimeter-Wave Radar Based on Radio-Over-Fiber and Optical Frequency Multiplier. J. Lightwave Technol. 2016, 34, 4835–4843. [Google Scholar] [CrossRef]
- Nsengiyumva, F.; Pichot, C.; Aliferis, I. Detection of debris (FOD) on runways in W-band: Relevance and validity domain of two-dimensional approaches. In Proceedings of the IEEE International Conference on Electromagnetics in Advanced Applications, Turin, Italy, 7–11 September 2015; pp. 117–120. [Google Scholar] [CrossRef]
- Jin, E.; Yan, D.; Zhang, Z. FOD Detection on Airport Runway with Clutter Map CFAR Plane Technique. In Communications, Signal Processing, and Systems; Springer: Berlin, Germany, 2012; Volume 202, pp. 335–342. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Yu, X. CFAR Detection Method in Multi-target Environments for Foreign Object Debris Surveillance Radar. In The Proceedings of the Second International Conference on Communications, Signal Processing, and Systems; Springer International Publishing: Berlin, Germany, 2014; Volume 246, pp. 533–540. [Google Scholar] [CrossRef]
- He, Z.; Miao, C.; Zhao, Y. Millimeter Wave Radar for FOD Detection on Airport Runway Based on SAR Principle. J. Microwav. 2017, S1, 230–233. [Google Scholar]
- Cong, X.; Liu, J.; Long, K. Millimeter-wave spotlight circular synthetic aperture radar (scsar) imaging for Foreign Object Debris on airport runway. In Proceedings of the IEEE International Conference on Signal Processing, Hangzhou, China, 19–23 October 2014; pp. 1968–1972. [Google Scholar] [CrossRef]
- Ao, D.; Wang, X.; Wang, H. Modeling of Foreign Objects Debris Detection Radar on Airport Runway. In Proceedings of the 2012 International Conference on Information Technology and Software Engineering; Springer: Berlin, Germany, 2013; pp. 115–123. [Google Scholar] [CrossRef]
- Kohmura, A.; Futatsumori, S.; Yonemoto, N.; Okada, K. Optical fiber connected millimeter-wave radar for FOD detection on runway. In Proceedings of the European Radar Conference, Nuremberg, Germany, 9–11 October 2013; pp. 41–44, ISBN 978-2-87487-033-0. [Google Scholar]
- Blacknell, D. Target detection in correlated SAR clutter. IEEE Proc. Radar Sonar Navig. 2002, 147, 9–16. [Google Scholar] [CrossRef]
- Soumekh, M.; Himed, B. SAR-MTI processing of multi-channel airborne radar measurement (MCARM) data. In Proceedings of the 2002 IEEE Radar Conference, Long Beach, CA, USA, 25 April 2002; pp. 24–28. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Wang, H.; Park, S. A deterministic least-squares approach to space-time adaptive processing (STAP). IEEE Trans. Antennas Propag. 2001, 49, 91–103. [Google Scholar] [CrossRef]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid Convergence Rate in Adaptive Arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, 10, 853–863. [Google Scholar] [CrossRef]
- Gerlach, K.; Blunt, S.D.; Picciolo, M.L. Robust adaptive matched filtering using the FRACTA algorithm. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 929–945. [Google Scholar] [CrossRef]
- Huang, L.; Thompson, E.A.; Schmithorst, V.; Holland, S.K.; Talavage, T.M. Partially Adaptive STAP Algorithm Approaches to Functional MRI. IEEE Trans. Biomed. Eng. 2009, 56, 518–521. [Google Scholar] [CrossRef]
- Ginolhac, G.; Forster, P.; Pascal, F.; Ovarlez, J.P. Performance of Two Low-Rank STAP Filters in a Heterogeneous Noise. IEEE Trans. Signal Process. 2012, 61, 57–61. [Google Scholar] [CrossRef]
- Fa, R.; Lamare, R.C.D.; Wang, L. Reduced-Rank STAP Schemes for Airborne Radar Based on Switched Joint Interpolation, Decimation and Filtering Algorithm. IEEE Trans. Signal Process. 2010, 58, 4182–4194. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Wang, H.; Fa, R. Knowledge-aided STAP with sparse-recovery by exploiting spatio-temporal sparsity. IET Signal Process. 2016, 10, 150–161. [Google Scholar] [CrossRef]
- Yang, K.; Bar-Shalom, Y.; Willett, P. Sparsity-Based STAP Using Alternating Direction Method with Gain/Phase Errors. IEEE Trans. Aerosp. Electron. Syst. 2017, 99. [Google Scholar] [CrossRef]
- Riedl, M.; Potter, L.C. Knowledge-Aided Bayesian Space-Time Adaptive Processing. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1850–1861. [Google Scholar] [CrossRef]
- Wang, P.; Li, H.; Himed, B. A Bayesian Parametric Test for Multichannel Adaptive Signal Detection in Nonhomogeneous Environments. IEEE Signal Process. Lett. 2010, 17, 351–354. [Google Scholar] [CrossRef]
- Wen, C.; Peng, J.; Zhou, Y.; Wu, J. Enhanced Three-Dimensional Joint Domain Localized STAP for Airborne FDA-MIMO Radar under Dense False-Target Jamming Scenario. IEEE Sens. J. 2018, 18, 4154–4166. [Google Scholar] [CrossRef]
- Zhang, S.; He, Z.; Jun, L.; Wang, Y. A Robust Colored-loading Factor Optimization Approach for KA-STAP. J. Electron. Inf. Technol. 2016, 38, 1942–1949. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, T.; Wu, J.; Duan, J. Robust training samples selection algorithm based on spectral similarity for space–time adaptive processing in heterogeneous interference environments. IET Radar Sonar Navig. 2015, 9, 778–782. [Google Scholar] [CrossRef]
- Han, S.; Fan, C.; Huang, X. A novel training sample selection method for STAP based on clutter sparse recovery. In Proceedings of the IEEE Progress in Electromagnetic Research Symposium, 2016 Congress on Image and Signal Processing, Shanghai, China, 8–11 August 2016. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.; Wang, H. Radar echo modeling of Foreign Objects Debris detection on airport runways. J. Terahertz Sci. Electron. Inf. Technol. 2013, 11, 917–921. [Google Scholar] [CrossRef]
- Mehdi, G.; Miao, J. Millimetre Wave FMCW Radar for Foreign Object Debris (FOD) Detection at Airport Runways. In Proceedings of the 9th International Conference, Applied Science & Technology, Islamabad, Pakistan, 9–12 January 2012; pp. 407–412. [Google Scholar] [CrossRef]
- Rao, N.; Chen, X.; Zhou, J. Research on Ground Modelling of Airborne Cognitive Radar Based on Digital Elevation Model Data. J. Univ. Electron. Sci. Technol. Chin. 2016, 45, 511–519. [Google Scholar] [CrossRef]
- Sun, G.; He, Z.; Tong, J.; Zhang, X. Knowledge-Aided Covariance Matrix Estimation via Kronecker Product Expansions for Airborne STAP. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1–5. [Google Scholar] [CrossRef]
- AC 150/5220-24 Airport Foreign Object Debris Detection Equipment. Available online: https://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentID/99719 (accessed on 30 September 2009).
- Brennan, L.E.; Malle, J.D.; Reed, L.S. Theory of Adaptive Radar. IEEE Trans. Aerosp. Electron. Syst. 1973, 9, 237–252. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Klemm, R. Applications of Space-Time Adaptive Processing; IET Digital Library: London, UK, 2004; pp. 154–196. ISBN 9780852969243. [Google Scholar]
- Qin, L. Research on Robust Space-Time Adaptive Processing for Airborne Radar. Ph.D. Thesis, National University of Defence Technology, Changsha, China, June 2017. [Google Scholar]
- Zhang, X.; Li, Y.; Yang, X.; Long, T. Sub-Array Weighting UN-MUSIC: A Unified Framework and Optimal Weighting Strategy. IEEE Signal Process. Lett. 2014, 21, 871–874. [Google Scholar] [CrossRef]

| Surface Type | Concrete Runway | Lawn (Height ≤ 0.5 m) | ||||
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Value | −49 | 32 | 20 | −21 | 10 | 6 |
| Data Number | Date | Rf Frequency | Frequency Step | Azimuth | Azimuth Step | Grazing Angle |
|---|---|---|---|---|---|---|
| Dataset 1 | 16 September 2014 | 10 GHz | \ | −180–180 deg | 0.1 deg | 5/10/15 deg |
| Dataset 2 | 16 December 2014 | 8–12 GHz | 10 MHz |
| Parameter | Symbol | Value | Parameter | Symbol | Value | |
|---|---|---|---|---|---|---|
| SAR | number of pulses in a CPI | 3 | number of antenna elements | 4 | ||
| PRI | 0.1 ms | ULA spacing | 0.5 | |||
| beam width in azimuth | 20° | beam width in downwards | 2.4° | |||
| transmit power | 100 mW | antenna gain | 48 dBi | |||
| scale | 1 | \ | \ | \ | ||
| Scene knowledge | distance | 50 m | platform height | 2 m | ||
| runway width | 50 m | \ | \ | \ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Huo, K.; Zhang, X.; Jiang, W.; Chen, Y. A Clutter-Analysis-Based STAP for Moving FOD Detection on Runways. Sensors 2019, 19, 549. https://doi.org/10.3390/s19030549
Yang X, Huo K, Zhang X, Jiang W, Chen Y. A Clutter-Analysis-Based STAP for Moving FOD Detection on Runways. Sensors. 2019; 19(3):549. https://doi.org/10.3390/s19030549
Chicago/Turabian StyleYang, Xiaoqi, Kai Huo, Xinyu Zhang, Weidong Jiang, and Yong Chen. 2019. "A Clutter-Analysis-Based STAP for Moving FOD Detection on Runways" Sensors 19, no. 3: 549. https://doi.org/10.3390/s19030549
APA StyleYang, X., Huo, K., Zhang, X., Jiang, W., & Chen, Y. (2019). A Clutter-Analysis-Based STAP for Moving FOD Detection on Runways. Sensors, 19(3), 549. https://doi.org/10.3390/s19030549





