Health-Aware Model-Predictive Control of a Cooperative AGV-Based Production System
Abstract
1. Introduction
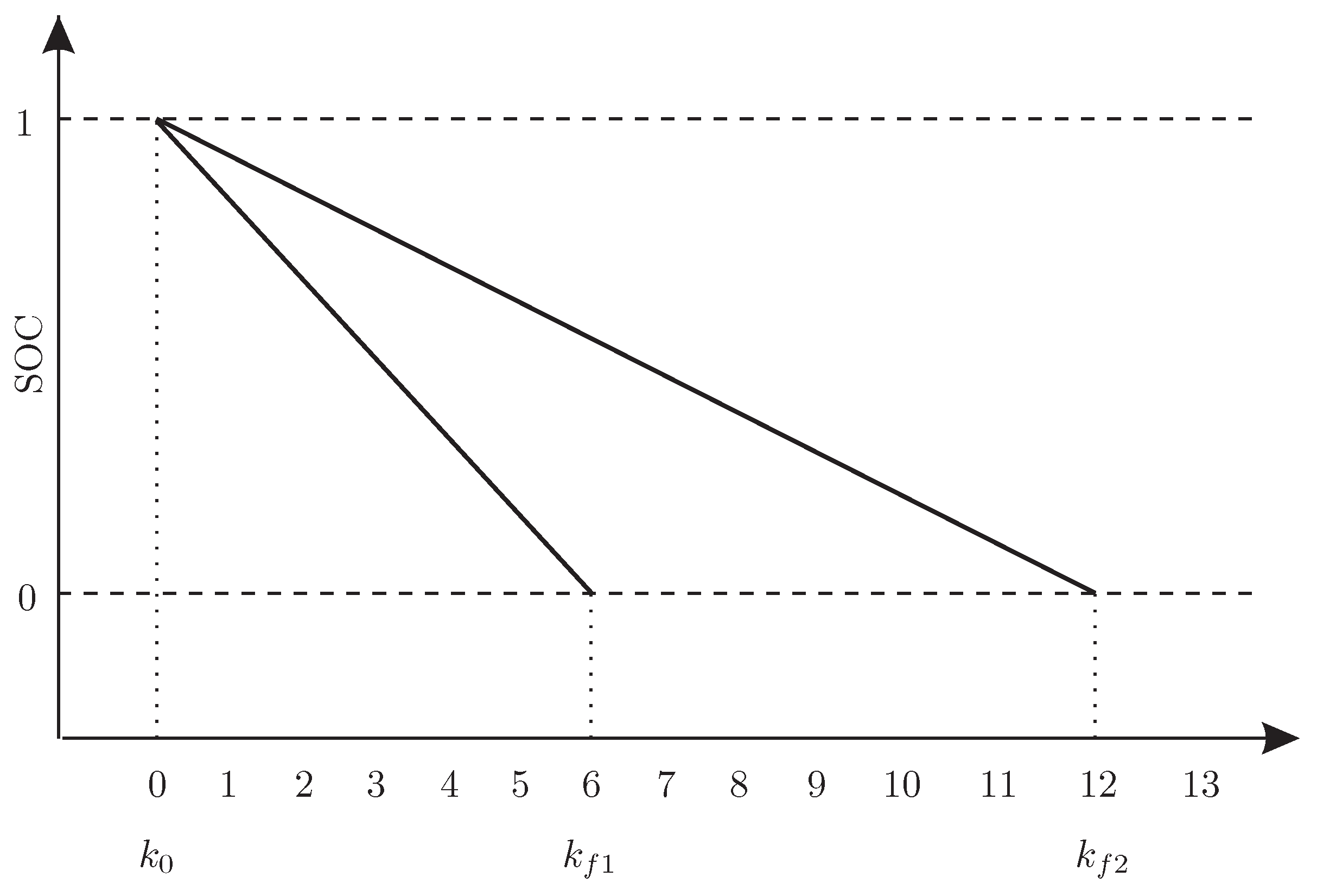
- The SOH is a number of cycles from a given SOC down to zero.
- How to design a framework allowing trustworthy estimation of SOC and SOH of AGV batteries along with incorporation of this knowledge within the predictive control strategy of the assembly system?
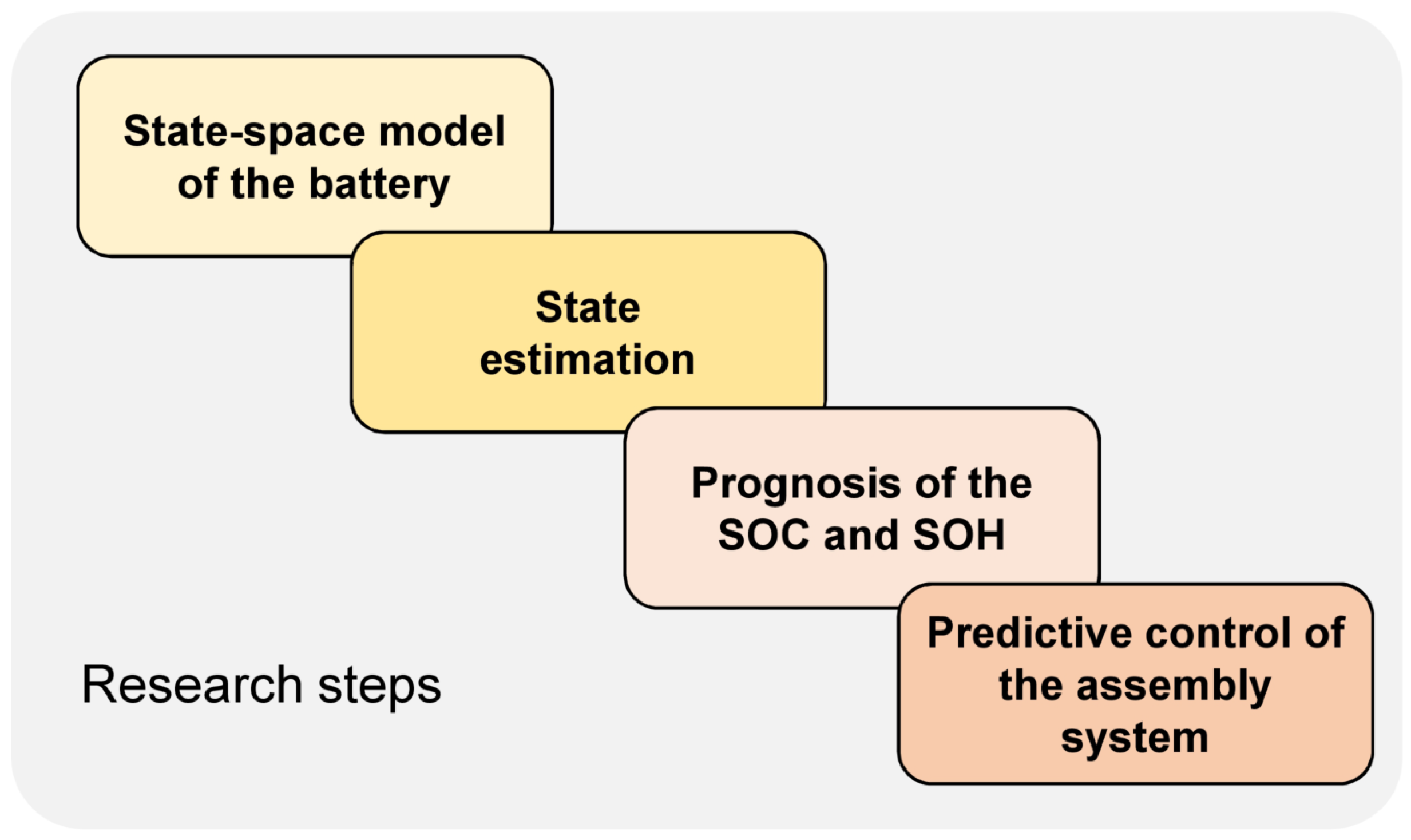
- Firstly, a state-space model of a battery is derived from the literature.
- Secondly, algorithms, which allow estimation of AGV-battery SOC based on current and voltage sensor measurements, are developed.
- Thirdly, algorithms, which allow the prognosis of the SOH based on the evolution of SOC, are developed.
- Fourthly, control-scheduling algorithms, which allow optimal distribution of workload between two cooperating AGVs, taking into account their SOH, are developed.
2. State of the Art
2.1. Prognosis of the SOH of Technical Systems
2.2. Models of Battery Ageing
2.3. Predictive Control of Assembly Systems
3. Seat-Assembly System
- k—is the event counter associated with the realization of k seat frame transportation,
- —is the start time of the first AGV for k-th event counter,
- —is the start time of the second AGV for k-th event counter,
- —is the seat frame arrival time k-th event counter,
- —is the delivery time of seat frame, which must be transported for k-th event counter,
- —is the forward transportation time between assembly stations for k-th event counter,
- —is the backward transportation time between assembly stations for k-th event counter.
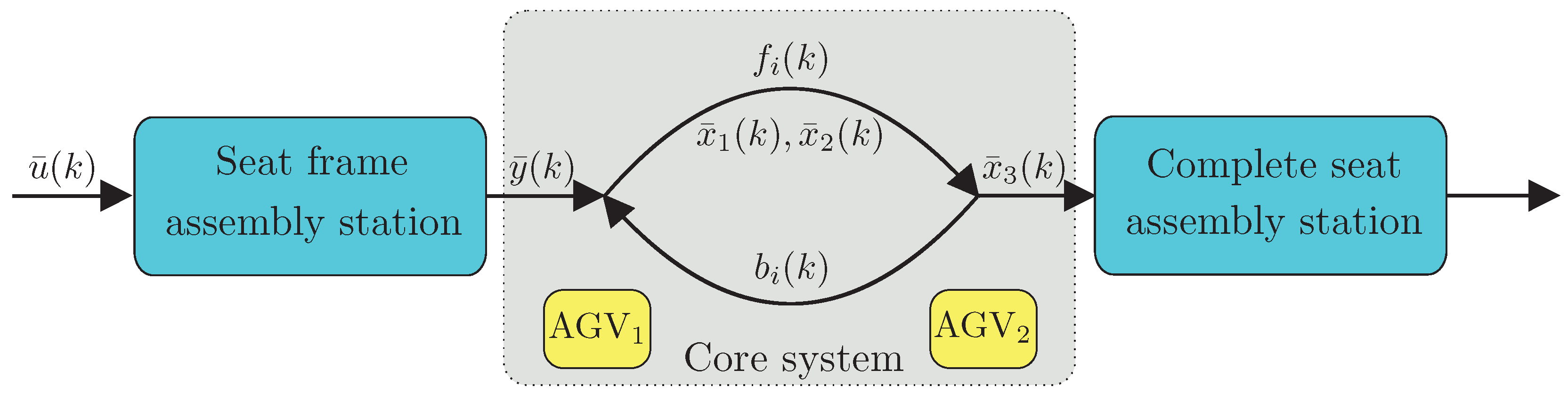
- Assembly stations: seat frame and complete seat;
- Core system: containing two cooperating AGVs. It consists of two AGVs, which can realize a single task. Thus, the problem is to spread the work load among these two cooperating AGVs in such a way to optimize their battery consumption process;
- AGV-battery SOC: battery state estimator (Section 4);
- Remaining AGV cycles: a state-of-charge prediction mechanism (Section 5).
- AGV MPC: a health-aware predictive control (Section 7).
- Assembling system MPC: the seat frame assembly station MPC.
4. Estimation of the Battery State
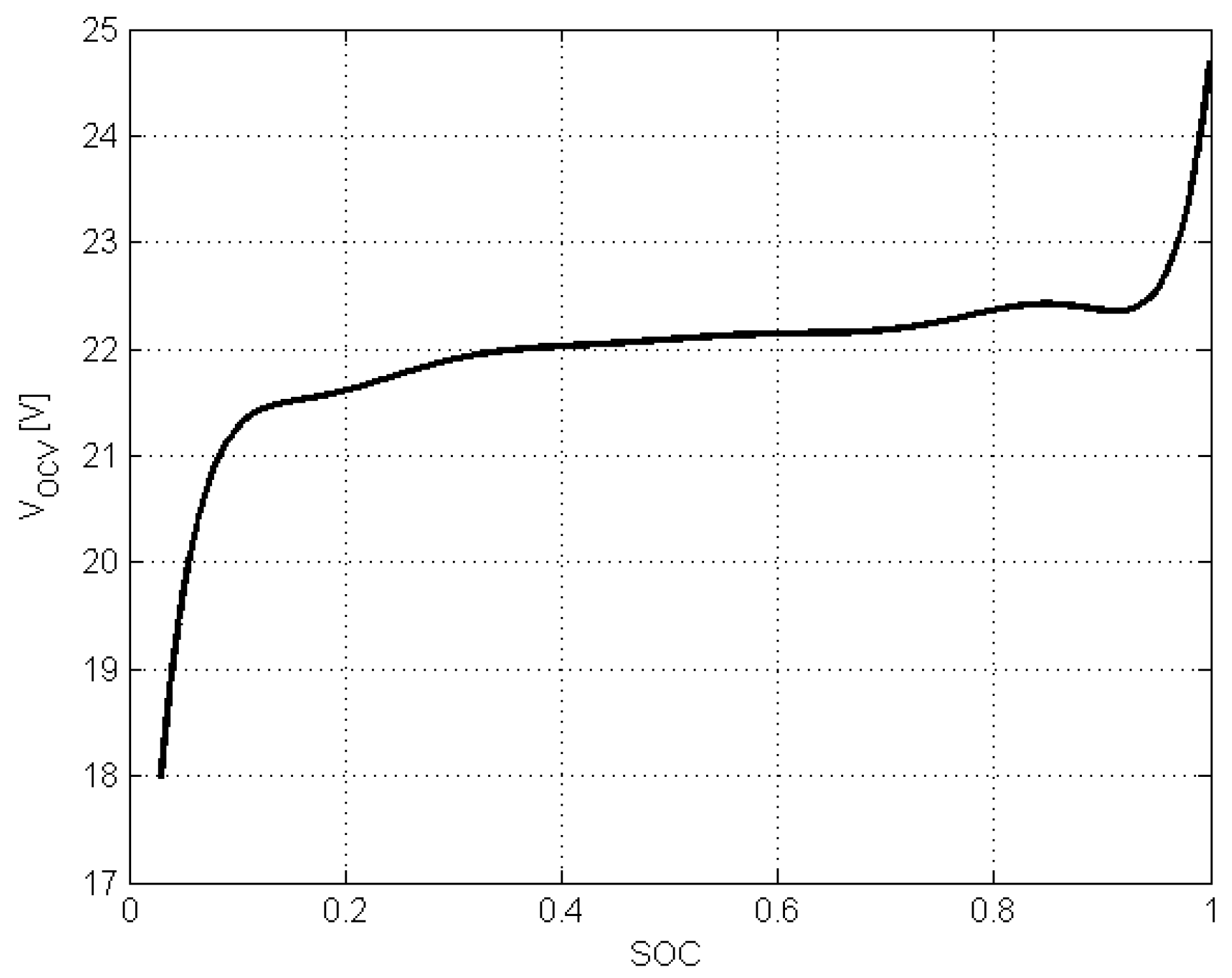
- SOC is within the range ;
- the function linking SOC and is positive and monotonic.
- Off-line:
- On-line
- Set and .
- Obtain the state estimate according to (9).
- Set and go to Step 2.
5. Prognosis of the Remaining SOC
- Set , and , with being a sufficiently large positive constant.
- Set and go to Step 2.
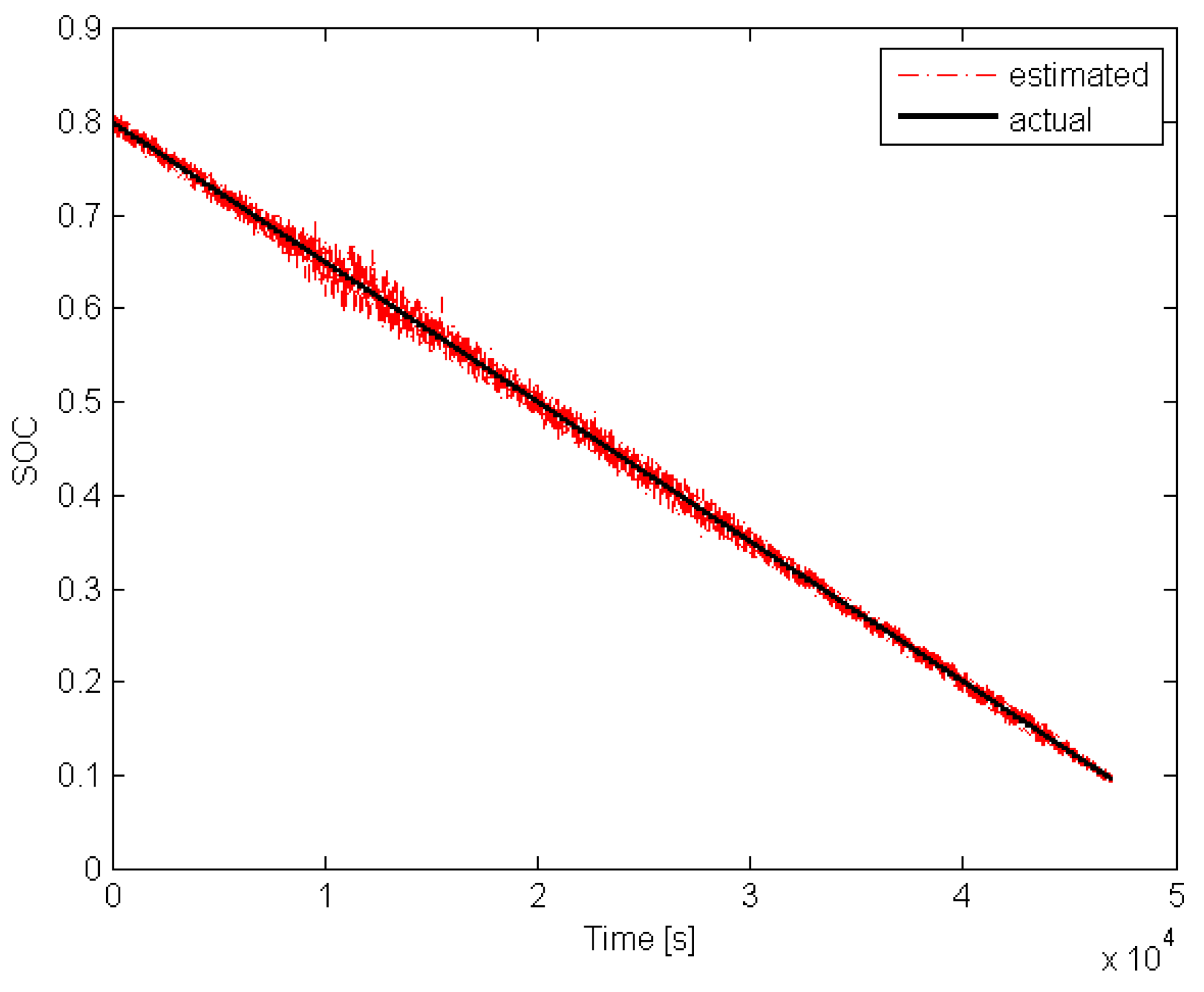
6. Performance Evaluation
7. Predictive Control of the Assembly System
7.1. MPC of Cooperative AGVs
- first, the designed system must follow some predefined trajectory that can be defined as scheduling constraints of the form:where is the upper bound of at k.
- the second set of constraint concerns the performance of the AGVs:The possibly time-varying upper bounds is connected to the minimum speed of the AGVs.
- the last constraint is the rate of change one:where is lower bound of the change rate.
7.2. Health-Aware MPC of Cooperative AGVs
8. Verification and Experimental Results
- Scenario 1:—predictive control without H-A features.
- Scenario 2:—predictive control with H-A features, AGV batteries with equal SOC.
- Scenario 3:—predictive control with H-A features, SOC of smaller than SOC of .
9. Summary and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Hu, X.; Cao, D.; Egardt, B. Condition Monitoring in Advanced Battery Management Systems: Moving Horizon Estimation Using a Reduced Electrochemical Model. IEEE/ASME Trans. Mechatron. 2018, 23, 167–178. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive nonlinear model-based fault diagnosis of Li-ion batteries. IEEE Trans. Ind. Electron. 2015, 62, 1002–1011. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka-Guth, T.; Sauer, D. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. A support vector machine-based state-of-health estimation method for lithium-ion batteries under electric vehicle operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 270, 793–803. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Khorasgani, H.; Biswas, G.; Sankararaman, S. Methodologies for system-level remaining useful life prediction. Reliab. Eng. Syst. Saf. 2016, 154, 8–18. [Google Scholar] [CrossRef]
- Wang, H.K.; Li, Y.F.; Huang, H.Z.; Jin, T. Near-extreme system condition and near-extreme remaining useful time for a group of products. Reliab. Eng. Syst. Saf. 2017, 162, 103–110. [Google Scholar] [CrossRef]
- Kodagoda, K.; Wijesoma, W.; Teoh, E. Fuzzy speed and steering control of an AGV. IEEE Trans. Control Syst. Technol. 2002, 10, 112–120. [Google Scholar] [CrossRef]
- Wang, J.; Steiber, J.; Surampudi, B. Autonomous ground vehicle control system for high-speed and safe operation. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008. [Google Scholar]
- Stetter, R.; Witczak, M.; Pazera, M. Virtual Diagnostic Sensors Design for an Automated Guided Vehicle. Appl. Sci. 2018, 8, 702. [Google Scholar] [CrossRef]
- Adams, D. Health Monitoring of Structural Materials and Components: Methods with Applications; Wiley-Interscience: New York, NY, USA, 2007. [Google Scholar]
- Farrar, C.; Worden, K. An Introduction to Structural Health Monitoring. Philos. Trans. R. Soc. A 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Duong, B.; Khan, S.; Shon, D.; Im, K.; Park, J.; Lim, D.S.; Jang, B.; Kim, J.M. A Reliable Health Indicator for Fault Prognosis of Bearings. Sensors 2018, 18, 3740. [Google Scholar] [CrossRef] [PubMed]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer: New York, NY, USA, 2016. [Google Scholar]
- Mrugalska, B. Towards Enhanced Performance of Neural-Network-Based Fault Detection Using an Sequential D-Optimum Experimental Design. Appl. Sci. 2018, 8, 1290. [Google Scholar] [CrossRef]
- Holder, K.; Zech, A.; Ramsaier, M.; Stetter, R.; Niedermeier, H.P.; Rudolph, S.; Till, M. Model-Based Requirements Management in Gear Systems Design Based On Graph-Based Design Languages. Appl. Sci. 2017, 7, 1112. [Google Scholar] [CrossRef]
- Ramsaier, M.; Holder, K.; Zech, A.; Stetter, R.; Rudolph, S.; Till, M. Digital representation of product functions in multicopter design. In Proceedings of the 21st International Conference on Engineering Design (ICED 17), Vancouver, BC, Canada, 21–25 August 2017; Volume 1: Resource Sensitive Design, Design Research Applications and Case Studies. The University of British Columbia: Vancouver, BC, Canada, 2017. [Google Scholar]
- Heng, A.; Zhang, S.; Tan, A.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H. Remaining useful life estimation—A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Kan, M.; Tan, A.; Mathew, J. A review on prognostic techniques for non-stationary and non-linear rotating systems. Mech. Syst. Signal Process. 2015, 62, 1–20. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, M.; Mao, Z. Remaining Useful Life Estimation of Aircraft Engines Using a Modified Similarity and Supporting Vector Machine (SVM) Approach. Energies 2018, 11, 28. [Google Scholar] [CrossRef]
- Pecht, M. Prognostics and Health Management of Electronics; Wiley-Interscience: New York, NY, USA, 2010. [Google Scholar]
- Pecht, M.; Jaai, R. A prognostics and health management roadmap for information and electronics-rich systems. Microelectron. Reliab. 2010, 50, 317–323. [Google Scholar] [CrossRef]
- Sikorska, J.; Hodkiewicz, M.; Ma, L. Prognostic modelling options for remaining useful life estimation by industry. Mech. Syst. Signal Process. 2011, 25, 1803–1836. [Google Scholar] [CrossRef]
- Liao, L.; Koetting, F. Review of Hybrid Prognostics Approaches for Remaining Useful Life Prediction of Engineered Systems, and an Application to Battery Life Prediction. IEEE Trans. Reliab. 2014, 63, 191–207. [Google Scholar] [CrossRef]
- Pham, H.T.; Yang, B.S. Estimation and forecasting of machine health condition using ARMA/GARCH model. Mech. Syst. Signal Process. 2010, 24, 546–558. [Google Scholar] [CrossRef]
- Peng, Y.; Dong, M.; Zuo, M.J. Current status of machine prognostics in condition-based maintenance: A review. Int. J. Adv. Manuf. Technol. 2010, 50, 297–313. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.A.; Medjaher, K.; Zerhouni, N.; Tripot, G. A Data-Driven Failure Prognostics Method Based on Mixture of Gaussians Hidden Markov Models. IEEE Trans. Reliab. 2012, 61, 491–503. [Google Scholar] [CrossRef]
- Li, K.; Wu, J.; Zhang, Q.; Su, L.; Chen, P. New Particle Filter Based on GA for Equipment Remaining Useful Life Prediction. Sensors 2017, 17, 696. [Google Scholar] [CrossRef]
- Singleton, R.K.; Strangas, E.G.; Aviyente, S. Extended Kalman Filtering for Remaining-Useful-Life Estimation of Bearings. IEEE Trans. Ind. Electron. 2015, 62, 1781–1790. [Google Scholar] [CrossRef]
- Yousfi, B.; Raïssi, T.; Amairi, M.; Aoun, M. Set-membership methodology for model-based prognosis. ISA Trans. 2017, 66, 216–225. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, C.; Kong, X.; Zhang, W.; Zhang, Z. Online updating with a wiener-process-based prediction model using UKF algorithm for remaining useful life estimation. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangjiajie, China, 24–27 August 2014; pp. 305–309. [Google Scholar] [CrossRef]
- Mosallam, A.; Medjaher, K.; Zerhouni, N. Data-driven prognostic method based on Bayesian approaches fordirect remaining useful life prediction. J. Intell. Manuf. 2016, 27, 1037–1048. [Google Scholar] [CrossRef]
- Sankararaman, S. Significance, interpretation, and quantification of uncertainty in prognostics and remaining useful life prediction. Mech. Syst. Signal Process. 2015, 52–53, 228–247. [Google Scholar] [CrossRef]
- Goebel, K.; Saha, B.; Saxena, A.; Celaya, J.; Christophersen, J. Prognostics in battery health management. IEEE Instrum. Meas. Mag. 2008, 11, 33–40. [Google Scholar] [CrossRef]
- Dong, M.; He, D. A segmental hidden semi-Markov model (HSMM)-based diagnostics and prognostics framework and methodology. Mech. Syst. Signal Process. 2007, 21, 2248–2266. [Google Scholar] [CrossRef]
- Benkedjouh, T.; Medjaher, K.; Zerhouni, N.; Rechak, S. Health assessment and life prediction of cutting tools based on support vector regression. J. Intell. Manuf. 2015, 26, 213–223. [Google Scholar] [CrossRef]
- Huang, R.; Xi, L.; Li, X.; Liu, C.; Qiu, H.; Lee, J. Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods. Mech. Syst. Signal Process. 2007, 21, 193–207. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Tae Lee, J.; Yushin, G. Li-ion battery materials: Present and future. Materialstoday 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Li, Q.; Chen, J.; Fan, L.; Kong, X.; Lu, Y. Progress in electrolytes for rechargeable Li-based batteries and beyond. Green Energy Environ. 2016, 1, 18–42. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K.; Poll, S.; Christophersen, J. Prognostics Methods for Battery Health Monitoring Using a Bayesian Framework. IEEE Trans. Instrum. Meas. 2009, 58, 291–296. [Google Scholar] [CrossRef]
- He, W.; Willard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster–Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.; Chung, J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
- Remmlinger, J.; Buchholz, M.; Soczka-Guth, T.; Dietmayer, K. On-board state-of-health monitoring of lithium-ion batteries using linear parameter-varying models. J. Power Sources 2013, 239, 689–695. [Google Scholar] [CrossRef]
- Hua, Y.; Cordoba-Arenas, A.; Warner, N.; Rizzoni, G. A multi time-scale state-of-charge and state-of-health estimation framework using nonlinear predictive filter for lithium-ion battery pack with passive balance control. J. Power Sources 2015, 280, 293–312. [Google Scholar] [CrossRef]
- Widodo, A.; Shim, M.C.; Caesarendra, W.; Yang, B.S. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Zou, C.; Hu, X.; Dey, S.; Zhang, L.; Tang, X. Nonlinear Fractional-Order Estimator With Guaranteed Robustness and Stability for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 5951–5961. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, H.; Zou, C.; Li, Z.; Zhang, L. Co-Estimation of State of Charge and State of Health for Lithium-Ion Batteries Based on Fractional-Order Calculus. IEEE Trans. Veh. Technol. 2018, 67, 10319–10329. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Barre, A.; Deguilhem, B.; Grolleau, S.; Gerad, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Rezvanizaniani, S.; Liu, Z.; Chen, Y.; Lee, J. Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility. J. Power Sources 2014, 256, 110–124. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Taborelli, C.; Onori, S. Advanced battery management system design for SOC/SOH estimation for e-bikes applications. Int. J. Powertrains 2016, 5, 325–357. [Google Scholar] [CrossRef]
- Seybold, L.; Witczak, M.; Majdzik, P.; Stetter, R. Towards Robust Predictive Fault–Tolerant Control for a Battery Assembly System. Int. J. Appl. Math. Comput. Sci. 2015, 25, 849–862. [Google Scholar] [CrossRef]
- Majdzik, P.; Akielaszek-Witczak, A.; Seybold, L.; Stetter, R.; Mrugalska, B. A fault-tolerant approach to the control of a battery assembly system. Control Eng. Pract. 2016, 55, 139–148. [Google Scholar] [CrossRef]
- Paoli, A.; Sartini, M.; Lafortune, S. Active fault tolerant control of discrete event systems using online diagnostics. Automatica 2011, 47, 639–649. [Google Scholar] [CrossRef]
- Polak, M.; Majdzik, P.; Banaszak, Z.; Wojcik, R. The performance evaluation tool for automated prototyping of concurrent cyclic processes. Fundam. Inform. 2004, 60, 269–289. [Google Scholar]
- Baccelli, F.; Cohen, G.; Olsder, G.; Quadrat, J. Synchronization and linearity: An algebra for discrete event systems. J. Oper. Res. Soc. 1994, 45, 118–119. [Google Scholar]
- Butkovic, P. Max-Linear Systems: Theory and Algorithms; Springer: NewYork, NY, USA, 2010. [Google Scholar]
- Elkins, D.; Huang, N.; Alden, J. Agile manufacturing systems in the automotive industry. Int. J. Prod. Econ. 2004, 91, 201–214. [Google Scholar] [CrossRef]
- Hamrol, A. A New Look at Some Aspects of Maintenance and Improvements of Production Processes. Manag. Prod. Eng. Rev. 2018, 9, 34–43. [Google Scholar]
- Hoshino, S.; Seki, H.; Naka, Y. Development of a Flexible and Agile Multi-robot Manufacturing System. In Proceedings of the 17th World Congress The International Federation of Automatic Control, Seoul, Korea, 6–11 July 2008. [Google Scholar]
- Wagner, S.M.; Silveira-Camargos, V. Decision model for the application of just-in-sequence. Int. J. Prod. Res. 2011, 49, 5713–5736. [Google Scholar] [CrossRef]
- Stetter, R.; Paczynski, A. Intelligent Steering System for Electrical Power Trains. In Proceedings of the Emobility—Electrical Power Train, Leipzig, Germany, 8–9 November 2010; pp. 1–6. [Google Scholar]
- Ziemniak, P.; Stania, M.; Stetter, R. Mechatronics Engineering on the Example of an Innovative Production Vehicle. In DS 58-1: Proceedings of the ICED’09 17th International Conference on Engineering Design, Palo Alto, CA, USA, 24–27 August 2009; Norell Bergendahl, M., Grimheden, M., Leifer, L., Skogstad, P., Lindemann, U., Eds.; Design Society: Glasgow, Scotland, 2009; Volume 1, pp. 61–72. [Google Scholar]
- Van den Boom, T.; De Schutter, B. Modelling and control of discrete event systems using switching max-plus-linear systems. Control Eng. Pract. 2006, 14, 1199–1211. [Google Scholar] [CrossRef]
- Schutter, B.D.; van den Boom, T. Model predictive control for max-plus-linear discrete event systems. Automatica 2001, 37, 1049–1056. [Google Scholar] [CrossRef]
- Alessandri, A.; Baglietto, M.; Battistelli, G. Design of state estimators for uncertain linear systems using quadratic boundedness. Automatica 2006, 42, 497–502. [Google Scholar] [CrossRef]
- Mrugalska, B. A bounded-error approach to actuator fault diagnosis and remaining useful life prognosis of Takagi-Sugeno fuzzy systems. ISA Trans. 2018, 80, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Ding, B. Constrained robust model predictive control via parameter-dependent dynamic output feedback. Automatica 2010, 46, 1517–1523. [Google Scholar] [CrossRef]
- Ding, B. Dynamic output feedback predictive control for nonlinear systems represented by a Takagi–Sugeno model. IEEE Trans. Fuzzy Syst. 2011, 19, 831–843. [Google Scholar] [CrossRef]
- Snihir, I.; Rey, W.; Verbitskiy, E.; Belfadhel-Ayeb, A.; Notten, P. Battery open-circuit voltage estimation by a method of statistical analysis. J. Power Sources 2006, 159, 1484–1487. [Google Scholar] [CrossRef]
- Abichandani, P.; Benson, H.; Kam, M. Mathematical Programming Approaches for Multi-Vehicle Motion Planning: Linear, Nonlinear, and Mixed Integer Programming. Found. Trends Robot. 2011, 2, 261–338. [Google Scholar]










© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mrugalska, B.; Stetter, R. Health-Aware Model-Predictive Control of a Cooperative AGV-Based Production System. Sensors 2019, 19, 532. https://doi.org/10.3390/s19030532
Mrugalska B, Stetter R. Health-Aware Model-Predictive Control of a Cooperative AGV-Based Production System. Sensors. 2019; 19(3):532. https://doi.org/10.3390/s19030532
Chicago/Turabian StyleMrugalska, Beata, and Ralf Stetter. 2019. "Health-Aware Model-Predictive Control of a Cooperative AGV-Based Production System" Sensors 19, no. 3: 532. https://doi.org/10.3390/s19030532
APA StyleMrugalska, B., & Stetter, R. (2019). Health-Aware Model-Predictive Control of a Cooperative AGV-Based Production System. Sensors, 19(3), 532. https://doi.org/10.3390/s19030532





