Improving the Topside Profile of Ionosonde with TEC Retrieved from Spaceborne Polarimetric SAR
Abstract
:1. Introduction
2. Methods for TEC Retrieval and Topside Profile Modification
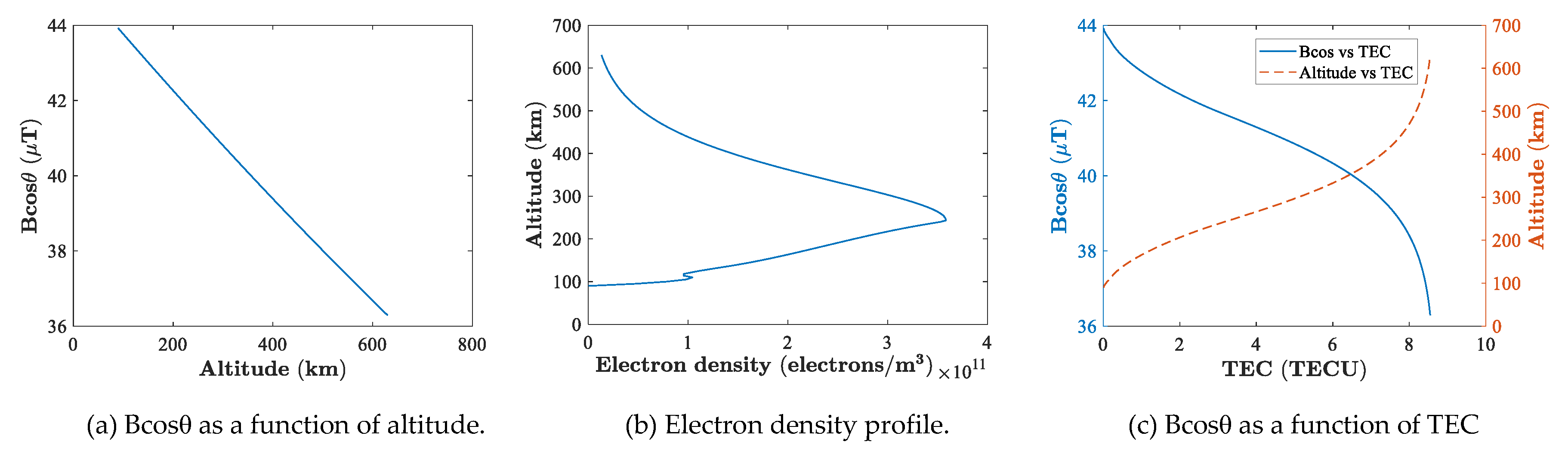
2.1. TEC Retrieval from PolSAR
2.2. Improving the Topside Profile Model of Ionosonde with Known TEC
3. Data Details
3.1. Data for Estimating TEC Precision of PolSAR
3.2. Data for Modeling the Topside Profile of Ionosonde
4. Results and Discussions
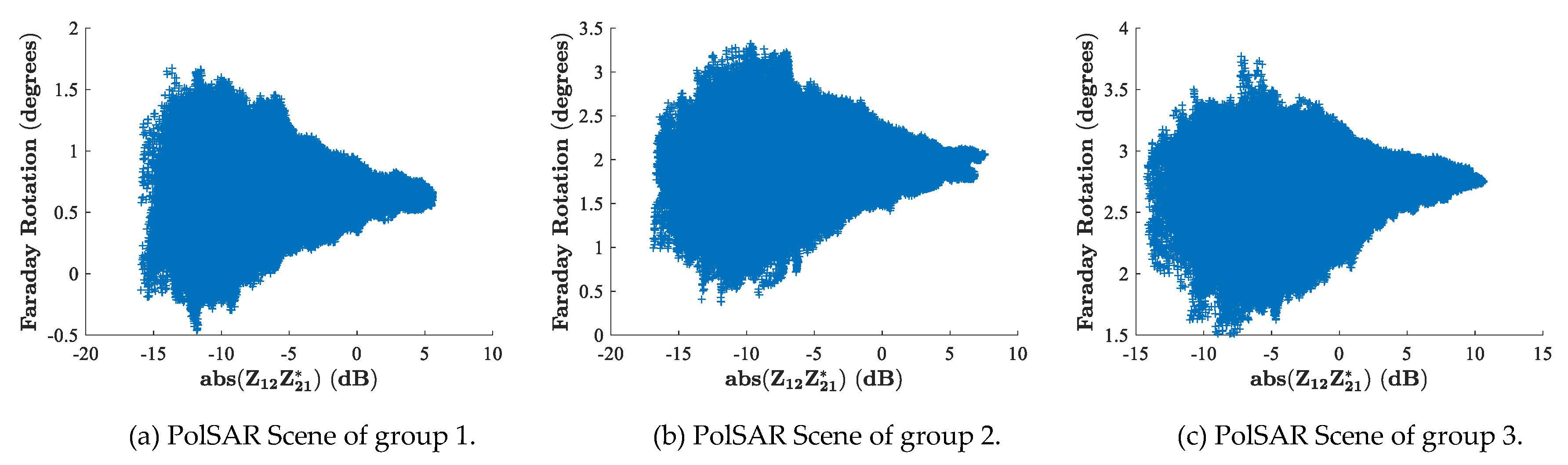
4.1. Validation of the Precision of PolSAR in Estimating TEC
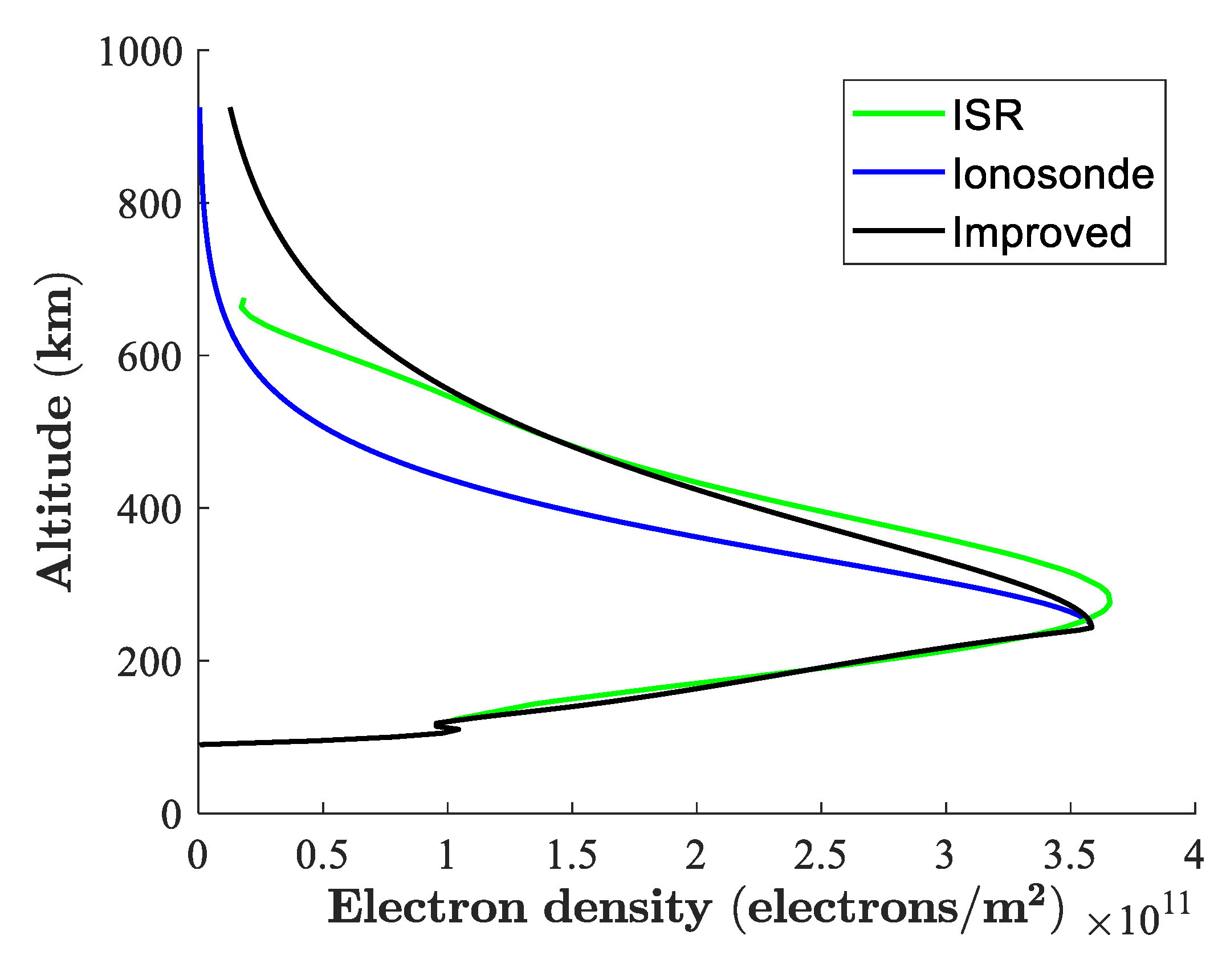
4.2. Modeling the Topside Profile of Ionosonde with New HT
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yizengaw, E.; Dyson, P.L.; Essex, E.A.; Moldwin, M.B. Ionosphere dynamics over the southern hemisphere during the 31 March 2001 severe magnetic storm using multi-instrument measurement data. Ann. Geophys. ANGEO 2005, 23, 707–721. [Google Scholar] [CrossRef]
- Wen, D.; Yuan, Y.; Ou, J.; Zhang, K. Ionospheric response to the geomagnetic storm on August 21, 2003 over China using GNSS-based tomographic technique. IEEE Trans. Geosci. Remote. Sens. 2010, 48, 3212–3217. [Google Scholar] [CrossRef]
- Zhao, H.-S.; Xu, Z.-W.; Wu, J.; Wang, Z.-G. Ionospheric tomography by combining vertical and oblique sounding data with TEC retrieved from a tri-band beacon. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.-S.; Xu, Z.-W.; Wu, J.; Quegan, S. Ionospheric tomography of small-scale disturbances with a triband beacon: A numerical study. Radio Sci. 2010, 45. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Fu, L.; Wang, J.; Zhang, C. Studying ionosphere responses to a geomagnetic storm in June 2015 with multi-constellation observations. Remote. Sens. 2018, 10, 666. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Galkin, I.A. Global ionospheric radio observatory (GIRO). Earth Planets Space 2011, 63, 377–381. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Huang, X. Deducing topside profiles and total electron content from bottomside ionograms. Adv. Space Res. 2001, 27, 23–30. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Huang, X.; Galkin, I.A.; Paznukhov, V.; Kozlov, A. Recent advances in real-time analysis of ionograms and ionospheric drift measurements with digisondes. J. Atmos. Sol. Terr. Phys. 2005, 67, 1054–1062. [Google Scholar] [CrossRef]
- Huang, X.; Reinisch, B.W. Vertical electron content from ionograms in real time. Radio Sci. 2001, 36, 335–342. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Chen, L.; Liu, L.; Yang, J.; Lu, Z.; Feng, J.; Zhao, H.-S. Robust computerized ionospheric tomography based on spaceborne polarimetric SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 4022–4031. [Google Scholar] [CrossRef]
- Pi, X.; Freeman, A.; Chapman, B.; Rosen, P.; Li, Z. Imaging ionospheric inhomogeneities using spaceborne synthetic aperture radar. J. Geophys. Res. Space Phys. 2011, 116, A04303. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Xu, Z.-W.; Zhao, H.-S. TEC retrieval from spaceborne SAR data and its applications. J. Geophys. Res. Space Phys. 2014, 119, 8648–8659. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.S.; Papathanassiou, K.P.; Scheiber, R.; Quegan, S. Correcting distortion of polarimetric SAR data induced by ionospheric scintillation. IEEE Trans. Geosci. Remote. Sens. 2015, 53, 6319–6335. [Google Scholar] [CrossRef]
- Qi, R.; Jin, Y. Analysis of the effects of Faraday rotation on spaceborne polarimetric SAR observations at P-band. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1115–1122. [Google Scholar] [CrossRef]
- Freeman, A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1617–1624. [Google Scholar] [CrossRef]
- Bickel, S.H.; Bates, R.H.T. Effects of magneto-ionic propagation on the polarization scattering matrix. Proc. IEEE 1965, 53, 1089–1091. [Google Scholar] [CrossRef]
- Rogers, N.C.; Quegan, S.; Kim, J.S.; Papathanassiou, K.P. Impacts of ionospheric scintillation on the BIOMASS P-band satellite SAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1856–1868. [Google Scholar] [CrossRef]
- Chen, J.; Quegan, S. Improved estimators of Faraday rotation in spaceborne polarimetric SAR data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 846–850. [Google Scholar] [CrossRef]
- Wang, C.; Liu, L.; Chen, L.; Feng, J.; Zhao, H.-S. Improved TEC retrieval based on spaceborne PolSAR data. Radio Sci. 2017, 52, 2016RS006116. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Dong, Z.; Liang, D. New Faraday rotation estimators based on polarimetric covariance matrix. IEEE Geosci. Remote Sens. Lett. 2014, 11, 133–137. [Google Scholar] [CrossRef]
- Meyer, F.J. Performance requirements for ionospheric correction of low-frequency SAR data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3694–3702. [Google Scholar] [CrossRef]
- Hartmann, G.K.; Leitinger, R. Range errors due to ionospheric and tropospheric effects for signal frequencies above 100 MHz. Bull. Géod. 1984, 58, 109–136. [Google Scholar] [CrossRef]
- Datta-Barua, S.; Walter, T.; Blanch, J.; Enge, P. Bounding higher-order ionosphere errors for the dual-frequency GPS user. Radio Sci. 2008, 43. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Chen, L.; Liu, L. A new analytical model to study the ionospheric effects on VHF/UHF wideband SAR imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4545–4557. [Google Scholar] [CrossRef]
- Poker Flat ISR station. Available online: http://isr.sri.com/madrigal/ (accessed on 8 February 2018).
- Digital Ionogram DataBase. Available online: http://ulcar.uml.edu/DIDBase/ (accessed on 5 February 2018).
- Borner, T.; Papathanassiou, K.P.; Marquart, N.; Zink, M.; Meadows, P.J.; Rye, A.J.; Wright, P.; Meininger, M.; Tell, B.R.; Traver, I.N. ALOS PALSAR products verification. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelon, Spain, 23–28 July 2007; pp. 5214–5217. [Google Scholar]
- Eriksson, L.E.B.; Sandberg, G.; Ulander, L.M.H.; Smith-Jonforsen, G.; Hallberg, B.; Folkesson, K.; Fransson, J.E.S.; Magnusson, M.; Olsson, H.; Gustavsson, A.; et al. ALOS PALSAR calibration and validation results from Sweden. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1589–1592. [Google Scholar]
- Meyer, F.J.; Nicoll, J.B. Prediction, detection, and correction of Faraday rotation in full-polarimetric L-band SAR data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3076–3086. [Google Scholar] [CrossRef]
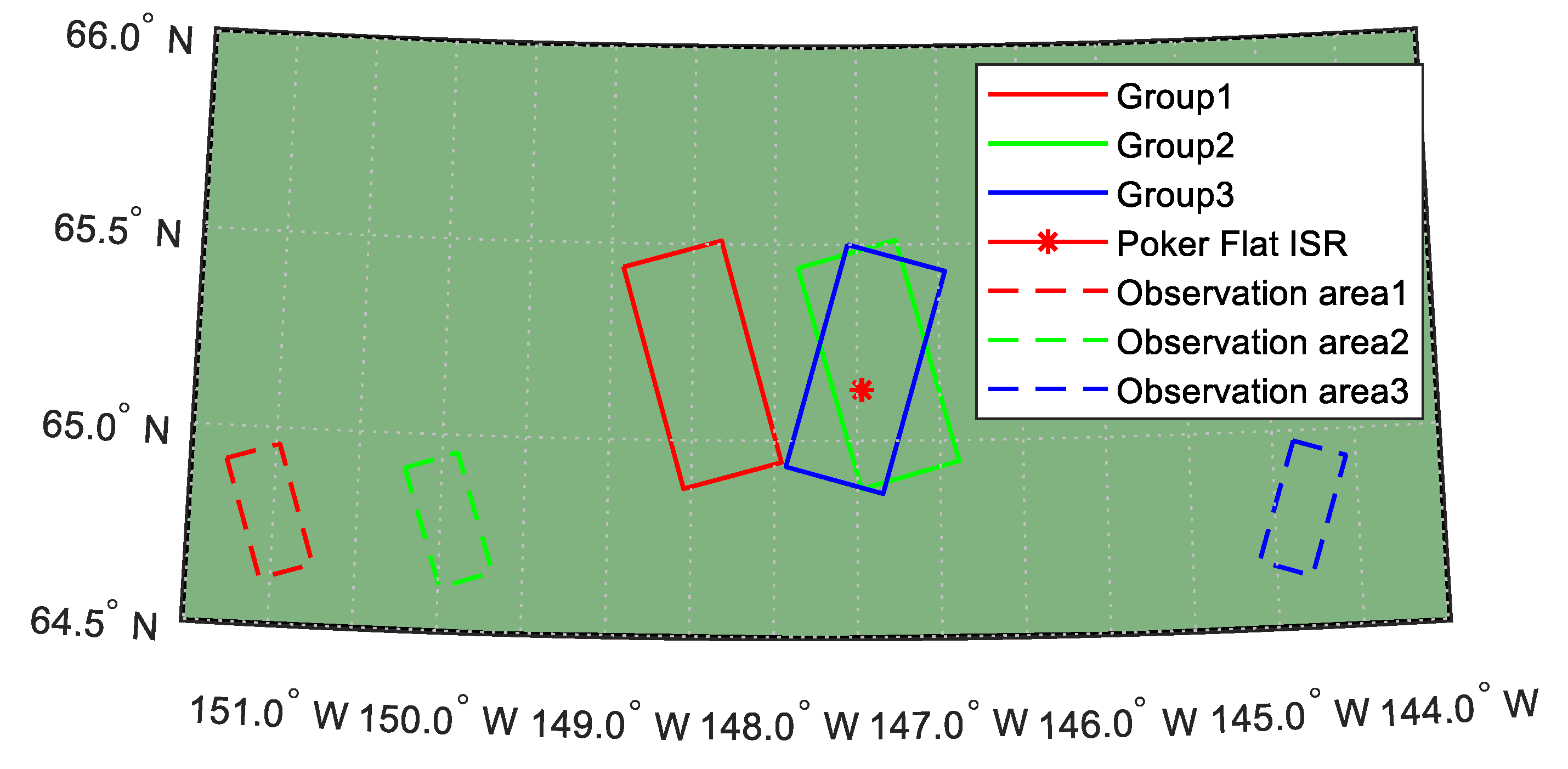
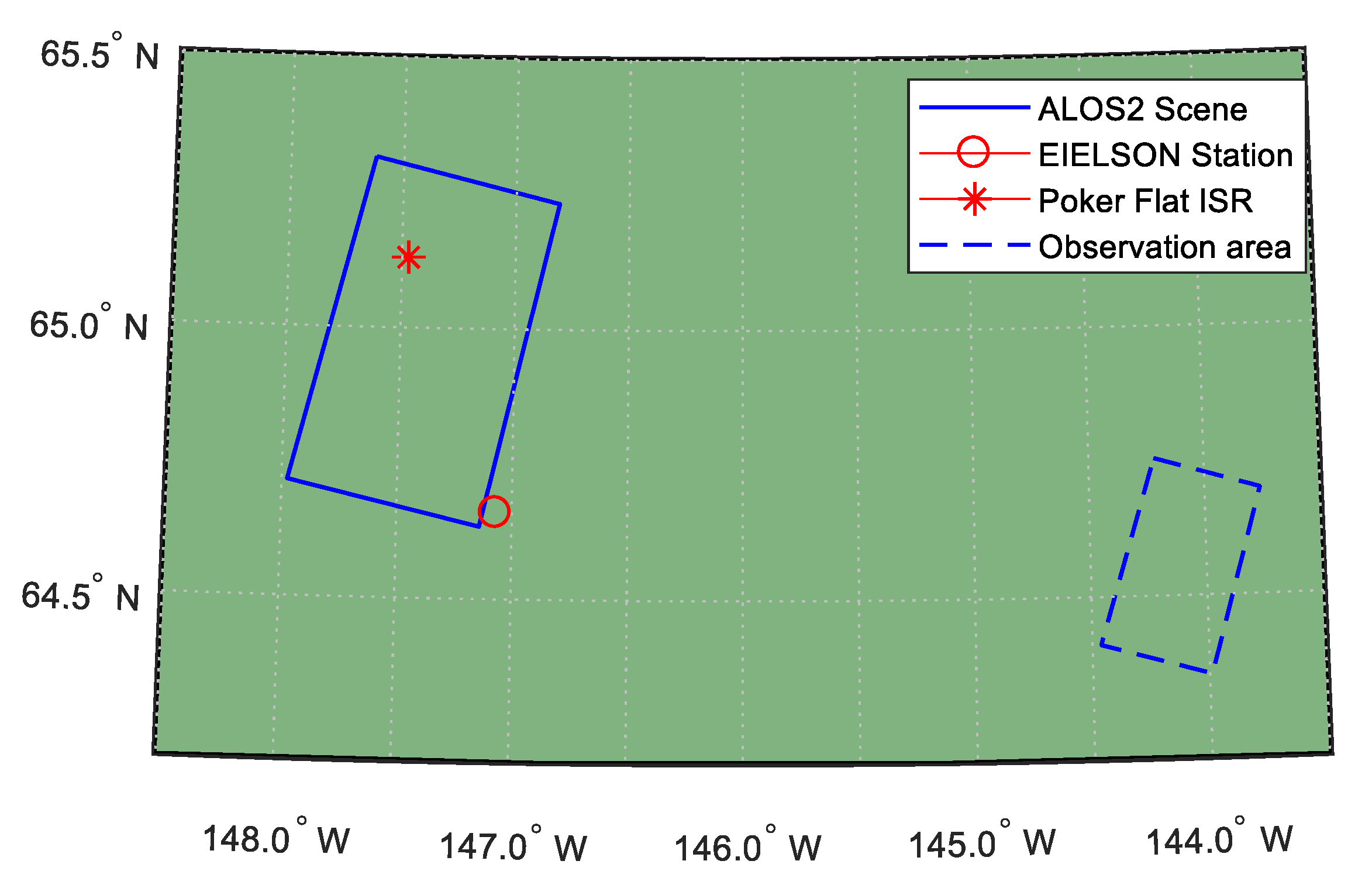
| Data Group | Instrument | Center Latitude | Center Longitude | Center Observation Time (UTC:Y/M/D HH/MM) | Piercing Latitude | Piercing Lontitude |
|---|---|---|---|---|---|---|
| 1 | PALSAR | 65.193 | −148.439 | 2011/03/19 07/32 | 64.786 | −151.022 |
| Poker Flat ISR | 65.130 | −147.471 | 2011/03/19 07/30 | 64.650 | −148.000 | |
| 2 | PALSAR | 65.194 | −147.369 | 2011/03/31 07/28 | 64.782 | −149.949 |
| Poker Flat ISR | 65.130 | −147.471 | 2011/03/31 07/28 | 65.130 | −147.471 | |
| 3 | PALSAR | 65.183 | −147.450 | 2010/08/06 21/06 | 64.800 | −144.832 |
| Poker Flat ISR | 65.130 | −147.471 | 2010/08/06 21/08 | 65.370 | −145.070 |
| Instrument | Center Latitude | Center Longitude | Center Observation Time (UTC: Y/M/D HH/MM) | Piercing Latitude | Piercing Longitude |
|---|---|---|---|---|---|
| PALSAR | 65.193 | −148.439 | 2014/08/29 22/24 | 64.603 | −144.362 |
| Poker Flat ISR | 65.130 | −147.471 | 2014/08/29 22/20 | 65.130 | −147.471 |
| EIELSON station | 64.660 | −147.070 | 2014/08/29 22/15 | 64.660 | −147.070 |
| Instrument. | Group 1 | Group 2 | Group 3 |
|---|---|---|---|
| Poker Flat ISR | 1.484 | 5.700 | 7.365 |
| PolSAR (300 km) | 1.514 (0.324) | 4.646 (0.444) | 6.812 (0.351) |
| PolSAR (400 km) | 1.586 (0.340) | 4.864 (0.465) | 7.112 (0.367) |
| PolSAR (500 km) | 1.660 (0.355) | 5.092 (0.487) | 7.434 (0.384) |
| Deviation (400 km) | 0.102 | 0.836 | 0.253 |
| Poker Flat ISR (average) | 1.46 | 5.71 | 7.86 |
| GNSS | 6 | 12.5 | 10.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Guo, W.; Zhao, H.; Chen, L.; Wei, Y.; Zhang, Y. Improving the Topside Profile of Ionosonde with TEC Retrieved from Spaceborne Polarimetric SAR. Sensors 2019, 19, 516. https://doi.org/10.3390/s19030516
Wang C, Guo W, Zhao H, Chen L, Wei Y, Zhang Y. Improving the Topside Profile of Ionosonde with TEC Retrieved from Spaceborne Polarimetric SAR. Sensors. 2019; 19(3):516. https://doi.org/10.3390/s19030516
Chicago/Turabian StyleWang, Cheng, Wulong Guo, Haisheng Zhao, Liang Chen, Yiwen Wei, and Yuanyuan Zhang. 2019. "Improving the Topside Profile of Ionosonde with TEC Retrieved from Spaceborne Polarimetric SAR" Sensors 19, no. 3: 516. https://doi.org/10.3390/s19030516
APA StyleWang, C., Guo, W., Zhao, H., Chen, L., Wei, Y., & Zhang, Y. (2019). Improving the Topside Profile of Ionosonde with TEC Retrieved from Spaceborne Polarimetric SAR. Sensors, 19(3), 516. https://doi.org/10.3390/s19030516






