Measurement Matrix Construction for Large-area Single Photon Compressive Imaging
Abstract
1. Introduction
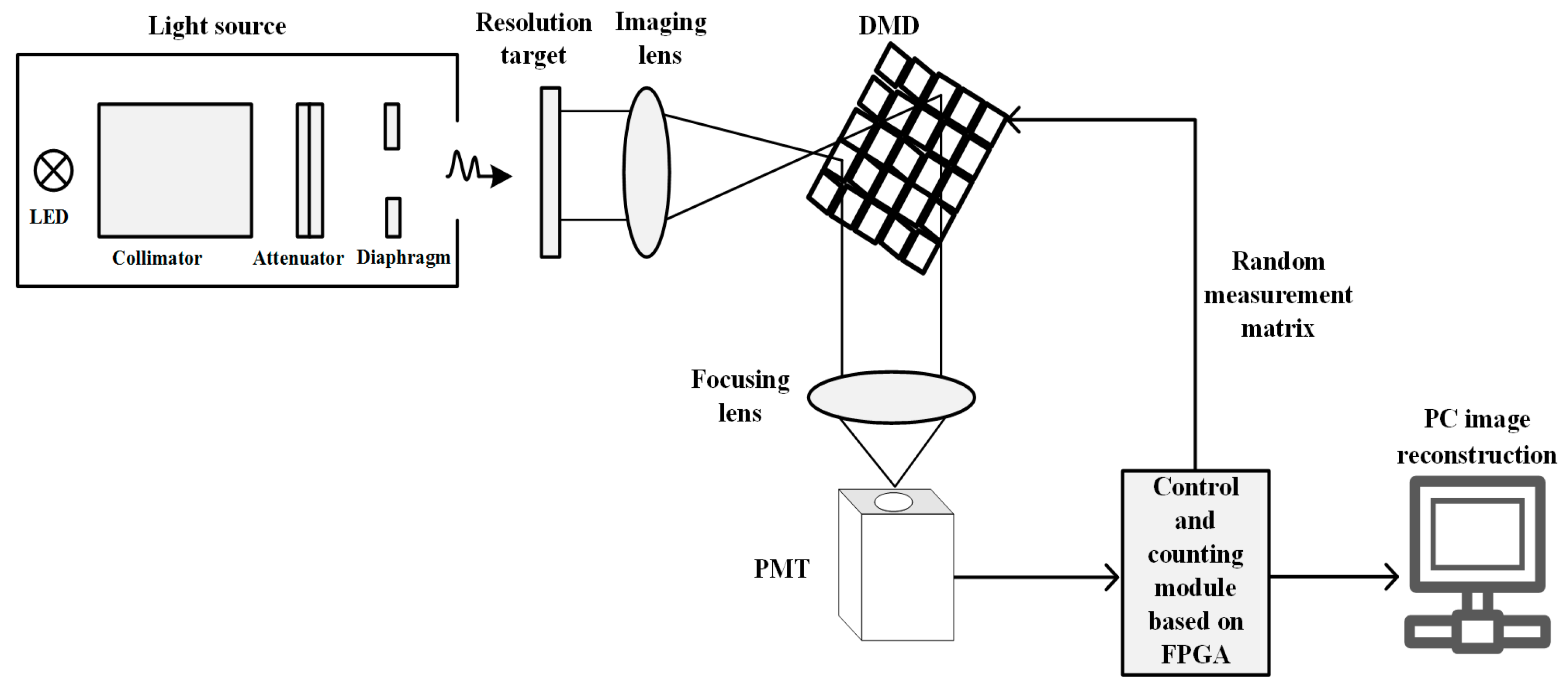
2. Principle and Realization of Experimental System
3. Construction of Measurement Matrix and Theoretical Analysis
3.1. Construction of Measurement Matrix
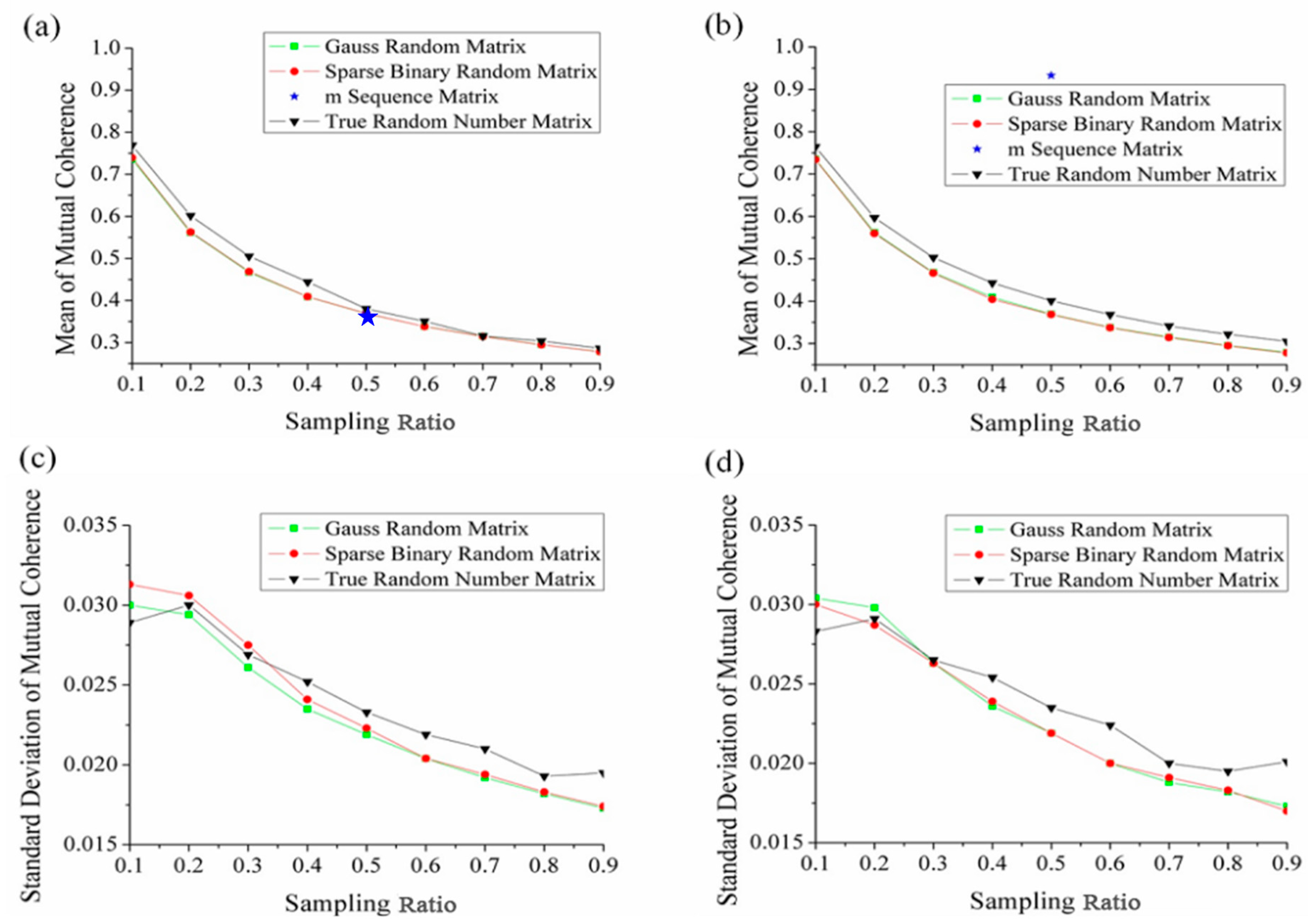
3.2. Theoretical Analysis of Matrix Performance
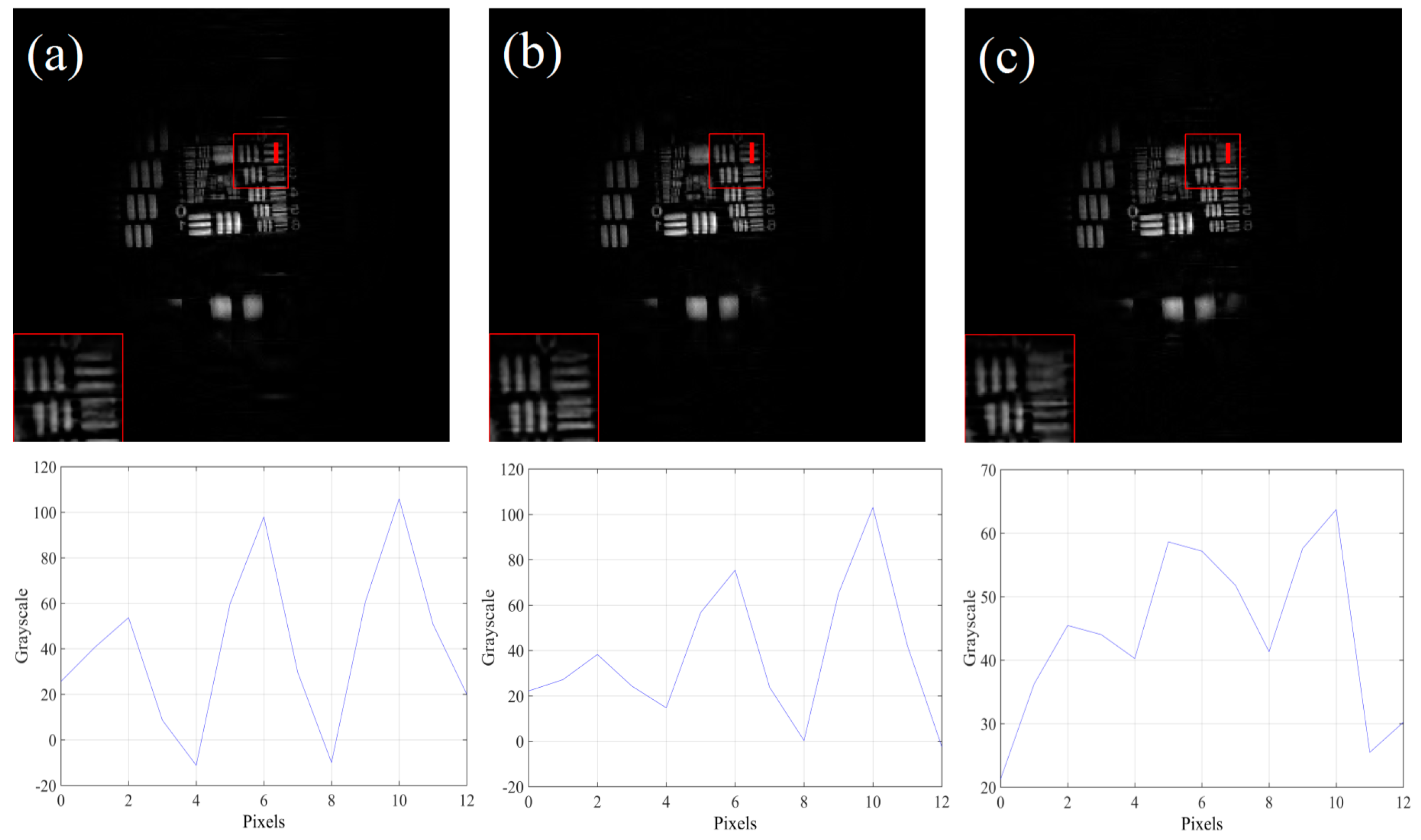
4. Experimental Performance Verification
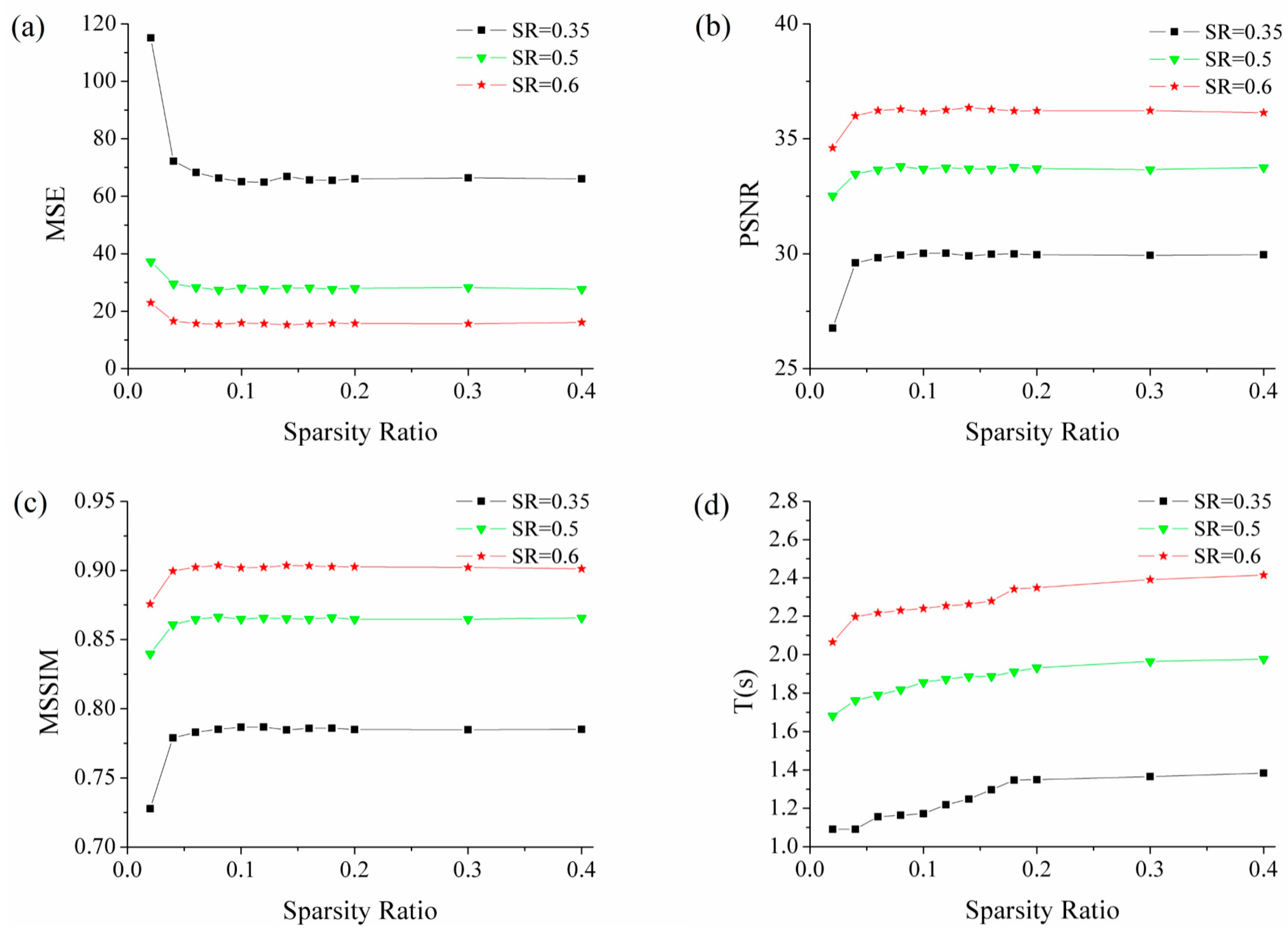
4.1. Influence of Sparsity Ratio on Imaging Quality
4.2. Influence of Compressive Sampling Ratio on Imaging Quality
4.3. Comparison of Imaging Performance of Different Measurement Matrices
4.4. Influence of Poisson Noise on Imaging Quality
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Studer, V.; Bobin, J.; Chahid, M.; Moussavi, H.; Candès, E.J.; Dahan, M. Compressive fluorescence microscopy for biological and hyperspectral imaging. Proc. Natl. Acad. Sci. USA 2012, 109, 1679–1687. [Google Scholar] [CrossRef] [PubMed]
- Becker, W.; Bergmann, A.; Hink, M.A.; König, K.; Benndorf, K.; Biskup, C. Fluorescence lifetime imaging by time-correlated single-photon counting. Microsc. Res. Tech. 2003, 63, 58–66. [Google Scholar]
- Pourmorteza, A.; Symons, R.; Sandfort, V.; Mallek, M.; Fuld, M.K.; Henderson, G.; Jones, E.C.; Malayeri, A.A.; Folio, L.; Bluemke, D.A. Abdominal Imaging with Contrast-enhanced Photon-counting CT: First Human Experience. Radiology 2016, 279, 239–245. [Google Scholar] [CrossRef] [PubMed]
- Taguchi, K.; Iwanczyk, J.S. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Med. Phys. 2013, 40, 100901. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.K. Applications of Compressed Sensing in Super-sensitivity Time-resolved Spectral Imaging; University of Chinese Academy of Sciences: Beijing, China, 2015. [Google Scholar]
- Liu, Y.; Shi, J.; Zeng, G. Single-photon-counting polarization ghost imaging. Appl. Opt. 2016, 55, 10347–10351. [Google Scholar] [PubMed]
- Liu, X.F.; Yu, W.K.; Yao, X.R.; Dai, B.; Li, L.Z.; Wang, C.; Zhai, G.J. Measurement dimensions compressed spectral imaging with a single point detector. Opt. Commun. 2016, 365, 173–179. [Google Scholar]
- Kirmani, A.; Venkatraman, D.; Shin, D.; Colaco, A.; Wong, F.N.C.; Shapiro, J.H.; Goyal, V.K. First-photon imaging. Science 2014, 343, 58–61. [Google Scholar] [CrossRef]
- Yu, W.K.; Liu, X.F.; Yao, X.R.; Wang, C.; Zhai, G.J.; Zhao, Q. Single-photon compressive imaging with some performance benefits over raster scanning. Phys. Lett. A 2014, 378, 3406–3411. [Google Scholar] [CrossRef]
- Sun, M.J.; Edgar, M.P.; Gibson, G.M.; Sun, B.; Radwell, N.; Lamb, R.; Padgett, M.J. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Commun. 2016, 7, 12010. [Google Scholar] [CrossRef]
- Morris, P.A.; Aspden, R.S.; Bell, J.E.C.; Boyd, R.W.; Padgett, M.J. Imaging with a small number of photons. Nat. Commun. 2015, 6, 5913. [Google Scholar] [CrossRef]
- Luo, Q.; Just, F.; Leuchs, G.; Chekhova, M.V. Autonomous absolute calibration of an ICCD camera in single-photon detection regime. Opt. Express 2016, 24, 26444–26453. [Google Scholar]
- Zhao, P.; Cui, S. An improved weak light detector used for infrared Imaging guidance system. Opt.-Int. J. Light Electron Opt. 2016, 127, 2316. [Google Scholar] [CrossRef]
- Milnes, J.S.; Conneely, T.M.; Horsfield, C.J.; Lapington, J. Area and extraction field analysis of the analogue saturation of 40 mm microchannel plate photomultiplier tubes. Rev. Sci. Instrum. 2018, 89, 10K104. [Google Scholar] [CrossRef] [PubMed]
- Leach, S.A.; Lapington, J.S.; Milnes, J.S.; Conneely, T.; Bugalho, R.; Tavernier, S. Operation of microchannel plate PMTs with TOFPET multichannel timing electronics. Nucl. Instrum. Methods Phys. Res. Sect. A 2018. [Google Scholar] [CrossRef]
- Calvi, M.; Carniti, P.; Cassina, L.; Gotti, C.; Maino, M.; Matteuzzi, C.; Pessina, G. Characterization of the Hamamatsu H12700A-03 and R12699-03 multi-anode photomultiplier tubes. J. Instrum. 2015, 10, P09021. [Google Scholar] [CrossRef]
- Martinenghi, E.; Di Sieno, L.; Contini, D.; Sanzaro, M.; Pifferi, A.; Dalla Mora, A. Time-resolved single-photon detection module based on silicon photomultiplier: A novel building block for time-correlated measurement systems. Rev. Sci. Instrum. 2016, 87, 073101. [Google Scholar] [CrossRef] [PubMed]
- Della Rocca, F.M.; Nedbal, J.; Tyndall, D.; Krstajić, N.; Li, D.D.-U.; Ameer-Beg, S.M.; Henderson, R.K. Real-time fluorescence lifetime actuation for cell sorting using a CMOS SPAD silicon photomultiplier. Opt. Lett. 2016, 41, 673–676. [Google Scholar]
- Henderson, R.K.; Johnston, N.; Chen, H.; Li, D.D.U.; Hungerford, G.; Hirsch, R.; David, M.; Philip, Y.; Birch, D.J. A 192 × 128 Time Correlated Single Photon Counting Imager in 40 nm CMOS Technology. In Proceedings of the ESSCIRC 2018-IEEE 44th European Solid State Circuits Conference (ESSCIRC) IEEE, Dresden, Germany, 3–6 September 2018; pp. 54–57. [Google Scholar]
- Bronzi, D.; Villa, F.; Tisa, S.; Tosi, A.; Zappa, F. SPAD Figures of merit for photon-counting, photon-timing, and imaging applications: A review. IEEE Sens. J. 2016, 16, 3–12. [Google Scholar] [CrossRef]
- Dutton, N.A.; Gyongy, I.; Parmesan, L.; Gnecchi, S.; Calder, N.; Rae, B.R.; Sara, P.; Lindsay, A.G.; Henderson, R.K. A SPAD-based QVGA image sensor for single-photon counting and quanta imaging. IEEE Trans. Electron Devices 2016, 63, 189–196. [Google Scholar]
- Romberg, J. Imaging via compressive sampling. IEEE Sign. Proc. Mag. 2008, 25, 14–20. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Proc. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Proc. Mag. 2007, 24, 118. [Google Scholar] [CrossRef]
- Pian, Q.; Yao, R.; Sinsuebphon, N.; Intes, X. Compressive hyperspectral time-resolved wide-field fluorescence lifetime imaging. Nat. Photonics 2017, 11, 411. [Google Scholar] [CrossRef] [PubMed]
- Hadfield, R.H. Single-photon detectors for optical quantum information applications. Nat. Photonics 2009, 3, 696–705. [Google Scholar]
- Patel, K.A.; Dynes, J.F.; Sharpe, A.W.; Yuan, Z.L.; Penty, R.V.; Shields, A.J. Gigacount/second photon detection with InGaAs avalanche photodiodes. Electron. Lett. 2012, 48, 111–113. [Google Scholar] [CrossRef]
- Yu, W.K.; Liu, X.F.; Yao, X.R.; Wang, C.; Gao, S.Q.; Zhai, G.J.; Qing, Z.; Ge, M.L. Single photon counting imaging system via compressive sensing. arXiv, 2012; preprint. arXiv:1202.5866. [Google Scholar]
- Yu, W.K.; Yao, X.R.; Liu, X.F.; Zhai, G.J.; Zhao, Q. Compressed sensing for ultra-weak light counting imaging. Opt. Precis. Eng. 2012, 20, 2283. [Google Scholar]
- Howell, J.C. Compressive depth map acquisition using a single photon-counting detector: Parametric signal processing meets sparsity. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 96–102. [Google Scholar]
- Howland, G.A.; Lum, D.J.; Ware, M.R.; Howell, J.C. Photon counting compressive depth mapping. Opt. Express 2013, 21, 23822–23837. [Google Scholar]
- Dai, H.D.; Gu, G.H.; He, W.J.; Ye, L.; Mao, T.Y.; Chen, Q. Adaptive compressed photon counting 3D imaging based on wavelet trees and depth map sparse representation. Opt. Express 2016, 24, 26080–26096. [Google Scholar] [CrossRef]
- Tiwari, V.; Bansod, P.P.; Kumar, A. Designing sparse sensing matrix for compressive sensing to reconstruct high resolution medical images. Cogent Eng. 2015, 2, 1017244. [Google Scholar] [CrossRef]
- Obermeier, R.; Martinez-Lorenzo, J.A. Sensing Matrix Design via Mutual Coherence Minimization for Electromagnetic Compressive Imaging Applications. IEEE Trans. Comput. Imaging 2017, 3, 217–229. [Google Scholar]
- Yan, Q.R.; Wang, H.; Yuan, C.L.; Li, B.; Wang, Y.H. Large-area single photon compressive imaging based on multiple micro-mirrors combination imaging method. Opt. Express 2018, 26, 19080–19090. [Google Scholar] [PubMed]
- Wu, Y. Research on Measure Matrix for Compressive Sensing; XiDian University: Xian, China, 2012. [Google Scholar]
- Zepernick, H.J.; Finger, A. Pseudo Random Signal Processing: Theory and Application; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Dang, K.; Ma, L.; Tian, Y.; Zhang, H.; Ru, L.; Li, X. Construction of the compressive sensing measurement matrix based on m sequences. J. Xidian Univ. 2015, 42, 186. [Google Scholar]
- Yan, Q.; Zhao, B.; Hua, Z.; Liao, Q.; Yang, H. High-speed quantum-random number generation by continuous measurement of arrival time of photons. Rev. Sci. Instrum. 2015, 86, 073113. [Google Scholar] [CrossRef]
- Yan, Q.; Zhao, B.; Liao, Q.; Zhou, N. Multi-bit quantum random number generation by measuring positions of arrival photons. Rev. Sci. Instrum. 2014, 85, 103116. [Google Scholar] [CrossRef] [PubMed]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar]
- Candès, E.J.; Romberg, J.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Comm. Pure Appl. Math 2006, 59, 1207. [Google Scholar] [CrossRef]
- Cai, T.; Wang, L.; Xu, G. Stable Recovery of Sparse Signals and an Oracle Inequality. IEEE Trans. Inf. Theory 2010, 56, 3516–3522. [Google Scholar] [CrossRef]
- Donoho, D.L.; Huo, X. Uncertainty Principles and Ideal Atomic Decomposition. IEEE Trans. Inf. Theory 1999, 47, 2845–2862. [Google Scholar]
- Elad, M.; Bruckstein, A.M. A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Trans. Inf. Theory 2002, 48, 2558–2567. [Google Scholar] [CrossRef]
- Jiao, L.C.; Yang, S.Y.; Liu, F.; Hou, B. Development and prospect of compressive sensing. Acta Electron. Sin. 2011, 39, 1651. [Google Scholar]

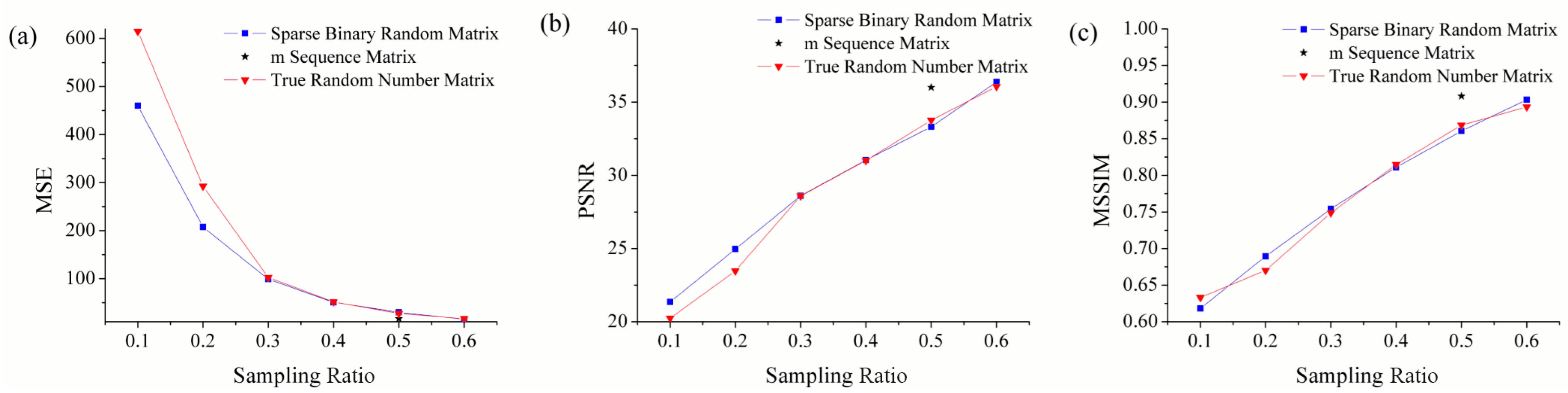

| Evaluation Index | MSE | PSNR | MSSIM |
|---|---|---|---|
| Sparse binary random matrix | 29.6249 | 33.3144 | 0.8607 |
| m sequence matrix | 16.3040 | 36.0078 | 0.9081 |
| True random number matrix | 27.3209 | 33.7658 | 0.8685 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yan, Q.; Li, B.; Yuan, C.; Wang, Y. Measurement Matrix Construction for Large-area Single Photon Compressive Imaging. Sensors 2019, 19, 474. https://doi.org/10.3390/s19030474
Wang H, Yan Q, Li B, Yuan C, Wang Y. Measurement Matrix Construction for Large-area Single Photon Compressive Imaging. Sensors. 2019; 19(3):474. https://doi.org/10.3390/s19030474
Chicago/Turabian StyleWang, Hui, Qiurong Yan, Bing Li, Chenglong Yuan, and Yuhao Wang. 2019. "Measurement Matrix Construction for Large-area Single Photon Compressive Imaging" Sensors 19, no. 3: 474. https://doi.org/10.3390/s19030474
APA StyleWang, H., Yan, Q., Li, B., Yuan, C., & Wang, Y. (2019). Measurement Matrix Construction for Large-area Single Photon Compressive Imaging. Sensors, 19(3), 474. https://doi.org/10.3390/s19030474





