Finite-Time Attitude Stabilization Adaptive Control for Spacecraft with Actuator Dynamics
Abstract
1. Introduction
2. Mathematical Model with Actuator Dynamics
2.1. Notation
2.2. Attitude Dynamics and Kinematics
2.3. Actuator Dynamics
2.4. Assumptions and Lemmas
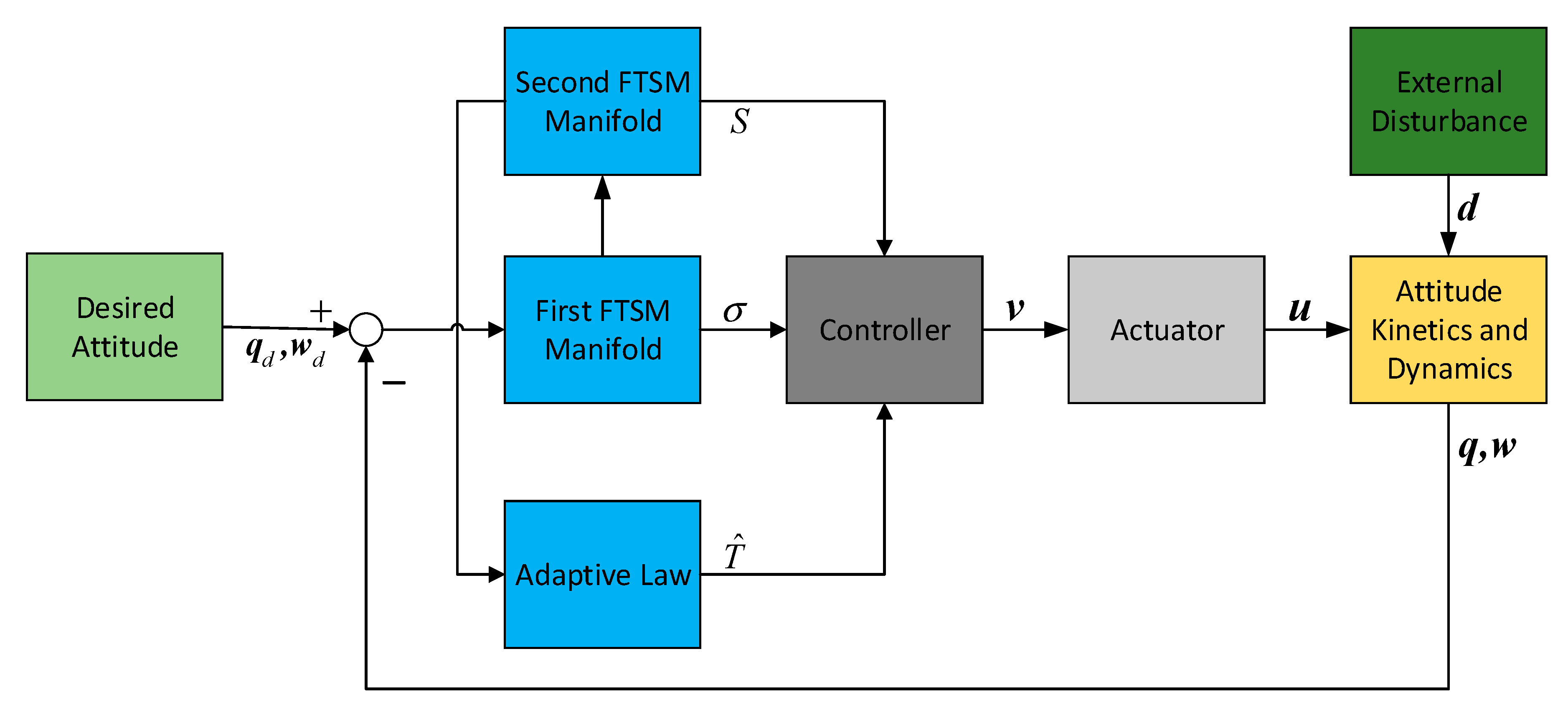
3. Attitude Control Law with Actuator Dynamics Design
3.1. Basic Double FTSM Control Law Design
3.2. Adaptive Double FTSM Control Law Design
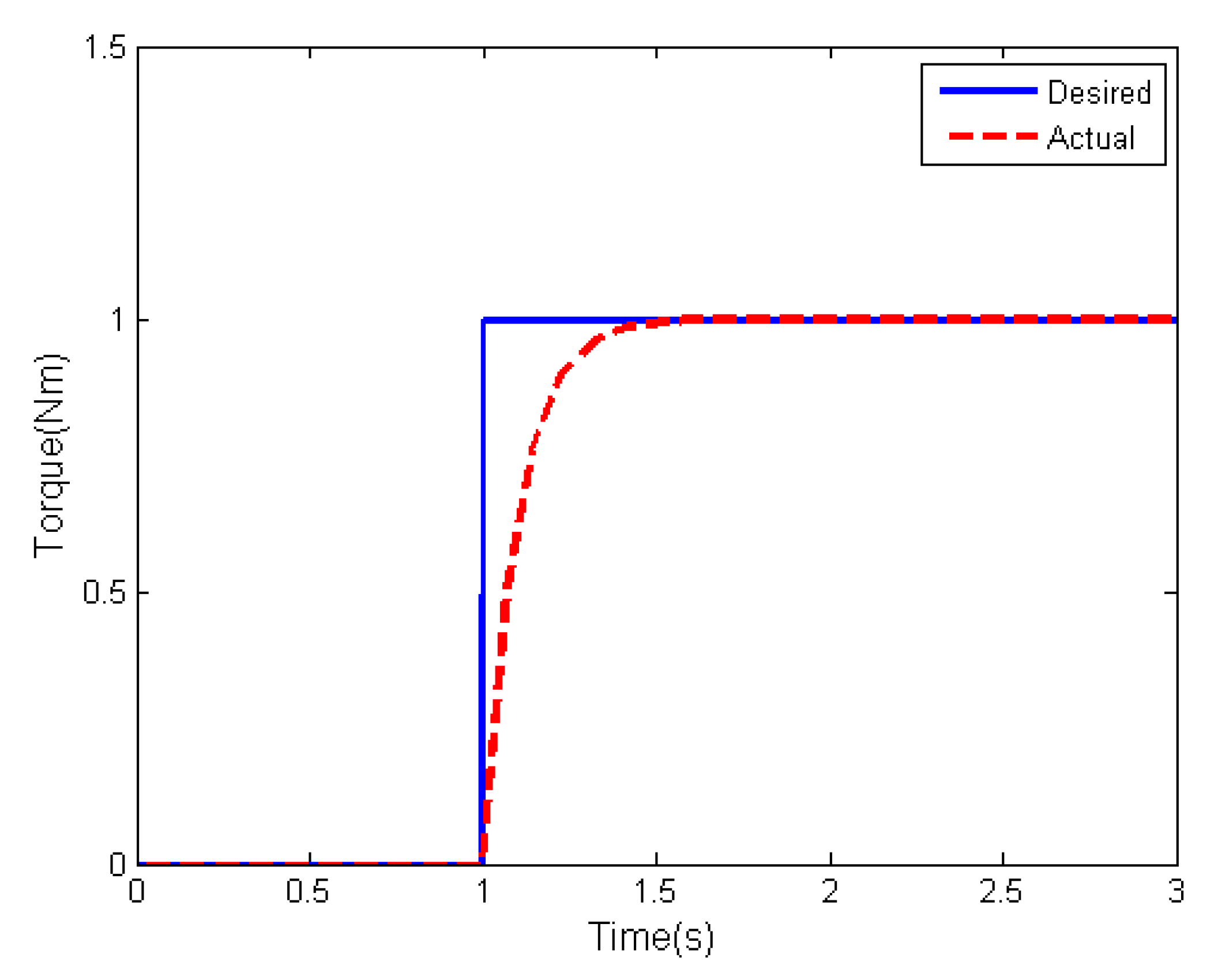
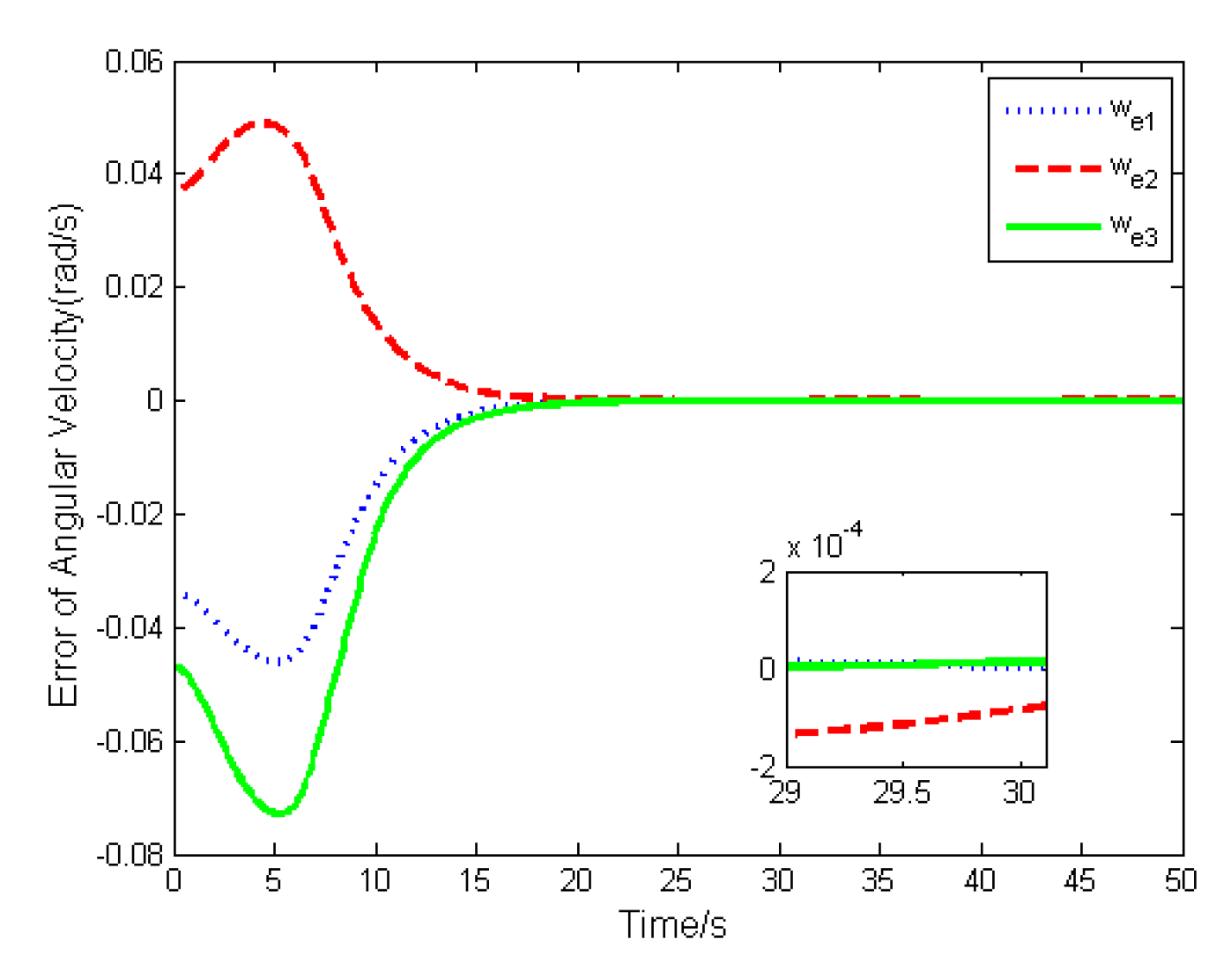
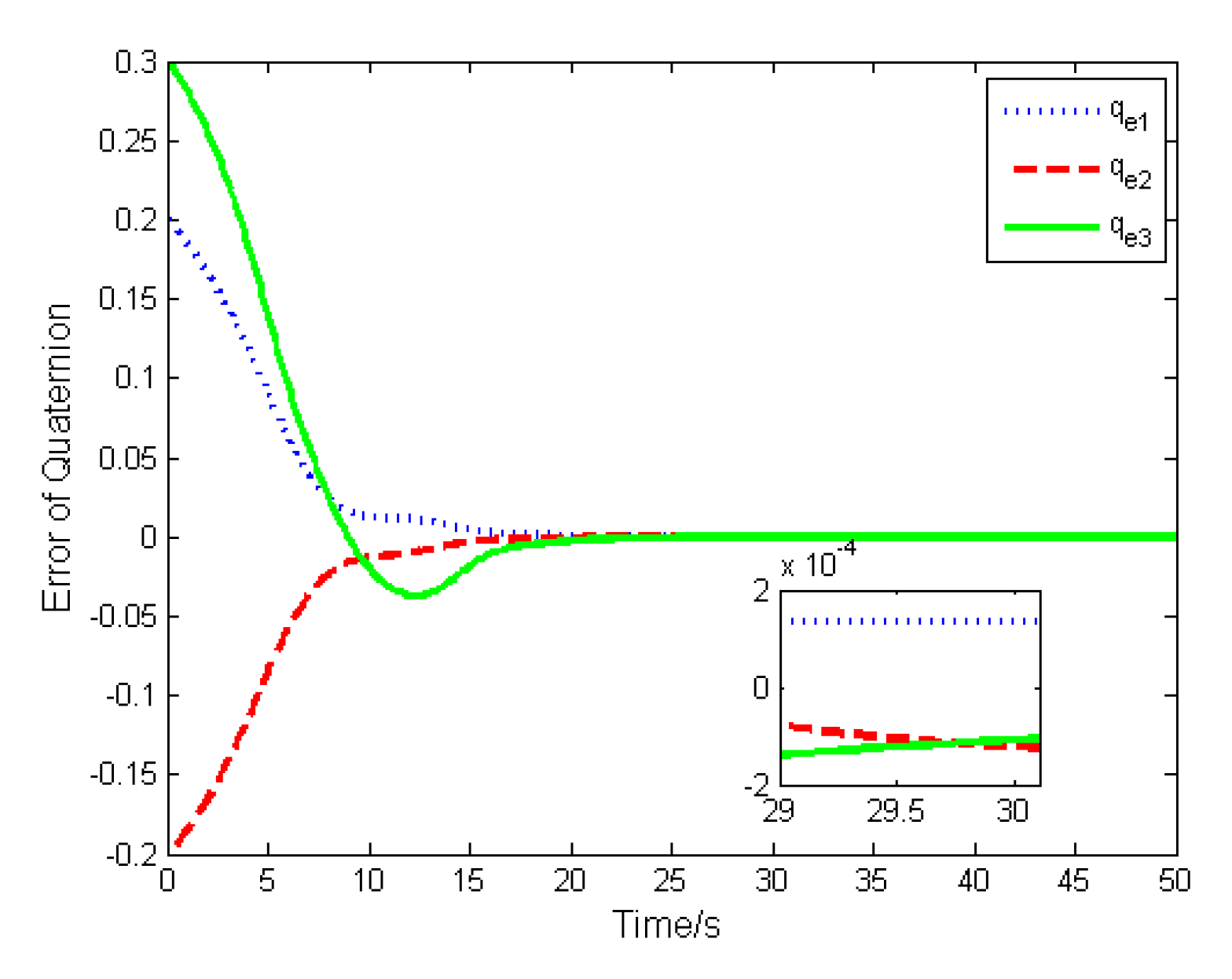
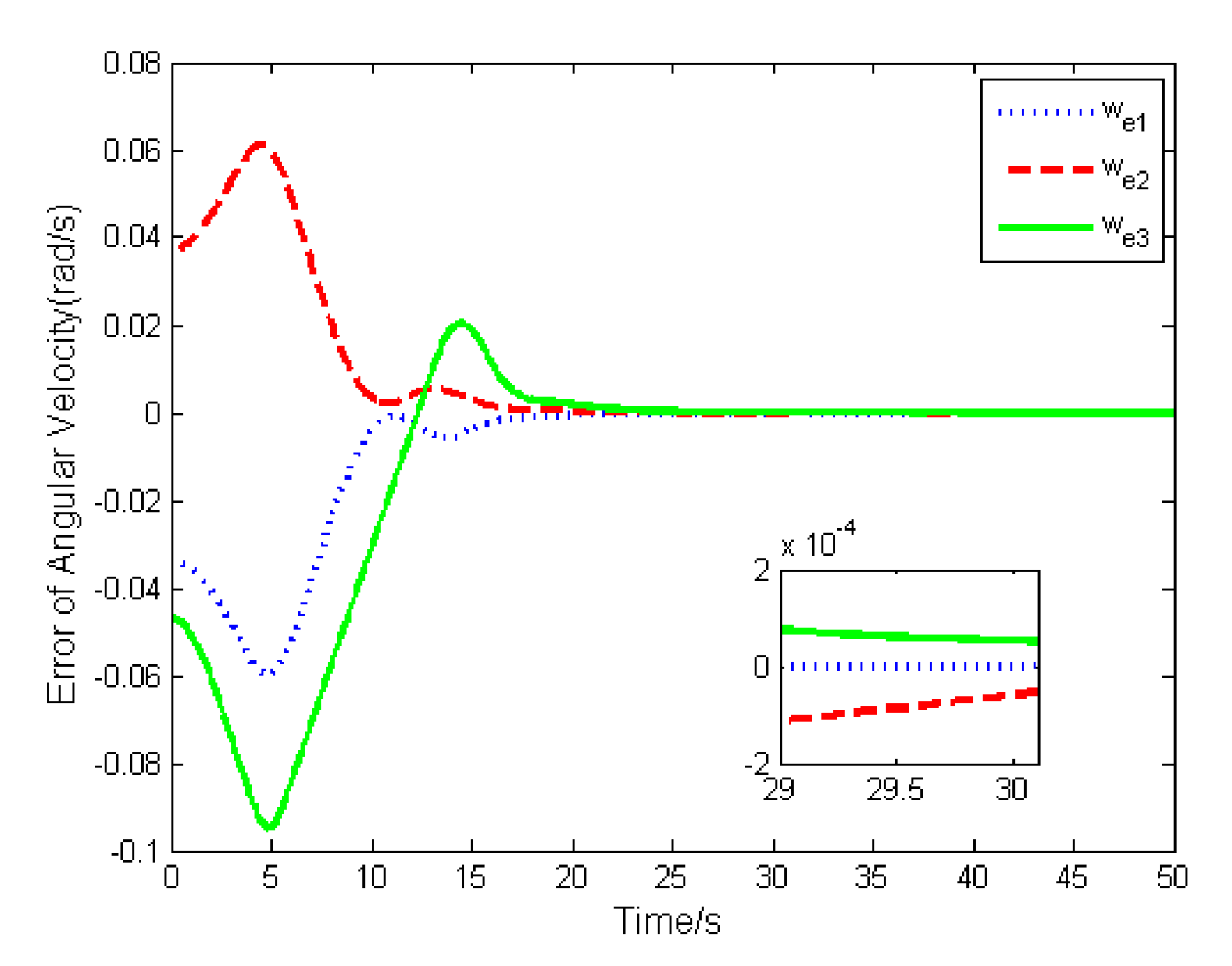
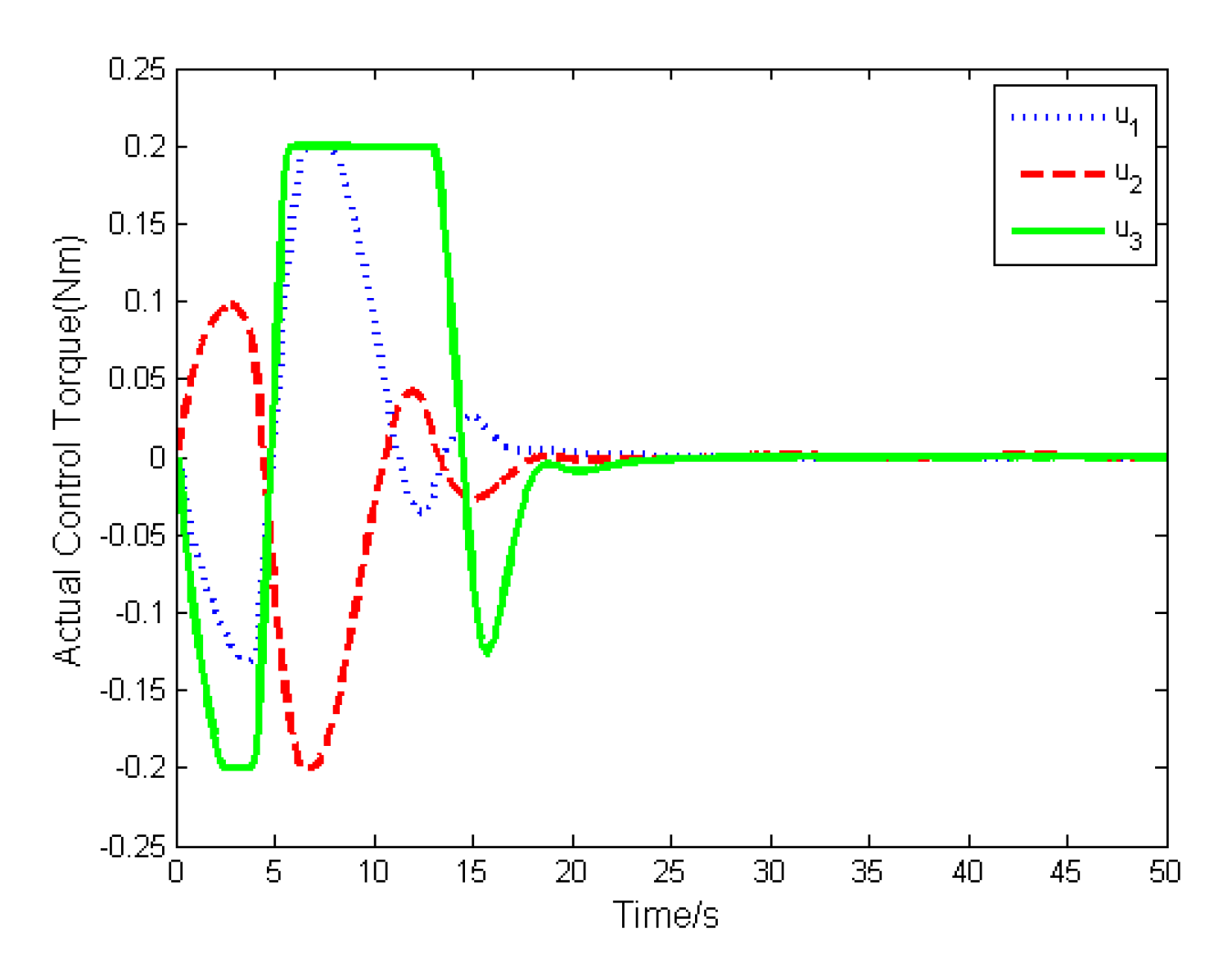
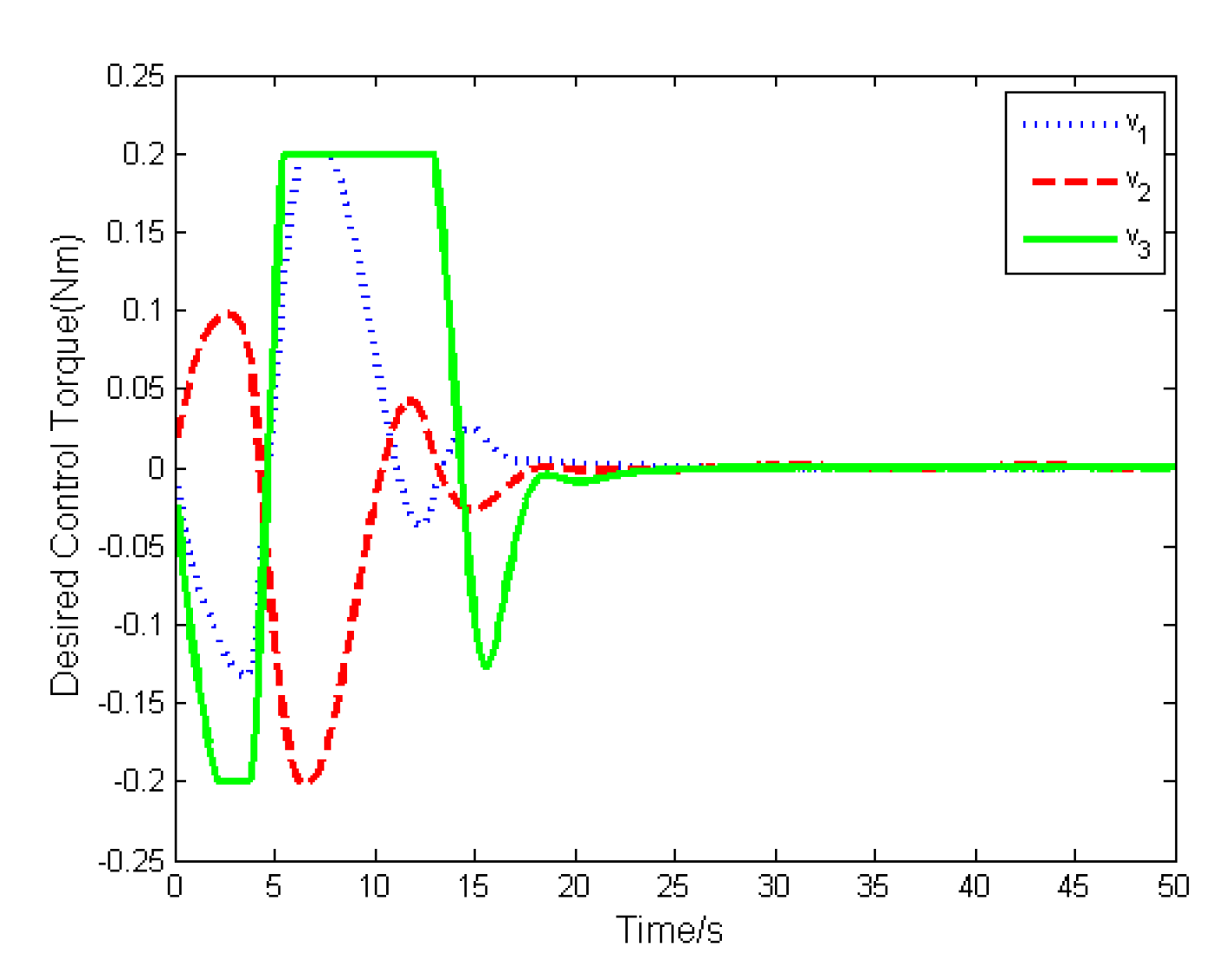
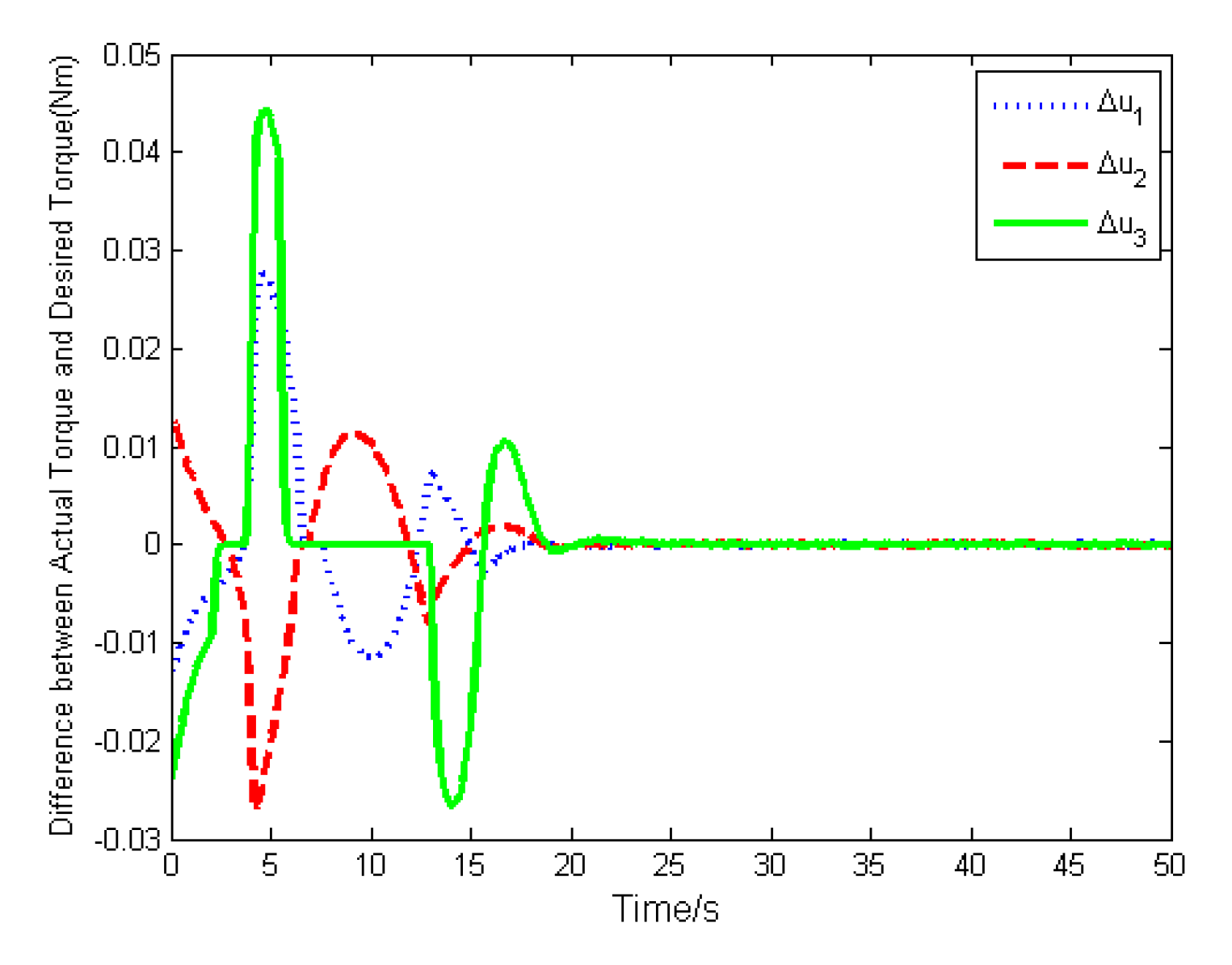
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Hu, Q.; Tan, X.; Akella, M.R. Finite-Time Fault-Tolerant Spacecraft Attitude Control with Torque Saturation. J. Guid. Control Dyn. 2017, 40, 2524–2537. [Google Scholar] [CrossRef]
- Song, Z.; Li, H.; Sun, K. Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique. ISA Trans. 2014, 53, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, P.M.; Janardhanan, S.; Nabi, M. Rigid Spacecraft Attitude Control Using Adaptive Non-singular Fast Terminal Sliding Mode. J. Control Autom. Electr. Syst. 2015, 26, 115–124. [Google Scholar] [CrossRef]
- Zou, A.-M.; Kumar, K.D. Finite-Time Attitude Tracking Control for Spacecraft Using Terminal Sliding Mode and Chebyshev Neural Network. IEEE Trans. Syst. Man Cybern. Part B 2011, 41, 950–963. [Google Scholar]
- Kritiansen, R.; Hagen, D. Modeling of Actuator Dynamics for Spacecraft Attitude Control. J. Guid. Control Dyn. 2009, 32, 1022–1025. [Google Scholar] [CrossRef]
- Hu, Q.; Cao, J.; Zhang, Y. Robust Backstepping Sliding Mode Attitude Tracking and Vibration Damping of Flexible Spacecraft with Actuator Dynamics. J. Aerosp. Eng. 2009, 22, 139–152. [Google Scholar] [CrossRef]
- Xiao, B.; Hu, Q.; Zhang, Y.; Huo, X. Fault-Tolerant Tracking Control of Spacecraft with Attitude-Only Measurement Under Actuator Failures. J. Guid. Control Dyn. 2014, 37, 838–849. [Google Scholar] [CrossRef]
- Han, Y.; Biggs, J.D.; Cui, N. Adaptive Fault-Tolerant Control of Spacecraft Attitude Dynamics with Actuator Failures. J. Guid. Control Dyn. 2015, 38, 2033–2042. [Google Scholar] [CrossRef]
- Ruiter, A.H.J. Adaptive Spacecraft Attitude Tracking Control with Actuator Saturation. J. Guid. Control Dyn. 2010, 33, 1692–1695. [Google Scholar] [CrossRef]
- Tiwari, P.M.; Janardhanan, S.; Nabi, M. Rigid spacecraft attitude control using adaptive integral second order sliding mode. Aerosp. Sci. Technol. 2015, 42, 50–57. [Google Scholar] [CrossRef]
- Thakur, D.; Srikant, S.; Akella, M.R. Adaptive Attitude-Tracking Control of Spacecraft with Uncertain Time-Varying Inertia Parameters. J. Guid. Control Dyn. 2015, 38, 41–52. [Google Scholar] [CrossRef]
- Zhong, C.; Guo, Y.; Yu, Z.; Wang, L.; Chen, Q. Finite-Time attitude control for flexible spacecraft with unknown bounded disturbance. Tras. Inst. Meas. Control 2016, 38, 240–249. [Google Scholar] [CrossRef]
- Hu, Q. Sliding mode attitude control with L2-gain performance and vibration of flexible spacecraft with actuator dynamics. Acta Astronaut. 2010, 67, 572–583. [Google Scholar] [CrossRef]
- Shuster, M.D. A Survey of Attitude Representations. J. Astronaut. Sci. 1993, 41, 439–517. [Google Scholar]
- Bhat, S.P.; Bernstein, D.S. Finite-Time Stability of Continuous Autonomous Systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Krupp, D.R.; Shkolnikov, I.A.; Shtessel, Y.B. 2-sliding mode control for nonlinear plants with parametric and dynamic uncertainties. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, CO, USA, 14–17 August 2000; pp. 1–9. [Google Scholar]
- Krupp, D.; Shtessel, Y.B. Chattering-free Sliding Mode Control with Unmodeled Dynamics. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999; pp. 530–534. [Google Scholar]
- Shen, Q.; Wang, D.; Zhu, S.; Poh, E.K. Finite-Time Fault-Tolerant Attitude Stabilization for Spacecraft With Actuator Saturation. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2390–2405. [Google Scholar] [CrossRef]
- Krstic, M.; Kanellakopoulos, L.; Kokotovic, P. Nonlinear Adaptive Control Design; Wiley Press: New York, NY, USA, 1995. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Ye, D.; Mu, Z.; Sun, Z.; Wu, S. Finite-Time Attitude Stabilization Adaptive Control for Spacecraft with Actuator Dynamics. Sensors 2019, 19, 5568. https://doi.org/10.3390/s19245568
Wang C, Ye D, Mu Z, Sun Z, Wu S. Finite-Time Attitude Stabilization Adaptive Control for Spacecraft with Actuator Dynamics. Sensors. 2019; 19(24):5568. https://doi.org/10.3390/s19245568
Chicago/Turabian StyleWang, Chunbao, Dong Ye, Zhongcheng Mu, Zhaowei Sun, and Shufan Wu. 2019. "Finite-Time Attitude Stabilization Adaptive Control for Spacecraft with Actuator Dynamics" Sensors 19, no. 24: 5568. https://doi.org/10.3390/s19245568
APA StyleWang, C., Ye, D., Mu, Z., Sun, Z., & Wu, S. (2019). Finite-Time Attitude Stabilization Adaptive Control for Spacecraft with Actuator Dynamics. Sensors, 19(24), 5568. https://doi.org/10.3390/s19245568





