Object-Based Image Analysis Applied to Low Altitude Aerial Imagery for Potato Plant Trait Retrieval and Pathogen Detection
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site and Dataset
2.2. Sampling and Modeling
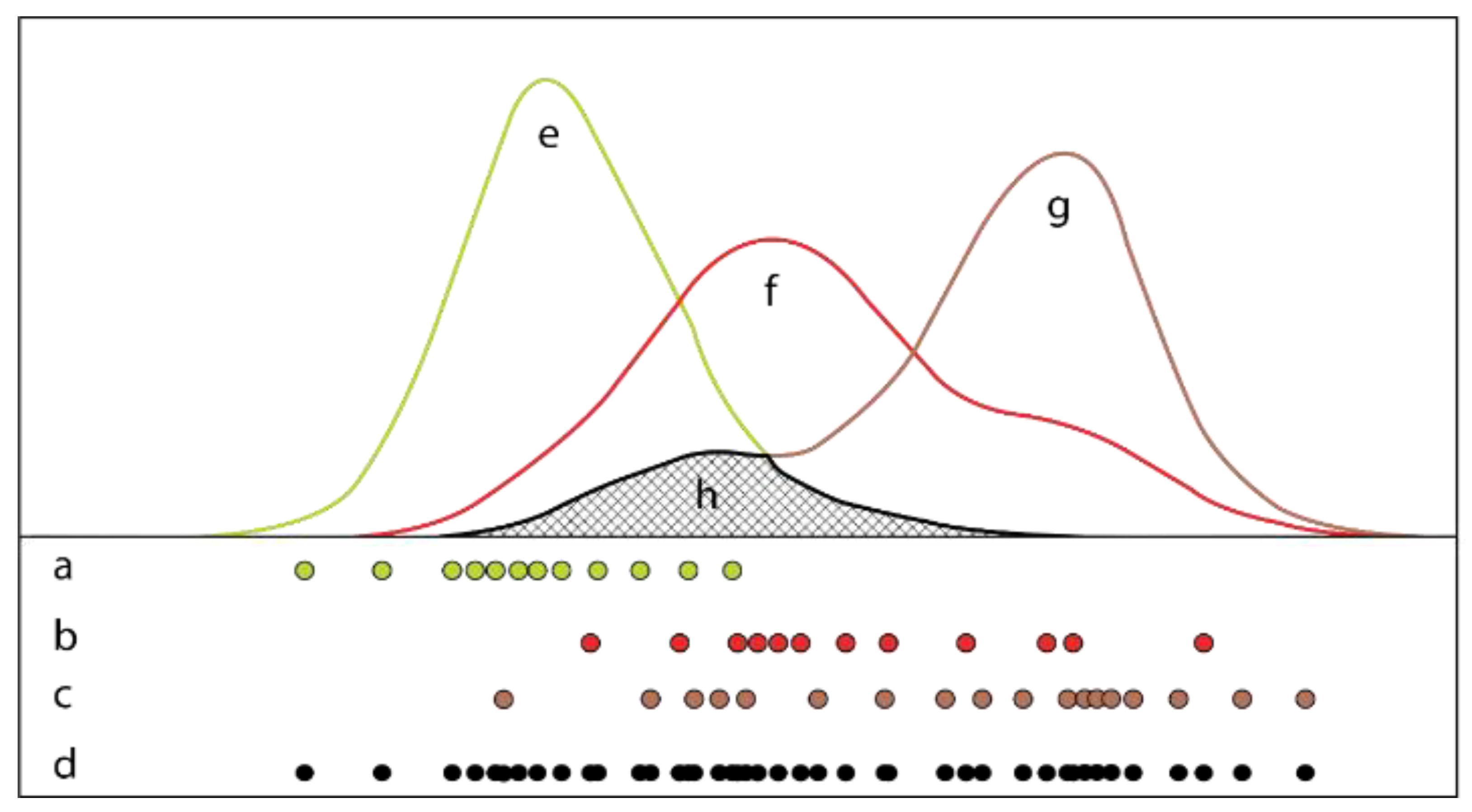
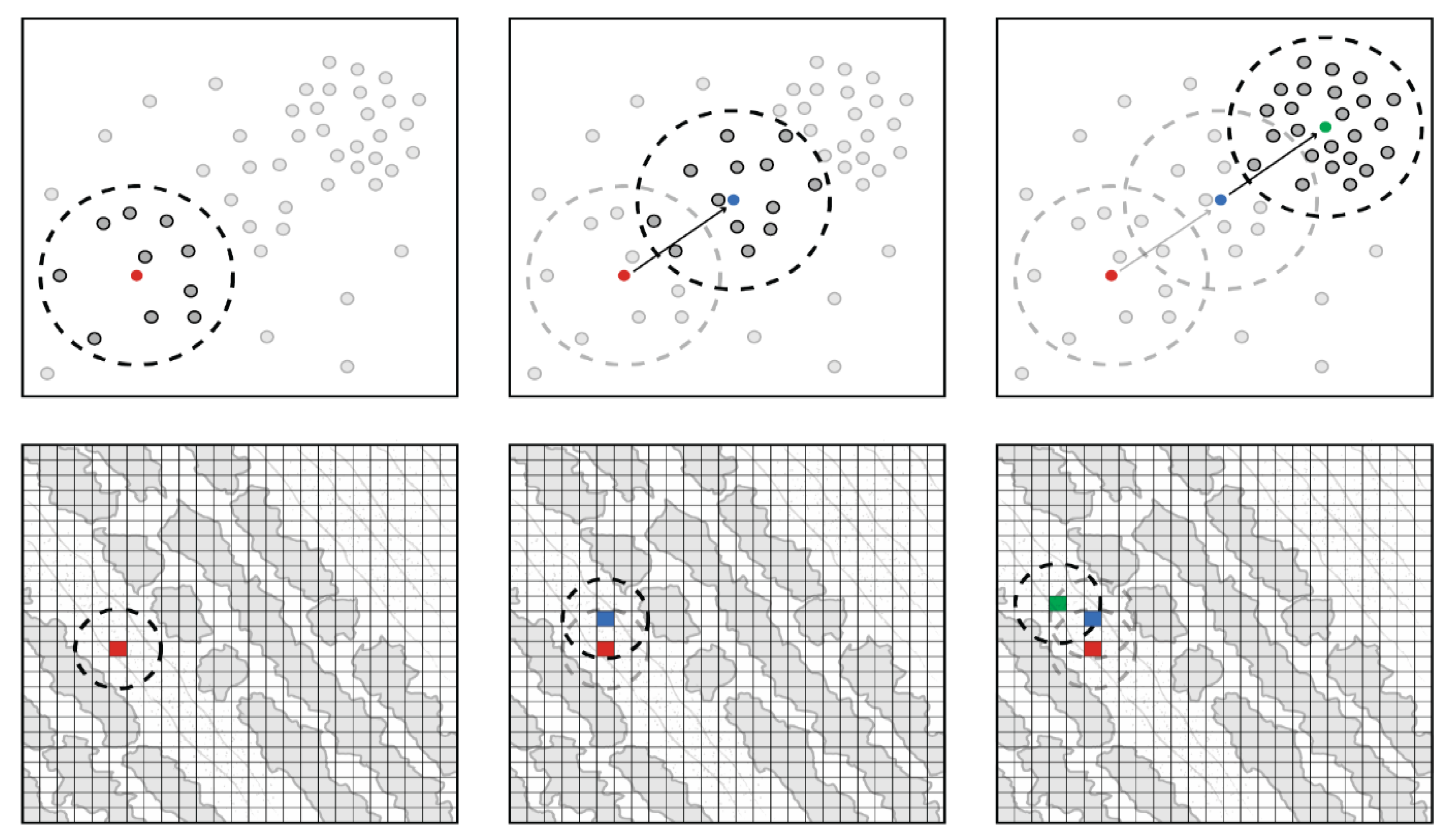
2.3. Initial Plant Mapping
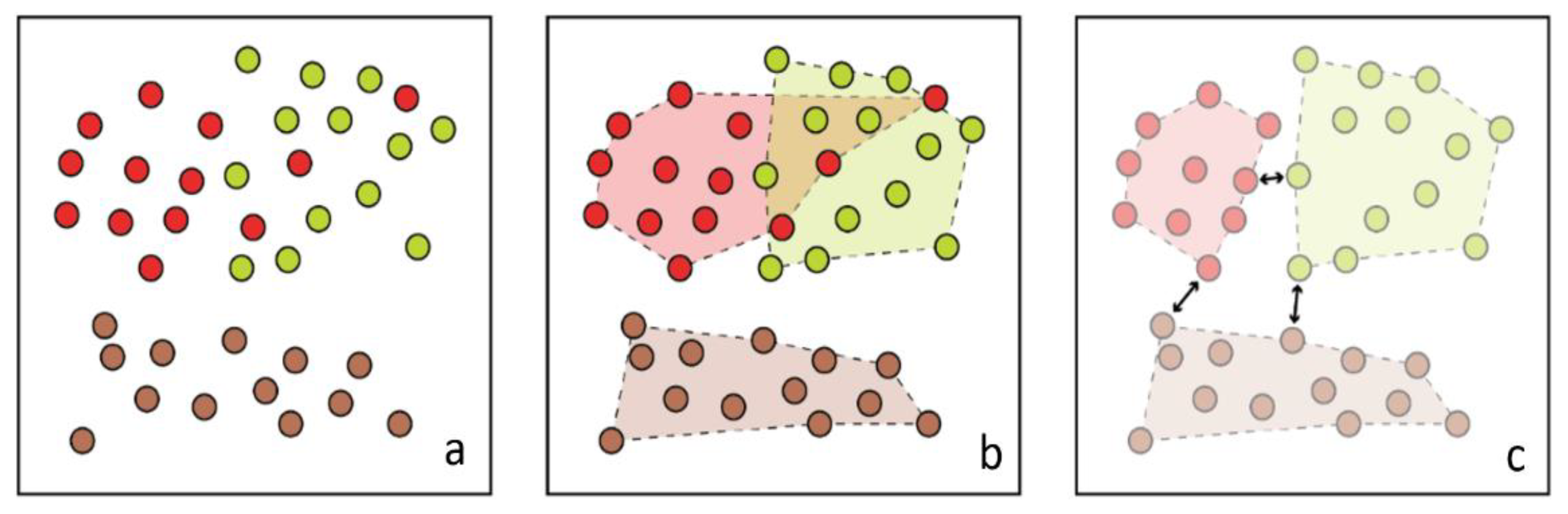
2.4. Class Expansion and Classification
3. Results
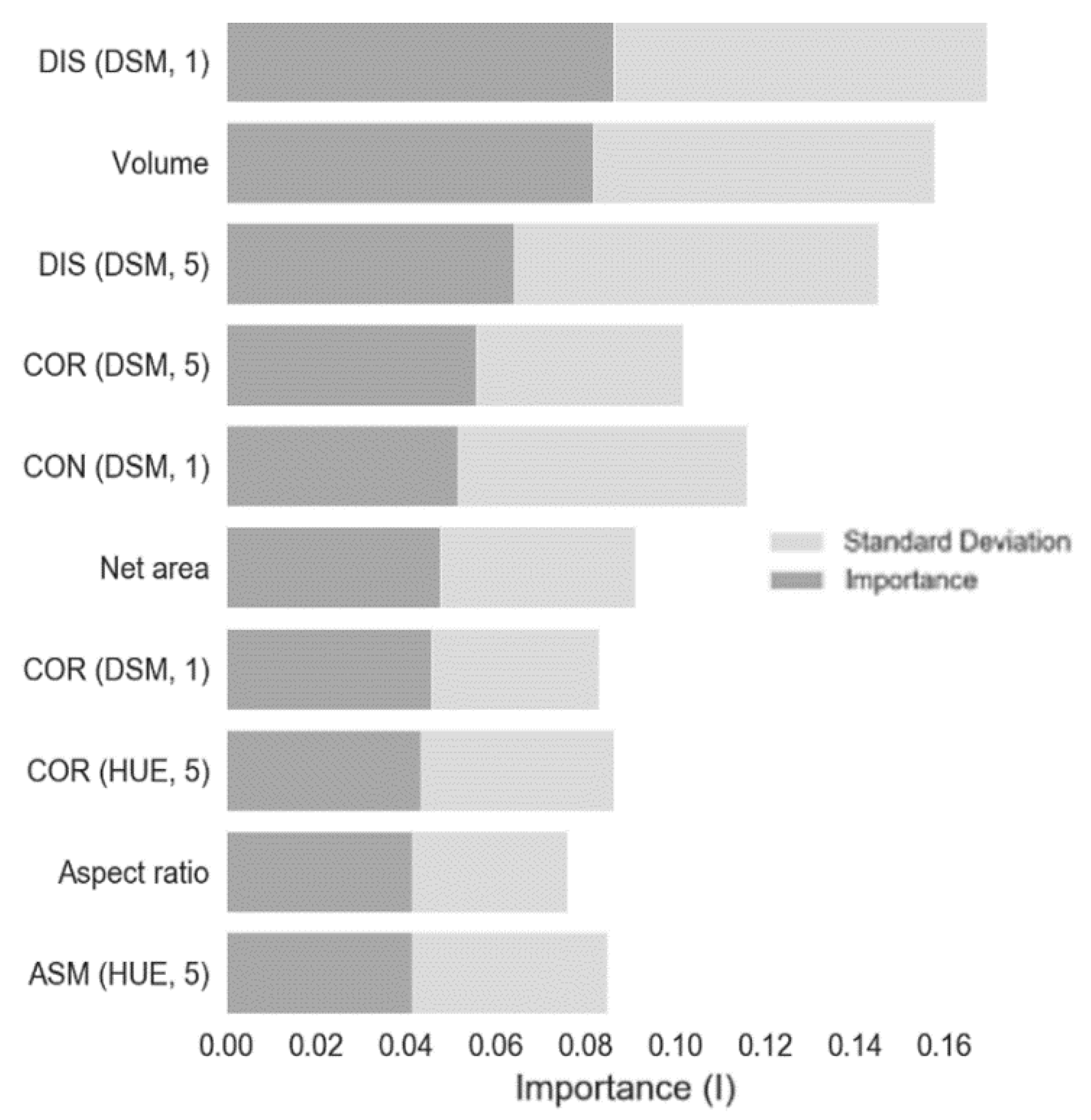
3.1. Separability and Performance
3.2. Disease Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Healthy (µ) | Diseased (µ) | T Values | P Values | |
|---|---|---|---|---|
| Volume | 72.7668 | 61.566 | 7.44281 | 0 |
| # Flowers | 7.64118 | 6.38235 | 2.78653 | 0.00564 |
| Aspect Ratio | 1.06597 | 1.06297 | 0.39755 | 0.69125 |
| Solidity | 0.05259 | 0.06375 | −2.217 | 0.02733 |
| Net Area (m2) | 0.50749 | 0.46247 | 6.11125 | 0 |
| Perimeter (m) | 6.22416 | 5.7683 | 3.29756 | 0.00108 |
| Contrast 1 (DSM) | 111.887 | 140.36 | −6.0246 | 0 |
| Dissimilarity 1 (DSM) | 5.00174 | 5.56444 | −5.9483 | 0 |
| Homogeneity 1 (DSM) | 0.33563 | 0.32129 | 4.3921 | 0.00002 |
| ASM 1 (DSM) | 0.001 | 0.00082 | 5.26375 | 0 |
| Energy 1 (DSM) | 0.03113 | 0.02835 | 5.40393 | 0 |
| Correlation 1 (DSM) | 0.9672 | 0.96978 | −2.6944 | 0.0074 |
| Contrast 5 (DSM) | 759.653 | 933.711 | −5.9451 | 0 |
| Dissimilarity 5 (DSM) | 17.7592 | 19.8636 | −6.1313 | 0 |
| Homogeneity 5 (DSM) | 0.07983 | 0.07286 | 4.44554 | 0.00001 |
| ASM 5 (DSM) | 0.00033 | 0.00029 | 4.0238 | 0.00007 |
| Energy 5 (DSM) | 0.01786 | 0.01686 | 4.04216 | 0.00007 |
| Correlation 5 (DSM) | 0.75588 | 0.78134 | −4.2657 | 0.00003 |
| Contrast 1 (Hue) | 30.6429 | 31.2285 | −0.5783 | 0.56345 |
| Dissimilarity 1 (Hue) | 3.92445 | 3.97107 | −0.7314 | 0.46502 |
| Homogeneity 1 (Hue) | 0.24755 | 0.24455 | 0.84087 | 0.40102 |
| ASM 1 (Hue) | 0.00406 | 0.00368 | 3.21612 | 0.00143 |
| Energy 1 (Hue) | 0.06311 | 0.06009 | 3.37492 | 0.00082 |
| Correlation 1 (Hue) | 0.64758 | 0.68589 | −4.8532 | 0 |
| Contrast 5 (Hue) | 67.2367 | 71.6527 | −2.4429 | 0.01508 |
| Dissimilarity 5 (Hue) | 6.08534 | 6.30297 | −2.7502 | 0.00628 |
| Homogeneity 5 (Hue) | 0.16461 | 0.15893 | 2.96378 | 0.00326 |
| ASM 5 (Hue) | 0.00313 | 0.00277 | 4.29112 | 0.00002 |
| Energy 5 (Hue) | 0.05551 | 0.05213 | 4.48815 | 0.00001 |
| Correlation 5 (Hue) | 0.19399 | 0.2515 | −5.3375 | 0 |
References
- United Nations. World Population Prospects 2019: Highlights (ST/ESA/SER.A/423); United Nations: New York, NY, USA, 2019. [Google Scholar]
- Food and Agriculture Organization of the United Nations. The Future of Food and Agriculture: Trends and Challenges; FAO: Rome, Italy, 2017. [Google Scholar]
- Food and Agriculture, Organization of the United Nations. The state of the world′s land and water resources for food and agriculture (SOLAW)—Managing systems at risk. In The State of the World′s Land and Water Resources for Food and Agriculture, Managing Systems at Risk; Earthscan: London, UK, 2011; ISBN 978-1-84971-326-9. [Google Scholar]
- Savary, S.; Ficke, A.; Aubertot, J.N.; Hollier, C. Crop losses due to diseases and their implications for global food production losses and food security. Food Secur. 2012, 4, 519–537. [Google Scholar] [CrossRef]
- Sankaran, S.; Mishra, A.; Ehsani, R.; Davis, C. A review of advanced techniques for detecting plant diseases. Comput. Electron. Agric. 2010, 72, 1–13. [Google Scholar] [CrossRef]
- Atli Benediktsson, J.; Chaunussot, J.; Moon, W. Advances in Very-High-Resolution Remote Sensing. Proc. IEEE 2013, 101, 566–569. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Perspectives for Remote Sensing with Unmanned Aerial Vehicles in Precision Agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Raparelli, E.; Bajocco, S. A bibliometric analysis on the use of unmanned aerial vehicles in agricultural and forestry studies. Int. J. Remote Sens. 2019, 40, 9070–9083. [Google Scholar] [CrossRef]
- Sugiura, R.; Tsuda, S.; Tamiya, S.; Itoh, A.; Nishiwaki, K.; Murakami, N.; Nuske, S. Field phenotyping system for the assessment of potato late blight resistance using RGB imagery from an unmanned aerial vehicle. Biosyst. Eng. 2016, 148, 1–10. [Google Scholar] [CrossRef]
- Singh, R.P.; Valkonen, J.P.T.; Gray, S.M.; Boonham, N.; Jones, R.A.C.; Kerlan, C.; Schubert, J. Discussion paper: The naming of Potato virus Y strains infecting potato. Arch. Virol. 2008, 153, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Toth, I.K.; Bell, K.S.; Holeva, M.C.; Birch, P.R.J. Soft rot erwiniae: From genes to genomes. Mol. Plant Pathol. 2003, 4, 17–30. [Google Scholar] [CrossRef]
- Hay, G.J.; Niemann, K.O.; McLean, G.F. An object-specific image-texture analysis of H-resolution forest imagery. Remote Sens. Environ. 1996, 55, 108–122. [Google Scholar] [CrossRef]
- Hamuda, E.; Glavin, M.; Jones, E. A survey of image processing techniques for plant extraction and segmentation in the field. Comput. Electron. Agric. 2016, 125, 184–199. [Google Scholar] [CrossRef]
- Kerkech, M.; Hafiane, A.; Canals, R. Deep leaning approach with colorimetric spaces and vegetation indices for vine diseases detection in UAV images. Comput. Electron. Agric. 2018, 155, 237–243. [Google Scholar] [CrossRef]
- Castilla, G.; Hay, G.J. Image Objects and Geographic Objects. In Object-Based Image Analysis. Lecture Notes in Geoinformation and Cartography; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 91–110. [Google Scholar] [CrossRef]
- Lang, S.; Hay, G.J.; Baraldi, A.; Tiede, D.; Blaschke, T. GEOBIA achievements and spatial opportunities in the era of big Earth observation data. ISPRS Int. J. Geo-Inf. 2019, 8, 474. [Google Scholar] [CrossRef]
- Lang, S. Object-based image analysis for remote sensing applications: Modeling reality—Dealing with complexity. In Object-Based Image Analysis; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–27. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Tiede, D. Geographic Object-Based Image Analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Leng, W.; Liu, K.; Liu, L.; He, Z.; Zhu, Y. Object-Based mangrove species classification using unmanned aerial vehicle hyperspectral images and digital surface models. Remote Sens. 2018, 10, 89. [Google Scholar] [CrossRef]
- Baatz, M.; Hoffmann, C.; Willhauck, G. Progressing from Object-Based to Object-Oriented Image Analysis. In Object-Based Image Analysis. Lecture Notes in Geoinformation and Cartography; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 29–42. [Google Scholar] [CrossRef]
- Weih, R.C.; Riggan, N.D. Object-based classification vs. pixel-based classification: Comparitive importance of multi-resolution imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 4–7. [Google Scholar]
- Hernández-Hernández, J.L.; García-Mateos, G.; González-Esquiva, J.M.; Escarabajal-Henarejos, D.; Ruiz-Canales, A.; Molina-Martínez, J.M. Optimal color space selection method for plant/soil segmentation in agriculture. Comput. Electron. Agric. 2016, 122, 124–132. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. UAV Remote sensing for urban vegetation mapping using random forest and texture analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef]
- Barbedo, J.G. Digital image processing techniques for detecting, quantifying and classifying plant diseases. SpringerPlus 2013, 2, 660–671. [Google Scholar] [CrossRef]
- Suomalainen, J.; Anders, N.; Iqbal, S.; Roerink, G.; Franke, J.; Wenting, P.; Kooistra, L. A lightweight hyperspectral mapping system and photogrammetric processing chain for unmanned aerial vehicles. Remote Sens. 2014, 6, 11013–11030. [Google Scholar] [CrossRef]
- Polder, G.; Blok, P.M.; de Villiers, H.A.C.; van der Wolf, J.M.; Kamp, J. Potato virus Y detection in seed potatoes using deep learning on hyperspectral images. Front. Plant Sci. 2019, 10. [Google Scholar] [CrossRef]
- García-Mateos, G.; Hernández-Hernández, J.L.; Escarabajal-Henarejos, D.; Jaén-Terrones, S.; Molina-Martínez, J.M. Study and comparison of color models for automatic image analysis in irrigation management applications. Agric. Water Manag. 2015, 151, 158–166. [Google Scholar] [CrossRef]
- Turlach, B.A. Bandwidth Selection in Kernel Density Estimation: A Review. CORE Inst. Stat. 1993, 23–493. [Google Scholar]
- Scott, D.W. Scott′s rule. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 497–502. [Google Scholar] [CrossRef]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
- Michel, J.; Youssefi, D.; Grizonnet, M. Stable mean-shift algorithm and its application to the segmentation of arbitrarily large remote sensing images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 952–964. [Google Scholar] [CrossRef]
- Mahlein, A.-K. Present and Future Trends in Plant Disease Detection. Plant Dis. 2016, 100, 1–11. [Google Scholar] [CrossRef]
- Su, W.; Li, J.; Chen, Y.; Liu, Z.; Zhang, J.; Low, T.M.; Hashim, S.A.M. Textural and local spatial statistics for the object-oriented classification of urban areas using high resolution imagery. Int. J. Remote Sens. 2008, 29, 3105–3117. [Google Scholar] [CrossRef]
- Pascale, D. A review of RGB color spaces from xyY to R′G′B′. Babel Color 2003, 18, 1–35. Available online: http://scholar.google.com/scholar?hl=enbtnG=Searchq=intitle:A+Review+of+RGB+color+spaces+from+xyY+to+R′G′B#0 (accessed on 5 May 2019).
- James, G.; Witen, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R. In Performance Evaluation; Elsevier: Austin, TX, USA, 2017; Volume 64. [Google Scholar] [CrossRef]
- Shih, P.; Liu, C. Comparative assessment of content-based face image retrieval in different color spaces. J. Pattern Recognit. Artif. Intell. 2005, 19, 873–893. [Google Scholar] [CrossRef]
- Tian, L.F.; Slaughter, D.C. Environmentally adaptive segmentation algorithm for outdoor image segmentation. Comput. Electron. Agric. 1998, 21, 153–168. [Google Scholar] [CrossRef]
- Strahler, A.H.; Woodcock, C.E.; Smith, J.A. On the nature of models in remote sensing. Remote Sens. Environ. 1986, 20, 121–139. [Google Scholar] [CrossRef]
- Gibson-Poole, S.; Humphris, S.; Toth, I.; Hamilton, A. Identification of the onset of disease within a potato crop using a UAV equipped with un-modified and modified commercial off-the-shelf digital cameras. Adv. Anim. Biosci. 2017, 8, 812–816. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Peña, J.M. An automatic object-based method for optimal thresholding in UAV images: Application for vegetation detection in herbaceous crops. Comput. Electron. Agric. 2015, 114, 43–52. [Google Scholar] [CrossRef]
- Mahlein, A.-K.; Kuska, M.T.; Thomas, S.; Wahabzada, M.; Behmann, J.; Rascher, U.; Kersting, K. Quantitative and qualitative phenotyping of disease resistance of crops by hyperspectral sensors: Seamless interlocking of phytopathology, sensors, and machine learning is needed! Curr. Opin. Plant Biol. 2019, 50, 156–162. [Google Scholar] [CrossRef] [PubMed]
- Mafanya, M.; Tsele, P.; Botai, J.; Manyama, P.; Swart, B.; Monate, T. Evaluating pixel and object based image classification techniques for mapping plant invasions from UAV derived aerial imagery: Harrisia pomanensis as a case study. ISPRS J. Photogramm. Remote Sens. 2017, 129, 1–11. [Google Scholar] [CrossRef]
- Prokop, R.J.; Reeves, A.P. A survey of moment-based techniques for unoccluded object representation and recognition. CVGIP Graph. Models Image Process. 1992, 54, 438–460. [Google Scholar] [CrossRef]
- Sebari, I.; He, D.C. Automatic fuzzy object-based analysis of VHSR images for urban objects extraction. ISPRS J. Photogramm. Remote Sens. 2013, 79, 171–184. [Google Scholar] [CrossRef]

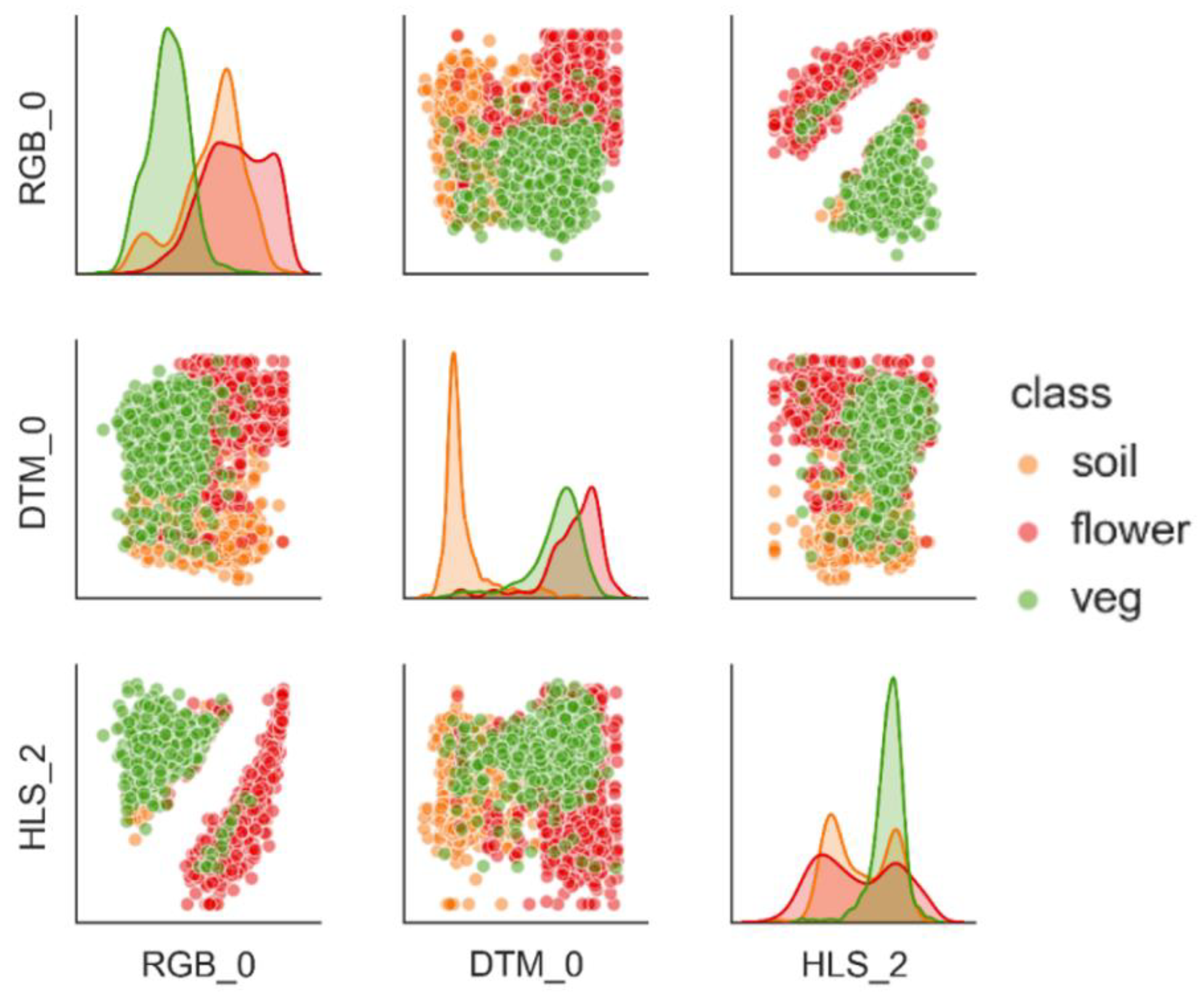

| Transformation | Purpose | # | Source |
|---|---|---|---|
| rgb | Normalize luminance | 3 | [27] |
| YUV | Compression (video) | 3 | [27] |
| HSV | Intuitive color representation | 3 | [27] |
| HLS | Intuitive color representation | 3 | [27] |
| LAB | Uniform color representation | 3 | [27] |
| LUV | Uniform color representation | 3 | [27] |
| XYZ | Modeling the human retina | 3 | [27] |
| I1I2I3 | Decorrelate primary colors | 3 | [27] |
| EXR | Emphasize red tones | 1 | [13] |
| EXB | Emphasize blue tones | 1 | [13] |
| EXG | Emphasize green tones | 1 | [13] |
| CIVE | Emphasize green tones | 1 | [13] |
| # | Color Definition | MCC(veg) | MCC(Flower) | MCC(Soil) | MCC(µ) | Overlap |
|---|---|---|---|---|---|---|
| 5 | DSM_0,HLS_2,HSV_0,LUV_1,LUV_2 | 0.860262 | 0.649457 | 0.883537 | 0.51032 | 0.002226 |
| DSM_0,YUV_2,HLS_2,HSV_0,LUV_2 | 0.857509 | 0.63696 | 0.881851 | 0.50556 | 0.002472 | |
| DSM_0,I23_1,I23_2,LUV_1,LUV_2 | 0.845499 | 0.625602 | 0.869054 | 0.49758 | 0.001609 | |
| DSM_0,YUV_2,HLS_2,HSV_0,YUV_1 | 0.854386 | 0.604864 | 0.881494 | 0.49469 | 0.002744 | |
| 3 | DSM_0,HSV_0,HLS_1 | 0.834355 | 0.537583 | 0.871446 | 0.46829 | 0.00611 |
| DSM_0,YUV_0,HSV_0 | 0.835072 | 0.535683 | 0.868721 | 0.46711 | 0.005786 | |
| RGB_1,DSM_0,HSV_2 | 0.838721 | 0.523977 | 0.873642 | 0.46484 | 0.003734 | |
| RGB_0,DSM_0,HSV_2 | 0.775362 | 0.55155 | 0.814206 | 0.45313 | 0.003568 | |
| 1 | DSM_0 | 0.6276 | 0.19633 | 0.83016 | 0.32548 | 0.021265 |
| RGB_2 | 0.57866 | 0.43062 | 0.50568 | 0.32044 | 0.100627 | |
| XYZ_2 | 0.57112 | 0.42312 | 0.49702 | 0.31516 | 0.100731 | |
| HSV_0 | 0.70743 | 0.13215 | 0.79449 | 0.30469 | 0.047911 |
| F1 | MCC | Model Parameters | ||
|---|---|---|---|---|
| base model | healthy | 0.73 | trees = 10 bootstrap = true max features = none minimal split size = 2 minimal leaf size = 1 | |
| diseased | 0.68 | |||
| avg/total | 0.7 | 0.41 | ||
| optimized model | healthy | 0.75 | trees = 100 bootstrap = true max features = 20 minimal split size = 2 minimal leaf size = 1 | |
| diseased | 0.72 | |||
| avg/total | 0.73 | 0.47 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siebring, J.; Valente, J.; Domingues Franceschini, M.H.; Kamp, J.; Kooistra, L. Object-Based Image Analysis Applied to Low Altitude Aerial Imagery for Potato Plant Trait Retrieval and Pathogen Detection. Sensors 2019, 19, 5477. https://doi.org/10.3390/s19245477
Siebring J, Valente J, Domingues Franceschini MH, Kamp J, Kooistra L. Object-Based Image Analysis Applied to Low Altitude Aerial Imagery for Potato Plant Trait Retrieval and Pathogen Detection. Sensors. 2019; 19(24):5477. https://doi.org/10.3390/s19245477
Chicago/Turabian StyleSiebring, Jasper, João Valente, Marston Heracles Domingues Franceschini, Jan Kamp, and Lammert Kooistra. 2019. "Object-Based Image Analysis Applied to Low Altitude Aerial Imagery for Potato Plant Trait Retrieval and Pathogen Detection" Sensors 19, no. 24: 5477. https://doi.org/10.3390/s19245477
APA StyleSiebring, J., Valente, J., Domingues Franceschini, M. H., Kamp, J., & Kooistra, L. (2019). Object-Based Image Analysis Applied to Low Altitude Aerial Imagery for Potato Plant Trait Retrieval and Pathogen Detection. Sensors, 19(24), 5477. https://doi.org/10.3390/s19245477








