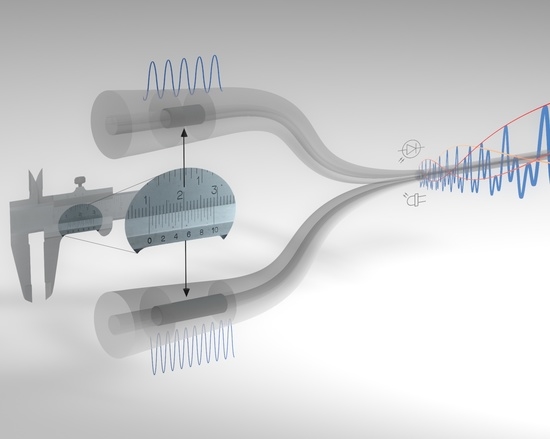
Optical Harmonic Vernier Effect: A New Tool for High Performance Interferometric Fiber Sensors
Abstract
1. Introduction
2. Theoretical Considerations
2.1. Fundamental Optical Vernier Effect
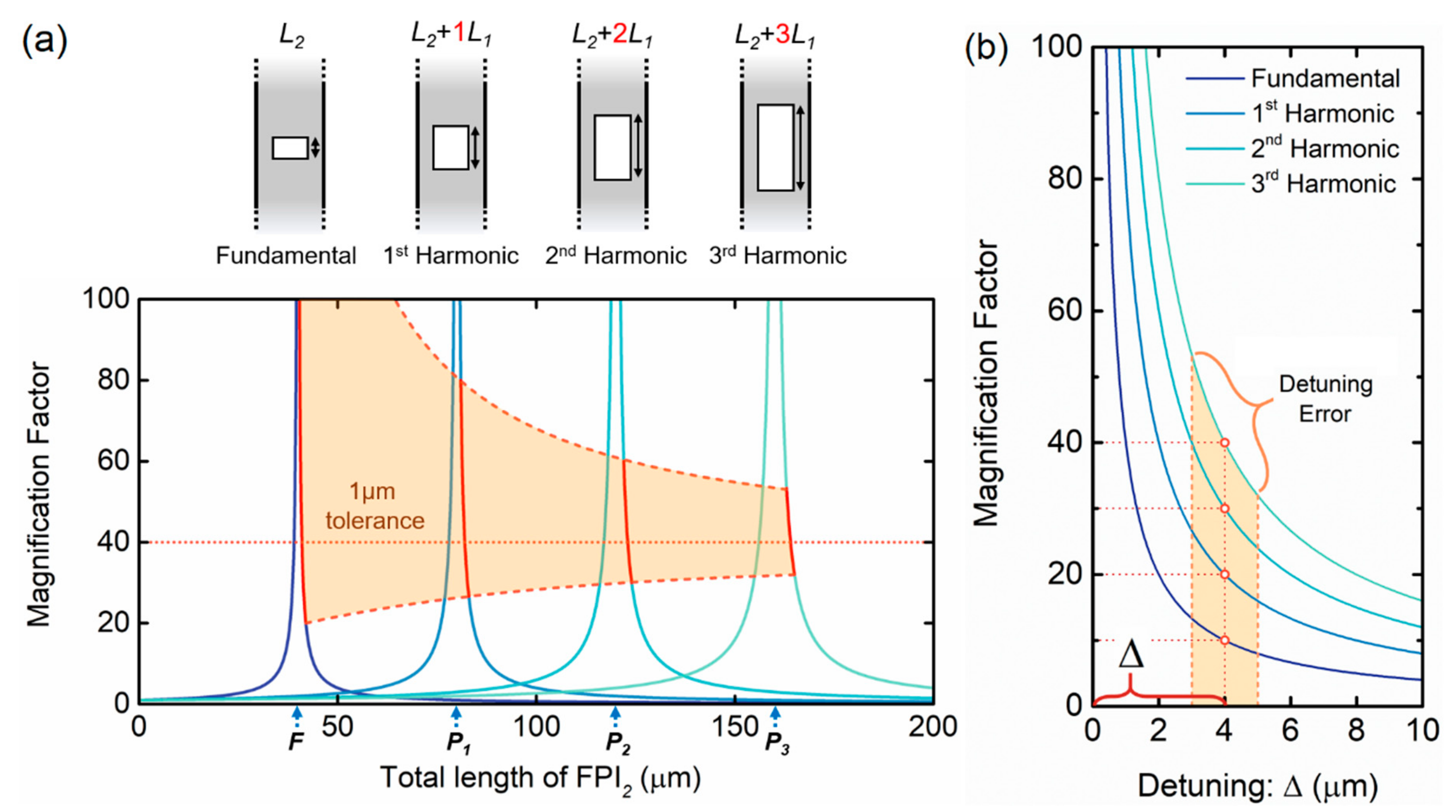
2.2. Optical Harmonic Vernier Effect
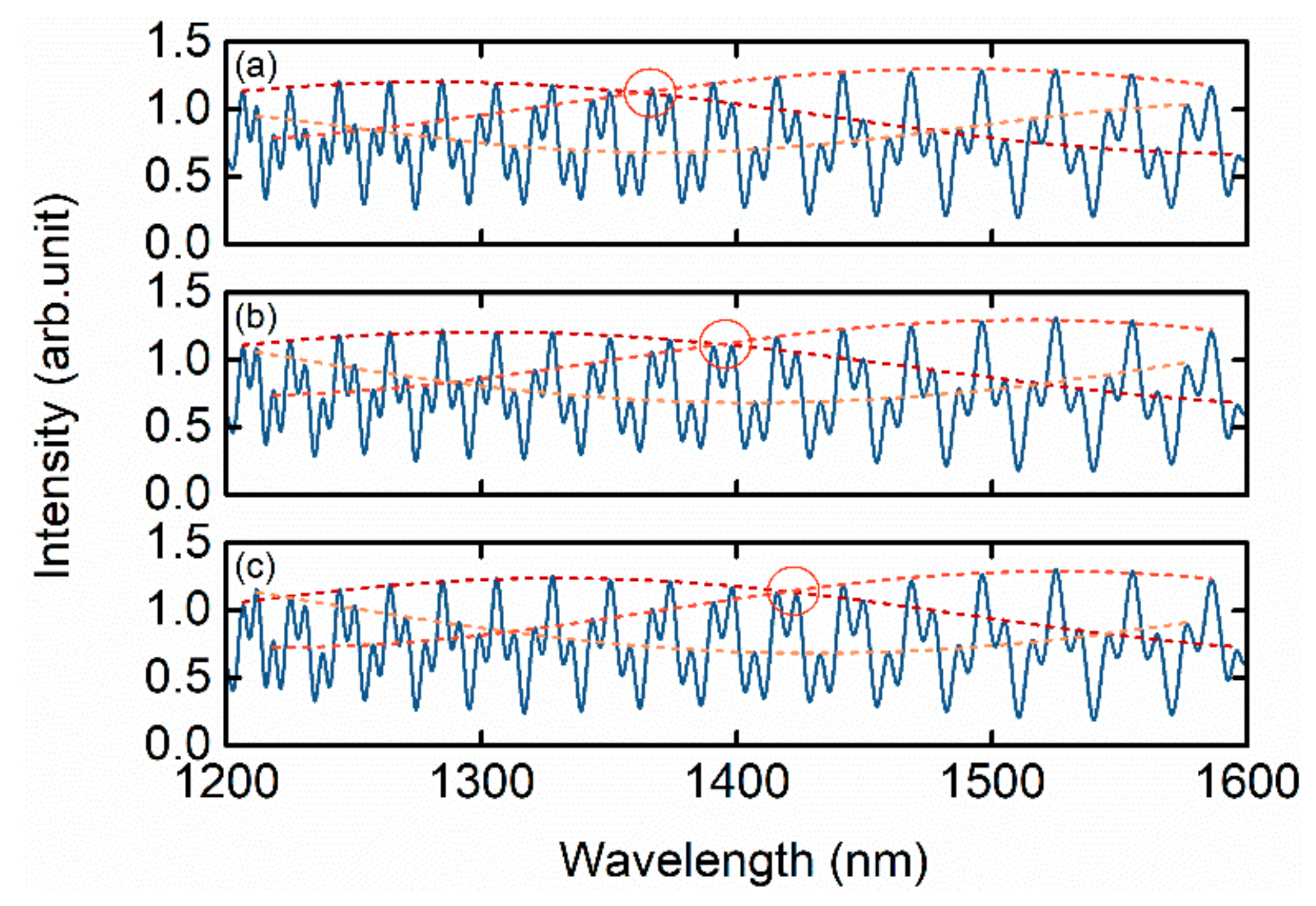
3. Results
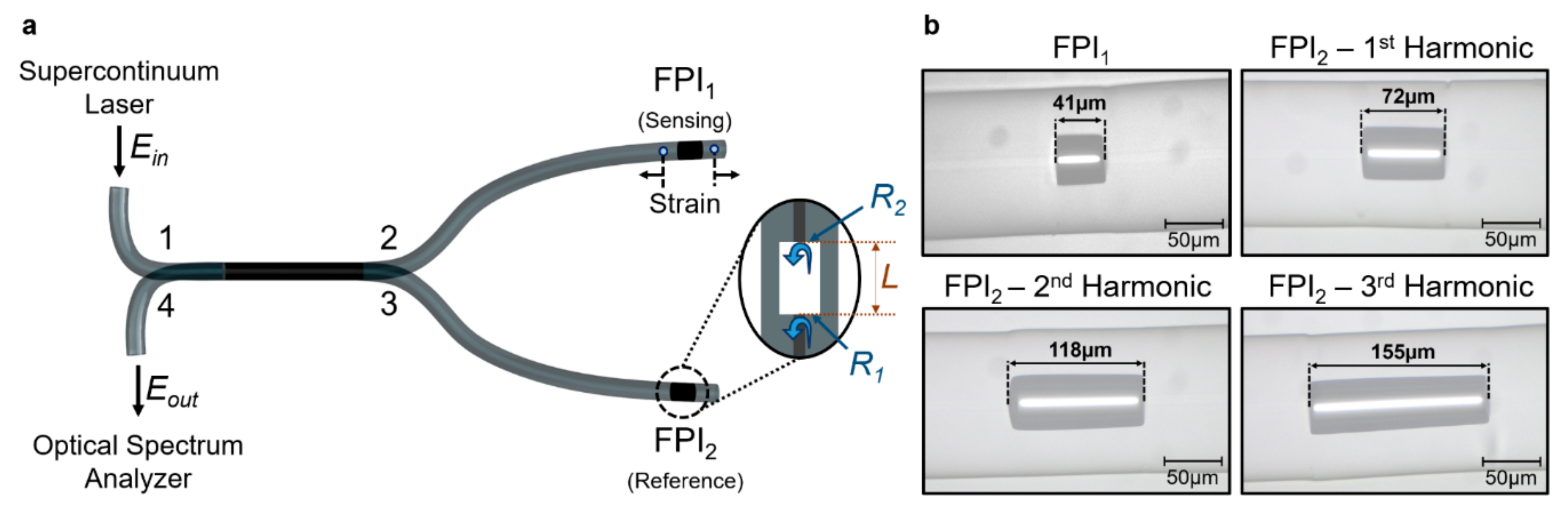
3.1. Experimental Setup
3.2. Sensor Fabrication
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Reflected Light Intensity for the Fundamental Optical Vernier Effect
Appendix B. Derivation of the Free Spectral Range (FSR) of the Envelope and Magnification Factor (M-Factor) for the Fundamental Vernier Effect

Appendix C. Derivation of the Free Spectral Range (FSR) of the Envelope for the First Optical Vernier Effect Harmonic and Generalization for Any Harmonic Order
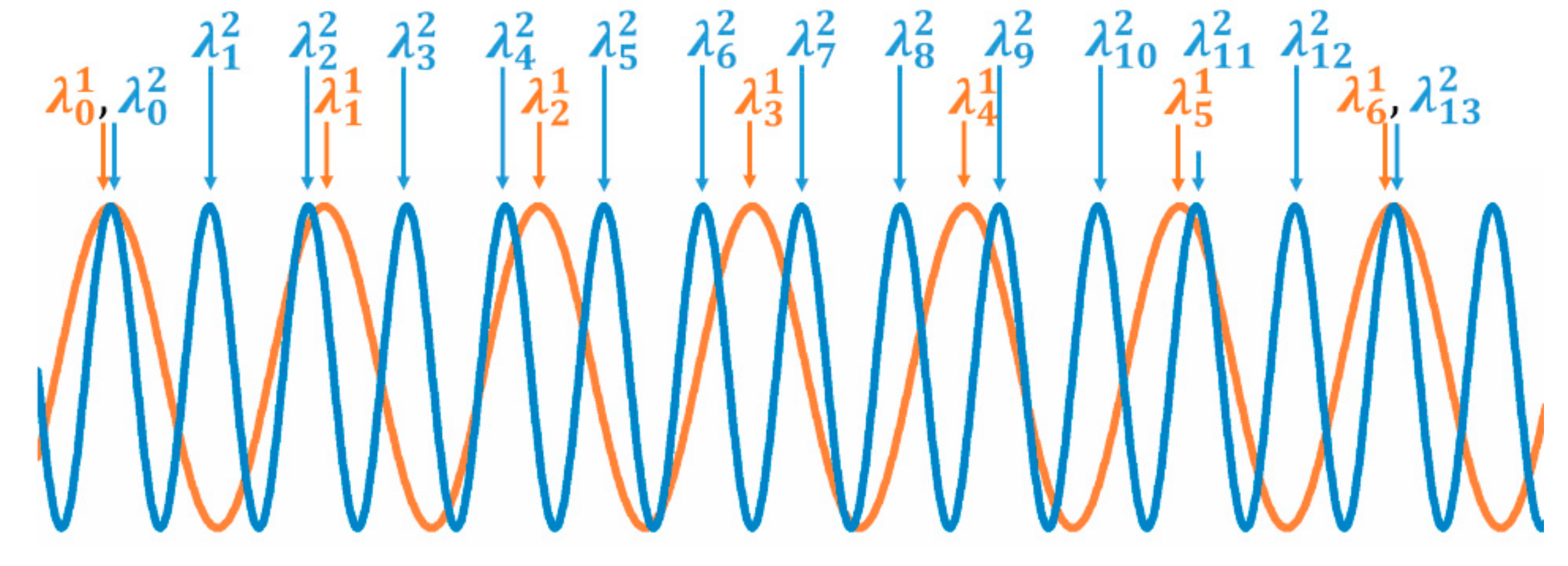
Appendix D. Example of the Spectral Shift
References
- Yao, T.; Pu, S.; Zhao, Y.; Li, Y. Ultrasensitive refractive index sensor based on parallel-connected dual Fabry-Perot interferometers with Vernier effect. Sens. Actuators A Phys. 2019, 290, 14–19. [Google Scholar] [CrossRef]
- Chen, P.; Dai, Y.; Zhang, D.; Wen, X.; Yang, M. Cascaded-cavity Fabry-Perot interferometric gas pressure sensor based on Vernier effect. Sensors 2018, 18, 3677. [Google Scholar] [CrossRef] [PubMed]
- Quan, M.; Tian, J.; Yao, Y. Ultra-high sensitivity Fabry–Perot interferometer gas refractive index fiber sensor based on photonic crystal fiber and Vernier effect. Opt. Lett. 2015, 40, 4891–4894. [Google Scholar] [CrossRef] [PubMed]
- Nan, T.; Liu, B.; Wu, Y.; Wang, J.; Mao, Y.; Zhao, L.; Sun, T.; Wang, J. Ultrasensitive strain sensor based on Vernier-effect improved parallel structured fiber-optic Fabry-Perot interferometer. Opt. Express 2019, 27, 17239–17250. [Google Scholar] [CrossRef] [PubMed]
- Gomes, A.D.; Becker, M.; Dellith, J.; Zibaii, M.I.; Latifi, H.; Rothhardt, M.; Bartelt, H.; Frazão, O. Multimode Fabry–Perot Interferometer Probe Based on Vernier Effect for Enhanced Temperature Sensing. Sensors 2019, 19, 453. [Google Scholar] [CrossRef]
- Zhang, P.; Tang, M.; Gao, F.; Zhu, B.; Fu, S.; Ouyang, J.; Shum, P.P.; Liu, D. Cascaded fiber-optic Fabry-Perot interferometers with Vernier effect for highly sensitive measurement of axial strain and magnetic field. Opt. Express 2014, 22, 19581–19588. [Google Scholar] [CrossRef]
- Zhang, P.; Tang, M.; Gao, F.; Zhu, B.; Zhao, Z.; Duan, L.; Fu, S.; Ouyang, J.; Wei, H.; Shum, P.P.; et al. Simplified hollow-core fiber-based Fabry–Perot interferometer with modified Vernier effect for highly sensitive high-temperature measurement. IEEE Photonics J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, P.; Lv, R.; Liu, X. Highly sensitive airflow sensor based on Fabry–Perot interferometer and Vernier effect. J. Light. Technol. 2016, 34, 5351–5356. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Zhao, Y.; Jiang, J.; He, X.; Yang, W.; Zhu, Z.; Gao, W.; Li, L. Sensitivity-enhanced temperature sensor by hybrid cascaded configuration of a Sagnac loop and a F-P cavity. Opt. Express 2017, 25, 33290–33296. [Google Scholar] [CrossRef]
- Zhang, J.; Liao, H.; Lu, P.; Jiang, X.; Fu, X.; Ni, W.; Liu, D.; Zhang, J. Ultrasensitive temperature sensor with cascaded fiber optic Fabry–Perot interferometers based on Vernier effect. IEEE Photonics J. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Kong, L.; Zhang, Y.; Zhang, W.; Zhang, Y.; Yu, L.; Yan, T.; Geng, P. Cylinder-type fiber-optic Vernier probe based on cascaded Fabry–Perot interferometers with a controlled FSR ratio. Appl. Opt. 2018, 57, 5043–5047. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, C.; Xu, B.; Wang, D.; Yang, M. Optical cascaded Fabry–Perot interferometer hydrogen sensor based on vernier effect. Opt. Commun. 2018, 414, 166–171. [Google Scholar] [CrossRef]
- Lin, H.; Liu, F.; Guo, H.; Zhou, A.; Dai, Y. Ultra-highly sensitive gas pressure sensor based on dual side-hole fiber interferometers with Vernier effect. Opt. Express 2018, 26, 28763–28772. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Xia, L.; Li, W.; Xia, J. Highly sensitive Fabry–Perot demodulation based on coarse wavelength sampling and Vernier effect. IEEE Photonics Technol. Lett. 2019, 31, 487–490. [Google Scholar] [CrossRef]
- Zhao, Y.; Tong, R.; Chen, M.; Peng, Y. Relative humidity sensor based on Vernier effect with GQDs-PVA un-fully filled in hollow core fiber. Sens. Actuators A Phys. 2019, 285, 329–337. [Google Scholar] [CrossRef]
- Liu, L.; Ning, T.; Zheng, J.; Pei, L.; Li, J.; Cao, J.; Gao, X.; Zhang, C. High-sensitivity strain sensor implemented by hybrid cascaded interferometers and the Vernier-effect. Opt. Laser Technol. 2019, 119, 105591. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y.; Guo, H.; Zhou, A.; Yuan, L. Highly sensitive vector curvature sensor based on two juxtaposed fiber Michelson interferometers with Vernier-like effect. IEEE Sens. J. 2019, 19, 2148–2154. [Google Scholar] [CrossRef]
- Flores, R.; Janeiro, R.; Viegas, J. Optical fibre Fabry-Pérot interferometer based on inline microcavities for salinity and temperature sensing. Sci. Rep. 2019, 9, 9556. [Google Scholar] [CrossRef]
- Hou, L.; Zhao, C.; Xu, B.; Mao, B.; Shen, C.; Wang, D.N. Highly sensitive PDMS-filled Fabry–Perot interferometer temperature sensor based on the Vernier effect. Appl. Opt. 2019, 58, 4858–4865. [Google Scholar] [CrossRef]
- Deng, J.; Wang, D.N. Ultra-sensitive strain sensor based on femtosecond laser inscribed in-fiber reflection mirrors and vernier effect. J. Light. Technol. 2019, 37, 4935–4939. [Google Scholar] [CrossRef]
- Xie, M.; Gong, H.; Zhang, J.; Zhao, C.-L.; Dong, X. Vernier effect of two cascaded in-fiber Mach-Zehnder interferometers based on a spherical-shaped structure. Appl. Opt. 2019, 58, 6204–6210. [Google Scholar] [CrossRef] [PubMed]
- Ullah, U.; Yasin, M.; Kiraz, A.; Cheema, M.I. Digital sensor based on multicavity fiber interferometers. J. Opt. Soc. Am. B 2019, 36, 2587–2592. [Google Scholar] [CrossRef]
- Liu, S.; Lu, P.; Chen, E.; Ni, W.; Liu, D.; Zhang, J.; Lian, Z. Vernier effect of fiber interferometer based on cascaded PANDA polarization maintaining fiber. Chinese Opt. Lett. 2019, 17, 080601. [Google Scholar] [CrossRef]
- Paixão, T.; Araújo, F.; Antunes, P. Highly sensitive fiber optic temperature and strain sensor based on an intrinsic Fabry–Perot interferometer fabricated by a femtosecond laser. Opt. Lett. 2019, 44, 4833–4836. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Shao, L.; Lang, T.; Gu, G.; Zhang, X.; Liu, Y.; Song, X.; Song, Z.; Feng, J.; Buczynski, R.; et al. Dual Mach-Zehnder interferometer based on side-hole fiber for high-sensitivity refractive index sensing. IEEE Photonics J. 2019, 1. [Google Scholar] [CrossRef]
- Su, H.; Zhang, Y.; Zhao, Y.; Ma, K.; Qi, K.; Guo, Y.; Zhu, F. Parallel double-FPIs temperature sensor based on suspended-core microstructured optical fiber. IEEE Photonics Technol. Lett. 2019, 1. [Google Scholar] [CrossRef]
- Tian, J.; Li, Z.; Sun, Y.; Yao, Y. High-sensitivity fiber-optic strain sensor based on the Vernier effect and separated Fabry—Perot interferometers. J. Light. Technol. 2019, 1. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, B.; Wu, J.; Zhao, L.; Sun, T.; Mao, Y.; Nan, T.; Wang, J. A transverse load sensor with ultra-sensitivity employing Vernier-effect improved parallel-structured fiber-optic Fabry-Perot interferometer. IEEE Access 2019, 7, 120297–120303. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, L.; Zhao, Y.; Zhou, A.; Yuan, L. Bending sensor with parallel fiber Michelson interferometers based on Vernier-like effect. Opt. Laser Technol. 2019, 120, 105679. [Google Scholar] [CrossRef]
- Ying, Y.; Zhao, C.; Gong, H.; Shang, S.; Hou, L. Demodulation method of Fabry-Perot sensor by cascading a traditional Mach-Zehnder interferometer. Opt. Laser Technol. 2019, 118, 126–131. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Jiang, J.; Zhao, Y.; He, X.; Li, L. High-sensitive all-fiber Fabry-Perot interferometer gas refractive index sensor based on lateral offset splicing and Vernier effect. Optik (Stuttg). 2019, 196, 163181. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, UK, 1999; ISBN 9780521642224. [Google Scholar]

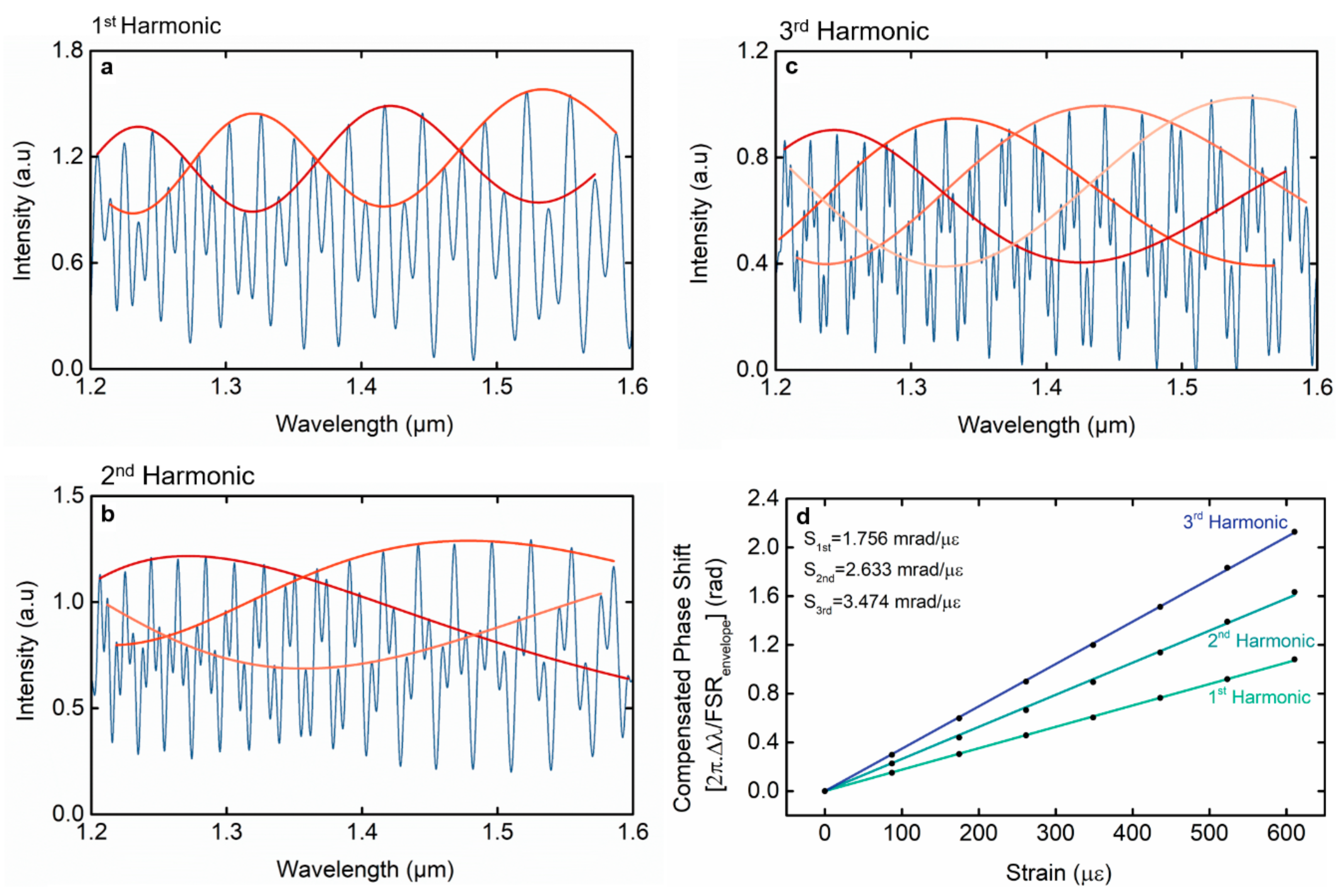
| Experimental Strain Sensitivity (pm/με) | Compensated Phase Sensitivity (mrad/ με) | M-Factor by FSRenvelope Equation (11) | M-Factor by Sensitivities Equation (7) | M-Factor by FSR/M-factor by Fundamental Vernier Effect | |
|---|---|---|---|---|---|
| 1st Harmonic | 27.6 | 1.765 | 8.38 | 8.18 | 1.95 (2) |
| 2nd Harmonic | 93.4 | 2.633 | 28.41 | 27.70 | 2.93 (3) |
| 3rd Harmonic | 59.6 | 3.474 | 18.32 | 17.70 | 3.86 (4) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomes, A.D.; Ferreira, M.S.; Bierlich, J.; Kobelke, J.; Rothhardt, M.; Bartelt, H.; Frazão, O. Optical Harmonic Vernier Effect: A New Tool for High Performance Interferometric Fiber Sensors. Sensors 2019, 19, 5431. https://doi.org/10.3390/s19245431
Gomes AD, Ferreira MS, Bierlich J, Kobelke J, Rothhardt M, Bartelt H, Frazão O. Optical Harmonic Vernier Effect: A New Tool for High Performance Interferometric Fiber Sensors. Sensors. 2019; 19(24):5431. https://doi.org/10.3390/s19245431
Chicago/Turabian StyleGomes, André D., Marta S. Ferreira, Jörg Bierlich, Jens Kobelke, Manfred Rothhardt, Hartmut Bartelt, and Orlando Frazão. 2019. "Optical Harmonic Vernier Effect: A New Tool for High Performance Interferometric Fiber Sensors" Sensors 19, no. 24: 5431. https://doi.org/10.3390/s19245431
APA StyleGomes, A. D., Ferreira, M. S., Bierlich, J., Kobelke, J., Rothhardt, M., Bartelt, H., & Frazão, O. (2019). Optical Harmonic Vernier Effect: A New Tool for High Performance Interferometric Fiber Sensors. Sensors, 19(24), 5431. https://doi.org/10.3390/s19245431