Multiple Simultaneous Ranging in IR-UWB Networks
Abstract
1. Introduction
2. Multiple Simultaneous Ranging
2.1. Proposed Method
- Step 1: Node M determines the transmission timestamps for the first and third packets to follow , based on its current timestamp value and the properly pre-specified value of .
- Step 2: Node M transmits the first packet at the determined time, while other nodes are in receiver mode.
- Step 3: Upon completion of the transmission and reception, all nodes except node M retrieve and store the corresponding reception timestamps. Then node A prepares for transmission of the second packet, while other nodes enter the receiver mode.
- Step 4: Node A transmits the second packet, while other nodes are in receiver mode.
- Step 5: Upon completion of the transmission and reception, node A retrieves and stores the corresponding transmission timestamp, while other nodes retrieve and store the corresponding reception timestamps. Then node M computes using Equations (6) and (12), and prepares for transmission of the third packet, which will carry the value of , while other nodes enter the receiver mode.
- Step 6: Node M transmits the third packet at the determined time, while other nodes are in receiver mode.
- Step 7: Upon completion of the transmission and reception, all nodes except node M retrieve and store the corresponding reception timestamps. Node A also stores the received value of .
- Step 9: All anchor nodes send all the time difference of reception values, i.e., node A sends and while each passive anchor node X sends , to a computing unit via a communication backbone.
- Step 10: For each anchor node X, the computing unit computes using Equation (16), and then multiplies the result with the speed of light to obtain the corresponding range.
- Step 1: Node A determines the transmission timestamps for the first and third packets to follow , based on its current timestamp value and the properly pre-specified value of .
- Step 2: Node A transmits the first packet at the determined time, while other nodes are in receiver mode.
- Step 3: Upon completion of the transmission and reception, all nodes except node A retrieve and store the corresponding reception timestamps. Then node M prepares for transmission of the second packet, while other nodes enter the receiver mode.
- Step 4: Node M transmits the second packet, while other nodes are in receiver mode.
- Step 5: Upon completion of the transmission and reception, node M retrieves and stores the corresponding transmission timestamp, while other nodes retrieve and store the corresponding reception timestamps. Then node A prepares for transmission of the third packet, while other nodes enter the receiver mode.
- Step 6: Node A transmits the third packet at the determined time, while other nodes are in receiver mode.
- Step 7: Upon completion of the transmission and reception, all nodes except node A retrieve and store the corresponding reception timestamps.
- Step 9: Node M transmits a wireless data packet carrying the value of to node A.
- Step 10: All anchor nodes send all the time difference of reception values, i.e., node A sends and while each passive anchor node X sends , to a computing unit via a communication backbone.
- Step 11: For each anchor node X, the computing unit computes using Equation (17), and then multiplies the result with the speed of light to obtain the corresponding range.
- Step 1: Node A transmits the first packet, while other nodes are in receiver mode.
- Step 2: Upon completion of the transmission and reception, each node , retrieves and stores the corresponding reception timestamp, and also determines using Equation (21).
- Step 3: While other nodes enter the receiver mode, node M determines a suitable transmission timestamp for the second packet from the obtained reception timestamp of the first packet, and then computes using Equation (18).
- Step 4: Node M transmits the second packet carrying the value of at the determined time, while other nodes are in receiver mode.
- Step 5: Upon completion of the transmission and reception, each node , retrieves and stores the corresponding reception timestamp, and node A also stores the received value of .
- Step 7: All anchor nodes send all the time difference of reception values, i.e., node A sends and while each passive anchor node X sends , to a computing unit via a communication backbone.
- Step 8: For each anchor node X, the computing unit computes using Equation (17), and then multiplies the result with the speed of light to obtain the corresponding range.
2.2. Unification with Recent Methods
2.3. Effect of Clock Offset
2.4. Effect of Timestamp Error
3. Numerical Results
3.1. Air Time Occupancy
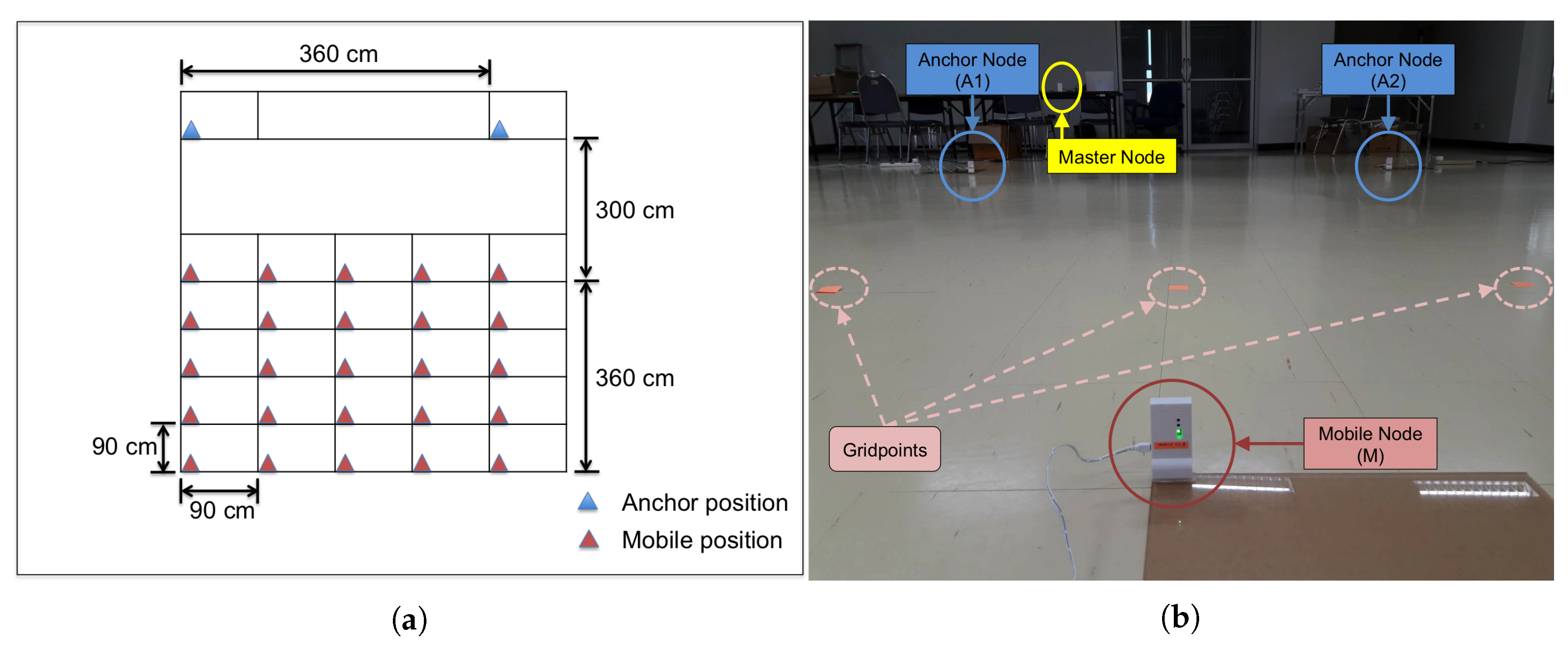
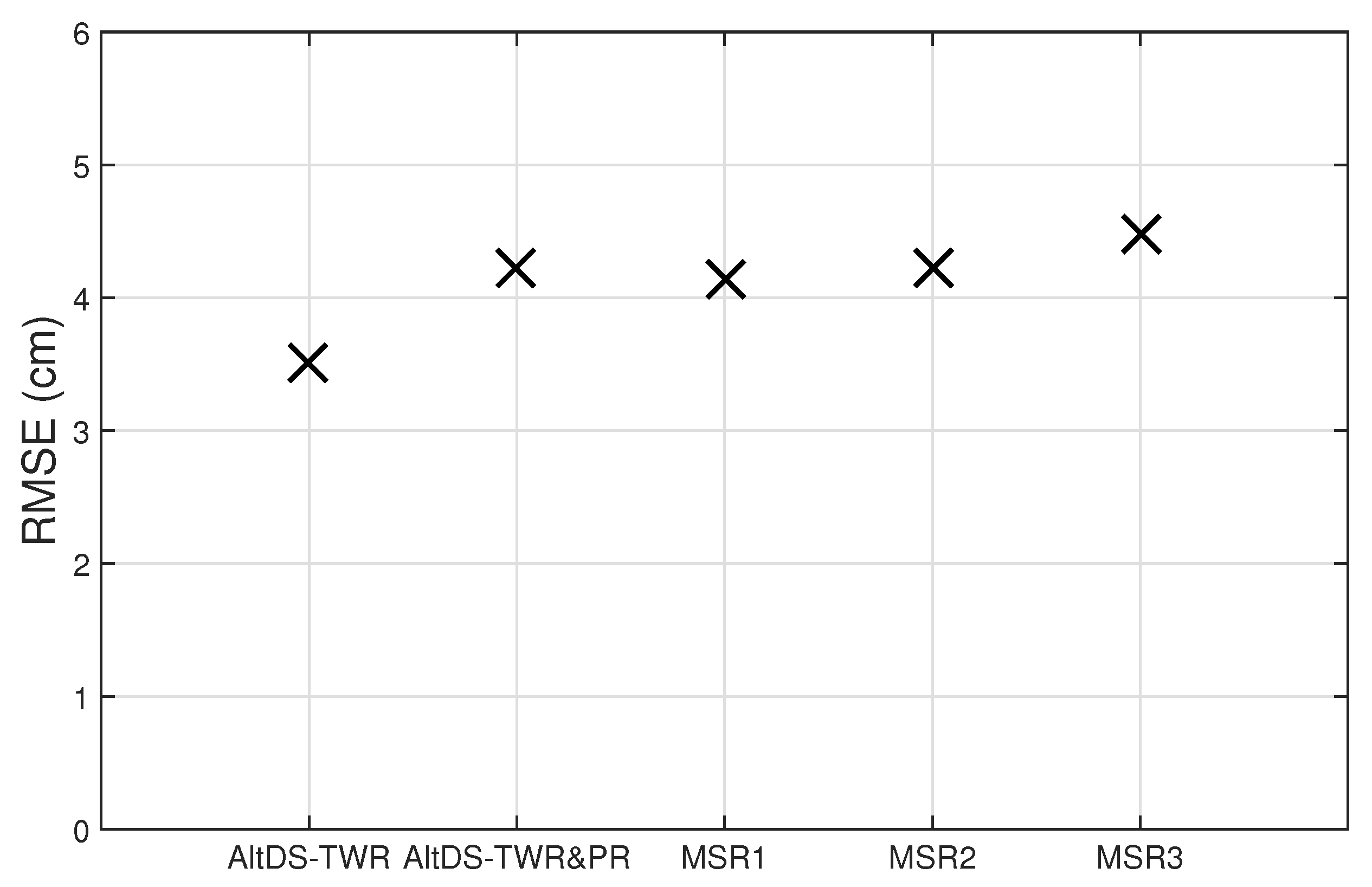
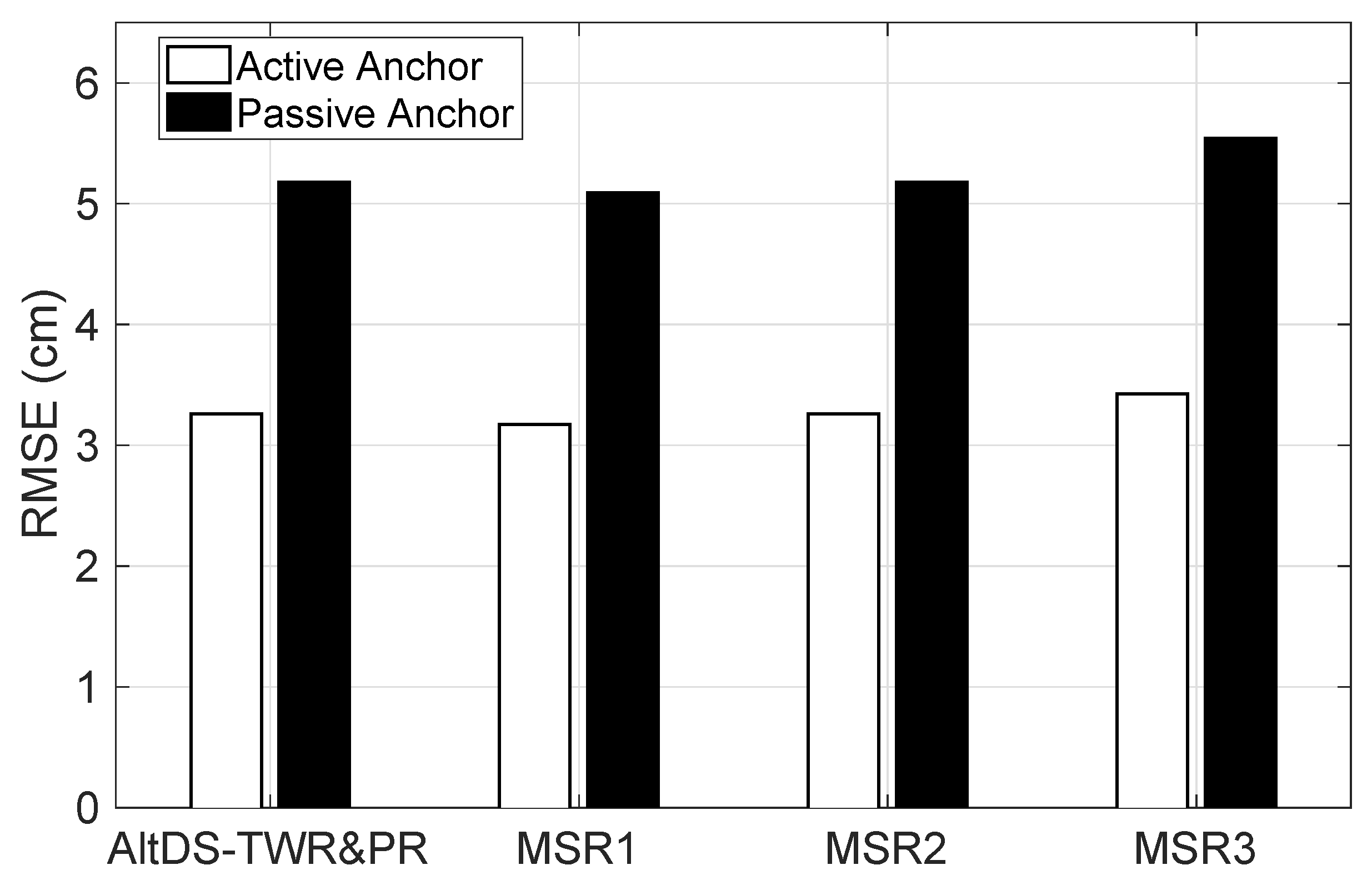
3.2. Experimental Evaluation
4. Further Extensions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ferreira, A.F.G.; Fernandes, D.M.A.; Catarino, A.P.; Monteiro, J.L. Localization and Positioning Systems for Emergency Responders: A Survey. IEEE Commun. Surv. Tutor. 2017, 19, 2836–2870. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. arXiv 2017, arXiv:1709.01015. [Google Scholar] [CrossRef]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef]
- Gandhi, G.M.; Rama, P. GPS based Multi-hop Communication with Localization in Subterranean Wireless Sensor Networks. Procedia Comput. Sci. 2015, 57, 1189–1198. [Google Scholar] [CrossRef]
- Du, H.; Zhang, C.; Ye, Q.; Xu, W.; Kibenge, P.L.; Yao, K. A hybrid outdoor localization scheme with high-position accuracy and low-power consumption. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 4. [Google Scholar] [CrossRef]
- IEEE 802.15.4a. IEEE Standard for Information Technology—Local and Metropolitan Area Networks—Specific Requirements—Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (WPANs): Amendment 1: Add Alternate PHYs; Technical Report; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Karapistoli, E.; Pavlidou, F.; Gragopoulos, I.; Tsetsinas, I. An overview of the IEEE 802.15.4a Standard. IEEE Commun. Mag. 2010, 48, 47–53. [Google Scholar] [CrossRef]
- IEEE 802.15.4. IEEE Standard for Local and Metropolitan Area Networks—Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs); Technical Report; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Alhadhrami, S.; Al-Ammar, M.; Al-Khalifa, H. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Dong, X. High-Accuracy Localization Platform Using Asynchronous Time Difference of Arrival Technology. IEEE Trans. Instrum. Meas. 2017, 66, 1728–1742. [Google Scholar] [CrossRef]
- Wu, Y.; Chaudhari, Q.; Serpedin, E. Clock Synchronization of Wireless Sensor Networks. IEEE Signal Process. Mag. 2011, 28, 124–138. [Google Scholar] [CrossRef]
- Gholami, M.R.; Gezici, S.; Strom, E.G. TDOA Based Positioning in the Presence of Unknown Clock Skew. IEEE Trans. Commun. 2013, 61, 2522–2534. [Google Scholar] [CrossRef]
- Wang, H.; Shao, L.; Li, M.; Wang, B. A Global Clock Skew Estimation Scheme for Hierarchical Wireless Sensor Networks. IEEE Access 2017, 5, 20333–20338. [Google Scholar] [CrossRef]
- Xue, Y.; Su, W.; Wang, H.; Yang, D.; Ma, J. A Model on Indoor Localization System Based on the Time Difference Without Synchronization. IEEE Access 2018, 6, 34179–34189. [Google Scholar] [CrossRef]
- Neirynck, D.; Luk, E.; McLaughlin, M. An alternative double-sided two-way ranging method. In Proceedings of the 2016 13th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 19–20 October 2016. [Google Scholar]
- Jiang, Y.; Leung, V.C.M. An Asymmetric Double Sided Two-Way Ranging for Crystal Offset. In Proceedings of the 2007 International Symposium on Signals, Systems and Electronics, Montreal, QC, Canada, 30 July– 2 August 2007; pp. 525–528. [Google Scholar]
- Lian Sang, C.; Adams, M.; Hörmann, T.; Hesse, M.; Porrmann, M. Numerical and Experimental Evaluation of Error Estimation for Two-Way Ranging Methods. Sensors 2019, 19, 616. [Google Scholar] [CrossRef]
- Horvath, K.A.; Ill, G.; Milnkovich, A. Passive extended double-sided two-way ranging with alternative calculation. In Proceedings of the 2017 IEEE 17th International Conference on Ubiquitous Wireless Broadband (ICUWB), Salamanca, Spain, 12–15 September 2017. [Google Scholar]
- Horvath, K.A.; Ill, G.; Milnkovich, A. Passive extended double-sided two-way ranging algorithm for UWB positioning. In Proceedings of the 2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN), Milan, Italy, 4–7 July 2017; pp. 482–487. [Google Scholar]
- Decawave Ltd. DW1000 User Manual. Available online: https://www.decawave.com/sites/default/files/resources/dw1000_user_manual_2.11.pdf (accessed on 4 December 2019).
- Decawave Ltd. DW1000 Device Driver Application Programming Interface (API) Guide. Available online: https://decaforum.decawave.com/uploads/default/original/1X/8b220e1e26fea4ebd83f0b0e5ef42eb9a251310d.pdf (accessed on 4 December 2019).
- Decawave Ltd. APS011 Application Note, Sources of error in DW1000 Based Two-Way ranging (TWR) Schemes. Available online: https://www.decawave.com/wp-content/uploads/2018/10/APS011_Sources-of-Error-in-Two-Way-Ranging-Schemes_v1.1.pdf (accessed on 4 December 2019).
- Decawave Ltd. Decawave DWM1001 Datasheet. Available online: https://www.decawave.com/sites/default/files/dwm1001_datasheet.pdf (accessed on 4 December 2019).
- Liu, R.; Yuen, C.; Do, T.; Jiao, D.; Liu, X.; Tan, U. Cooperative relative positioning of mobile users by fusing IMU inertial and UWB ranging information. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5623–5629. [Google Scholar]
| Schemes | Air Time Occupancy | Required Number of |
|---|---|---|
| (Packets) | Packets (for ) | |
| AltDS-TWR (w/o combined transmissions) | 12 | |
| AltDS-TWR (w/combined transmissions) | 6 | |
| AltDS-TWR&PR | 4 | 4 |
| MSR1 | 3 | 3 |
| MSR2 | 4 | 4 |
| MSR3 | 2 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.; Demeechai, T. Multiple Simultaneous Ranging in IR-UWB Networks. Sensors 2019, 19, 5415. https://doi.org/10.3390/s19245415
Shah S, Demeechai T. Multiple Simultaneous Ranging in IR-UWB Networks. Sensors. 2019; 19(24):5415. https://doi.org/10.3390/s19245415
Chicago/Turabian StyleShah, Shashi, and Tanee Demeechai. 2019. "Multiple Simultaneous Ranging in IR-UWB Networks" Sensors 19, no. 24: 5415. https://doi.org/10.3390/s19245415
APA StyleShah, S., & Demeechai, T. (2019). Multiple Simultaneous Ranging in IR-UWB Networks. Sensors, 19(24), 5415. https://doi.org/10.3390/s19245415





