Robust Statistics for GNSS Positioning under Harsh Conditions: A Useful Tool?
Abstract
1. Introduction
2. Robust Statistics Principles
2.1. Dictionary of Robust Statistics Terms
2.2. Robust Estimates for Regression Problems
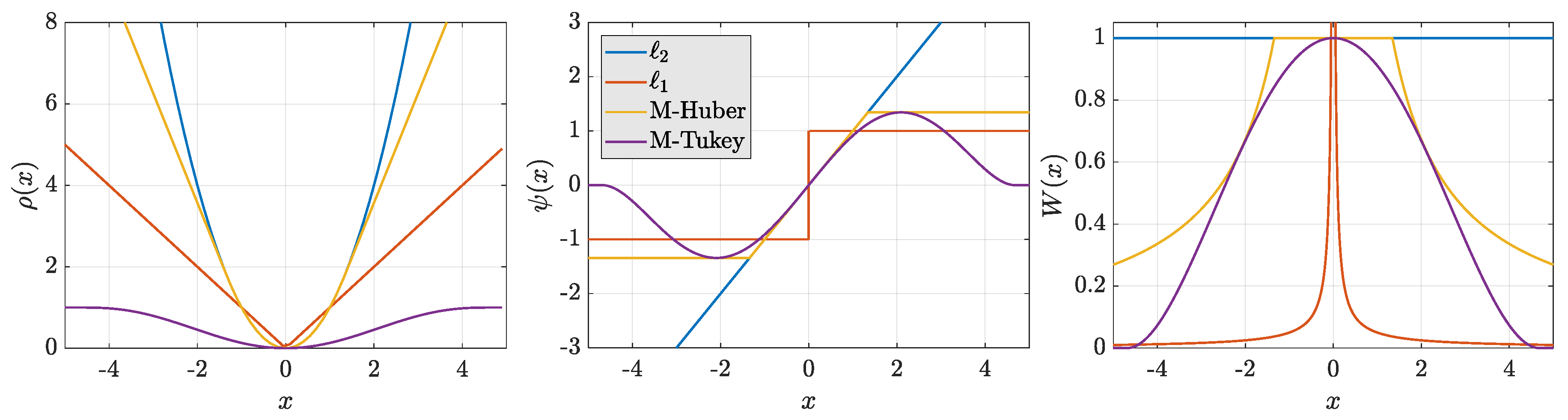
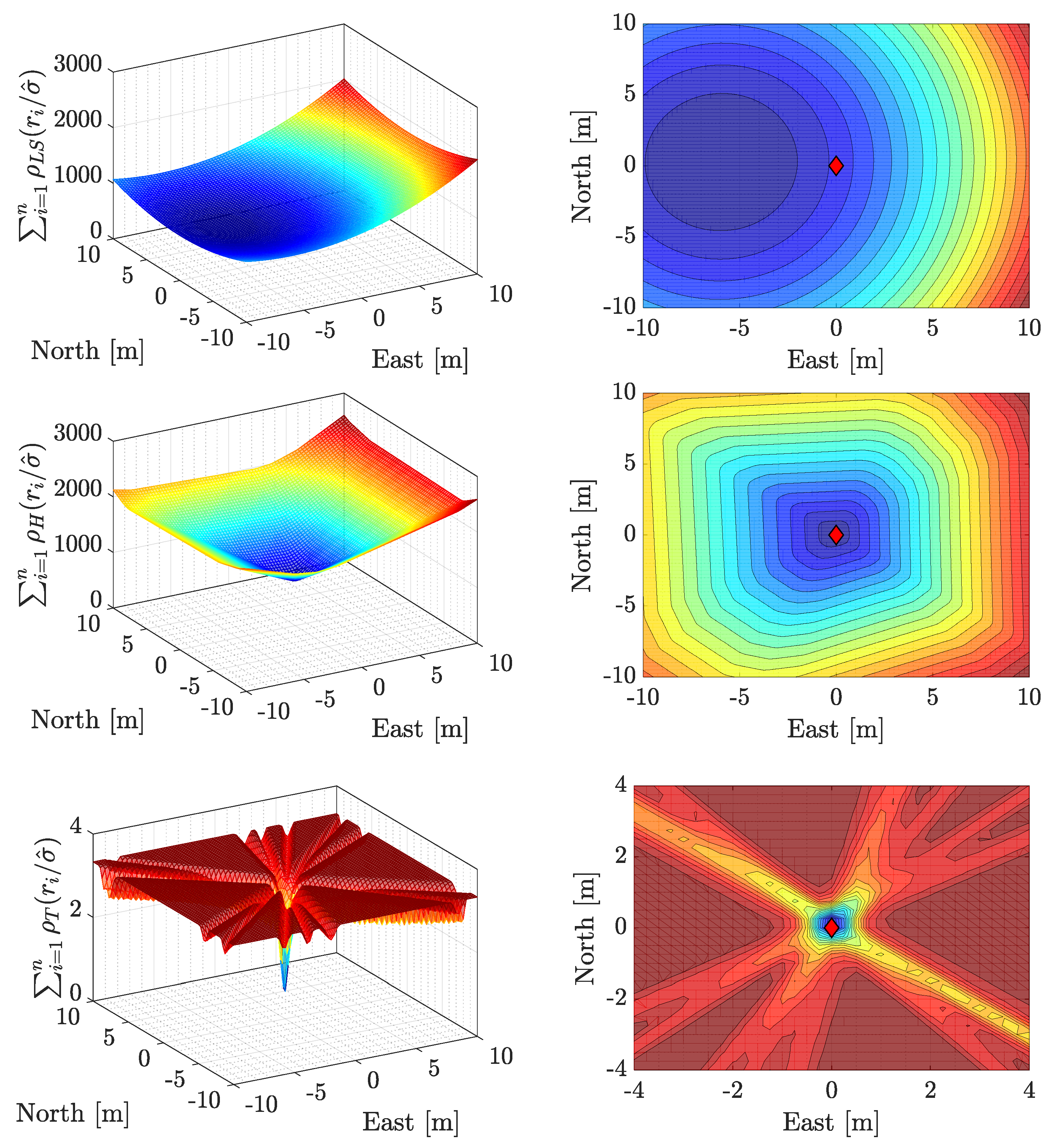
2.2.1. Huber and Tukey Families of Loss Functions
2.2.2. M-Estimator
2.2.3. S-Estimator
2.2.4. MM-Estimator
- (1)
- Compute an initial consistent S-estimate of , namely , with a high breakdown point but possibly low normal efficiency.
- (2)
- Compute an M-estimate of the scale of the residuals using the high breakdown point estimate .
- (3)
- Compute the regression M-estimate initialized at , considering the robust scale estimate and using a recursive IRLS approach.
3. Robust Statistics for GNSS Positioning
| Algorithm 1: IRLS procedure for robust GNSS SPP. |
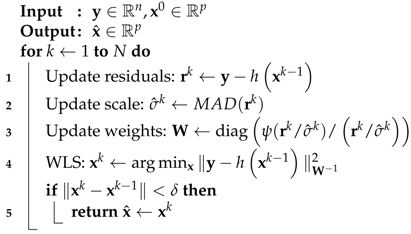 |
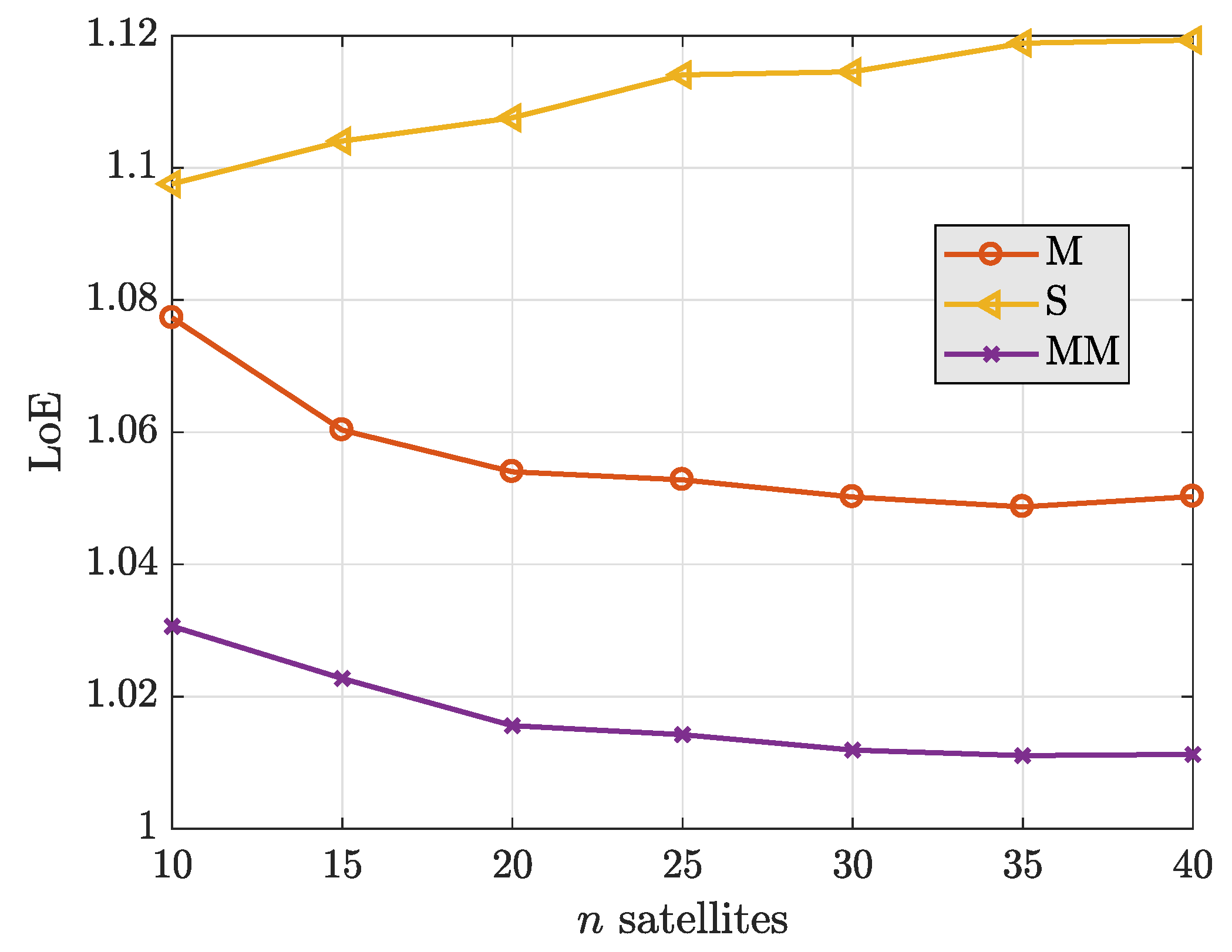
4. Loss-of-Efficiency in Robust PVT Solvers
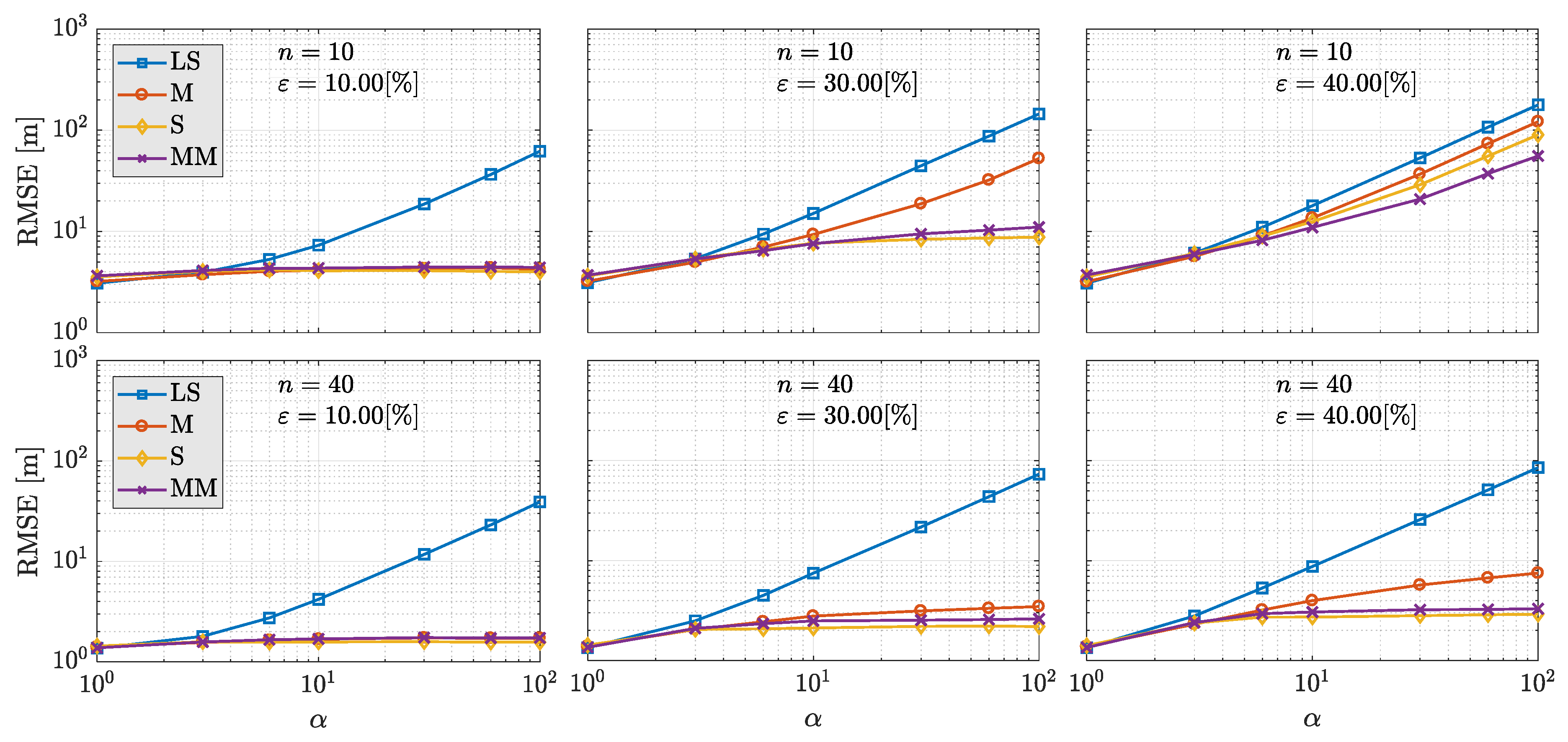
5. Test and Results
5.1. Simulated Environment
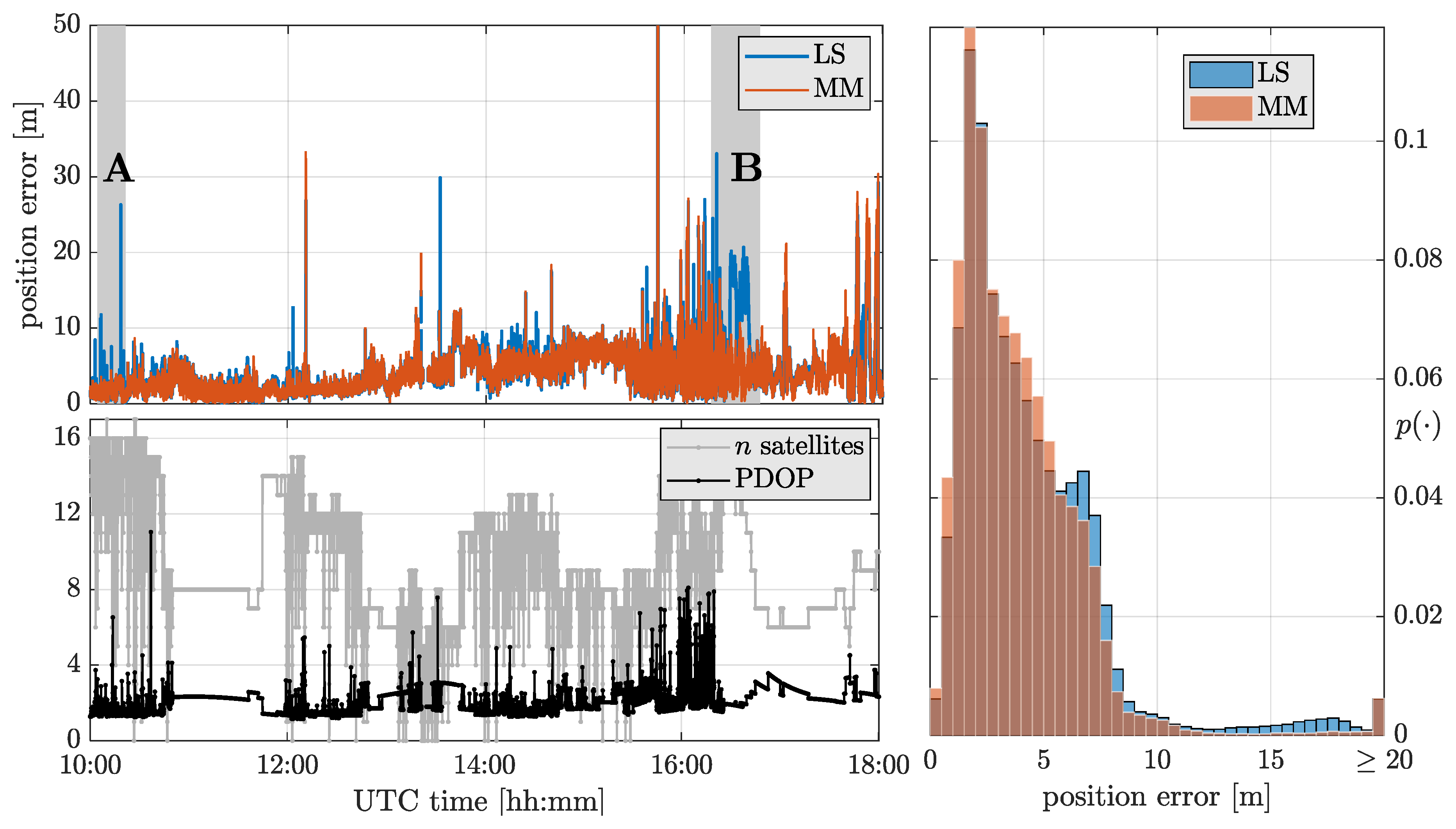
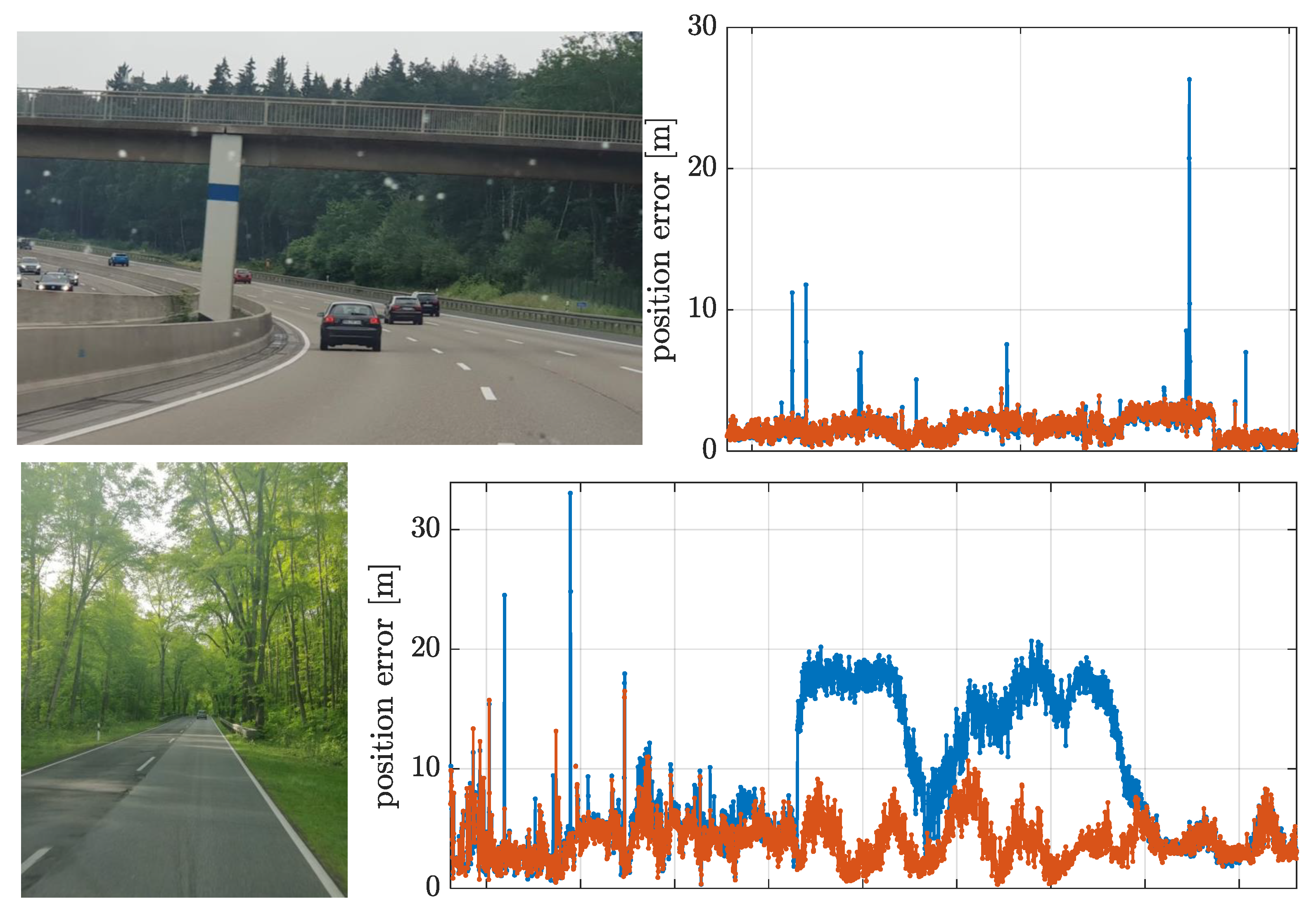
5.2. Experimentation under Real Harsh Conditions
6. Outlook and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Williams, N.; Wu, G.; Closas, P. Impact of positioning uncertainty on eco-approach and departure of connected and automated vehicles. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1081–1087. [Google Scholar]
- Dardari, D.; Luise, M.; Falletti, E. Satellite and Terrestrial Radio Positioning Techniques: A Signal Processing Perspective; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Amin, M.G.; Closas, P.; Broumandan, A.; Volakis, J.L. Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proc. IEEE 2016, 104, 1169–1173. [Google Scholar] [CrossRef]
- Medina, D.; Lass, C.; Pérez-Marcos, E.; Ziebold, R.; Closas, P.; García, J. On GNSS Jamming Threat from the Maritime Navigation Perspective. In Proceedings of the 22st International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, 2–5 July 2019. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A. Advanced RAIM user algorithm description: Integrity support message processing, fault detection, exclusion, and protection level calculation. In Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 2828–2849. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P.; Wallner, S.; Amarillo Fernandez, F.; Dellago, R.; Ioannides, R.; Fernandez Hernandez, I.; Belabbas, B.; Spletter, A.; et al. Critical Elements for a Multi-Constellation Advanced RAIM. Navig. J. Inst. Navig. 2013, 60, 53–69. [Google Scholar] [CrossRef]
- Angrisano, A.; Gioia, C.; Gaglione, S.; Del Core, G. GNSS reliability testing in signal-degraded scenario. Int. J. Navig. Obs. 2013, 2013, 870365. [Google Scholar] [CrossRef][Green Version]
- Angrisano, A.; Gaglione, S.; Gioia, C. RAIM algorithms for aided GNSS in urban scenario. In Proceedings of the 2012 Ubiquitous Positioning, Indoor Navigation, and Location Based Service (UPINLBS), Helsinki, Finland, 3–4 October 2012; pp. 1–9. [Google Scholar]
- Rippl, M.; Schroth, G.; Belabbas, B.; Meurer, M. A probabilistic assessment on the Range Consensus (RANCO) RAIM Algorithm. In Proceedings of the ION International Technical Meeting (ITM), Anaheim, CA, USA, 26–28 January 2009; pp. 248–255. [Google Scholar]
- Jiang, Z.; Groves, P.D.; Ochieng, W.Y.; Feng, S.; Milner, C.D.; Mattos, P.G. Multi-constellation GNSS multipath mitigation using consistency checking. In Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 19–23 September 2011; pp. 3889–3902. [Google Scholar]
- Hampel, F.R. A general qualitative definition of robustness. Ann. Math. Stat. 1971, 42, 1887–1896. [Google Scholar] [CrossRef]
- Huber, P.J. Robust regression: Asymptotics, conjectures and Monte Carlo. Ann. Stat. 1973, 1, 799–821. [Google Scholar] [CrossRef]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J.; Salibián-Barrera, M. Robust Statistics: Theory and Methods (with R); Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Zoubir, A.M.; Koivunen, V.; Chakhchoukh, Y.; Muma, M. Robust estimation in signal processing: A tutorial-style treatment of fundamental concepts. IEEE Signal Process. Mag. 2012, 29, 61–80. [Google Scholar] [CrossRef]
- Zhang, Z. Determining the epipolar geometry and its uncertainty: A review. Int. J. Comput. Vis. 1998, 27, 161–195. [Google Scholar] [CrossRef]
- Malis, E.; Marchand, E. Experiments with robust estimation techniques in real-time robot vision. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 223–228. [Google Scholar]
- Leski, J.M. Robust weighted averaging [of biomedical signals]. IEEE Trans. Biomed. Eng. 2002, 49, 796–804. [Google Scholar] [CrossRef]
- Muma, M.; Zoubir, A.M. Robust model order selection for corneal height data based on τ estimation. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4096–4099. [Google Scholar]
- Mili, L.; Cheniae, M.G.; Rousseeuw, P.J. Robust state estimation of electric power systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1994, 41, 349–358. [Google Scholar] [CrossRef]
- Borio, D.; Closas, P. A fresh look at GNSS anti-jamming. Inside GNSS 2017, 12, 54–61. [Google Scholar]
- Borio, D. Robust signal processing for GNSS. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 150–158. [Google Scholar] [CrossRef]
- Borio, D. Myriad Non-Linearity for GNSS Robust Signal Processing. IET Radar Sonar Navig. 2017, 11, 1467–1476. [Google Scholar] [CrossRef]
- Borio, D.; Closas, P. Complex Signum Non-Linearity for Robust GNSS Signal Mitigation. IET Radar Sonar Navig. 2018, 12, 900–909. [Google Scholar]
- Borio, D.; Li, H.; Closas, P. Huber’s Non-Linearity for GNSS Interference Mitigation. Sensors 2018, 18, 2217. [Google Scholar] [CrossRef] [PubMed]
- Borio, D.; Closas, P. Robust Transform Domain Signal Processing for GNSS. Navigation 2019, 66, 305–323. [Google Scholar] [CrossRef]
- Li, H.; Borio, D.; Closas, P. Dual-Domain Robust GNSS Interference Mitigation. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 21–25 September 2019. [Google Scholar]
- Kuusniemi, H.; Wieser, A.; Lachapelle, G.; Takala, J. User-level reliability monitoring in urban personal satellite-navigation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1305–1318. [Google Scholar] [CrossRef]
- Knight, N.L.; Wang, J. A comparison of outlier detection procedures and robust estimation methods in GPS positioning. J. Navig. 2009, 62, 699–709. [Google Scholar] [CrossRef]
- Fallahi, K.; Cheng, C.T.; Fattouche, M. Robust positioning systems in the presence of outliers under weak GPS signal conditions. IEEE Syst. J. 2012, 6, 401–413. [Google Scholar] [CrossRef]
- Pozo-Pérez, J.A.; Medina, D.; Herrera-Pinzón, I.; Heßelbarth, A.; Ziebold, R. Robust Outlier Mitigation in Multi-Constellation GNSS-based Positioning for Waterborne Applications. In Proceedings of the 2017 International Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 30 January–2 February 2017; pp. 1330–1343. [Google Scholar]
- Pesonen, H. Robust estimation techniques for GNSS positioning. In Proceedings of the NAV07—The Navigation Conference and Exhibition, London, UK, 31 October–1 November 2007. [Google Scholar]
- Medina, D.; Romanovas, M.; Herrera-Pinzón, I.; Ziebold, R. Robust position and velocity estimation methods in integrated navigation systems for inland water applications. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 491–501. [Google Scholar]
- Crespillo, O.G.; Medina, D.; Skaloud, J.; Meurer, M. Tightly coupled GNSS/INS integration based on robust M-estimators. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 1554–1561. [Google Scholar]
- Teunissen, P.J. Least-squares estimation of the integer GPS ambiguities. In Proceedings of the Invited Lecture, Section IV Theory and Methodology, General Meeting of the International Association of Geodesy, Beijing, China, 8–13 August 1993. [Google Scholar]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Li, H.; Medina, D.; Vilà-Valls, J.; Closas, P. Robust Kalman Filter for RTK Positioning Under Signal-Degraded Scenarios. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Medina, D.; Li, H.; Vilà-Valls, J.; Closas, P. On Robust Statistics for GNSS Single Point Positioning. In Proceedings of the 2019 22nd International Conference on Intelligent Transportation Systems (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Blankenship, T.K.; Kriztman, D.; Rappaport, T.S. Measurements and simulation of radio frequency impulsive noise in hospitals and clinics. In Proceedings of the 1997 IEEE 47th Vehicular Technology Conference. Technology in Motion, Phoenix, AZ, USA, 4–7 May 1997; Volume 3, pp. 1942–1946. [Google Scholar]
- Middleton, D. Non-Gaussian noise models in signal processing for telecommunications: New methods an results for class A and class B noise models. IEEE Trans. Inf. Theory 1999, 45, 1129–1149. [Google Scholar] [CrossRef]
- Etter, P.C. Underwater Acoustic Modeling and Simulation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics: The Approach Based on Influence Functions; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zoubir, A.M.; Koivunen, V.; Ollila, E.; Muma, M. Robust Statistics for Signal Processing; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Huber, P.J. The 1972 Wald Lecture Robust Statistics: A Review. Ann. Math. Stat. 1972, 43, 1041–1067. [Google Scholar] [CrossRef]
- Donoho, D.L.; Huber, P.J. The notion of breakdown point. In A Festschrift for Erich L. Lehmann; CRC Press: Boca Raton, FL, USA, 1983; pp. 157–184. [Google Scholar]
- Davies, P.L. Aspects of robust linear regression. Ann. Stat. 1993, 21, 1843–1899. [Google Scholar] [CrossRef]
- Hampel, F.R. The influence curve and its role in robust estimation. J. Am. Stat. Assoc. 1974, 69, 383–393. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Croux, C. Alternatives to the median absolute deviation. J. Am. Stat. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- Subirana, J.S.; Hernandez-Pajares, M.; Zornoza, J.M.J. GNSS Data Processing: Fundamentals and Algorithms; European Space Agency: Paris, France, 2013. [Google Scholar]
- Walter, T.; Enge, P. Weighted RAIM for precision approach. In Proceedings of the 8th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1995), Palm Springs, CA, USA, 12–15 September 1995; Volume 8, pp. 1995–2004. [Google Scholar]
- SC-159, R.F. Minimum Operational SPerformancetandards for Global Positioning System/Wide Area Augmentation System Airborne Equipment; RTCA: Washington, DC, USA, 2006. [Google Scholar]
- Circiu, M.S.; Meurer, M.; Felux, M.; Gerbeth, D.; Thölert, S.; Vergara, M.; Enneking, C.; Sgammini, M.; Pullen, S.; Antreich, F. Evaluation of GPS L5 and Galileo E1 and E5a performance for future multifrequency and multiconstellation GBAS. Navig. J. Inst. Navig. 2017, 64, 149–163. [Google Scholar] [CrossRef]
- Li, B. Stochastic modeling of triple-frequency BeiDou signals: Estimation, assessment and impact analysis. J. Geod. 2016, 90, 593–610. [Google Scholar] [CrossRef]
- Medina, D.; Gibson, K.; Ziebold, R.; Closas, P. Determination of Pseudorange Error Models and Multipath Characterization under Signal-Degraded Scenarios. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 3446–3456. [Google Scholar]
- Maronna, R.A.; Yohai, V.J. Correcting MM estimates for “fat” data sets. Comput. Stat. Data Anal. 2010, 54, 3168–3173. [Google Scholar] [CrossRef]
- Natural Resources Canada. Tools and Applications: Precise Point Positioning. 2019. Available online: https://www.nrcan.gc.ca/maps-tools-and-publications/tools/geodetic-reference-systems-tools/tools-applications/10925#ppp (accessed on 25 October 2019).

| Simulation parameters | |
|---|---|
| Number of satellites n | {10,40} |
| Percentage of outliers | {0,10,30,40} |
| Outlier magnitude | {1,3,6,10,30,60,100} |
| Robust parameters | |
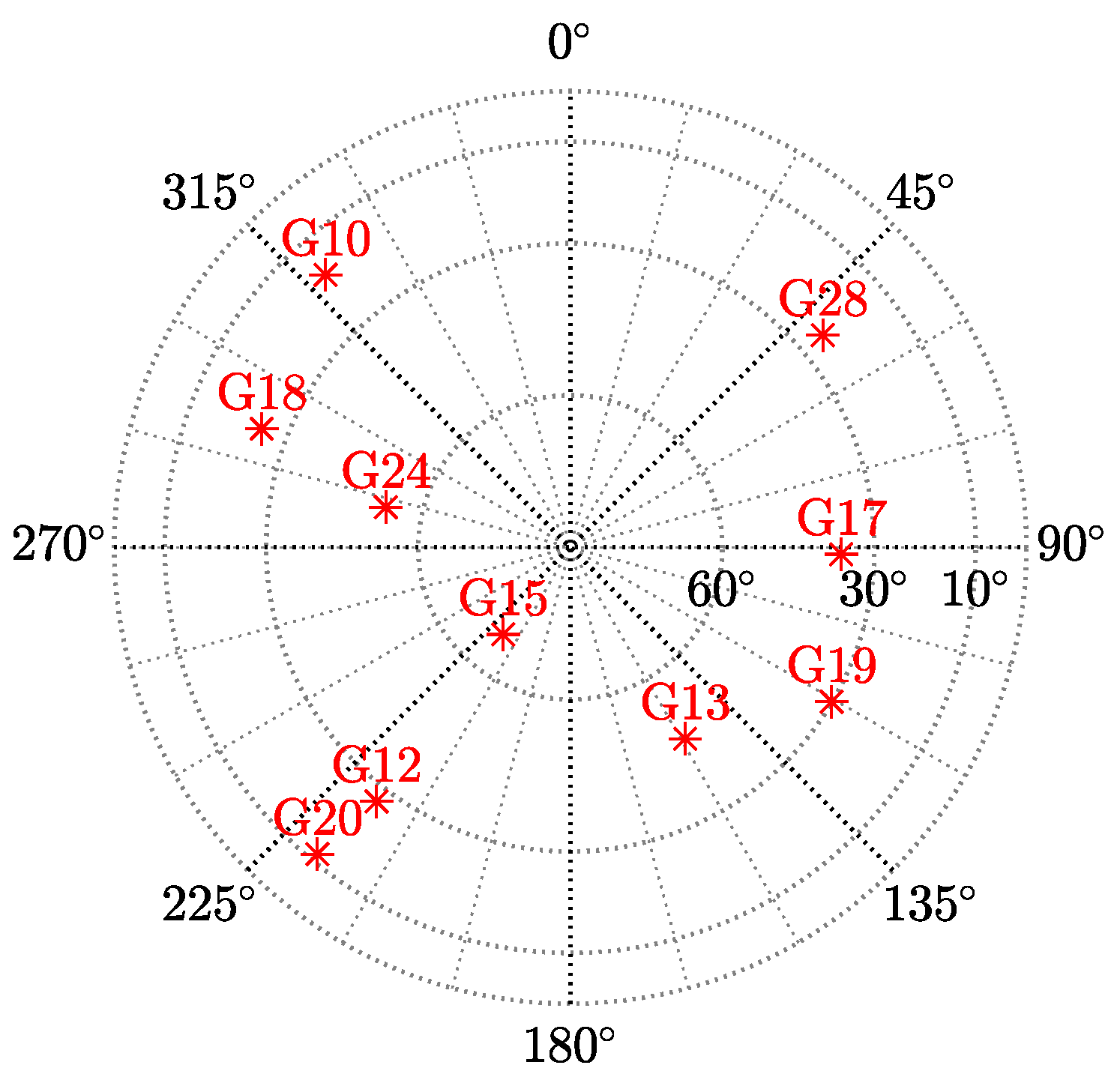
| Single-constellation scenario setup | |
| UTC time | |
| Location | Koblenz, Germany |
| (502156 N, 73555 E) | |
| PDOP | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina, D.; Li, H.; Vilà-Valls, J.; Closas, P. Robust Statistics for GNSS Positioning under Harsh Conditions: A Useful Tool? Sensors 2019, 19, 5402. https://doi.org/10.3390/s19245402
Medina D, Li H, Vilà-Valls J, Closas P. Robust Statistics for GNSS Positioning under Harsh Conditions: A Useful Tool? Sensors. 2019; 19(24):5402. https://doi.org/10.3390/s19245402
Chicago/Turabian StyleMedina, Daniel, Haoqing Li, Jordi Vilà-Valls, and Pau Closas. 2019. "Robust Statistics for GNSS Positioning under Harsh Conditions: A Useful Tool?" Sensors 19, no. 24: 5402. https://doi.org/10.3390/s19245402
APA StyleMedina, D., Li, H., Vilà-Valls, J., & Closas, P. (2019). Robust Statistics for GNSS Positioning under Harsh Conditions: A Useful Tool? Sensors, 19(24), 5402. https://doi.org/10.3390/s19245402








