Dilated Skip Convolution for Facial Landmark Detection
Abstract
1. Introduction
- To the best of our knowledge, this is the first work to exploit FC-DenseNets as a local detector with a heatmap regression to predict dense heatmaps from the given image.
- We designed a thorough dilated skip convolution (DSC) network that can refine the estimated heatmaps of the facial key points by combining a stack of dilated convolutions and a skip-connections method.
- We developed a robust method to estimate the initial facial shape to work in challenging conditions.
2. Related Works
2.1. Regression-Based Methods
2.2. Fully Convolutional Heatmap Regression Methods
Fully Convolutional DenseNets
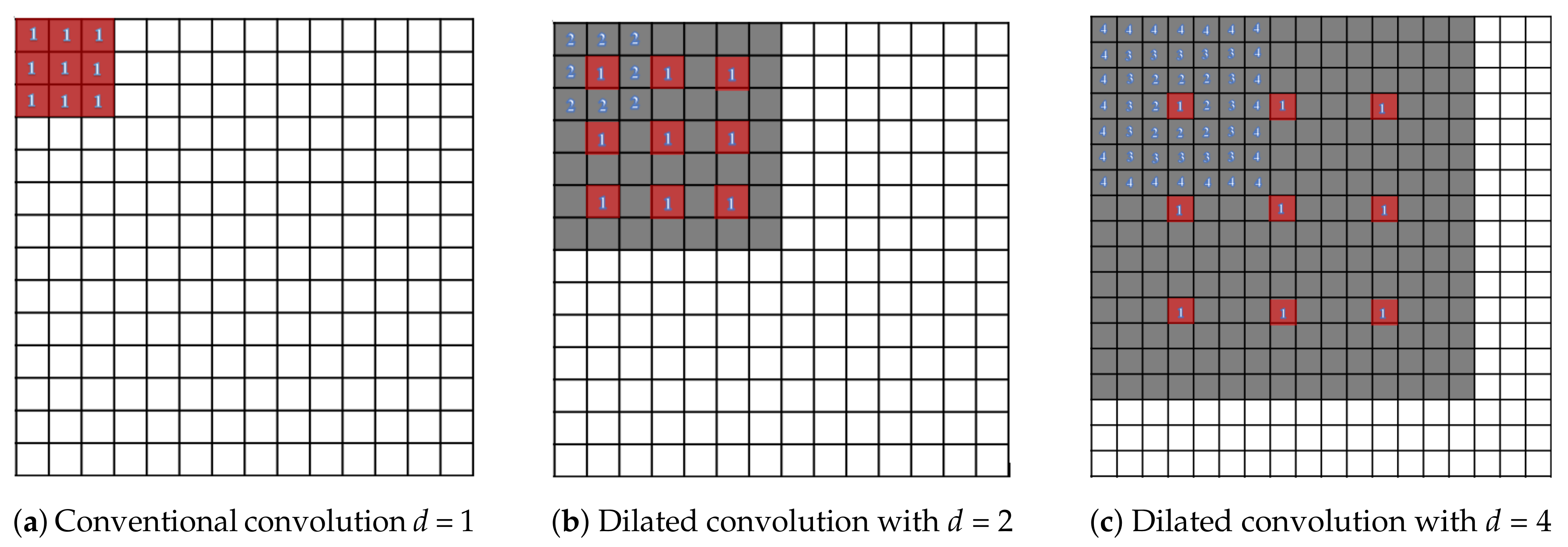
2.3. Dilated Convolutions
3. Methods
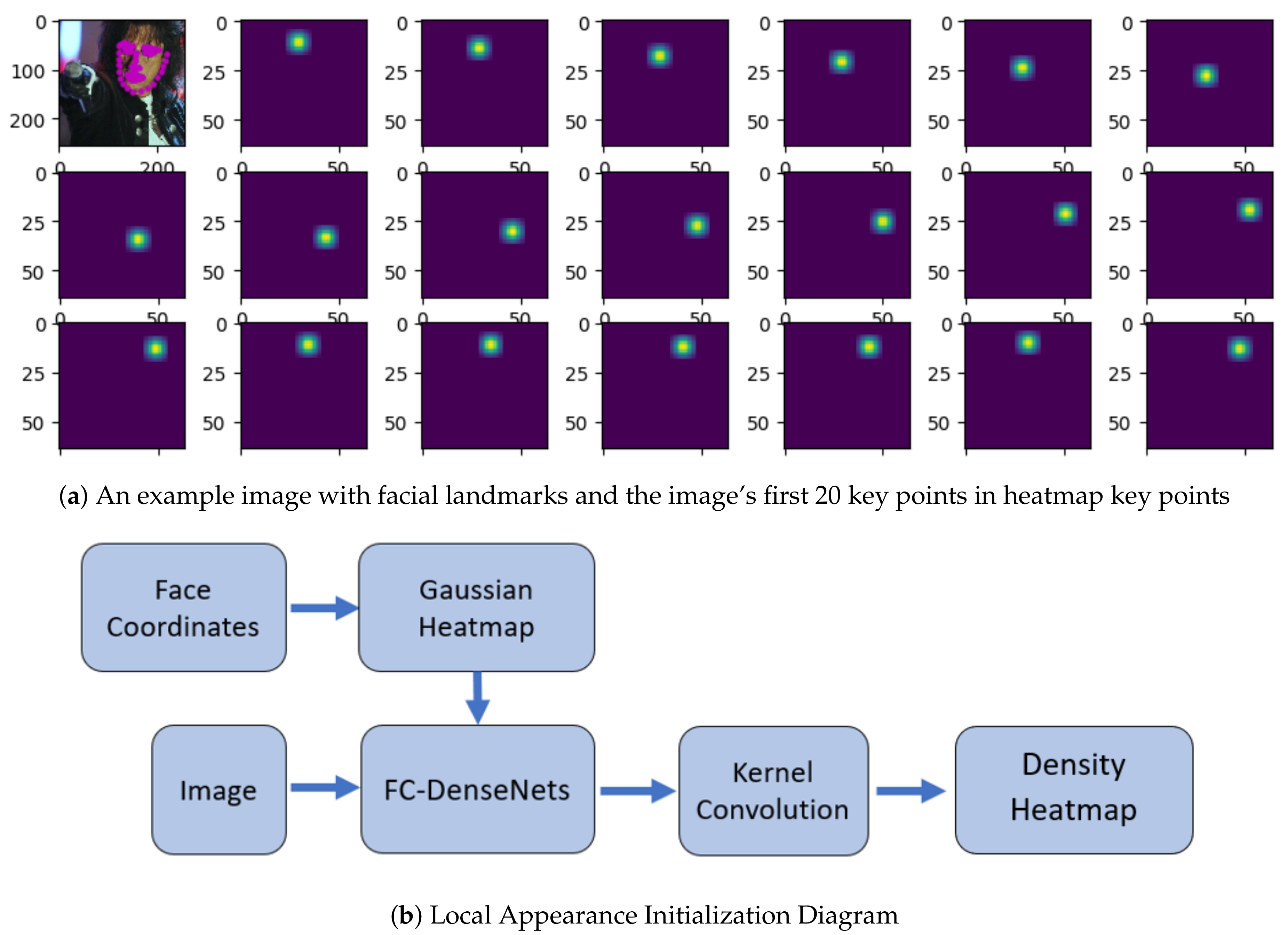
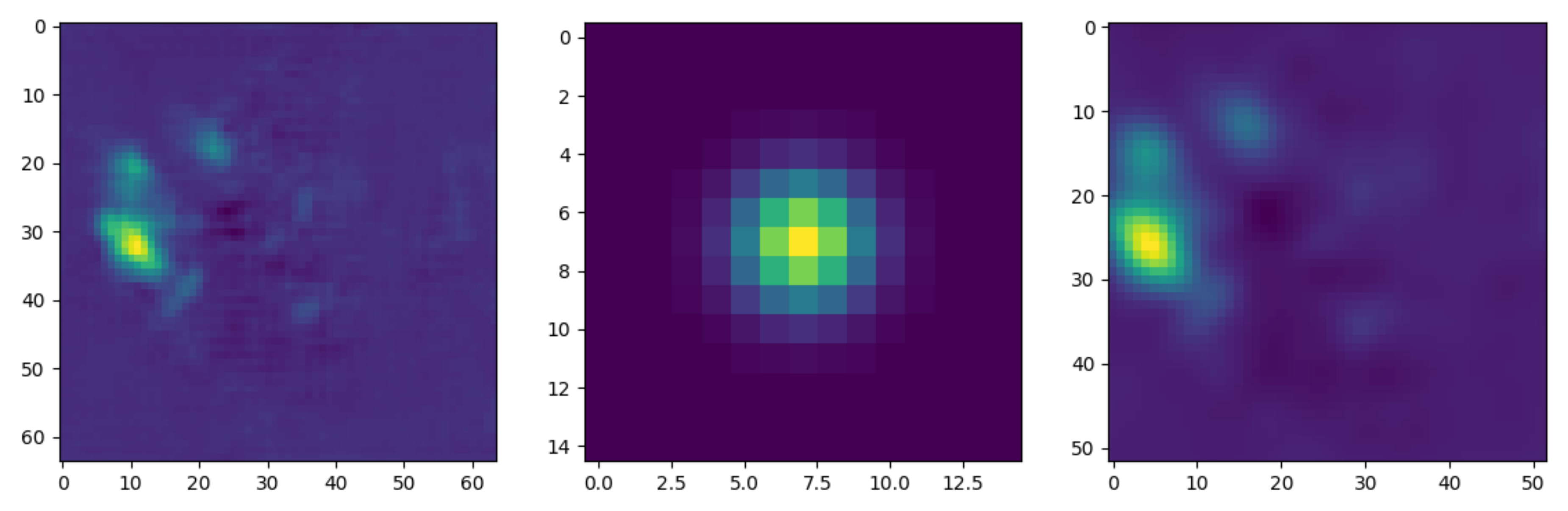
3.1. Local Appearance Initialization Networks
Kernel Convolution
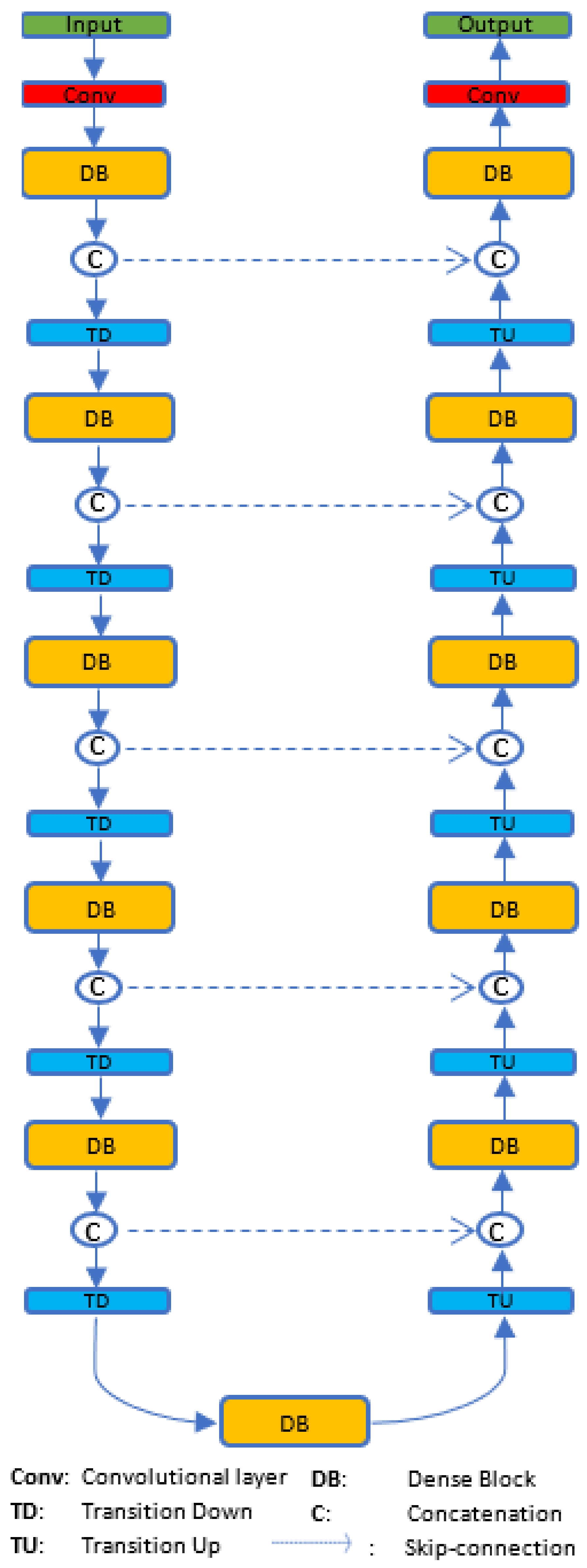
3.2. Dilated Skip Convolution Network for Shape Refinement
| Algorithm 1 Dilated skip convolution for facial landmark detection |
 |
4. Experiments
4.1. Datasets and Data Augmentation
4.1.1. Datasets
- 300W-LP [23]: 300W Large Pose (300W-LP) dataset consists of 61,225 images with 68 key points for each facial image in both 2D landmarks and the 2D projections of 3D landmarks. It is a synthetically-enlarged version of the 300W for obtaining face appearance in larger poses.
- LFPW [20]: The Labeled Face Parts in-the-Wild (LFPW) dataset has 1035 images divided into two parts: 811 images for training and 224 images for testing.
- HELEN [21]: HELEN consists of 2000 training and 330 test images with highly accurate, detailed and consistent annotations of the primary facial components. It uses annotated Flickr images.
- 300W [22]: The 300 faces in-the-Wild (300W) dataset consists of 3148 images with 68 annotated points on each face for training sets collected from three wild datasets such as LFPW [20], AFW [47] and HELEN [21]. There are three subsets for testing: challenging, common and full set. For the challenging subset, we collected the images from iBUG [48] dataset which contains 135 images; for the common subset, we collected 554 images from the testing sets of HELEN and LFPW datasets; for the full set subset, we merged the challenging and common subsets (689 images).
- AFLW 2000-3D [23]: Annotated Facial Landmarks in the Wild with 2000 three-dimensional images (AFLW 2000-3D) is a 3D face dataset constructed with 2D landmarks from the first 2000 images with yaw angles between ±90 of AFLW [49] samples. It varies expression and illumination conditions. However, some annotations, especially larger poses or occluded faces, are not very accurate.
4.1.2. Data Augmentation
4.2. Experimental Setting
4.2.1. Implementation Detail
4.2.2. Evaluation
4.3. Comparison with State-of-the-Art Algorithms
4.3.1. Comparison with LFPW Dataset
4.3.2. Comparison with HELEN Dataset
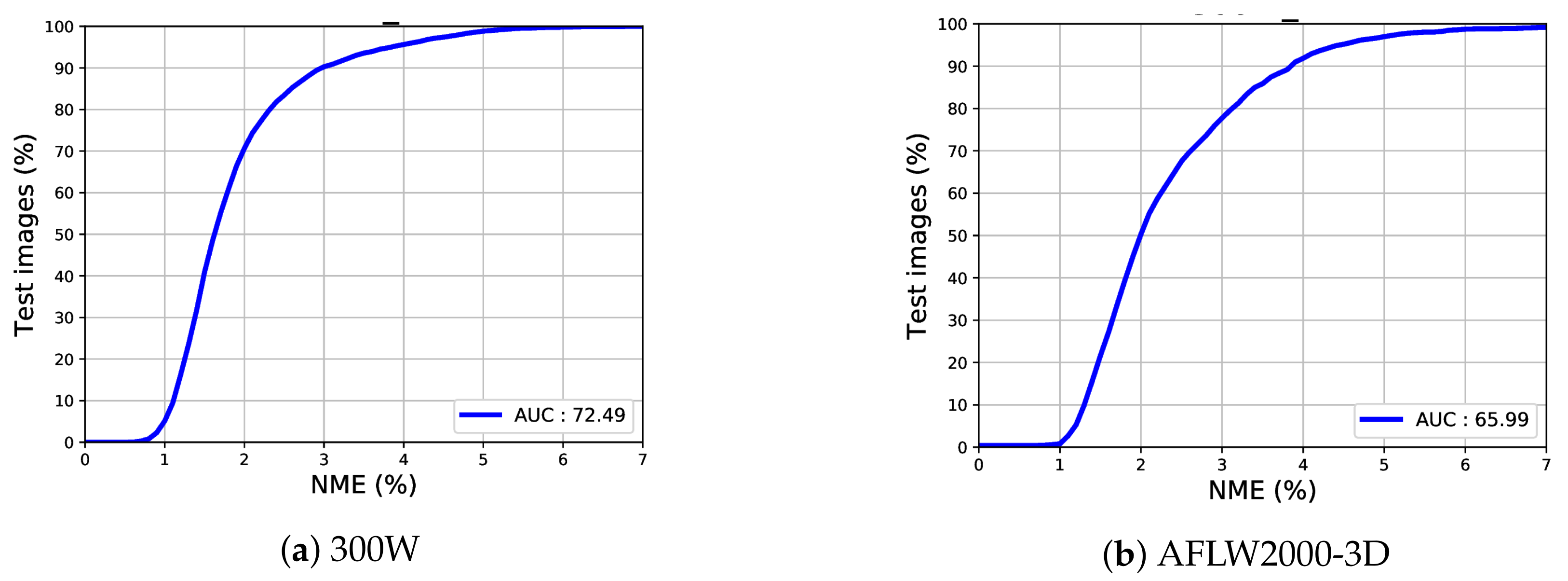
4.3.3. Comparison with 300W Dataset
4.3.4. Comparison of the AFLW2000-3D Dataset
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 300W | 300 faces in-the-Wild |
| 3D | Three-dimensional |
| AFLW 2000-3D | Annotated Facial Landmarks in the Wild with 2000 three-dimension |
| AUC | Area Under the Curve |
| CED | Cumulative Error Distribution |
| CLM | Constrained Local Model |
| CNN | Convolutional Neural Network |
| DCNN | Deep Convolutional Neural Network |
| DenseNets | Densely Connected Convolutional Networks |
| DSC | Dilated Skip Convolution |
| FCNs | Fully Convolutional Networks |
| GPU | Graphics Processing Unit |
| LAI | Local Appearance Initialization |
| LFPW | The Labeled Face Parts in-the-Wild |
| NME | Normalized Mean Error |
| ReLU | Rectified Linear Unit |
References
- Wu, Y.; Ji, Q. Facial Landmark Detection: A Literature Survey. Int. J. Comput. Vis. 2017, 1–28. [Google Scholar] [CrossRef]
- Corneanu, C.A.; Simón, M.O.; Cohn, J.F.; Guerrero, S.E. Survey on RGB, 3D, Thermal, and Multimodal Approaches for Facial Expression Recognition: History, Trends, and Affect-Related Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1548–1568. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.H.; Phillips, P.; Dong, Z.C.; Zhang, Y.D. Intelligent facial emotion recognition based on stationary wavelet entropy and Jaya algorithm. Neurocomputing 2018, 272, 668–676. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Lu, H.; Zhou, X.; Phillips, P.; Liu, Q.; Wang, S. Facial Emotion Recognition Based on Biorthogonal Wavelet Entropy, Fuzzy Support Vector Machine, and Stratified Cross Validation. IEEE Access 2016, 4, 8375–8385. [Google Scholar] [CrossRef]
- Xiong, X.; De la Torre, F. Supervised Descent Method and Its Applications to Face Alignment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 532–539. [Google Scholar]
- Koppen, P.; Feng, Z.H.; Kittler, J.; Awais, M.; Christmas, W.; Wu, X.J.; Yin, H.F. Gaussian mixture 3D morphable face model. Pattern Recognit. 2018, 74, 617–628. [Google Scholar] [CrossRef]
- Sinha, G.; Shahi, R.; Shankar, M. Human Computer Interaction. In Proceedings of the 2010 3rd International Conference on Emerging Trends in Engineering and Technology, Goa, India, 19–21 November 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Bulat, A.; Tzimiropoulos, G. How far are we from solving the 2D & 3D Face Alignment problem? (and a dataset of 230, 000 3D facial landmarks). CoRR 2017. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q.; Sun, Z.; Liu, Y. Combining data-driven and model-driven methods for robust facial landmark detection. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2409–2422. [Google Scholar] [CrossRef]
- Shi, H.; Wang, Z. Improved Stacked Hourglass Network with Offset Learning for Robust Facial Landmark Detection. In Proceedings of the 2019 9th International Conference on Information Science and Technology (ICIST), Hulunbuir, China, 2–5 August 2019; pp. 58–64. [Google Scholar] [CrossRef]
- Cao, X.; Wei, Y.; Wen, F.; Sun, J. Face alignment by explicit shape regression. Int. J. Comput. Vis. 2014, 107, 177–190. [Google Scholar] [CrossRef]
- Luo, P.; Wang, X.; Tang, X. Hierarchical face parsing via deep learning. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2480–2487. [Google Scholar]
- Wu, W.; Yang, S. Leveraging Intra and Inter-Dataset Variations for Robust Face Alignment. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Fischer, P.; Dosovitskiy, A.; Brox, T. Descriptor Matching with Convolutional Neural Networks: A Comparison to SIFT. arXiv 2014, arXiv:1405.5769. [Google Scholar]
- Wu, Y.; Wang, Z.; Ji, Q. Facial feature tracking under varying facial expressions and face poses based on restricted boltzmann machines. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 3452–3459. [Google Scholar]
- Lai, H.; Xiao, S.; Pan, Y.; Cui, Z.; Feng, J.; Xu, C.; Yin, J.; Yan, S. Deep recurrent regression for facial landmark detection. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 1144–1157. [Google Scholar] [CrossRef]
- Belagiannis, V.; Zisserman, A. Recurrent human pose estimation. In Proceedings of the 2017 12th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2017), Washington, DC, USA, 30 May–3 June 2017; pp. 468–475. [Google Scholar]
- Merget, D.; Rock, M.; Rigoll, G. Robust Facial Landmark Detection via a Fully-Convolutional Local-Global Context Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 781–790. [Google Scholar]
- Jégou, S.; Drozdzal, M.; Vazquez, D.; Romero, A.; Bengio, Y. The one hundred layers tiramisu: Fully convolutional densenets for semantic segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1175–1183. [Google Scholar]
- Belhumeur, P.N.; Jacobs, D.W.; Kriegman, D.J.; Kumar, N. Localizing Parts of Faces Using a Consensus of Exemplars. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2930–2940. [Google Scholar] [CrossRef] [PubMed]
- Le, V.; Brandt, J.; Lin, Z.; Bourdev, L.; Huang, T.S. Interactive Facial Feature Localization. In Computer Vision—ECCV 2012; Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 679–692. [Google Scholar]
- Sagonas, C.; Tzimiropoulos, G.; Zafeiriou, S.; Pantic, M. 300 Faces in-the-Wild Challenge: The First Facial Landmark Localization Challenge. In Proceedings of the 2013 IEEE International Conference on Computer Vision Workshops, Sydney, Australia, 2–8 December 2013; pp. 397–403. [Google Scholar] [CrossRef]
- Zhu, X.; Lei, Z.; Liu, X.; Shi, H.; Li, S.Z. Face Alignment Across Large Poses: A 3D Solution. CoRR 2015. [Google Scholar] [CrossRef]
- Bulat, A.; Tzimiropoulos, Y. Convolutional aggregation of local evidence for large pose face alignment. In Proceedings of the British Machine Vision Conference (BMVC), 19–22 September 2016; Richard, C., Wilson, E.R.H., Smith, W.A.P., Eds.; BMVA Press: York, UK, 2016; pp. 86.1–86.12. [Google Scholar] [CrossRef]
- Zhang, J.; Shan, S.; Kan, M.; Chen, X. Coarse-to-Fine Auto-Encoder Networks (CFAN) for Real-Time Face Alignment. In Computer Vision–ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 1–16. [Google Scholar]
- Xu, X.; Kakadiaris, I.A. Joint Head Pose Estimation and Face Alignment Framework Using Global and Local CNN Features. In Proceedings of the 2017 12th IEEE International Conference on Automatic Face Gesture Recognition (FG 2017), Washington, DC, USA, 30 May–3 June 2017; pp. 642–649. [Google Scholar] [CrossRef]
- Benini, S.; Khan, K.; Leonardi, R.; Mauro, M.; Migliorati, P. Face analysis through semantic face segmentation. Signal Process. Image Commun. 2019, 74, 21–31. [Google Scholar] [CrossRef]
- Benini, S.; Khan, K.; Leonardi, R.; Mauro, M.; Migliorati, P. FASSEG: A FAce semantic SEGmentation repository for face image analysis. Data Brief 2019, 24, 103881. [Google Scholar] [CrossRef] [PubMed]
- Toshev, A.; Szegedy, C. DeepPose: Human Pose Estimation via Deep Neural Networks. CoRR 2013. [Google Scholar] [CrossRef]
- Newell, A.; Yang, K.; Deng, J. Stacked Hourglass Networks for Human Pose Estimation. arXiv 2016, arXiv:1603.06937. [Google Scholar]
- Jain, A.; Tompson, J.; LeCun, Y.; Bregler, C. MoDeep: A Deep Learning Framework Using Motion Features for Human Pose Estimation. arXiv 2014, arXiv:1409.7963. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. arXiv 2016, arXiv:1608.06993. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; Omnipress: Madison, WI, USA, 2010; pp. 807–814. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Wang, Z.; Ji, S. Smoothed Dilated Convolutions for Improved Dense Prediction. CoRR 2018. [Google Scholar] [CrossRef]
- Van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.W.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Kalchbrenner, N.; van den Oord, A.; Simonyan, K.; Danihelka, I.; Vinyals, O.; Graves, A.; Kavukcuoglu, K. Video Pixel Networks. arXiv 2016, arXiv:1610.00527. [Google Scholar]
- Kalchbrenner, N.; Espeholt, L.; Simonyan, K.; van den Oord, A.; Graves, A.; Kavukcuoglu, K. Neural Machine Translation in Linear Time. arXiv 2016, arXiv:1610.10099. [Google Scholar]
- Pfister, T.; Charles, J.; Zisserman, A. Flowing ConvNets for Human Pose Estimation in Videos. arXiv 2015, arXiv:1506.02897. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the Neural Information Processing Systems (NIPS 2017) Workshop on Autodiff, Long Beach, CA, USA, 8 December 2017. [Google Scholar]
- Burgos-Artizzu, X.P.; Perona, P.; Dollár, P. Robust face landmark estimation under occlusion. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 1513–1520. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Mairal, J.; Koniusz, P.; Harchaoui, Z.; Schmid, C. Convolutional Kernel Networks. In Advances in Neural Information Processing Systems 27, 8–13 December 2014; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; MIT Press: Montreal, QC, Canada, 2014; Volume 2, pp. 2627–2635. [Google Scholar]
- Wang, L.; Yin, B.; Guo, A.; Ma, H.; Cao, J. Skip-connection convolutional neural network for still image crowd counting. Appl. Intell. 2018, 48, 3360–3371. [Google Scholar] [CrossRef]
- Zhu, X.; Ramanan, D. Face detection, pose estimation, and landmark localization in the wild. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2879–2886. [Google Scholar] [CrossRef]
- Sagonas, C.; Tzimiropoulos, G.; Zafeiriou, S.; Pantic, M. A Semi-automatic Methodology for Facial Landmark Annotation. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Portland, OR, USA, 23–28 June 2013; IEEE Computer Society: Washington, DC, USA, 2013; pp. 896–903. [Google Scholar] [CrossRef]
- Köstinger, M.; Wohlhart, P.; Roth, P.M.; Bischof, H. Annotated Facial Landmarks in the Wild: A large-scale, real-world database for facial landmark localization. In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 2144–2151. [Google Scholar] [CrossRef]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Zhu, S.; Li, C.; Loy, C.C.; Tang, X. Face alignment by coarse-to-fine shape searching. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4998–5006. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, E.; Mo, Y.; Liu, J.; Cao, Z. Delving Deep Into Coarse-To-Fine Framework for Facial Landmark Localization. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Kowalski, M.; Naruniec, J.; Trzcinski, T. Deep Alignment Network: A convolutional neural network for robust face alignment. arXiv 2017, arXiv:1706.01789. [Google Scholar]
- Tzimiropoulos, G.; Pantic, M. Gauss-Newton Deformable Part Models for Face Alignment In-the-Wild. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1851–1858. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Q.; Zhang, K. Stacked Hourglass Network for Robust Facial Landmark Localisation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Wei, S.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional Pose Machines. arXiv 2016, arXiv:1602.00134. [Google Scholar]
- Liu, Y.; Jourabloo, A.; Ren, W.; Liu, X. Dense Face Alignment. arXiv 2017, arXiv:1709.01442. [Google Scholar]
- Ren, S.; Cao, X.; Wei, Y.; Sun, J. Face Alignment at 3000 FPS via Regressing Local Binary Features. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1685–1692. [Google Scholar] [CrossRef]
- Xiao, S.; Feng, J.; Xing, J.; Lai, H.; Yan, S.; Kassim, A. Robust Facial Landmark Detection via Recurrent Attentive-Refinement Networks. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 57–72. [Google Scholar]
- Bhagavatula, C.; Zhu, C.; Luu, K.; Savvides, M. Faster Than Real-time Facial Alignment: A 3D Spatial Transformer Network Approach in Unconstrained Poses. arXiv 2017, arXiv:1707.05653. [Google Scholar]
- Yan, J.; Lei, Z.; Yi, D.; Li, S.Z. Learn to Combine Multiple Hypotheses for Accurate Face Alignment. In Proceedings of the 2013 IEEE International Conference on Computer Vision Workshops, Sydney, Australia, 2–8 December 2013; pp. 392–396. [Google Scholar] [CrossRef]




| Layer | Number of Feature Maps |
|---|---|
| Input | 3 |
| 3 × 3 convolution | 36 |
| DB (4 layers) + TD | 84 |
| DB (4 layers) + TD | 144 |
| DB (4 layers) + TD | 228 |
| DB (4 layers) + TD | 348 |
| DB (4 layers) + TD | 492 |
| DB (4 layers) | 672 |
| DB (4 layers) + TU | 816 |
| DB (4 layers) + TU | 612 |
| DB (4 layers) + TU | 434 |
| DB (4 layers) + TU | 288 |
| DB (4 layers) + TU | 192 |
| 1 | 68 (keypoints) |
| Filter Size | Dilation Factor | Activation Function |
|---|---|---|
| 3 × 3 | d = 1 | ReLU |
| 3 × 3 | d = 1 | ReLU |
| 3 × 3 | d = 2 | ReLU |
| 3 × 3 | d = 4 | ReLU |
| 3 × 3 | d = 8 | ReLU |
| 3 × 3 | d = 16 | ReLU |
| 3 × 3 | d = 32 | ReLU |
| Dataset | Landmark | Pose | Image |
|---|---|---|---|
| Training | |||
| HELEN | 68 | ±45 | 2000 |
| LFPW | 68 | ±45 | 811 |
| 300W | 68 | ±45 | 3148 |
| 300W-LP | 68 | ±90 | 61,225 |
| Testing | |||
| HELEN | 68 | ±45 | 330 |
| LFPW | 68 | ±45 | 224 |
| 300W | 68 | ±45 | 689 |
| AFLW2000-3D | 68 | ±90 | 2000 |
| Method | 68 pts |
|---|---|
| Zhu et al. [52] | 8.29 |
| DRMF [53] | 6.57 |
| RCPR [43] | 5.67 |
| SDM [5] | 5.67 |
| GN-DPM [54] | 5.92 |
| CFAN [25] | 5.44 |
| CFSS [51] | 4.87 |
| CFSS Practical [51] | 4.90 |
| Ours | 3.52 |
| Method | 68 pts |
|---|---|
| Zhu et al. [52] | 8.16 |
| DRMF [53] | 6.70 |
| ESR [11] | 5.70 |
| RCPR [43] | 5.93 |
| SDM [5] | 5.50 |
| GN-DPM [54] | 5.69 |
| CFAN [25] | 5.53 |
| CFSS [51] | 4.63 |
| CFSS Practical [51] | 4.72 |
| TCDCN [55] | 4.60 |
| Ours | 3.11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chim, S.; Lee, J.-G.; Park, H.-H. Dilated Skip Convolution for Facial Landmark Detection. Sensors 2019, 19, 5350. https://doi.org/10.3390/s19245350
Chim S, Lee J-G, Park H-H. Dilated Skip Convolution for Facial Landmark Detection. Sensors. 2019; 19(24):5350. https://doi.org/10.3390/s19245350
Chicago/Turabian StyleChim, Seyha, Jin-Gu Lee, and Ho-Hyun Park. 2019. "Dilated Skip Convolution for Facial Landmark Detection" Sensors 19, no. 24: 5350. https://doi.org/10.3390/s19245350
APA StyleChim, S., Lee, J.-G., & Park, H.-H. (2019). Dilated Skip Convolution for Facial Landmark Detection. Sensors, 19(24), 5350. https://doi.org/10.3390/s19245350





