Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms
Abstract
:1. Introduction
2. Preliminaries and Related Works
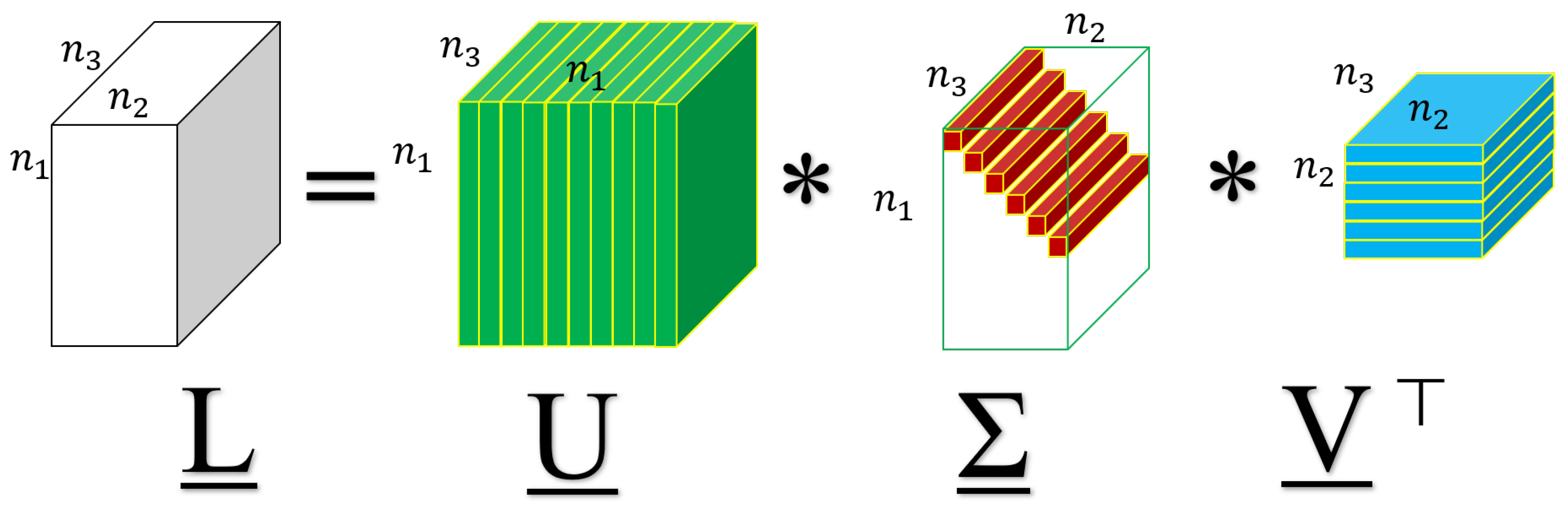
2.1. Tensor Singular Value Decomposition
2.2. Related Works
3. Theoretical Guarantee for Stable Tensor Principal Component Pursuit
3.1. The Proposed STPCP
- (I).
- (II).
- (III).
- When and , the proposed STPCP further degenerates to Robust Principal Component Analysis (RPCA) [46] given as follows:
3.2. A Theorem for Stable Recovery
- (I).
- (II).
- (III).
- When and , the proposed STPCP has consistent theoretical guarantee with the analysis of RPCA [46].
4. Algorithms
4.1. An ADMM Algorithm
- Update . We update by minimizing with other variables fixed as follows:Taking derivatives of the right-hand side of Equation (31) with respect to and respectively, and setting the results zero, we obtain:Resolving the above equation group yields:where ⊘ denotes entry-wise division and denotes the tensor all whose entries are 1.
- Update . We update by minimizing with other variables fixed as follows
- Update . The Lagrangian multipliers are updated by gradient ascent as follows:
| Algorithm 1 Solving Problem (29) using ADMM. |
4.2. A Faster Algorithm
- Update : We update by minimizing with other variables fixed as follows:Taking derivatives of the right-hand side with respect to and respectively, and setting the results zero, we obtain:Resolving the above equation group yields:
- Update . We update by minimizing with other variables fixed as followswhere operator is defined in Lemma 5 as follows.Lemma 5.([51]) Given any tensors , suppose tensor has t-SVD , where and . Then, the problem:has a closed-form solution as:
- Update :We update by minimizing with other variables fixed as follows:The equality in Equation (49) holds because according to , we have:
- Update . The Lagrangian multipliers are updated by gradient ascent as follows:
| Algorithm 2 Solving Problem (40) using ADMM. |
5. Experiments
5.1. Synthetic Data
- (I).
- (Exact recovery in the noiseless setting.) Our analysis guarantees that the underlying low-rank tensor and sparse tensor can be exactly recovered in the noiseless setting. This statement will be checked in Section 5.1.1.
- (II).
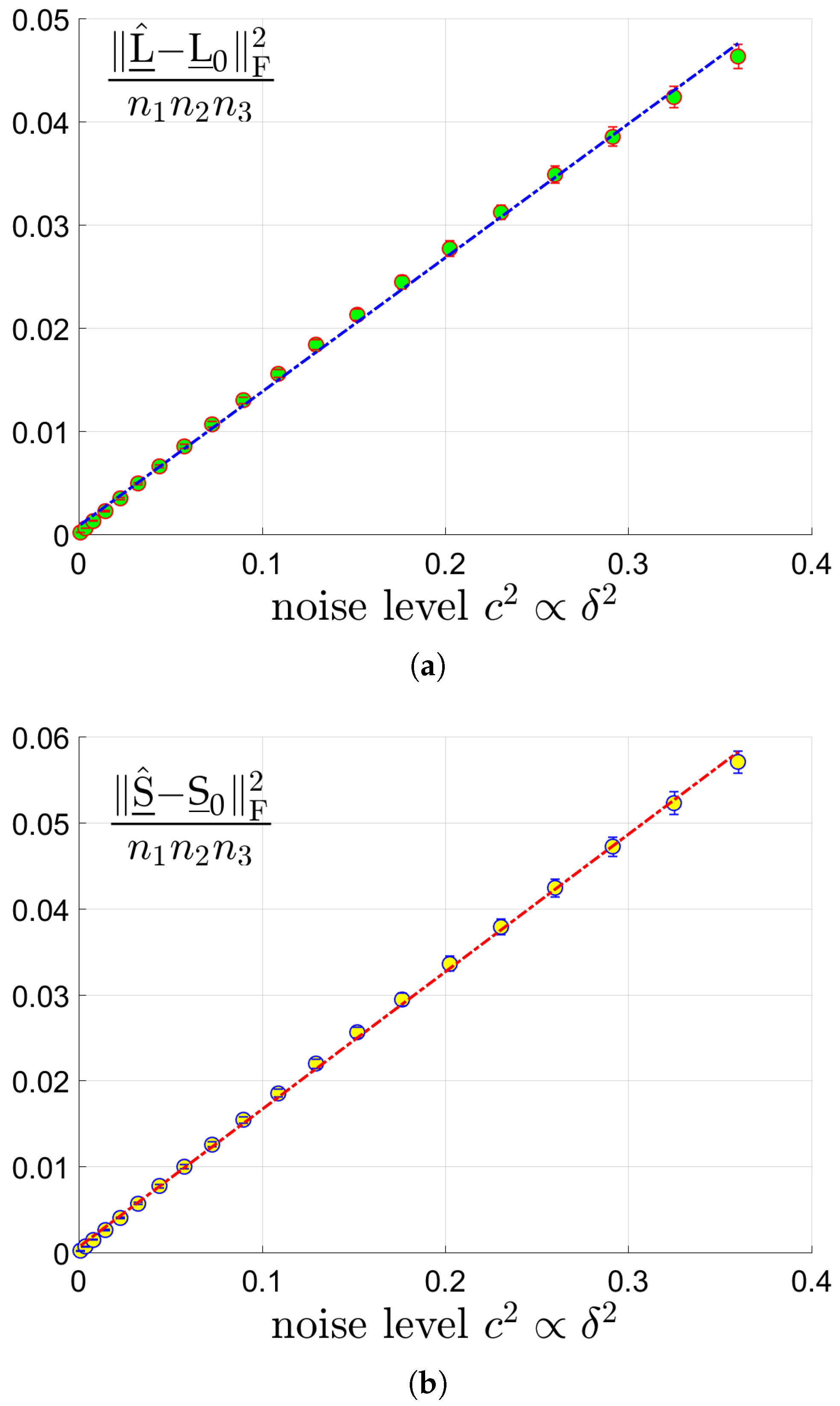
- (Linear scaling of errors with the noise level.) In Theorem 1, the estimation errors on and scales linearly with the noise level . This statement will be checked in Section 5.1.2.
5.1.1. Exact Recovery in the Noiseless Setting
5.1.2. Linear Scaling of Errors with the Noise Level
5.2. Real Data Sets
- (I).
- NN-I: tensor recovery based on matrix nuclear norms of frontal slices formulated as follows:This model will be used for image restoration in Section 5.2.1. Please note that Model (53) is equivalent to parallel matrix recovery on each frontal slice.
- (II).
- NN-II: tensor recovery based on matrix nuclear norm formulated as follows:where with defined as the vectorization [40] of frontal slices , for all . This model will be used for video restoration in Section 5.2.2.
- (III).
- SNN: tensor recovery based on SNN formulated as follows:where is the mode-i matriculation of tensor , for all .
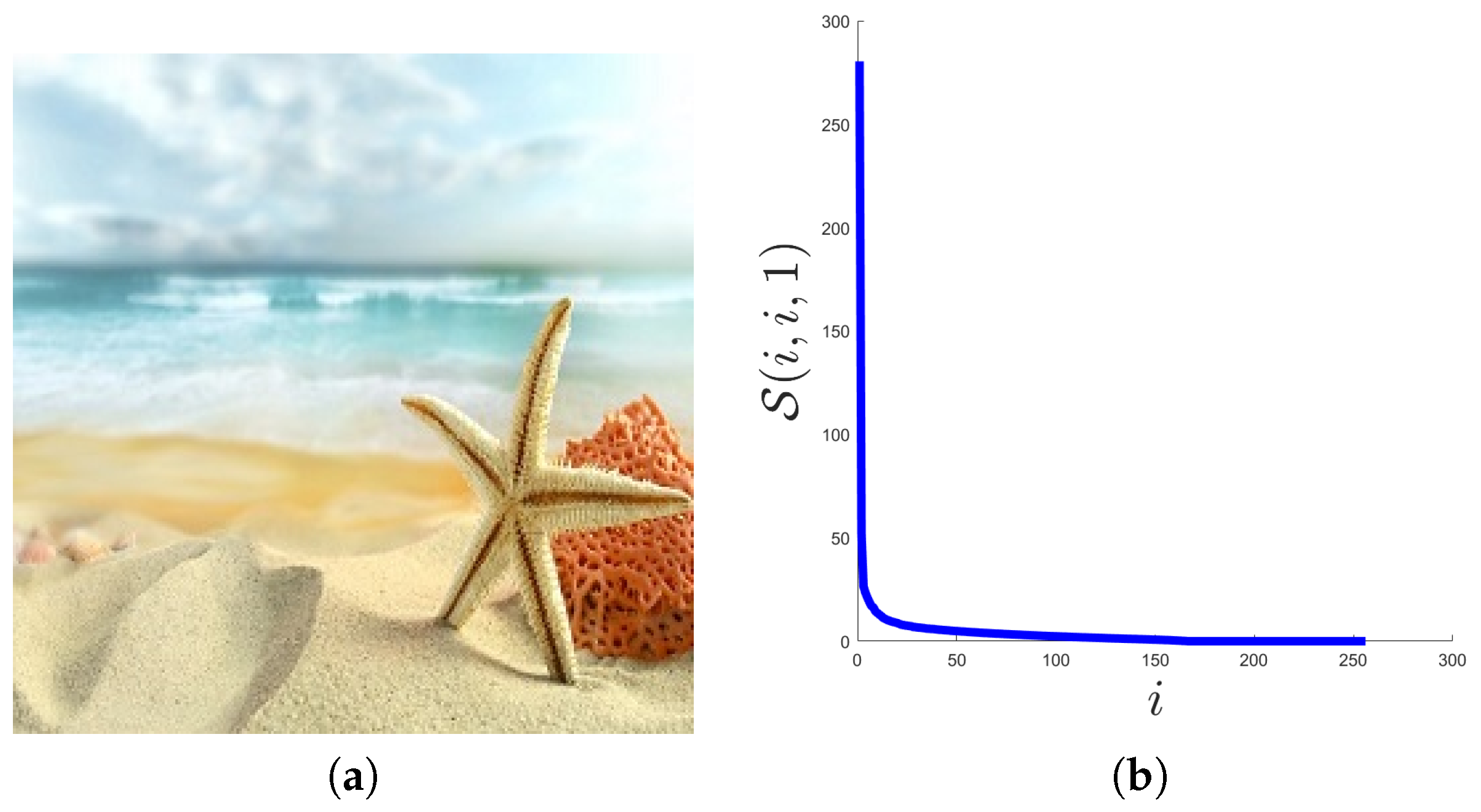
5.2.1. Color Images
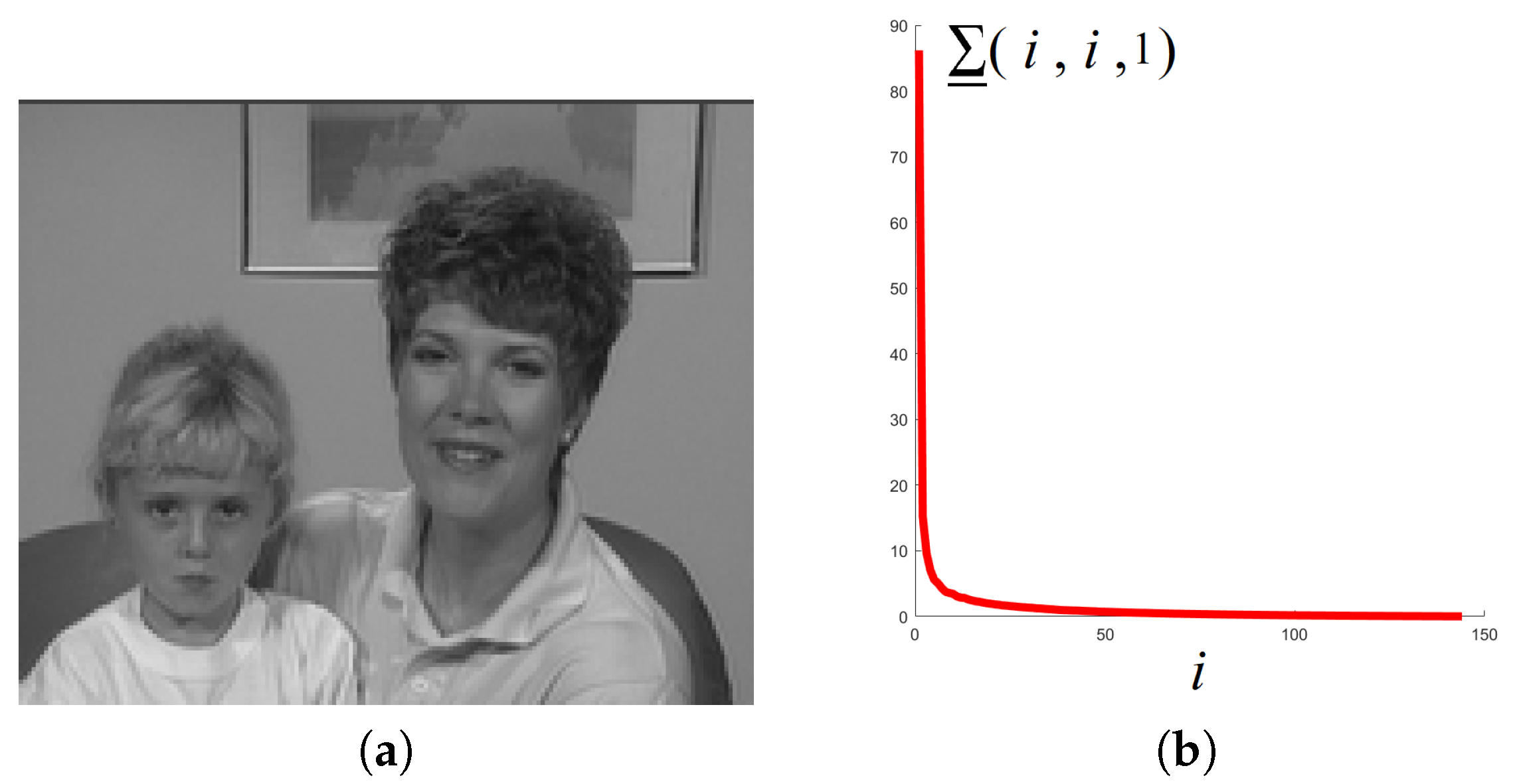
5.2.2. Videos
6. Conclusions
- By recursively applying DFT over successive modes higher than 3 and then unfolding the obtained tensor into 3-way [57], the proposed algorithms and theoretical analysis can be extended to higher-way tensors.
- By using the overlapped orientation invariant tubal nuclear norm [58], we can extend the proposed algorithm to higher-order cases and obtain orientation invariance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Lemmas and Theorems
Appendix A.1. The Proof of Theorem 1
Appendix A.1.1. Key Lemmas for the Proof of Theorem 1
Appendix A.1.2. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
Appendix A.3. Proof of Lemma 4
Appendix A.4. Proof of Theorem 3
References
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Hao, R.; Yin, W.; Su, Z. Parallel matrix factorization for low-rank tensor completion. Inverse Probl. Imaging 2015, 9, 601–624. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Shang, F. An Efficient Matrix Factorization Method for Tensor Completion. IEEE Signal Process. Lett. 2013, 20, 307–310. [Google Scholar] [CrossRef]
- Wang, A.; Wei, D.; Wang, B.; Jin, Z. Noisy Low-Tubal-Rank Tensor Completion Through Iterative Singular Tube Thresholding. IEEE Access 2018, 6, 35112–35128. [Google Scholar] [CrossRef]
- Tan, H.; Feng, G.; Feng, J.; Wang, W.; Zhang, Y.J.; Li, F. A tensor-based method for missing traffic data completion. Transp. Res. Part C 2013, 28, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Lu, B.L. Discriminative extreme learning machine with supervised sparsity preserving for image classification. Neurocomputing 2017, 261, 242–252. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; De Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef] [Green Version]
- Vaswani, N.; Bouwmans, T.; Javed, S.; Narayanamurthy, P. Robust subspace learning: Robust PCA, robust subspace tracking, and robust subspace recovery. IEEE Signal Process. Mag. 2018, 35, 32–55. [Google Scholar] [CrossRef] [Green Version]
- Cichocki, A.; Lee, N.; Oseledets, I.; Phan, A.H.; Zhao, Q.; Mandic, D.P. Tensor Networks for Dimensionality Reduction and Large-scale Optimization: Part 1 Low-Rank Tensor Decompositions. Found. Trends® Mach. Learn. 2016, 9, 249–429. [Google Scholar] [CrossRef] [Green Version]
- Yuan, M.; Zhang, C.H. On Tensor Completion via Nuclear Norm Minimization. Found. Comput. Math. 2016, 16, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Candès, E.J.; Tao, T. The power of convex relaxation: Near-optimal matrix completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef] [Green Version]
- Hillar, C.J.; Lim, L. Most Tensor Problems Are NP-Hard. J. ACM 2009, 60, 45. [Google Scholar] [CrossRef]
- Yuan, M.; Zhang, C.H. Incoherent Tensor Norms and Their Applications in Higher Order Tensor Completion. IEEE Trans. Inf. Theory 2017, 63, 6753–6766. [Google Scholar] [CrossRef]
- Tomioka, R.; Suzuki, T. Convex tensor decomposition via structured schatten norm regularization. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1331–1339. [Google Scholar]
- Semerci, O.; Hao, N.; Kilmer, M.E.; Miller, E.L. Tensor-Based Formulation and Nuclear Norm Regularization for Multienergy Computed Tomography. IEEE Trans. Image Process. 2014, 23, 1678–1693. [Google Scholar] [CrossRef] [Green Version]
- Mu, C.; Huang, B.; Wright, J.; Goldfarb, D. Square Deal: Lower Bounds and Improved Relaxations for Tensor Recovery. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 73–81. [Google Scholar]
- Zhao, Q.; Meng, D.; Kong, X.; Xie, Q.; Cao, W.; Wang, Y.; Xu, Z. A Novel Sparsity Measure for Tensor Recovery. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 271–279. [Google Scholar]
- Wei, D.; Wang, A.; Wang, B.; Feng, X. Tensor Completion Using Spectral (k, p) -Support Norm. IEEE Access 2018, 6, 11559–11572. [Google Scholar] [CrossRef]
- Tomioka, R.; Hayashi, K.; Kashima, H. Estimation of low-rank tensors via convex optimization. arXiv 2010, arXiv:1010.0789. [Google Scholar]
- Chretien, S.; Wei, T. Sensing tensors with Gaussian filters. IEEE Trans. Inf. Theory 2016, 63, 843–852. [Google Scholar] [CrossRef] [Green Version]
- Ghadermarzy, N.; Plan, Y.; Yılmaz, Ö. Near-optimal sample complexity for convex tensor completion. arXiv 2017, arXiv:1711.04965. [Google Scholar] [CrossRef] [Green Version]
- Ghadermarzy, N.; Plan, Y.; Yılmaz, Ö. Learning tensors from partial binary measurements. arXiv 2018, arXiv:1804.00108. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Shang, F.; Fan, W.; Cheng, J.; Cheng, H. Generalized Higher-Order Orthogonal Iteration for Tensor Decomposition and Completion. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1763–1771. [Google Scholar]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Lu, C.; Feng, J.; Lin, Z.; Yan, S. Exact Low Tubal Rank Tensor Recovery from Gaussian Measurements. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 1948–1954. [Google Scholar]
- Jiang, J.Q.; Ng, M.K. Exact Tensor Completion from Sparsely Corrupted Observations via Convex Optimization. arXiv 2017, arXiv:1708.00601. [Google Scholar]
- Xie, Y.; Tao, D.; Zhang, W.; Liu, Y.; Zhang, L.; Qu, Y. On Unifying Multi-view Self-Representations for Clustering by Tensor Multi-rank Minimization. Int. J. Comput. Vis. 2018, 126, 1157–1179. [Google Scholar] [CrossRef] [Green Version]
- Ely, G.T.; Aeron, S.; Hao, N.; Kilmer, M.E. 5D seismic data completion and denoising using a novel class of tensor decompositions. Geophysics 2015, 80, V83–V95. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Aeron, S.; Aggarwal, V.; Wang, X.; Wu, M. Adaptive Sampling of RF Fingerprints for Fine-grained Indoor Localization. IEEE Trans. Mob. Comput. 2016, 15, 2411–2423. [Google Scholar] [CrossRef] [Green Version]
- Wang, A.; Lai, Z.; Jin, Z. Noisy low-tubal-rank tensor completion. Neurocomputing 2019, 330, 267–279. [Google Scholar] [CrossRef]
- Sun, W.; Chen, Y.; Huang, L.; So, H.C. Tensor Completion via Generalized Tensor Tubal Rank Minimization using General Unfolding. IEEE Signal Process. Lett. 2018, 25, 868–872. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.Y.; Aeron, S.; Aggarwal, V.; Wang, X. Low-tubal-rank tensor completion using alternating minimization. arXiv 2016, arXiv:1610.01690. [Google Scholar]
- Liu, X.Y.; Wang, X. Fourth-order tensors with multidimensional discrete transforms. arXiv 2017, arXiv:1705.01576. [Google Scholar]
- Gu, Q.; Gui, H.; Han, J. Robust tensor decomposition with gross corruption. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1422–1430. [Google Scholar]
- Wang, A.; Jin, Z.; Tang, G. Robust tensor decomposition via t-SVD: Near-optimal statistical guarantee and scalable algorithms. Signal Process. 2020, 167, 107319. [Google Scholar] [CrossRef]
- Zhang, Z.; Aeron, S. Exact Tensor Completion Using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
- Goldfarb, D.; Qin, Z. Robust low-rank tensor recovery: Models and algorithms. SIAM J. Matrix Anal. Appl. 2014, 35, 225–253. [Google Scholar] [CrossRef] [Green Version]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Cheng, L.; Wu, Y.C.; Zhang, J.; Liu, L. Subspace identification for DOA estimation in massive/full-dimension MIMO systems: Bad data mitigation and automatic source enumeration. IEEE Trans. Signal Process. 2015, 63, 5897–5909. [Google Scholar] [CrossRef]
- Cheng, L.; Xing, C.; Wu, Y.C. Irregular Array Manifold Aided Channel Estimation in Massive MIMO Communications. IEEE J. Sel. Top. Signal Process. 2019, 13, 974–988. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhou, G.; Zhang, L.; Cichocki, A.; Amari, S.I. Bayesian robust tensor factorization for incomplete multiway data. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 736–748. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Cheung, Y. Bayesian Low-Tubal-Rank Robust Tensor Factorization with Multi-Rank Determination. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, X.; Wright, J.; Candes, E.; Ma, Y. Stable principal component pursuit. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 12–18 June 2010; pp. 1518–1522. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Tensors via Convex Optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Peng, Y.; Lu, B.L. Robust structured sparse representation via half-quadratic optimization for face recognition. Multimed. Tools Appl. 2017, 76, 8859–8880. [Google Scholar] [CrossRef]
- Liu, G.; Yan, S. Active subspace: Toward scalable low-rank learning. Neural Comput. 2012, 24, 3371–3394. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Jin, Z.; Yang, J. A Factorization Strategy for Tensor Robust PCA; ResearchGate: Berlin, Germany, 2019. [Google Scholar]
- Jiang, Q.; Ng, M. Robust Low-Tubal-Rank Tensor Completion via Convex Optimization. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 2649–2655. [Google Scholar]
- Kernfeld, E.; Kilmer, M.; Aeron, S. Tensor–tensor products with invertible linear transforms. Linear Algebra Its Appl. 2015, 485, 545–570. [Google Scholar] [CrossRef]
- Lu, C.; Peng, X.; Wei, Y. Low-Rank Tensor Completion With a New Tensor Nuclear Norm Induced by Invertible Linear Transforms. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5996–6004. [Google Scholar]
- Liu, X.Y.; Aeron, S.; Aggarwal, V.; Wang, X. Low-tubal-rank tensor completion using alternating minimization. In Proceedings of the SPIE Defense+ Security, Baltimore, MD, USA, 17–21 April 2016; International Society for Optics and Photonics: Bellingham, DC, USA, 2016; p. 984809. [Google Scholar]
- Zhou, P.; Lu, C.; Lin, Z.; Zhang, C. Tensor Factorization for Low-Rank Tensor Completion. IEEE Trans. Image Process. 2018, 27, 1152–1163. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.D.; Shafer, R.; Larue, B. An Order-p Tensor Factorization with Applications in Imaging. SIAM J. Sci. Comput. 2013, 35, A474–A490. [Google Scholar] [CrossRef]
- Wang, A.; Jin, Z. Orientation Invariant Tubal Nuclear Norms Applied to Robust Tensor Decomposition. Available online: https://www.researchgate.net/publication/329116872_Orientation_Invariant_Tubal_Nuclear_Norms_Applied_to_Robust_Tensor_Decomposition (accessed on 3 December 2019).

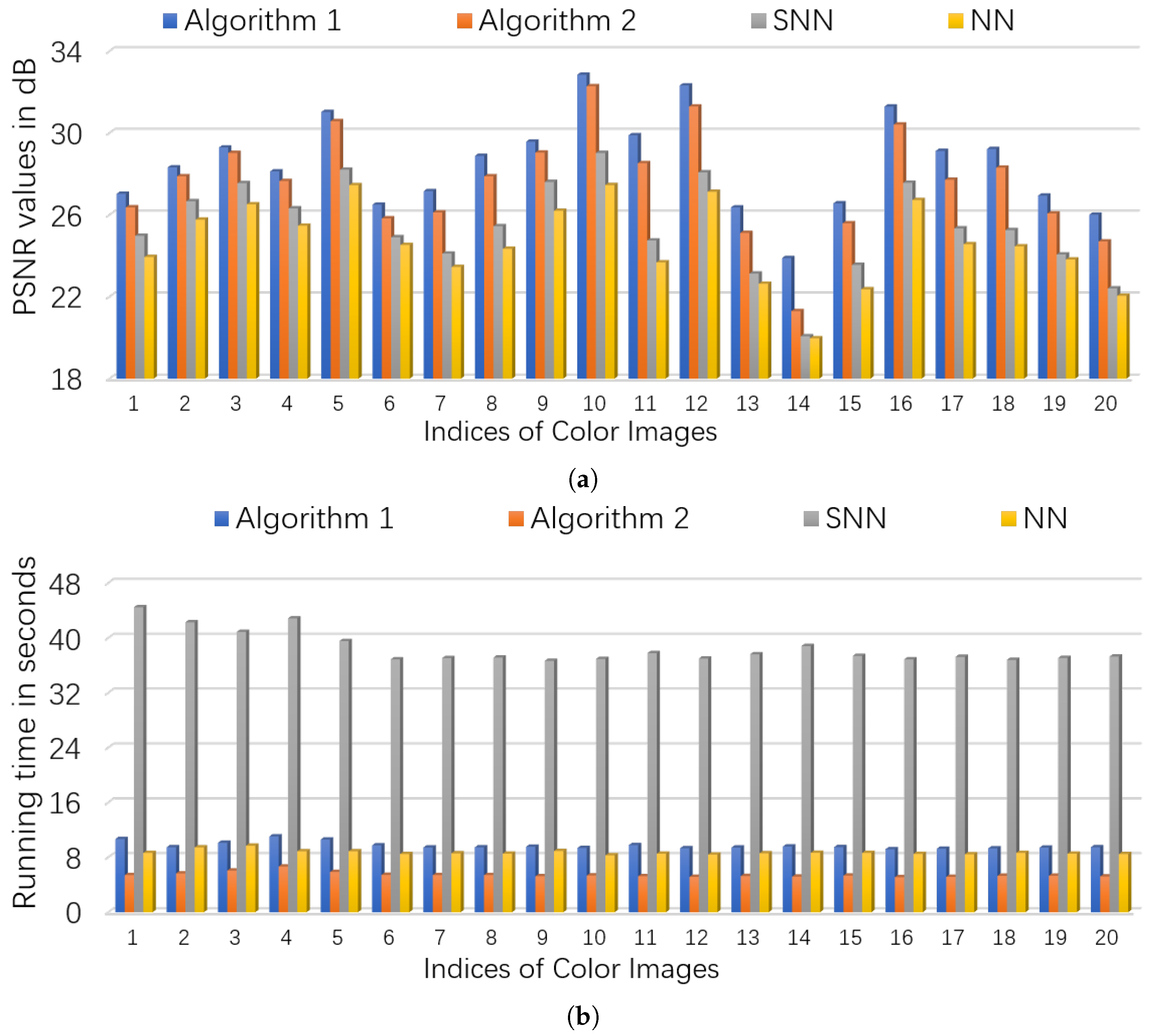
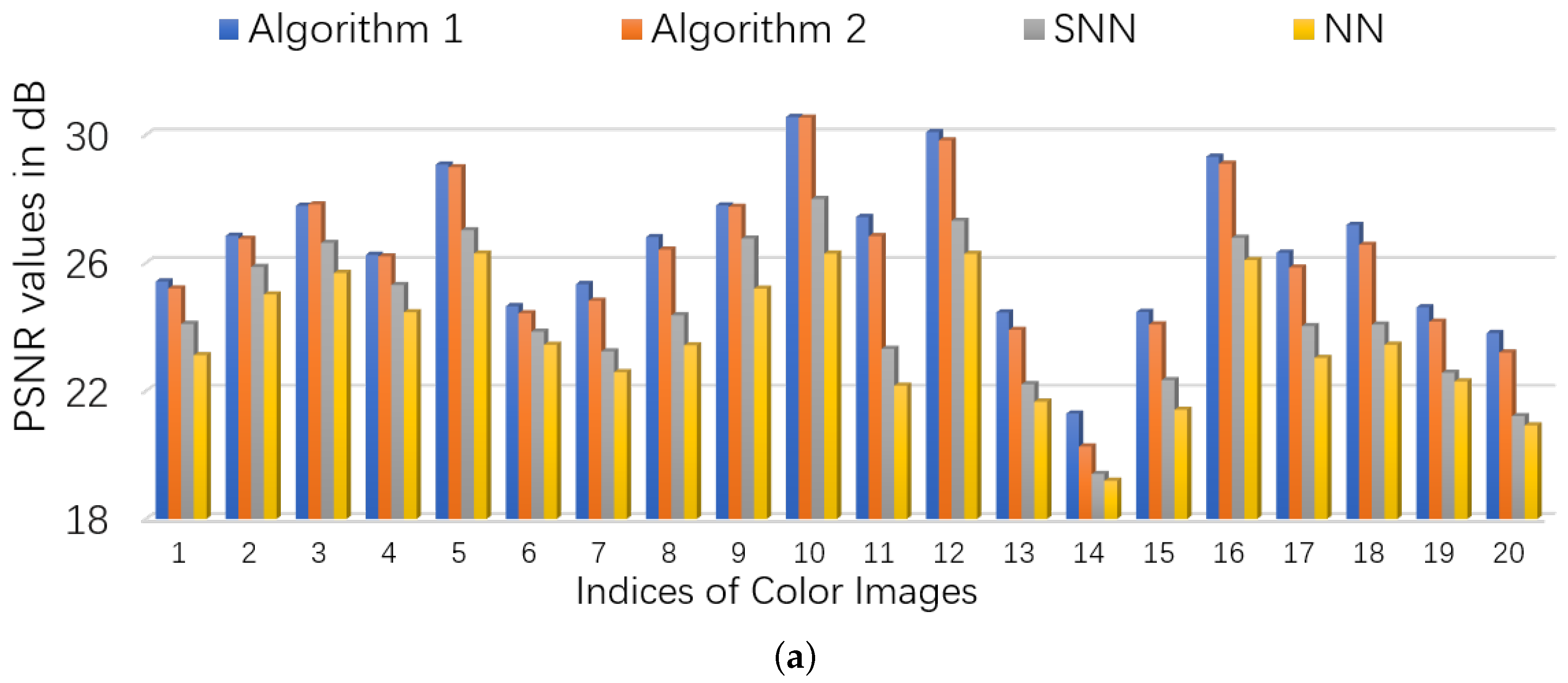
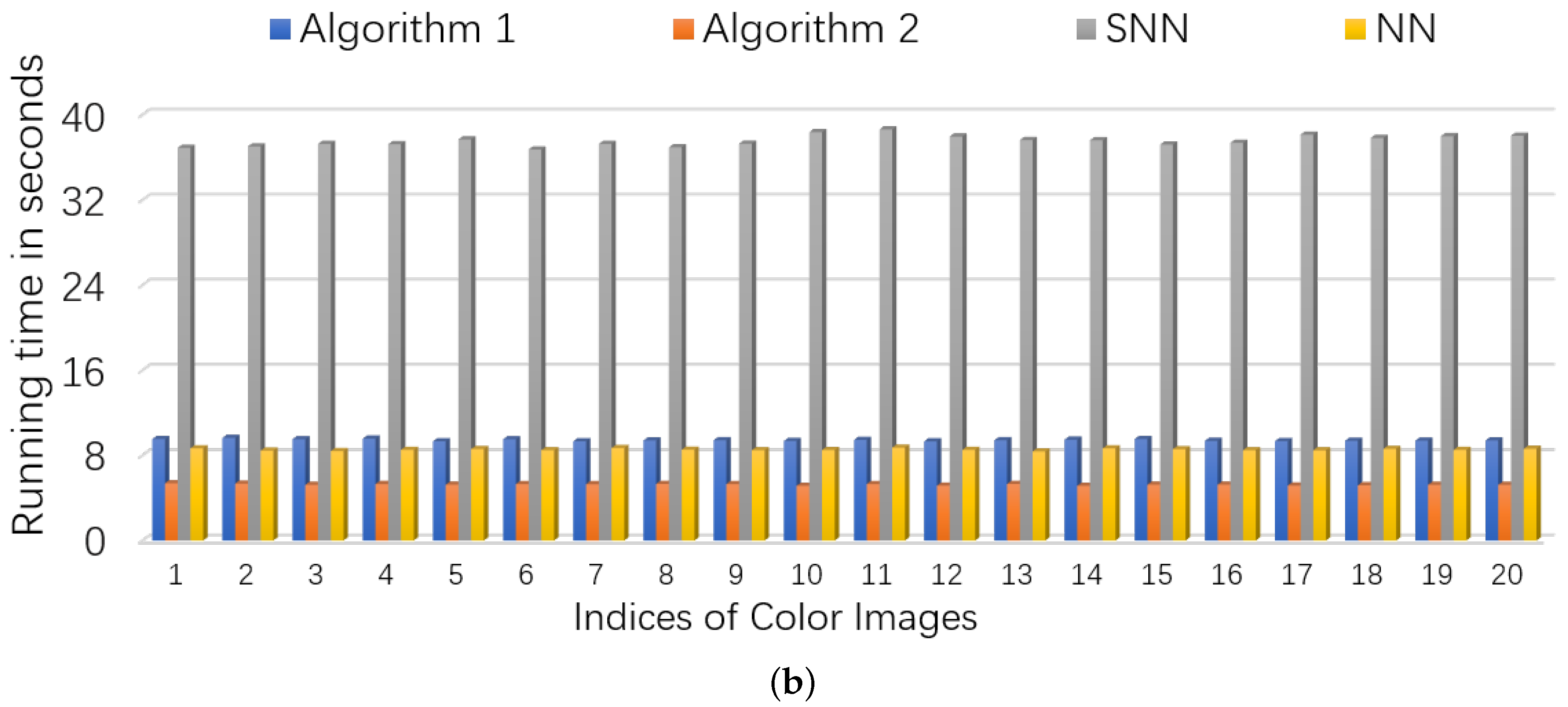

| n | Method | time/s | |||||
|---|---|---|---|---|---|---|---|
| 100 | 5 | Algorithm 1 | 5 | 3.63 | |||
| Algorithm 2 | 5 | 1.76 | |||||
| 160 | 8 | Algorithm 1 | 8 | 9.52 | |||
| Algorithm 2 | 8 | 4.42 | |||||
| 200 | 10 | Algorithm 1 | 10 | 14.16 | |||
| Algorithm 2 | 10 | 7.44 |
| n | Method | time/s | |||||
|---|---|---|---|---|---|---|---|
| 100 | 5 | Algorithm 1 | 5 | 4.43 | |||
| Algorithm 2 | 5 | 1.82 | |||||
| 160 | 8 | Algorithm 1 | 8 | 10.45 | |||
| Algorithm 2 | 8 | 5.15 | |||||
| 200 | 10 | Algorithm 1 | 10 | 18.97 | |||
| Algorithm 2 | 10 | 8.04 |
| n | Method | time/s | |||||
|---|---|---|---|---|---|---|---|
| 100 | 5 | Algorithm 1 | 5 | 3.87 | |||
| Algorithm 2 | 5 | 1.69 | |||||
| 160 | 8 | Algorithm 1 | 8 | 9.64 | |||
| Algorithm 2 | 8 | 4.46 | |||||
| 200 | 10 | Algorithm 1 | 10 | 14.78 | |||
| Algorithm 2 | 10 | 7.77 |
| Data Set | Index | NN, Model (54) | SNN, Model (55) | Algorithm 1 | Algorithm 2 | |
|---|---|---|---|---|---|---|
| Akiyo | (0.9,0.1) | PSNR | 31.74 | 32.09 | 33.94 | 33.36 |
| time/s | 29.48 | 51.13 | 20.10 | 12.39 | ||
| (0.8,0.2) | PSNR | 30.59 | 30.70 | 32.44 | 32.07 | |
| time/s | 30.65 | 51.17 | 19.53 | 14.92 | ||
| Silent | (0.9,0.1) | PSNR | 28.26 | 30.39 | 31.74 | 31.23 |
| time/s | 28.91 | 49.79 | 21.21 | 14.76 | ||
| (0.8,0.2) | PSNR | 26.95 | 27.60 | 30.42 | 30.07 | |
| time/s | 36.51 | 60.81 | 22.43 | 15.62 | ||
| Carphone | (0.9,0.1) | PSNR | 26.87 | 28.79 | 29.15 | 28.94 |
| time/s | 28.55 | 47.17 | 22.12 | 14.41 | ||
| (0.8,0.2)) | PSNR | 26.12 | 26.43 | 28.17 | 27.99 | |
| time/s | 26.72 | 49.21 | 20.55 | 14.74 | ||
| Claire | (0.9,0.1) | PSNR | 30.56 | 32.20 | 34.27 | 34.02 |
| time/s | 29.75 | 47.32 | 21.43 | 13.52 | ||
| (0.8,0.2) | PSNR | 29.94 | 30.43 | 32.96 | 32.78 | |
| time/s | 29.43 | 50.46 | 19.47 | 13.04 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, W.; Wei, D.; Zhang, R. Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms. Sensors 2019, 19, 5335. https://doi.org/10.3390/s19235335
Fang W, Wei D, Zhang R. Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms. Sensors. 2019; 19(23):5335. https://doi.org/10.3390/s19235335
Chicago/Turabian StyleFang, Wei, Dongxu Wei, and Ran Zhang. 2019. "Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms" Sensors 19, no. 23: 5335. https://doi.org/10.3390/s19235335
APA StyleFang, W., Wei, D., & Zhang, R. (2019). Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms. Sensors, 19(23), 5335. https://doi.org/10.3390/s19235335




