Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms
Abstract
1. Introduction
2. Preliminaries and Related Works
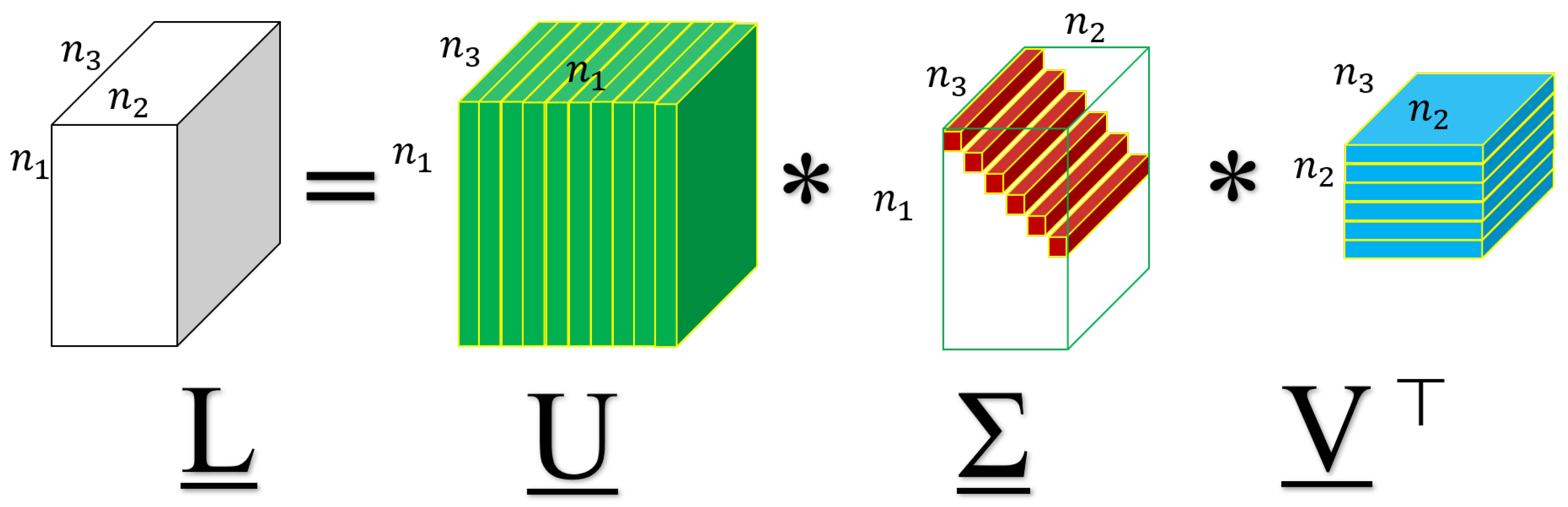
2.1. Tensor Singular Value Decomposition
2.2. Related Works
3. Theoretical Guarantee for Stable Tensor Principal Component Pursuit
3.1. The Proposed STPCP
- (I).
- (II).
- (III).
- When and , the proposed STPCP further degenerates to Robust Principal Component Analysis (RPCA) [46] given as follows:
3.2. A Theorem for Stable Recovery
- (I).
- (II).
- (III).
- When and , the proposed STPCP has consistent theoretical guarantee with the analysis of RPCA [46].
4. Algorithms
4.1. An ADMM Algorithm
- Update . We update by minimizing with other variables fixed as follows:Taking derivatives of the right-hand side of Equation (31) with respect to and respectively, and setting the results zero, we obtain:Resolving the above equation group yields:where ⊘ denotes entry-wise division and denotes the tensor all whose entries are 1.
- Update . We update by minimizing with other variables fixed as follows
- Update . The Lagrangian multipliers are updated by gradient ascent as follows:
| Algorithm 1 Solving Problem (29) using ADMM. |
4.2. A Faster Algorithm
- Update : We update by minimizing with other variables fixed as follows:Taking derivatives of the right-hand side with respect to and respectively, and setting the results zero, we obtain:Resolving the above equation group yields:
- Update . We update by minimizing with other variables fixed as followswhere operator is defined in Lemma 5 as follows.Lemma 5.([51]) Given any tensors , suppose tensor has t-SVD , where and . Then, the problem:has a closed-form solution as:
- Update :We update by minimizing with other variables fixed as follows:The equality in Equation (49) holds because according to , we have:
- Update . The Lagrangian multipliers are updated by gradient ascent as follows:
| Algorithm 2 Solving Problem (40) using ADMM. |
5. Experiments
5.1. Synthetic Data
- (I).
- (Exact recovery in the noiseless setting.) Our analysis guarantees that the underlying low-rank tensor and sparse tensor can be exactly recovered in the noiseless setting. This statement will be checked in Section 5.1.1.
- (II).
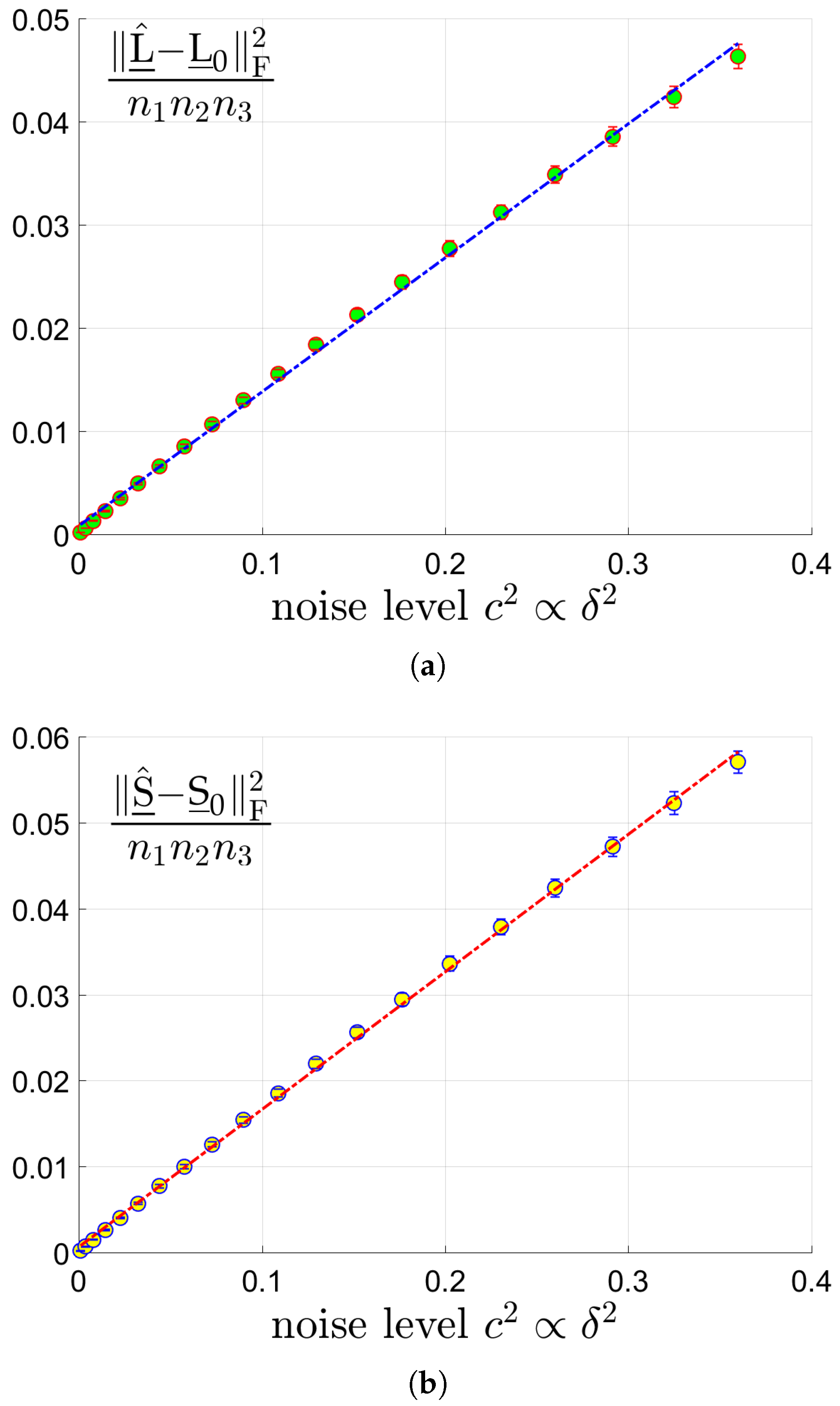
- (Linear scaling of errors with the noise level.) In Theorem 1, the estimation errors on and scales linearly with the noise level . This statement will be checked in Section 5.1.2.
5.1.1. Exact Recovery in the Noiseless Setting
5.1.2. Linear Scaling of Errors with the Noise Level
5.2. Real Data Sets
- (I).
- NN-I: tensor recovery based on matrix nuclear norms of frontal slices formulated as follows:This model will be used for image restoration in Section 5.2.1. Please note that Model (53) is equivalent to parallel matrix recovery on each frontal slice.
- (II).
- NN-II: tensor recovery based on matrix nuclear norm formulated as follows:where with defined as the vectorization [40] of frontal slices , for all . This model will be used for video restoration in Section 5.2.2.
- (III).
- SNN: tensor recovery based on SNN formulated as follows:where is the mode-i matriculation of tensor , for all .
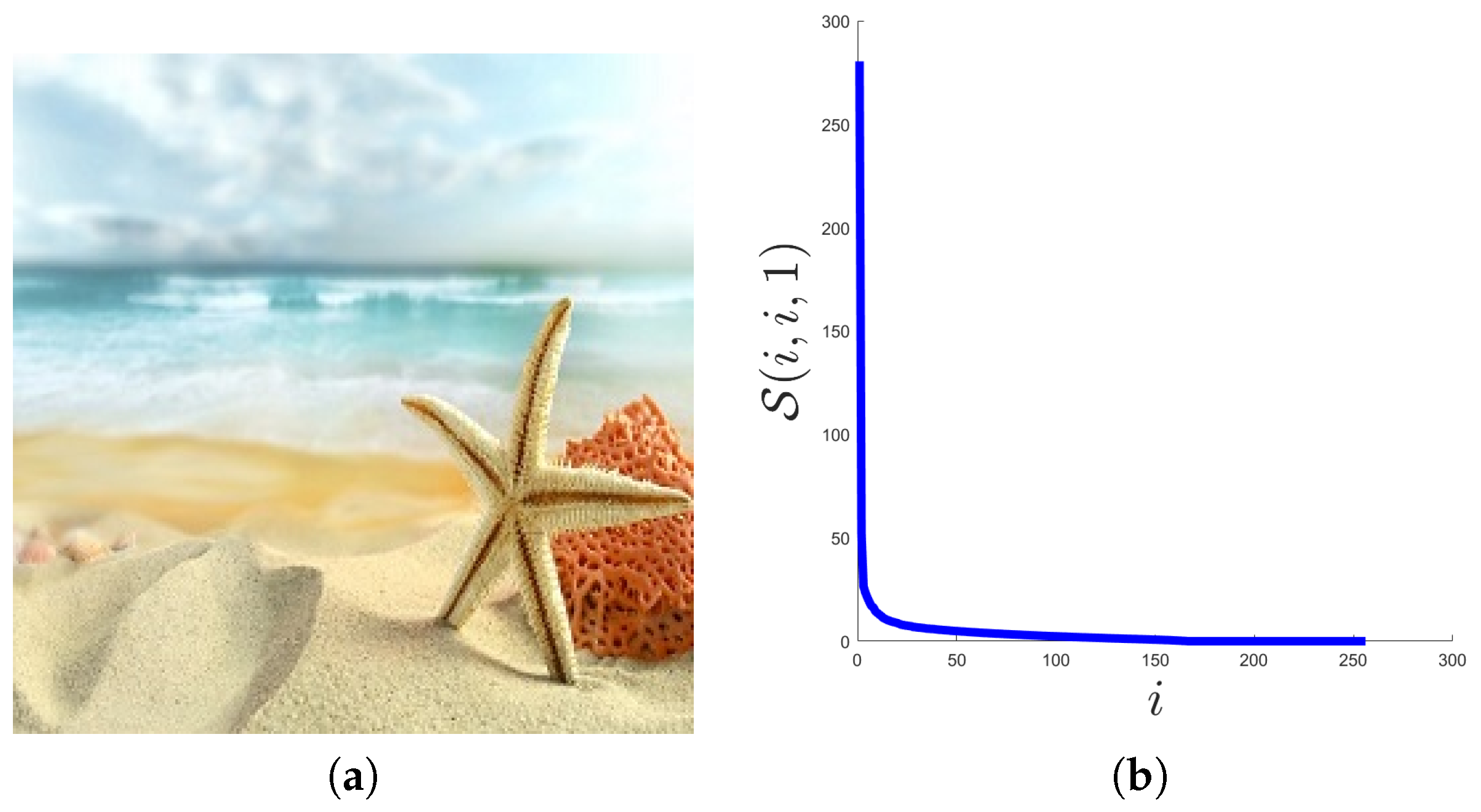
5.2.1. Color Images
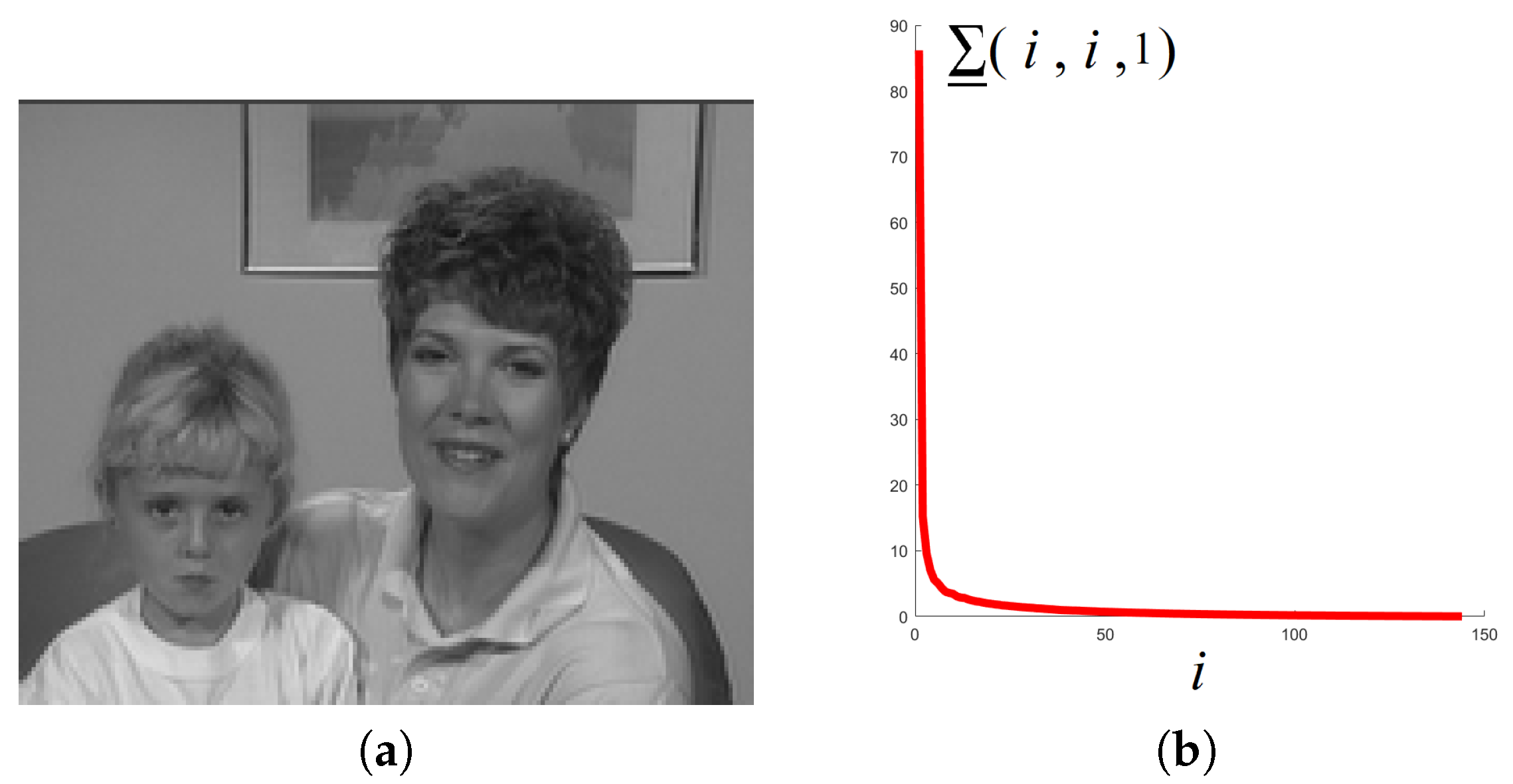
5.2.2. Videos
6. Conclusions
- By recursively applying DFT over successive modes higher than 3 and then unfolding the obtained tensor into 3-way [57], the proposed algorithms and theoretical analysis can be extended to higher-way tensors.
- By using the overlapped orientation invariant tubal nuclear norm [58], we can extend the proposed algorithm to higher-order cases and obtain orientation invariance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Lemmas and Theorems
Appendix A.1. The Proof of Theorem 1
Appendix A.1.1. Key Lemmas for the Proof of Theorem 1
Appendix A.1.2. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
Appendix A.3. Proof of Lemma 4
Appendix A.4. Proof of Theorem 3
References
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Xu, Y.; Hao, R.; Yin, W.; Su, Z. Parallel matrix factorization for low-rank tensor completion. Inverse Probl. Imaging 2015, 9, 601–624. [Google Scholar] [CrossRef]
- Liu, Y.; Shang, F. An Efficient Matrix Factorization Method for Tensor Completion. IEEE Signal Process. Lett. 2013, 20, 307–310. [Google Scholar] [CrossRef]
- Wang, A.; Wei, D.; Wang, B.; Jin, Z. Noisy Low-Tubal-Rank Tensor Completion Through Iterative Singular Tube Thresholding. IEEE Access 2018, 6, 35112–35128. [Google Scholar] [CrossRef]
- Tan, H.; Feng, G.; Feng, J.; Wang, W.; Zhang, Y.J.; Li, F. A tensor-based method for missing traffic data completion. Transp. Res. Part C 2013, 28, 15–27. [Google Scholar] [CrossRef]
- Peng, Y.; Lu, B.L. Discriminative extreme learning machine with supervised sparsity preserving for image classification. Neurocomputing 2017, 261, 242–252. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; De Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef]
- Vaswani, N.; Bouwmans, T.; Javed, S.; Narayanamurthy, P. Robust subspace learning: Robust PCA, robust subspace tracking, and robust subspace recovery. IEEE Signal Process. Mag. 2018, 35, 32–55. [Google Scholar] [CrossRef]
- Cichocki, A.; Lee, N.; Oseledets, I.; Phan, A.H.; Zhao, Q.; Mandic, D.P. Tensor Networks for Dimensionality Reduction and Large-scale Optimization: Part 1 Low-Rank Tensor Decompositions. Found. Trends® Mach. Learn. 2016, 9, 249–429. [Google Scholar] [CrossRef]
- Yuan, M.; Zhang, C.H. On Tensor Completion via Nuclear Norm Minimization. Found. Comput. Math. 2016, 16, 1–38. [Google Scholar] [CrossRef]
- Candès, E.J.; Tao, T. The power of convex relaxation: Near-optimal matrix completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef]
- Hillar, C.J.; Lim, L. Most Tensor Problems Are NP-Hard. J. ACM 2009, 60, 45. [Google Scholar] [CrossRef]
- Yuan, M.; Zhang, C.H. Incoherent Tensor Norms and Their Applications in Higher Order Tensor Completion. IEEE Trans. Inf. Theory 2017, 63, 6753–6766. [Google Scholar] [CrossRef]
- Tomioka, R.; Suzuki, T. Convex tensor decomposition via structured schatten norm regularization. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1331–1339. [Google Scholar]
- Semerci, O.; Hao, N.; Kilmer, M.E.; Miller, E.L. Tensor-Based Formulation and Nuclear Norm Regularization for Multienergy Computed Tomography. IEEE Trans. Image Process. 2014, 23, 1678–1693. [Google Scholar] [CrossRef]
- Mu, C.; Huang, B.; Wright, J.; Goldfarb, D. Square Deal: Lower Bounds and Improved Relaxations for Tensor Recovery. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 73–81. [Google Scholar]
- Zhao, Q.; Meng, D.; Kong, X.; Xie, Q.; Cao, W.; Wang, Y.; Xu, Z. A Novel Sparsity Measure for Tensor Recovery. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 271–279. [Google Scholar]
- Wei, D.; Wang, A.; Wang, B.; Feng, X. Tensor Completion Using Spectral (k, p) -Support Norm. IEEE Access 2018, 6, 11559–11572. [Google Scholar] [CrossRef]
- Tomioka, R.; Hayashi, K.; Kashima, H. Estimation of low-rank tensors via convex optimization. arXiv 2010, arXiv:1010.0789. [Google Scholar]
- Chretien, S.; Wei, T. Sensing tensors with Gaussian filters. IEEE Trans. Inf. Theory 2016, 63, 843–852. [Google Scholar] [CrossRef]
- Ghadermarzy, N.; Plan, Y.; Yılmaz, Ö. Near-optimal sample complexity for convex tensor completion. arXiv 2017, arXiv:1711.04965. [Google Scholar] [CrossRef]
- Ghadermarzy, N.; Plan, Y.; Yılmaz, Ö. Learning tensors from partial binary measurements. arXiv 2018, arXiv:1804.00108. [Google Scholar] [CrossRef]
- Liu, Y.; Shang, F.; Fan, W.; Cheng, J.; Cheng, H. Generalized Higher-Order Orthogonal Iteration for Tensor Decomposition and Completion. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1763–1771. [Google Scholar]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Lu, C.; Feng, J.; Lin, Z.; Yan, S. Exact Low Tubal Rank Tensor Recovery from Gaussian Measurements. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 1948–1954. [Google Scholar]
- Jiang, J.Q.; Ng, M.K. Exact Tensor Completion from Sparsely Corrupted Observations via Convex Optimization. arXiv 2017, arXiv:1708.00601. [Google Scholar]
- Xie, Y.; Tao, D.; Zhang, W.; Liu, Y.; Zhang, L.; Qu, Y. On Unifying Multi-view Self-Representations for Clustering by Tensor Multi-rank Minimization. Int. J. Comput. Vis. 2018, 126, 1157–1179. [Google Scholar] [CrossRef]
- Ely, G.T.; Aeron, S.; Hao, N.; Kilmer, M.E. 5D seismic data completion and denoising using a novel class of tensor decompositions. Geophysics 2015, 80, V83–V95. [Google Scholar] [CrossRef]
- Liu, X.; Aeron, S.; Aggarwal, V.; Wang, X.; Wu, M. Adaptive Sampling of RF Fingerprints for Fine-grained Indoor Localization. IEEE Trans. Mob. Comput. 2016, 15, 2411–2423. [Google Scholar] [CrossRef]
- Wang, A.; Lai, Z.; Jin, Z. Noisy low-tubal-rank tensor completion. Neurocomputing 2019, 330, 267–279. [Google Scholar] [CrossRef]
- Sun, W.; Chen, Y.; Huang, L.; So, H.C. Tensor Completion via Generalized Tensor Tubal Rank Minimization using General Unfolding. IEEE Signal Process. Lett. 2018, 25, 868–872. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Liu, X.Y.; Aeron, S.; Aggarwal, V.; Wang, X. Low-tubal-rank tensor completion using alternating minimization. arXiv 2016, arXiv:1610.01690. [Google Scholar]
- Liu, X.Y.; Wang, X. Fourth-order tensors with multidimensional discrete transforms. arXiv 2017, arXiv:1705.01576. [Google Scholar]
- Gu, Q.; Gui, H.; Han, J. Robust tensor decomposition with gross corruption. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1422–1430. [Google Scholar]
- Wang, A.; Jin, Z.; Tang, G. Robust tensor decomposition via t-SVD: Near-optimal statistical guarantee and scalable algorithms. Signal Process. 2020, 167, 107319. [Google Scholar] [CrossRef]
- Zhang, Z.; Aeron, S. Exact Tensor Completion Using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
- Goldfarb, D.; Qin, Z. Robust low-rank tensor recovery: Models and algorithms. SIAM J. Matrix Anal. Appl. 2014, 35, 225–253. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Cheng, L.; Wu, Y.C.; Zhang, J.; Liu, L. Subspace identification for DOA estimation in massive/full-dimension MIMO systems: Bad data mitigation and automatic source enumeration. IEEE Trans. Signal Process. 2015, 63, 5897–5909. [Google Scholar] [CrossRef]
- Cheng, L.; Xing, C.; Wu, Y.C. Irregular Array Manifold Aided Channel Estimation in Massive MIMO Communications. IEEE J. Sel. Top. Signal Process. 2019, 13, 974–988. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhou, G.; Zhang, L.; Cichocki, A.; Amari, S.I. Bayesian robust tensor factorization for incomplete multiway data. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 736–748. [Google Scholar] [CrossRef]
- Zhou, Y.; Cheung, Y. Bayesian Low-Tubal-Rank Robust Tensor Factorization with Multi-Rank Determination. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, X.; Wright, J.; Candes, E.; Ma, Y. Stable principal component pursuit. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 12–18 June 2010; pp. 1518–1522. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Tensors via Convex Optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Peng, Y.; Lu, B.L. Robust structured sparse representation via half-quadratic optimization for face recognition. Multimed. Tools Appl. 2017, 76, 8859–8880. [Google Scholar] [CrossRef]
- Liu, G.; Yan, S. Active subspace: Toward scalable low-rank learning. Neural Comput. 2012, 24, 3371–3394. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Jin, Z.; Yang, J. A Factorization Strategy for Tensor Robust PCA; ResearchGate: Berlin, Germany, 2019. [Google Scholar]
- Jiang, Q.; Ng, M. Robust Low-Tubal-Rank Tensor Completion via Convex Optimization. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 2649–2655. [Google Scholar]
- Kernfeld, E.; Kilmer, M.; Aeron, S. Tensor–tensor products with invertible linear transforms. Linear Algebra Its Appl. 2015, 485, 545–570. [Google Scholar] [CrossRef]
- Lu, C.; Peng, X.; Wei, Y. Low-Rank Tensor Completion With a New Tensor Nuclear Norm Induced by Invertible Linear Transforms. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5996–6004. [Google Scholar]
- Liu, X.Y.; Aeron, S.; Aggarwal, V.; Wang, X. Low-tubal-rank tensor completion using alternating minimization. In Proceedings of the SPIE Defense+ Security, Baltimore, MD, USA, 17–21 April 2016; International Society for Optics and Photonics: Bellingham, DC, USA, 2016; p. 984809. [Google Scholar]
- Zhou, P.; Lu, C.; Lin, Z.; Zhang, C. Tensor Factorization for Low-Rank Tensor Completion. IEEE Trans. Image Process. 2018, 27, 1152–1163. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.D.; Shafer, R.; Larue, B. An Order-p Tensor Factorization with Applications in Imaging. SIAM J. Sci. Comput. 2013, 35, A474–A490. [Google Scholar] [CrossRef]
- Wang, A.; Jin, Z. Orientation Invariant Tubal Nuclear Norms Applied to Robust Tensor Decomposition. Available online: https://www.researchgate.net/publication/329116872_Orientation_Invariant_Tubal_Nuclear_Norms_Applied_to_Robust_Tensor_Decomposition (accessed on 3 December 2019).

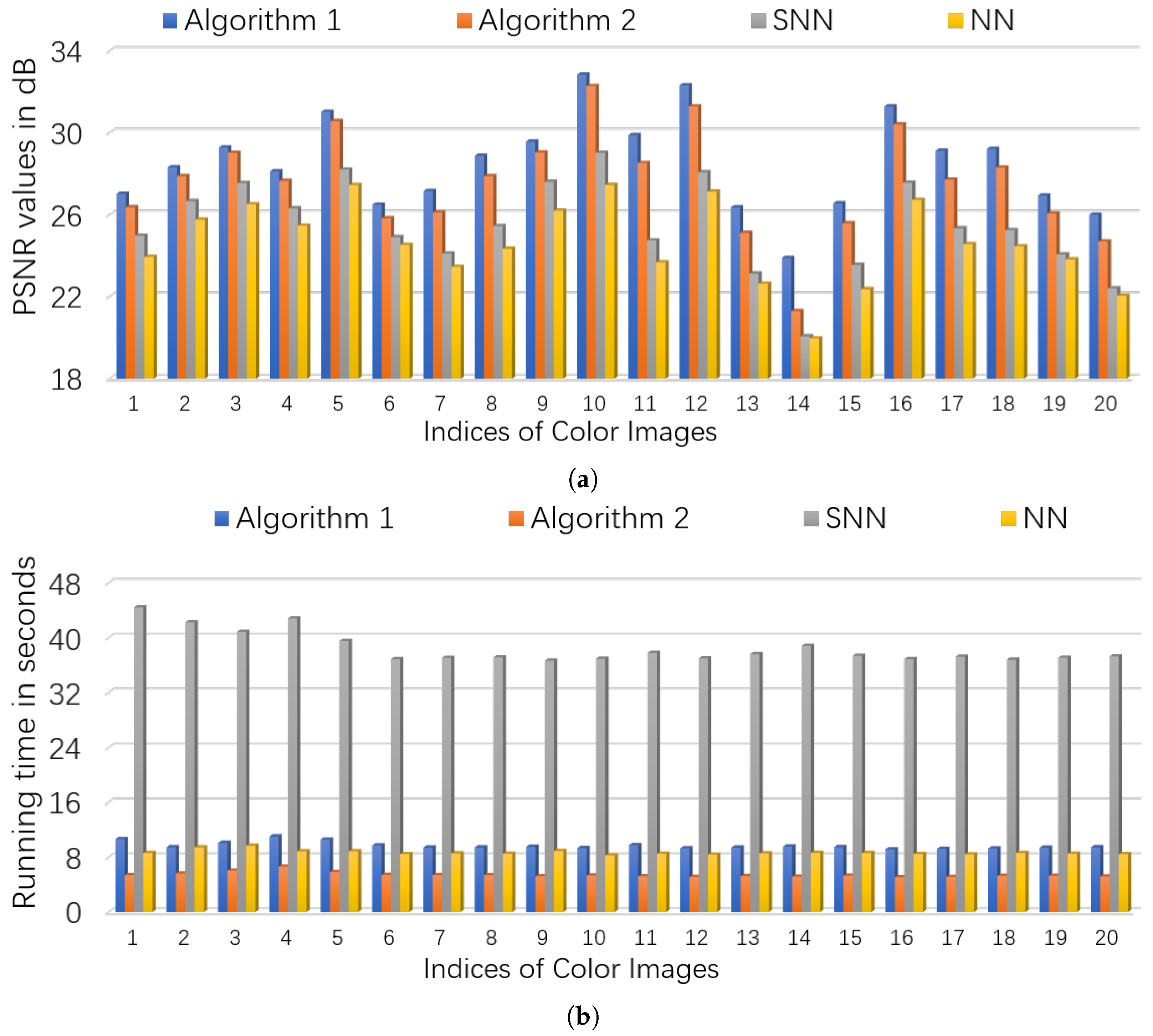
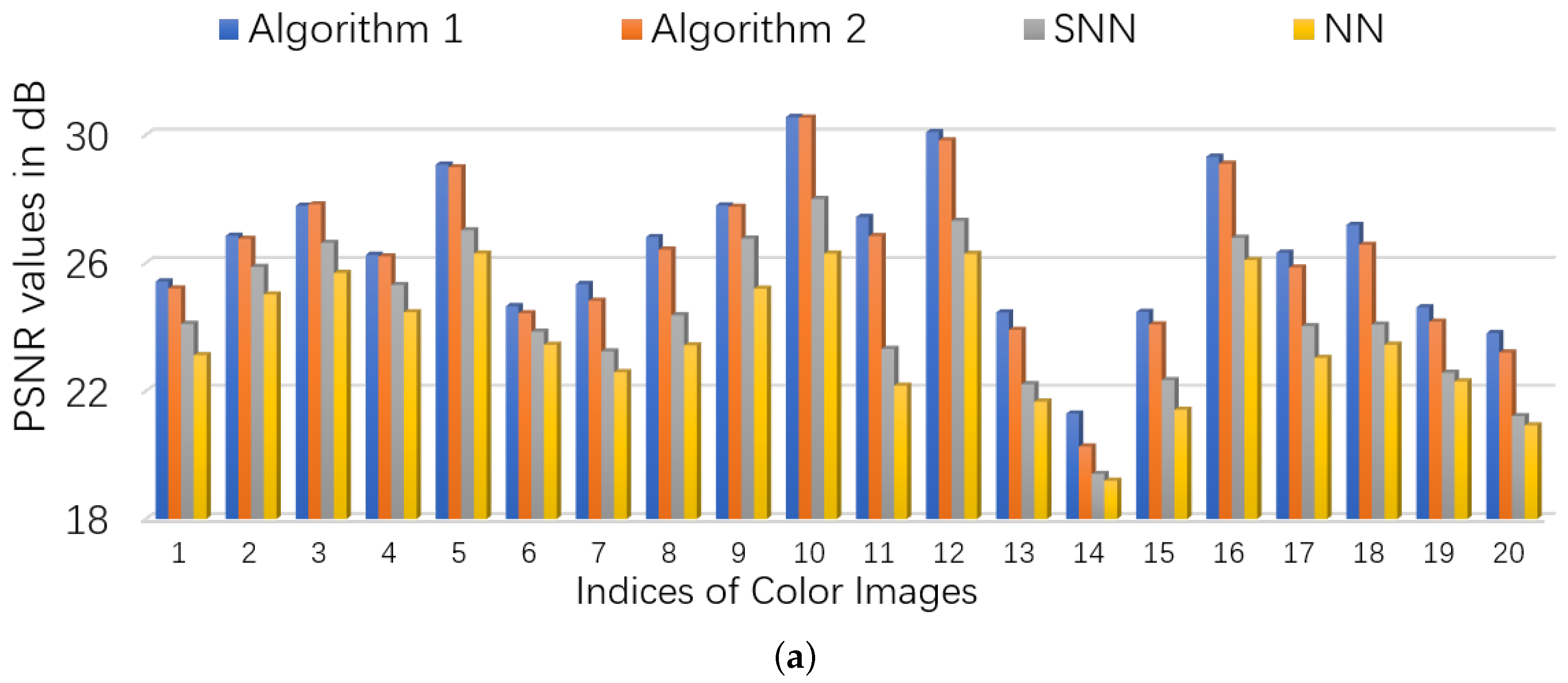
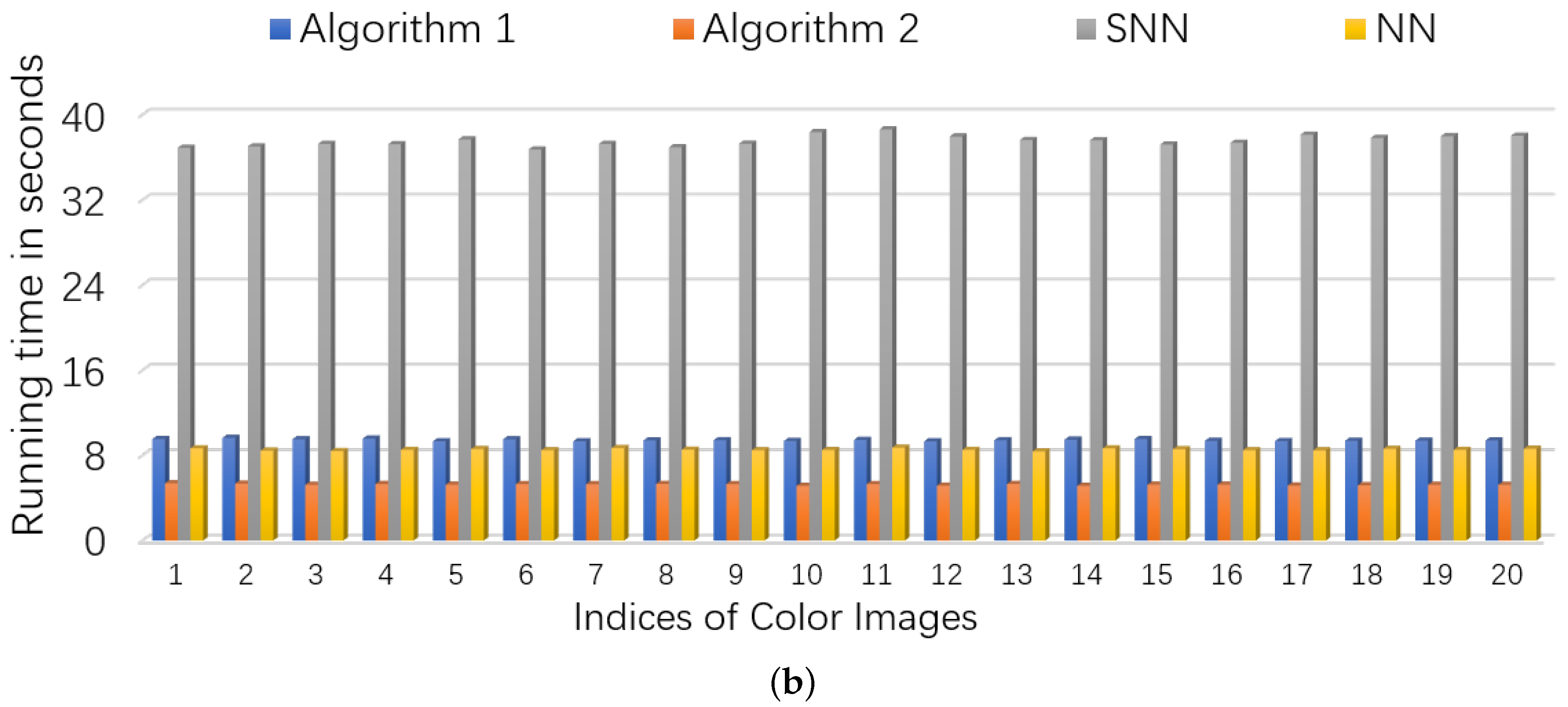

| n | Method | time/s | |||||
|---|---|---|---|---|---|---|---|
| 100 | 5 | Algorithm 1 | 5 | 3.63 | |||
| Algorithm 2 | 5 | 1.76 | |||||
| 160 | 8 | Algorithm 1 | 8 | 9.52 | |||
| Algorithm 2 | 8 | 4.42 | |||||
| 200 | 10 | Algorithm 1 | 10 | 14.16 | |||
| Algorithm 2 | 10 | 7.44 |
| n | Method | time/s | |||||
|---|---|---|---|---|---|---|---|
| 100 | 5 | Algorithm 1 | 5 | 4.43 | |||
| Algorithm 2 | 5 | 1.82 | |||||
| 160 | 8 | Algorithm 1 | 8 | 10.45 | |||
| Algorithm 2 | 8 | 5.15 | |||||
| 200 | 10 | Algorithm 1 | 10 | 18.97 | |||
| Algorithm 2 | 10 | 8.04 |
| n | Method | time/s | |||||
|---|---|---|---|---|---|---|---|
| 100 | 5 | Algorithm 1 | 5 | 3.87 | |||
| Algorithm 2 | 5 | 1.69 | |||||
| 160 | 8 | Algorithm 1 | 8 | 9.64 | |||
| Algorithm 2 | 8 | 4.46 | |||||
| 200 | 10 | Algorithm 1 | 10 | 14.78 | |||
| Algorithm 2 | 10 | 7.77 |
| Data Set | Index | NN, Model (54) | SNN, Model (55) | Algorithm 1 | Algorithm 2 | |
|---|---|---|---|---|---|---|
| Akiyo | (0.9,0.1) | PSNR | 31.74 | 32.09 | 33.94 | 33.36 |
| time/s | 29.48 | 51.13 | 20.10 | 12.39 | ||
| (0.8,0.2) | PSNR | 30.59 | 30.70 | 32.44 | 32.07 | |
| time/s | 30.65 | 51.17 | 19.53 | 14.92 | ||
| Silent | (0.9,0.1) | PSNR | 28.26 | 30.39 | 31.74 | 31.23 |
| time/s | 28.91 | 49.79 | 21.21 | 14.76 | ||
| (0.8,0.2) | PSNR | 26.95 | 27.60 | 30.42 | 30.07 | |
| time/s | 36.51 | 60.81 | 22.43 | 15.62 | ||
| Carphone | (0.9,0.1) | PSNR | 26.87 | 28.79 | 29.15 | 28.94 |
| time/s | 28.55 | 47.17 | 22.12 | 14.41 | ||
| (0.8,0.2)) | PSNR | 26.12 | 26.43 | 28.17 | 27.99 | |
| time/s | 26.72 | 49.21 | 20.55 | 14.74 | ||
| Claire | (0.9,0.1) | PSNR | 30.56 | 32.20 | 34.27 | 34.02 |
| time/s | 29.75 | 47.32 | 21.43 | 13.52 | ||
| (0.8,0.2) | PSNR | 29.94 | 30.43 | 32.96 | 32.78 | |
| time/s | 29.43 | 50.46 | 19.47 | 13.04 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, W.; Wei, D.; Zhang, R. Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms. Sensors 2019, 19, 5335. https://doi.org/10.3390/s19235335
Fang W, Wei D, Zhang R. Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms. Sensors. 2019; 19(23):5335. https://doi.org/10.3390/s19235335
Chicago/Turabian StyleFang, Wei, Dongxu Wei, and Ran Zhang. 2019. "Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms" Sensors 19, no. 23: 5335. https://doi.org/10.3390/s19235335
APA StyleFang, W., Wei, D., & Zhang, R. (2019). Stable Tensor Principal Component Pursuit: Error Bounds and Efficient Algorithms. Sensors, 19(23), 5335. https://doi.org/10.3390/s19235335




