A Comparison of the Influence of Vegetation Cover on the Precision of an UAV 3D Model and Ground Measurement Data for Archaeological Investigations: A Case Study of the Lepelionys Mound, Middle Lithuania
Abstract
1. Introduction
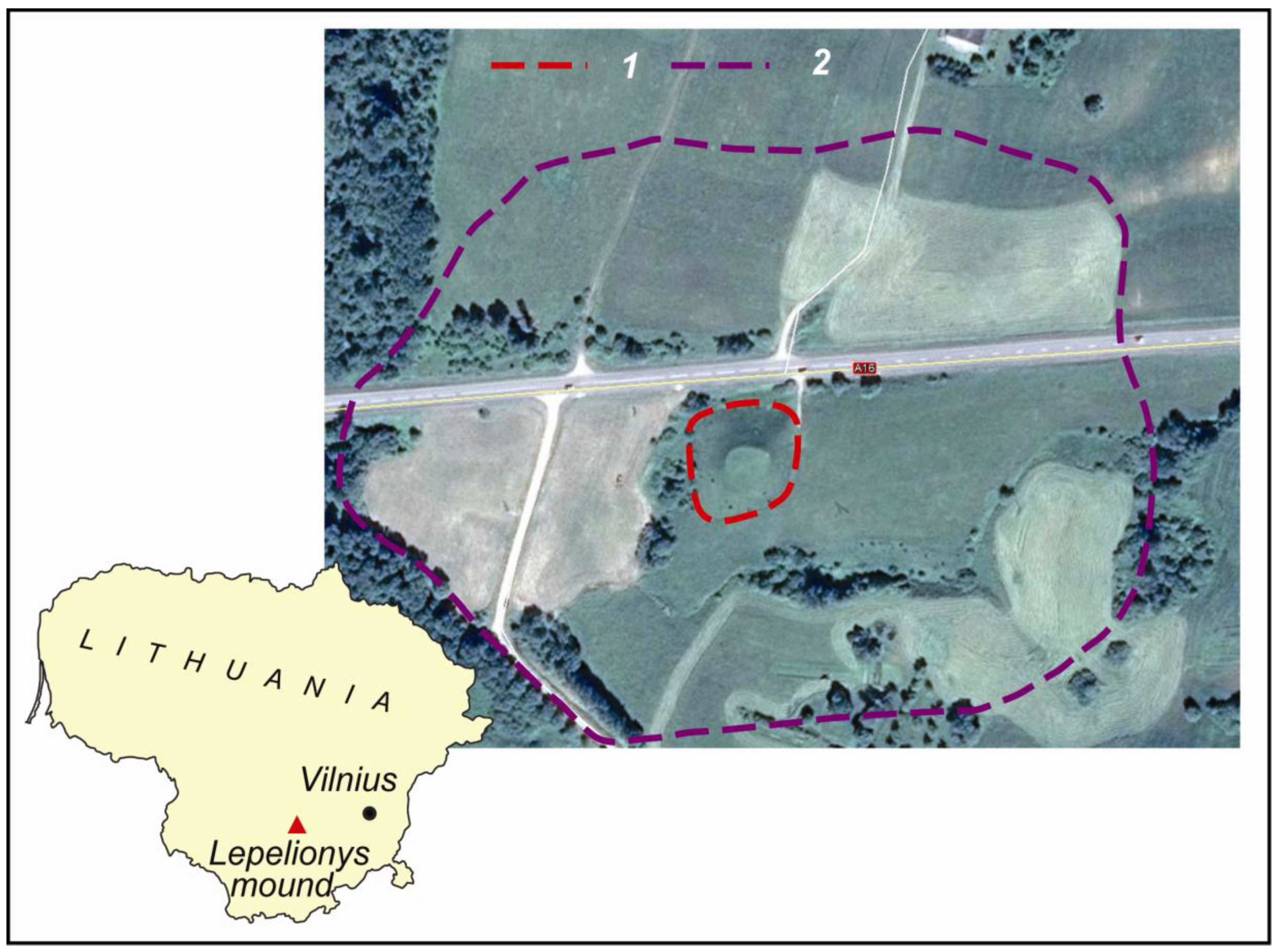
2. Research Object, Materials, and Methods
- (i)
- Organic waste was thrown at the foot of the mound;
- (ii)
- In the territory of the ancient settlement the ground was excavated for substructures of buildings and the soil (sediment) was poured beside the walls of the building;
- (iii)
- The ancient settlement was surrounded by palisades, the stakes of which were driven into the ground and the excavated soil fortified the foundation of the fence;
- (iv)
- Organic and mineral waste (ceramic fragments, bones of the animals used for food, worn out shoes, and clothes) was thrown over the palisade of the settlement.
3. Results
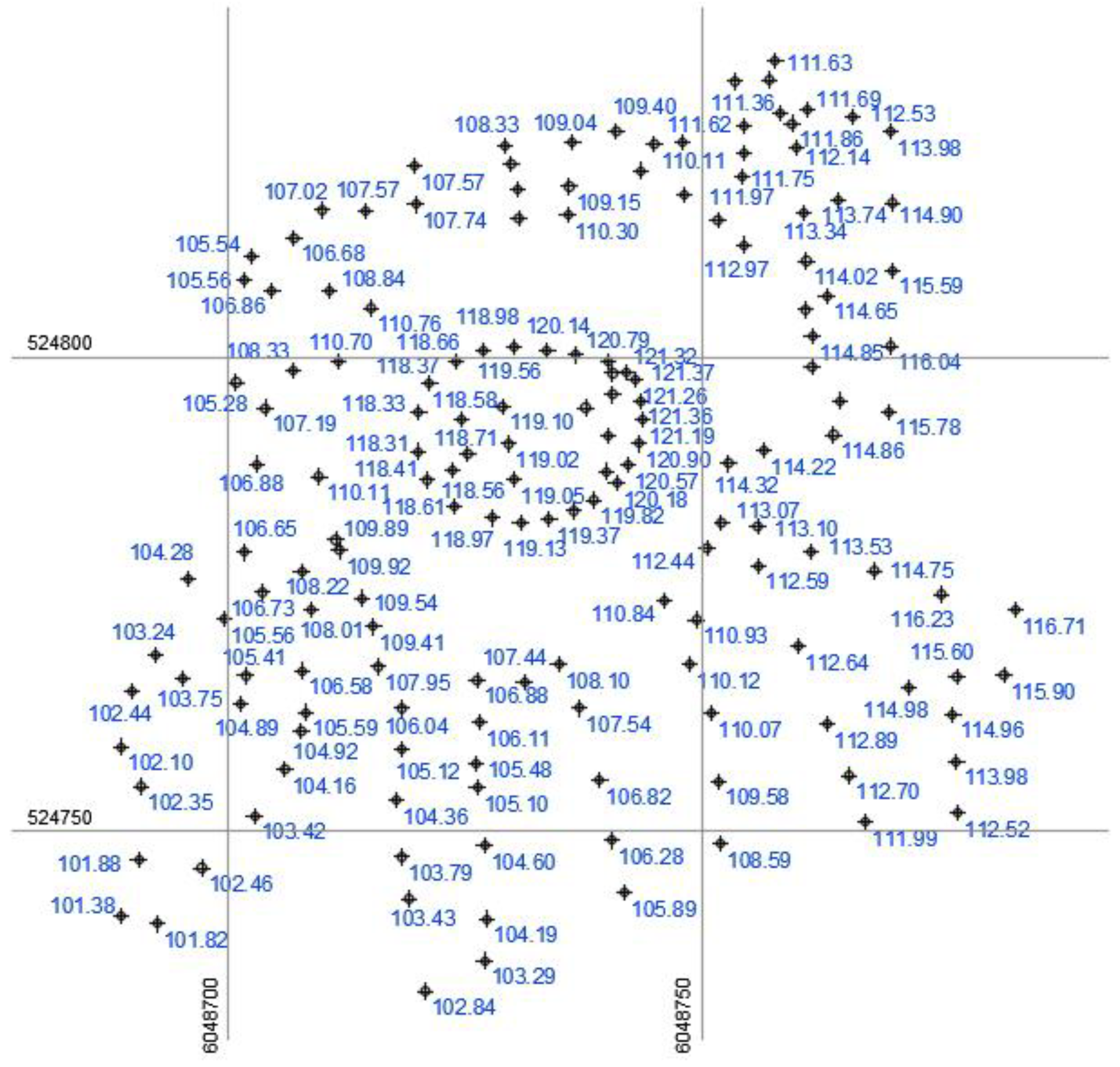
3.1. Creating a Two-Dimensional (2D) Relief Model
3.2. Drawing of a Topographic Plan
4. Discussion
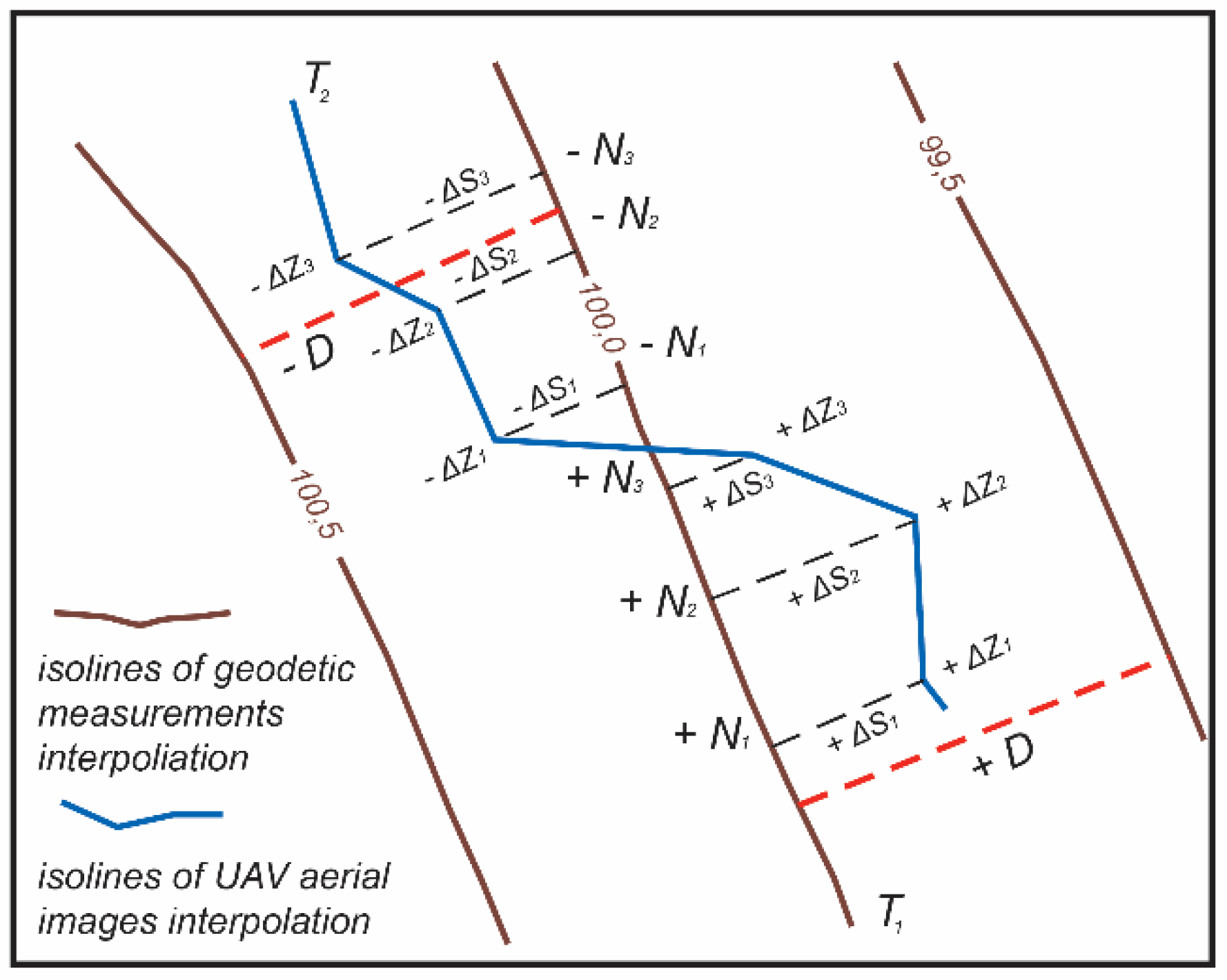
4.1. Evaluation of the Precision of theAaerial Images
4.2. Evaluation of the Influence of Vegetation Covers
5. Conclusions
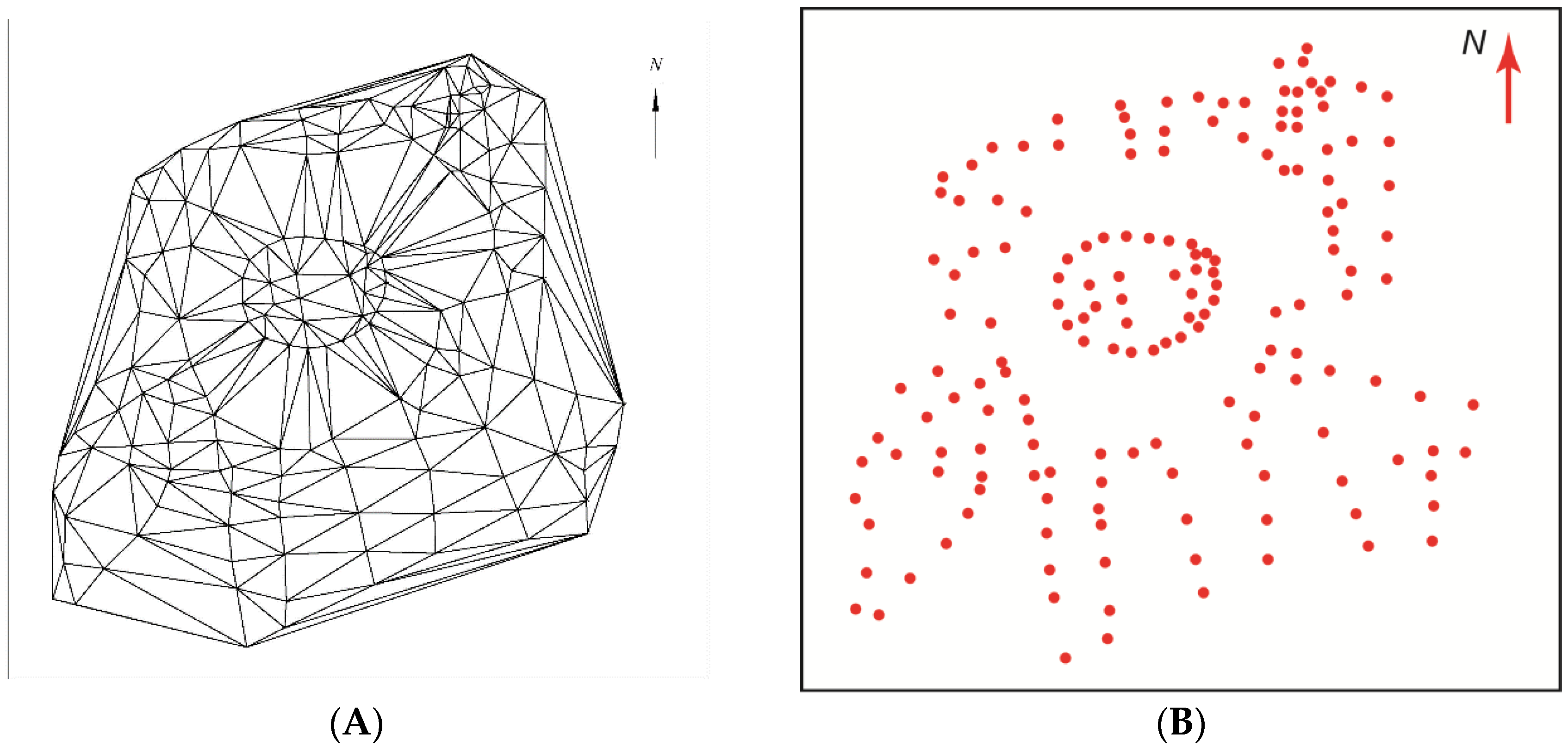
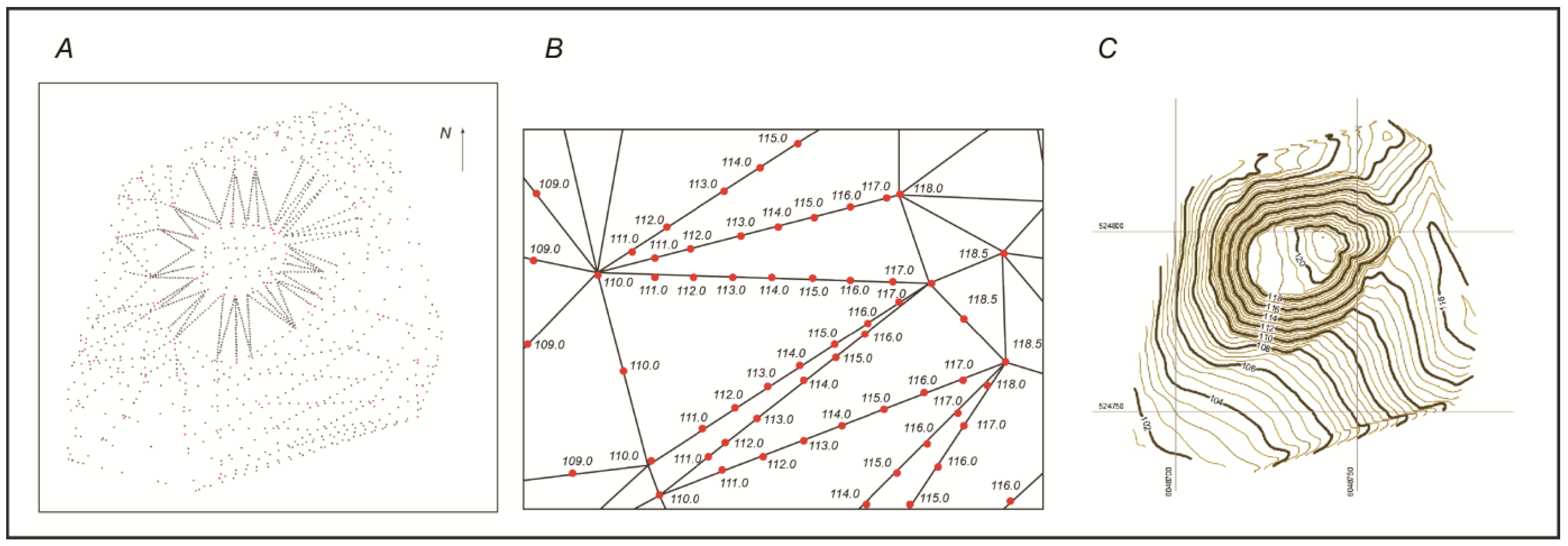
- The “Circle_3p” computer program designed by Artūras Bautrėnas, an associate professor of the Department of Cartography and Geoinformatics, employs the classical method of Delaunay and ensures a consistent systemic selection of points.
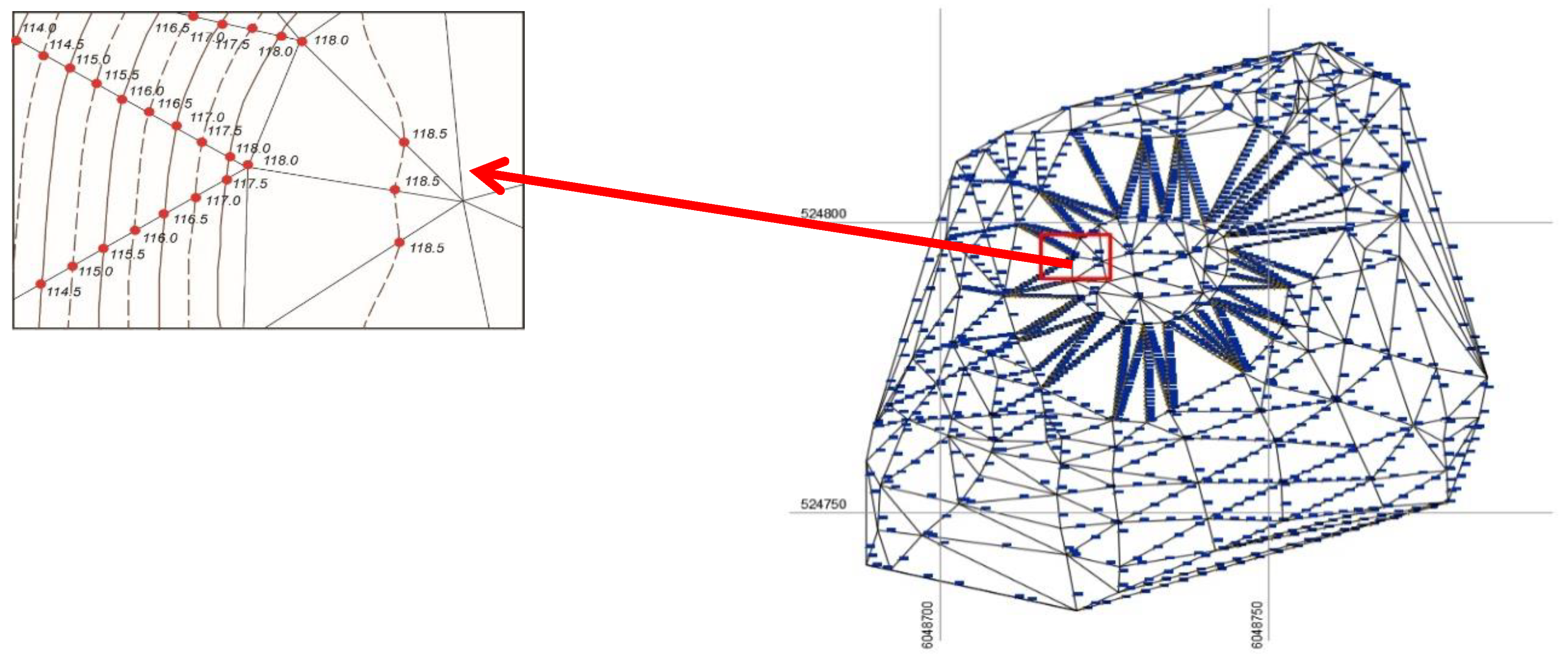
- The use of “Circle 3p” for the analysis of aerial photographs of the Lepelionys Mound has shown that the program needs to be improved by adding elements for the correction of the isolines.
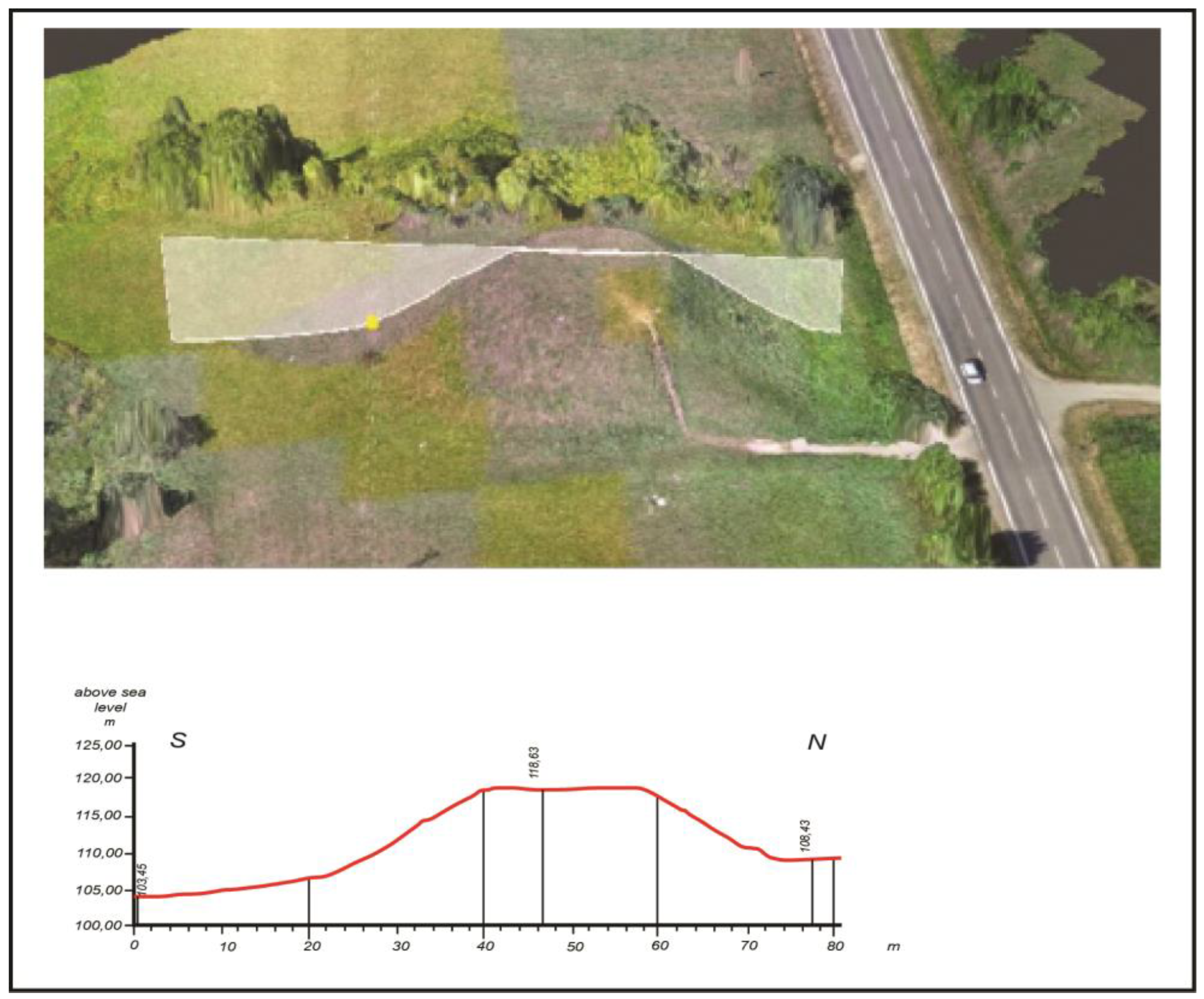
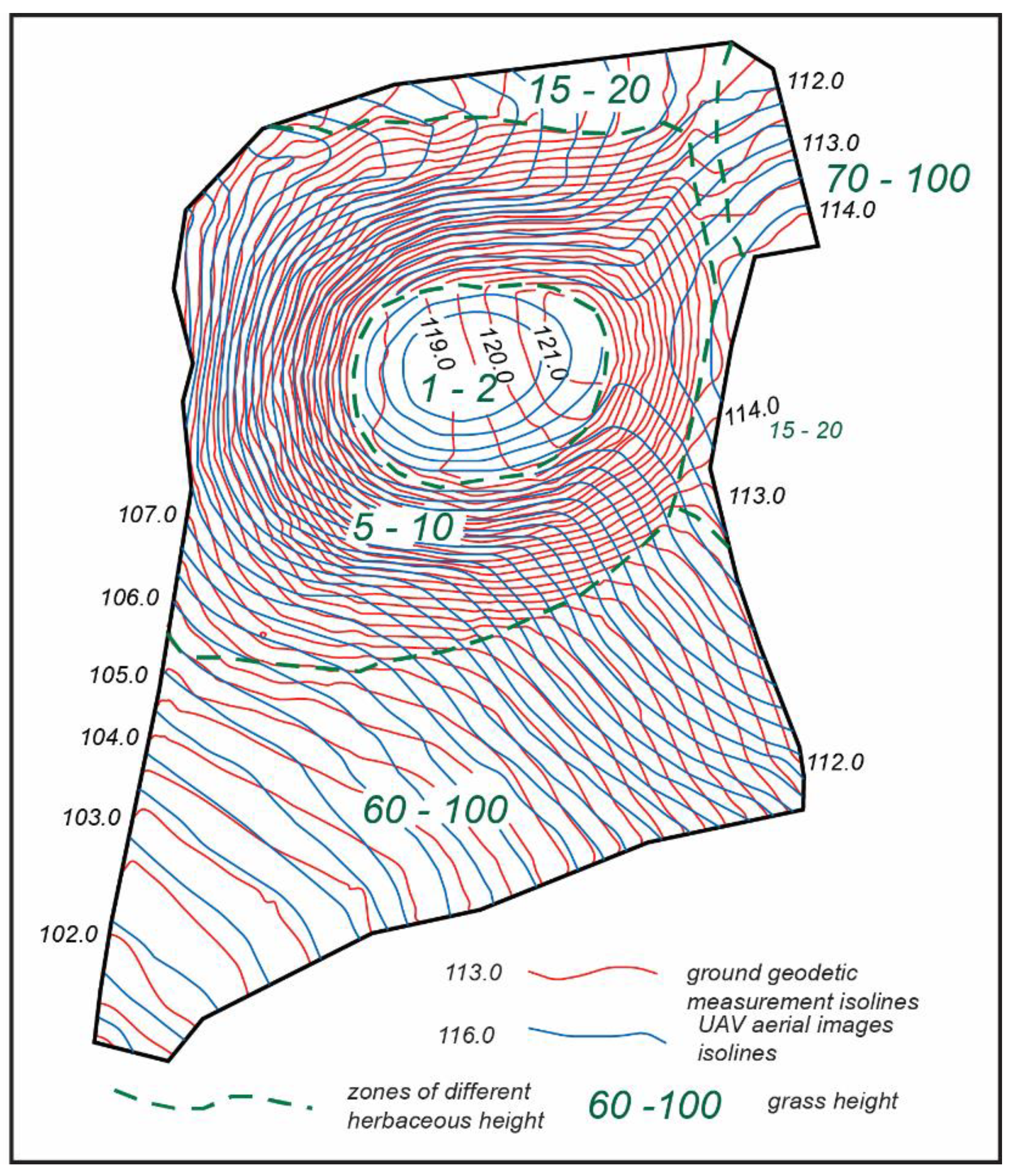
- A comparison of the results of the geodetic measurements and the UAV images, showed that the best overlaps of surface microform isolines are on steep slopes. On the flat top of the mound surface, microform variance makes up 0.7 to 1.0 m. This is due to the rare density of the interpolation points calculated by the program “Circle_3p”. The variance of the isolines at the foot of the mound reaches 0.45 to 0.7 m (medium-height grass) and 0.95 to 1.35 m (high grass). The study has shown that external factors have a significant influence on the identification of the mound relief microforms.
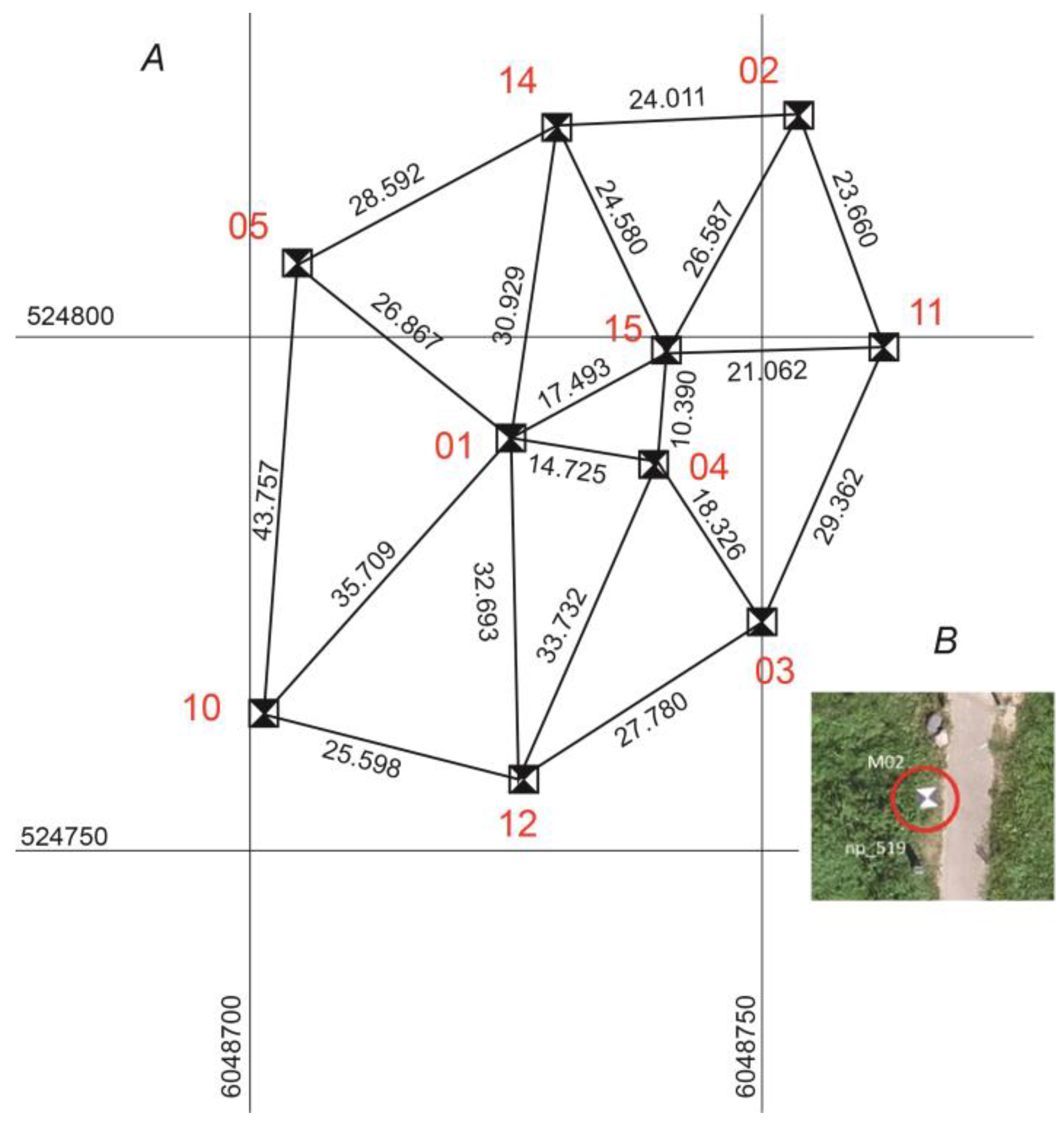
- The research related to the GCPs position and shows that five GCPs arranged at the edges and the center of the object give the best accuracy as compared with other variations (three on the top, four on the edge, and ten GCPs).
- The unnatural curvature of isolines in the UAV 3D model, resulting in the abundance of unnatural surface microforms, is due to the interpolation techniques used to determine the isoline position, specifically the calculation of the interfaces between numerous point pairs.
Author Contributions
Funding
Conflicts of Interest
References
- Jones, R.J.A.; Evans, R. Soil and crop marks in the recognition of archaeological sites by air photography. In Aerial Reconnaissance for Archaeology; Wilson, D.R., Ed.; The Council for British Archaeology: London, UK, 1975; pp. 1–11. [Google Scholar]
- Remondino, F.; El-Hakim, S. Image-based 3D modelling, a review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Parcaks, S.H. Satellite Remote Sensing for Archaeology; Routledge: London, UK; New York, NY, USA, 2009; p. 312. [Google Scholar]
- Bäumker, M.; Przybilla, H.-J. Investigations on the accuracy of the navigation data of unmanned aerial vehicles using the example of the system microcopter. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 113–118. [Google Scholar]
- Deseilligny, M.; De Luca, L.; Remondino, F. Automated image-based procedures for accurate artifacts 3D modeling and orthoimages. In Proceedings of the XXIIIth International CIPA Simposium, Prague, Czech Republic, 12–16 September 2011; pp. 291–299. [Google Scholar]
- Chiabrando, F.; Nex, F.; Piatti, D.; Rinaudo, F. UAV and RPV systems for photogrammetric surveys in archaeological areas, two tests in the Piedmont Region (Italy). J. Archaeol. Sci. 2011, 38, 697–710. [Google Scholar] [CrossRef]
- Lasaponara, R.; Masini, N. Satellite remote sensing in archaeology, past, present and future perspectives. J. Archaeol Sci. 2011, 38, 1995–2002. [Google Scholar] [CrossRef]
- Lasaponara, R.; Masini, N. (Eds.) Satellite Remote Sensing: A New Tool for Archaeology; Springer: Heidelberg, Germany, 2012; p. 364. [Google Scholar]
- Lasaponara, R.; Masini, N. Satellite synthetic aperture radar in archaeology and cultural landscape: An overview. Archaeol. Prospect. 2013, 20, 71–78. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications, a review. Appl. Geomat. 2013, 6, 1–15. [Google Scholar] [CrossRef]
- Hugenholtz, C.H.; Whitehead, K.; Brown, O.W.; Barchyn, T.E.; Moorman, B.J.; LeClair, A.J.; Riddell, K.; Hamilton, T. Geomorphological mapping with a small unmanned aircraft system (SUAS), feature detection and accuracy assessment of a photogrammetrically-derived digital terrain model. Geomorphology 2013, 194, 16–24. [Google Scholar] [CrossRef]
- Whitehead, K.; Hugenholtz, C.H. Remote sensing of the environment with small unmanned aircraft systems (UAS): A review of progress and challenges. J. Unmanned Veh. Syst. 2014, 2, 69–85. [Google Scholar] [CrossRef]
- Whitehead, K.; Hugenholtz, C.H.; Myshak, S.; Brown, O.W.; LeClair, A.J.; Tamminga, A.; Barchyn, T.E.; Moorman, B.J.; Eaton, B. Remote sensing of the environment with small unmanned aircraft systems (UAS): Scientific and commercial applications. J. Unmanned Veh. Syst. 2014, 2, 86–102. [Google Scholar] [CrossRef]
- Themistocleous, K.; Agapiou, A.; Cuca, B.; Hadjimitsis, D.G. Unmanned aerial systems and spectroscopy for remote sensing applications in archaeology. Int. Arch. Photogramm. Remote Sens. Spati. Inf. Sci. 2015, XL-7/W3, 1419–1423. [Google Scholar] [CrossRef]
- Hadjimitsis, D.G.; Themistocleous, K.; Agapiou, A. Monitoring Archaeological Site Landscapes in Cyprus using multi-temporal atmospheric corrected image data. Int. J. Archit. Comput. 2009, 7, 121–138. [Google Scholar] [CrossRef]
- Agapiou, A.; Hadjimitsis, D.G.; Themistocleous, K.; Papadavid, G.; Toulios, L. Detection of archaeological crop marks in Cyprus using vegetation indices from Landsat TM/ETM+ satellite images and field spectroscopy measurements. Proc. SPIE 2010, 7831, 78310V. [Google Scholar]
- Ruzgienė, B.; Berteška, T.; Gečytė, S.; Jakubauskienė, E.; Aksamitauskas, V.Č. The surface modelling based on UAV photogrammetry and qualitative estimation. Measurement 2015, 73, 619–627. [Google Scholar] [CrossRef]
- Sužiedelytė-Visockienė, J.; Bručas, D.; Bagdžiūnaitė, R.; Puzienė, R.; Stanionis, A.; Ragauskas, U. Remotely-piloted aerial system for photogrammetry: Orthoimage generation for mapping applications. Geografie 2016, 121, 349–367. [Google Scholar]
- Campana, S. Drones in archaeology. State-of-the-art and future perspectives. Archaeol. Prospect. 2017, 24, 275–296. [Google Scholar] [CrossRef]
- Traviglia, A.; Torsello, A. Landscape pattern detection in archaeological remote sensing. Geosciences 2017, 7, 128. [Google Scholar] [CrossRef]
- Masini, N.; Marzo, C.; Manzari, P.; Belmonte, A.; Sabia, C.; Lasaponara, R. On the characterization of temporal and spatial patterns of archaeological crop-marks. J. Cult. Herit. 2018, 32, 124–132. [Google Scholar] [CrossRef]
- Cowley, D.C.; Moriarty, C.H.; Geddes, G.; Brown, G.L.; Wade, T.; Nichol, C.J. UAVs in context: Archaeological airborne recording in a national body of survey and record. Drones 2018, 56, 2. [Google Scholar] [CrossRef]
- Tapete, D. Remote sensing and geosciences for archaeology. Geosciences 2018, 7, 41. [Google Scholar] [CrossRef]
- Konstantinos, K.G.; Soura, K.; Koukouvelas, I.K.; Argyropoulos, N.G. UAV vs classical aerial photogrammetry for archaeological studies. J. Archaeol. Sci. Rep. 2017, 14, 758–773. [Google Scholar]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodríguez-Pérez, J.R.; Ordóñez, C. Accuracy of unmanned aerial vehicle (UAV) and SfM photogrammetry survey as a function of the number and location of ground control points used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef]
- Shahbazi, M.; Sohn, G.; Théau, J.; Menard, P. Development and evaluation of a UAV-photogrammetry system for precise 3D environmental modeling. Sensors 2015, 15, 27493–27524. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generating georectified mosaics from ultra-high resolution unmanned aerial vehicle (UAV) imagery, based on structure from motion (SFM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Shahbazi, M.; Sohn, G.; Théau, J.; Menard, P. Robust structure-from-motion computation: Application to open-pit mine surveying from unmanned aerial images. J. Unmanned Veh. Syst. 2017, 5, 126–145. [Google Scholar] [CrossRef]
- Mian, O.; Lutes, J.; Lipa, G.; Hutton, J.J.; Gavelle, E.; Borghini, S. Accuracy assessment of direct georeferencing for photogrammetric applications on small unmanned aerial platforms. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 40, 77–83. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial accuracy of UAV-derived orthoimagery and topography: Comparing photogrammetric models processed with direct geo-referencing and ground control points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Cella, U.M.; Roncella, R.; Santise, M. Testing the accuracy and repeatability of UAV blocks oriented with GNSS-supported aerial triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; Cella, U.M.; di Roncella, R.; Santise, M. Quality assessment of DSMs produced from UAV flights georeferenced with on-board RTK positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]
- Buivydas, U. The Settlement at the foot of Lepelionys Hill Fort. In Archaeological Research in Lithuania; Lithuanian Archaeological Society: Vilnius, Lithuania, 2006; pp. 65–66. [Google Scholar]
- Banytė-Rowell, R.; Baronas, D.; Kazakevičius, V.; Vaškevičiūtė, I.; Zabiela, G. History of Lithuania; Zabiela, G., Ed.; The Lithuanian Institute of History: Vilnius, Lithuania, 2007; Volume 2, p. 518. [Google Scholar]
- Jovaiša, E. The Aestii: Genesis; Lithuanian University of Educational Sciences: Vilnius, Lithuania, 2013; Volume 1, p. 379. [Google Scholar]
- Jovaiša, E. The Aestii: Evolution; Lithuanian University of Educational Sciences: Vilnius, Lithuania, 2014; Volume 2, p. 351. [Google Scholar]
- Viršilienė, J.; Zabiela, G. Revived Mounds; The Lithuanian Institute of History: Vilnius, Lithuania, 2018; p. 219. [Google Scholar]
- Berni, J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Baluja, J.; Diago, M.P.; Balda, P.; Zorer, R.; Meggio, F.; Morales, F.; Tardaguila, J. Assessment of vineyard water status variability by thermal and multispectral imagery using an unmanned aerial vehicle (UAV). Irrig. Sci. 2012, 30, 511–522. [Google Scholar] [CrossRef]
- Bellvert, J.; Zarco-Tejada, P.J.; Girona, J.; Fereres, E. Mapping crop water stress index in a Pinot-Noir vineyard: Comparing ground measurements with thermal remote sensing imagery from an unmanned aerial vehicle. Precis. Agric. 2013, 15, 361–376. [Google Scholar] [CrossRef]
- Chisholm, R.A.; Cui, J.; Lum, S.K.Y.; Chen, B.M. UAV LiDAR for below-canopy forest surveys. J. Unmanned Veh. Syst. 2013, 1, 61–68. [Google Scholar] [CrossRef]
- Huesca, M.; Merino-de-Miguel, S.; González-Alonso, F.; Martinez, S.; Miguel Cuevas, J.; Calle, A. Using AHS hyper-spectral images to study forest vegetation recovery after a fire. Int. J. Remote Sens. 2013, 34, 4025–4048. [Google Scholar] [CrossRef]
- Knoth, C.; Klein, B.; Prinz, T.; Kleinebecker, T. Unmanned aerial vehicles as innovative remote sensing platforms for high-resolution infrared imagery to support restoration monitoring in cut-over bogs. Appl. Veg. Sci. 2013, 16, 509–517. [Google Scholar] [CrossRef]
- Mozas-Calvache, A.T.; Pérez-García, J.L.; Cardernal-Escarcena, F.J.; Delgado, J.; Mata-de-Castro, E. Comparison of low altitude photogrammetric methods for obtaining DEMs and orthoimages of archaeological sites. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 577–581. [Google Scholar] [CrossRef]
- Erny, G.; Gutierrez, G.; Friedman, A.; Godsey, M.; Gradoz, M. Archaeological topography: Comparing digital photogrammetry taken with unmanned aerial vehicles (UAVs) versus standard surveys with total stations. In Proceedings of the 80th Annual Meeting of the Society for American Archaeology, San Francisco, CA, USA, 15–19 April 2015; p. 409. [Google Scholar]
- Mesas-Carracosa, F.-J.; Notario-Garcia, M.D.; Meroño de Larriva, J.E.; García-Ferre, A. An analysis of the influence of flight parameters in the generation of unmanned aerial vehicle (UAV) orthomosaics to survey archaeological areas. Sensors 2016, 16, 1838. [Google Scholar] [CrossRef]
- Mian, O.; Lutes, J.; Lipa, G.; Hutton, J.J.; Gavelle, E.; Borghini, S. Direct georeferencing on small unmanned aerial platforms for improved reliability and accuracy of mapping without the need for ground control points. In Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Toronto, ON, Canada, 30 August–2 September 2015; Volume XL-1/W4, pp. 397–402. [Google Scholar]
- Agüera–Vega, F.; Carvajal–Ramirez, F.; Martínez–Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Measurement 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Fryskowska, A.; Kedzierski, M.; Walczykowski, P.; Wierzbicki, D.; Delis, P.; Lada, A. Effective detection of sub-surface archaeological features from laser scanning point clouds and imagery data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 245–251. [Google Scholar] [CrossRef]
- Carvajal-Ramírez, F.; Navarro-Ortega, A.D.; Agüera-Vega, F.; Martínez-Carricondo, P.; Mancini, F. Virtual reconstruction of damaged archaeological sites based on unmanned aerial vehicle photogrammetry and 3D modelling: Study case of a southeastern Iberia production area in the Bronze Age. J. Int. Meas. Conf. 2019, 136, 225–236. [Google Scholar] [CrossRef]
- Juškaitis, V. Report of Archaeological Research in 2007 of the Ancient Settlement of the Lepelionys Mound (22593, Prienai District); Trakai Historical Museum: Trakai, Lithuania, 2009. [Google Scholar]
- Juškaitis, V. The settlement at the foot of the lepelionys hill fort site. In Archaeological Research in Lithuania; The Lithuanian Institute of History: Vilnius, Lithuania, 2007; pp. 73–74. [Google Scholar]
- Fang, T.; Piegl, L. Algorithm for Delaunay triangulation and convex hull computation using a sparse matrix. Comput. Aided Des. 1992, 24, 425–436. [Google Scholar] [CrossRef]
- Hacigüzeller, P. Collaborative mapping in the age of ubiquitous internet: An archaeological perspective. Digit. Class. Online 2017, 3, 5–16. [Google Scholar]
- Perkins, C. Community Mapping. Cartogr. J. 2007, 44, 127–137. [Google Scholar] [CrossRef]
- Lee, D. Map Orkney Month: Imagining Archaeological Mappings. Livingmaps Rev. 2016, 1, 1–25. [Google Scholar]




| Hovering Accuracy (GPS Mode) | Vertical: 0.5 m; Horizontal: 2.5 m |
|---|---|
| Max angular velocity | Pitch: 300°/s; Yaw: 150°/s |
| Max tilt angle | 35° |
| Max ascent and descent speed | 5 m/s; 4 m/s |
| Max speed | 22 m/s |
| Max wind speed resistance | 10 m/s |
| Max service ceiling above take-off point | 120 m |
| Type and model | X3; FC350 |
| Total and effective pixels | 12.76 M; 12.4 M |
| Max capacity | 64 GB |
| Maximal image size | 4000 × 3000 |
| ISO range | Photo- 100–1600; Video- 100–3200. |
| The electronic shutter speed | 8 s–1/8000 s |
| A field of view (FOV) | 94° |
| Supported file formats | Photo: JPEG, DNG; Video: MP4/MOV (MPEG-4 AVC/H.264) |
| Types of electronic media | Micro SD. Maximal capacity 64 GB. Class 10 or UHS-1 |
| Sensor width (mm) | 6.17 |
| Focal length (mm) | 4.55 |
| Altitude (m) | 50 |
| Image width | 4000 |
| Image height | 3000 |
| GSD (cm/pixel) | 1.695054945 |
| Width (m) | 67.8021978 |
| Height (m) | 50.85164835 |
| Line No. | Variance of Equal Height Isolines in Plane Position, m | Slope Inclination, Degree in Brackets (Mean Slope Inclination Values) | Remarks |
|---|---|---|---|
| 1 | 0.91 | 0 | The top of the mound, mown grass |
| 2 | 0.71 | 0 | The top of the mound, mown grass |
| 3 | 0.86 | 0 | The top of the mound, mown grass |
| 4 | 0.94 | 0 | The top of the mound, mown grass |
| 5 | 0.89 | 0 | The top of the mound, mown grass |
| 6 | 0.60 | 30–40 | The slope of the mound, short grass (0.1 m) |
| 7 | 0.36 | 30–40 | The slope of the mound, short grass (0.1 m) |
| 8 | 0.54 | 30–40 | The slope of the mound, short grass (0.1 m) |
| 9 | 0.36 | 30–40 | The slope of the mound, short grass (0.1 m) |
| 10 | 0.34 | 30–40 | The slope of the mound, short grass (0.1 m) |
| 11 | 0.36 | 30–40 | The slope of the mound, short grass (0.1 m) |
| 12 | 0.96 | 21–26 | The foot of the mound, high grass (0.5 m) |
| 13 | 1.26 | 21–26 | The foot of the mound, high grass (0.5 m) |
| 14 | 1.09 | 21–26 | The foot of the mound, high grass (0.5 m) |
| 15 | 1.32 | 21–26 | The foot of the mound, high grass (0.5 m) |
| 16 | 0.91 | 21–26 | The foot of the mound, high grass (0.5 m) |
| 17 | 0.45 | 14–19 | The foot of the mound, medium-high grass (0.2 m) |
| 18 | 0.67 | 14–19 | The foot of the mound, medium-high grass (0.2 m) |
| 19 | 0.71 | 14–19 | The foot of the mound, medium-high grass (0.2 m) |
| 20 | 0.54 | 14–19 | The foot of the mound, medium-high grass (0.2 m) |
| 21 | 0.63 | 14–19 | The foot of the mound, medium-high grass (0.2 m) |
| No. | GPS | DEM | Error Size (m) | Absolute Error Size (mm) |
|---|---|---|---|---|
| np-507 | ||||
| X | 6048772.162 | 6048772.216 | −0.054 | 54 |
| Y | 524809.995 | 524810.072 | −0.077 | 77 |
| Z | 112.138 | 112.212 | −0.074 | 74 |
| np-508 | ||||
| X | 6048771.963 | 6048771.971 | −0.008 | 8 |
| Y | 524810.078 | 524810.066 | 0.012 | 12 |
| Z | 112.757 | 112.785 | −0.028 | 28 |
| np-515 | ||||
| X | 6048774.378 | 6048774.393 | −0.015 | 15 |
| Y | 524804.426 | 524804.440 | −0.014 | 14 |
| Z | 111.620 | 111.644 | −0.024 | 24 |
| np-522 | ||||
| X | 6048769.132 | 6048769.230 | −0.098 | 98 |
| Y | 524803.655 | 524803.700 | −0.045 | 45 |
| Z | 111.896 | 111.940 | −0.044 | 44 |
| np-530 | ||||
| X | 6048769.708 | 6048769.740 | −0.032 | 32 |
| Y | 524793.519 | 524793.562 | −0.043 | 43 |
| Z | 110.071 | 110.140 | −0.069 | 69 |
| np-560 | ||||
| X | 6048716.410 | 6048716.452 | −0.042 | 42 |
| Y | 524751.812 | 524751.892 | −0.080 | 80 |
| Z | 105.409 | 105.368 | 0.041 | 41 |
| np-582 | ||||
| X | 6048712.964 | 6048712.978 | −0.014 | 14 |
| Y | 524768.387 | 524768.400 | −0.013 | 13 |
| Z | 106.038 | 106.006 | 0.032 | 32 |
| np-586 | ||||
| X | 6048692.869 | 6048692.835 | 0.034 | 34 |
| Y | 524769.123 | 524769.100 | 0.023 | 23 |
| Z | 103.427 | 103.394 | 0.033 | 33 |
| np-587 | ||||
| X | 6048692.729 | 6048692.734 | −0.005 | 5 |
| Y | 524769.143 | 524769.154 | −0.011 | 11 |
| Z | 104.131 | 104.107 | 0.024 | 24 |
| np-596 | ||||
| X | 6048715.725 | 6048715.685 | 0.040 | 40 |
| Y | 524781.260 | 524781.290 | −0.030 | 30 |
| Z | 107.443 | 107.399 | 0.044 | 44 |
| Absolute Error (mm) | |||
|---|---|---|---|
| Point No. | X | Y | Z |
| np-507 | 54 | 77 | 74 |
| np-508 | 8 | 12 | 28 |
| np-515 | 15 | 14 | 24 |
| np-522 | 98 | 45 | 44 |
| np-530 | 32 | 43 | 69 |
| np-560 | 42 | 80 | 41 |
| np-582 | 14 | 13 | 32 |
| np-586 | 34 | 23 | 33 |
| np-587 | 5 | 11 | 24 |
| np-596 | 40 | 30 | 44 |
| Point No. | 3 Marks | 4 Marks | 5 Marks | 7 Marks | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | x | y | z | x | y | z | |
| np-507 | 402 | 608 | 514 | 309 | 194 | 263 | 56 | 80 | 51 | 48 | 70 | 73 |
| np-508 | 86 | 105 | 56 | 36 | 42 | 42 | 11 | 12 | 26 | 10 | 9 | 19 |
| np-515 | 175 | 193 | 64 | 78 | 14 | 10 | 15 | 8 | 25 | 13 | 16 | 26 |
| np-522 | 95 | 145 | 574 | 48 | 33 | 254 | 95 | 56 | 57 | 88 | 39 | 49 |
| np-530 | 954 | 657 | 1419 | 692 | 170 | 164 | 48 | 46 | 52 | 37 | 38 | 55 |
| np-560 | 400 | 492 | 194 | 387 | 308 | 406 | 45 | 84 | 48 | 43 | 78 | 47 |
| np-582 | 102 | 266 | 88 | 56 | 32 | 39 | 16 | 11 | 28 | 11 | 15 | 29 |
| np-586 | 729 | 371 | 803 | 524 | 498 | 527 | 35 | 25 | 31 | 30 | 28 | 27 |
| np-587 | 109 | 145 | 188 | 64 | 75 | 84 | 17 | 14 | 26 | 9 | 16 | 22 |
| np-596 | 701 | 398 | 239 | 471 | 480 | 341 | 42 | 32 | 46 | 45 | 33 | 43 |
| Isoline Height | Number of Deviation a | Maximum Plane Deviation, m b | Average of Plane Deviation, m c | Maximum of Height Deviation, m d | Average of Height Deviation, m e | Proportional Deviation f | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| − | + | − | + | − | + | − | + | − | + | ||
| The foot of the mound. Height of the grass was 60–100 cm | |||||||||||
| 102.00 | 138 | 232 | 0.619 | 1.569 | 0.269 | 0.556 | −0.109 | +0.117 | −0.051 | +0.038 | +0.005 |
| 102.50 | 741 | 399 | 6.653 | 2.527 | 1.539 | 0.834 | −0.338 | +0.214 | −0.091 | +0.071 | −0.034 |
| 103.00 | 449 | 632 | 5.791 | 2.116 | 0.961 | 0.864 | −0.778 | +0.216 | −0.110 | +0.085 | +0.004 |
| 103.50 | 377 | 431 | 3.950 | 1.663 | 0.569 | 0.698 | −0.480 | +0.186 | −0.064 | +0.079 | +0.012 |
| 104.00 | 732 | 635 | 1.355 | 2.162 | 0.497 | 0.765 | −0.167 | +0.213 | −0.064 | +0.081 | +0.003 |
| 104.50 | 882 | 863 | 2.301 | 1.822 | 0.787 | 0.569 | −0.277 | +0.293 | −0.086 | +0.080 | −0.004 |
| 105.00 | 877 | 608 | 1.720 | 1.726 | 0.577 | 0.566 | −0.190 | +0.245 | −0.063 | +0.091 | 0.000 |
| 105.50 | 744 | 631 | 1.693 | 1.463 | 0.539 | 0.446 | −0.199 | +0.271 | −0.074 | +0.075 | −0.005 |
| 106.00 | 536 | 356 | 1.629 | 0.902 | 0.449 | 0.276 | −0.233 | +0.139 | −0.066 | +0.048 | −0.021 |
| 106.50 | 532 | 222 | 1.534 | 0.513 | 0.420 | 0.197 | −0.282 | +0.120 | −0.077 | +0.043 | −0.042 |
| 107.00 | 318 | 251 | 0.771 | 0.959 | 0.310 | 0.293 | −0.197 | +0.179 | −0.074 | +0.059 | −0.016 |
| 107.50 | 258 | 254 | 0.518 | 0.818 | 0.214 | 0.225 | −0.126 | +0.176 | −0.047 | +0.048 | +0.000 |
| 108.00 | 203 | 303 | 0.681 | 0.799 | 0.265 | 0.253 | −0.182 | +0.183 | −0.066 | +0.060 | +0.009 |
| 108.50 | 70 | 382 | 0.355 | 0.969 | 0.127 | 0.330 | −0.109 | +0.174 | −0.037 | +0.062 | +0.047 |
| 109.00 | 416 | 242 | 1.021 | 0.508 | 0.401 | 0.135 | −0.174 | +0.147 | −0.075 | +0.040 | −0.033 |
| 109.50 | 374 | 319 | 1.736 | 0.700 | 0.469 | 0.254 | −0.406 | +0.163 | −0.115 | +0.059 | −0.035 |
| 110.00 | 212 | 305 | 0.776 | 0.415 | 0.250 | 0.166 | −0.167 | +0.090 | −0.064 | +0.036 | −0.005 |
| 110.50 | 344 | 189 | 1.251 | 0.449 | 0.322 | 0.132 | −0.238 | +0.103 | −0.066 | +0.030 | −0.032 |
| 111.00 | 449 | 336 | 1.401 | 0.575 | 0.412 | 0.211 | −0.298 | +0.199 | −0.093 | +0.064 | −0.026 |
| 111.50 | 451 | 361 | 1.055 | 1.080 | 0.438 | 0.332 | −0.251 | +0.289 | −0.103 | +0.081 | −0.022 |
| 112.00 | 537 | 206 | 1.843 | 0.779 | 0.585 | 0.270 | −0.341 | +0.141 | −0.113 | +0.048 | −0.069 |
| The slopes of the mound. Height of the grass was 5 to 10 cm | |||||||||||
| 110.00 | 138 | 137 | 0.422 | 0.695 | 0.205 | 0.325 | 0.197 | +0.424 | −0.096 | +0.148 | +0.027 |
| 110.50 | 112 | 158 | 0.349 | 0.477 | 0.159 | 0.195 | 0.197 | +0.272 | −0.086 | +0.107 | +0.027 |
| 111.00 | 162 | 124 | 0.326 | 0.3 | 0.114 | 0.109 | 0.184 | +0.184 | −0.064 | +0.064 | −0.006 |
| 111.50 | 169 | 118 | 0.355 | 0.358 | 0.154 | 0.133 | −0.21 | +0.234 | −0.089 | +0.088 | −0.014 |
| 112.00 | 144 | 144 | 0.384 | 0.406 | 0.159 | 0.139 | −0.247 | +0.255 | −0.01 | +0.091 | −0.001 |
| 112.50 | 146 | 137 | 0.347 | 0.381 | 0.138 | 0.137 | −0.256 | +0.246 | −0.098 | +0.096 | −0.004 |
| 113.00 | 125 | 122 | 0.297 | 0.291 | 0.12 | 0.12 | −0.227 | +0.196 | −0.09 | +0.082 | −0.002 |
| 113.50 | 115 | 113 | 0.272 | 0.265 | 0.124 | 0.116 | −0.182 | +0.189 | −0.083 | +0.081 | +0.001 |
| 114.00 | 110 | 100 | 0.251 | 0.213 | 0.12 | 0.105 | −0.161 | +0.161 | −0.08 | +0.073 | −0.007 |
| 114.50 | 103 | 108 | 0.277 | 0.288 | 0.123 | 0.132 | −0.202 | +0.207 | −0.008 | +0.01 | +0.005 |
| 115.00 | 120 | 125 | 0.339 | 0.362 | 0.141 | 0.171 | −0.199 | +0.248 | −0.092 | +0.116 | +0.013 |
| 115.50 | 115 | 139 | 0.378 | 0.329 | 0.181 | 0.137 | −0.249 | +0.219 | −0.124 | +0.099 | −0.001 |
| 116.00 | 120 | 111 | 0.34 | 0.245 | 0.151 | 0.109 | −0.257 | +0.17 | −0.108 | +0.078 | −0.018 |
| 116.50 | 95 | 124 | 0.206 | 0.237 | 0.095 | 0.097 | −0.159 | +0.155 | 0.072 | +0.066 | +0.007 |
| 117.00 | 119 | 88 | 0.267 | 0.222 | 0.119 | 0.108 | −0.185 | +0.16 | −0.082 | +0.078 | −0.02 |
| 117.50 | 95 | 107 | 0.268 | 0.285 | 0.137 | 0.134 | −0.168 | +0.207 | −0.085 | +0.096 | +0.009 |
| 118.00 | 91 | 100 | 0.271 | 0.274 | 0.132 | 0.131 | −0.185 | +0.176 | −0.096 | +0.082 | −0.002 |
| 118.50 | 90 | 99 | 0.259 | 0.278 | 0.115 | 0.117 | −0.193 | +0.183 | −0.009 | +0.075 | −0.002 |
| 119.00 | 110 | 68 | 0.27 | 0.242 | 0.122 | 0.112 | −0.184 | +0.158 | −0.087 | +0.075 | −0.026 |
| 119.50 | 612 | 73 | 0.236 | 0.222 | 0.103 | 0.088 | −0.159 | +0.123 | −0.079 | +0.049 | −0.009 |
| 120.00 | 87 | 92 | 0.254 | 0.405 | 0.094 | 0.123 | −0.217 | +0.177 | −0.072 | +0.063 | −0.003 |
| 120.50 | 70 | 132 | 0.247 | 0.253 | 0.05 | 0.081 | −0.245 | +0.114 | −0.041 | +0.044 | +0.014 |
| 121.00 | 57 | 50 | 0.116 | 0.159 | 0.063 | 0.069 | −0.127 | +0.127 | −0.041 | +0.071 | +0.043 |
| The top of the mound. Height of the grass was 1 to 2 cm | |||||||||||
| 121.00 | 71 | 151 | 0.468 | 0.443 | 0.260 | 0.240 | −0.297 | +0.055 | −0.107 | +0.031 | −0.013 |
| 120.50 | 153 | 183 | 0.396 | 0.754 | 0.111 | 0.310 | −0.070 | +0.101 | −0.021 | +0.048 | +0.017 |
| 120.00 | 86 | 251 | 0.373 | 0.466 | 0.148 | 0.269 | −0.042 | +0.091 | −0.018 | +0.051 | +0.033 |
| 119.50 | 151 | 225 | 0.274 | 0.694 | 0.114 | 0.238 | −0.048 | +0.125 | −0.018 | +0.044 | +0.019 |
| 119.00 | 205 | 395 | 0.736 | 0.585 | 0.256 | 1.228 | −0.197 | +0.419 | −0.033 | +0.114 | +0.064 |
| 118.50 | 107 | 490 | 0.647 | 2.373 | 0.302 | 0.804 | −0.235 | +0.196 | −0.106 | +0.074 | +0.042 |
| 121.00 | 71 | 151 | 0.468 | 0.443 | 0.260 | 0.240 | −0.297 | +0.055 | −0.107 | +0.031 | −0.013 |
| 120.50 | 153 | 183 | 0.396 | 0.754 | 0.111 | 0.310 | −0.070 | +0.101 | −0.021 | +0.048 | +0.017 |
| 120.00 | 86 | 251 | 0.373 | 0.466 | 0.148 | 0.269 | −0.042 | +0.091 | −0.018 | +0.051 | +0.033 |
| 119.50 | 151 | 225 | 0.274 | 0.694 | 0.114 | 0.238 | −0.048 | +0.125 | −0.018 | +0.044 | +0.019 |
| 119.00 | 205 | 395 | 0.736 | 0.585 | 0.256 | 1.228 | −0.197 | +0.419 | −0.033 | +0.114 | +0.064 |
| 118.50 | 107 | 490 | 0.647 | 2.373 | 0.302 | 0.804 | −0.235 | +0.196 | −0.106 | +0.074 | +0.042 |
| 121.00 | 71 | 151 | 0.468 | 0.443 | 0.260 | 0.240 | −0.297 | +0.055 | −0.107 | +0.031 | −0.013 |
| 120.50 | 153 | 183 | 0.396 | 0.754 | 0.111 | 0.310 | −0.070 | +0.101 | −0.021 | +0.048 | +0.017 |
| 120.00 | 86 | 251 | 0.373 | 0.466 | 0.148 | 0.269 | −0.042 | +0.091 | −0.018 | +0.051 | +0.033 |
| 119.50 | 151 | 225 | 0.274 | 0.694 | 0.114 | 0.238 | −0.048 | +0.125 | −0.018 | +0.044 | +0.019 |
| 119.00 | 205 | 395 | 0.736 | 0.585 | 0.256 | 1.228 | −0.197 | +0.419 | −0.033 | +0.114 | +0.064 |
| 118.50 | 107 | 490 | 0.647 | 2.373 | 0.302 | 0.804 | −0.235 | +0.196 | −0.106 | +0.074 | +0.042 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Česnulevičius, A.; Bautrėnas, A.; Bevainis, L.; Ovodas, D. A Comparison of the Influence of Vegetation Cover on the Precision of an UAV 3D Model and Ground Measurement Data for Archaeological Investigations: A Case Study of the Lepelionys Mound, Middle Lithuania. Sensors 2019, 19, 5303. https://doi.org/10.3390/s19235303
Česnulevičius A, Bautrėnas A, Bevainis L, Ovodas D. A Comparison of the Influence of Vegetation Cover on the Precision of an UAV 3D Model and Ground Measurement Data for Archaeological Investigations: A Case Study of the Lepelionys Mound, Middle Lithuania. Sensors. 2019; 19(23):5303. https://doi.org/10.3390/s19235303
Chicago/Turabian StyleČesnulevičius, Algimantas, Artūras Bautrėnas, Linas Bevainis, and Donatas Ovodas. 2019. "A Comparison of the Influence of Vegetation Cover on the Precision of an UAV 3D Model and Ground Measurement Data for Archaeological Investigations: A Case Study of the Lepelionys Mound, Middle Lithuania" Sensors 19, no. 23: 5303. https://doi.org/10.3390/s19235303
APA StyleČesnulevičius, A., Bautrėnas, A., Bevainis, L., & Ovodas, D. (2019). A Comparison of the Influence of Vegetation Cover on the Precision of an UAV 3D Model and Ground Measurement Data for Archaeological Investigations: A Case Study of the Lepelionys Mound, Middle Lithuania. Sensors, 19(23), 5303. https://doi.org/10.3390/s19235303




