Pre-Processing of Panchromatic Images to Improve Object Detection in Pansharpened Images
Abstract
1. Introduction
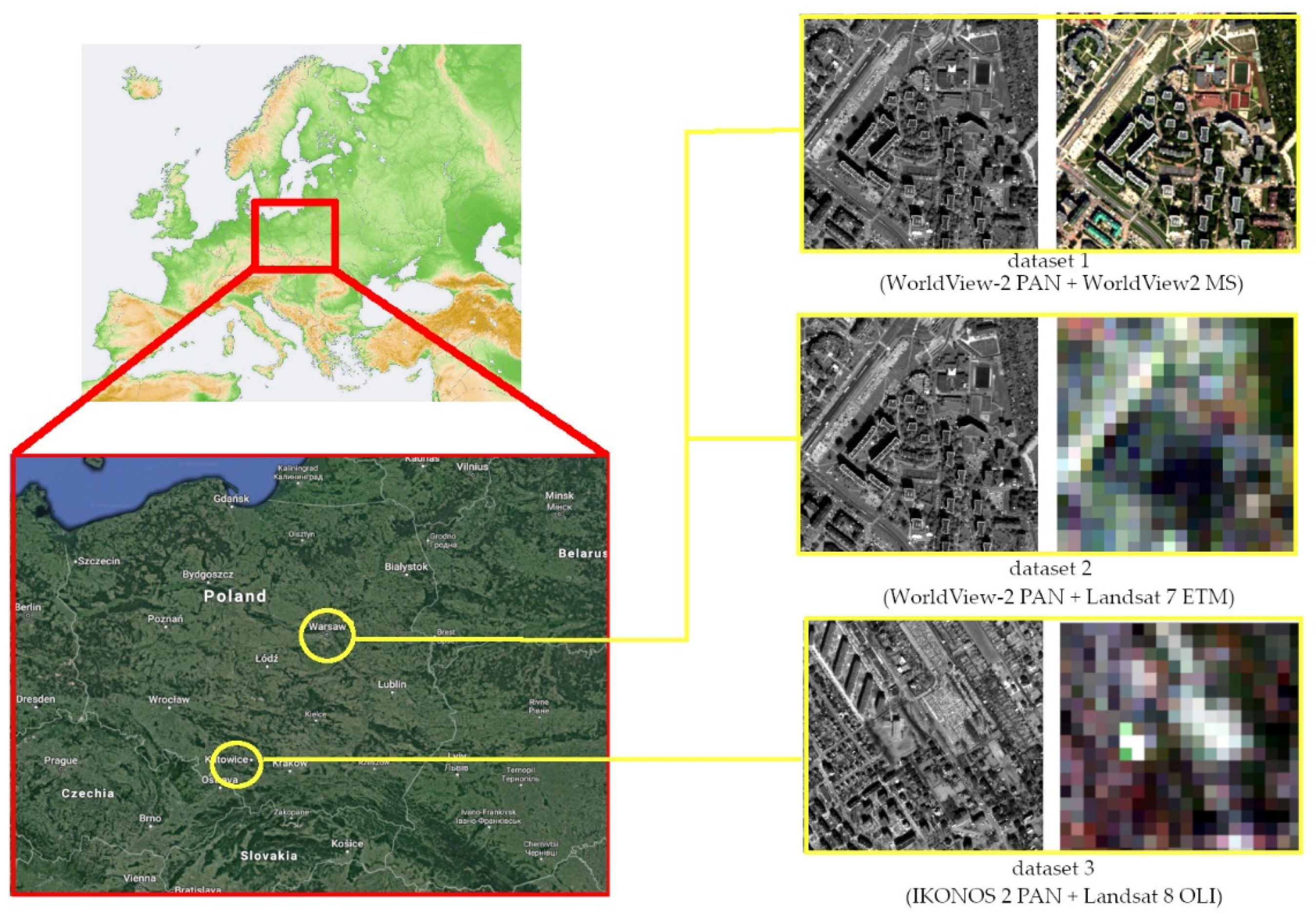
2. Materials
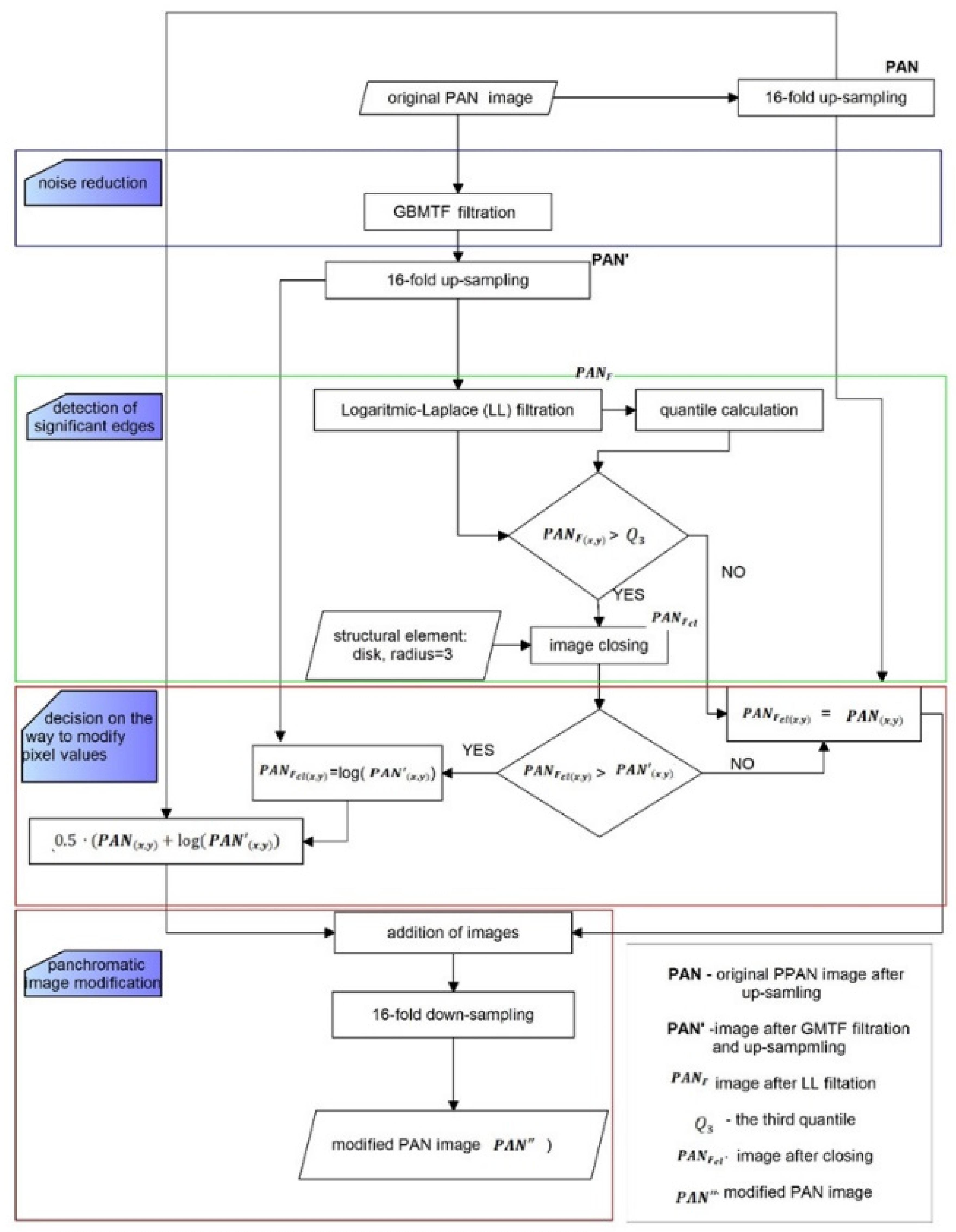
3. Methods
4. Results
4.1. Spatial Quality Assessment
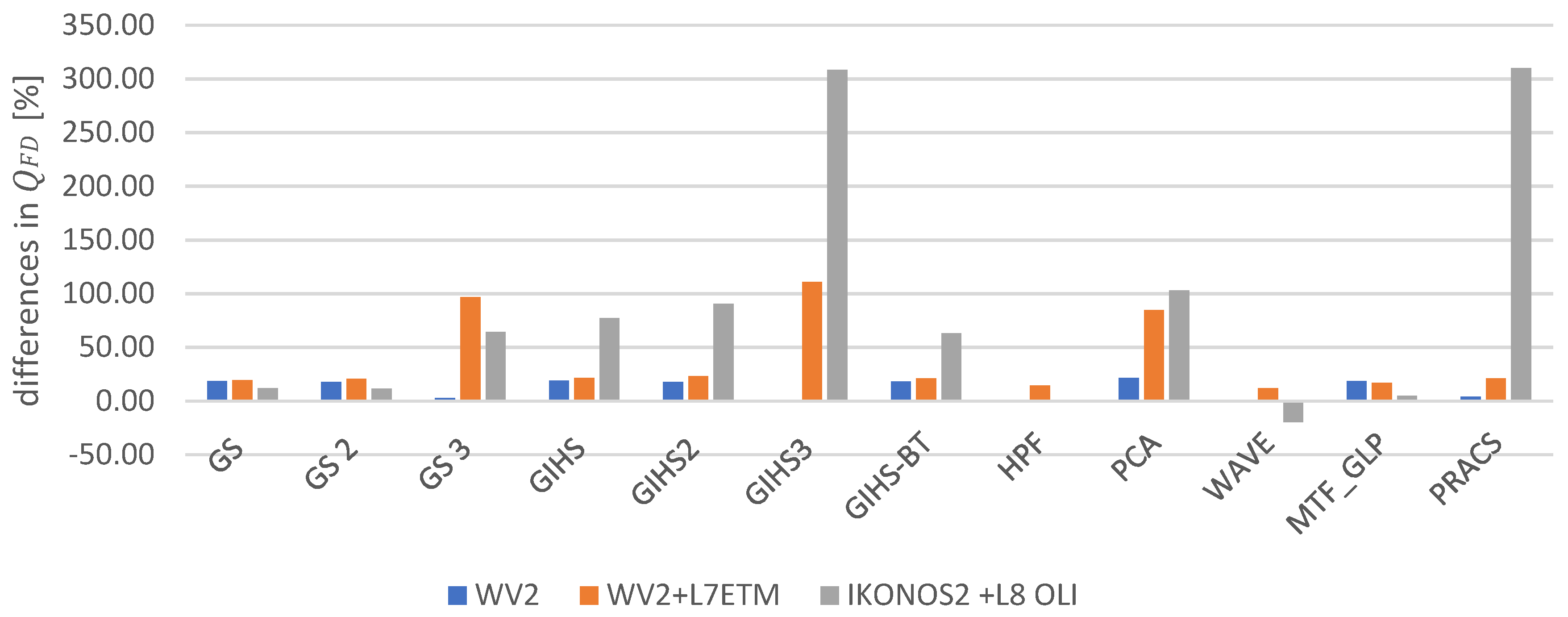
4.2. Features-Detector-Based Quality Index
4.3. Image Segmentation
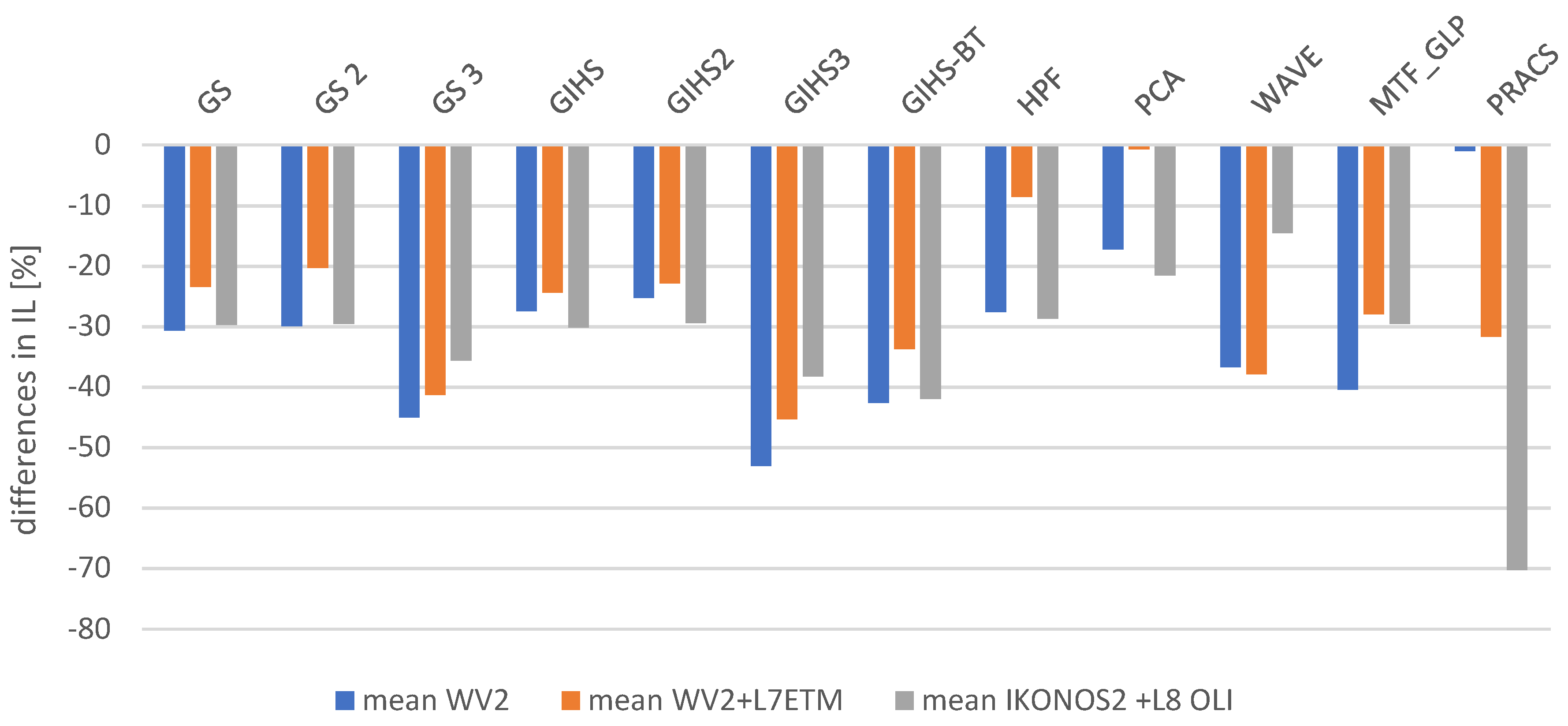
4.4. Spectral Quality Assessment
4.5. Accuracy Assessment
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fonseca, L.; Namikawa, L.; Castejon, E.; Carvalho, L.; Pinho, C.; Pagamisse, A. Image Fusion for Remote Sensing Applications. In Image Fusion and Its Applications; Zheng, Y., Ed.; InTech: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef]
- Su, W.; Sun, Z.; Chen, W.-H.; Zhang, X.; Yao, C.; Wu, J.; Huang, J.; Zhu, D. Joint Retrieval of Growing Season Corn Canopy LAI and Leaf Chlorophyll Content by Fusing Sentinel-2 and MODIS Images. Remote Sens. 2019, 11, 2409. [Google Scholar] [CrossRef]
- Noviello, M.; Ciminale, M.; De Pasquale, V. Combined application of pansharpening and enhancement methods to improve archaeological cropmark visibility and identification in QuickBird imagery: Two case studies from Apulia, Southern Italy. J. Archaeol. Sci. 2013, 40, 3604–3613. [Google Scholar] [CrossRef]
- Amarsaikhan, D.; Blotevogel, H.H.; Van Genderen, J.L.; Ganzorig, M.; Gantuya, R.; Nergui, B. Fusing high-resolution SAR and optical imagery for improved urban land cover study and classification. Int. J. Image Data Fusion 2010, 1, 83–97. [Google Scholar] [CrossRef]
- Ma, X.; Li, C.; Tong, X.; Liu, S. A New Fusion Approach for Extracting Urban Built-up Areas from Multisource Remotely Sensed Data. Remote Sens. 2019, 11, 2516. [Google Scholar] [CrossRef]
- Orych, A. Review of methods for determining the spatial resolution of UAVsensors. In Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Toronto, ON, Canada, 30 August–2 September 2015. [Google Scholar]
- Ehlers, M.; Jacobsen, K.; Schiewe, J. High Resolution Image Data and GIS. In ASPRS Manual of GIS; Madden, M., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2009; pp. 721–777. [Google Scholar]
- Jolliffe, I. Principal Component Analysis; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Maurer, T. How to pan-sharpen images using the Gram-Schmidt pan-sharpen method-a recipe. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Hannover, Germany, 21–24 May 2013; Volume XL-1/W1. [Google Scholar]
- Craig, A.L.; Bernard, V.B.; Inventor Eastman Kodak Co. Assigne. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 09,069,232, 29 April 1998. [Google Scholar]
- Al-Wassai, F.A.; Kalyankar, N.V.; Al-Zuky, A.A. The IHS transformations based image fusion. arXiv 2011, arXiv:1107.4396. [Google Scholar]
- Tu, T.M.; Huang, P.S.; Hung, C.L.; Chang, C.P. A fast intensity-hue-saturation fusion technique with spectral adjustment for IKONOS imagery. IEEE Trans. Geosci. Remote Sens. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Tu, T.; Lee, Y.C.; Chang, C.P.; Huang, P.S. Adjustable intensity-hue-saturation and Brovey transform fusion technique for IKONOS/QuickBird imagery. Opt. Eng. 2005, 44, 116201. [Google Scholar] [CrossRef]
- Gangkofner, U.G.; Pradhan, P.S.; Holcomb, D.W. Optimizing the high-pass filter addition technique for image fusion. Photogramm. Eng. Remote Sens. 2008, 74, 1107–1118. [Google Scholar] [CrossRef]
- Pajares, G.; De La Cruz, J.M. A wavelet-based image fusion tutorial. Pattern Recognit. 2004, 37, 1855–1872. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, G. An IHS an wavelet integrated approach to improve pansharpening visual quality of natural colour IKONOS and QuickBird images. Inf. Fusion 2005, 6, 225–234. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geosci. Remote Sens. Lett. 2013, 11, 930–934. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, M.; Choi, J.; Kim, Y. Image fusion of spectrally nonoverlapping imagery using SPCA and MTF-based filters. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2295–2299. [Google Scholar] [CrossRef]
- Choi, J.; Yu, K.; Kim, Y. A new adaptive component-substitution-based satellite image fusion by using partial replacement. IEEE Trans. Geosci. Remote Sens. 2010, 49, 295–309. [Google Scholar] [CrossRef]
- Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1847–1857. [Google Scholar] [CrossRef]
- Zhang, H.K.; Huang, B. A new look at image fusion methods from a Bayesian perspective. Remote Sens. 2015, 7, 6828–6861. [Google Scholar] [CrossRef]
- Qu, J.; Lei, J.; Li, Y.; Dong, W.; Zeng, Z.; Chen, D. Structure Tensor-Based Algorithm for Hyperspectral and Panchromatic Images Fusion. Remote Sens. 2018, 10, 373. [Google Scholar] [CrossRef]
- Choi, J.; Park, H.; Seo, D. Pansharpening Using Guided Filtering to Improve the Spatial Clarity of VHR Satellite Imagery. Remote Sens. 2019, 11, 633. [Google Scholar] [CrossRef]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1753–1761. [Google Scholar]
- Li, Z.; Cheng, C. A CNN-Based Pan-Sharpening Method for Integrating Panchromatic and Multispectral Images Using Landsat 8. Remote Sens. 2019, 11, 2606. [Google Scholar] [CrossRef]
- Hu, J.; He, Z.; Wu, J. Deep Self-Learning Network for Adaptive Pansharpening. Remote Sens. 2019, 11, 2395. [Google Scholar] [CrossRef]
- Fryskowska, A.; Wojtkowska, M.; Delis, P.; Grochala, A. Some Aspects of Satellite Imagery Integration from EROS B and LANDSAT 8. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 647–652. [Google Scholar]
- Grochala, A.; Kedzierski, M. A Method of Panchromatic Image Modification for Satellite Imagery Data Fusion. Remote Sens. 2017, 9, 639. [Google Scholar] [CrossRef]
- Jenerowicz, A.; Siok, K.; Woroszkiewicz, M.; Orych, A. The Fusion of Satellite and UAV Data: Simulation of High Spatial Resolution Band. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XIX; International Society for Optics and Photonics: Warsaw, Poland, 2017; Volume 10421, p. 104211Z. [Google Scholar]
- Sekrecka, A.; Kedzierski, M. Integration of Satellite Data with High Resolution Ratio: Improvement of Spectral Quality with Preserving Spatial Details. Sensors 2018, 18, 4418. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Zhou, C.; Huang, L.; Yang, X.; Xu, B.; Liang, D. Fusion of Unmanned Aerial Vehicle Panchromatic and Hyperspectral Images Combining Joint Skewness-Kurtosis Figures and a Non-Subsampled Contourlet Transform. Sensors 2018, 18, 3467. [Google Scholar] [CrossRef] [PubMed]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 6, 697–698. [Google Scholar]
- DIGITAL GLOBE. Available online: https://www.digitalglobe.com/products/satellite-imagery (accessed on 6 July 2019).
- NASA. Available online: http://landsat.gsfc.nasa.gov (accessed on 6 July 2019).
- Shreyamsha Kumar, B.K. Image Denoising based on Gaussian/Bilateral Filter and its Method Noise Thresholding. Signal Image Video Process 2012, 7, 1159–1172. [Google Scholar] [CrossRef]
- Zhang, M.; Gunturk, B.K. Multiresolution bilateral filtering for image denoising. IEEE Trans. Image Process. 2008, 17, 2324–2333. [Google Scholar] [CrossRef]
- Borkowski, A.; Głowienka, E.; Hejmanowska, B.; Kwiatkowska-Malina, J.; Kwolek, M.; Michałowska, K.; Mikrut, S.; Pekala, A.; Pirowski, T.; Zabrzeska-Gasiorek, B. GIS and Remote Sensing in Environmental Monitoring; Głowienka, E., Ed.; Rzeszow School of Engineering and Economics, Neiko Print & Publishing: Tarnobrzeg, Poland, 2015; pp. 7–48. [Google Scholar]
- Zhou, H.; Wu, J.; Zhang, J. Digital Image Processing: Part II; Bookboon: London, UK, 2010; pp. 34–46. ISBN 978-87-7681-542-4. [Google Scholar]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up Robust Features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Terriberry, T.B.; French, L.M.; Helmsen, J. GPU accelerating speeded-up robust features. Proc. 3DPVT 2008, 8, 355–362. [Google Scholar]
- Schouten, T.E.; Gebbinck, M.S.K. Quality measures for image segmentation using generated images. In Image Signal Process. Remote Sens. 1995, 2579, 411–422. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Lu, L. Why is image quality assessment so difficult? In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002. [Google Scholar]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Ranchin, T.; Wald, L. Fusion of High Spatial and Spectral Resolution Images: The ARSIS Concept and its Implementation. Photogramm. Eng. Remote Sens. 2000, 66, 49–61. [Google Scholar]
- Wald, L. Quality of High Resolution Synthesised Images: Is There a Simple Criterion? Available online: https://hal.archives-ouvertes.fr/hal-00395027/document (accessed on 3 October 2019).
- Ranchin, T.; Aiazzi, B.; Alparone, L.; Baronti, S.; Wald, L. Image fusion—The ARSIS concept and some successful implementation schemes. ISPRS J. Photogramm. Remote Sens. 2003, 58, 4–18. [Google Scholar] [CrossRef]
- Selva, M.; Santurri, L.; Baronti, S. On the Use of the Expanded Image in Quality Assessment of Pansharpened Images. IEEE Geosc. Remote Sens. Lett. 2018, 15, 320–324. [Google Scholar] [CrossRef]
- Liu, J.G. Smoothing Filter-based Intensity Modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Choi, J.; Yeom, J.; Chang, A.; Byun, Y.; Kim, Y. Hybrid pansharpening algorithm for high spatial resolution satellite imagery to improve spatial quality. IEEE Geosci. Remote Sens. Lett. 2012, 10, 490–494. [Google Scholar] [CrossRef]
- Gonzalo, C.; Lillo-Saavedra, M. A directed search algorithm for setting the spectral–spatial quality trade-off of fused images by the wavelet à trous method. Can. J. Remote Sens. 2008, 34, 367–375. [Google Scholar] [CrossRef]
- Marcello, J.; Medina, A.; Eugenio, F. Evaluation of spatial and spectral effectiveness of pixel-level fusion techniques. IEEE Geosci. Remote Sens. Lett. 2012, 10, 432–436. [Google Scholar] [CrossRef]
- Gillmann, C.; Arbelaez, P.; Hernandez, J.; Hagen, H.; Wischgoll, T. An Uncertainty-Aware Visual System for Image Pre-Processing. J. Imaging 2018, 4, 109. [Google Scholar] [CrossRef]





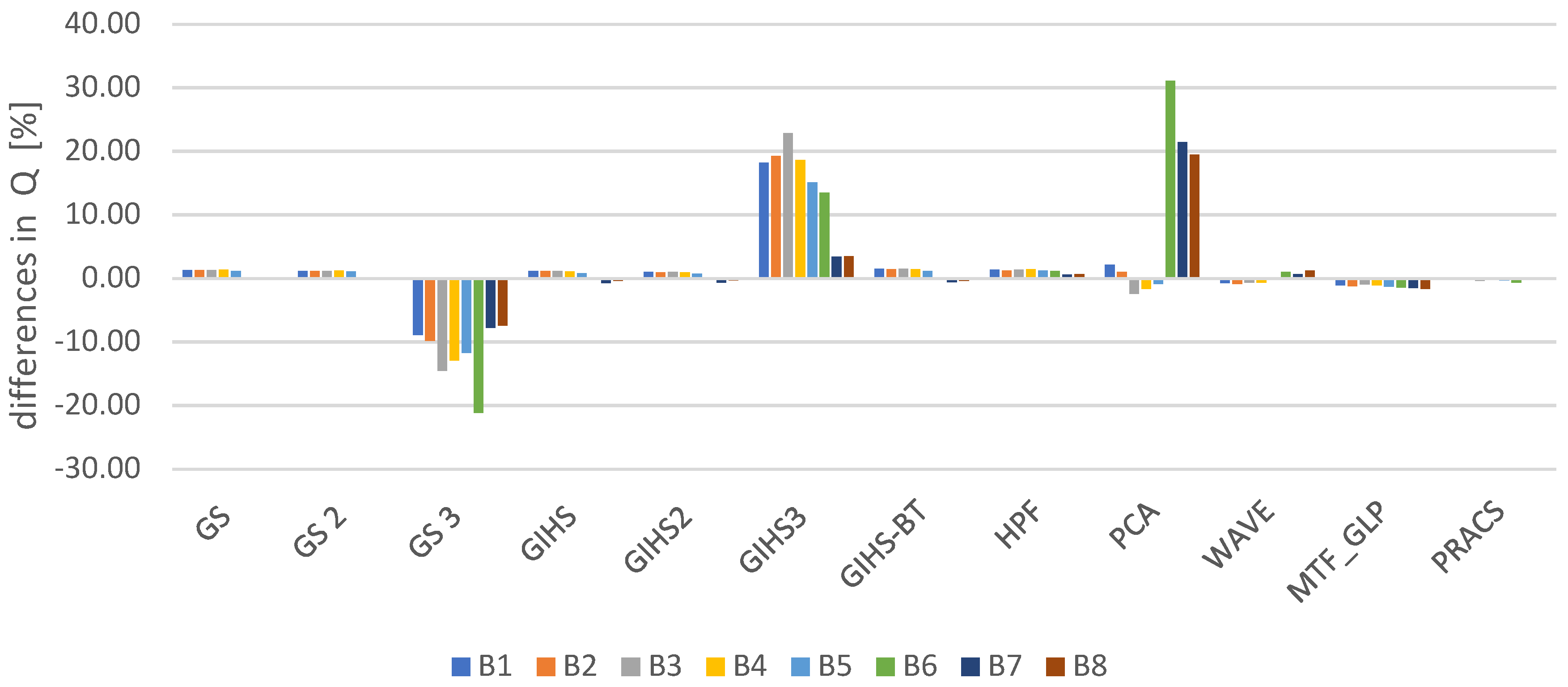

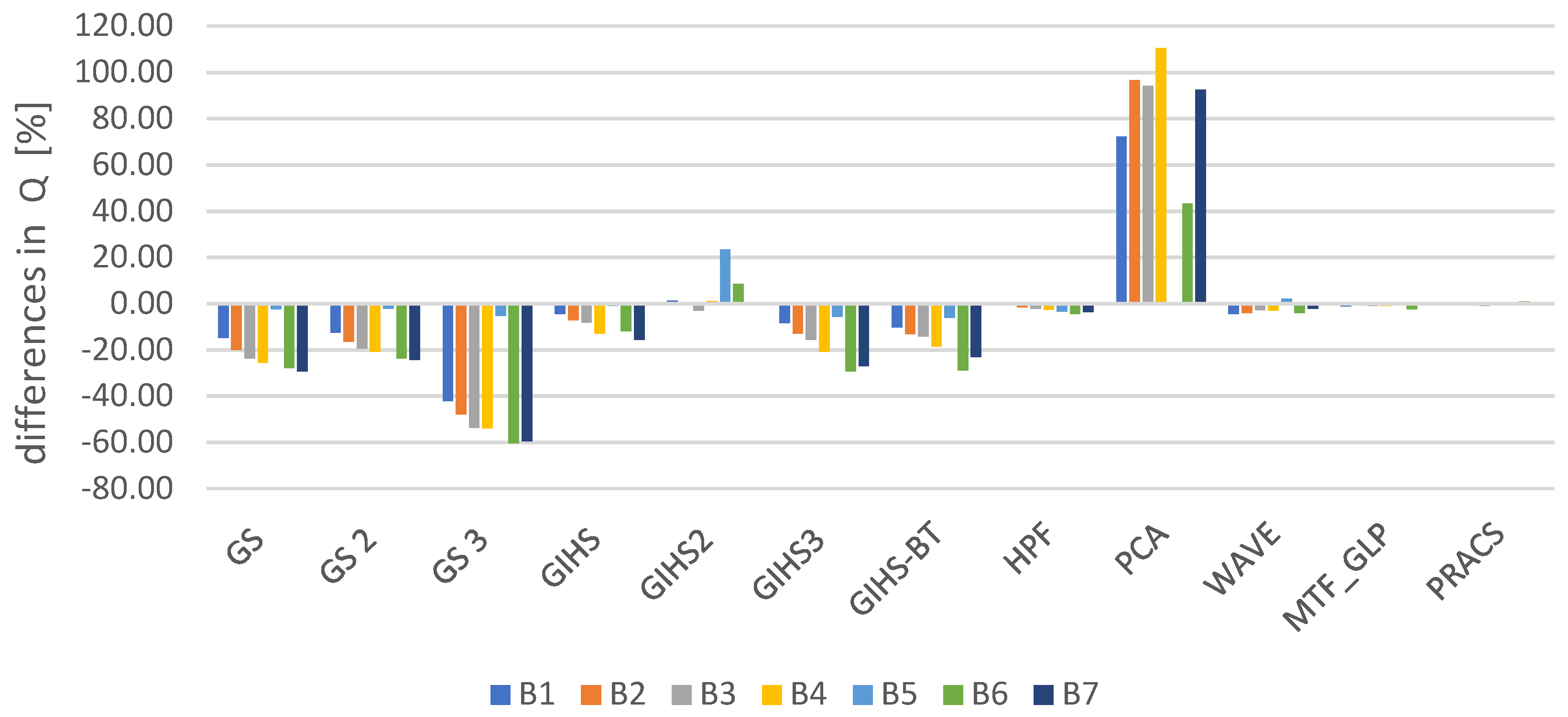


| Method | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 |
|---|---|---|---|---|---|---|---|---|
| GS class | 0.75 | 0.80 | 0.93 | 0.88 | 0.86 | 0.92 | 0.70 | 0.67 |
| GS mod | 0.94 | 1.00 | 1.16 | 1.10 | 1.07 | 1.03 | 0.74 | 0.71 |
| GS 2 class | 0.73 | 0.77 | 0.89 | 0.85 | 0.84 | 0.89 | 0.68 | 0.65 |
| GS 2 mod | 0.91 | 0.96 | 1.10 | 1.06 | 1.03 | 0.99 | 0.72 | 0.69 |
| GS 3 class | 0.72 | 0.76 | 0.87 | 0.83 | 0.83 | 0.84 | 0.66 | 0.63 |
| GS 3 mod | 0.75 | 0.80 | 0.90 | 0.87 | 0.86 | 0.84 | 0.66 | 0.62 |
| GIHS class | 0.56 | 0.58 | 0.62 | 0.62 | 0.59 | 0.88 | 0.65 | 0.64 |
| GIHS mod | 0.71 | 0.71 | 0.80 | 0.74 | 0.70 | 1.01 | 0.72 | 0.70 |
| GIHS 2 class | 0.55 | 0.57 | 0.60 | 0.60 | 0.59 | 0.86 | 0.63 | 0.63 |
| GIHS 2 mod | 0.68 | 0.69 | 0.76 | 0.72 | 0.68 | 0.96 | 0.70 | 0.69 |
| GIHS 3 class | 0.61 | 0.62 | 0.66 | 0.67 | 0.64 | 0.85 | 0.63 | 0.63 |
| GIHS 3 mod | 0.61 | 0.62 | 0.66 | 0.65 | 0.63 | 0.84 | 0.61 | 0.62 |
| GIHS BT class | 0.54 | 0.55 | 0.62 | 0.63 | 0.60 | 0.93 | 0.70 | 0.73 |
| GIHS BT mod | 0.66 | 0.66 | 0.76 | 0.74 | 0.71 | 1.04 | 0.81 | 0.83 |
| HPF class | 0.89 | 0.90 | 0.99 | 0.98 | 0.93 | 1.05 | 0.95 | 0.94 |
| HPF mod | 0.91 | 0.91 | 1.00 | 0.98 | 0.95 | 1.06 | 0.94 | 0.93 |
| PCA class | 0.69 | 0.70 | 0.92 | 0.94 | 0.78 | 0.67 | 0.55 | 0.55 |
| PCA mod | 0.97 | 1.00 | 1.11 | 1.18 | 1.07 | 0.70 | 0.55 | 0.55 |
| Wave class | 0.89 | 0.96 | 0.96 | 0.92 | 0.93 | 1.17 | 0.92 | 0.90 |
| Wave mod | 0.90 | 0.97 | 0.96 | 0.92 | 0.93 | 1.19 | 0.92 | 0.89 |
| MTF_GLP or | 0.69 | 0.70 | 0.77 | 0.76 | 0.76 | 0.91 | 0.80 | 0.83 |
| MTF_GLP mod | 0.85 | 0.86 | 0.94 | 0.87 | 0.92 | 1.03 | 0.93 | 0.97 |
| PRACS or | 0.55 | 0.56 | 0.60 | 0.60 | 0.58 | 0.74 | 0.60 | 0.60 |
| PRACS mod | 0.57 | 0.58 | 0.66 | 0.55 | 0.63 | 0.79 | 0.62 | 0.63 |
| Method | b1 | b2 | b3 | b4 | b5 | b6 |
|---|---|---|---|---|---|---|
| GS class | 0.64 | 0.82 | 0.77 | 0.61 | 0.92 | 0.90 |
| GS mod | 0.76 | 0.98 | 0.92 | 0.71 | 1.11 | 1.07 |
| GS 2 class | 0.55 | 0.69 | 0.65 | 0.54 | 0.78 | 0.76 |
| GS 2 mod | 0.66 | 0.85 | 0.79 | 0.63 | 0.95 | 0.91 |
| GS 3 class | 0.44 | 0.57 | 0.54 | 0.44 | 0.69 | 0.65 |
| GS 3 mod | 0.85 | 1.18 | 1.11 | 0.72 | 1.40 | 1.34 |
| GIHS class | 0.84 | 0.83 | 0.80 | 0.78 | 0.80 | 0.82 |
| GIHS mod | 1.00 | 1.00 | 0.97 | 0.96 | 0.98 | 0.99 |
| GIHS 2 class | 0.80 | 0.80 | 0.76 | 0.74 | 0.75 | 0.78 |
| GIHS 2 mod | 0.99 | 0.98 | 0.94 | 0.91 | 0.93 | 0.95 |
| GIHS 3 class | 0.71 | 0.71 | 0.67 | 0.63 | 0.66 | 0.68 |
| GIHS 3 mod | 1.45 | 1.46 | 1.42 | 1.36 | 1.42 | 1.43 |
| GIHS BT class | 0.84 | 0.84 | 0.79 | 0.82 | 01 | 0.80 |
| GIHS BT mod | 1.00 | 1.00 | 0.97 | 0.98 | 0.98 | 0.98 |
| HPF class | 0.24 | 0.23 | 0.24 | 0.23 | 0.23 | 0.23 |
| HPF mod | 0.28 | 0.27 | 0.27 | 0.27 | 0.26 | 0.26 |
| PCA class | 0.07 | 0.26 | 0.21 | 0.26 | 0.90 | 0.51 |
| PCA mod | 0.21 | 0.46 | 0.41 | 0.49 | 1.11 | 0.74 |
| Wave class | 0.46 | 0.48 | 0.47 | 0.44 | 0.46 | 0.51 |
| Wave mod | 0.53 | 0.53 | 0.54 | 0.50 | 0.49 | 0.55 |
| MTF_GLP or | 0.67 | 0.67 | 0.66 | 0.67 | 0.65 | 0.65 |
| MTF_GLP mod | 0.92 | 0.92 | 0.92 | 0.05 | 0.90 | 0.91 |
| PRACS or | 0.78 | 0.83 | 0.78 | 0.16 | 0.61 | 0.51 |
| PRACS mod | 1.15 | 1.13 | 1.09 | 0.16 | 0.91 | 0.77 |
| Method | b1 | b2 | b3 | b4 | b5 | b6 | b7 |
|---|---|---|---|---|---|---|---|
| GS class | 0.77 | 0.79 | 0.87 | 0.81 | 0.03 | 0.76 | 0.85 |
| GS mod | 0.85 | 0.88 | 0.98 | 0.92 | 0.02 | 0.85 | 0.96 |
| GS 2 class | 0.72 | 0.74 | 0.83 | 0.77 | 0.02 | 0.73 | 0.81 |
| GS 2 mod | 0.79 | 0.81 | 0.92 | 0.86 | 0.02 | 0.82 | 0.92 |
| GS 3 class | 0.55 | 0.56 | 0.63 | 0.58 | 0.03 | 0.53 | 0.61 |
| GS 3 mod | 0.89 | 0.93 | 1.05 | 0.95 | 0.02 | 0.87 | 1.00 |
| GIHS class | 0.43 | 0.45 | 0.48 | 0.38 | 0.04 | 0.46 | 0.44 |
| GIHS mod | 0.76 | 0.79 | 0.80 | 0.72 | 0.20 | 0.81 | 0.78 |
| GIHS 2 class | 0.35 | 0.37 | 0.38 | 0.29 | 0.03 | 0.38 | 0.34 |
| GIHS 2 mod | 0.67 | 0.70 | 0.67 | 0.60 | 0.17 | 0.74 | 0.63 |
| GIHS 3 class | 0.26 | 0.26 | 0.24 | 0.20 | 0.03 | 0.26 | 0.22 |
| GIHS 3 mod | 0.98 | 1.00 | 1.00 | 0.92 | 0.37 | 1.01 | 0.97 |
| GIHS BT class | 0.42 | 0.44 | 0.50 | 0.52 | 0.51 | 78 | 0.60 |
| GIHS BT mod | 0.72 | 0.75 | 0.80 | 0.80 | 0.73 | 0.99 | 0.86 |
| HPF class | 0.29 | 0.29 | 0.29 | 0.29 | 0.27 | 0.28 | 0.28 |
| HPF mod | 0.28 | 0.29 | 0.29 | 0.29 | 0.27 | 0.27 | 0.27 |
| PCA class | 0.76 | 0.76 | 0.69 | 0.89 | 0.01 | 0.01 | 0.40 |
| PCA mod | 1.04 | 1.05 | 1.00 | 1.09 | 0.05 | 0.06 | 0.82 |
| MTF_GLP or | 0.71 | 0.73 | 0.71 | 0.70 | 0.75 | 0.71 | 0.72 |
| MTF_GLP mod | 0.74 | 0.75 | 0.74 | 0.36 | 0.80 | 0.76 | 0.76 |
| PRACS or | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 |
| PRACS mod | 0.05 | 0.07 | 0.10 | 0.01 | 0.01 | 0.03 | 0.05 |
| WorldView-2 (PAN and MS) | WorldView-2 (PAN) and Landsat 7 ETM (MS) | IKONOS-2 (PAN) and Landsat 8 OLI (MS) | ||||
|---|---|---|---|---|---|---|
| Class | Mod | Class | Mod | Class | Mod | |
| Buildings | 0.92 | 0.94 | 0.68 | 0.78 | 0.48 | 0.63 |
| Walkways and paths | 0.66 | 0.84 | 0.58 | 0.74 | 0.15 | 0.46 |
| Roads | 0.97 | 0.97 | 0.74 | 0.78 | 0.68 | 0.56 |
| Lanes on the roads | 0.20 | 0.86 | 0.20 | 0.88 | 0.00 | 0.00 |
| Grass | 0.98 | 0.97 | 0.90 | 0.92 | 0.66 | 0.64 |
| Trees | 0.90 | 0.91 | 0.71 | 0.75 | 0.34 | 0.37 |
| Parking lots and playgrounds | 0.88 | 0.92 | 0.77 | 0.86 | 0.36 | 0.39 |
| All | 0.79 | 0.92 | 0.65 | 0.82 | 0.38 | 0.44 |
| Method | WorldView-2 (PAN and MS) | WorldView-2 (PAN) and Landsat 7 ETM (MS) | IKONOS-2 (PAN) and Landsat 8 OLI (MS) | |||
|---|---|---|---|---|---|---|
| X [m] | Y [m] | X [m] | Y [m] | X [m] | Y [m] | |
| GS | 0.1 | −0.1 | 0.1 | 0.1 | −0.1 | 0.1 |
| GS 2 | 0.1 | −0.1 | 0.1 | −0.1 | 0.1 | −0.1 |
| GS 3 | 0.1 | −0.2 | 0.1 | −0.1 | 0.1 | 0.1 |
| GIHS | 0.1 | −0.2 | 0.1 | −0.2 | 0.1 | −0.6 |
| GIHS2 | 0.1 | −0.1 | 0.1 | −0.1 | −0.2 | −0.3 |
| GIHS3 | 0.1 | −0.1 | 0.1 | 0.1 | −0.2 | −0.1 |
| GIHS-BT | 0.2 | −0.2 | 0.1 | −0.1 | 0.1 | 0.1 |
| HPF | 0.1 | −0.2 | 0.1 | 0.1 | 0.1 | −0.4 |
| PCA | −0.1 | −0.2 | 0.1 | −0.2 | 0.1 | −0.3 |
| WAVE | 0.5 | −0.2 | 0.3 | 0.4 | 0.9 | 1.2 |
| MTF_GLP | 0.1 | −0.1 | 0.2 | 0.2 | 0.1 | −0.1 |
| PRACS | 0.1 | −0.2 | 0.1 | −0.1 | 0.1 | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekrecka, A.; Kedzierski, M.; Wierzbicki, D. Pre-Processing of Panchromatic Images to Improve Object Detection in Pansharpened Images. Sensors 2019, 19, 5146. https://doi.org/10.3390/s19235146
Sekrecka A, Kedzierski M, Wierzbicki D. Pre-Processing of Panchromatic Images to Improve Object Detection in Pansharpened Images. Sensors. 2019; 19(23):5146. https://doi.org/10.3390/s19235146
Chicago/Turabian StyleSekrecka, Aleksandra, Michal Kedzierski, and Damian Wierzbicki. 2019. "Pre-Processing of Panchromatic Images to Improve Object Detection in Pansharpened Images" Sensors 19, no. 23: 5146. https://doi.org/10.3390/s19235146
APA StyleSekrecka, A., Kedzierski, M., & Wierzbicki, D. (2019). Pre-Processing of Panchromatic Images to Improve Object Detection in Pansharpened Images. Sensors, 19(23), 5146. https://doi.org/10.3390/s19235146







