Tensor-Based Subspace Tracking for Time-Delay Estimation in GNSS Multi-Antenna Receivers
Abstract
1. Introduction
Notation
2. Data Model
2.1. Pre-Correlation Signal Model
2.2. Post-Correlation Signal Model
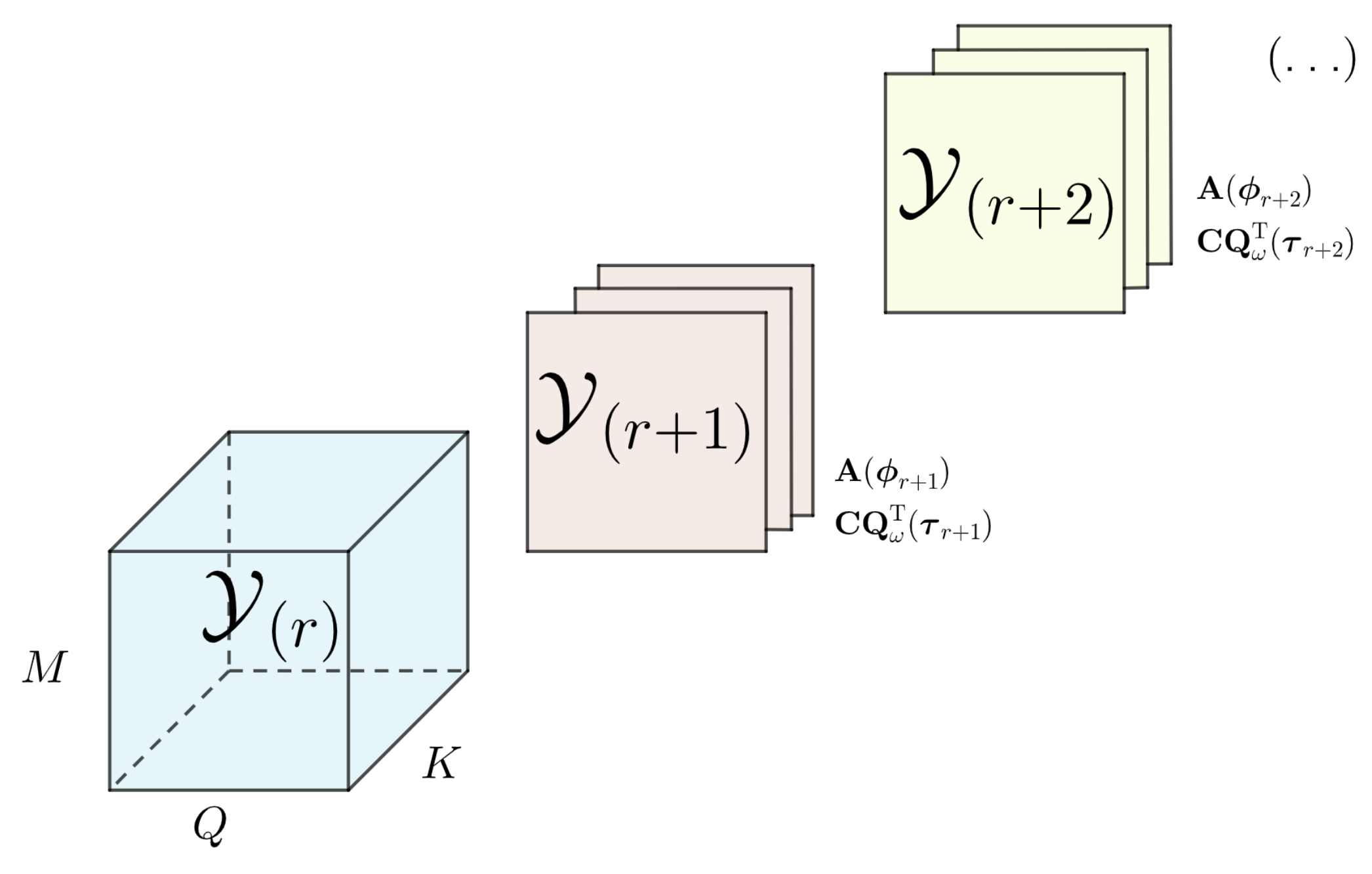
3. Proposed Tensor-Based Subspace Tracking Framework
3.1. PAST–HOSVD/TDE
3.2. PAST–DoA/KRF
3.3. Computational Complexity
| Algorithm 1: PAST–HOSVD time-delay estimation. |
|
| Algorithm 2: PAST–DoA/KRF time-delay estimation. |
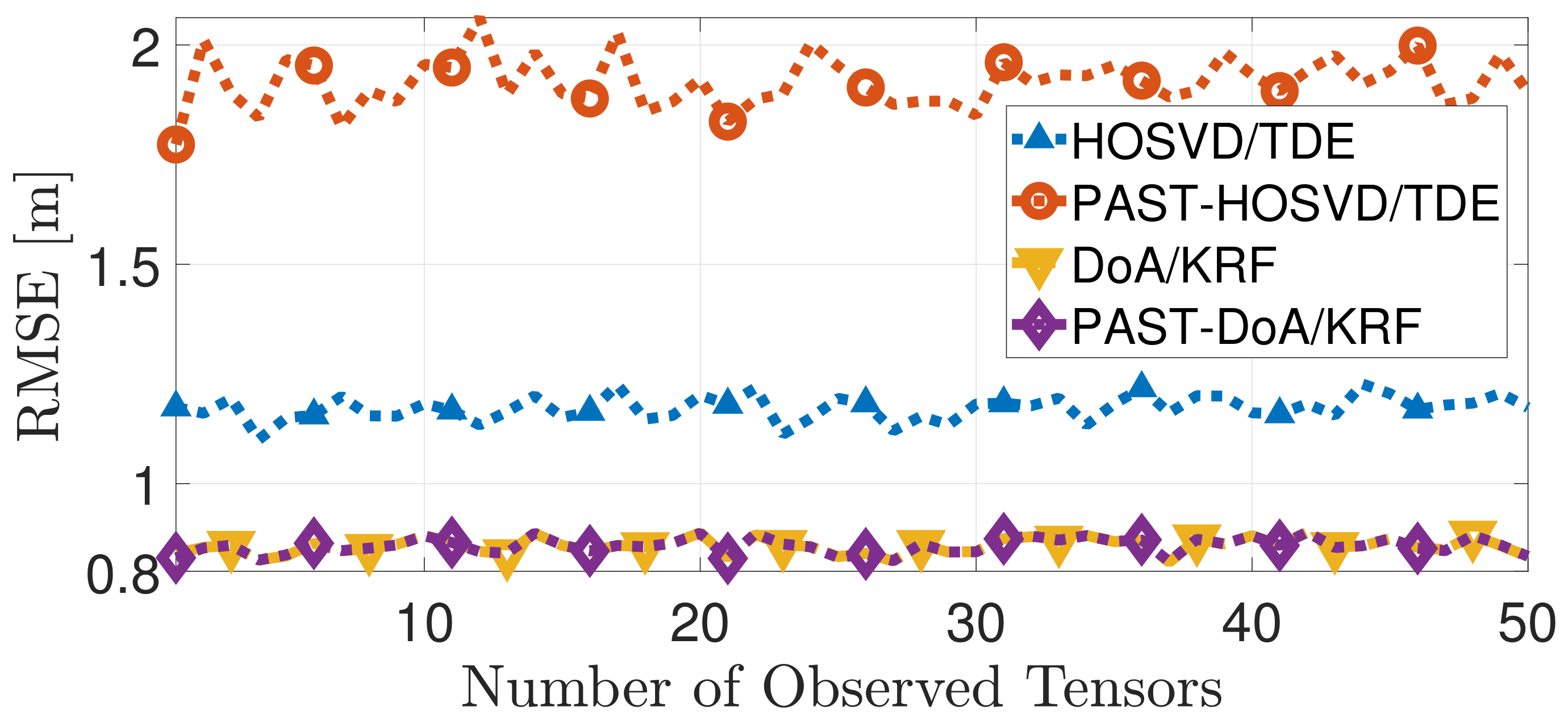
4. Simulations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite Systems |
| LOS | Line of Sight |
| NLOS | non-Line of Sight |
| SVD | Singular Value Decomposition |
| HOSVD | High Order Singular Value Decomposition |
| SCA | Safety-Critical Applications |
| LCA | Liability Critical Applications |
| PARAFAC | Parallel Factor Analysis |
| HOSVD/TDE | High Order Singular Value Decomposition based Time Delay Estimation |
| DOA/KRF | DoA/Khatri-Rao Factorization |
| SECSI | Semi-algebraic framework for approximate Canonical Polyadic Decompositions via |
| Simultaneous Matrix Diagonalizations | |
| CPD-GEVD | Canonical Polyadic Decomposition by Generalized Eigenvalue Decomposition |
| PAST | Projection Approximation Subspace Tracking |
| FAPI | Fast Approximated Power Iteration |
| FDPM | Fast Data Projection Method |
| FBA | Forward-Backward Averaging |
| ESPS | Expanded Spatial Smoothing |
| ESPRIT | Estimation of Signal Parameters via Rotational Invariance Techniques |
| KRF | Khatri-Rao factorization |
| DLR | German Aerospace Center |
| SMR | Signal to Multipath Ratio |
| MC | Monte Carlo |
| LPA | Largest Principal Angle |
Appendix A
| Algorithm A1: DoA/KRF Time-delay estimation [11]. |
|
References
- Teunissen, P.J.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kang, C.; Lee, S.; Chung, C.C. On-Road Vehicle Localization with GPS under Long Term Failure of a Vision Sensor. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015; pp. 1638–1643. [Google Scholar] [CrossRef]
- Uchida, K.; Arai, N.; Moriya, K.; MiYamoto, Y.; Kakihara, T.; Tokai, T. Development of automatic system for monitoring fishing effort in conger-eel tube fishery using radio frequency identification and global positioning system. Fish. Sci. 2005, 71, 992–1002. [Google Scholar] [CrossRef]
- Esau, T.; Zaman, Q.; Groulx, D.; Corscadden, K.; Chang, Y.; Schumann, A.; Havard, P. Economic analysis for smart sprayer application in wild blueberry fields. Precis. Agric. 2016, 17, 753–765. [Google Scholar] [CrossRef]
- Soubielle, J.; Fijalkow, I.; Duvaut, P.; Bibaut, A. GPS positioning in a multipath environment. IEEE Trans. Signal Process. 2002, 50, 141–150. [Google Scholar] [CrossRef]
- Van Nee, R.; Siereveld, J.; Fenton, P.; Townsend, B. The multipath estimating delay lock loop: approaching theoretical accuracy limits. In Proceedings of the 1994 IEEE Position, Location and Navigation Symposium, Las Vegas, NV, USA, 11–15 April 1994; pp. 246–251. [Google Scholar] [CrossRef]
- Pillai, S.; Kwon, B. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Tie-Jun, S.; Wax, M.; Kailath, R.A. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]
- Harshman, R.A. Foundations of the PARAFAC procedure: Models and conditions for an “explanatory” multimodal factor analysis. Ucla Work. Pap. Phon. 1970, 16, 1–84. [Google Scholar]
- Hammoud, B.; Antreich, F.; Nossek, J.A.; Nossek, J.A.; da Costa, J.P.C.L.; de Almeida, A.L.F. Tensor-Based Approach for Time-Delay Estimation. In Proceedings of the 20th International ITG Workshop on Smart Antennas, Munich, Germany, 9–11 March 2016; pp. 1–7. [Google Scholar]
- De Lima, D.V.; da Costa, J.P.C.L.; Antreich, F.; Miranda, R.K.; del Galdo, G. High Resolution Time-Delay Estimation via Direction of Arrival Estimation and Khatri-Rao Factorization for Multipath Mitigation. In Proceedings of the 21th International ITG Workshop on Smart Antennas, Berlin, Germany, 15–17 March 2017; pp. 1–8. [Google Scholar]
- Da Rosa Zanatta, M.; de Mendonça, F.L.L.; Antreich, F.; de Lima, D.V.; Miranda, R.K.; Galdo, G.D.; da Costa, J.P.C.L. Tensor-based time-delay estimation for second and third generation global positioning system. Digit. Signal Process. 2019, 92, 1–19. [Google Scholar] [CrossRef]
- De Lima, D.V.; da Costa, J.P.C.L.; Antreich, F.; Miranda, R.K.; Del Galdo, G. Time-Delay estimation via CPD-GEVD applied to tensor-based GNSS arrays with errors. In Proceedings of the 2017 IEEE 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Curacao, The Netherlands, 10–13 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Nion, D.; Sidiropoulos, N.D. Adaptive Algorithms to Track the PARAFAC Decomposition of a Third-Order Tensor. IEEE Trans. Signal Process. 2009, 57, 2299–2310. [Google Scholar] [CrossRef]
- Owsley, N. Adaptive data orthogonalization. In Proceedings of the IEEE International Conference on Acoustics Speech, and Signal Processing, Tulsa, Oklahoma, USA, 10–12 April 1978; Volume 3, pp. 109–112. [Google Scholar] [CrossRef]
- Karasalo, I. Estimating the covariance matrix by signal subspace averaging. IEEE Trans. Acoust. Speech, Signal Process. 1986, 34, 8–12. [Google Scholar] [CrossRef]
- Yang, B. Projection approximation subspace tracking. IEEE Trans. Signal Process. 1995, 43, 95–107. [Google Scholar] [CrossRef]
- Badeau, R.; David, B.; Richard, G. Fast approximated power iteration subspace tracking. IEEE Trans. Signal Process. 2005, 53, 2931–2941. [Google Scholar] [CrossRef]
- Doukopoulos, X.G.; Moustakides, G.V. The fast Data Projection Method for stable subspace tracking. In Proceedings of the 2005 13th European Signal Processing Conference, Antalya, Turkey, 4–8 September 2005; pp. 1–4. [Google Scholar]
- Doukopoulos, X.G.; Moustakides, G.V. Fast and Stable Subspace Tracking. IEEE Trans. Signal Process. 2008, 56, 1452–1465. [Google Scholar] [CrossRef]
- Roemer, F.; Kasnakli, E.K.; Yao, C.; Haardt, M. Tensor subspace tracking via Kronecker structured projections (TeTraKron). In Proceedings of the 2013 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), St. Martin, France, 15–18 December 2013; pp. 212–215. [Google Scholar] [CrossRef]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.D.; Abed-Meraim, K.; Linh-Trung, N. On Adaptive PARAFAC Decomposition of Three-Way Tensors. hal-01295020. 2016. Available online: https://hal.inria.fr/hal-01295020 (accessed on 20 November 2019).
- Sun, J.; Tao, D.; Papadimitriou, S.; Yu, P.S.; Faloutsos, C. Incremental tensor analysis: Theory and applications. Acm Trans. Knowl. Discov. Data Tkdd 2008, 2, 11. [Google Scholar] [CrossRef]
- Hu, W.; Li, X.; Zhang, X.; Shi, X.; Maybank, S.; Zhang, Z. Incremental tensor subspace learning and its applications to foreground segmentation and tracking. Int. J. Comput. Vis. 2011, 91, 303–327. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Abed-Meraim, K.; Linh-Trung, N. Fast tensor decompositions for big data processing. In Proceedings of the 2016 International Conference on Advanced Technologies for Communications (ATC), Hanoi, Vietnam, 12–14 October 2016; pp. 215–221. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Xiong, J.; Liu, K.; da Costa, J.P.C.L.; Wang, W. Bayesian information criterion for multidimensional sinusoidal order selection. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3106–3110. [Google Scholar] [CrossRef]
- Da Costa, J.P.C.L.; Haardt, M.; Romer, F.; Del Galdo, G. Enhanced Model Order Estimation using Higher-Order Arrays. In Proceedings of the 2007 Conference Record of the Forty-First Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 200; pp. 412–416. [CrossRef]
- Da Costa, J.P.C.L.; Roemer, F.; Haardt, M.; de Sousa, R.T., Jr. Multidimensional model order selection. Eurasip J. Adv. Signal Process. 2011, 2011, 26. [Google Scholar] [CrossRef][Green Version]
- Selva, J. Efficient Multipath Mitigation in Navigation Systems. Ph.D. Thesis, Universitat Politènica de Catalunya – UPC, Barcelona, Spain, 2004. [Google Scholar]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. A Multilinear Singular Value Decomposition. Siam J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef]
- Gomes, P.R.; de Almeida, A.L.; da Costa, J.P.C.; Del Galdo, G. Tensor-based methods for blind spatial signature estimation under arbitrary and unknown source covariance structure. Digit. Signal Process. 2017, 62, 197–210. [Google Scholar] [CrossRef]
- Gomes, P.R.; da Costa, J.P.C.; de Almeida, A.L.; de Sousa, R.T., Jr. Tensor-based multiple denoising via successive spatial smoothing, low-rank approximation and reconstruction for R-D sensor array processing. Digit. Signal Process. 2019, 89, 1–7. [Google Scholar] [CrossRef]
- Cheng, Y.; Roemer, F.; Khatib, O.; Haardt, M. Tensor subspace Tracking via Kronecker structured projections (TeTraKron) for time-varying multidimensional harmonic retrieval. Eurasip J. Adv. Signal Process. 2014, 2014, 123. [Google Scholar] [CrossRef]
- De Lima, D.V.; da Costa, J.P.C.L.; Maranhão, J.P.A.; de Sousa, R.T., Jr. Time-delay estimation via procrustes estimation and Khatri-Rao factorization for GNSS multipath mitigation. In Proceedings of the 2017 11th International Conference on Signal Processing and Communication Systems (ICSPCS), Gold Coast, QLD, Australia, 13–15 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Da Costa, J.P.C.L.; Roemer, F.; Weis, M.; Haardt, M. Robust R-D parameter estimation via closed-form PARAFAC. In Proceedings of the 2010 International ITG Workshop on Smart Antennas (WSA), Bremen, Germany, 23–24 February 201; pp. 99–106. [CrossRef]
- Golub, G.H.G.H.; Van Loan, C.F. Matrix Computations; The Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Cuntz, M.; Konovaltsev, A.; Hornbostel, A.; Neves, E.S.; Dreher, A. GALANT—Galileo Antenna and Receiver Demonstrator for Safety-Critical Applications. In Proceedings of the 2007 European Conference on Wireless Technologies, Munich, Germany, 8–10 October 2007; pp. 59–61. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcez, C.C.R.; de Lima, D.V.; Miranda, R.K.; Mendonça, F.; da Costa, J.P.C.L.; de Almeida, A.L.F.; de Sousa, R.T., Jr. Tensor-Based Subspace Tracking for Time-Delay Estimation in GNSS Multi-Antenna Receivers. Sensors 2019, 19, 5076. https://doi.org/10.3390/s19235076
Garcez CCR, de Lima DV, Miranda RK, Mendonça F, da Costa JPCL, de Almeida ALF, de Sousa RT Jr. Tensor-Based Subspace Tracking for Time-Delay Estimation in GNSS Multi-Antenna Receivers. Sensors. 2019; 19(23):5076. https://doi.org/10.3390/s19235076
Chicago/Turabian StyleGarcez, Caio C. R., Daniel Valle de Lima, Ricardo Kehrle Miranda, Fábio Mendonça, João Paulo C. L. da Costa, André L. F. de Almeida, and Rafael T. de Sousa, Jr. 2019. "Tensor-Based Subspace Tracking for Time-Delay Estimation in GNSS Multi-Antenna Receivers" Sensors 19, no. 23: 5076. https://doi.org/10.3390/s19235076
APA StyleGarcez, C. C. R., de Lima, D. V., Miranda, R. K., Mendonça, F., da Costa, J. P. C. L., de Almeida, A. L. F., & de Sousa, R. T., Jr. (2019). Tensor-Based Subspace Tracking for Time-Delay Estimation in GNSS Multi-Antenna Receivers. Sensors, 19(23), 5076. https://doi.org/10.3390/s19235076






