Vision-Based Multirotor Following Using Synthetic Learning Techniques
Abstract
1. Introduction
2. Contribution
- A robust detection technique was trained with a novel approach based on synthetic photorealistic images generated by a commercial game engine. The synthetic multirotor image dataset, utilized in this work for detector training, was also released as an open-source dataset.
- Problem formulation under the reinforcement-learning framework was designed in order to achieve learning convergence for a motion-control agent with a state-of-the-art deep reinforcement-learning algorithm and within the context of high-dimensional continuous state and action spaces. The agent was trained in a simulated environment and tested in real-flight experiments (refer to Figure 1).
- A novel motion-control strategy for object following is introduced where camera gimbal movement is coupled with multirotor motion during multirotor following.
3. Related Work
3.1. Autonomous Aerial Pursuit
3.2. Monocular Vision-Based Object Following
3.3. Reinforcement Learning for Real-World Robotics
3.4. Multirotor In-Flight Detection and Tracking
3.5. Object Detection with Synthetic Images
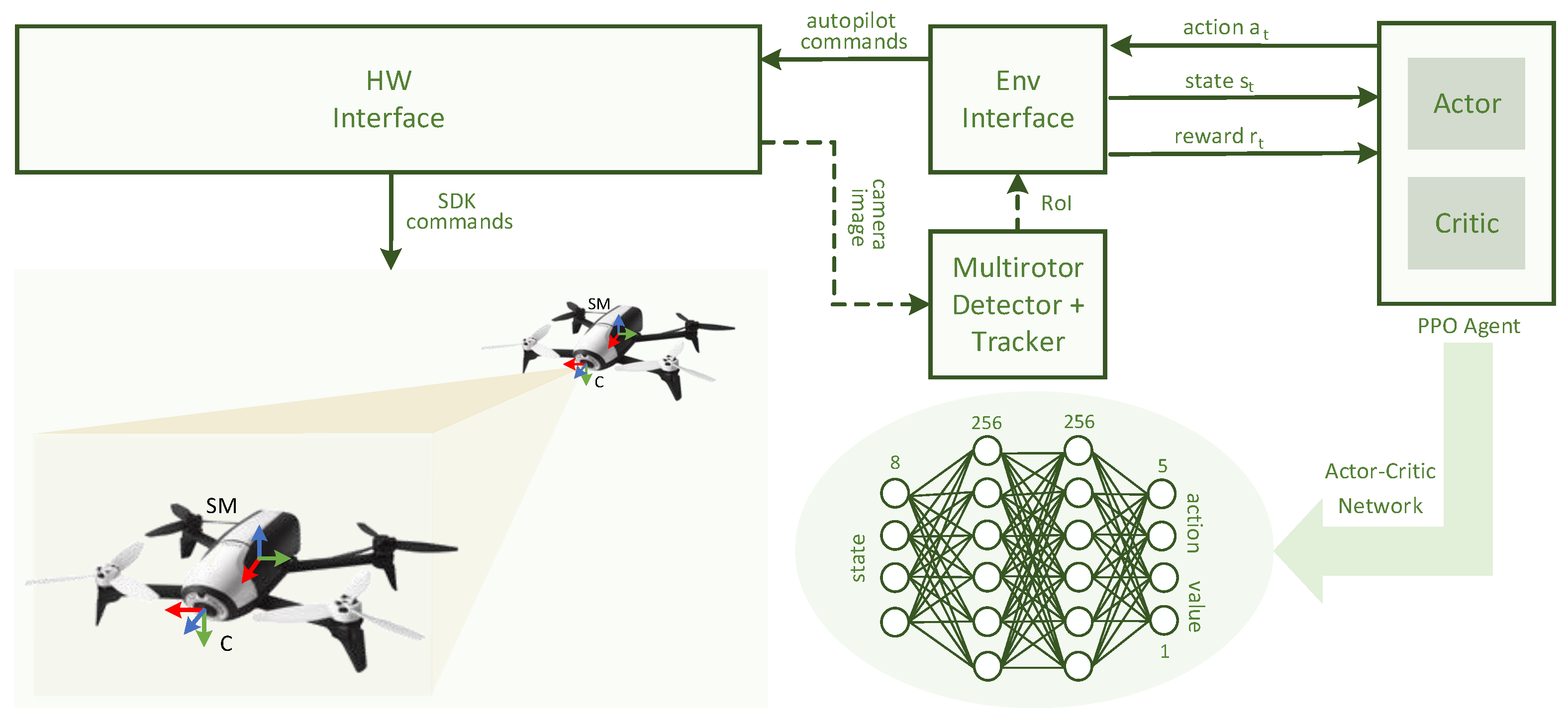
4. Vision-Based Multirotor Following Approach
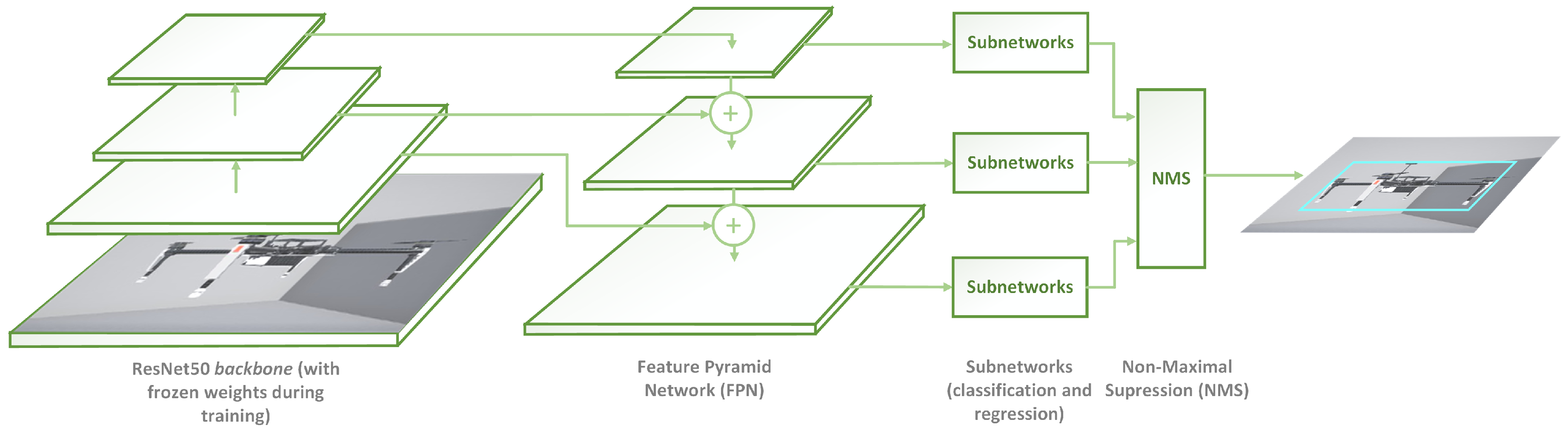
4.1. Multirotor Detector
4.2. Image-Based Tracker
4.3. Motion-Control Policy
4.3.1. Problem Formulation
4.3.2. System and Network Architecture
5. Experiments
5.1. Experiment Setup
5.1.1. Simulation
5.1.2. Real Flight
5.2. Training Methodology
5.2.1. Multirotor Detector
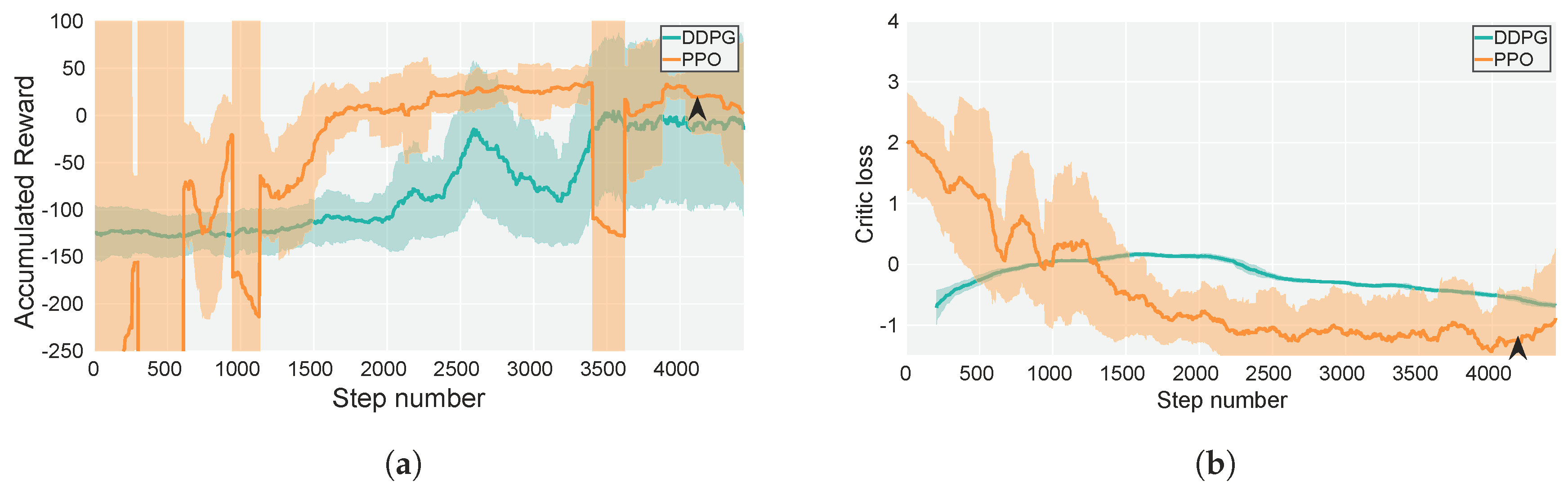
5.2.2. Motion-Control Policy
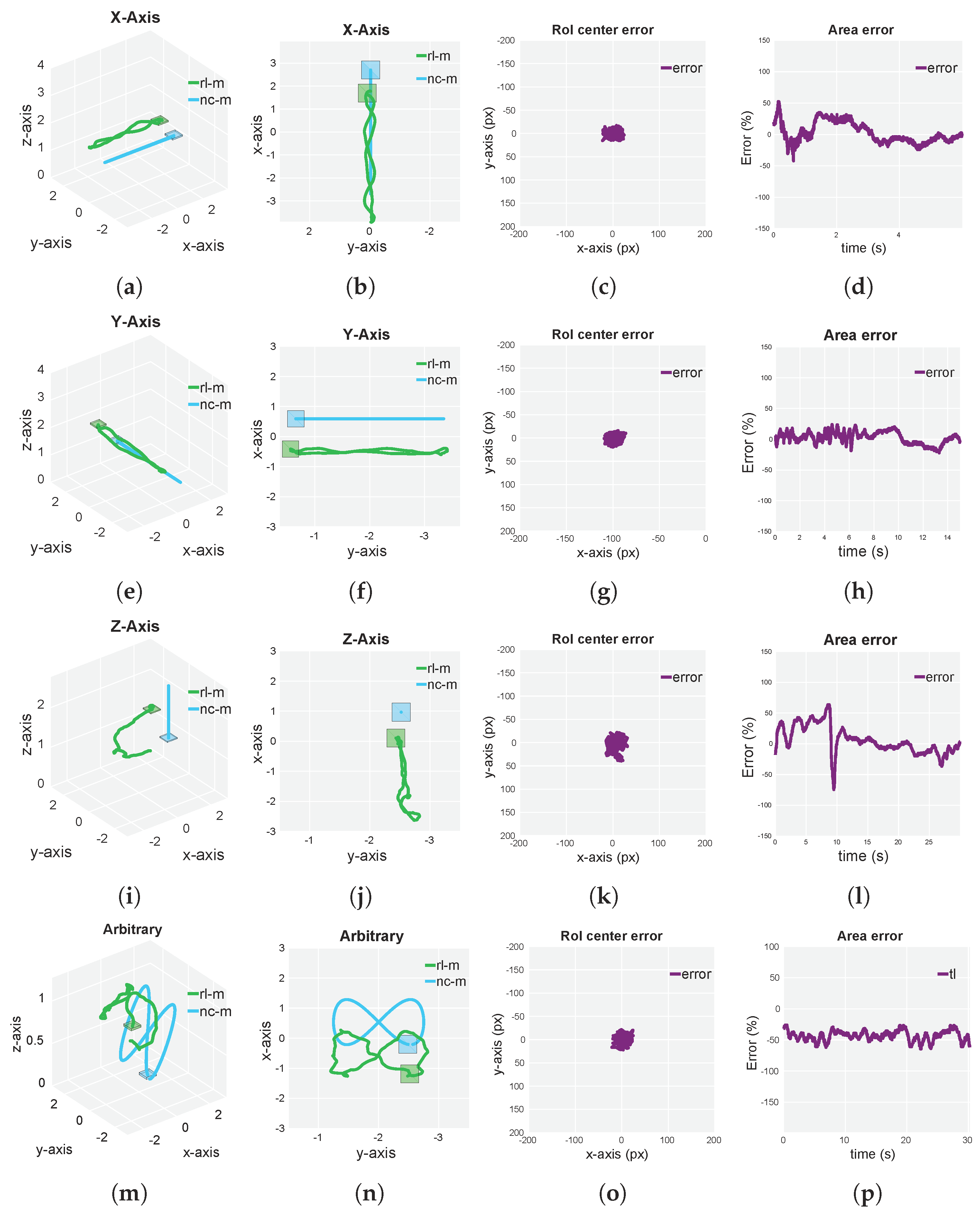
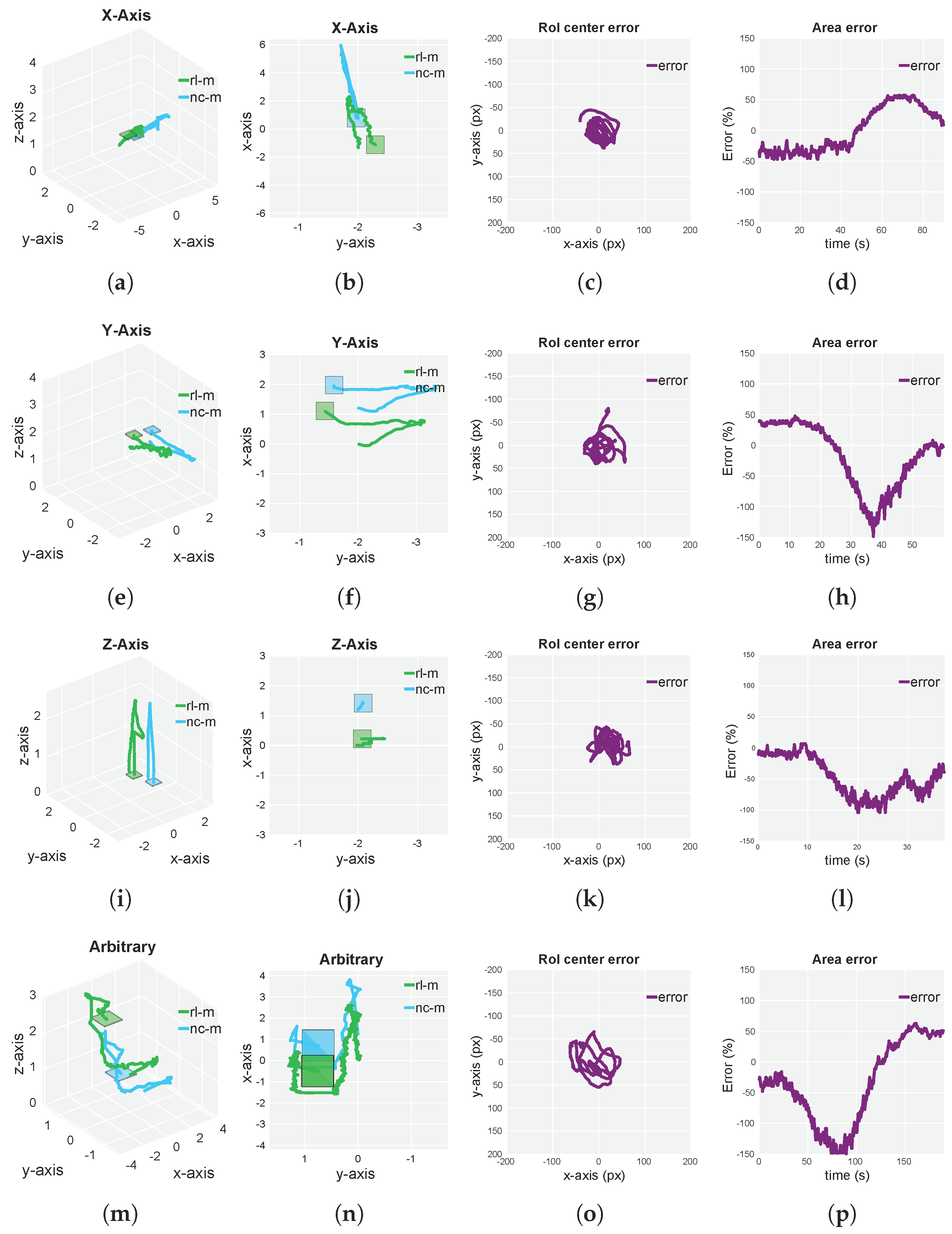
5.3. Simulated and Real-Flight Experiments
6. Discussion
7. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| UPM | Universidad Politécnica de Madrid |
| CSIC | Consejo Superior de Investigaciones Científicas |
| DOF | Degrees Of Freedom |
| FC | Flight Controller |
| RGB | Red Green Blue |
| UAV | Unmanned Aerial Vehicle |
| PID | Proportional Integral Derivative |
| RoI | Region of Interest |
| HOG | Histogram Of Gradients |
| LBP | Local Binary Patterns |
| CAD | Computer-Aided Design |
| CNN | Convolutional Neural Network |
| NC-M | Noncooperative Multirotor |
| RL-M | Reinforcement-Learning-based Multirotor |
| FPN | Feature Pyramid Network |
| FL | Focal Loss |
| DCF | Discriminative Correlation Filter |
| DDPG | Deep Deterministic Policy Gradients |
| TRPO | Trust-Region Policy Optimization |
| PPO | Proximal Policy Optimization |
| FOV | Field Of View |
| ROS | Robotic Operating System |
| COCO | Common Objects in COntext |
| AP | Average Precision |
| EKF | Extended Kalman Filter |
References
- Tan, J.; Zhang, T.; Coumans, E.; Iscen, A.; Bai, Y.; Hafner, D.; Bohez, S.; Vanhoucke, V. Sim-to-real: Learning agile locomotion for quadruped robots. arXiv 2018, arXiv:1804.10332. [Google Scholar]
- Rodriguez-Ramos, A.; Sampedro, C.; Bavle, H.; Moreno, I.G.; Campoy, P. A Deep Reinforcement Learning Technique for Vision-Based Autonomous Multirotor Landing on a Moving Platform. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1010–1017. [Google Scholar]
- Hwangbo, J.; Sa, I.; Siegwart, R.; Hutter, M. Control of a quadrotor with reinforcement learning. IEEE Robot. Autom. Lett. 2017, 2, 2096–2103. [Google Scholar] [CrossRef]
- Rozantsev, A.; Lepetit, V.; Fua, P. On rendering synthetic images for training an object detector. Comput. Vis. Image Underst. 2015, 137, 24–37. [Google Scholar] [CrossRef]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Chen, Y.; Li, W.; Sakaridis, C.; Dai, D.; Van Gool, L. Domain adaptive faster r-cnn for object detection in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake, UT, USA, 18–22 June 2018; pp. 3339–3348. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Tai, L.; Yun, P.; Xiong, Y.; Liu, M.; Boedecker, J.; Burgard, W. Vr-goggles for robots: Real-to-sim domain adaptation for visual control. IEEE Robot. Autom. Lett. 2019, 4, 1148–1155. [Google Scholar] [CrossRef]
- Rozantsev, A.; Lepetit, V.; Fua, P. Detecting flying objects using a single moving camera. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 879–892. [Google Scholar] [CrossRef]
- Li, J.; Ye, D.H.; Chung, T.; Kolsch, M.; Wachs, J.; Bouman, C. Multi-target detection and tracking from a single camera in Unmanned Aerial Vehicles (UAVs). In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Deajeon, Korea, 9–14 October 2016; pp. 4992–4997. [Google Scholar]
- Opromolla, R.; Fasano, G.; Accardo, D. A Vision-Based Approach to UAV Detection and Tracking in Cooperative Applications. Sensors 2018, 18, 3391. [Google Scholar] [CrossRef]
- Zengin, U.; Dogan, A. Cooperative target pursuit by multiple UAVs in an adversarial environment. Robot. Autonom. Syst. 2011, 59, 1049–1059. [Google Scholar] [CrossRef]
- Yamasaki, T.; Balakrishnan, S. Sliding mode based pure pursuit guidance for UAV rendezvous and chase with a cooperative aircraft. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010. [Google Scholar]
- Alexopoulos, A.; Schmidt, T.; Badreddin, E. Cooperative pursue in pursuit-evasion games with unmanned aerial vehicles. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015. [Google Scholar]
- Ma, L.; Hovakimyan, N. Vision-based cyclic pursuit for cooperative target tracking. J. Guid. Control Dyn. 2013, 36, 617–622. [Google Scholar] [CrossRef]
- Yamasaki, T.; Enomoto, K.; Takano, H.; Baba, Y.; Balakrishnan, S. Advanced pure pursuit guidance via sliding mode approach for chase UAV. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10 August–13 August 2009. [Google Scholar]
- Pestana, J.; Sanchez-Lopez, J.; Saripalli, S.; Campoy, P. Computer vision based general object following for gps-denied multirotor unmanned vehicles. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014. [Google Scholar]
- Teuliere, C.; Eck, L.; Marchand, E. Chasing a moving target from a flying UAV. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Choi, H.; Kim, Y. UAV guidance using a monocular-vision sensor for aerial target tracking. Control Eng. Pract. 2014, 22, 10–19. [Google Scholar] [CrossRef]
- Li, R.; Pang, M.; Zhao, C.; Zhou, G.; Fang, L. Monocular long-term target following on uavs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 29–37. [Google Scholar]
- Mueller, M.; Sharma, G.; Smith, N.; Ghanem, B. Persistent aerial tracking system for uavs. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Deajeon, Korea, 9–14 October 2016; pp. 1562–1569. [Google Scholar]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-learning-detection. Pattern Anal. Mach. Intell. 2011, 34, 1409–1422. [Google Scholar] [CrossRef] [PubMed]
- Hare, S.; Golodetz, S.; Saffari, A.; Vineet, V.; Cheng, M.M.; Hicks, S.L.; Torr, P.H. Struck: Structured output tracking with kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2096–2109. [Google Scholar] [CrossRef] [PubMed]
- Kassab, M.A.; Maher, A.; Elkazzaz, F.; Baochang, Z. UAV Target Tracking By Detection via Deep Neural Networks. In Proceedings of the 2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; pp. 139–144. [Google Scholar]
- Maher, A.; Taha, H.; Zhang, B. Realtime multi-aircraft tracking in aerial scene with deep orientation network. J. Real-Time Image Process. 2018, 15, 495–507. [Google Scholar] [CrossRef]
- Yao, N.; Anaya, E.; Tao, Q.; Cho, S.; Zheng, H.; Zhang, F. Monocular vision-based human following on miniature robotic blimp. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3244–3249. [Google Scholar]
- Nägeli, T.; Oberholzer, S.; Plüss, S.; Alonso-Mora, J.; Hilliges, O. Flycon: Real-Time Environment-Independent Multi-View Human Pose Estimation with Aerial Vehicles. In Proceedings of the SIGGRAPH Asia 2018 Technical, Tokio, Japan, 4–7 December 2018; p. 182. [Google Scholar]
- Rafi, F.; Khan, S.; Shafiq, K.; Shah, M. Autonomous target following by unmanned aerial vehicles. In Proceedings of the Unmanned Systems Technology VIII. International Society for Optics and Photonics, San Jose, CA, USA, 20–21 January 2006. [Google Scholar]
- Qadir, A.; Neubert, J.; Semke, W.; Schultz, R. On-Board Visual Trackingwith Unmanned Aircraft System (UAS); American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. [Google Scholar]
- Andrychowicz, M.; Baker, B.; Chociej, M.; Jozefowicz, R.; McGrew, B.; Pachocki, J.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning Dexterous in-Hand Manipulation. arXiv 2018, arXiv:1808.00177. [Google Scholar]
- James, S.; Wohlhart, P.; Kalakrishnan, M.; Kalashnikov, D.; Irpan, A.; Ibarz, J.; Levine, S.; Hadsell, R.; Bousmalis, K. Sim-to-Real via Sim-to-Sim: Data-efficient Robotic Grasping via Randomized-to-Canonical Adaptation Networks. arXiv 2018, arXiv:1812.07252. [Google Scholar]
- Sampedro, C.; Rodriguez-Ramos, A.; Gil, I.; Mejias, L.; Campoy, P. Image-Based Visual Servoing Controller for Multirotor Aerial Robots Using Deep Reinforcement Learning. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 979–986. [Google Scholar]
- Kang, K.; Belkhale, S.; Kahn, G.; Abbeel, P.; Levine, S. Generalization through simulation: Integrating simulated and real data into deep reinforcement learning for vision-based autonomous flight. arXiv 2019, arXiv:1902.03701. [Google Scholar]
- Sadeghi, F.; Levine, S. CAD2RL: Real single-image flight without a single real image. arXiv 2016, arXiv:1611.04201. [Google Scholar]
- Wang, F.; Zhou, B.; Chen, K.; Fan, T.; Zhang, X.; Li, J.; Tian, H.; Pan, J. Intervention Aided Reinforcement Learning for Safe and Practical Policy Optimization in Navigation. arXiv 2018, arXiv:1811.06187. [Google Scholar]
- Gökçe, F.; Üçoluk, G.; Şahin, E.; Kalkan, S. Vision-based detection and distance estimation of micro unmanned aerial vehicles. Sensors 2015, 15, 23805–23846. [Google Scholar] [CrossRef]
- Fu, C.; Duan, R.; Kircali, D.; Kayacan, E. Onboard robust visual tracking for UAVs using a reliable global-local object model. Sensors 2016, 16, 1406. [Google Scholar] [CrossRef] [PubMed]
- Hinterstoisser, S.; Lepetit, V.; Wohlhart, P.; Konolige, K. On pre-trained image features and synthetic images for deep learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Peng, X.; Sun, B.; Ali, K.; Saenko, K. Learning deep object detectors from 3d models. In Proceedings of the IEEE International Conference on Computer Vision, Las Condes, Chile, 11–18 December 2015. [Google Scholar]
- Shrivastava, A.; Pfister, T.; Tuzel, O.; Susskind, J.; Wang, W.; Webb, R. Learning from simulated and unsupervised images through adversarial training. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Tremblay, J.; Prakash, A.; Acuna, D.; Brophy, M.; Jampani, V.; Anil, C.; To, T.; Cameracci, E.; Boochoon, S.; Birchfield, S. Training deep networks with synthetic data: Bridging the reality gap by domain randomization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–23 June 2018; pp. 969–977. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 379–387. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venezia, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Alabachi, S.; Sukthankar, G.; Sukthankar, R. Customizing Object Detectors for Indoor Robots. arXiv 2019, arXiv:1902.10671. [Google Scholar]
- Lin, T.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venezia, Italy, 22–29 October 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Danelljan, M.; Bhat, G.; Shahbaz Khan, F.; Felsberg, M. Eco: Efficient convolution operators for tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.I.; Moritz, P. Trust Region Policy Optimization. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Andrychowicz, M.; Wolski, F.; Ray, A.; Schneider, J.; Fong, R.; Welinder, P.; McGrew, B.; Tobin, J.; Abbeel, O.P.; Zaremba, W. Hindsight experience replay. In Proceedings of the Advances in Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; pp. 5048–5058. [Google Scholar]
- Dorigo, M.; Colombetti, M. Robot Shaping: An Experiment in Behavior Engineering; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Furrer, F.; Burri, M.; Achtelik, M.; Siegwart, R. Rotors—A modular gazebo mav simulator framework. In Robot Operating System (ROS); Springer: Cham, Switzerland, 2016. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]


| Training | Validation | Training | Validation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (only NC-M) | (only NC-M) | (full) | (full) | |||||||||
| Epoch | AP | AP | AP | AP | AP | AP | AP | AP | AP | AP | AP | AP |
| 0 | 0.73 | 0.98 | 0.54 | 0.24 | 0.35 | 0.30 | 0.30 | 0.58 | 0.54 | 0.59 | 0.73 | 0.69 |
| 1 | 0.91 | 0.99 | 0.99 | 0.25 | 0.35 | 0.31 | 0.69 | 0.83 | 0.76 | 0.73 | 0.96 | 0.85 |
| 2 | 0.92 | 0.99 | 0.99 | 0.63 | 0.93 | 0.70 | 0.76 | 0.88 | 0.83 | 0.75 | 0.96 | 0.87 |
| 3 | 0.94 | 0.99 | 0.99 | 0.61 | 0.92 | 0.70 | 0.76 | 0.88 | 0.83 | 0.73 | 0.95 | 0.85 |
| 4 | 0.93 | 0.99 | 0.99 | 0.64 | 0.93 | 0.75 | 0.85 | 0.95 | 0.92 | 0.75 | 0.97 | 0.89 |
| 5 | 0.95 | 0.99 | 0.99 | 0.61 | 0.89 | 0.69 | 0.95 | 0.99 | 0.98 | 0.74 | 0.95 | 0.87 |
| 6 | 0.95 | 0.99 | 0.99 | 0.60 | 0.89 | 0.68 | 0.95 | 0.98 | 0.98 | 0.73 | 0.96 | 0.88 |
| Simulation | Real Flights | |||||
|---|---|---|---|---|---|---|
| Experiment | Center error (px) | Center error (px) | ||||
| scenario | Avg | Max | Min | Avg | Max | Min |
| X-axis | 5.79 | 24 | 0 | 15.15 | 44 | 0 |
| Y-axis | 5.72 | 27 | 0 | 22.35 | 80 | 0 |
| Z-axis | 7.58 | 39 | 0 | 20.31 | 66 | 0 |
| Arbitrary | 5.7 | 24 | 0 | 26.71 | 65 | 0 |
| Experiment | Area error (%) | Area error (%) | ||||
| scenario | Avg | Max | Min | Avg | Max | Min |
| X-axis | 13.61 | 52.51 | 0.16 | 33.59 | 57.38 | 0 |
| Y-axis | 8.59 | 24.10 | 0.16 | 44.02 | 148 | 0 |
| Z-axis | 17.41 | 74.51 | 0 | 47.12 | 104 | 0 |
| Arbitrary | 10.94 | 47.56 | 0 | 63.99 | 162.8 | 0.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Ramos, A.; Alvarez-Fernandez, A.; Bavle, H.; Campoy, P.; How, J.P. Vision-Based Multirotor Following Using Synthetic Learning Techniques. Sensors 2019, 19, 4794. https://doi.org/10.3390/s19214794
Rodriguez-Ramos A, Alvarez-Fernandez A, Bavle H, Campoy P, How JP. Vision-Based Multirotor Following Using Synthetic Learning Techniques. Sensors. 2019; 19(21):4794. https://doi.org/10.3390/s19214794
Chicago/Turabian StyleRodriguez-Ramos, Alejandro, Adrian Alvarez-Fernandez, Hriday Bavle, Pascual Campoy, and Jonathan P. How. 2019. "Vision-Based Multirotor Following Using Synthetic Learning Techniques" Sensors 19, no. 21: 4794. https://doi.org/10.3390/s19214794
APA StyleRodriguez-Ramos, A., Alvarez-Fernandez, A., Bavle, H., Campoy, P., & How, J. P. (2019). Vision-Based Multirotor Following Using Synthetic Learning Techniques. Sensors, 19(21), 4794. https://doi.org/10.3390/s19214794







