Three-Point Inverse and Forward Kinematic Algorithms for Circle Measurement from Distributed Displacement Sensor Network
Abstract
1. Introduction
2. Materials and Methods
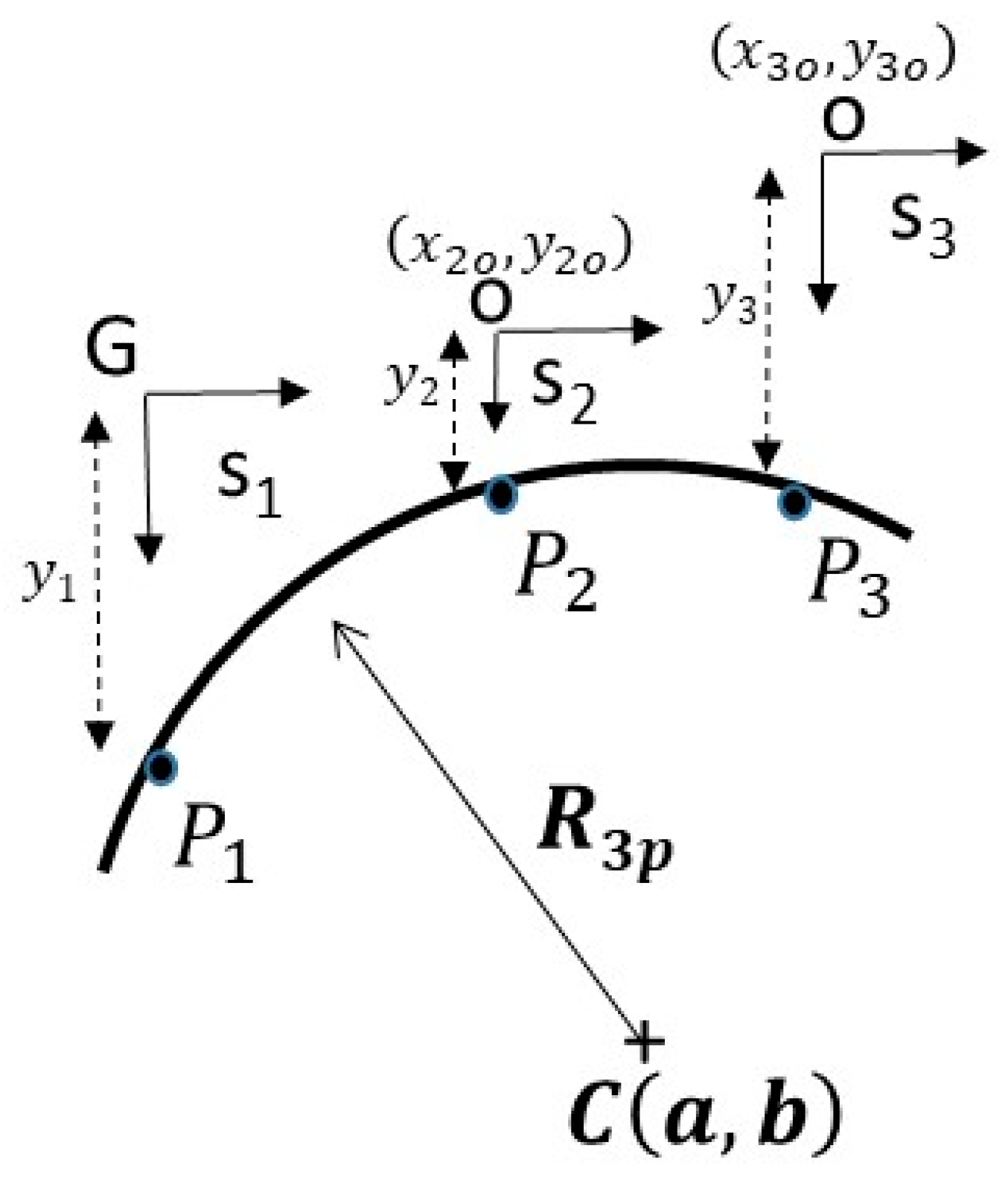
- Three-point inverse kinematic algorithm (TPIK): a calibration procedure that references the local coordinates of each sensor into one global coordinate system (G). This produces system parameters whose values are based on a numerical solution of mixed non-linear equations. Further discussion to follow in Section 2.2.
- Three-point forward kinematic algorithm (TPFK): a closed form solution that algebraically fits the transformed data points through the circumference of a circle. Further discussion to follow in Section 2.1.
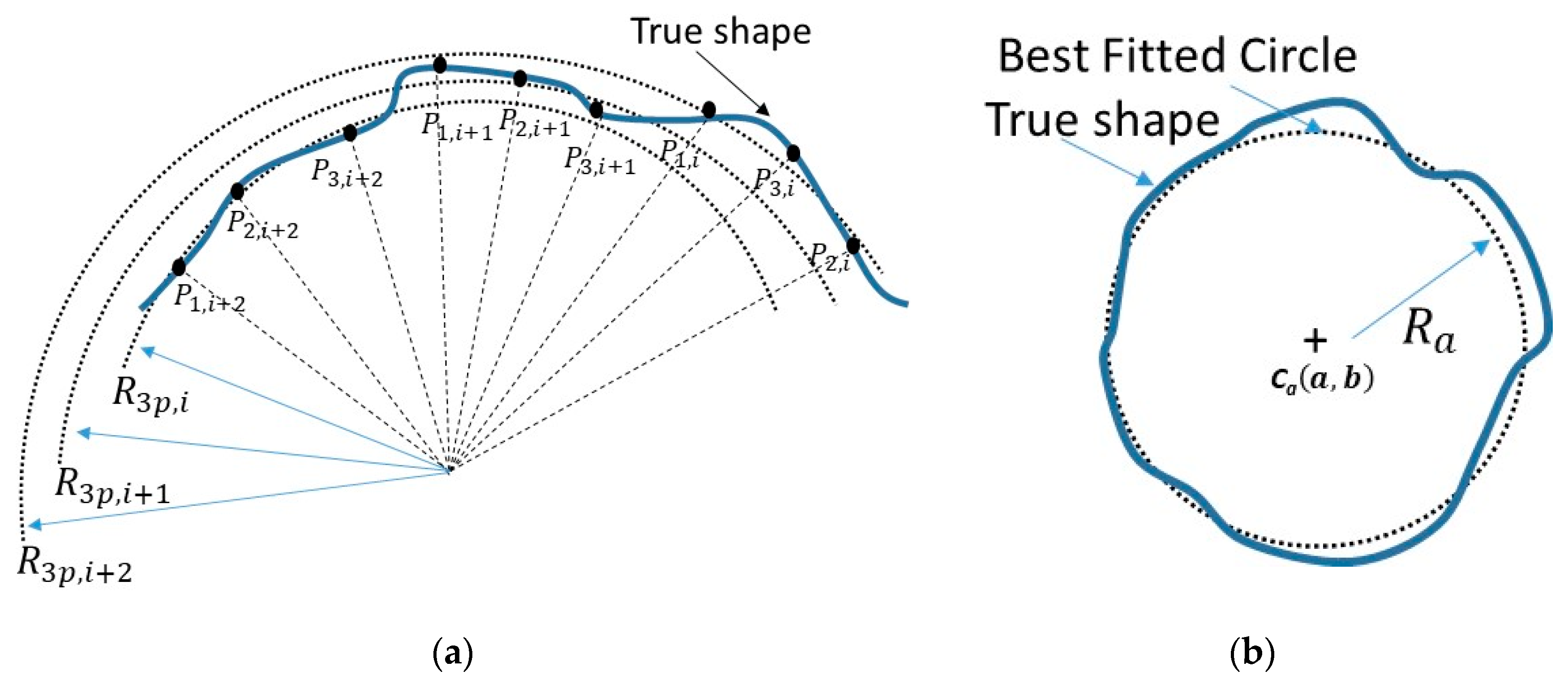
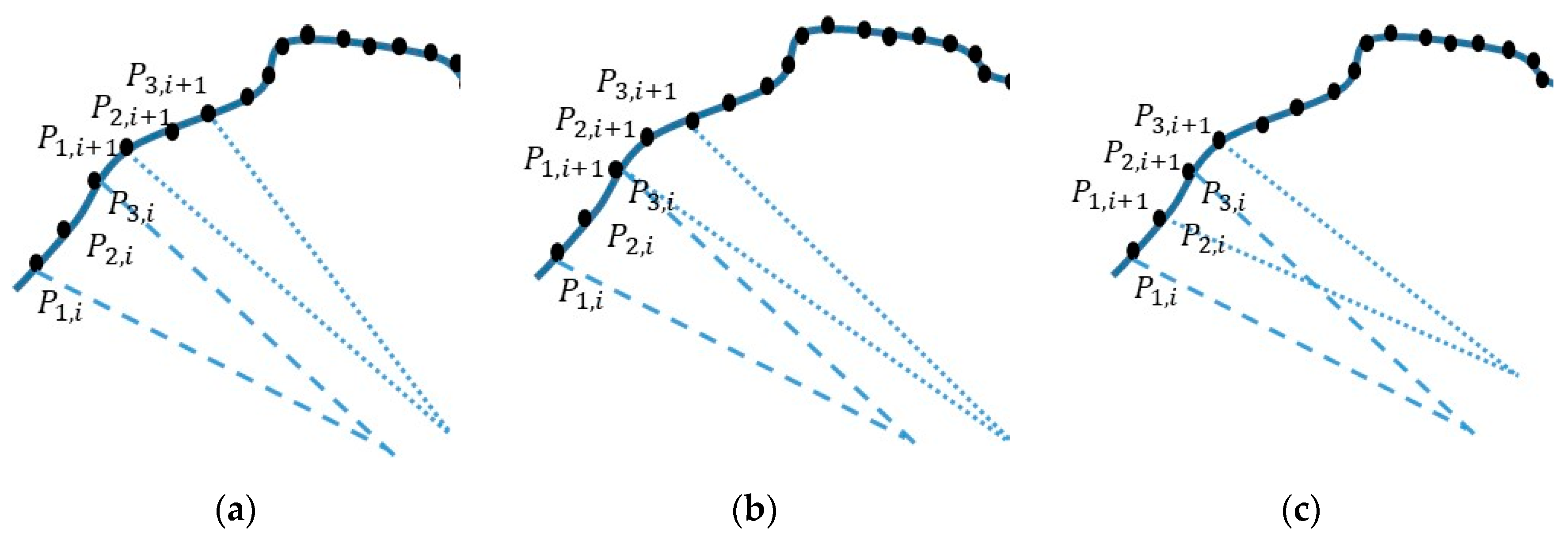
2.1. Three-Point Forward Kinematics (TPFK) Algorithm—Recovery of Circle Geometry
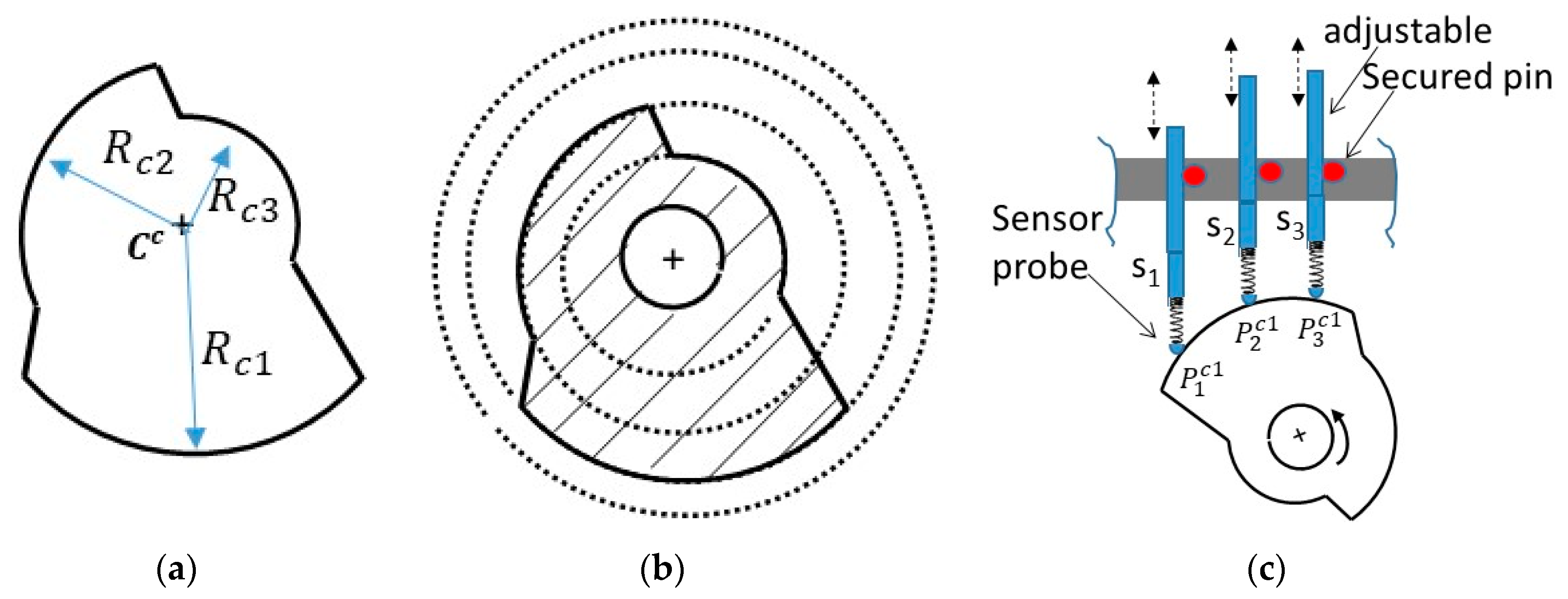
2.2. Three-Point Inverse Kinematics (TPIK) Algorithm—Calibration Procedures
2.3. Roundness Index Based on TPIK and TPFK Algorithms
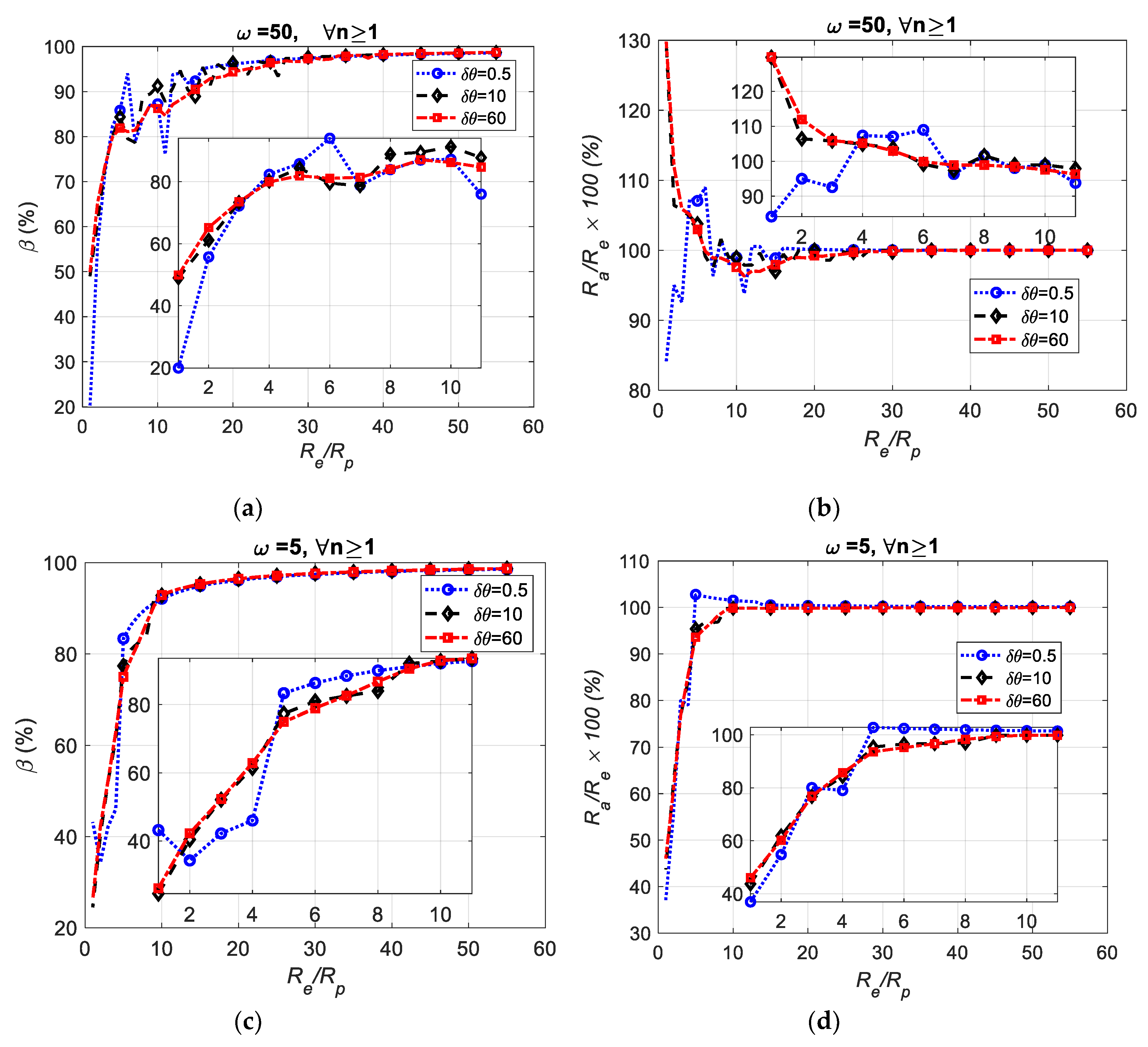
3. Results and Discussion
3.1. Validation of the TPIK Algorithm by Mathematical Simulation
3.2. Validation of the TPFK Algorithm by Mathematical Simulation
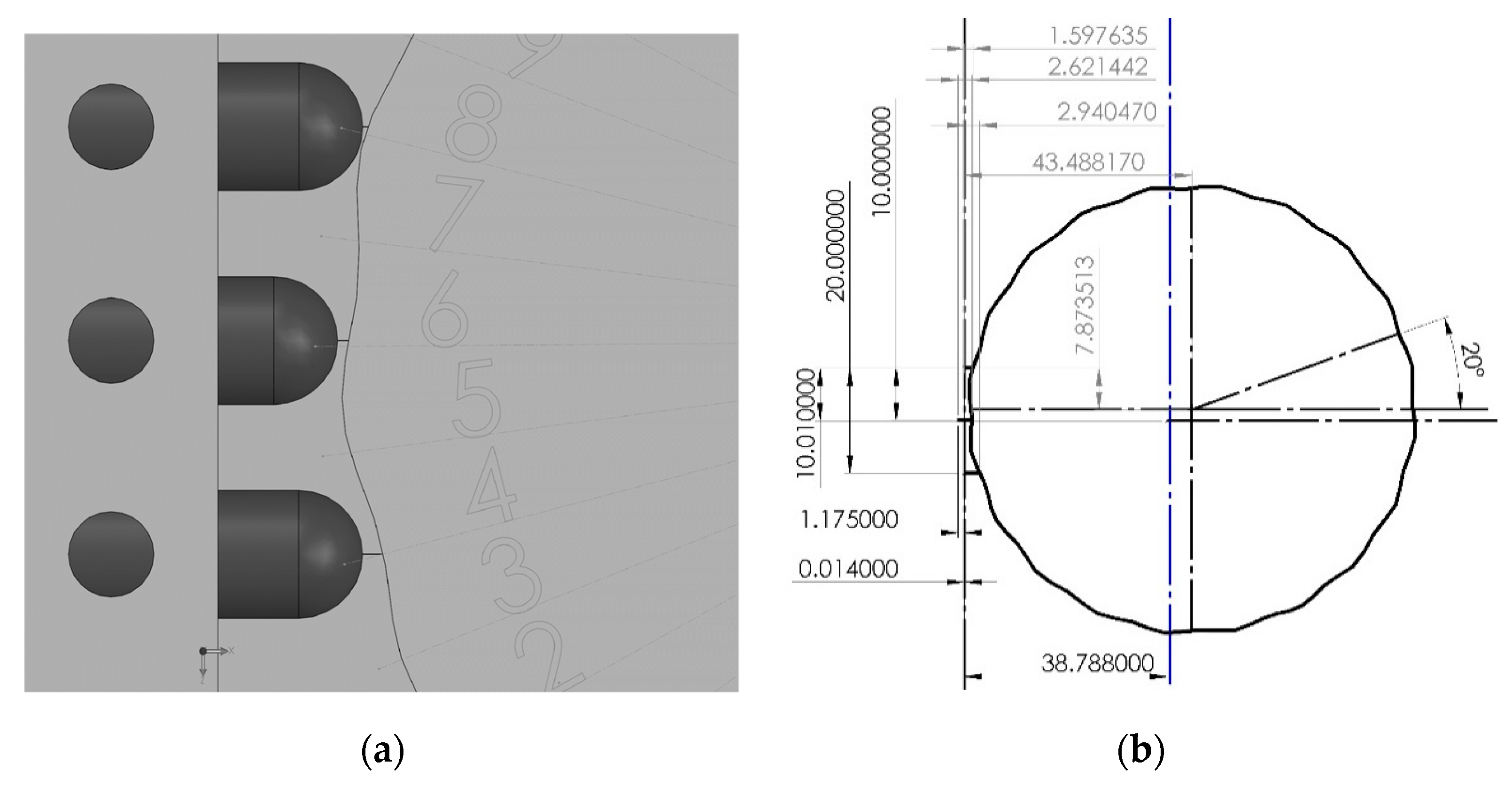
3.3. Validation of the TPIK Algorithm by CAD Simulation
3.4. Validation of the TPFK Algorithm by CAD Simulation
3.5. Study of the Roundness Index Based on the Mathematical Model
3.6. Study of Roundness Index Based on CAD Model
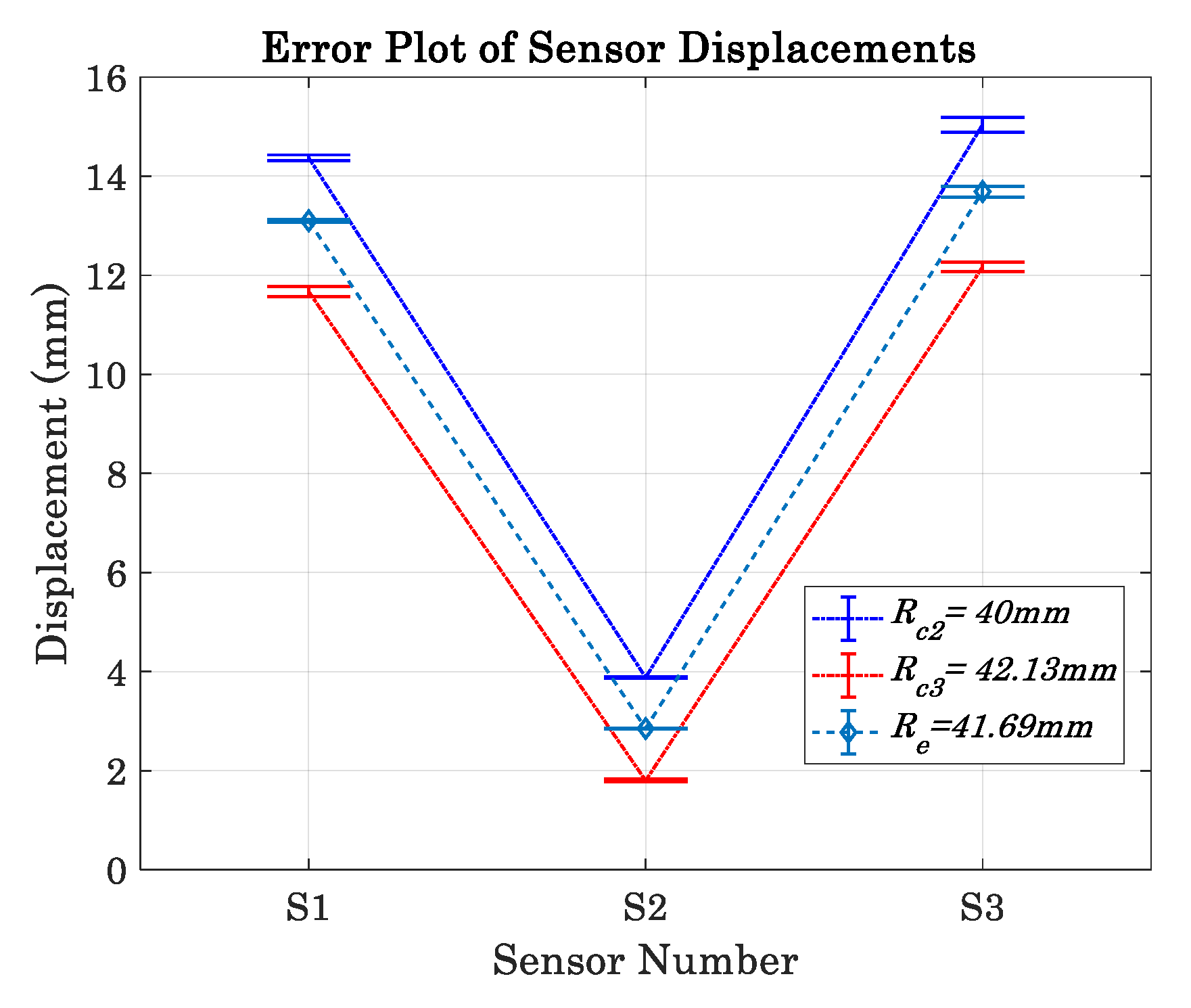
3.7. Validation of the TPIK and TPFK Algorithms Based on the Empirical Study
4. Conclusions and Future Work
Funding
Acknowledgments
Conflicts of Interest
References
- Umbach, D.; Jones, K.N. A few methods for fitting circles to data. IEEE Trans. Instrum. Measure. 2003, 52, 1881–1885. [Google Scholar] [CrossRef]
- Safaee-Rad, R.; Tchoukanov, I.; Smith, K.C.; Benhabib, B. Three-dimensional location estimation of circular features for machine vision. IEEE Trans. Robot. Autom. 1992, 8, 624–640. [Google Scholar] [CrossRef]
- Traband, M.T.; Medeiros, D.J.; Chandra, M.J. A statistical approach to tolerance evaluation for circles and cylinders. IIE Trans. (Inst. Ind. Eng.) 2004, 36, 777–785. [Google Scholar] [CrossRef]
- Landau, U.M. Estimation of a circular arc center and its radius. Comput. Vis. Gr. Image Process. 1987, 38, 317–326. [Google Scholar] [CrossRef]
- Thomas, S.M.; Chan, Y.-T. A simple approach for the estimation of circular arc center and its radius. Comput. Vis. Gr. Image Process. 1989, 45, 362–370. [Google Scholar] [CrossRef]
- Thom, A. A statistical examination of the megalithic sites in Britain. J. R. Stat. Soc. Ser. A 1955, 118, 275–295. [Google Scholar] [CrossRef]
- Robinson, S.M. Fitting spheres by the method of least squares. Commun. ACM 1961, 4, 491. [Google Scholar] [CrossRef]
- Lin, S.; Jusko, O.; Härtig, F.; Seewig, J. A least squares algorithm for fitting data points to a circular arc cam. Measurement 2017, 102, 170–178. [Google Scholar] [CrossRef]
- Hopp, T.H. Computational metrology. Manuf. Rev. 1993, 6, 295. [Google Scholar]
- Schwenke, H.; Knapp, W.; Haitjema, H.; Weckenmann, A.; Schmitt, R.; Delbressine, F. Geometric error measurement and compensation of machines—an update. CIRP Annals. 2008, 57, 660–675. [Google Scholar] [CrossRef]
- Phillips, S.D.; Borchardt, B.; Abackerli, A.J.; Shakarji, C.; Sawyer, D.; Murray, P.; Rasnick, B.; Summerhays, K.D.; Baldwin, J.M.; Henke, R.P.; et al. The validation of CMM task specific measurement uncertainty software. In Proceedings of the ASPE 2003 Summer Topical Meeting “Coordinate Measuring Machines”, Charlotte, NC, USA, 25–26 June 2003; pp. 25–26. [Google Scholar]
- Pegna, J.; Guo, C. Computational metrology of the circle. In Proceedings of the Computer Graphics International (Cat. No. 98EX149), Hannover, Germany, 26–26 June 1998; pp. 350–363. [Google Scholar]
- Rusu, C.; Tico, M.; Kuosmanen, P.; Delp, E.J. Classical geometrical approach to circle fitting—Review and new developments. J. Electron. Imaging 2003, 12, 179–194. [Google Scholar]
- De Guevara, I.L.; Muñoz, J.; De Cózar, O.D.; Blázquez, E.B. Robust fitting of circle arcs. J. Math. Imaging Vis. 2011, 40, 147–161. [Google Scholar] [CrossRef]
- Brandon, J.A.; Cowley, A. A weighted least squares method for circle fitting to frequency response data. J. Sound Vib. 1983, 89, 419–424. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Raja, J. Computational Surface and Roundness Metrology; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Zelniker, E.E.; Clarkson, I.V.L. A statistical analysis of the Delogne—Kåsa method for fitting circles. Digit. Signal Process. 2006, 16, 498–522. [Google Scholar] [CrossRef]
- Hopp, T.H. The Sensitivity of Three-Point Circle Fitting; NIST Report NISTIR-5501; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994. [Google Scholar]
- MathWorks. Matlab. 2019. Available online: https://www.MathWorks.com (accessed on 1 April 2019).
- SolidWorks. SolidWorks. 2019. Available online: https://www.SolidWorks.com (accessed on 13 March 2019).
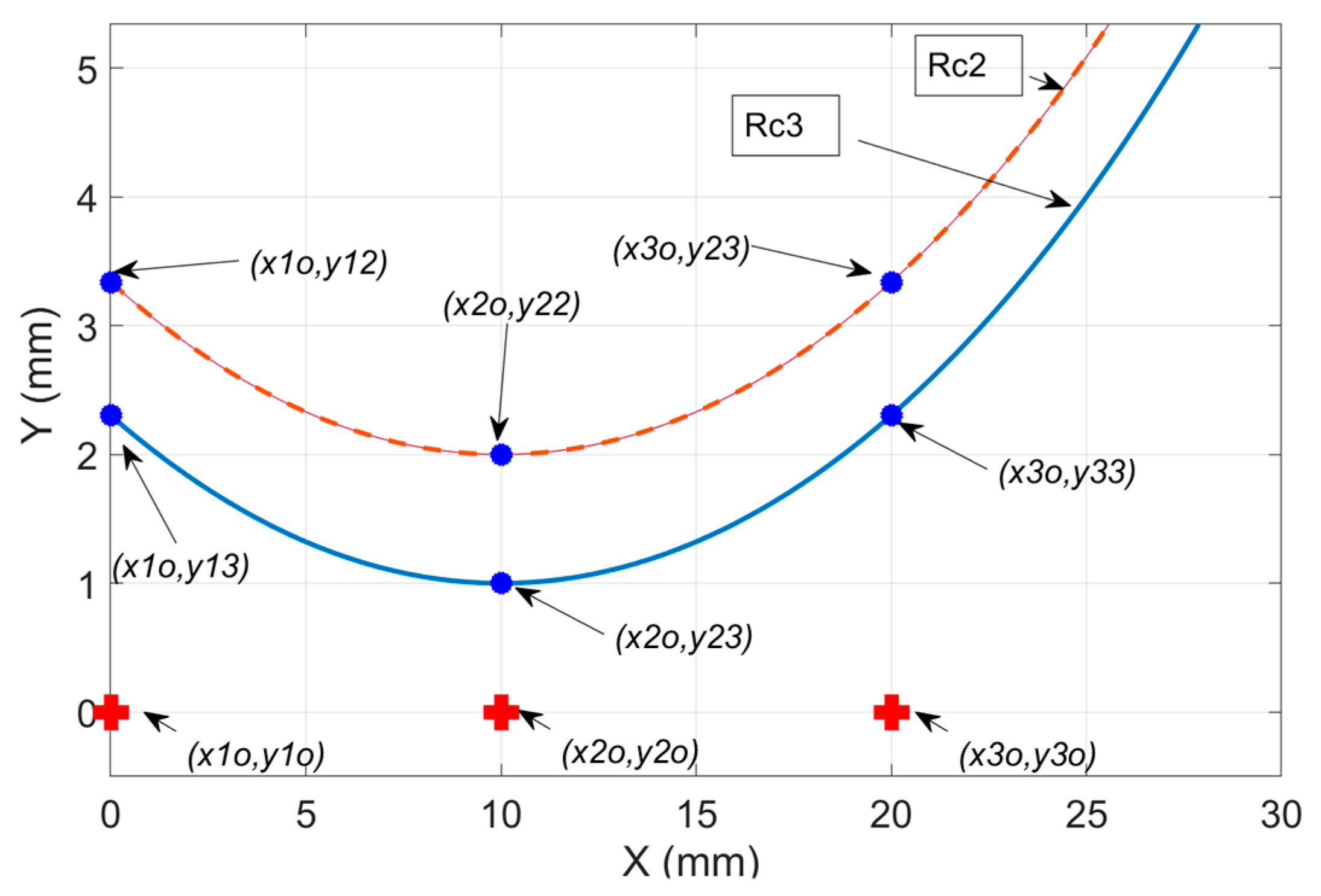

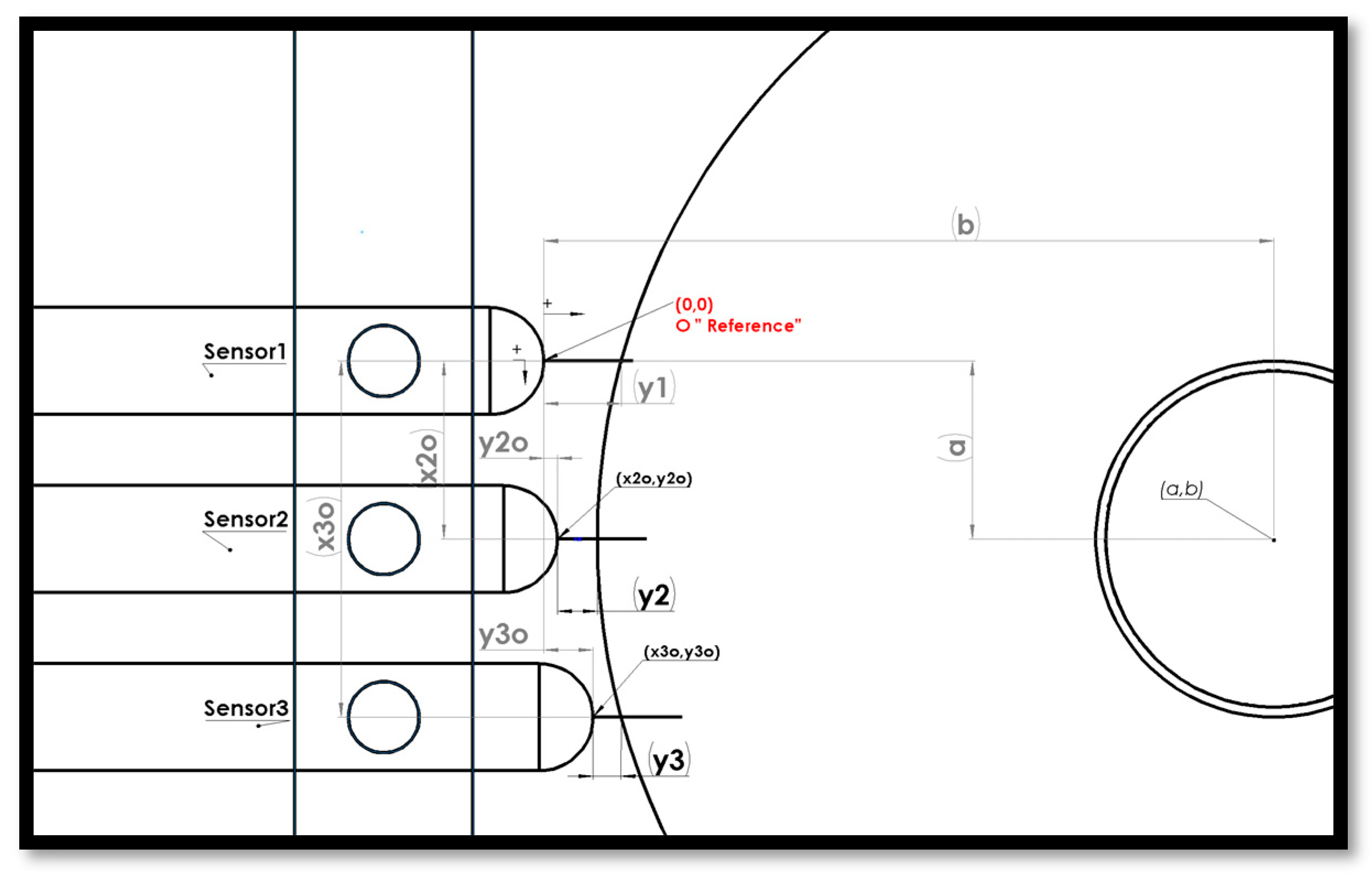
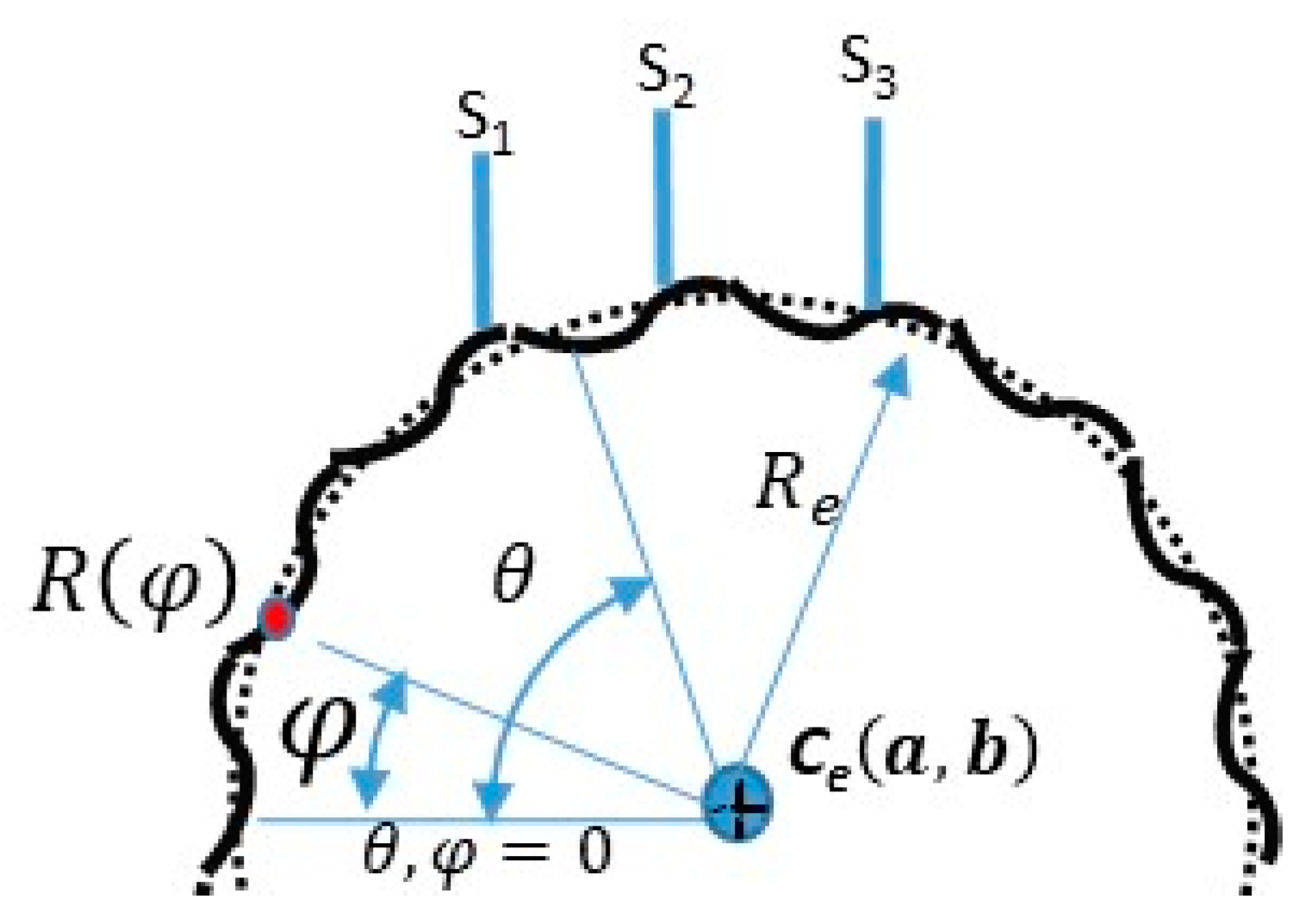
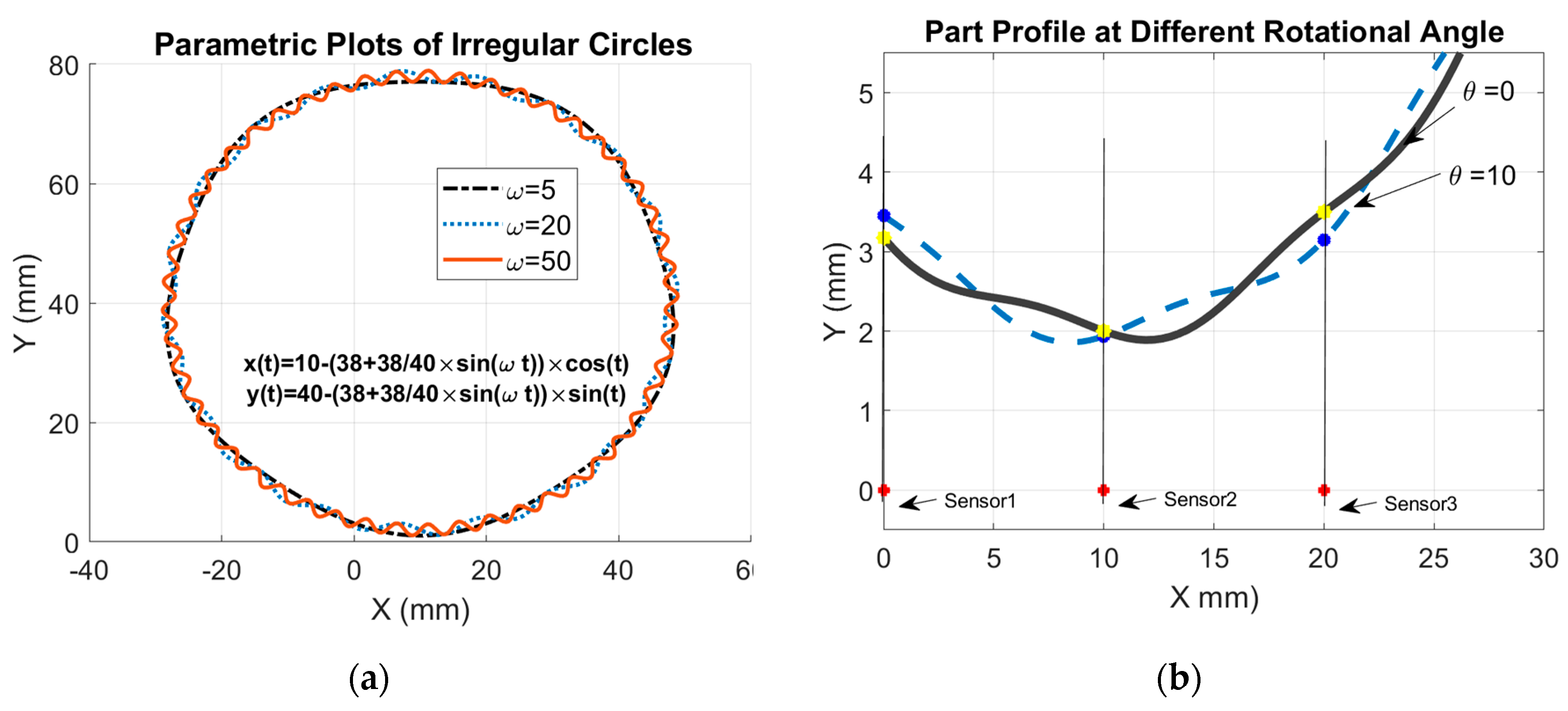

| Sensor | Simulated | Sensor | Simulated |
|---|---|---|---|
| 3.33939 mm | 2.30385 mm | ||
| 2.00000 mm | 1.0000 mm | ||
| 3.33939 mm | 2.30385 mm | ||
| Test | Initial Guess | # Iterations to Convergence | |||||||
|---|---|---|---|---|---|---|---|---|---|
| True solution is obtained from the parametric equations: | 10.000 | 20.000 | 0.000 | 0.000 | 10.000 | 40.000 | |||
| Trial 1 | [8,19,1,1,9,39] | 23 | 0.000534 | 9.998 | 19.998 | 0.000 | 0.000 | 9.999 | 40.000 |
| Trial 2 | [12,18,2,1,4,35] | 95 (stopped) | 538.63 | 19.998 | 20.000 | 0.001 | 0.000 | 9.999 | 40.000 |
| Trial 3 | [8,13,2,3,12,43] | 95 (stopped) | 342.70 | 10.195 | 20.000 | 0.001 | 0.000 | 9.999 | 40.000 |
| Trial 4 | [15,25,2,2,15,50] | 52 | 10.085 | 10.017 | 19.998 | 0.000 | 0.000 | 9.999 | 40.000 |
| Trial 5 | [20,25,2,2,20,50] | 16 | 0.000538 | 10.000 | 19.998 | 0.000 | 0.000 | 9.999 | 40.000 |
| Trial 6 | [20,25,2,2,5,5] | 117 (stopped) | 0.56 × 1010 | 16.977 | 40.307 | 64.830 | −9.854 | 27.854 | 29.399 |
| Trial 7 | [1,1,1,1,1,1] | 106 (stopped) | 2.05 × 1010 | 9.5110 | 22.302 | −61.161 | 10.345 | 26.507 | −25.103 |
| Trial 8 | [15,25,−2,−2,15,50] | 15 | 0.000865 | 10.000 | 19.998 | 0.000 | 0.000 | 9.999 | 40.000 |
| Trial 9 | [20,25,−2,−2,20,50] | 45 | 0.000141 | 9.999 | 19.998 | 0.000 | 0.000 | 9.999 | 40.000 |
| Trial 10 | [8,19,1,−1,9,39] | 90 (stopped) | 526 × 1013 | 12.097 | 26.698 | 74.837 | −1.913 | 15.937 | 37.914 |
| True Radius R | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Calculation Based on True Values Sp = {10,20,0,0} | Calculation Based on Trial 5 in Table 2 Sp = {10,19.998,0,0} | ||||||||
| 38.000 | Values from Table 1 | 10.0000 | 40.0108 | 38.0108 | 9.999 | 40.0033 | 38.0033 | ||
| 39.000 | Values from Table 1 | 10.0000 | 39.9956 | 38.9956 | 9.999 | 39.9879 | 38.9879 | ||
| Sensor | Measurement (mm) | Sensor | Measurement (mm) |
|---|---|---|---|
| 2.130124 | 1.094501 | ||
| 1.963025 | 0.963052 | ||
| 2.138668 | 1.103195 | ||
| Trial # | Initial Guess | n | Ers 10−7 (mm2) | # Iterations | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| - | True * | 10.000 | 20.000 | −1.175 | −0.014 | 10.010 | 38.788 | - | - | |
| 1 | [10,20,−2,−1,11,39] | 6 | 10.010 | 20.000 | −1.1750 | −0.014 | 10.010 | 38.788 | 3.0458 | 108 (stopped) |
| 2 | [10,20,−2,0,9,39] | 6 | 10.012 | 20.002 | −1.175 | −0.014 | 10.012 | 38.788 | 2.1151 | 107 (stopped) |
| 3 | [12,21,2,1,11,38] | 6 | 9.048 | 17.536 | 72.354 | −3.990 | 17.060 | 36.135 | 50 | 94 (stopped) |
| 4 | [10,20,−1.175,−0.014,10.01,38.788] | 6 | 10.010 | 20.000 | −1.175 | −0.014 | 10.010 | 38.788 | 3.045 | 99 (stopped) |
| 5 | 5 | 10.010 | 20.000 | −1.175 | −0.014 | 10.010 | 38.788 | 1.2075 | 85 | |
| 6 | 4 | 10.006 | 20.000 | −1.175 | −0.014 | 10.010 | 38.788 | 43.69 | 97 (stopped) | |
| 7 | 3 | 9.927 | 19.987 | −1.152 | 0.027 | 9.927 | 38.811 | 1.1 | 8 | |
| 8 | 2 | 10.583 | 21.148 | −1.331 | −0.010 | 10.574 | 38.629 | 11 | 54 |
| Part True Re | Probes Measurement (mm), n = 3 | Calculated (mm) | Error (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Group 1: True part center location is fixed at (ae,be) | |||||||||
| 38.000 | Values from Table 3, n = 3 | 10.0092 | 38.7851 | 37.9971 | 0.001 | 0.003 | 0.003 | ||
| 38.250 | 1.871 | 1.713 | 1.880 | 10.0092 | 38.7831 | 38.2451 | 0.001 | 0.005 | 0.005 |
| 38.500 | 1.612 | 1.463 | 1.621 | 10.0093 | 38.7845 | 38.4965 | 0.001 | 0.003 | 0.004 |
| 38.750 | 1.353 | 1.213 | 1.362 | 10.0094 | 38.7895 | 38.7515 | 0.001 | 0.002 | 0.002 |
| 39.000 | Values from Table 3, n = 3 | 10.0113 | 38.7836 | 38.9956 | 0.001 | 0.004 | 0.004 | ||
| 39.250 | 0.836 | 0.713 | 0.845 | 10.0095 | 38.7809 | 39.2429 | 0.001 | 0.007 | 0.007 |
| 39.500 | 0.577 | 0.463 | 0.586 | 10.0096 | 38.7964 | 39.5084 | 0.000 | 0.008 | 0.008 |
| Group 2: Part center location is arbitrarily (unrestricted positioning) | |||||||||
| 38.000 | 8.268 | 9.303 | 10.742 | 5.5273 | 45.8615 | 37.9977 | - | - | 0.002 |
| 38.000 | 2.040 | 2.963 | 4.277 | 5.9495 | 39.5931 | 38.0215 | - | - | 0.022 |
| 38.000 | 2.408 | 2.244 | 2.422 | 10.000 | 39.0798 | 38.0108 | - | - | 0.011 |
| 38.000 | 1.067 | 0.903 | 1.081 | 10.000 | 37.7388 | 38.0108 | - | - | 0.011 |
| 38.000 | 1.540 | 1.376 | 1.554 | 10.000 | 38.2118 | 38.0108 | - | - | 0.011 |
| 38.000 | 1.364 | 0.660 | 0.310 | 11.9549 | 37.4382 | 38.0035 | - | - | 0.004 |
| 38.000 | 0.185 | 0.120 | 0.398 | 9.6352 | 36.9458 | 38.0026 | - | - | 0.003 |
| Inc. i | (°) | 20° | |||||
|---|---|---|---|---|---|---|---|
| Probes Measurement (mm), n = 3 | Calculated (mm) | ||||||
| 1 | 20 | 3.366 | 2.349 | 2.004 | 10.14 | 40.445 | 37.975 |
| 2 | 40 | 3.337 | 2.3440 | 2.024 | 9.943 | 40.337 | 38.003 |
| 3 | 60 | 3.314 | 2.307 | 1.987 | 9.883 | 39.452 | 38.024 |
| 4 | 80 | 3.351 | 2.325 | 1.981 | 10.097 | 39.859 | 37.989 |
| … | … | … | … | … | … | … | … |
| 12 | 320 | 3.354 | 2.355 | 2.024 | 10.041 | 40.590 | 37.986 |
| 13 | 340 | 3.315 | 2.318 | 2.004 | 9.860 | 39.731 | 38.023 |
| 14 | 360 | 3.333 | 2.310 | 1.975 | 10.008 | 39.519 | 38.006 |
| Average | = 37.9992 | ||||||
| True Part Center is Fixed and Rotated about a = 7.873513 and b = 43.48817 | ||||||
|---|---|---|---|---|---|---|
| Probes Measurement, n = 3 | Calculated | |||||
| 0 | 1.357 | 2.445 | 3.169 | 5.4487 | 52.8828 | 51.8131 |
| 2 | 1.598 | 2.622 | 2.941 | 5.9349 | 63.4376 | 62.1237 |
| 4 | 1.904 | 2.610 | 2.619 | 7.8732 | 62.9325 | 61.5343 |
| 6 | 2.118 | 2.413 | 2.379 | 9.3908 | 51.5730 | 50.3386 |
| 8 | 2.141 | 2.122 | 2.335 | 9.6553 | 40.5330 | 39.5875 |
| 10 | 1.972 | 1.875 | 2.488 | 9.1946 | 34.3121 | 33.6218 |
| 12 | 1.697 | 1.792 | 2.758 | 8.4051 | 32.6860 | 32.1086 |
| 14 | 1.433 | 1.906 | 3.033 | 7.3904 | 35.1336 | 34.5015 |
| 16 | 1.296 | 2.164 | 3.198 | 6.2524 | 41.9387 | 41.1208 |
| 18 | 1.357 | 2.445 | 3.169 | 5.4487 | 52.8828 | 51.8131 |
| 20 | 1.598 | 2.622 | 2.941 | 5.9349 | 63.4376 | 62.1237 |
| - | - | - | - | - | - | - |
| 358 | 1.296 | 2.164 | 3.198 | 6.2524 | 41.9387 | 41.1208 |
| Average | 7.7273 | 46.1588 | = 45.1944 | |||
| Sensor | Avg./SD (mm) | Measurement (mm) | Avg./SD (mm) | Measurement (mm) |
|---|---|---|---|---|
| S1 | (, sd12) | (14.37, 0.06) | (, sd13) | (11.67, 0.10) |
| S2 | (, sd22) | (3.88, 0.02) | (, sd13) | (1.80, 0.03) |
| S3 | (, sd32) | (15.04, 0.15) | (, sd13) | (12.17, 0.10) |
| Sensor | Avg./SD (mm) | Measurement (mm) |
|---|---|---|
| S1 | (, sd1) | (13.10, 0.03) |
| S2 | (, sd2) | (2.85, 0.01) |
| S3 | (, sd3) | (13.69,0.11) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayyas, M. Three-Point Inverse and Forward Kinematic Algorithms for Circle Measurement from Distributed Displacement Sensor Network. Sensors 2019, 19, 4679. https://doi.org/10.3390/s19214679
Mayyas M. Three-Point Inverse and Forward Kinematic Algorithms for Circle Measurement from Distributed Displacement Sensor Network. Sensors. 2019; 19(21):4679. https://doi.org/10.3390/s19214679
Chicago/Turabian StyleMayyas, Mohammad. 2019. "Three-Point Inverse and Forward Kinematic Algorithms for Circle Measurement from Distributed Displacement Sensor Network" Sensors 19, no. 21: 4679. https://doi.org/10.3390/s19214679
APA StyleMayyas, M. (2019). Three-Point Inverse and Forward Kinematic Algorithms for Circle Measurement from Distributed Displacement Sensor Network. Sensors, 19(21), 4679. https://doi.org/10.3390/s19214679





