An Alignment Method for Strapdown Inertial Navigation Systems Assisted by Doppler Radar on a Vehicle-Borne Moving Base
Abstract
1. Introduction
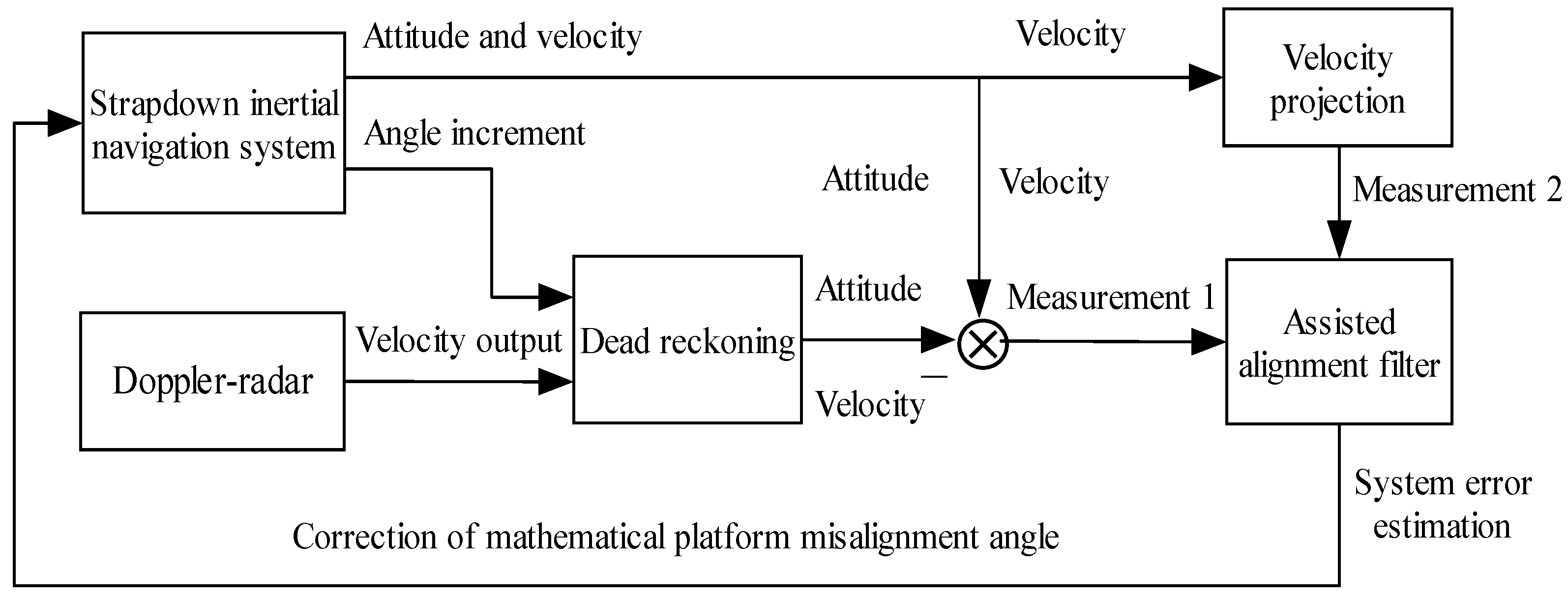
2. Moving-Base Alignment Scheme Using a Doppler-Radar-Assisted Strapdown Inertial Navigation System
3. Error Model of Gyro/Doppler Radar Dead Reckoning
3.1. Error Model of the Gyroscope and Doppler Radar
3.2. System Error Equation in Dead Reckoning
4. Doppler-Radar-Assisted Moving-Base Alignment Filtering Algorithm for Strapdown Inertial Navigation System
4.1. State Equation of Assisted Alignment Filter
4.2. Measurement Equation of Assisted Alignment Filter
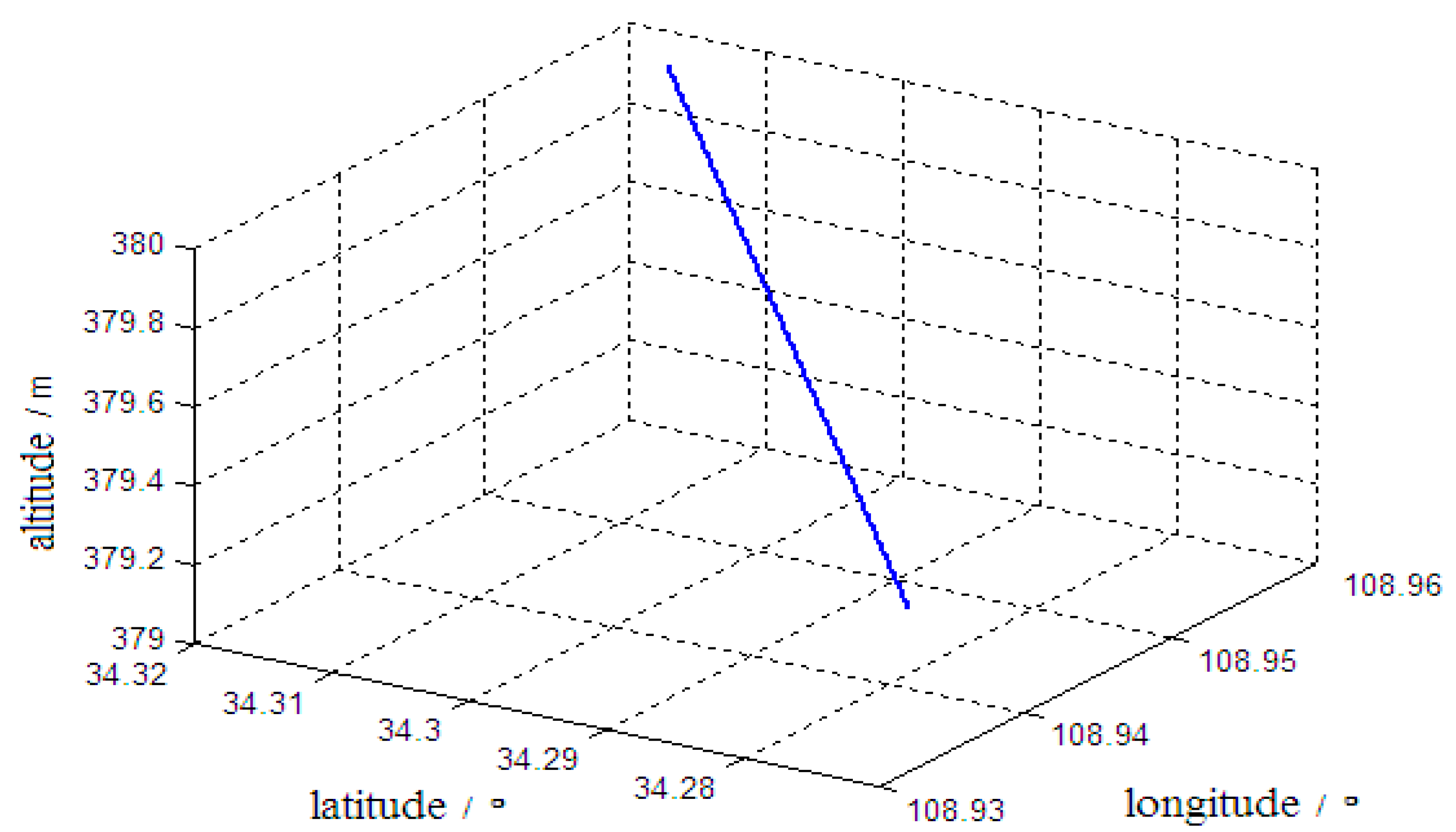
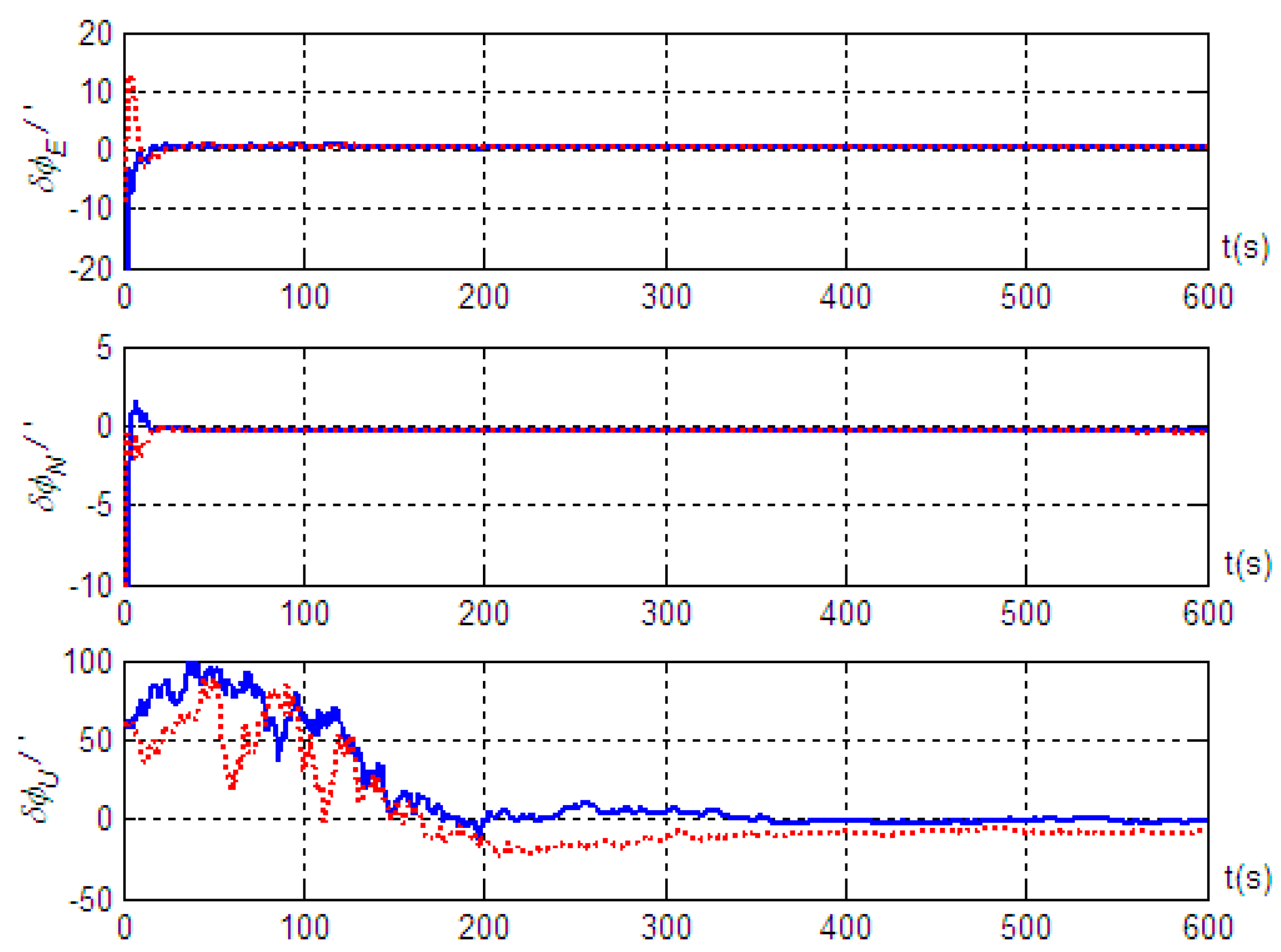
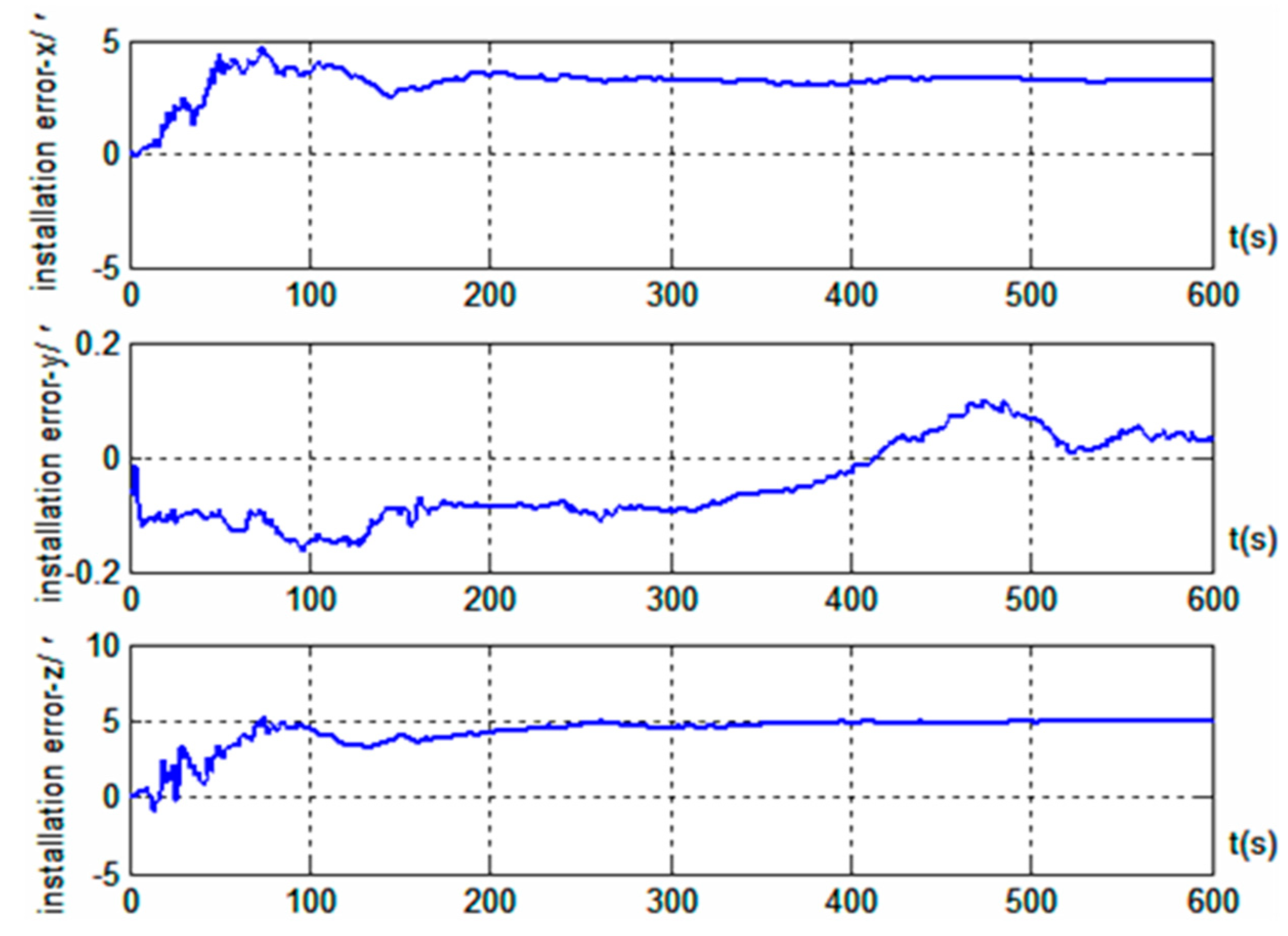
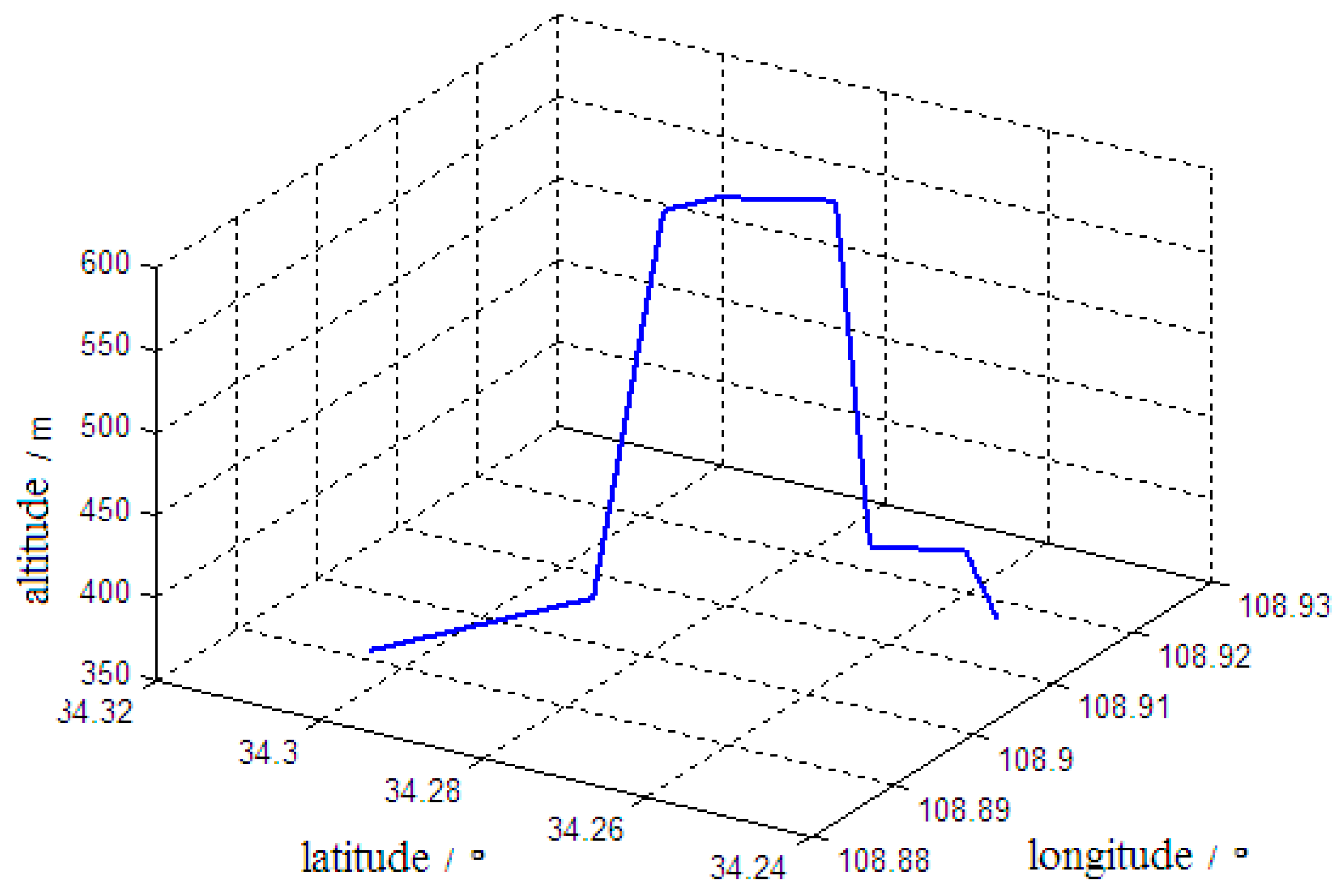
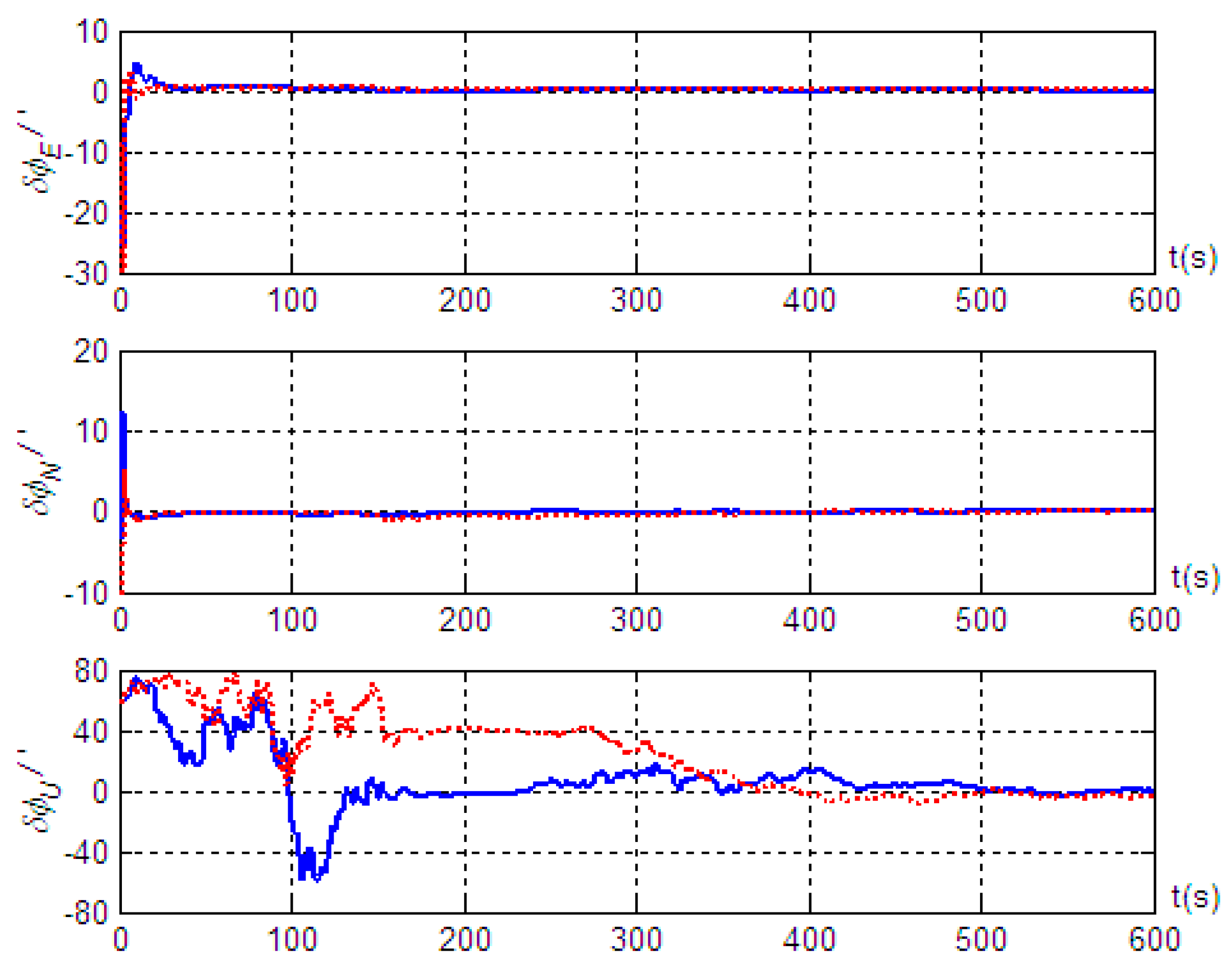
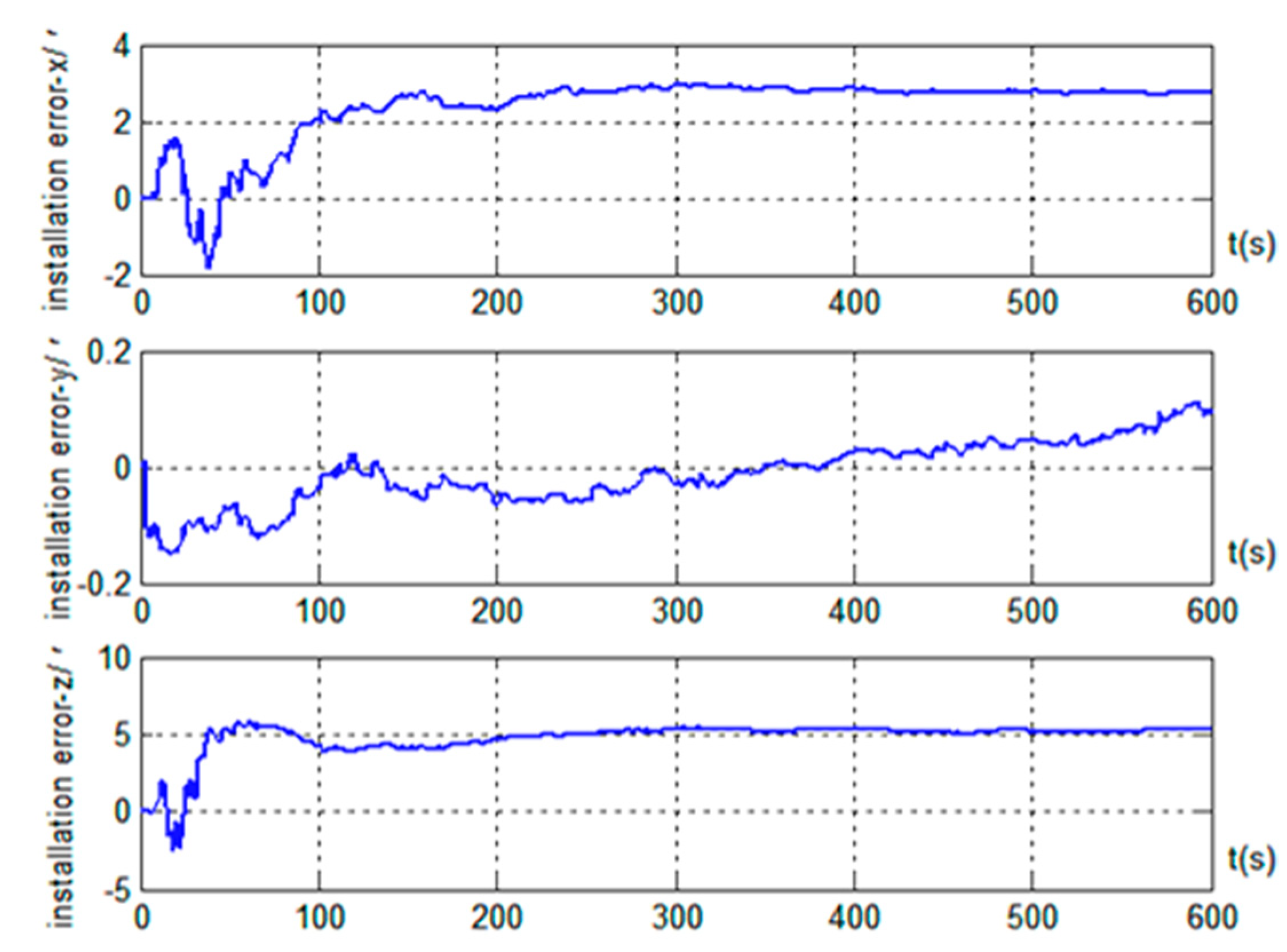
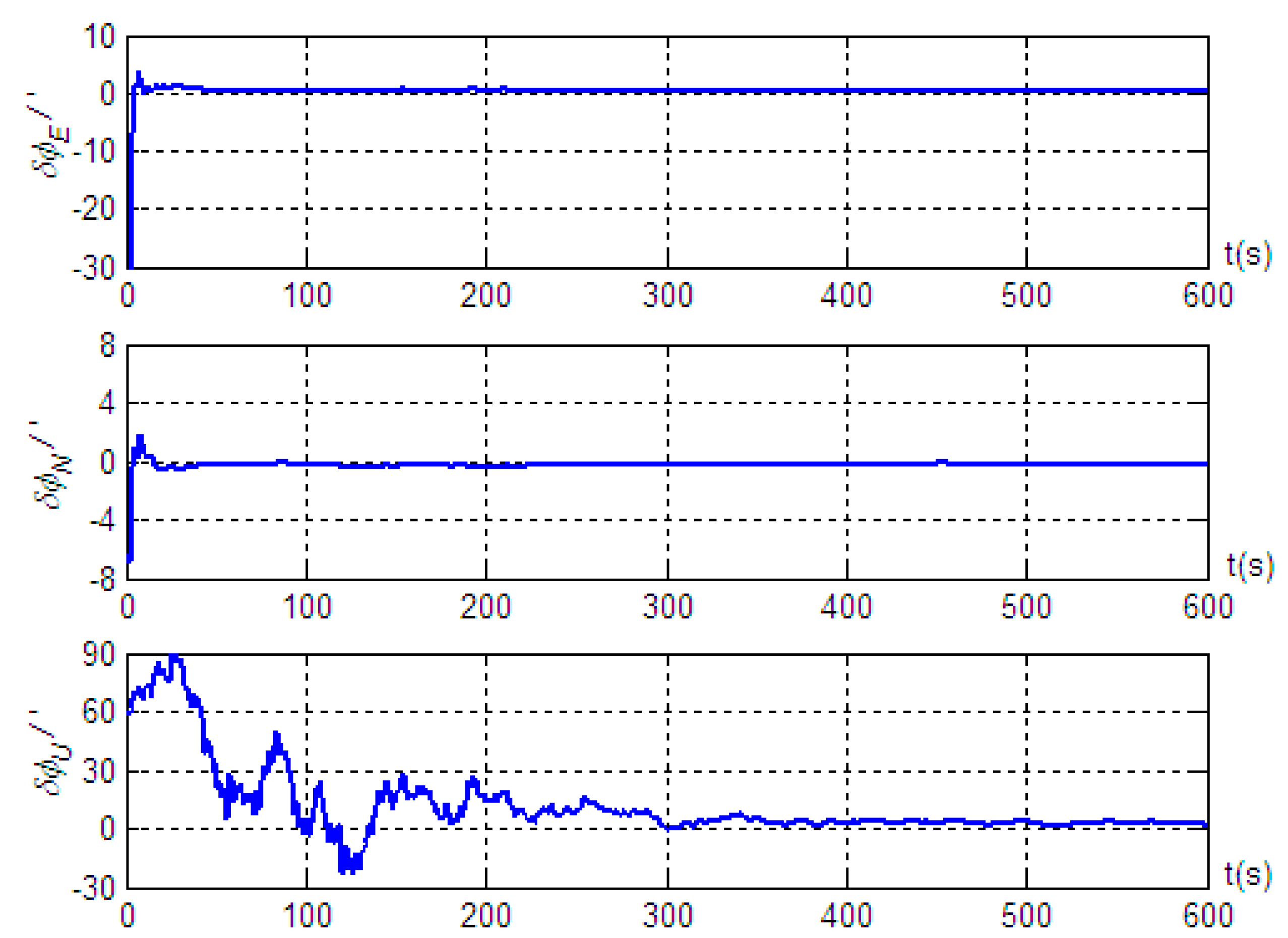
5. Simulation Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaygisiz, B.H.; Şen, B. In-motion alignment of a low-cost GPS/INS under large heading error. J. Navig. 2015, 68, 355–366. [Google Scholar] [CrossRef]
- Mei, C.B.; Qin, Y.Y.; Fu, Q.W.; Yan, G.M. In-motion alignment for SINS/GPS based on Rodrigues parameter and nonlinear measurement. J. Chin. Inert. Technol. 2015, 23, 739–745. [Google Scholar]
- Liu, C.; Wang, Z.Y.; Deng, H.F. Low accuracy SINS dynamic alignment method based on CKF aided by GPS location information. Sci. Surv. Mapp. 2016, 41, 155–159. [Google Scholar]
- Shin, H.C.; Yu, H.; Park, H.W. High-degree cubature Kalman filtering approach for GPS aided in-flight alignment of SDINS. J. Position. Navig. Timing 2015, 4, 181–186. [Google Scholar] [CrossRef]
- Hong, W.S.; Park, C.G. A multistage in-flight alignment with no initial attitude references for strapdown inertial navigation systems. Int. J. Aeronaut. Space Sci. 2017, 18, 565–573. [Google Scholar] [CrossRef]
- Li, B.G.; Hu, W.Y.; Wu, M. In-flight coarse alignment for aerostat strapdown inertial navigation system aided by single GPS antenna. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Compute, Shenyang, China, 20–22 December 2013; pp. 2807–2811. [Google Scholar]
- Yang, B.; Wang, Y.G.; Guo, Z.B.; Shan, B. Accurate independent alignment method of inertial navigation system for vehicles on moving base. J. Chin. Inert. Technol. 2015, 23, 580–584. [Google Scholar]
- Hu, J.; Cheng, X. A new in-motion initial alignment for land-vehicle SINS/OD integrated system. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium-PLANS, Monterey, CA, USA, 5–8 May 2014; pp. 407–412. [Google Scholar]
- Pan, J.; Zhang, C.; Zhang, X. Real-time accurate odometer velocity estimation aided by accelerometers. Measurement 2016, 91, 468–473. [Google Scholar] [CrossRef]
- Chang, L.B.; He, H.Y.; Qin, F.J. In-motion initial alignment for odometer-aided strapdown inertial navigation system based on attitude estimation. IEEE Sens. J. 2016, 17, 766–773. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wang, X. Kalman filtering-based in-motion coarse alignment for odometer-aided SINS. IEEE Trans. Instrum. Meas. 2017, 66, 3364–3377. [Google Scholar] [CrossRef]
- Golovan, A.A.; Nikitin, I.V. Combined use of strapdown inertial navigation systems and odometers from the standpoint of mechanics of inertial navigation systems. Part 1. Mosc. Univ. Mech. Bull. 2015, 70, 46–49. [Google Scholar] [CrossRef]
- Golovan, A.A.; Nikitin, I.V. Combined use of strapdown inertial navigation systems and odometers from the standpoint of mechanics of inertial navigation systems. Part 2. Mosc. Univ. Mech. Bull. 2015, 70, 101–105. [Google Scholar] [CrossRef]
- Jiang, X.L.; Wang, Y.G.; Yang, J.S.; Wen, C.B. Transfer alignment match method of land-launched missile. Mod. Def. Technol. 2015, 43, 88–93. [Google Scholar]
- Kang, C.W.; Park, C.G. Observability improvement of transfer alignment for ground launchers with engine vibration. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation, Tampa, FL, USA, 8–12 September 2014; pp. 1802–1806. [Google Scholar]
- Chang, L.B.; Li, Y.; Xue, B.Y. Initial alignment for Doppler velocity log-aided strapdown inertial navigation system with limited information. IEEE ASME Trans. Mechatron. 2017, 22, 329–338. [Google Scholar] [CrossRef]
- Kellner, D.; Barjenbruch, M.; Dietmayer, K.; Klappstein, J. Instantaneous lateral velocity estimation of a vehicle using Doppler radar. In Proceedings of the IEEE 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 877–884. [Google Scholar]
- Shariff, K.K.M.; Hoare, E.; Daniel, L.; Antoniou, M.; Cherniakov, M. Comparison of adaptive spectral estimation for vehicle speed measurement with radar sensors. Sensors 2017, 17, 751. [Google Scholar] [CrossRef] [PubMed]
- Guan, R.P.; Ristic, B.; Wang, L.P.; Moran, B.; Evans, R. Feature-based robot navigation using a Doppler-azimuth radar. Int. J. Control 2017, 90, 888–900. [Google Scholar] [CrossRef]
- Shuang, P.; Xu, H.; Nie, Y.F. A novel in-flight alignment algorithm for airborne strapdown INS with assistant of Doppler radar. In Proceedings of the Second International Conference on Mechatronics and Automatic Control, Beijing, China, 20–21 September 2014; pp. 1061–1070. [Google Scholar]
- Silva, F.O.; Hemerly, E.M.; Filho, W.C.L. Error analysis of analytical coarse alignment formulations for stationary SINS. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1777–1796. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Gao, W.; Diao, M.; Fei, Y. Coarse alignment of a shipborne strapdown inertial navigation system using star sensor. IET Sci. Meas. Technol. 2015, 9, 852–860. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Y.G.; Xue, L.; Shan, B.; Wang, B.C. Accurate integrated position and orientation method for vehicles based on strapdown inertial navigation system/Doppler radar. Meas. Control 2018, 51, 431–442. [Google Scholar]
- Jurman, D.; Jankovec, M.; Kamnik, R.; Topič, M. Calibration and data fusion solution for the miniature attitude and heading reference system. Sens. Actuators A Phys. 2007, 138, 411–420. [Google Scholar] [CrossRef]
- Skog, I.; Händel, P. Calibration of a MEMS inertial measurement unit. In Proceedings of the XVII IMEKO World Congress, Rio de Janeiro, Brazil, 17–22 September 2006; pp. 1–6. [Google Scholar]
- Panahandeh, G.; Skog, I.; Jansson, M. Calibration of the accelerometer triad of an inertial measurement unit, maximum likelihood estimation and Cramér-Rao bound. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010; pp. 1–6. [Google Scholar]
- Dorveaux, E.; Vissière, D.; Petit, N. On-the-field calibration of an array of sensors. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6795–6802. [Google Scholar]
- Dorveaux, E.; Vissiè, D.; Martin, A.P.; Petit, N. Iterative calibration method for inertial and magnetic sensors. In Proceedings of the 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, China, 16–18 December 2009; pp. 8296–8303. [Google Scholar]
- Tedaldi, D.; Pretto, A.; Menegatti, E. A robust and easy to implement method for IMU calibration without external equipments. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–5 June 2014; pp. 3042–3049. [Google Scholar]
- Xi, J.; He, M.; Liu, H.; Zheng, J. Admissible output consensualization control for singular multi-agent systems with time delays. J. Frankl. Inst. 2016, 353, 4074–4090. [Google Scholar] [CrossRef]
- Chatfield, A.B. Fundamentals of high accuracy inertial navigation. Prog. Astronaut. Aeronaut. 1997, 174, 15–32. [Google Scholar]
- Gebre-Egziabher, D.; Elkaim, G.H.; Powell, J.D.; Parkinson, B. A non-linear two-step estimation algorithm for calibrating solid-state strapdown magnetometers. In Proceedings of the 8th International St. Petersburg Conference on Navigation Systems, St. Petersburg, Russia, 28–30 May 2001; pp. 1–10. [Google Scholar]
- Tang, K.H.; Wang, J.L.; Li, W.L.; Wu, W.Q. A novel INS and Doppler sensors calibration method for long range underwater vehicle navigation. Sensors 2013, 13, 14583–14600. [Google Scholar] [CrossRef] [PubMed]
- Troni, G.; Whitcomb, L.L. Advances in in situ alignment calibration of Doppler and High/Low-end attitude sensors for underwater vehicle navigation: Theory and experimental evaluation. J. Field Robot. 2015, 32, 655–674. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Y.; Yang, T.; Li, C.Y.; Wang, Z.Q. A novel separation and calibration method for DVL and compass error in dead reckoning navigation systems. Meas. Sci. Technol. 2016, 27, 065003. [Google Scholar] [CrossRef]
- Kang, L.; Ye, L.; Song, K. A fast in-situ SINS and Doppler sensor calibration algorithm for underwater vehicle navigation. IEICE Electron. Express 2014, 11, 994–1004. [Google Scholar] [CrossRef][Green Version]
- Xu, X.S.; Pan, Y.F.; Zou, H.J. SINS/ DVL integrated navigation system based on adaptive filtering. J. Huazhong Univ. Sci. Technol. 2015, 43, 95–99. [Google Scholar]
- Li, W.L.; Zhang, L.D.; Sun, F.P.; Yang, L.; Chen, M.J.; Li, Y. Alignment calibration of IMU and Doppler sensors for precision INS/DVL integrated navigation. Opt. Int. J. Light Electron Opt. 2015, 126, 3872–3876. [Google Scholar] [CrossRef]
- Ying, Z.H.; Gao, C.F.; Wang, Q.; Wei, G.; Zhou, J.; Xie, Y.P. Application of high-accuracy laser Doppler velocimeter in self-contained land navigation system. Chin. J. Lasers 2017, 44, 159–166. [Google Scholar]
- Pierrottt, D.; Amzajerdian, F.; Petway, L. Flight test performance of a high precision navigation Doppler lindar. In Proceedings of the SPIE—Laser Radar Technology and Applications XIV, Orlando, FL, USA, 15–16 April 2009; pp. 7323–7334. [Google Scholar]
- Chen, H.J.; Nie, X.M.; Wang, M.C. Vehicle integrated navigation system based on two dimensional laser Doppler velocimeter. Infrared Laser Eng. 2018, 47, 218–224. [Google Scholar]
- Dissanayake, G.; Sukkarieh, S.; Nebot, E.M.; Durrant-whyte, H.F. The aiding of a low-cost strapdown inertial measurement unit using vehicle model constraints for land vehicle applications. IEEE Trans. Robot. Autom. 2001, 17, 731–747. [Google Scholar] [CrossRef]
- Wang, M.L.; Feng, G.Q.; Li, Y.F. MEMS-SINS navigation method aided by vehicle model. J. Chin. Inert. Technol. 2017, 25, 209–215. [Google Scholar]
- Yang, L.; Li, Y.; Wu, Y.L.; Rizos, C. An enhanced MEMSINS/GNSS integrated system with fault detection and exclusion capability for land vehicle navigation in urban areas. GPS Solut. 2014, 18, 593–603. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Xi, J.; Yang, J.; Xue, L. An Alignment Method for Strapdown Inertial Navigation Systems Assisted by Doppler Radar on a Vehicle-Borne Moving Base. Sensors 2019, 19, 4577. https://doi.org/10.3390/s19204577
Yang B, Xi J, Yang J, Xue L. An Alignment Method for Strapdown Inertial Navigation Systems Assisted by Doppler Radar on a Vehicle-Borne Moving Base. Sensors. 2019; 19(20):4577. https://doi.org/10.3390/s19204577
Chicago/Turabian StyleYang, Bo, Jianxiang Xi, Jian Yang, and Liang Xue. 2019. "An Alignment Method for Strapdown Inertial Navigation Systems Assisted by Doppler Radar on a Vehicle-Borne Moving Base" Sensors 19, no. 20: 4577. https://doi.org/10.3390/s19204577
APA StyleYang, B., Xi, J., Yang, J., & Xue, L. (2019). An Alignment Method for Strapdown Inertial Navigation Systems Assisted by Doppler Radar on a Vehicle-Borne Moving Base. Sensors, 19(20), 4577. https://doi.org/10.3390/s19204577




