A SINS/DVL Integrated Positioning System through Filtering Gain Compensation Adaptive Filtering
Abstract
1. Introduction
- (1)
- For the fusion of positioning information, we present a general framework for an integrated positioning fusion system based on adaptive Kalman filtering. It provides a general reference for information fusion methods.
- (2)
- We take full advantage of strong tracking filtering and adaptive filtering to propose and utilize an organic combination of a filtering gain compensation adaptive filter and a filtering gain compensation strong tracking filter to fuse the positioning information to obtain higher accuracy and a more stable positioning result.
- (3)
- The proposed SINS/DVL integrated positioning system based on a filtering gain compensation adaptive filter can enhance underwater positioning performance and also provides reference value for other information fusion systems.
2. Related Works
3. SINS/DVL Integrated Positioning System Based on a Filtering Gain Compensation Adaptive Kalman Filter
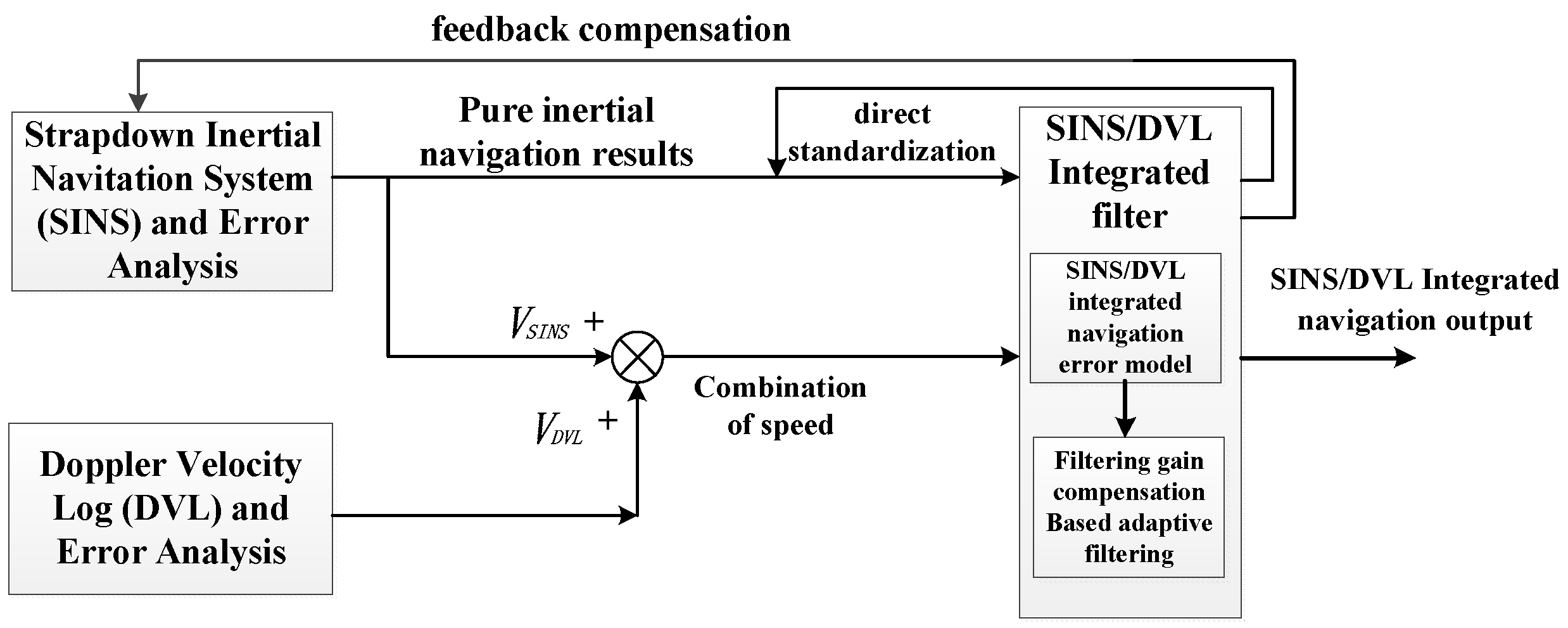
3.1. Framework for the SINS/DVL Integrated Positioning System
3.2. Strapdown Inertial Navigation Subsystem and Error Analysis
- Errors caused by inertial sensors: Inertial sensors, such as accelerometers or gyroscopes, may cause errors due to processing, assembly processes, or principal problems. This type of error is called systematic error. In the Strapdown Inertial Navigation/Doppler Velocity Logger integrated positioning system, such errors account for 90% of the total error.
- Errors in the computer operation process: The Strapdown Inertial Navigation System outputs the acceleration and attitude angles of the gyroscope and accelerometer, and the rest of the computational work is done by the computer. The calculation error includes the error in the Strapdown Inertial Navigation System and the error in the Kalman filter.
- Errors caused by mathematical models: When establishing the system model, we approximate the earth as a sphere in the calculation process. When using Newton’s second law as the inertial motion equation, and the speed of the aircraft is very high, the description of the aircraft’s motion will be insufficiently accurate.
- Errors caused by the initial alignment: These errors can be divided into the following:
- (1)
- Installation errors. Gyros and accelerometers can cause errors during installation.
- (2)
- Initial condition errors. Initial condition errors include heading, attitude and position, and zero errors in the gyroscope and accelerometer.
- (3)
- Calculation errors. The calculation errors of the navigation system are also called the calculation errors of the mathematical platform.
- (4)
- Instrument errors. This refers mainly to the errors in the drift that is generated by the gyroscope and the accelerometer and the error in the angular rate meter.
3.3. Doppler Velocity Log Subsystem and Error Analysis
3.4. SINS/DVL Integrated Adaptive Filter
3.4.1. Establishment of the Navigation Error Model
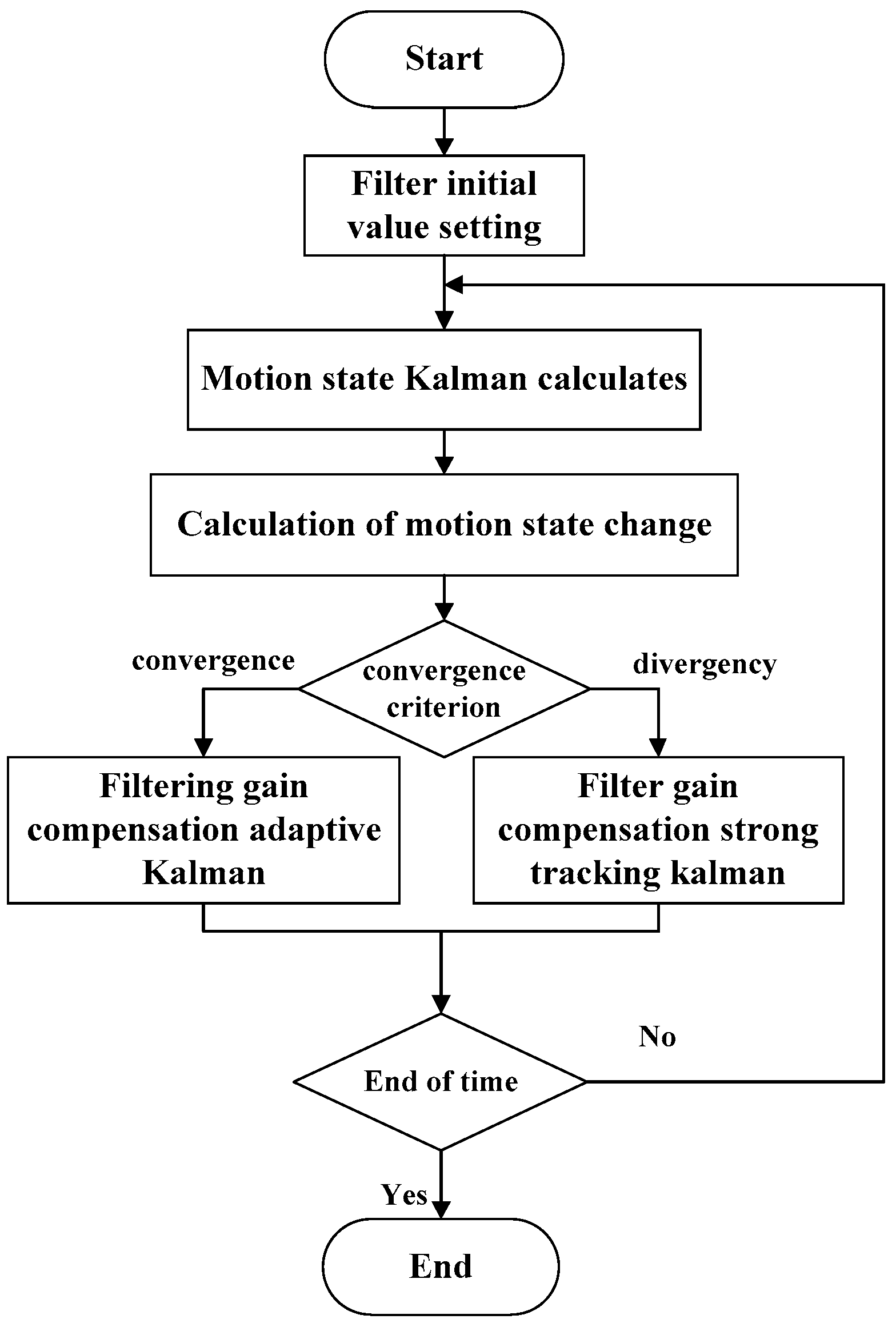
3.4.2. Filtering Gain Compensation-Based Adaptive Kalman Filter
4. Simulation Results and Analysis
4.1. Simulation Setup
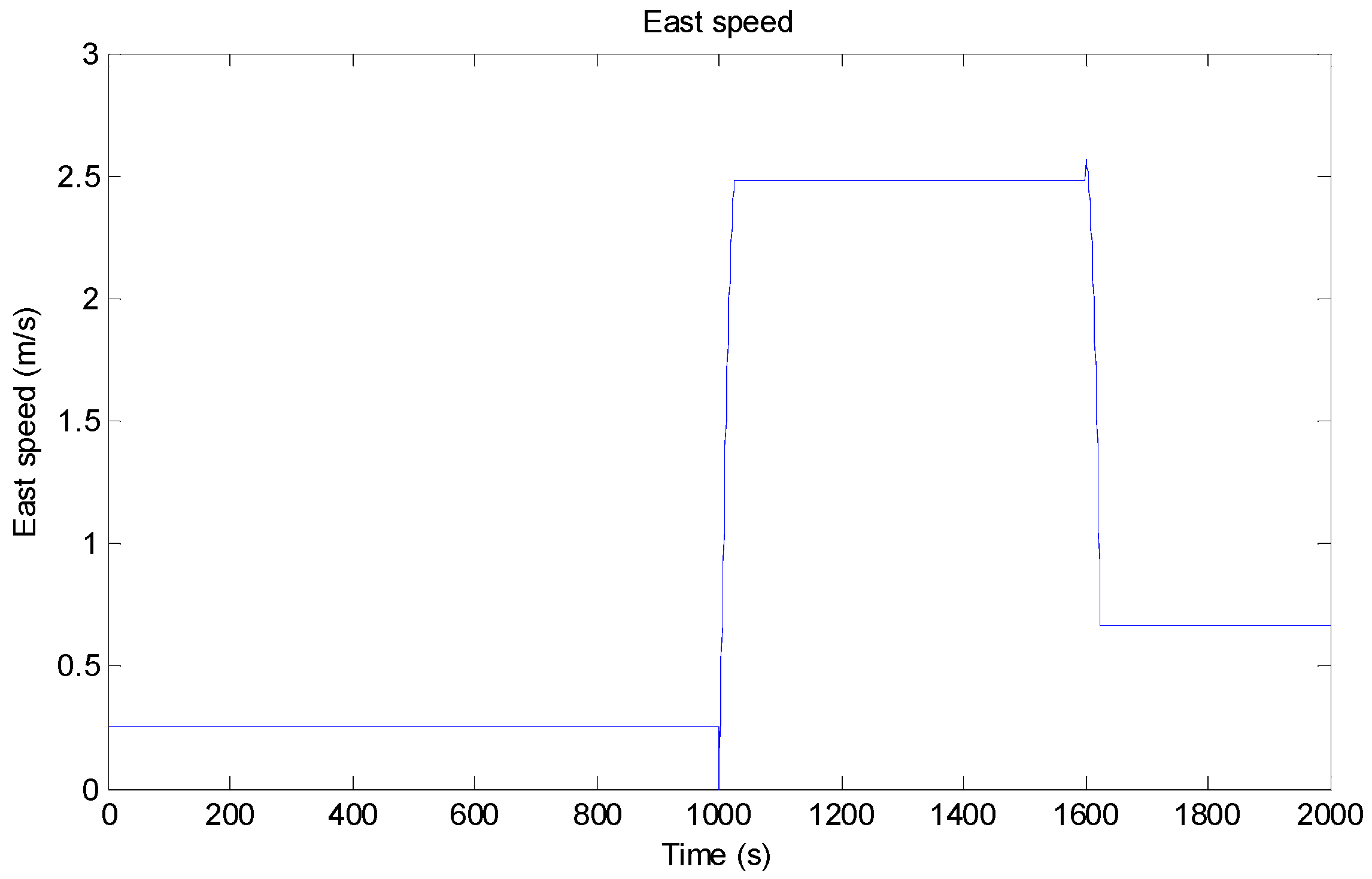
4.1.1. Motion Model and Simulation Design
4.1.2. Evaluation Metric
4.1.3. Reference Positioning Methods
4.2. Positioning Accuracy and Stability Evaluation
4.2.1. Positioning Accuracy Analysis
4.2.2. Positioning Stability Analysis
4.3. Positioning Efficiency Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, Y.P.; Yan, X.Z.; Luo, Q.H. A SINS/DVEL Integrated Navigation Positioning Method based on Improved Adaptive Filtering Technology. In Proceedings of the IEEE International Conference on Smart Internet of Things (SmartIOT), Tianjin, China, 9–11 July 2019; pp. 262–268. [Google Scholar]
- Yin, W.W.; Guo, S.L. Survey on Non-Satellite Underwater Navigation and Positioning Technology. Ship Electron. Eng. 2017, 37, 8–11. [Google Scholar]
- Chen, H.; Ma, L.; He, M.; Wang, X.; Huang, M. Artificial Bee Colony Optimizer Based on Bee Life-cycle for Stationary and Dynamic Optimization. IEEE Trans. Syst. Man Cybern. A Syst. Humans 2017, 47, 327–346. [Google Scholar] [CrossRef]
- Wei, G.; Wang, Q.; Peng, W. Accurate Evaluation of Vertical Tidal Displacement Determined by GPS Kinematic Precise Point Positioning: A Case Study of Hong Kong. Sensors 2019, 19, 2559. [Google Scholar] [CrossRef] [PubMed]
- Specht, M. Method of Evaluating the Positioning System Capability for Complying with the Minimum Accuracy Requirements for the International Hydrographic Organization Orders. Sensors 2019, 19, 3860. [Google Scholar] [CrossRef] [PubMed]
- Nowicki, M.R.; Skrzypczyński, P. Leveraging Visual Place Recognition to Improve Indoor Positioning with Limited Availability of WiFi Scans. Sensors 2019, 19, 3657. [Google Scholar] [CrossRef]
- Yan, X.; Luo, Q.; Yang, Y.; Liu, S.; Li, H.; Hu, C. ITL-MEPOSA: An Improved Trilateration Localization with Minimum Uncertainty Propagation and Optimized Selection of Anchor nodes for wireless sensor networks. IEEE Access 2019, 7, 53136–53146. [Google Scholar] [CrossRef]
- Leonard, J.J.; Bahr, A. Autonomous Underwater Vehicle Navigation. In Springer Handbook of Ocean Engineering; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Kinsey, J.C.; Eustice, R.M.; Whitcomb, L.L. A Survey of Underwater Vehicle Navigation: Recent Advances and New Challenges. In Proceedings of the Conference Maneuvering Control Marine Craft, Lisbon, Portugal, 20–22 September 2006. [Google Scholar]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and Localization: A Review. IEEE J. Oceanic Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Xu, T.L. The Research of SINS/DVL Integrated Navigation Technology. Master’s Thesis, Harbin Engineering University, Harbin, China, 2018. [Google Scholar]
- Zhu, Z.J. The Research of the Unknown Seabed Environment on AUV Integrated Navigation Technology. Master’s Thesis, Harbin Engineering University, Harbin, China, 2013. [Google Scholar]
- Dinc, M.; Hajiyev, C. Integration of Navigation Systems for Autonomous Underwater Vehicles. J. Marine Eng. Technol. 2015, 14, 32–43. [Google Scholar] [CrossRef]
- Larsen, M.B. High Performance Doppler-inertial Navigation-experimental Results. In Proceedings of the Ocean 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000. [Google Scholar]
- Jalving, B.; Gade, K.; Svartveit, K.; Willumsen, A.; Sørhagen, R. DVL Velocity Aiding in the HUGIN 1000 Integrated Inertial Navigation System. Model. Ident. Control 2004, 25, 223–235. [Google Scholar] [CrossRef]
- Hegrenæs, Ø.; Ramstad, A.; Pedersen, T.; Velasco, D. Validation of a New Generation DVL for Underwater Vehicle Navigation. In Proceedings of the IEEE/OES Autonomous Underwater Vehicles (AUV), Tokyo, Japan, 8 December 2016. [Google Scholar]
- Hu, G.; Gao, S.; Xue, L. A novel adaptive unscented Kalman filter. In Proceedings of the Third International Conference on Intelligent Control and Information Processing, Dalian, China, 15–17 July 2012. [Google Scholar]
- Liu, Y.; Xu, X.; Liu, X.; Yao, Y.; Wu, L.; Sun, J. A Self-Alignment Algorithm for SINS Based on Gravitational Apparent Motion and Sensor Data Denoising. Sensors 2015, 15, 9827–9853. [Google Scholar] [CrossRef] [PubMed]
- Dao, H.; Dai, S.; Dai, H. Error Analysis and Performance Improvement about the SINS/DVL Integrated Navigation System. J. Naval Aeronaut. Astronaut. Univ. 2012, 27, 84–88. [Google Scholar]
- Tan, C.; Zhu, X.; Su, Y.; Wang, Y.; Wu, Z.; Gu, D. A New Analytic Alignment Method for a SINS. Sensors 2015, 15, 27930–27953. [Google Scholar] [CrossRef] [PubMed]
- Brokloff, N. Matrix algorithm for Doppler sonar navigation. In Proceedings of the IEEE/MTS OCEANS, Brest, France, 13–16 September 1994. [Google Scholar]
- Guo, Y.S.; Fu, M.Y.; Deng, J.Q. SINS/DVL integrated navigation algorithm considering the impact of ocean currents. J. Chin. Inertial Technol. 2017, 25, 738–742. [Google Scholar]
- Savkin, A.V.; Petersen, I.R. Robust state estimation and model validation for discrete-time uncertain systems with deterministic description of noise and uncertainty. Automatica 1998, 34, 271–274. [Google Scholar] [CrossRef]
- Ghaorui, L.E.; Calafiore, G. Robust filtering for discrete-time systems with bounded noise and parametric uncertainty. IEEE Trans. Autom. Control 2001, 46, 1084–1089. [Google Scholar] [CrossRef]
- Wang, F.; Balakrishnan, V. Robust Kalman filters for linear time-varying systems with stochastic parametric uncertainties. IEEE Trans. Signal Process. 2002, 50, 803–813. [Google Scholar] [CrossRef]
- Kai, X.; Wei, C.; Liu, L. Robust extended Kalman filtering for nonlinear systems with stochastic uncertainties. IEEE Trans. Syst. Man Cybern. A Syst. Humans 2009, 40, 399–405. [Google Scholar] [CrossRef]
- Gao, W.; Li, J.; Zhou, G.; Li, Q. Adaptive Kalman Filtering with Recursive Noise Estimator for Integrated SINS/DVL Systems. J. Navig. 2015, 68, 142–161. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, M.; Tang, K.; Zhang, L. Square-Root Unscented Information Filter and Its Application in SINS/DVL Integrated Navigation. Sensors 2018, 18, 2069. [Google Scholar] [CrossRef] [PubMed]

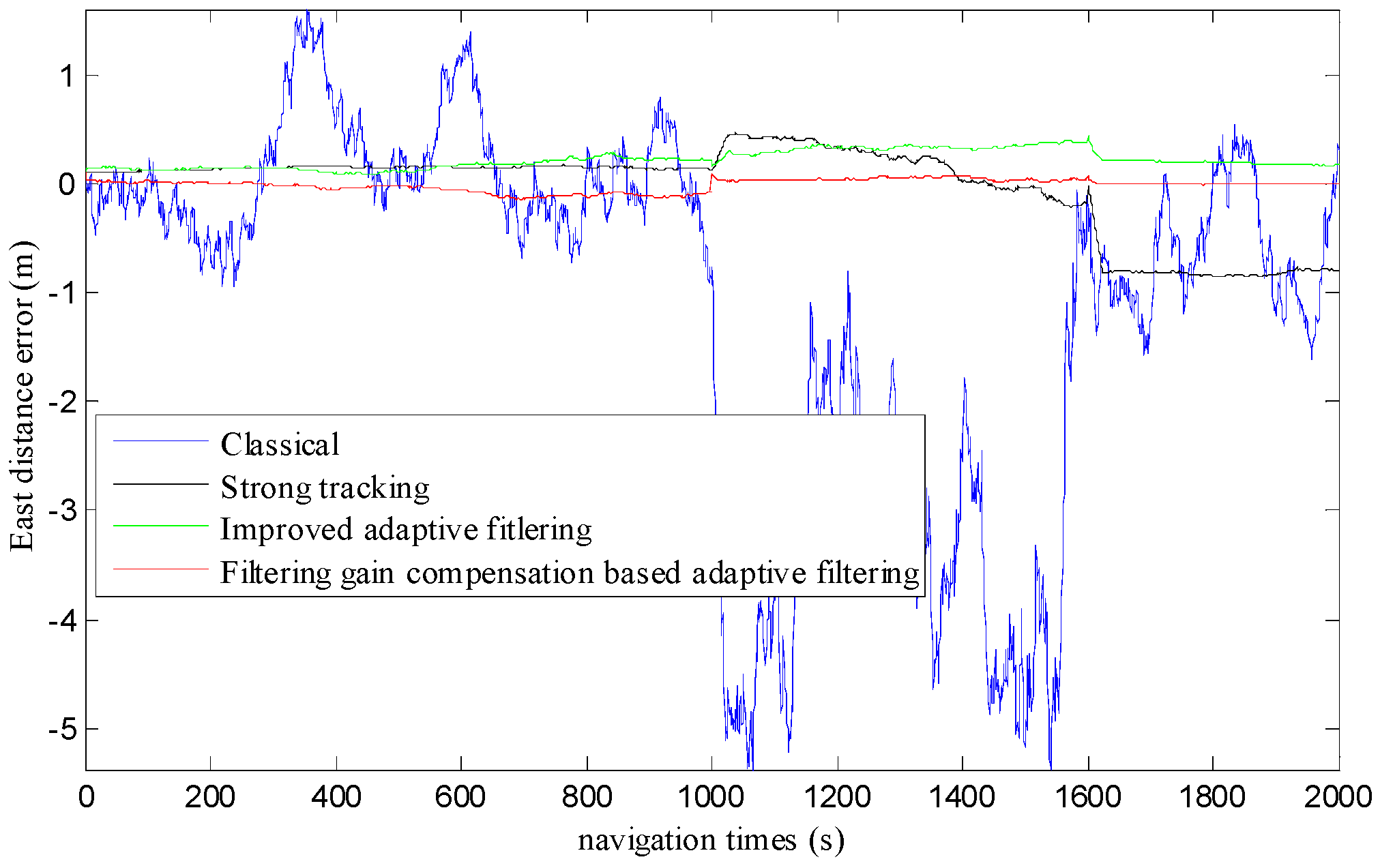
| Parameter | Classical | Strong Tracking | Improved Adaptive Filtering | Filtering Gain Compensation-Based Adaptive Filtering |
|---|---|---|---|---|
| Min (m) | –5.3766 | –0.8611 | 0.0845 | –0.1476 |
| Max (m) | 1.5984 | 0.4584 | 0.4353 | 0.1000 |
| Peak–peak (m) | 6.9751 | 1.3195 | 0.3509 | 0.2476 |
| Mean (m) | –1.0731 | –0.0342 | 0.2167 | –0.0140 |
| Improved | 98.70% | 59.06% | 106.46% | - |
| Parameter | Classical | Strong Tracking | Improved Adaptive Filtering | Filtering Gain Compensation-Based Adaptive Filtering |
|---|---|---|---|---|
| Average positioning time (s) | 0.40131 | 0.28413 | 0.3120 | 1.3474 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Yang, Y.; Luo, Q.; Chen, Y.; Hu, C. A SINS/DVL Integrated Positioning System through Filtering Gain Compensation Adaptive Filtering. Sensors 2019, 19, 4576. https://doi.org/10.3390/s19204576
Yan X, Yang Y, Luo Q, Chen Y, Hu C. A SINS/DVL Integrated Positioning System through Filtering Gain Compensation Adaptive Filtering. Sensors. 2019; 19(20):4576. https://doi.org/10.3390/s19204576
Chicago/Turabian StyleYan, Xiaozhen, Yipeng Yang, Qinghua Luo, Yunsai Chen, and Cong Hu. 2019. "A SINS/DVL Integrated Positioning System through Filtering Gain Compensation Adaptive Filtering" Sensors 19, no. 20: 4576. https://doi.org/10.3390/s19204576
APA StyleYan, X., Yang, Y., Luo, Q., Chen, Y., & Hu, C. (2019). A SINS/DVL Integrated Positioning System through Filtering Gain Compensation Adaptive Filtering. Sensors, 19(20), 4576. https://doi.org/10.3390/s19204576




