Exploring Deep Physiological Models for Nociceptive Pain Recognition
Abstract
1. Introduction
2. Materials and Methods
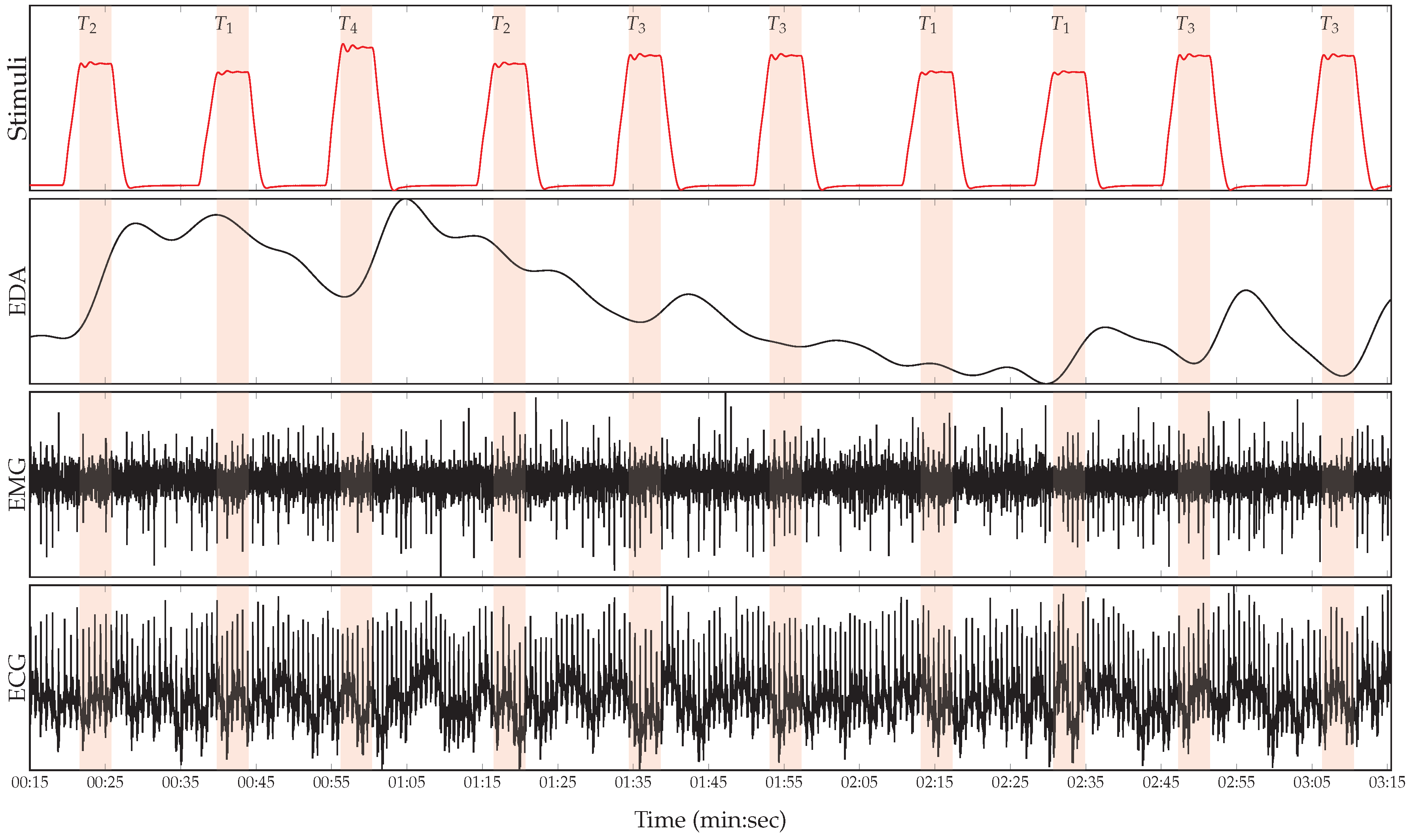
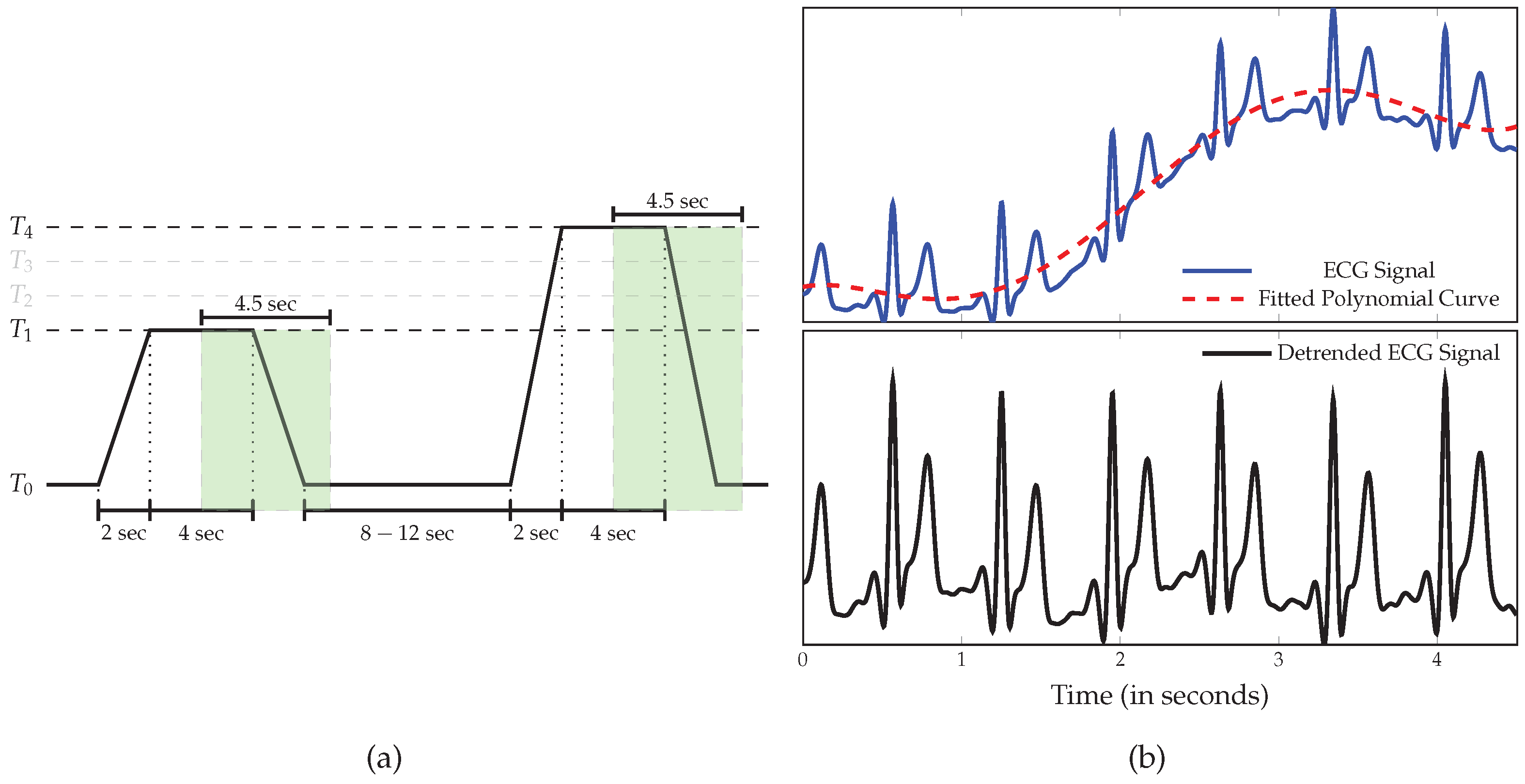
2.1. BioVid Heat Pain Database (BVDB)
2.2. Data Preprocessing
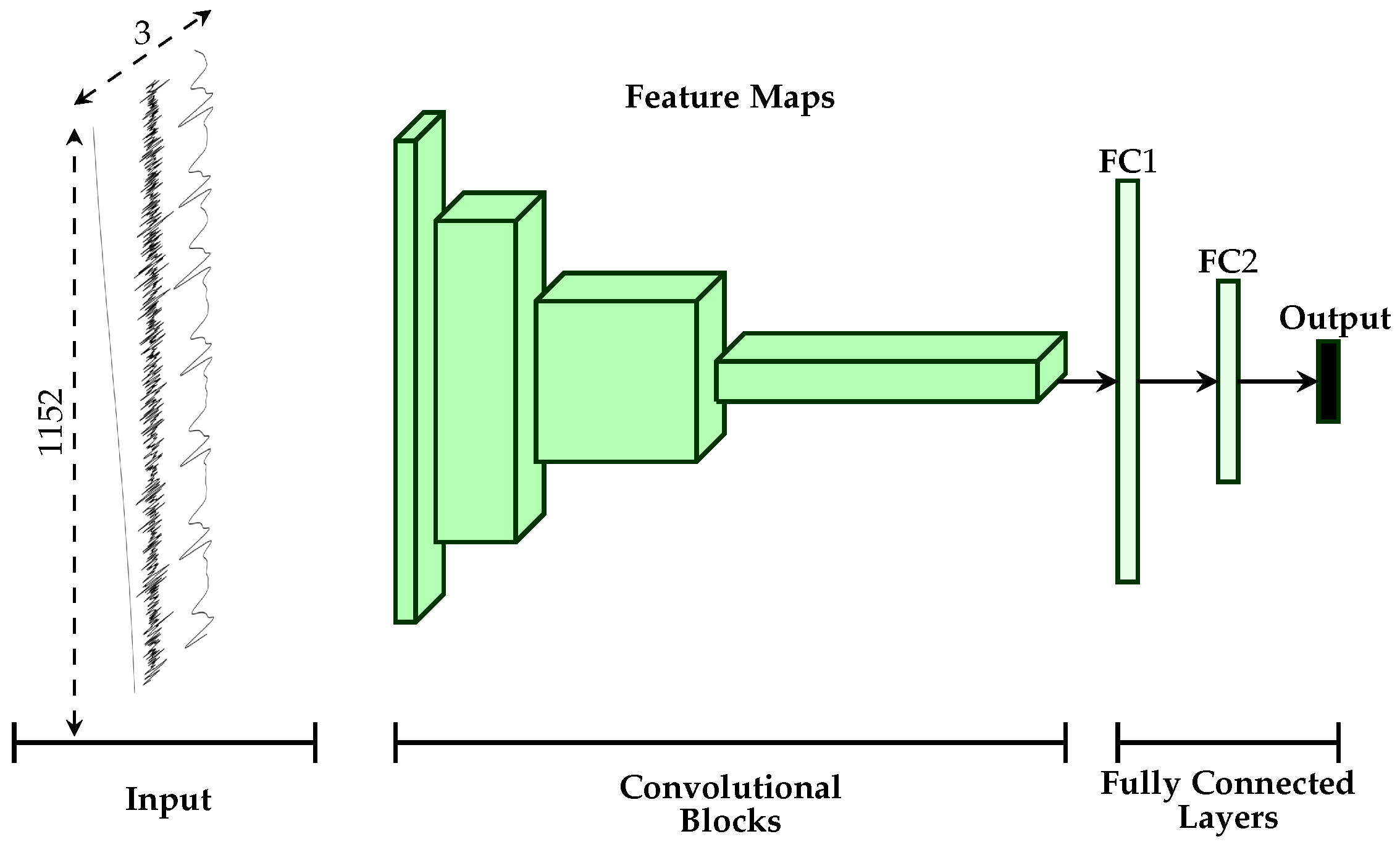
2.3. Uni-modal Deep Model Description
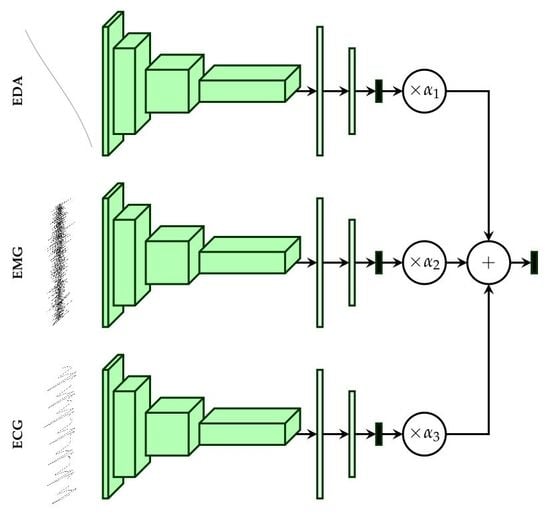
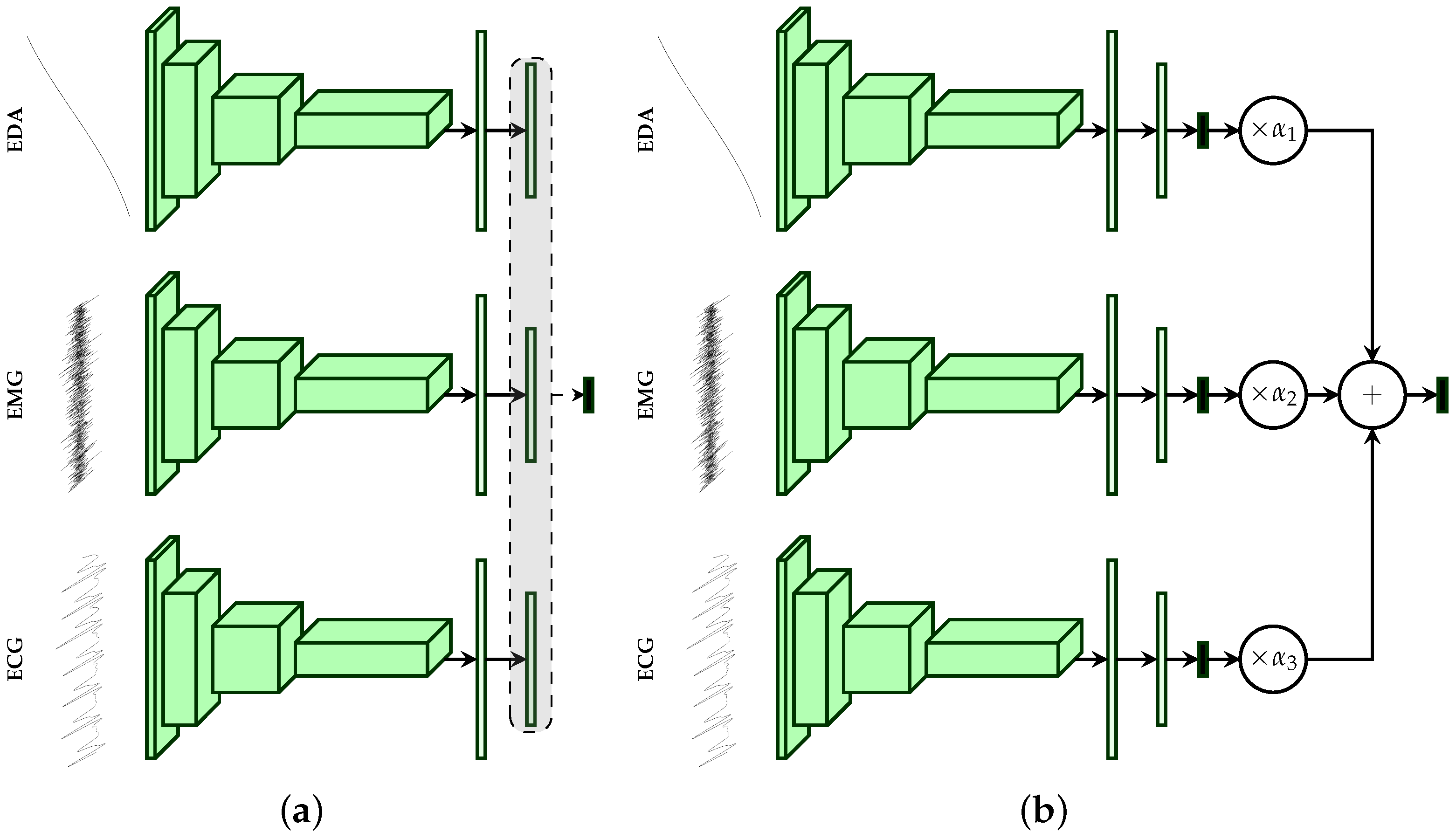
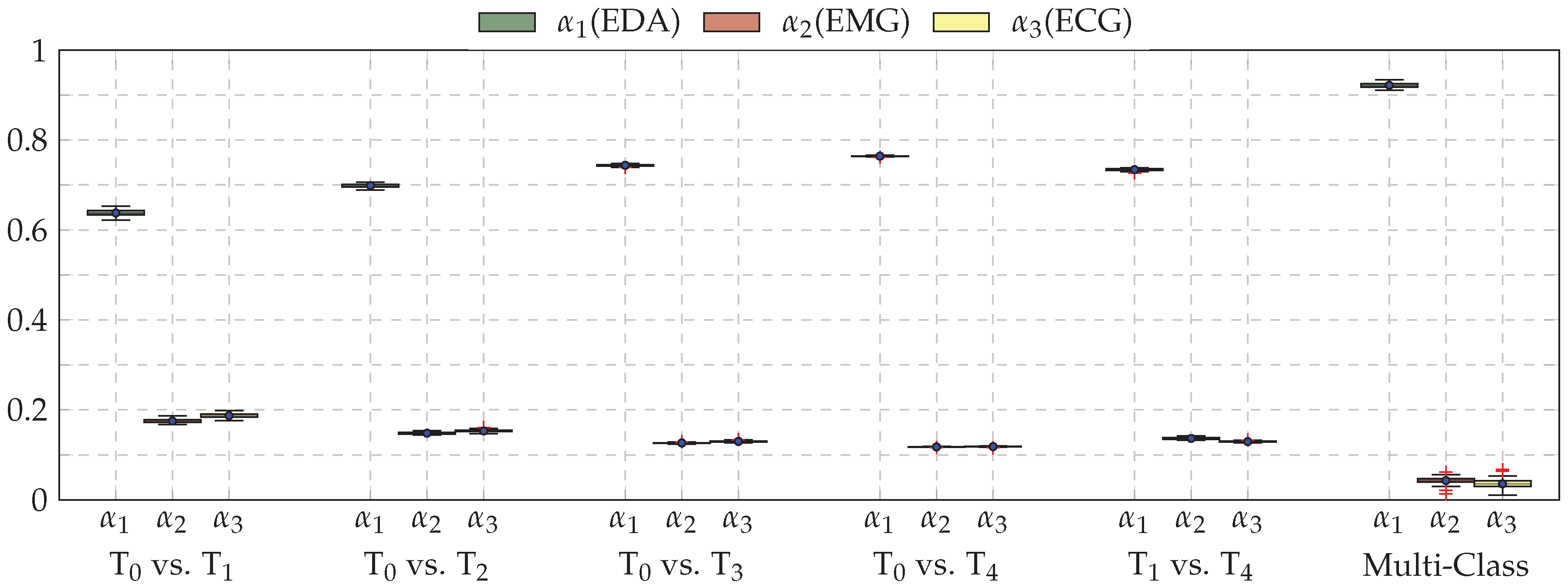
2.4. Multi-Modal Deep Model Description
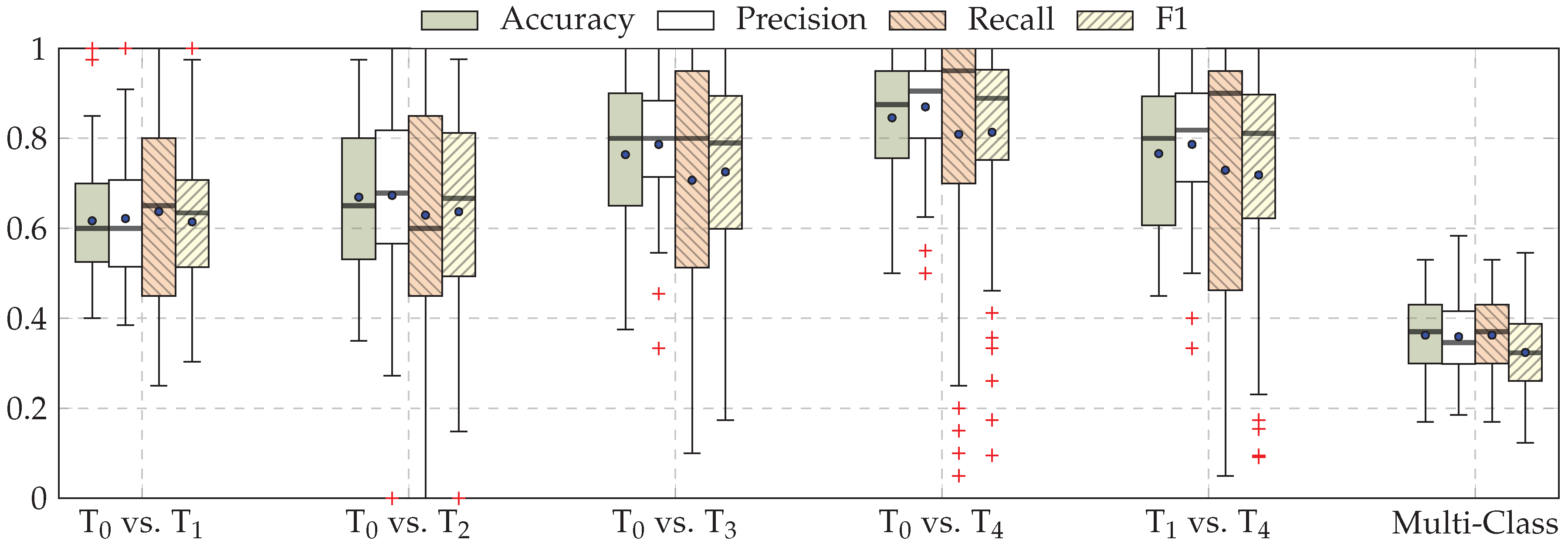
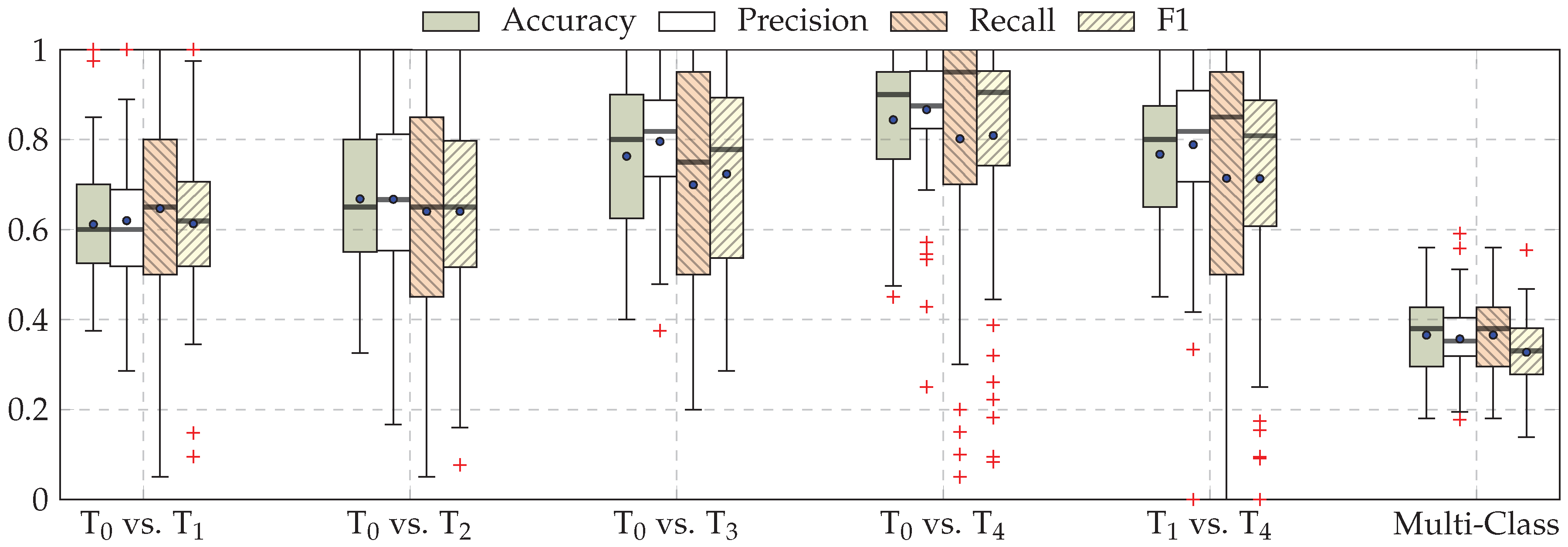
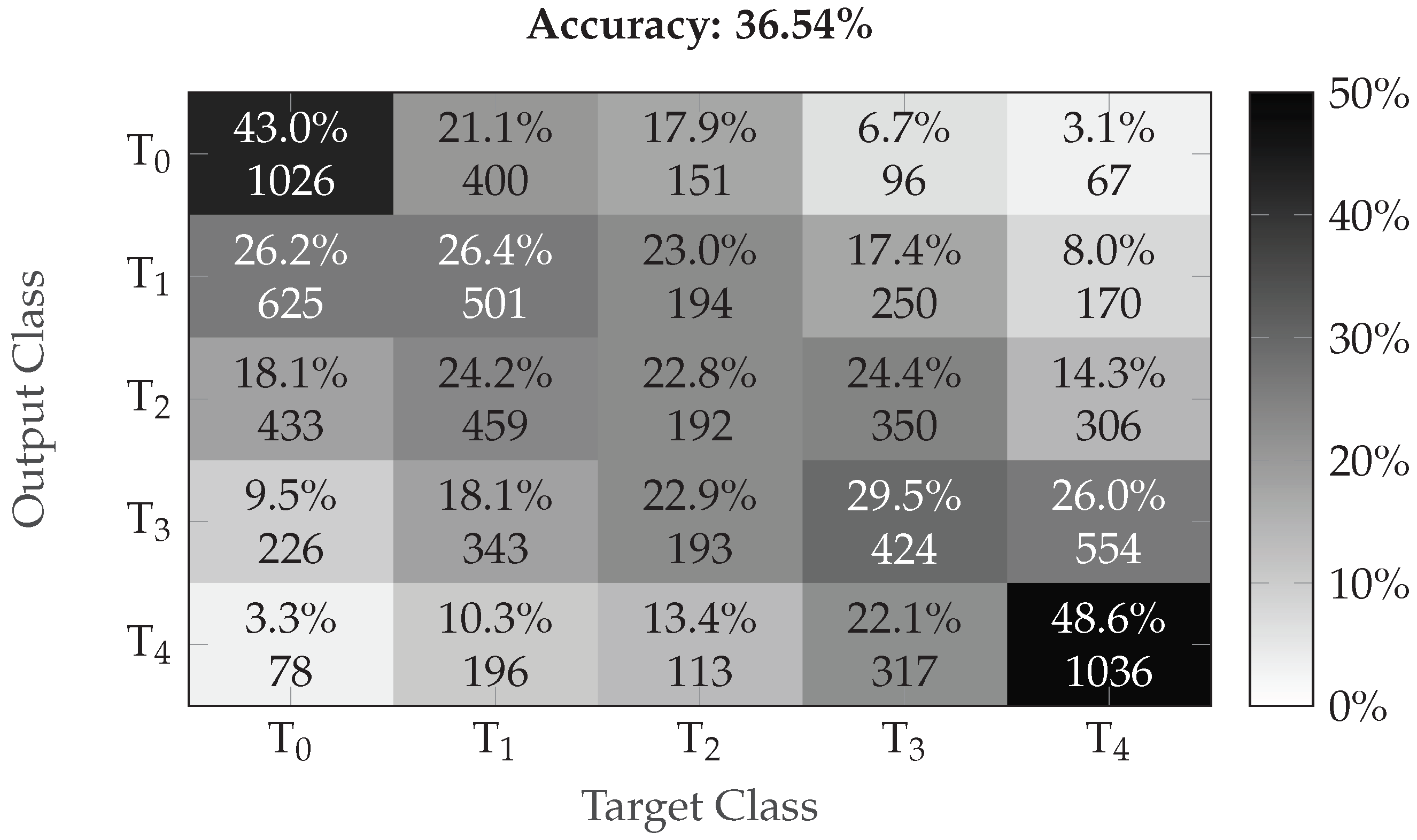
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolution Networks for Large-Scale Image Recognition. In Proceedings of the 3rd IAPR Asian Conference on Pattern Recognition (ACPR), Kuala Lumpur, Malaysia, 3–6 November 2015; pp. 730–734. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan Dumitru abd Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J.A. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Mohd Kamarufin, J.A.; Abdullah, A.; Sallehuddin, R. A Review of Deep Learning Architectures and Their Application. In Modeling, Design and Simulation of Systems; Springer: Singapore, 2017; pp. 83–94. [Google Scholar]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohammed, A.r.; Jaitly, N.; Senior, A.; Nguyen, P.; Sainath, T.N.; Kingsbury, B. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared View of Four Research Groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Zhang, Z.; Geiger, J.; Pohjalainen, J.; Mousa, A.E.D.; Jin, W.; Schuller, B. Deep Learning for Environmentallly Robust Speech Recognition: An Overview of Recent Developments. ACM Trans. Intell. Syst. Technol. 2018, 9, 49:1–49:28. [Google Scholar] [CrossRef]
- Costa-jussà, M.R. From Feature to Paradigm: Deep Learning in Machine Translation. J. Artif. Intell. Res. 2018, 61, 947–974. [Google Scholar] [CrossRef]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent Trends in Deep Learning Based Natural Language Processing [Review Article]. IEEE Comput. Intell. Mag. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Martinez, H.P.; Bengio, Y.; Yannakakis, G.N. Learning Deep Physiological Models of Affect. IEEE Comput. Intell. Mag. 2013, 8, 20–33. [Google Scholar] [CrossRef]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and application in vision. In Proceedings of the IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 253–256. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and Composing Robust features with Denoising Autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Proceedings of the International Joint Conference on Neural Networks, Washington, DC, USA, 1989; pp. 593–605. [Google Scholar]
- Zhong, Y.; Mengyuan, Z.; Yongxiong, W.; Jingdong, Y.; Jianhua, Z. Recognition of emotions using multimodal physiological signals and an ensemble deep learning model. Comput. Methods Programs Biomed. 2017, 140, 93–110. [Google Scholar]
- Santamaria-Granados, L.; Munoz-Organero, M.; Ramirez-González, G.; Abdulhay, E.; Arunkumar, N. Using Deep Convolutional Neural Network for Emotion Detection on a Physiological Signals Dataset (AMIGOS). IEEE Access 2018, 7, 57–67. [Google Scholar] [CrossRef]
- Kanjo, E.; Younis, E.M.; Ang, C.S. Deep learning analysis of mobile physiological, environmental and location sensor data for emotion detection. Inf. Fusion 2019, 49, 46–56. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Geng, W.; Du, Y.; Jin, W.; Wei, W.; Hu, Y.; Li, J. Gesture recognition by instantaneous surface EMG images. Sci. Rep. 2016, 6, 36571. [Google Scholar] [CrossRef] [PubMed]
- Xing, K.; Ding, Z.; Jiang, S.; Ma, X.; Yang, K.; Yang, C.; Li, X.; Jiang, F. Hand Gesture Recognition Based on Deep Learning Method. In Proceedings of the IEEE Third International Conference on Data Science in Cyberspace, Guangzhou, China, 18–21 June 2018; pp. 542–546. [Google Scholar]
- Zhai, X.; Jelfs, B.; Chan, R.H.M.; Tin, C. Self-Recalibrating Surface EMG Pattern Recognition for Neuroprosthesis Control Based on Convolutional Neural Network. Front. Neurosci. 2017, 11, 379. [Google Scholar] [CrossRef] [PubMed]
- Zia ur Rehman, M.; Waris, A.; Gilani, S.O.; Jochumsen, M.; Niazi, I.K.; HJamil, M.; Farina, D.; Kamavuako, E.N. Multiday EMG-Based Classification of Hand Motions with Deep Learning Techniques. Sensors 2018, 18, 2497. [Google Scholar] [CrossRef]
- Tayeb, Z.; Fedjaev, J.; Ghaboosi, N.; Richter, C.; Everding, L.; Qu, X.; Wu, Y.; Cheng, G.; Conradt, J. Validating Deep Neural Networks for Online Decoding of Motor Imagery Movements from EEG Signals. Sensors 2019, 19, 210. [Google Scholar] [CrossRef]
- Faust, O.; Hagiwara, Y.; Hong, T.J.; Lih, O.S.; Acharya, U.R. Deep Learning for Healthcare Applications based on Physiological Signals: A Review. Comput. Methods Programs Biomed. 2018, 161, 1–13. [Google Scholar] [CrossRef]
- Ganapathy, N.; Swaminathan, R.; Deserno, T.M. Deep Learning on 1-D Biosignals: A Taxonomy-based Survey. Yearb. Med. Inform. 2018, 27, 98–109. [Google Scholar] [CrossRef]
- Lim, H.; Kim, B.; Noh, G.J.; Yoo, S.K. A Deep Neural Network-Based Pain Classifier Using a Photoplethysmography Signal. Sensors 2019, 19, 384. [Google Scholar] [CrossRef]
- Abe, S. Support Vector Machines for Pattern Classification; Springer: London, UK, 2005. [Google Scholar]
- Jiang, M.; Mieronkoski, R.; Syrjälä, E.; Anzanpour, A.; Terävä, V.; Rahmani, A.M.; Salanterä, S.; Aantaa, R.; Hagelberg, N.; Liljeberg, P. Acute pain intensity monitoring with the classification of multiple physiological parameters. J. Clin. Monit. Comput. 2019, 33, 493–507. [Google Scholar] [CrossRef]
- Alazrai, R.; AL-Rawi, S.; Alwanni, H.; Daoud, M.I. Tonic Cold Pain Detection Using Choi-Williams Time-Frequency Distribution Analysis of EEG Signals: A Feasibility Study. Appl. Sci. 2019, 9, 3433. [Google Scholar] [CrossRef]
- Thiam, P.; Kessler, V.; Amirian, M.; Bellmann, P.; Layher, G.; Zhang, Y.; Velana, M.; Gruss, S.; Walter, S.; Traue, H.C.; et al. Multi-modal Pain Intensity Recognition based on the SenseEmotion Database. IEEE Trans. Affect. Comput. 2019, 1. [Google Scholar] [CrossRef]
- Thiam, P.; Schwenker, F. Multi-modal data fusion for pain intensity assessement and classification. In Proceedings of the 2017 Seventh International Conference on Image Processing Theory, Tools and Applications (IPTA), Montreal, QC, Canada, 28 November–1 December 2017; pp. 1–6. [Google Scholar]
- Velana, M.; Gruss, S.; Layher, G.; Thiam, P.; Zhang, Y.; Schork, D.; Kessler, V.; Gruss, S.; Neumann, H.; Kim, J.; et al. The SenseEmotion Database: A Multimodal Database for the Development and Systematic Validation of an Automatic Pain- and Emotion-Recognition System. In Multimodal Pattern Recognition of Social Signals in Human-Computer-Interaction; Springer International Publishing: Cham, Switzerland, 2017; pp. 127–139. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kessler, V.; Thiam, P.; Amirian, M.; Schwenker, F. Pain recognition with camera photoplethysmography. In Proceedings of the Seventh International Conference on Image Processing Theory, Tools and Applications (IPTA), Montreal, QC, Canada, 28 November–1 December 2017; pp. 1–5. [Google Scholar]
- Werner, P.; Al-Hamadi, A.; Niese, R.; Walter, S.; Gruss, S.; Traue, H.C. Automatic Pain Recognition from Video and Biomedical Signals. In Proceedings of the International Conference on Pattern Recognition (ICPR), Stockholm, Sweden, 24–28 August 2014; pp. 4582–4587. [Google Scholar]
- Walter, S.; Gruss, S.; Limbrecht-Ecklundt, K.; Traue, H.C.; Werner, P.; Al-Hamadi, A.; Diniz, N.; Silva, G.M.; Andrade, A.O. Automatic Pain Quantification using Autonomic Parameters. Psychol. Neurosci. 2014, 7, 363–380. [Google Scholar] [CrossRef]
- Gruss, S.; Treister, R.; Werner, P.; Traue, H.C.; Crawcour, S.; Andrade, A.; Walter, S. Pain Intensity Recognition Rates via Biopotential Feature Patterns with Support Vector Machines. PLoS ONE 2015, 10, 1–14. [Google Scholar] [CrossRef]
- Walter, S.; Gruss, S.; Ehleiter, H.; Tan, J.; Traue, H.C.; Crawcour, S.; Werner, P.; Al-Hamadi, A.; Andrade, A. The BioVid heat pain database data for the advancement and systematic validation of an automated pain recognition system. In Proceedings of the IEEE International Conference on Cybernetics, Lausanne, Switzerland, 13–15 June 2013; pp. 128–131. [Google Scholar]
- Kächele, M.; Thiam, P.; Amirian, M.; Schwenker, F.; Palm, G. Methods for Person-Centered Continuous Pain Intensity Assessment From Bio-Physiological Channels. IEEE J. Sel. Top. Signal Process. 2016, 10, 854–864. [Google Scholar] [CrossRef]
- Kächele, M.; Amirian, M.; Thiam, P.; Werner, P.; Walter, S.; Palm, G.; Schwenker, F. Adaptive Confidence Learning for the Personalization of Pain Intensity Estimation Systems. Evol. Syst. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Bellmann, P.; Thiam, P.; Schwenker, F. Chapter Multi-classifier-Systems: Architectures, Algorithms and Applications. In Computational Intelligence for Pattern Recognition; Springer: Cham, Switzerland, 2018; Volume 777, pp. 83–113. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Handwritten Digit Recognition with a Back-propagation Network. In Proceedings of the 2nd International Conference on Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1990; pp. 396–404. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Neural Network Learning by Exponential Linear Units (ELUs). In Proceedings of the 4th International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Pyakillya, B.; Kazachenko, N.; Mikhailovsky, N. Deep Learning for ECG Classification. J. Phys. Conf. Ser. 2017, 913, 012004. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Keras: The Python Deep Learning Library. 2015. Available online: https://keras.io (accessed on 16 October 2019).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, C.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 16 October 2019).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lopez-Martinez, D.; Picard, R. Continuous Pain Intensity Estimation from Autonomic Signals with Recurrent Neural Networks. In Proceedings of the 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 5624–5627. [Google Scholar]
- Kächele, M.; Werner, P.; Walter, S.; Al-Hamadi, A.; Schwenker, F. Bio-Visual Fusion for Person-Independent Recognition of Pain Intensity. In Multiple Classifier Systems (MCS); Springer: Cham, Switzerland, 2015; pp. 220–230. [Google Scholar]
- Kächele, M.; Thiam, P.; Amirian, M.; Werner, P.; Walter, S.; Schwenker, F.; Palm, G. Engineering Applications of Neural Networks. In Engineering Applications of Neural Networks, EANN 2015; Chapter Multimodal Data Fusion for Person-Independent, Continuous Estimation of Pain Intensity; Iliadis, L., Jayne, C., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 275–285. [Google Scholar]
- Werner, P.; Al-Hamadi, A.; Limbrecht-Ecklundt, K.; Walter, S.; Gruss, S.; Traue, H.C. Automatic Pain Assessment with Facial Activity Descriptors. IEEE Trans. Affect. Comput. 2017, 8, 286–299. [Google Scholar] [CrossRef]
- Jung, H.; Lee, S.; Yim, J.; Park, S.; Kim, J. Joint Fine-Tuning in Deep Neural Networks for Facial Expression. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2983–2991. [Google Scholar]
- Rodriguez, P.; Cucurull, G.; Gonzàlez, J.; Gonfaus, J.M.; Nasrollahi, K.; Moeslund, T.B.; Roca, F.X. Deep Pain: Exploiting Long Short-Term Memory Networks for Facial Expression Classification. IEEE Trans. Cybern. 2018, 1–11. [Google Scholar] [CrossRef]
- Yan, J.; Zheng, W.; Vui, Z.; Song, P. A Joint Convolutional Bidirectional LSTM Framework for Facial Expression Recognition. IEICE Trans. Inf. Syst. 2018, E101.D, 1217–1220. [Google Scholar] [CrossRef]
| EDA | EMG & ECG | ||||||
|---|---|---|---|---|---|---|---|
| Layer Name | No. Kernels (Units) | Kernel (Pool) Size | Stride | Layer Name | No. Kernels (Units) | Kernel (Pool) Size | Stride |
| Convolution | 16 | 3 | 1 | Convolution | 16 | 11 | 1 |
| Batch Normalisation | - | - | - | Batch Normalisation | - | - | - |
| Max Pooling | - | 2 | 2 | Max Pooling | - | 2 | 2 |
| Convolution | 16 | 3 | 1 | Dropout | - | - | - |
| Batch Normalisation | - | - | - | Convolution | 16 | 11 | 1 |
| Max Pooling | - | 2 | 2 | Batch Normalisation | - | - | - |
| Convolution | 32 | 3 | 1 | Max Pooling | - | 2 | 2 |
| Batch Normalisation | - | - | - | Dropout | - | - | - |
| Max Pooling | - | 2 | 2 | Convolution | 32 | 11 | 1 |
| Convolution | 32 | 3 | 1 | Batch Normalisation | - | - | - |
| Batch Normalisation | - | - | - | Max Pooling | - | 2 | 2 |
| Max Pooling | - | 2 | 2 | Dropout | - | - | - |
| Convolution | 64 | 3 | 1 | Convolution | 32 | 11 | 1 |
| Batch Normalisation | - | - | - | Batch Normalisation | - | - | - |
| Max Pooling | - | 2 | 2 | Max Pooling | - | 2 | 2 |
| Convolution | 64 | 3 | 1 | Dropout | - | - | - |
| Batch Normalisation | - | - | - | Convolution | 64 | 11 | 1 |
| Max Pooling | - | 2 | 2 | Batch Normalisation | - | - | - |
| Convolution | 128 | 3 | 1 | Max Pooling | - | 2 | 2 |
| Batch Normalisation | - | - | - | Dropout | - | - | - |
| Max Pooling | - | 2 | 2 | Convolution | 64 | 11 | 1 |
| Flatten | - | - | - | Batch Normalisation | - | - | - |
| Fully Connected | 1024 | - | - | Max Pooling | - | 2 | 2 |
| Dropout | - | - | - | Dropout | - | - | - |
| Fully Connected | 512 | - | - | Convolution | 128 | 11 | 1 |
| Dropout | - | - | - | Batch Normalisation | - | - | - |
| Fully Connected | c | - | - | Max Pooling | - | 2 | 2 |
| Flatten | - | - | - | ||||
| Dropout | - | - | - | ||||
| Fully Connected | 1024 | - | - | ||||
| Dropout | - | - | - | ||||
| Fully Connected | 512 | - | - | ||||
| Dropout | - | - | - | ||||
| Fully Connected | c | - | - | ||||
| Layer Name | No. Kernels (Units) | Kernel (Pool) Size | Stride |
|---|---|---|---|
| Convolution | 16 | ||
| Convolution | 16 | ||
| Batch Normalisation | - | - | - |
| Max Pooling | - | ||
| Dropout | - | - | - |
| Convolution | 32 | ||
| Batch Normalisation | - | - | - |
| Max Pooling | - | ||
| Dropout | - | - | - |
| Convolution | 32 | ||
| Batch Normalisation | - | - | - |
| Max Pooling | - | ||
| Dropout | - | - | - |
| Convolution | 64 | ||
| Batch Normalisation | - | - | - |
| Max Pooling | - | ||
| Dropout | - | - | - |
| Convolution | 64 | ||
| Batch Normalisation | - | - | - |
| Max Pooling | - | ||
| Flatten | - | - | - |
| Dropout | - | - | - |
| Fully Connected | 1024 | - | - |
| Dropout | - | - | - |
| Fully Connected | 512 | - | - |
| Dropout | - | - | - |
| Fully Connected | c | - | - |
| Method | ECG | EMG | EDA | Fusion |
|---|---|---|---|---|
| Werner et al. [36] | 62.00 | 57.90 | 73.80 | 74.10 |
| Kächele et al. [40,41] | 53.90 | 58.51 | 81.10 | 82.73 |
| Our Approaches (CNNs) | Early Fusion: Late Fusion (a): Late Fusion (b): |
| Task | ECG | EMG | EDA | Late Fusion (b) |
|---|---|---|---|---|
| vs. | † | a,b | ||
| vs. | † | a,b | ||
| vs. | † | a,b | ||
| vs. | † | a,b | ||
| vs. | a,b,† | |||
| Multi-Class | a,b,† |
| Measure | Binary Classification | Multi-Class Classification |
|---|---|---|
| Accuracy | ||
| Precision | ||
| Recall | ||
| F1 score | ||
| Method | vs. | vs. | vs. | vs. |
|---|---|---|---|---|
| Werner et al. [36] | 55.40 | 60.20 | 65.90 | 73.80 |
| Lopez-Martinez et al. [55] | 56.44 | 59.40 | 66.00 | 74.21 |
| Our Approach (CNN) |
| Approach | Description | Performance |
|---|---|---|
| Werner et al. [58] | Early Fusion with Random Forests (Head Pose and Facial Activity Descriptors) | 72.40 |
| Werner et al. [36] | Early Fusion with Random Forests (EDA, EMG, ECG, Video) | 77.80 |
| Kächele et al. [56] | Early Fusion with Random Forests (EDA, ECG, Video) | 78.90 |
| Kächele et al. [57] | Late Fusion with Random Forests and Pseudo-inverse (EDA, EMG, ECG, Video) | 83.10 |
| Our Approach (CNN) | Late Fusion (b) with CNNs (EDA, EMG, ECG) |
| Approach | Description | Performance |
|---|---|---|
| Kächele et al. [56] | Late Fusion with SVMs and Mean Aggregation (EMG (zygomaticus), EMG (corrugator), EMG (trapezius), ECG, EDA, Video) | 76.60 |
| Walter et al. [37] | Early Fusion with SVM (EMG (zygomaticus), EMG (corrugator), EMG (trapezius), ECG, EDA) | 77.05 |
| Our Approach (CNN) | Late Fusion (b) with CNNs (EMG (trapezius), ECG, EDA) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiam, P.; Bellmann, P.; Kestler, H.A.; Schwenker, F. Exploring Deep Physiological Models for Nociceptive Pain Recognition. Sensors 2019, 19, 4503. https://doi.org/10.3390/s19204503
Thiam P, Bellmann P, Kestler HA, Schwenker F. Exploring Deep Physiological Models for Nociceptive Pain Recognition. Sensors. 2019; 19(20):4503. https://doi.org/10.3390/s19204503
Chicago/Turabian StyleThiam, Patrick, Peter Bellmann, Hans A. Kestler, and Friedhelm Schwenker. 2019. "Exploring Deep Physiological Models for Nociceptive Pain Recognition" Sensors 19, no. 20: 4503. https://doi.org/10.3390/s19204503
APA StyleThiam, P., Bellmann, P., Kestler, H. A., & Schwenker, F. (2019). Exploring Deep Physiological Models for Nociceptive Pain Recognition. Sensors, 19(20), 4503. https://doi.org/10.3390/s19204503