Constrained MLAMBDA Method for Multi-GNSS Structural Health Monitoring
Abstract
1. Introduction
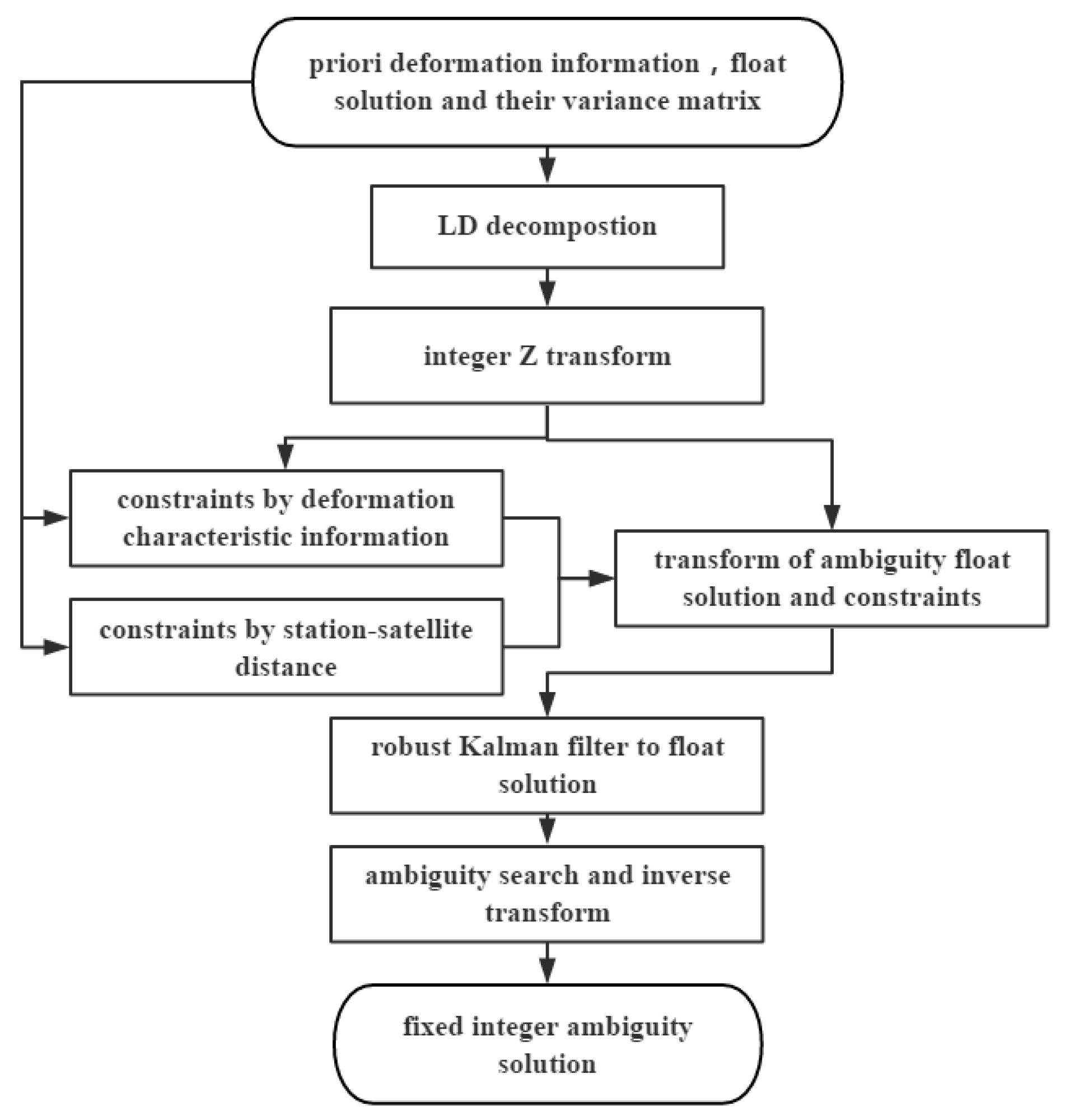
2. Materials and Methods
- Conduct decomposition of ambiguity variance matrix , where is the ambiguity variance matrix and is a diagonal matrix.
- Construct integer ambiguity transform matrix using matrix : .
- Transfer the float solution into a fixed solution ,where is the DD integer ambiguity. The constraints are also transformed to , where denotes the constraints.
- Search for the optimal integer ambiguity. The MLAMBDA method involves shrinking the search radius through updating the radius as , where is the serial number of the fixed ambiguity in matrix .
- Transfer the search result of DD ambiguities back to the integer ambiguities.
2.1. Constraint of Deformation Information
2.2. Constraints on Multi-GNSS MLAMBDA
3. Experiments and Analysis
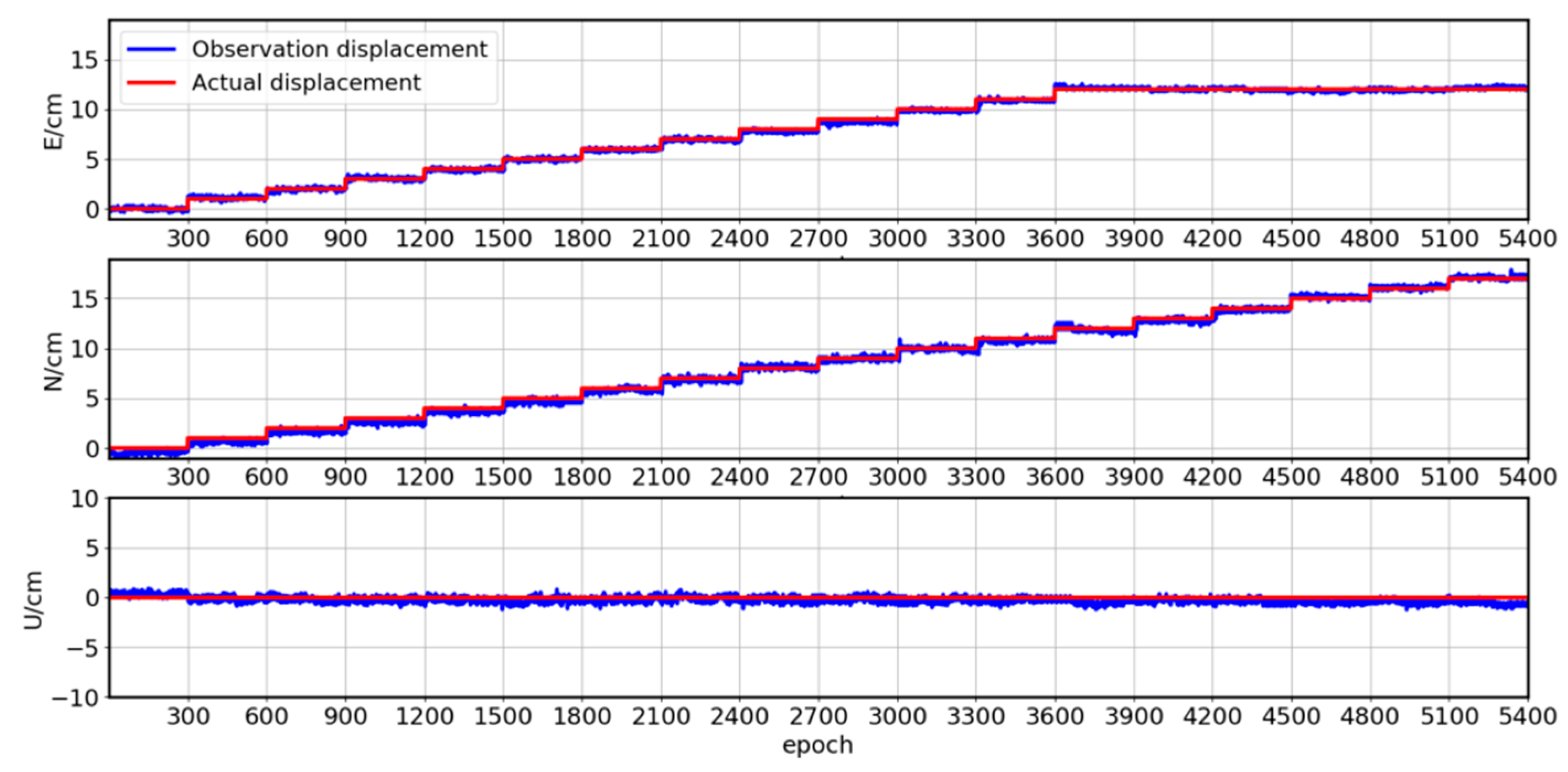
3.1. Experiment on the Baishazhou Bridge
3.2. Experiment on the Teaching Experiment Building of Wuhan University
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Lang, R.; Qin, H.; Zhou, K.; Cao, Y. A Real-Time Interference Monitoring Technique for GNSS Based on a Twin Support Vector Machine Method. Sensors 2016, 16, 329. [Google Scholar] [CrossRef] [PubMed]
- Barzaghi, R.; Cazzaniga, N.E.; De Gaetani, C.I.; Pinto, L.; Tornatore, V. Estimating and Comparing Dam Deformation Using Classical and GNSS Techniques. Sensors 2018, 18, 756. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Nguyen, D.T.; Xie, Y.; Xie, Y.; Owen, J.S.; Psimoulis, P.; Ince, S.; Chen, Q.; Ye, J.; Bhatia, P. Design and Implementation of a New System for Large Bridge Monitoring—GeoSHM. Sensors 2018, 18, 775. [Google Scholar] [CrossRef] [PubMed]
- Hatch, R. Instantaneous Ambiguity Resolution. In Proceedings of the Kinematic Systems in Geodesy, Surveying, and Remote Sensing, Banff, AB, Canada, 10–13 September 1990. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Chang, X.W.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Park, C.; Kim, I. Integer ambiguity resolution for GPS based attitude determination system. In Proceedings of the 37th SICE Annual Conference. International Session Papers, Chiba, Japan, 29–31 July 1998. [Google Scholar]
- Wang, B.; Miao, L.; Wang, S.; Shen, J. A constrained LAMBDA method for GPS attitude determination. GPS Solut. 2009, 13, 97–107. [Google Scholar] [CrossRef]
- Oliazadeh, N.; Landry, R.; Yeste-Ojeda, O.A.; Gagnon, E.; Wong, F. GPS-based attitude determination using RLS and LAMBDA methods. In Proceedings of the 2015 International Conference on Localization and GNSS (ICL-GNSS), Gothenburg, Sweden, 22–24 June 2015. [Google Scholar]
- Gong, A.; Zhao, X.; Pang, C.; Duan, R.; Wang, Y. GNSS Single Frequency, Single Epoch Reliable Attitude Determination Method with Baseline Vector Constraint. Sensors 2015, 15, 30093–30103. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Luzi, G.; Monserrat, O.; Crosetto, M. Ground-based synthetic aperture radar interferometry for deformation monitoring: A case study at Geheyan Dam, China. J. Appl. Remote. Sens. 2017, 11, 036030. [Google Scholar] [CrossRef]
- Wong, K.Y.; Lau, C.K.; Flint, A.R. Planning and implementation of the structural health monitoring system for cable-supported bridges in Hong Kong. In Proceedings of the SPIE’s 5th Annual International Symposium on Nondestructive Evaluation and Health Monitoring of Aging Infrastructure, Newport Beach, CA, USA, 6–8 March 2000. [Google Scholar]
- Meng, X.; Dodson, A.H.; Roberts, G.W. Detecting bridge dynamics with GPS and triaxial accelerometers. Eng. Struct. 2007, 29, 3178–3184. [Google Scholar] [CrossRef]
- Psimoulis, P.; Pytharouli, S.; Karambalis, D.; Stiros, S. Potential of global positioning system (GPS) to measure frequencies of oscillations of engineering structures. J. Sound Vib. 2008, 318, 606–623. [Google Scholar] [CrossRef]
- Yu, X.; Xu, S.; Gao, W.; Weical, L. Similar Single-Difference Model and Its Algorithm for Solving GPS Monitoring Deformation Directly at Single Epoch. Geo-Spat. Inf. Sci. 2002, 6, 51–56. [Google Scholar]
- Bai, Z.; Ren, C.; Jiang, G. Experimental Analysis of Continuous Deformation Monitoring Using the Whole Weekly Single Epoch Algorithm (in Chinese). J. Geod. Geodyn. 2014, 34, 96–99. [Google Scholar]
- Park, C.; Kim, I.; Lee, J.G.; Jee, G.-I. Efficient ambiguity resolution using constraint equation. In Proceedings of the Position, Location and Navigation Symposium—PLANS ’96, Atlanta, GA, USA, 22–25 April 1996. [Google Scholar]
- Dai, W. Single Epoch Ambiguity Resolution in Structure Monitoring Using GPS (in Chinese). Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 234–237. [Google Scholar]
- Koch, K.R.; Yang, Y. Robust Kalman filter for rank deficient observation models. J. Geod. 1998, 72, 436–441. [Google Scholar] [CrossRef]
- Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE baseline determination using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
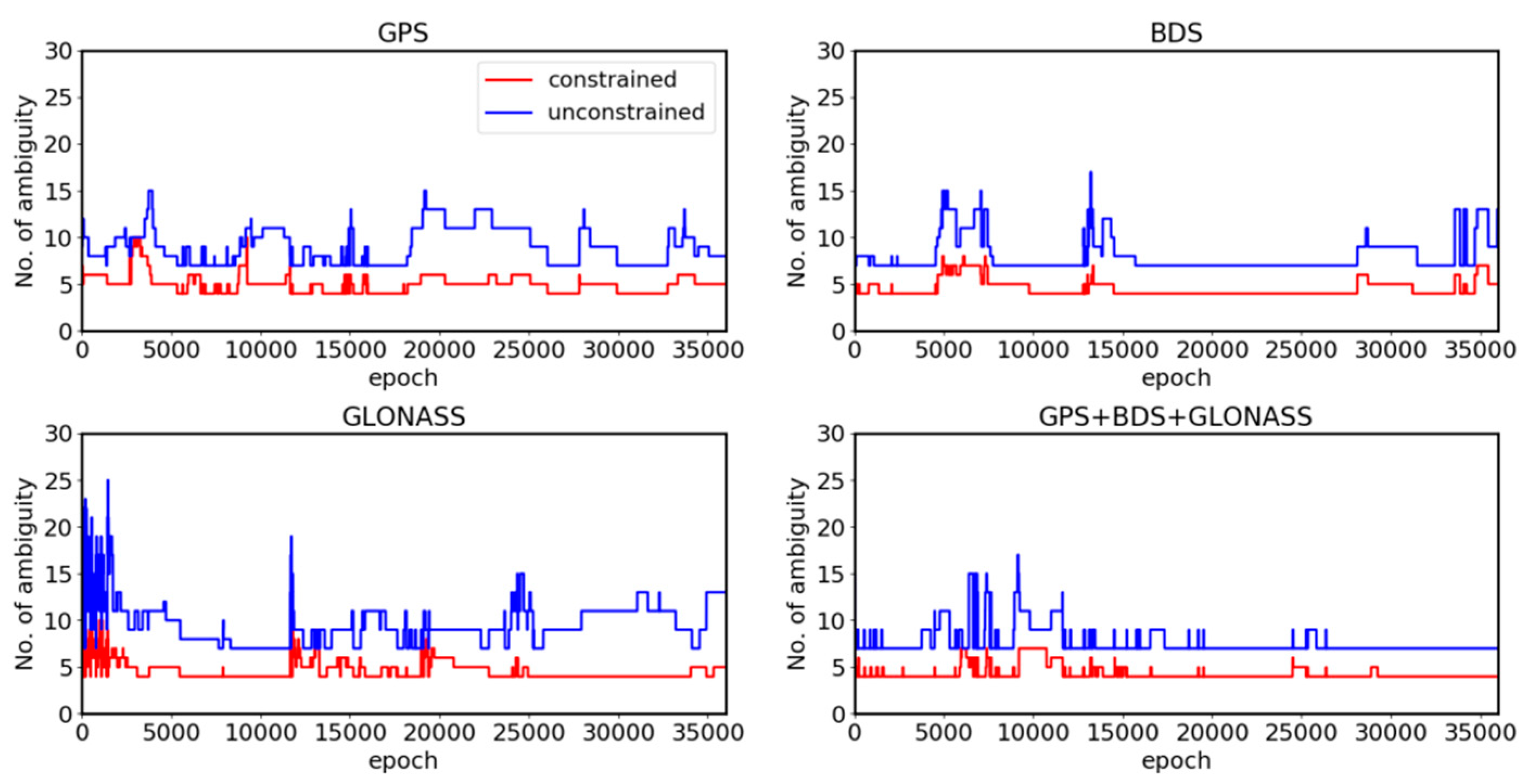
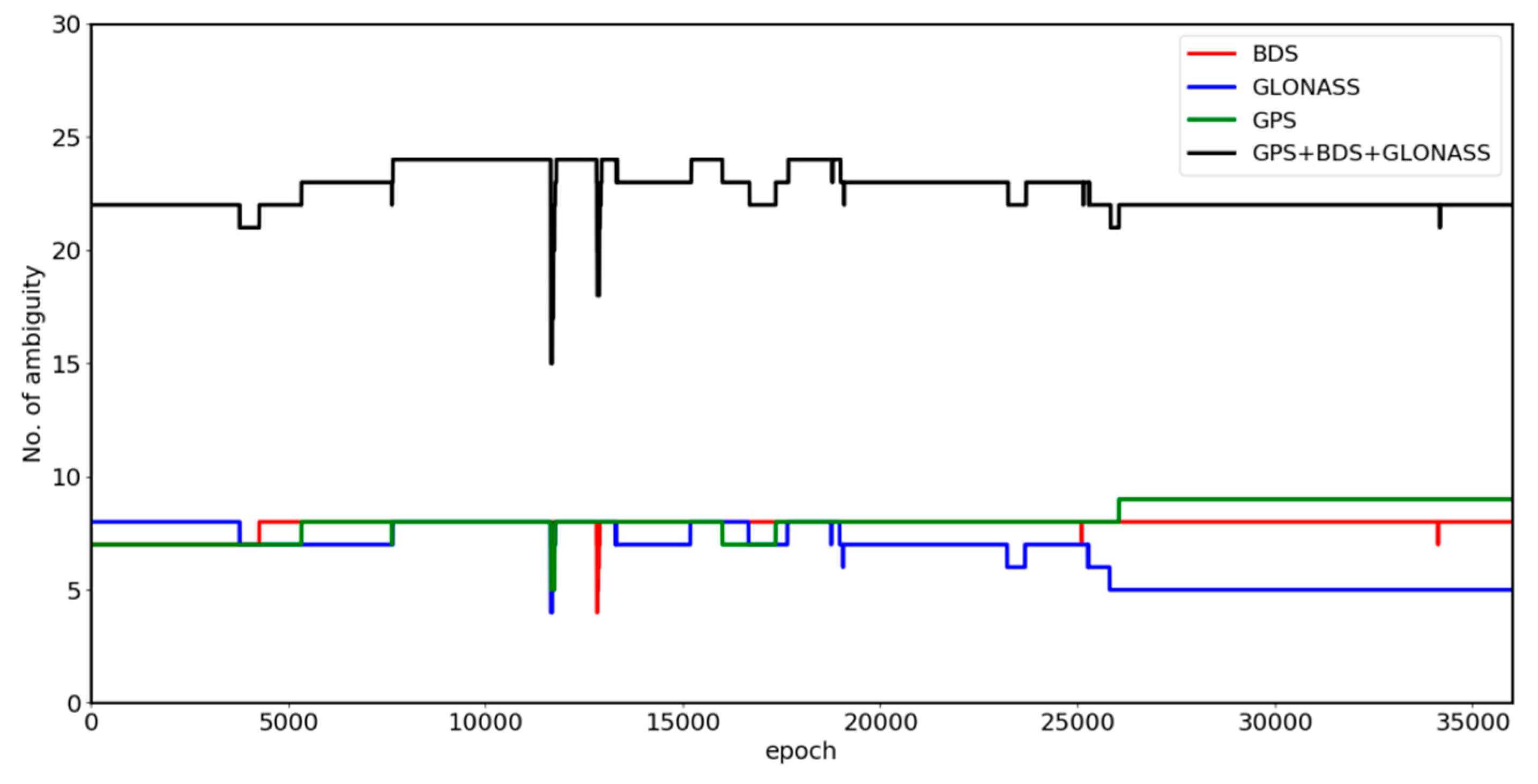
| Baseline Length (m) | Multi-GNSS | Method | Running Time (s) | Epoch-to-First Fixed Ambiguity | ASR (%) |
|---|---|---|---|---|---|
| 2480.4751 | GPS | constrained | 719.451 | 5 | 95.9 |
| unconstrained | 788.561 | 60 | 91.6 | ||
| BDS | constrained | 768.111 | 1 | 99.8 | |
| unconstrained | 838.462 | 51 | 99.6 | ||
| GLONASS | constrained | 674.581 | 2231 | 89.2 | |
| unconstrained | 760.271 | 5272 | 65.1 | ||
| GPS+BDS | constrained | 1162.402 | 1 | 94.0 | |
| unconstrained | 1280.622 | 1 | 87.6 | ||
| GPS+BDS+GLONASS | constrained | 1763.982 | 90 | 76.9 | |
| unconstrained | 1945.271 | 1655 | 66.3 |
| Multi-GNSS | Method | E | N | U | V |
|---|---|---|---|---|---|
| GPS | constrained | 6.13 | 7.84 | 13.56 | 16.82 |
| unconstrained | 9.51 | 11.03 | 18.47 | 23.52 | |
| BDS | constrained | 3.29 | 3.87 | 7.15 | 8.77 |
| unconstrained | 4.13 | 4.24 | 8.64 | 10.47 | |
| GLONASS | constrained | 11.84 | 13.57 | 24.52 | 35.35 |
| unconstrained | 176.42 | 195.52 | 403.12 | 481.52 | |
| GPS+BDS | constrained | 7.84 | 8.61 | 15.45 | 19.35 |
| unconstrained | 13.46 | 14.57 | 26.87 | 33.40 | |
| GPS+BDS+GLONASS | constrained | 72.14 | 85.21 | 143.87 | 182.11 |
| unconstrained | 154.58 | 162.82 | 334.87 | 403.17 |
| Baseline Length (m) | Method | Running Time (s) | ASR (%) |
|---|---|---|---|
| 427.8865 | constrained | 486.681 | 99.8 |
| unconstrained | 508.970 | 93.8 |
| E | N | U | V | ||
|---|---|---|---|---|---|
| Constrained | Internal accuracy | 2.65 | 2.14 | 4.31 | 5.49 |
| External accuracy | 3.89 | 3.22 | 5.05 | 7.14 | |
| Unconstrained | Internal accuracy | 3.05 | 2.69 | 5.13 | 6.53 |
| External accuracy | 3.98 | 3.54 | 6.11 | 8.11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Nie, G.; Chen, D.; Wu, S.; Wang, K. Constrained MLAMBDA Method for Multi-GNSS Structural Health Monitoring. Sensors 2019, 19, 4462. https://doi.org/10.3390/s19204462
Li H, Nie G, Chen D, Wu S, Wang K. Constrained MLAMBDA Method for Multi-GNSS Structural Health Monitoring. Sensors. 2019; 19(20):4462. https://doi.org/10.3390/s19204462
Chicago/Turabian StyleLi, Haiyang, Guigen Nie, Dezhong Chen, Shuguang Wu, and Kezhi Wang. 2019. "Constrained MLAMBDA Method for Multi-GNSS Structural Health Monitoring" Sensors 19, no. 20: 4462. https://doi.org/10.3390/s19204462
APA StyleLi, H., Nie, G., Chen, D., Wu, S., & Wang, K. (2019). Constrained MLAMBDA Method for Multi-GNSS Structural Health Monitoring. Sensors, 19(20), 4462. https://doi.org/10.3390/s19204462





