A Localization and Tracking Approach in NLOS Environment Based on Distance and Angle Probability Model
Abstract
:1. Introduction
2. System Model
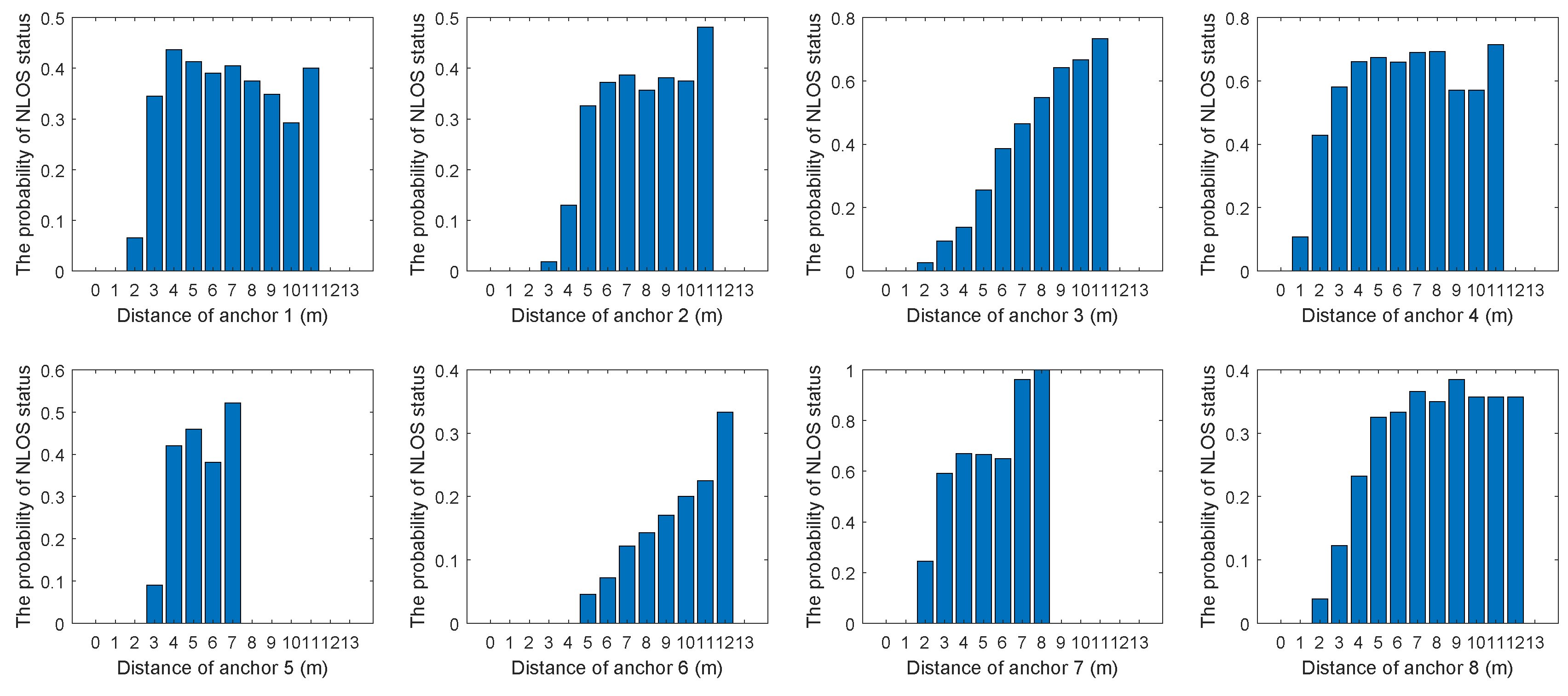
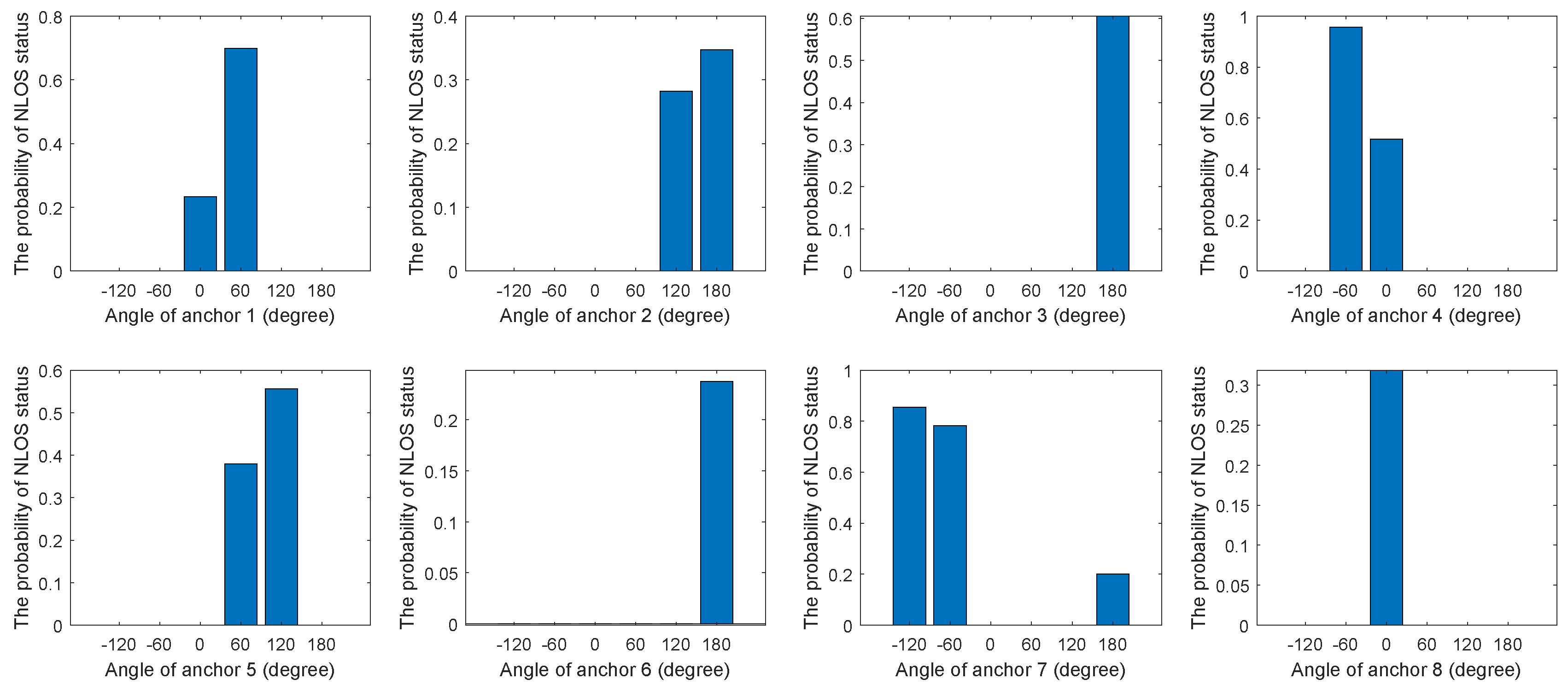
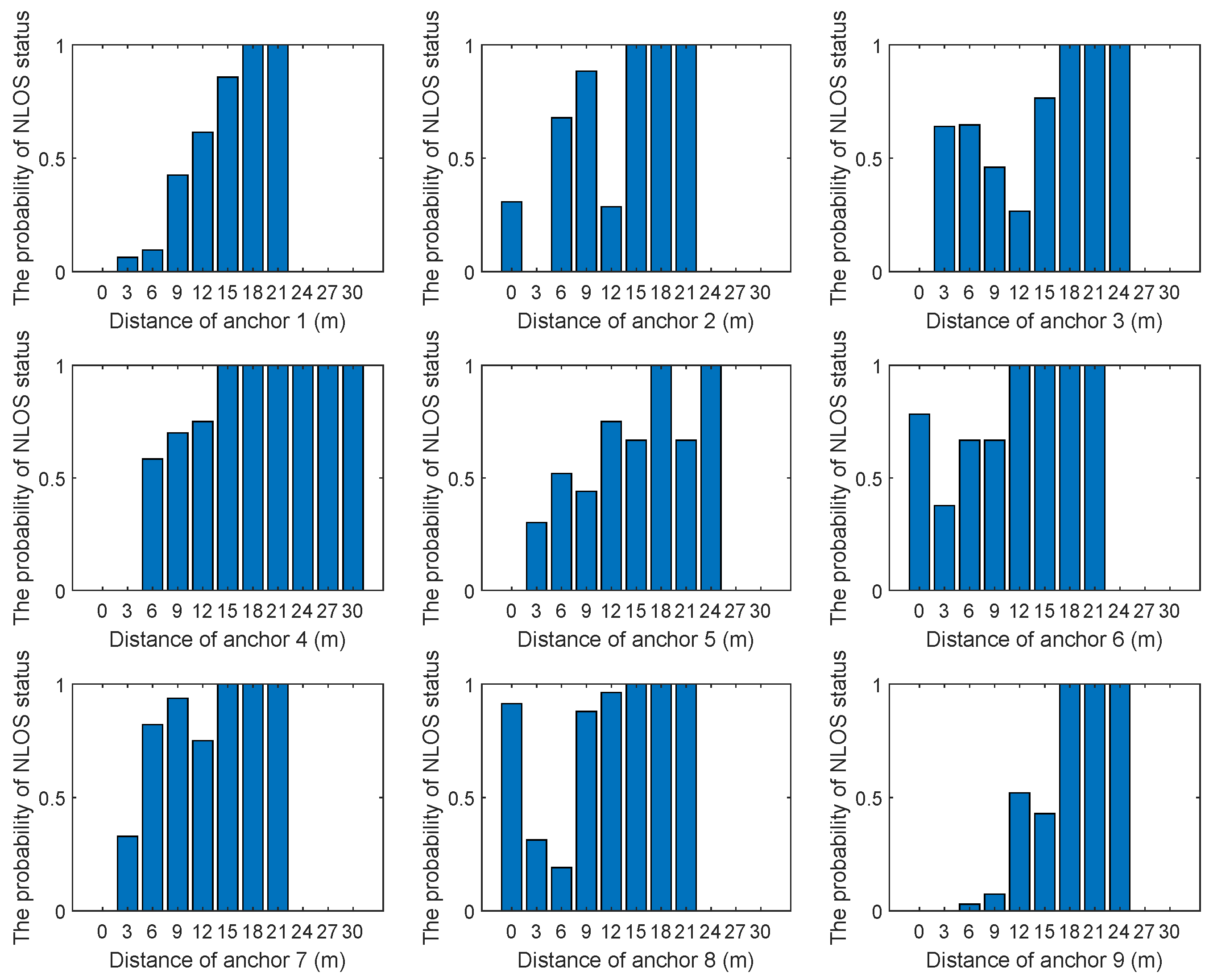
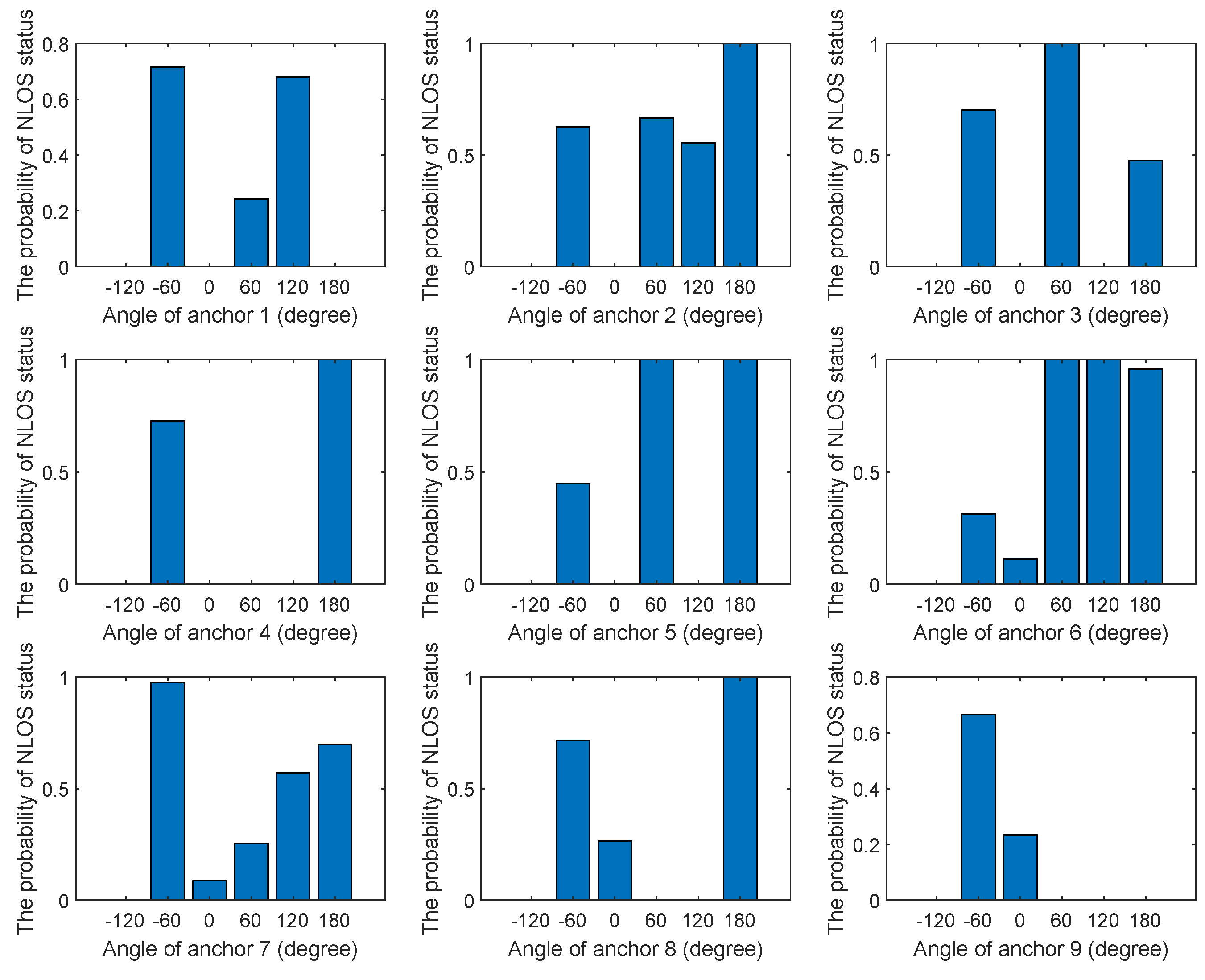
3. NLOS Propagation Occurrence Probability Model
| Algorithm 1 The probability acquisition method related to distance. |
|
| Algorithm 2 The probability acquisition method related to angle. |
|
4. Simplified Calculation of Maximum Likelihood Estimation
5. Localization Based on Extended Kalman Filter Algorithm
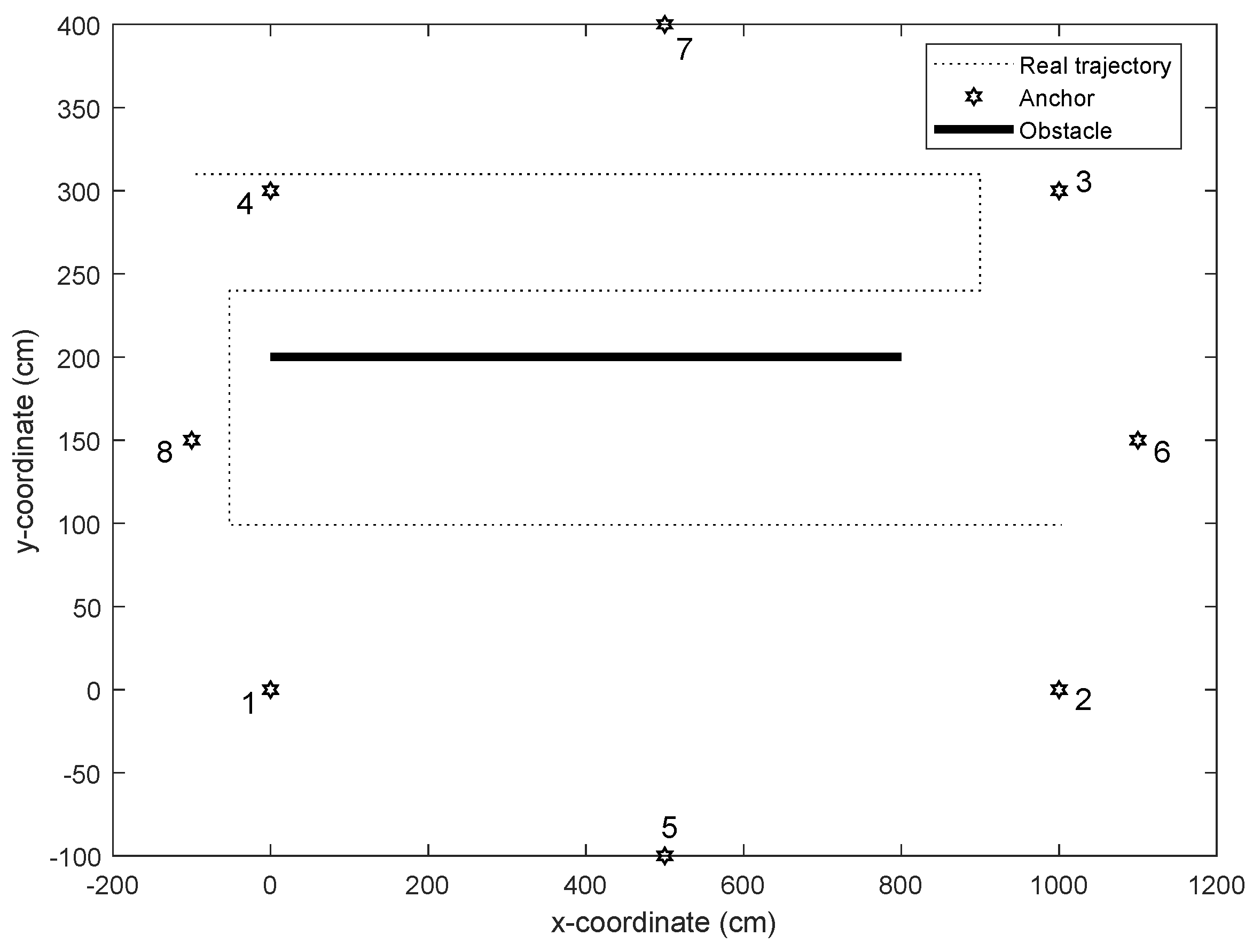
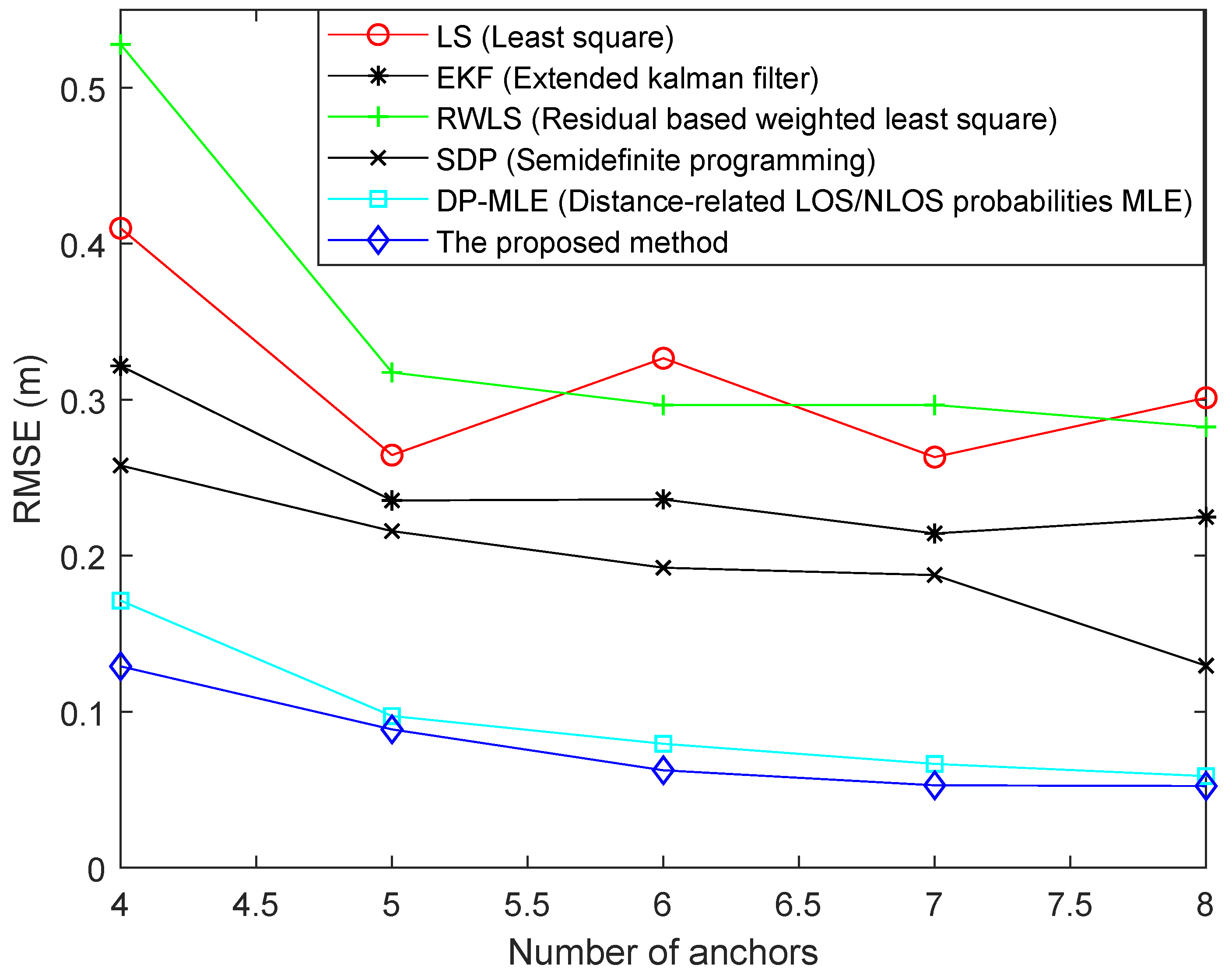
6. Simulation and Experimental Results
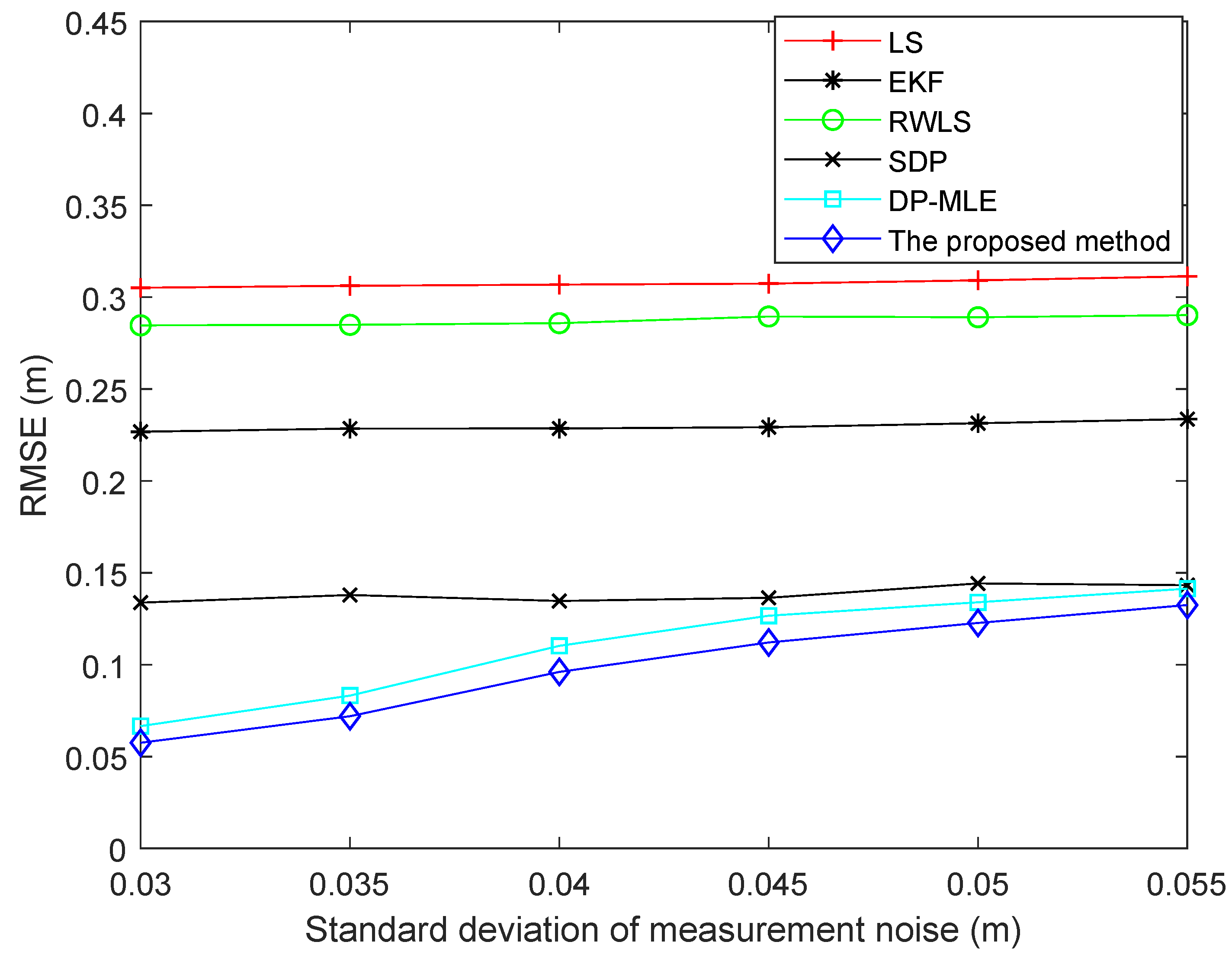
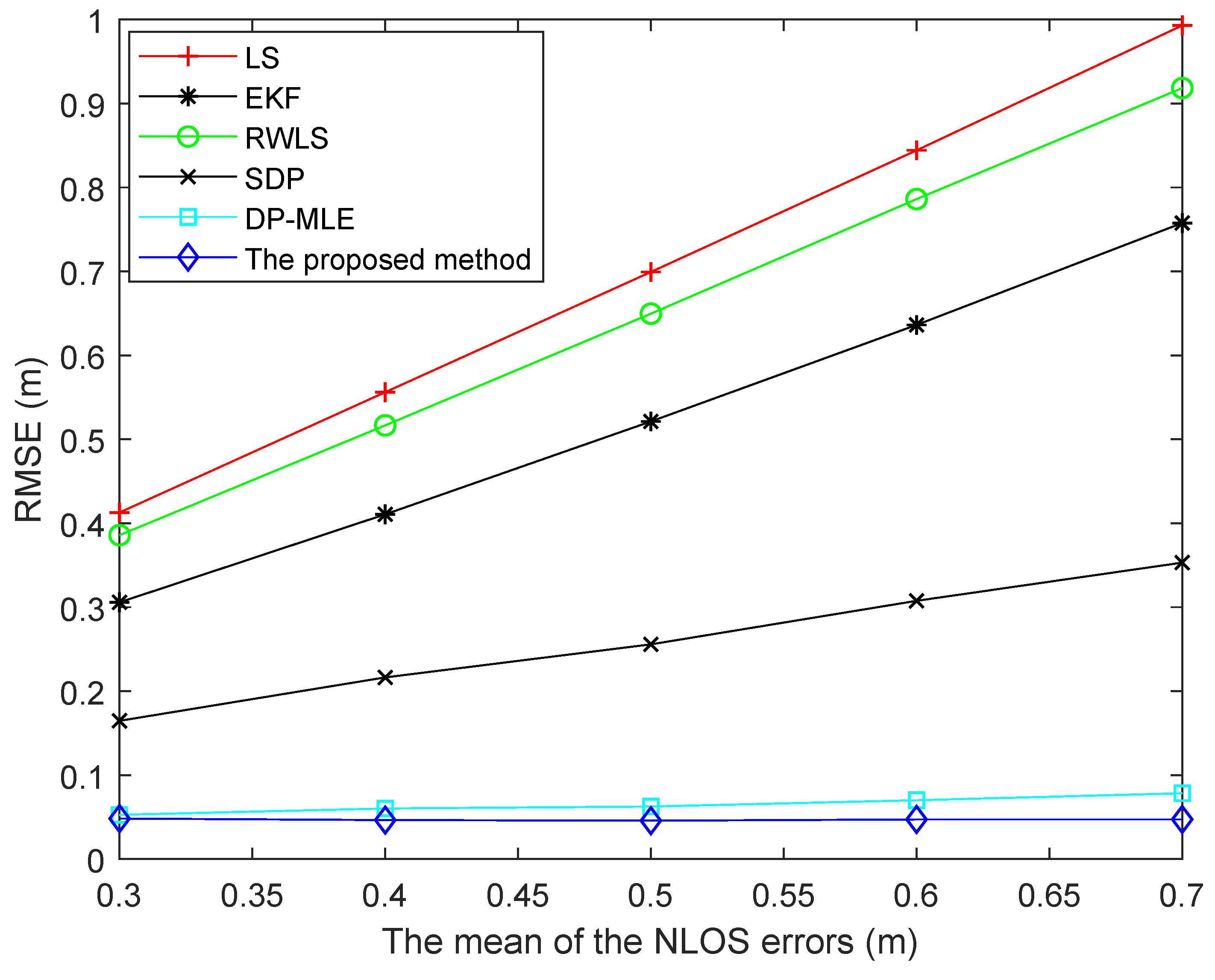
6.1. Simulation Results
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, H.; Cheng, P.; Shi, L.; Chen, J. Optimal DoS Attack Scheduling in Wireless Networked Control System. IEEE Trans. Control. Syst. Technol. 2016, 24, 843–852. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X. The IMU/UWB Fusion Positioning Algorithm Based on a Particle Filter. ISPRS Int. J. Geo-Inf. 2017, 6, 235. [Google Scholar] [CrossRef]
- Yu, C.; Lan, H.; Gu, F.; Fei, Y.; Naser, E. A Map/INS/Wi-Fi Integrated System for Indoor Location-Based Service Applications. Sensors 2017, 17, 1272. [Google Scholar] [CrossRef] [PubMed]
- Tseng, H.P.; Chan, C.Y.; Lin, J.Y.; Lin, B.D.; Wu, N.; Wang, M.T. Ray-Tracing-Assisted Fingerprinting Based on Channel Impulse Response Measurement for Indoor Positioning. IEEE Trans. Instrum. Meas. 2017, 66, 1032–1045. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Y.; Wang, Y.; Bi, Y.; Feng, L.; Xue, M. A Triple-Filter NLOS Localization Algorithm Based on Fuzzy C-means for Wireless Sensor Networks. Sensors 2019, 19, 1215. [Google Scholar] [CrossRef] [PubMed]
- Saska, M.; Baca, T.; Thomas, J.; Chudoba, J.; Preucil, L.; Krajnik, T.; Faigl, J.; Loianno, G.; Kumar, V. System for deployment of groups of unmanned micro aerial vehicles in GPS-denied environments using onboard visual relative localization. Auton. Robot. 2017, 41, 919–944. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, X.; Dai, G. Improving the indoor localization accuracy for CPS by reorganizing the fingerprint signatures. Int. J. Distrib. Sens. Netw. 2014, 10, 415710. [Google Scholar] [CrossRef]
- Pirzada, N.; Nayan, Y.M.; Subhan, F.; Abro, A.; Hassan, F.M.; Sakidin, H. Location Fingerprinting Technique for WLAN Device-Free Indoor Localization System. Wirel. Pers. Commun. 2017, 95, 445–455. [Google Scholar] [CrossRef]
- Li, J.; He, X.; Cai, Z.Y.; Xu, Q. Method of WiFi indoor location based on K-means and Random Forest. Control. Eng. China 2017, 24, 787–792. [Google Scholar]
- Lee, H.S.; Lim, K.I.; Lee, K.J. Method for improving indoor positioning accuracy using extended Kalman filter. Mob. Inf. Syst. 2016, 2016, 2369103. [Google Scholar] [CrossRef]
- Cai, S.; Liao, W.; Luo, C.; Li, M.; Huang, X.; Li, P. CRIL: An efficient online adaptive indoor localization system. IEEE Trans. Veh. Technol. 2017, 66, 4148–4160. [Google Scholar] [CrossRef]
- Liu, C.; Tian, Z.; Zhou, M.; Yang, X. Gene-Sequencing-Based Indoor Localization in Distributed Antenna System. IEEE Sens. J. 2017, 17, 6019–6028. [Google Scholar] [CrossRef]
- Jiang, W.; Yin, Z. Indoor localization with a signal tree. Multimed. Tools Appl. 2017, 76, 20317–20339. [Google Scholar] [CrossRef]
- Shi, X.; Mao, G.; Yang, Z.; Chen, J. MLE-based localization and performance analysis in probabilistic LOS/NLOS environment. Neurocomputing 2017, 270, 101–109. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R.; Montezuma, P. A Robust Bisection-based Estimator for TOA-based Target Localization in NLOS Environments. IEEE Commun. Lett. 2017, 21, 2488–2491. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H.; Li, Y.; Ansari, N. NLOS error mitigation for TOA-based localization via convex relaxation. IEEE Trans. Wirel. Commun. 2014, 13, 4119–4131. [Google Scholar] [CrossRef]
- Shi, X.; Yang, Z.; Chen, J. Localization accuracy of range-only sensors with additive and multiplicative noise. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 195–200. [Google Scholar]
- Yang, Z.; Shi, X.; Chen, J. Optimal Coordination of Mobile Sensors for Target Tracking Under Additive and Multiplicative Noises. IEEE Trans. Ind. Electron. 2014, 61, 3459–3468. [Google Scholar] [CrossRef]
- Li, C.; Qiu, Z.; Liu, C. An Improved Weighted K-Nearest Neighbor Algorithm for Indoor Positioning. Wirel. Pers. Commun. 2017, 96, 2239–2251. [Google Scholar] [CrossRef]
- Oussalah, M.; Alakhras, M.; Hussein, I.M. Multivariable fuzzy inference system for fingerprinting indoor localization. Fuzzy Sets Syst. 2015, 269, 65–89. [Google Scholar] [CrossRef]
- Li, J.; Wu, S. Non-parametric non-line-of-sight identification and estimation for wireless location. In Proceedings of the Computer Science and Service System (CSSS), Nanjing, China, 11–13 August 2012; pp. 81–84. [Google Scholar]
- Schroeder, J.; Galler, S.; Kyamakya, K.; Jobmann, K. NLOS detection algorithms for Ultra-Wideband localization. In Proceedings of the 4th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 22 March 2007; pp. 159–166. [Google Scholar]
- Borras, J.; Hatrack, P.; Mandayam, B.N. Decision theoretic framework for NLOS identification. In Proceedings of the 48th IEEE Vehicular Technology Conference, Ottawa, ON, Canada, 21 May 1998; pp. 1583–1587. [Google Scholar]
- Casas, R.; Marco, A.; Guerrero, J.J.; Falco, J. Robust estimator for non-line-of-sight error mitigation in indoor localization. EURASIP J. Appl. Signal Process. 2006, 2006, 156. [Google Scholar] [CrossRef]
- Venkatesh, S.; Buehrer, M.R. NLOS mitigation using linear programming in ultrawideband location-aware networks. IEEE Trans. Veh. Technol. 2007, 56, 3182–3198. [Google Scholar] [CrossRef]
- Marano, S.; Gifford, M.W.; Wymeersch, H.; Win, Z.M. NLOS identification and mitigation for localization based on UWB experimental data. IEEE J. Sel. Areas Commun. 2010, 28, 1026–1035. [Google Scholar] [CrossRef]
- Morelli, C.; Nicoli, M.; Rampa, V.; Spagnolini, U. Hidden Markov Models for Radio Localization in Mixed LOS/NLOS Conditions. IEEE Trans. Signal Process. 2007, 55, 1525–1542. [Google Scholar] [CrossRef]
- Lui, K.W.K.; So, C.H.; Ma, K.W. Maximum a posteriori approach to time-of-arrival-based localization in non-line-of-sight environment. IEEE Trans. Veh. Technol. 2009, 59, 1517–1523. [Google Scholar] [CrossRef]
- Gu, H.; Shi, Y.; Chen, Y. Cicada: A Highly-Precise Easy-Embedded and Omni-Directional Indoor Location Sensing System. In Proceedings of the International Conference on Advances in Grid and Pervasive Computing, Taichung, Taiwan, 3 May 2006; pp. 385–394. [Google Scholar]
- Yang, S.; Wang, B. Residual based weighted least square algorithm for Bluetooth/UWB indoor localization system. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 5959–5963. [Google Scholar]
- Dardari, D.; Sottile, F. WPR. B Database: Annex of N++ Deliverable WPR. B DB. 3. Progress Report II on Advanced Localization and Positioning Techniques: Data Fusion and Applications, Deliverable Number: DB, 3. 2010. Available online: https://www.academia.edu/2830567/216715_NEWCOM_Deliverable_Number_DB._3_Progress_Report_II_on_Advanced_Localization_and_Positioning_Techniques_Data_Fusion_and_Applications (accessed on 14 October 2019).
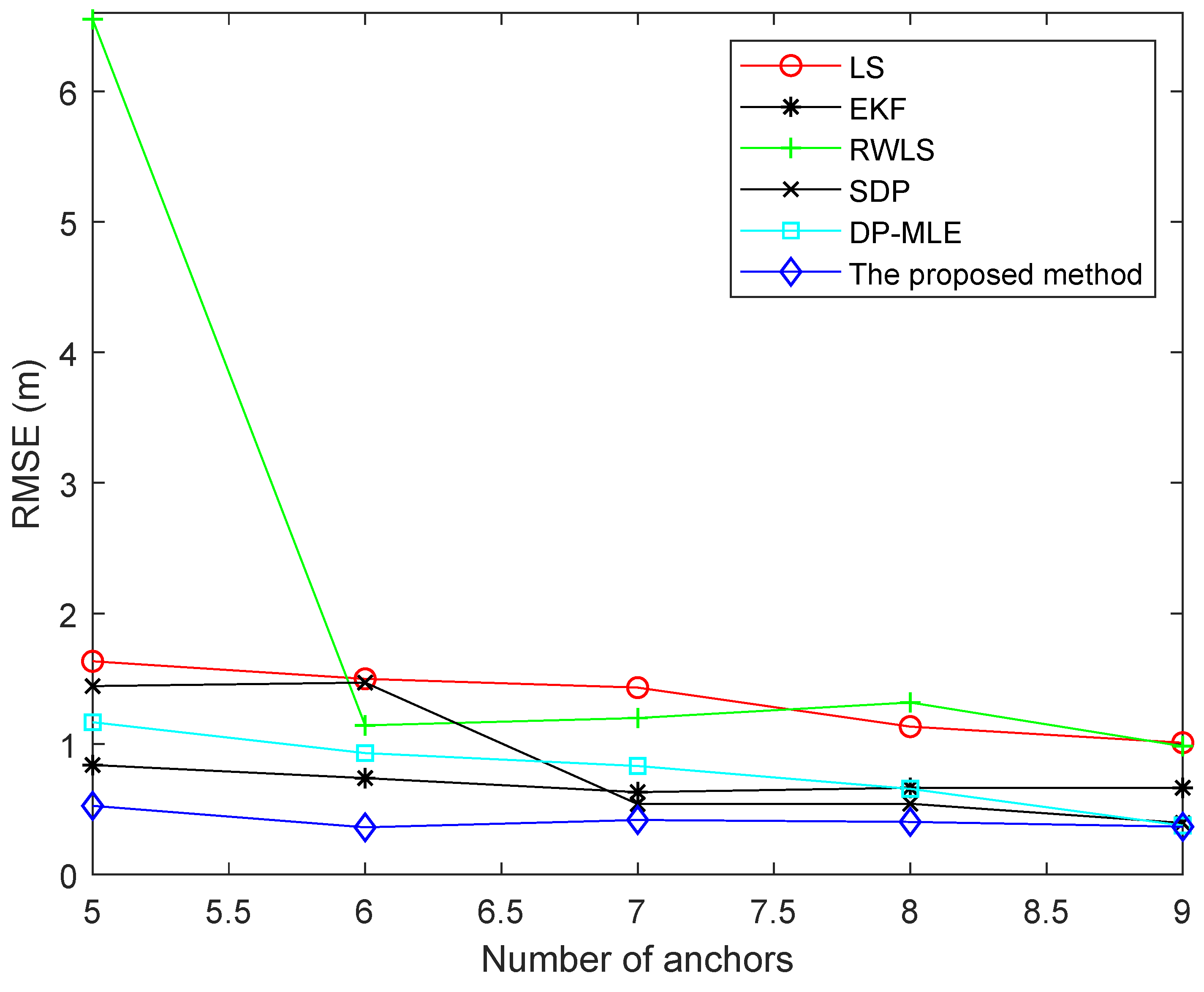
| Algorithm | Description |
|---|---|
| LS | Least square method |
| EKF | Extended kalman filtering algorithm [29] |
| RWLS | Residual based weighted least square algorithm [30] |
| SDP | Semidefinite programming method [16] |
| DP-MLE | Distance-related LOS/NLOS probabilities maximum likelihood estimation [14] |
| DAP-MLE | The proposed method |
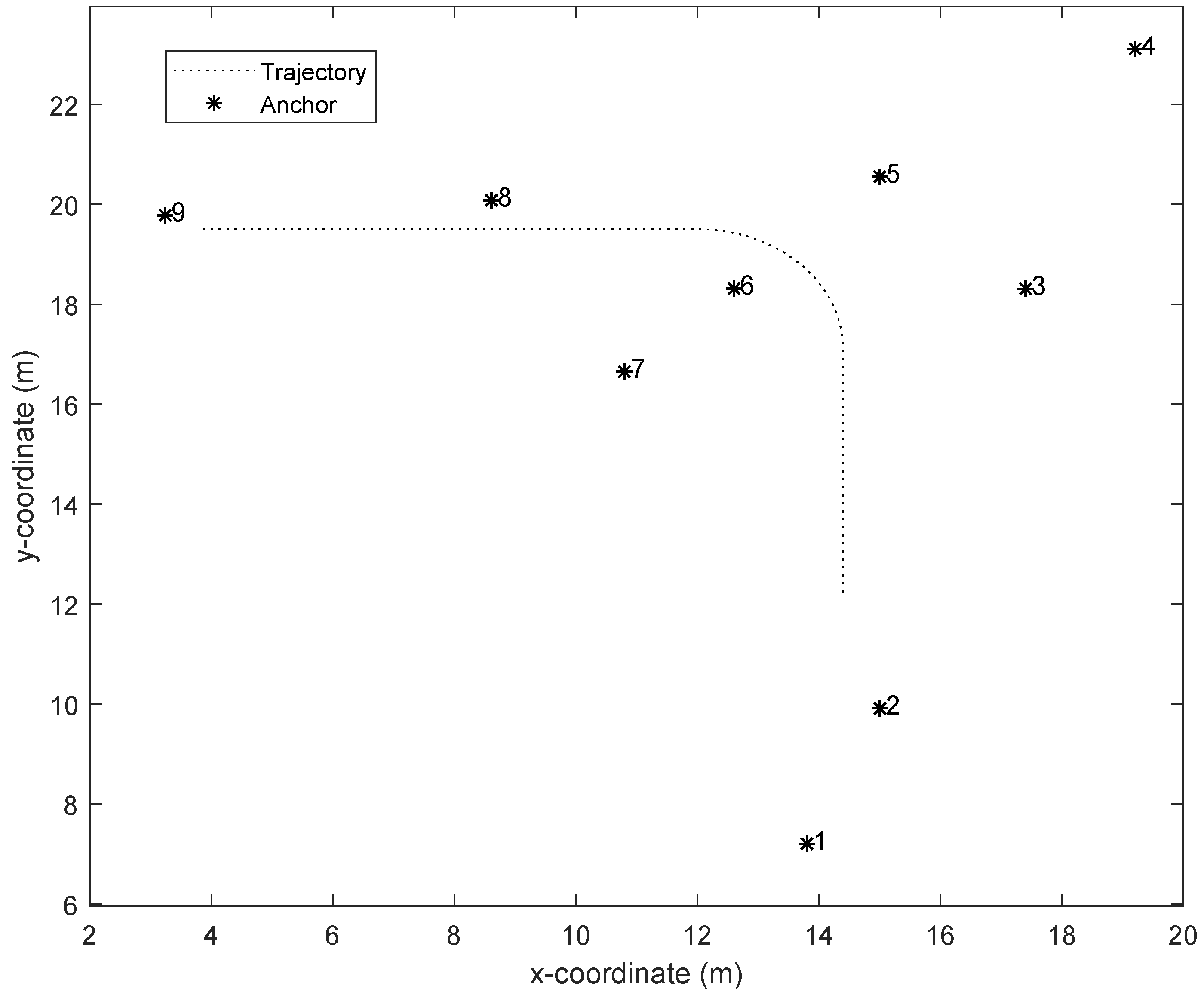
| Anchor ID | Coordinate X (m) | Coordinate Y (m) | Coordinate Z (m) |
|---|---|---|---|
| 8 | 13.80 | 7.20 | 1.13 |
| 9 | 15.00 | 9.91 | 1.13 |
| 11 | 17.40 | 18.31 | 1.13 |
| 12 | 19.21 | 23.11 | 1.13 |
| 13 | 15.00 | 20.56 | 1.13 |
| 14 | 12.60 | 18.31 | 1.13 |
| 15 | 10.80 | 16.65 | 1.13 |
| 16 | 8.61 | 20.08 | 1.13 |
| 17 | 3.24 | 19.78 | 1.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Wei, G.; Wang, J.; Zhang, D. A Localization and Tracking Approach in NLOS Environment Based on Distance and Angle Probability Model. Sensors 2019, 19, 4438. https://doi.org/10.3390/s19204438
Tian X, Wei G, Wang J, Zhang D. A Localization and Tracking Approach in NLOS Environment Based on Distance and Angle Probability Model. Sensors. 2019; 19(20):4438. https://doi.org/10.3390/s19204438
Chicago/Turabian StyleTian, Xin, Guoliang Wei, Jianhua Wang, and Dianchen Zhang. 2019. "A Localization and Tracking Approach in NLOS Environment Based on Distance and Angle Probability Model" Sensors 19, no. 20: 4438. https://doi.org/10.3390/s19204438
APA StyleTian, X., Wei, G., Wang, J., & Zhang, D. (2019). A Localization and Tracking Approach in NLOS Environment Based on Distance and Angle Probability Model. Sensors, 19(20), 4438. https://doi.org/10.3390/s19204438




