Combining Non-Uniform Time Slice and Finite Difference to Improve 3D Ghost Imaging
Abstract
:1. Introduction
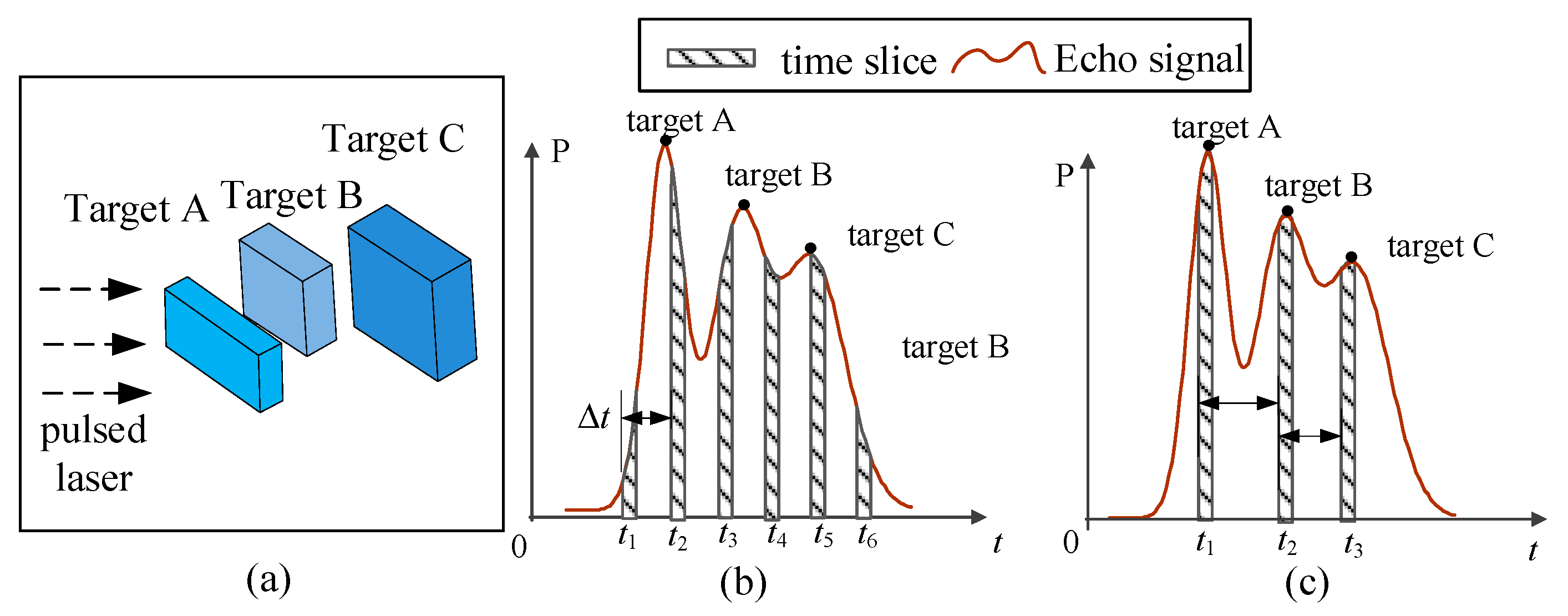
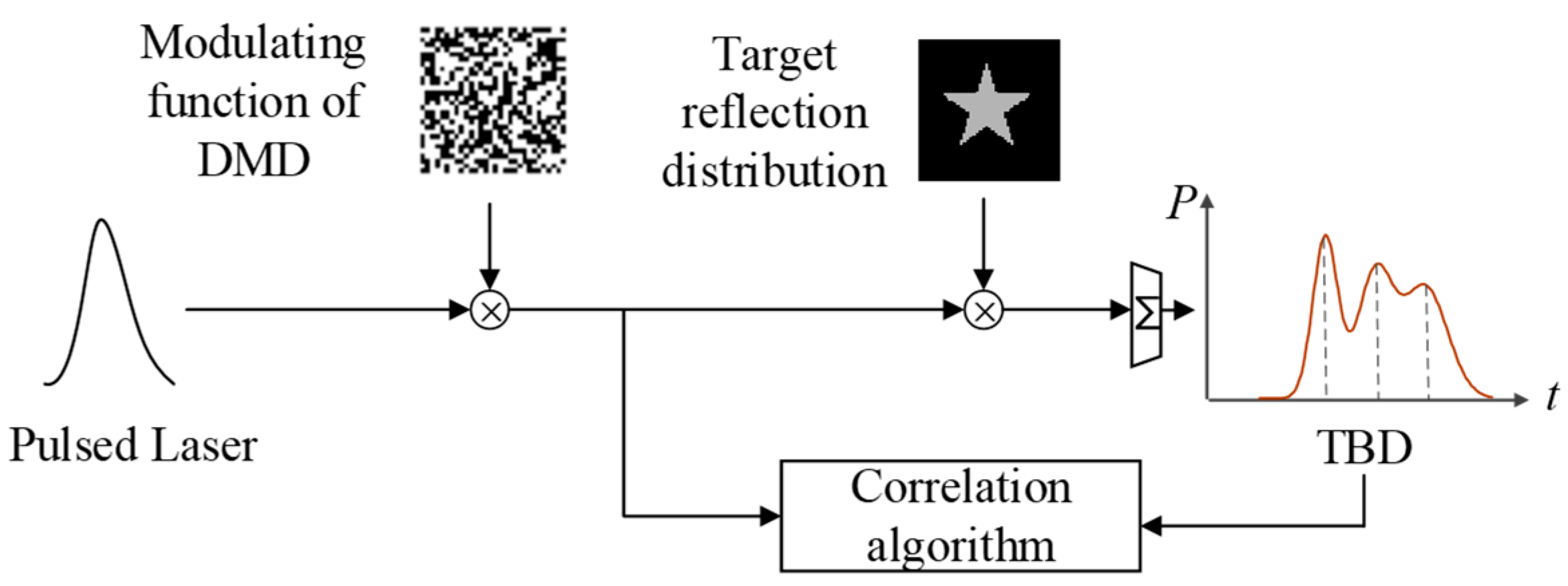
2. Method
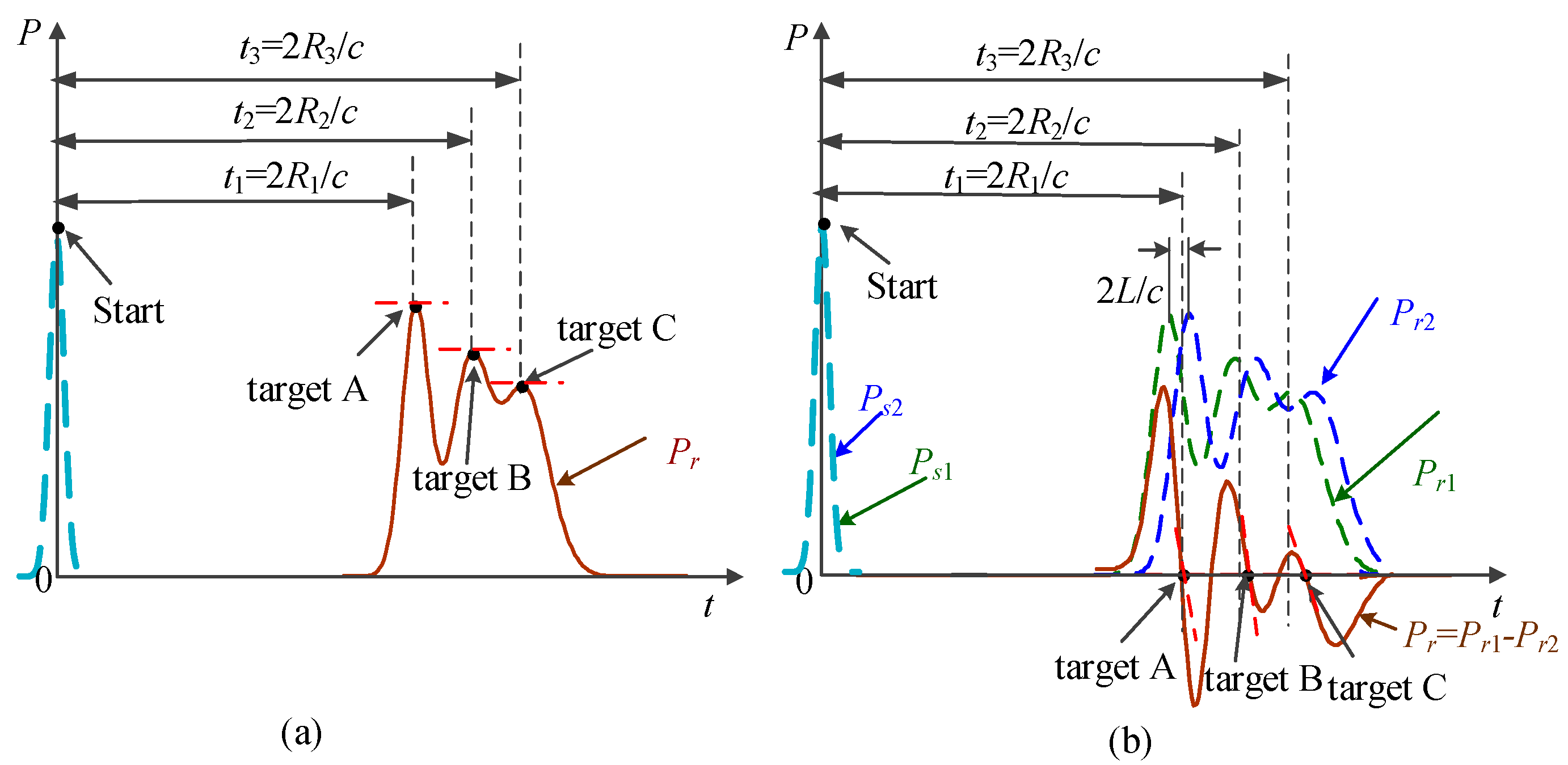
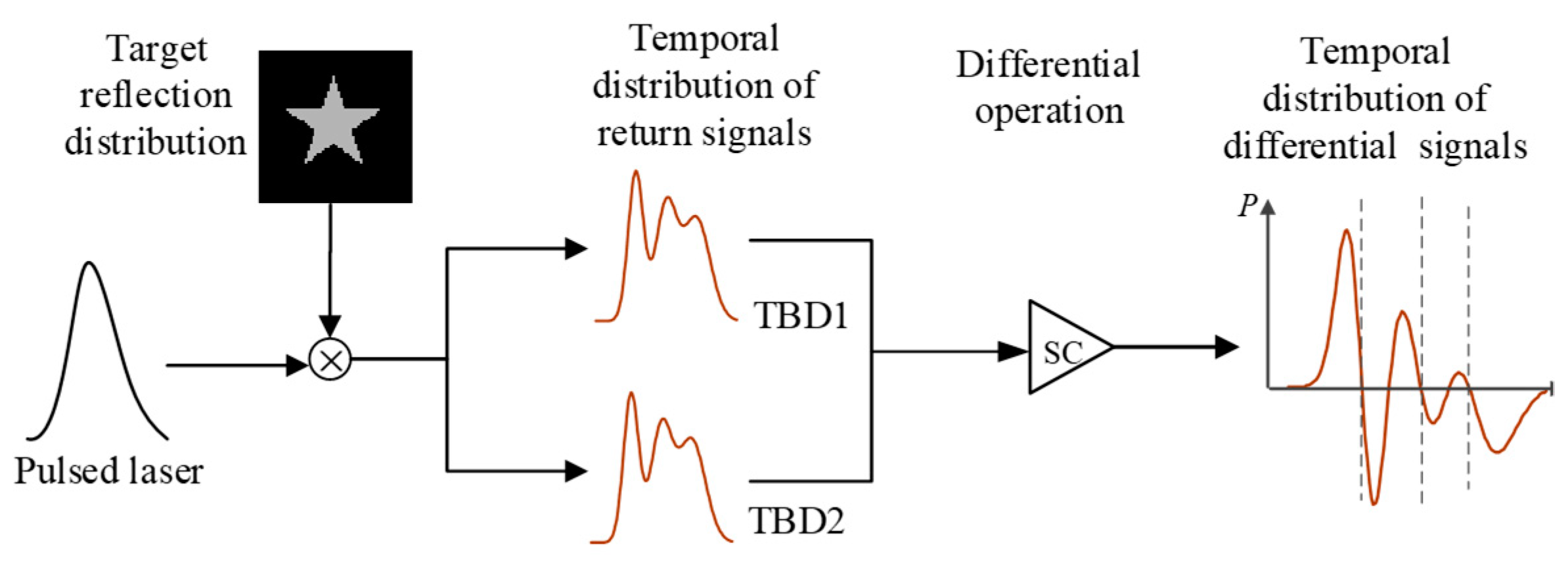
2.1. Combining NUTSM with Finite Difference
2.2. Theory
3. Simulations and Results
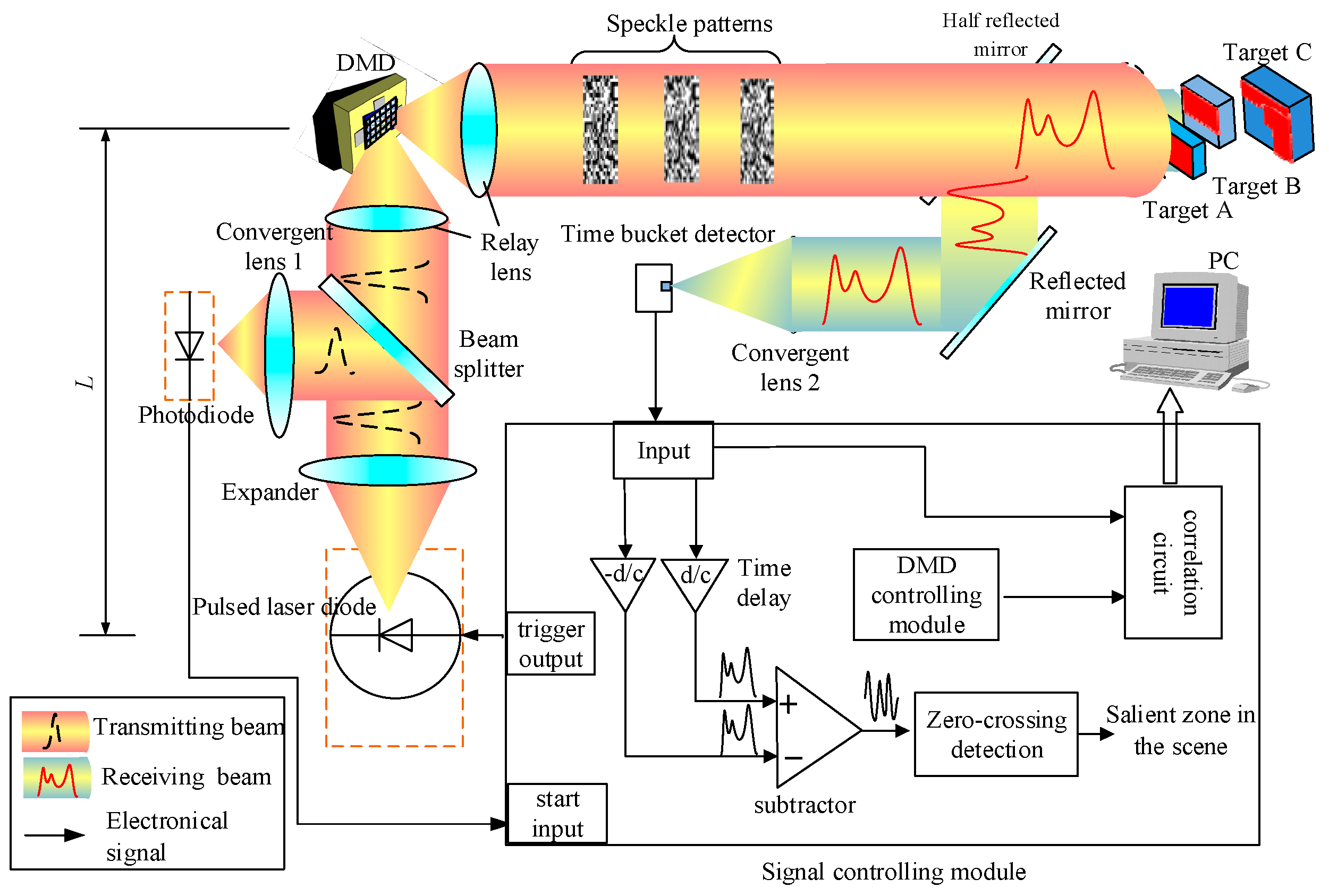
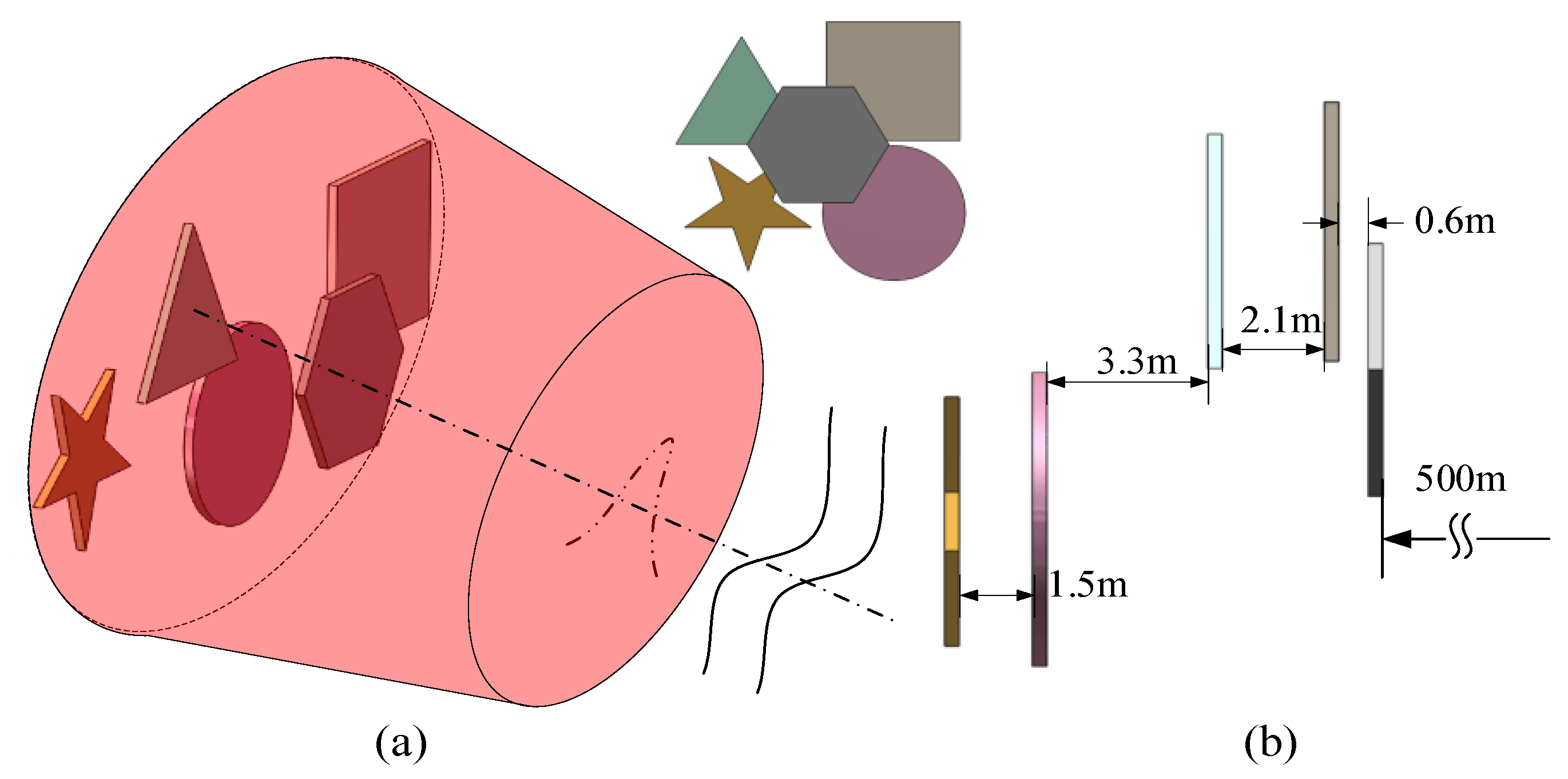
3.1. Simulation Setup
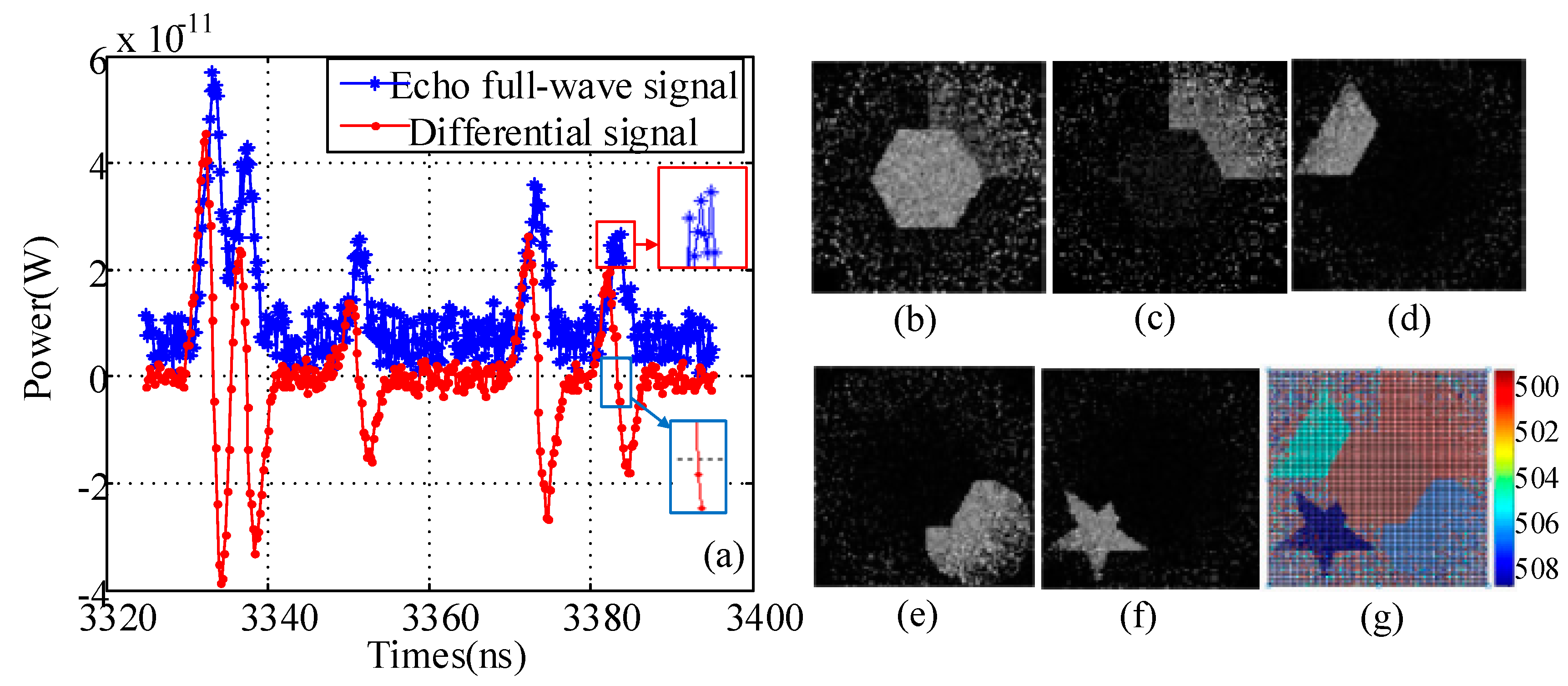
3.2. Modeling Verification
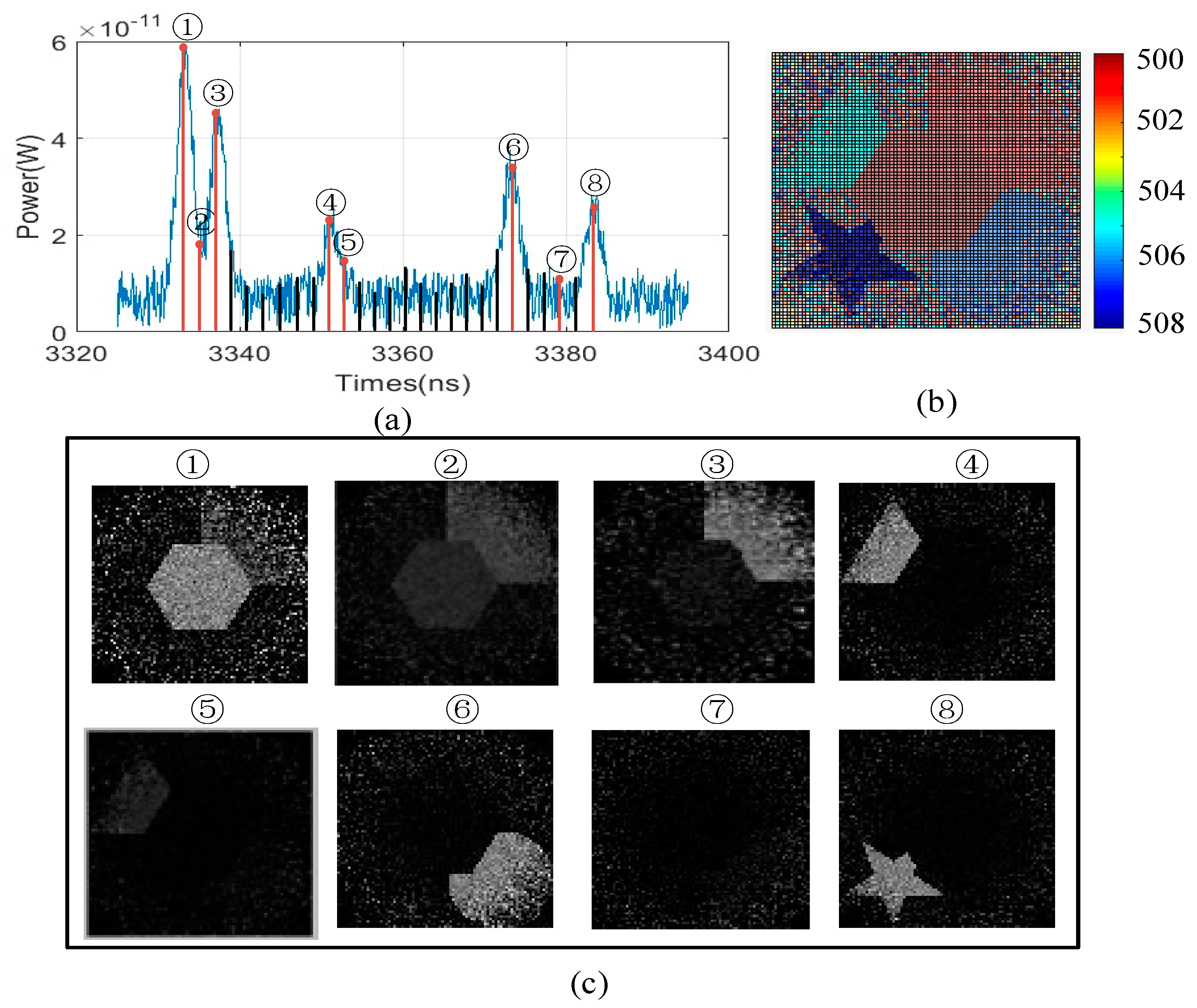
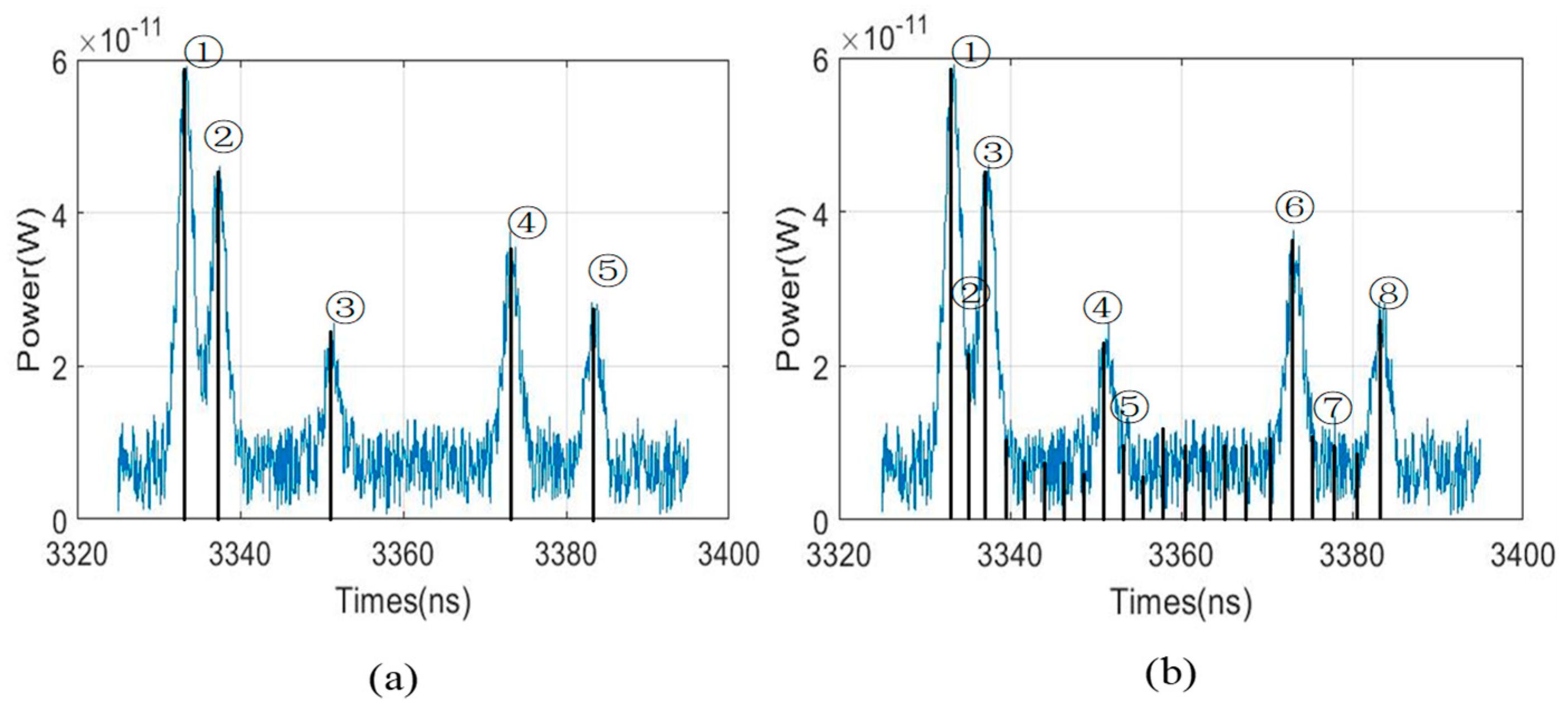
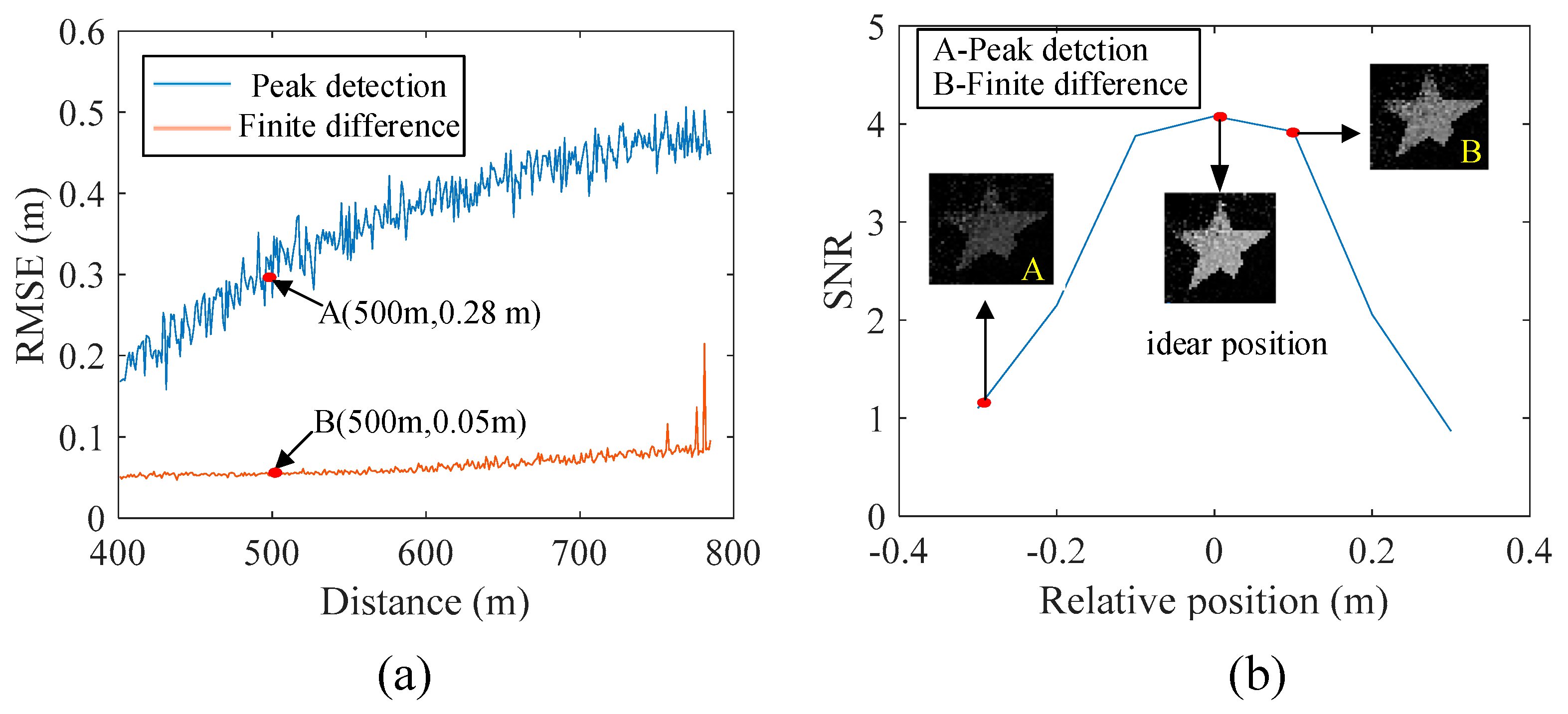
3.3. Comparative Results
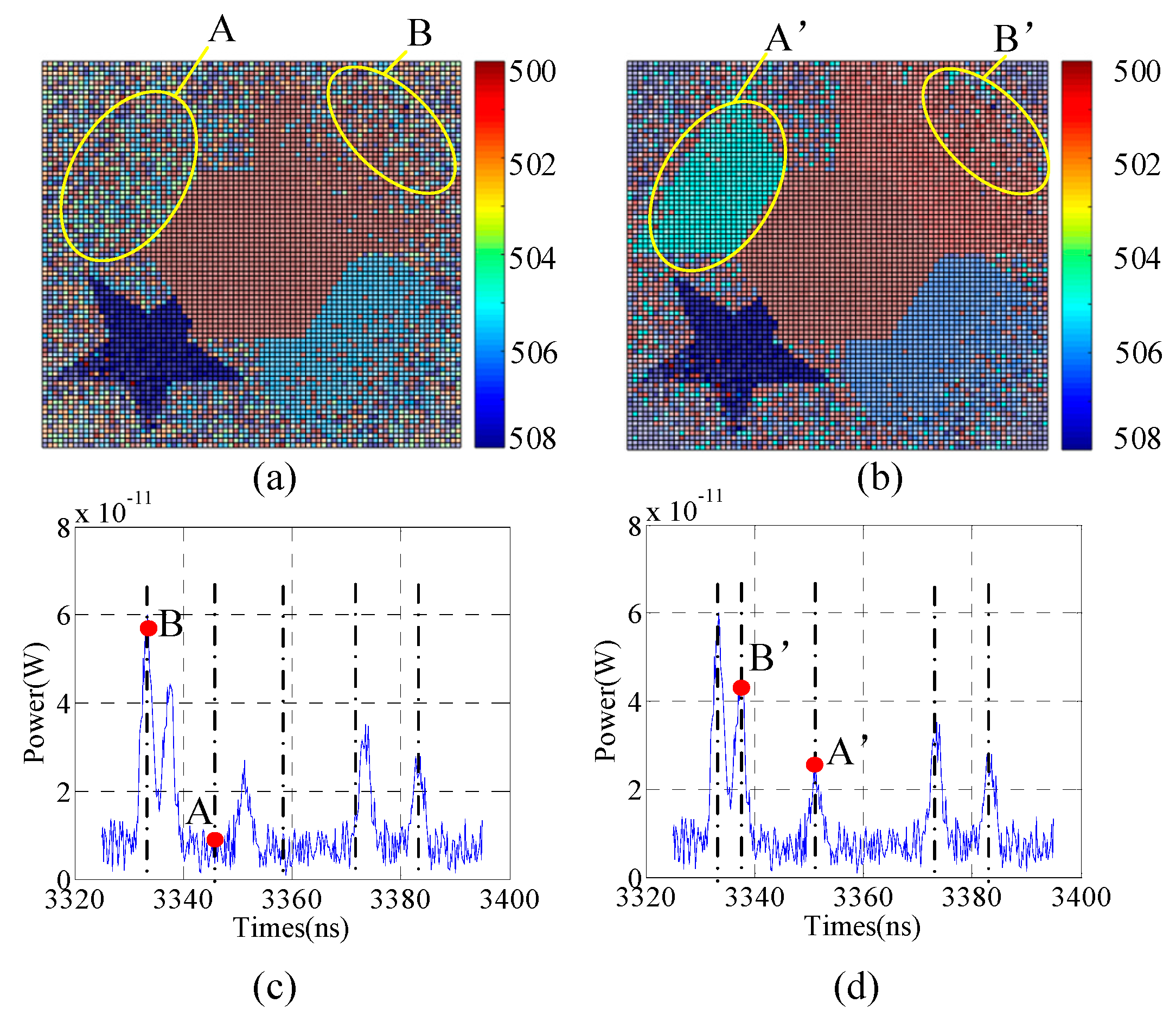
4. Discussion
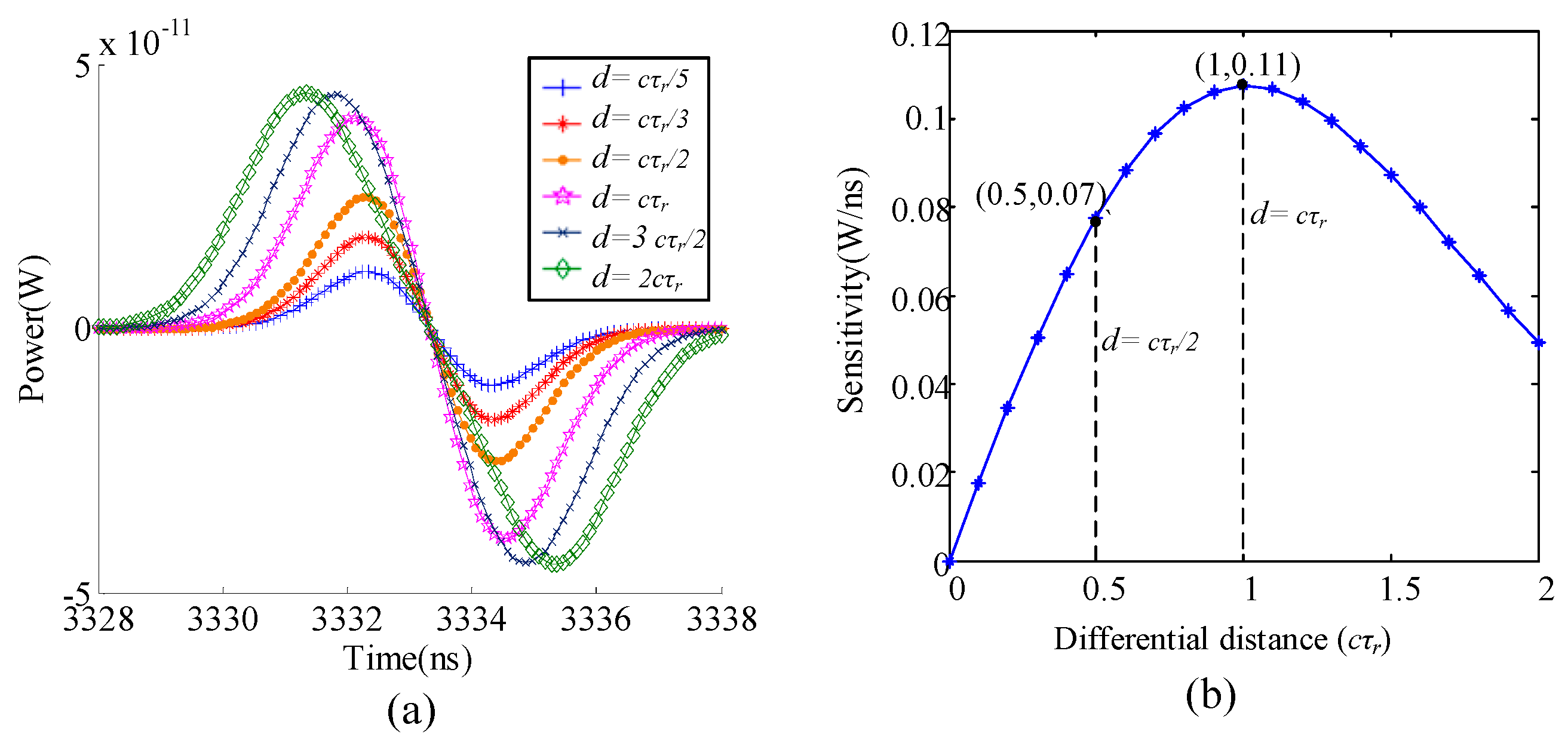
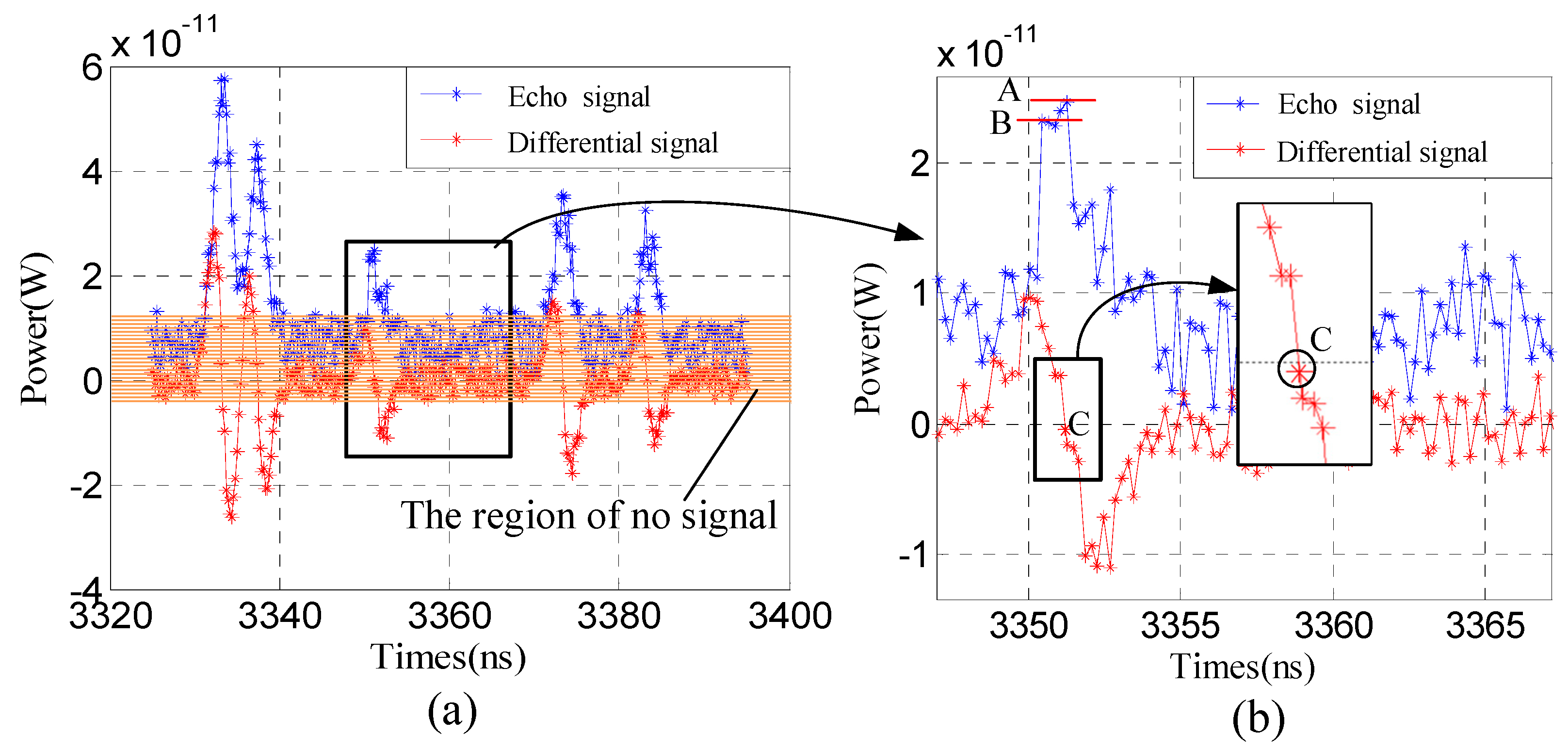
4.1. Optimal Differential Distance
4.2. Issue on Non Zero Crossing
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vu, T.T.; Ban, Y.; Qin, Y.; Niu, Z. Range determination for generating point clouds from airborne small footprint LiDAR waveforms. Opt. Express 2012, 20, 25935–25947. [Google Scholar]
- Foix, S.; Alenya, G.; Torras, C. Lock-in Time-of-Flight (ToF) Cameras: A Survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. An Integrated Framework for 3-D Modeling, Object Detection, and Pose Estimation From Point-Clouds. IEEE Trans. Instrum. Meas. 2015, 64, 683–693. [Google Scholar]
- Molebny, V.; Mcmanamon, P.; Steinvall, O.; Kobayashi, T.; Chen, W. Laser radar: Historical prospective—From the East to the West. Opt. Eng. 2016, 56, 031220. [Google Scholar] [CrossRef]
- Li, X.; Liang, Y. Surface characteristics modeling and performance evaluation of urban building materials using LiDAR data. Appl. Opt. 2015, 54, 4750–4759. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Gong, W.; Chen, M.; Li, E. Ghost imaging lidar via sparsity constraints. Appl. Phys. Lett. 2012, 101, 141123. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Jiang, H.; Zhao, H.; Li, X.; Zhu, S. Projector-defocusing rectification for Fourier single-pixel imaging. Opt. Express 2018, 26, 5005–5017. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.H.; Chen, W.; Penuelas, J.; Padgett, M.; Sun, M.J. 1000 fps computational ghost imaging using LED-based structured illumination. Opt. Express 2018, 26, 2427–2434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Basano, L.; Ottonello, P. Experiment in lensless ghost imaging with thermal light. Appl. Phys. Lett. 2006, 89, 061106. [Google Scholar] [CrossRef]
- Howland, G.A.; Lum, D.J.; Ware, M.R.; Howell, J.C. Photon counting compressive depth mapping. Opt. Express 2013, 21, 23822–23837. [Google Scholar] [CrossRef]
- Richmond, R.D. Direct-Detection LADAR Systems; SPIE Press: Bellingham, WA, USA, 2010. [Google Scholar]
- Gong, W.; Zhao, C.; Hong, Y.; Chen, M.; Xu, W.; Han, S. Three-dimensional ghost imaging lidar via sparsity constraint. Sci. Rep. 2016, 6, 26133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strekalov, D.V.; Sergienko, A.V.; Klyshko, D.N.; Shih, Y.H. Observation of two-photon “ghost” interference and diffraction. Phys. Rev. Lett. 1995, 74, 3600–3603. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Edgar, M.P.; Bowman, R.; Vittert, L.E.; Welsh, S.; Bowman, A.; Padgett, M.J. 3D computational imaging with single-pixel detectors. Science 2013, 340, 844–847. [Google Scholar] [CrossRef] [PubMed]
- Faccio, D.; Leach, J. Ghost Imaging in Three Dimensions. Science 2013, 340, 821–822. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wu, L.; Wang, X.; Dang, E. Gated viewing laser imaging with compressive sensing. Appl. Opt. 2012, 51, 2706–2712. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhang, Y.; Xu, L.; Yang, C.; Wang, Q.; Liu, Y.; Zhao, Y. Increasing the range accuracy of three-dimensional ghost imaging ladar using optimum slicing number method. Chin. Phys. B 2015, 24, 319–324. [Google Scholar] [CrossRef]
- Li, E.; Yu, H.; Han, S.; Gong, W. Structured image reconstruction for three-dimensional ghost imaging lidar. Opt. Express 2015, 23, 14541–14551. [Google Scholar]
- Zhang, Z.; Liu, S.; Peng, J.; Yao, M.; Zheng, G.; Zhong, J. Simultaneous spatial, spectral, and 3D compressive imaging via efficient Fourier single-pixel measurements. Optica 2018, 5, 315–319. [Google Scholar] [CrossRef]
- Jiang, H.; Zhu, S.; Zhao, H.; Xu, B.; Li, X. Adaptive regional single-pixel imaging based on the Fourier slice theorem. Opt. Express 2017, 25, 15118–15130. [Google Scholar] [CrossRef]
- Phillips, D.B.; Sun, M.J.; Taylor, J.M.; Edgar, M.P.; Barnett, S.M.; Gibson, G.M.; Padgett, M.J. Adaptive foveated single-pixel imaging with dynamic supersampling. Sci. Adv. 2016, 3, e1601782. [Google Scholar] [CrossRef]
- Howland, G.A.; Howell, J.C.; Dixon, P.B. Photon-counting compressive sensing laser radar for 3D imaging. Appl. Opt. 2011, 50, 5917–5920. [Google Scholar] [CrossRef] [PubMed]
- Budge, S.; Leishman, B.; Pack, R. Simulation and modeling of return waveforms from a ladar beam footprint in USU LadarSIM. Proc. SPIE 2006, 55, 308–312. [Google Scholar]
- Banakh, V.A.; Razenkov, I.A.; Smalikho, I.N. Laser echo signal amplification in a turbulent atmosphere. Appl. Opt. 2015, 54, 7301–7307. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.E. Effect of target surface orientation on the range precision of laser detection and ranging systems. J. Appl. Remote Sens. 2009, 3, 2527–2532. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Y.; Zhang, Y.; Sun, X. Range accuracy limitation of pulse ranging systems based on Geiger mode single-photon detectors. Appl. Opt. 2010, 49, 5561–5566. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Cao, J.; Hao, Q.; Xiao, Y.; Zhang, F.; Xia, W.; Zhang, K.; Yu, H. A Novel De-Noising Method for Improving the Performance of Full-Waveform LiDAR Using Differential Optical Path. Remote Sens. 2017, 9, 1109. [Google Scholar] [CrossRef]
- Marquès, J.R.; Geindre, J.P.; Amiranoff, F.; Audebert, P.; Gauthier, J.C.; Antonetti, A.; Grillon, G. Temporal and spatial measurements of the electron density perturbation produced in the wake of an ultrashort laser pulse. Phys. Rev. Lett. 1996, 76, 3566–3569. [Google Scholar] [CrossRef] [PubMed]
- Der, S.; Redman, B.; Chellappa, R. Simulation of error in optical radar range measurements. Appl. Opt. 1997, 36, 6869–6874. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z. Targets recognition using subnanosecond pulse laser range profiles. Opt. Express 2010, 18, 16788–16796. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Cao, J.; Hao, Q.; Zhang, K.; Cheng, Y.; Wang, Y.; Feng, Y. Combining Non-Uniform Time Slice and Finite Difference to Improve 3D Ghost Imaging. Sensors 2019, 19, 418. https://doi.org/10.3390/s19020418
Zhang F, Cao J, Hao Q, Zhang K, Cheng Y, Wang Y, Feng Y. Combining Non-Uniform Time Slice and Finite Difference to Improve 3D Ghost Imaging. Sensors. 2019; 19(2):418. https://doi.org/10.3390/s19020418
Chicago/Turabian StyleZhang, Fanghua, Jie Cao, Qun Hao, Kaiyu Zhang, Yang Cheng, Yingbo Wang, and Yongchao Feng. 2019. "Combining Non-Uniform Time Slice and Finite Difference to Improve 3D Ghost Imaging" Sensors 19, no. 2: 418. https://doi.org/10.3390/s19020418
APA StyleZhang, F., Cao, J., Hao, Q., Zhang, K., Cheng, Y., Wang, Y., & Feng, Y. (2019). Combining Non-Uniform Time Slice and Finite Difference to Improve 3D Ghost Imaging. Sensors, 19(2), 418. https://doi.org/10.3390/s19020418







