Robust Kalman Filter Aided GEO/IGSO/GPS Raw-PPP/INS Tight Integration
Abstract
1. Introduction
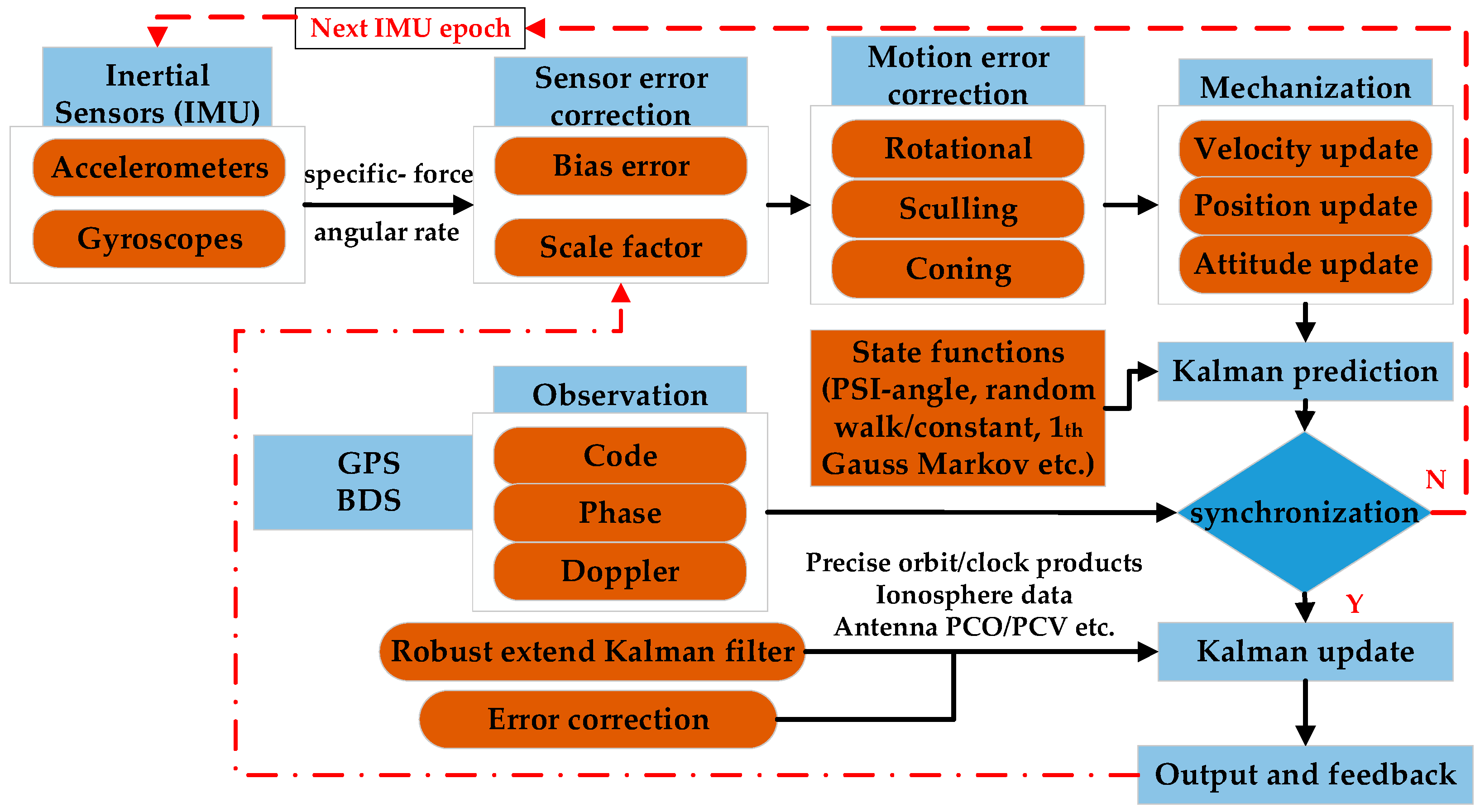
2. Methods
2.1. GEO/IGSO/GPS Raw PPP Model
2.2. INS Update
2.3. Robust Extended Kalman Filter Based PPP/INS Tight Integration
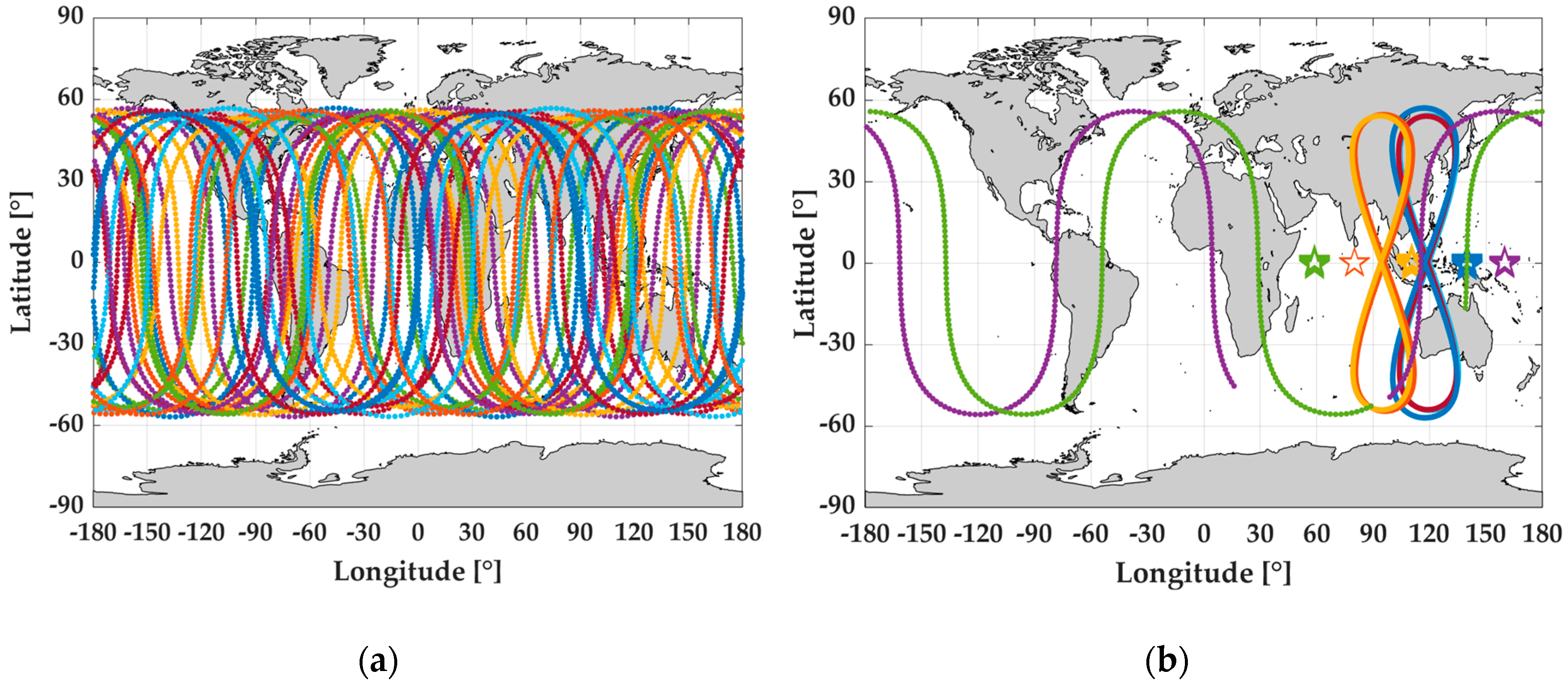
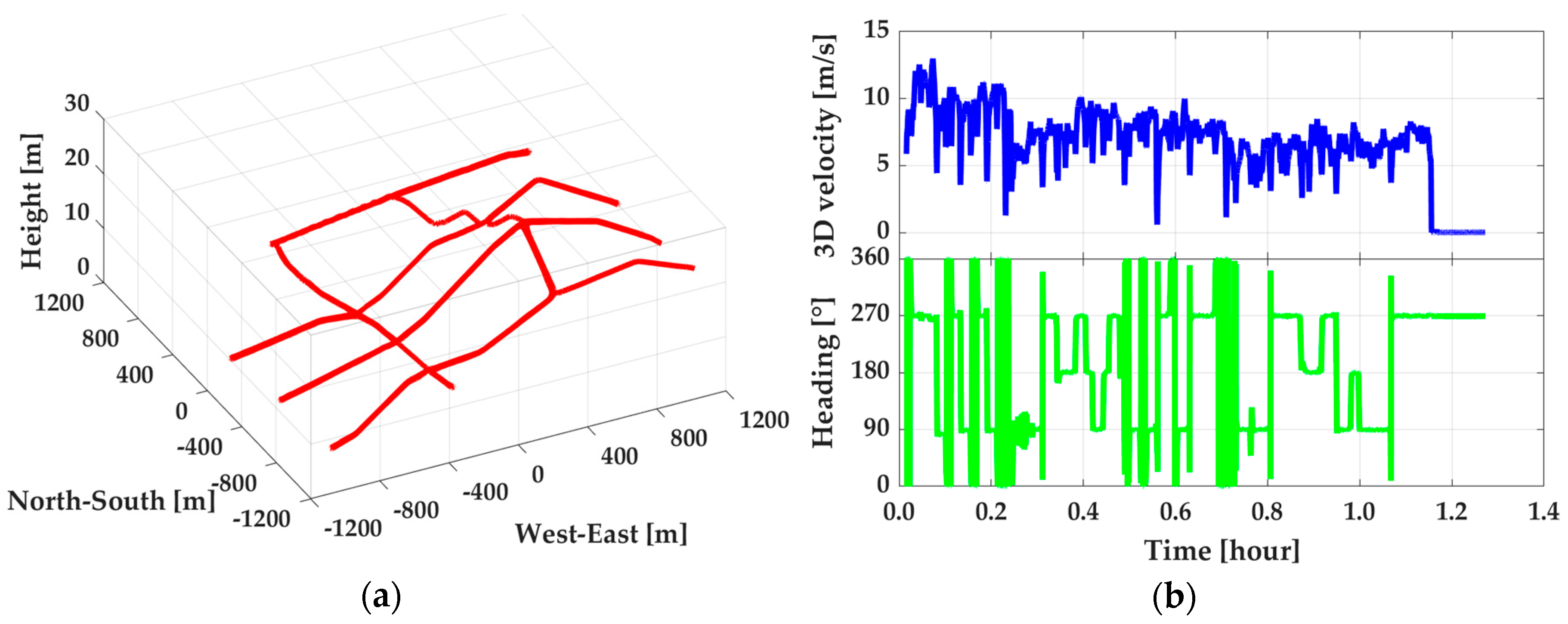
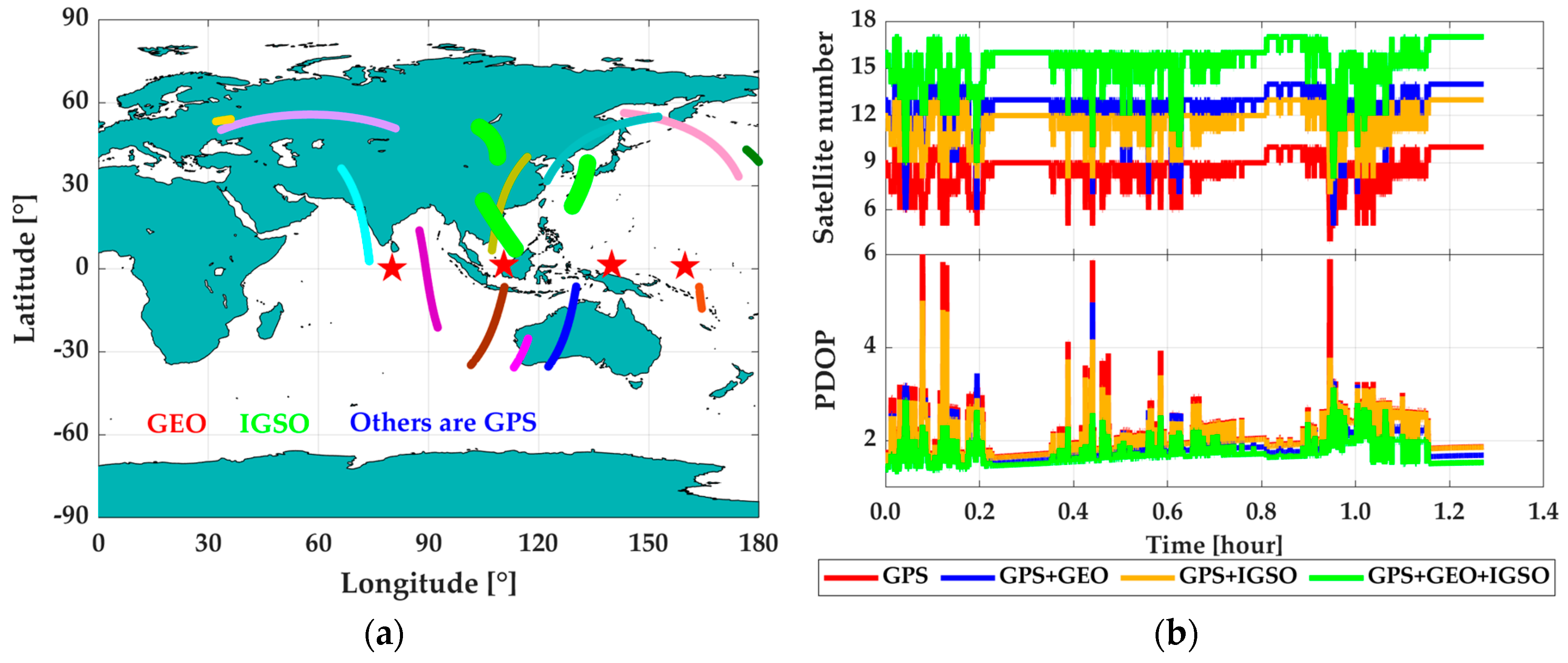
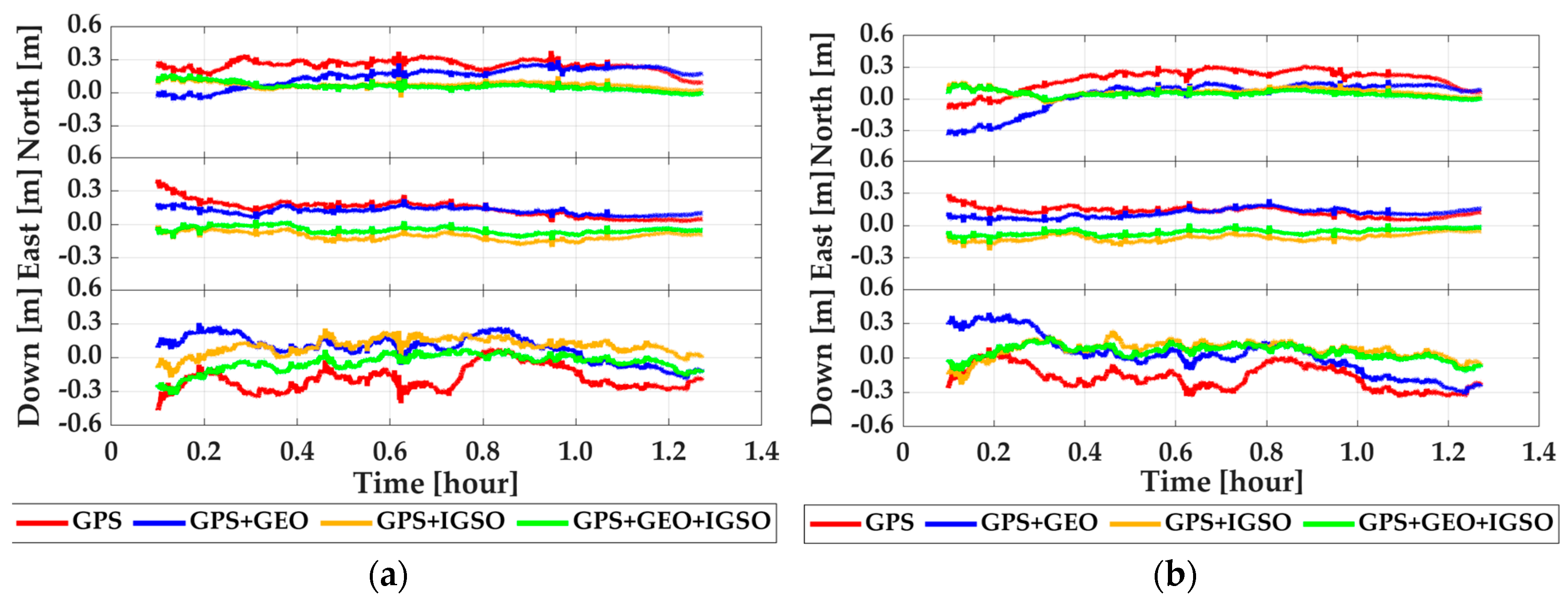
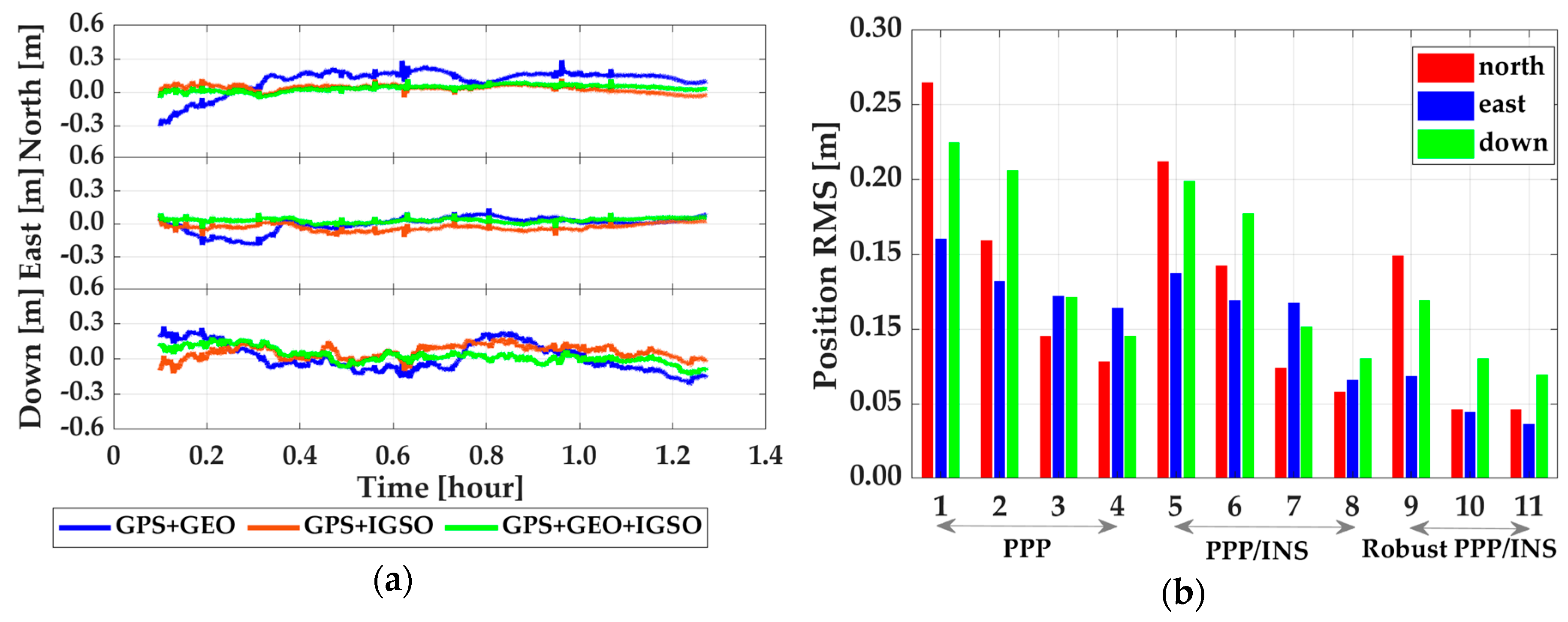
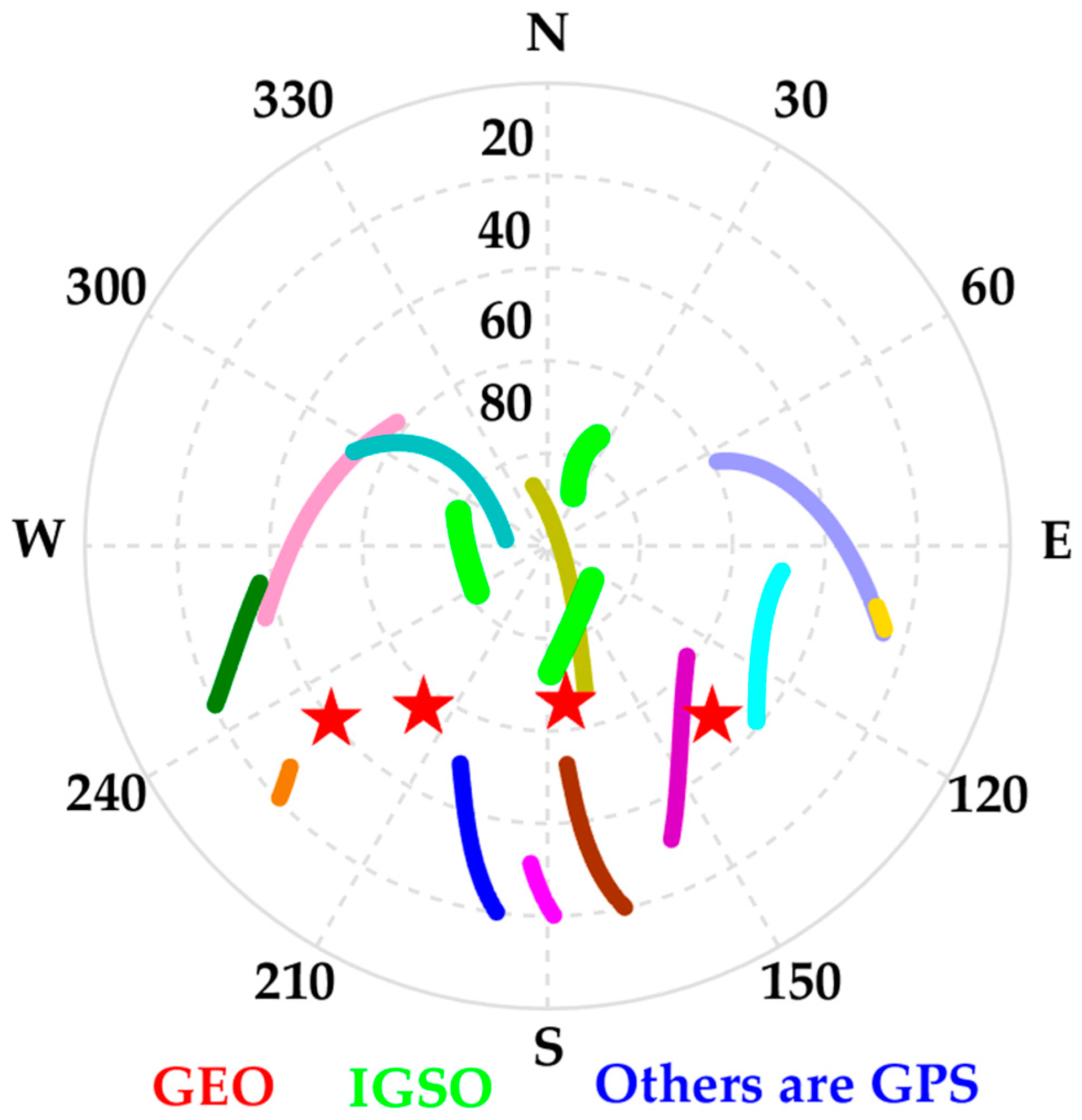
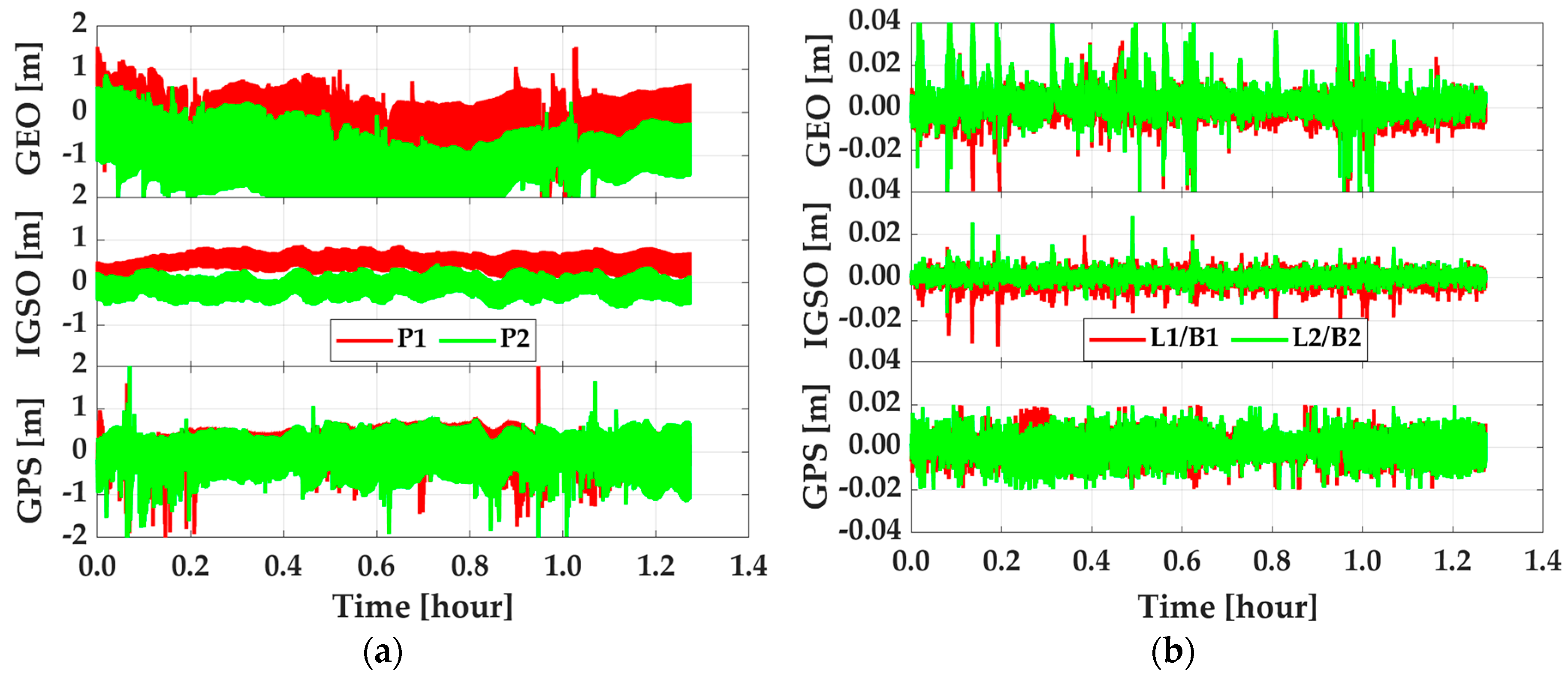
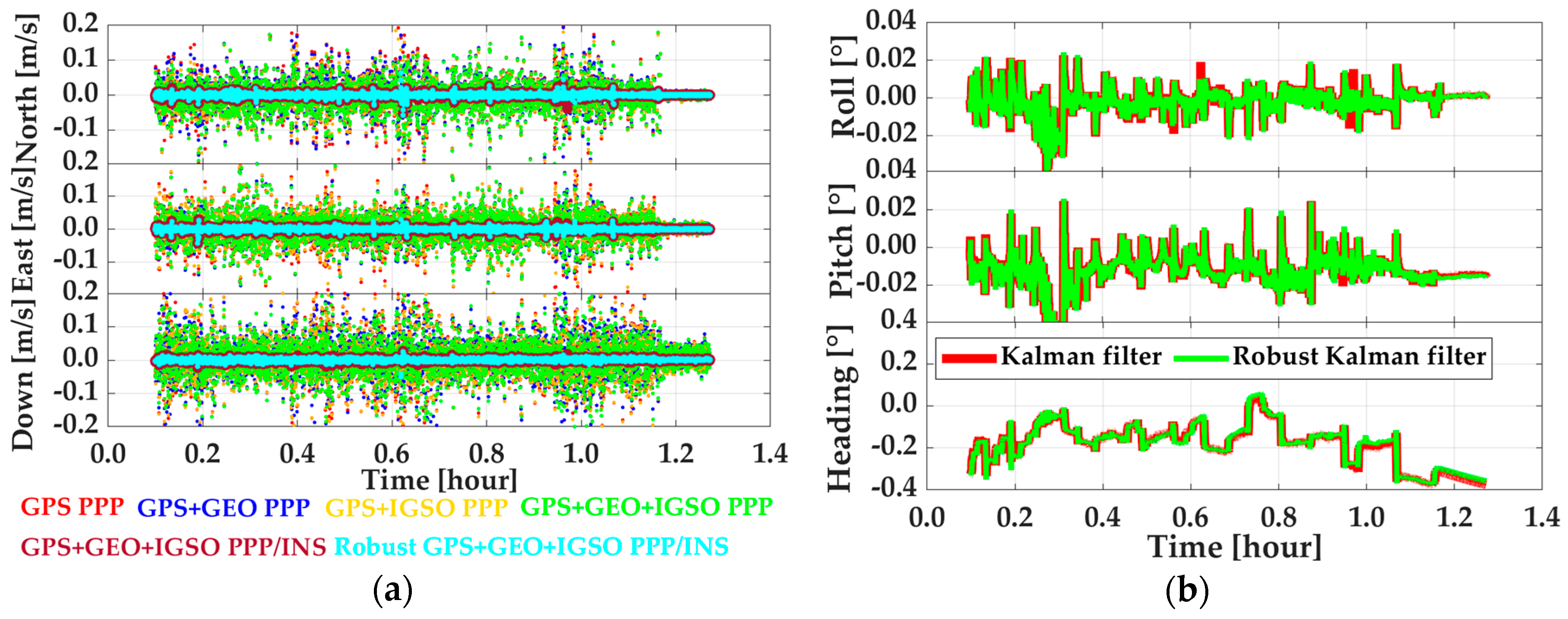
3. Tests, Results, and Discussion
3.1. Test Description
3.2. Performance Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Parkinson, B.W.; Enge, P.; Axelrad, P.; Spilker, J.J., Jr. Global Positioning System: Theory and Applications, Volume II; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1996. [Google Scholar]
- Azúa, B.M.; DeMets, C.; Masterlark, T. Strong interseismic coupling, fault afterslip, and viscoelastic flow before and after the Oct. 9, 1995 Colima-Jalisco earthquake: Continuous GPS measurements from Colima, Mexico. Geophys. Res. Lett. 2002, 29, 122-1–122-4. [Google Scholar]
- Larson, K.M.; Bodin, P.; Gomberg, J. Using 1-Hz GPS data to measure deformations caused by the Denali fault earthquake. Science 2003, 300, 1421–1424. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Shen, W.B.; Hwang, C.; Liao, C.; Zhang, T.; Zhang, G. Seasonal Mass Changes and Crustal Vertical Deformations Constrained by GPS and GRACE in Northeastern Tibet. Sensors 2016, 16, 1211. [Google Scholar] [CrossRef]
- Gendt, G.; Dick, G.; Reigber, C.H.; Tomassini, M.; Liu, Y.; Ramatschi, M. Demonstration of NRT GPS water vapor monitoring for numerical weather prediction in Germany. J. Meteorol. Soc. Jpn. 2003, 82, 360–370. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.A.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A.H. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv. Space Res. 2011, 47, 1664–1673. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X. Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing. GPS Solut. 2012, 16, 315–327. [Google Scholar]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of ionosphere-constrained precise point positioning and inertial navigation systems. Sensors 2015, 15, 5783–5802. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Sturze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Xu, J.; Tang, J.; Guo, H.; He, H. Contribution of the compass satellite navigation system to global PNT users. Chin. Sci. Bull. 2011, 56, 2813. [Google Scholar] [CrossRef]
- Li, M.; Qu, L.; Zhao, Q.; Guo, J.; Su, X.; Li, X. Precise point positioning with the BeiDou navigation satellite system. Sensors 2014, 14, 927–943. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- State Council Information Office (SCIO). China’s BeiDou Navigation Satellite System by the State Council Information Office of the People’s Republic of China (SCIO). 2016. Available online: http://www.beidou.gov.cn/xt/gfxz/201712/P020171221333863515306.pdf (accessed on 18 Mach 2017).
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M. Odometer and MEMS IMU enhancing PPP under weak satellite observability environments. Adv. Space Res. 2018, 62, 2494–2508. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Wang, J.; Tan, X. Performance analysis on carrier phase-based tightly-coupled GPS/BDS/INS integration in GNSS degraded and denied environments. Sensors 2015, 15, 8685–8711. [Google Scholar] [CrossRef]
- Cox, D.B., Jr. Integration of GPS with inertial navigation systems. Navigation 1978, 25, 236–245. [Google Scholar] [CrossRef]
- Farrell, J.; Barth, M. The Global Positioning System and Inertial Navigation; Mcgraw-Hill: New York, NY, USA, 1999; Volume 61. [Google Scholar]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solut. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Shin, E.H. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Thesis, Calgary University, Calgary, AB, Canada, 2005. [Google Scholar]
- Gao, Z.; Ge, M.; Shen, W.; Li, Y.; Chen, Q.; Zhang, H.; Niu, X. Evaluation on the impact of IMU grades on BDS+ GPS PPP/INS tightly coupled integration. Adv. Space Res. 2017, 60, 1283–1299. [Google Scholar] [CrossRef]
- Jan, S.S.; Tao, A.L. Comprehensive comparisons of satellite data, signals, and measurements between the BeiDou navigation satellite system and the global positioning system. Sensors 2016, 16, 689. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Liu, W.; Sun, G. Modernization milestone: BeiDou M2-S initial signal analysis. GPS Solut. 2016, 20, 125–133. [Google Scholar] [CrossRef]
- Xie, X.; Geng, T.; Zhao, Q.; Liu, J.; Wang, B. Performance of BDS-3: Measurement quality analysis, precise orbit and clock determination. Sensors 2017, 17, 1233. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.G.; Hwang, P.Y. Introduction to Random Signals and Applied Kalman Filtering; Wiley: New York, NY, USA, 1992; Volume 3. [Google Scholar]
- Koch, K.R.; Yang, Y. Robust Kalman filter for rank deficient observation models. J. Geod. 1998, 72, 436–441. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Z.; Ge, M.; Niu, X.; Huang, L.; Tu, R.; Li, X. On the convergence of ionospheric constrained precise point positioning (IC-PPP) based on undifferential uncombined raw GNSS observations. Sensors 2013, 13, 15708–15725. [Google Scholar] [CrossRef]
- Witchayangkoon, B. Elements of GPS precise point positioning. Ph.D. Thesis, University of Maine, Orono, ME, USA, December 2000. [Google Scholar]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, 3, 325–331. [Google Scholar] [CrossRef]
- Schaer, S.; Gurtner, W.; Feltens, J. IONEX: The ionosphere map exchange format version 1. In Proceedings of the IGS AC Workshop, Darmstadt, Germany, 9–11 February 1998; Volume 9. No. 11. [Google Scholar]
- Lan, H.; Yu, C.; Zhuang, Y.; Li, Y.; El-Sheimy, N. A novel kalman filter with state constraint approach for the integration of multiple pedestrian navigation systems. Micromachines 2015, 6, 926–952. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Li, Y.; Zhuang, Y.; Lan, H.; Zhang, P.; Niu, X.; El-Sheimy, N. Self-Contained Indoor Pedestrian Navigation Using Smartphone Sensors and Magnetic Features. IEEE Sens. J. 2016, 16, 7173–7182. [Google Scholar] [CrossRef]
- Zhuang, Y.; Li, Y.; Lan, H.; Syed, Z.; El-Sheimy, N. Smartphone-based WiFi access point localisation and propagation parameter estimation using crowdsourcing. Electron. Lett. 2015, 51, 1380–1382. [Google Scholar] [CrossRef]
- Li, Y.; Niu, X.; Cheng, Y.; Shi, C.; El-Sheimy, N. The Impact of Vehicle Maneuvers on the Attitude Estimation of GNSS/INS for Mobile Mapping. J. Appl. Geod. 2015, 9, 183–197. [Google Scholar]


| IMU Sensors | Gyro Bias (°/h) | Accelerometer Bias (mGal) | Forward (mm) | Right (mm) | Down (mm) |
|---|---|---|---|---|---|
| Navigation Grade | 0.001 | 25 | −122.0 | 613.1 | −109.0 |
| Tactical Grade | 0.5 | 500 | 114.0 | 429.0 | −151.5 |
| Data | PPP | PPP/INS | Robust PPP/INS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Down | North | East | Down | North | East | Down | |
| GPS | 0.265 | 0.160 | 0.225 | 0.212 | 0.137 | 0.199 | - | - | - |
| GPS + GEO | 0.159 | 0.132 | 0.206 | 0.142 | 0.119 | 0.177 | 0.149 | 0.068 | 0.119 |
| GPS + IGSO | 0.095 | 0.122 | 0.121 | 0.074 | 0.117 | 0.101 | 0.046 | 0.044 | 0.080 |
| GPS + GEO + IGSO | 0.078 | 0.114 | 0.095 | 0.058 | 0.066 | 0.080 | 0.046 | 0.036 | 0.069 |
| Residuals | P1(m) | P2(m) | L1/B1(m) | L2/B2(m) |
|---|---|---|---|---|
| GEO | 0.759 | 1.406 | 0.005 | 0.007 |
| IGSO | 0.491 | 0.292 | 0.004 | 0.003 |
| GPS | 0.307 | 0.424 | 0.003 | 0.004 |
| Data | PPP | PPP/INS | Robust PPP/INS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Down | North | East | Down | North | East | Down | |
| GPS | 0.0485 | 0.0438 | 0.0629 | 0.0044 | 0.0040 | 0.0039 | - | - | - |
| GPS + GEO | 0.0449 | 0.0399 | 0.0619 | 0.0043 | 0.0040 | 0.0038 | 0.0043 | 0.0040 | 0.0038 |
| GPS + IGSO | 0.0430 | 0.0418 | 0.0589 | 0.0042 | 0.0040 | 0.0036 | 0.0042 | 0.0040 | 0.0036 |
| GPS + GEO + IGSO | 0.0403 | 0.0392 | 0.0533 | 0.0040 | 0.0040 | 0.0036 | 0.0040 | 0.0040 | 0.0036 |
| Data | PPP/INS | Robust PPP/INS | ||||
|---|---|---|---|---|---|---|
| Roll | Pith | Heading | Roll | Pith | Heading | |
| GPS + GEO | 0.0065 | 0.0154 | 0.2044 | 0.0065 | 0.0154 | 0.2030 |
| GPS + IGSO | 0.0065 | 0.0153 | 0.2028 | 0.0065 | 0.0152 | 0.2023 |
| GPS + GEO + IGSO | 0.0065 | 0.0153 | 0.2025 | 0.0064 | 0.0152 | 0.1983 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Li, Y.; Zhuang, Y.; Yang, H.; Pan, Y.; Zhang, H. Robust Kalman Filter Aided GEO/IGSO/GPS Raw-PPP/INS Tight Integration. Sensors 2019, 19, 417. https://doi.org/10.3390/s19020417
Gao Z, Li Y, Zhuang Y, Yang H, Pan Y, Zhang H. Robust Kalman Filter Aided GEO/IGSO/GPS Raw-PPP/INS Tight Integration. Sensors. 2019; 19(2):417. https://doi.org/10.3390/s19020417
Chicago/Turabian StyleGao, Zhouzheng, You Li, Yuan Zhuang, Honglei Yang, Yuanjin Pan, and Hongping Zhang. 2019. "Robust Kalman Filter Aided GEO/IGSO/GPS Raw-PPP/INS Tight Integration" Sensors 19, no. 2: 417. https://doi.org/10.3390/s19020417
APA StyleGao, Z., Li, Y., Zhuang, Y., Yang, H., Pan, Y., & Zhang, H. (2019). Robust Kalman Filter Aided GEO/IGSO/GPS Raw-PPP/INS Tight Integration. Sensors, 19(2), 417. https://doi.org/10.3390/s19020417






