Pixelwise Phase Unwrapping Based on Ordered Periods Phase Shift
Abstract
:1. Introduction
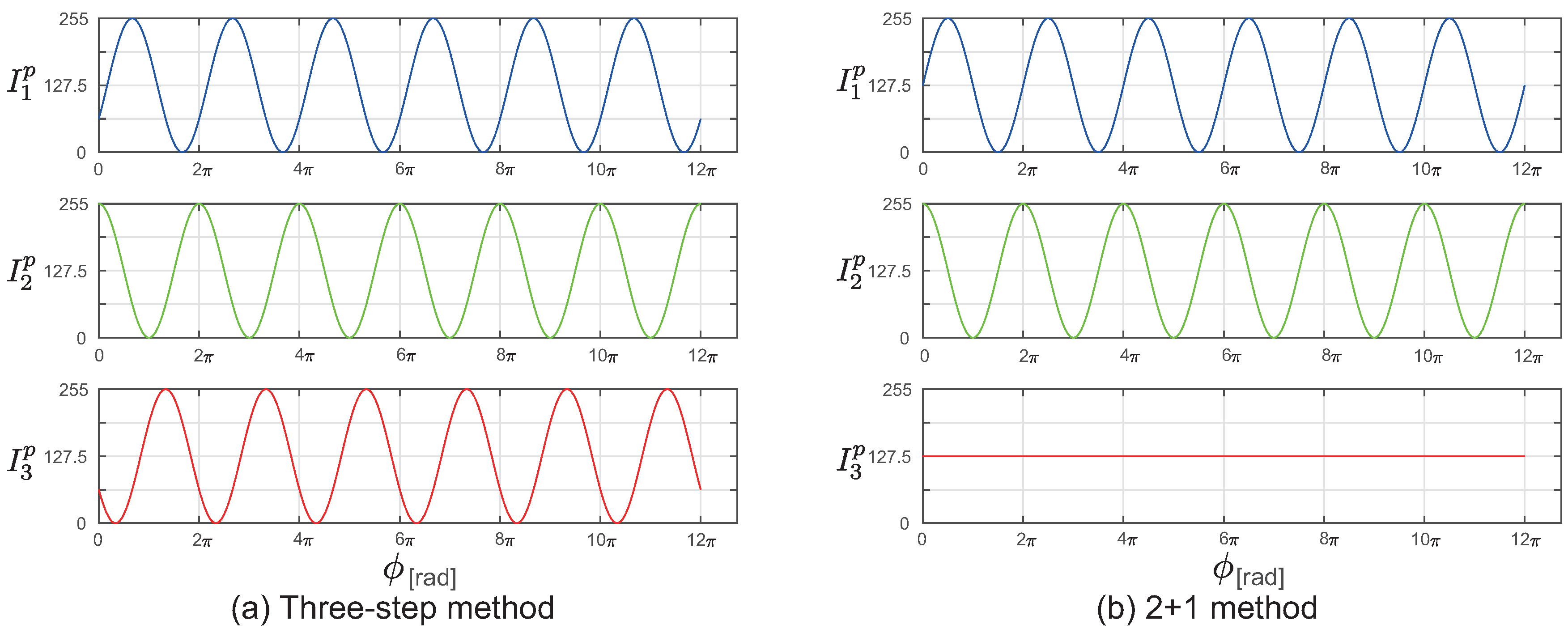
2. Related Methods
2.1. Basic Method
2.2. Phase Unwrapping
3. Proposed Method
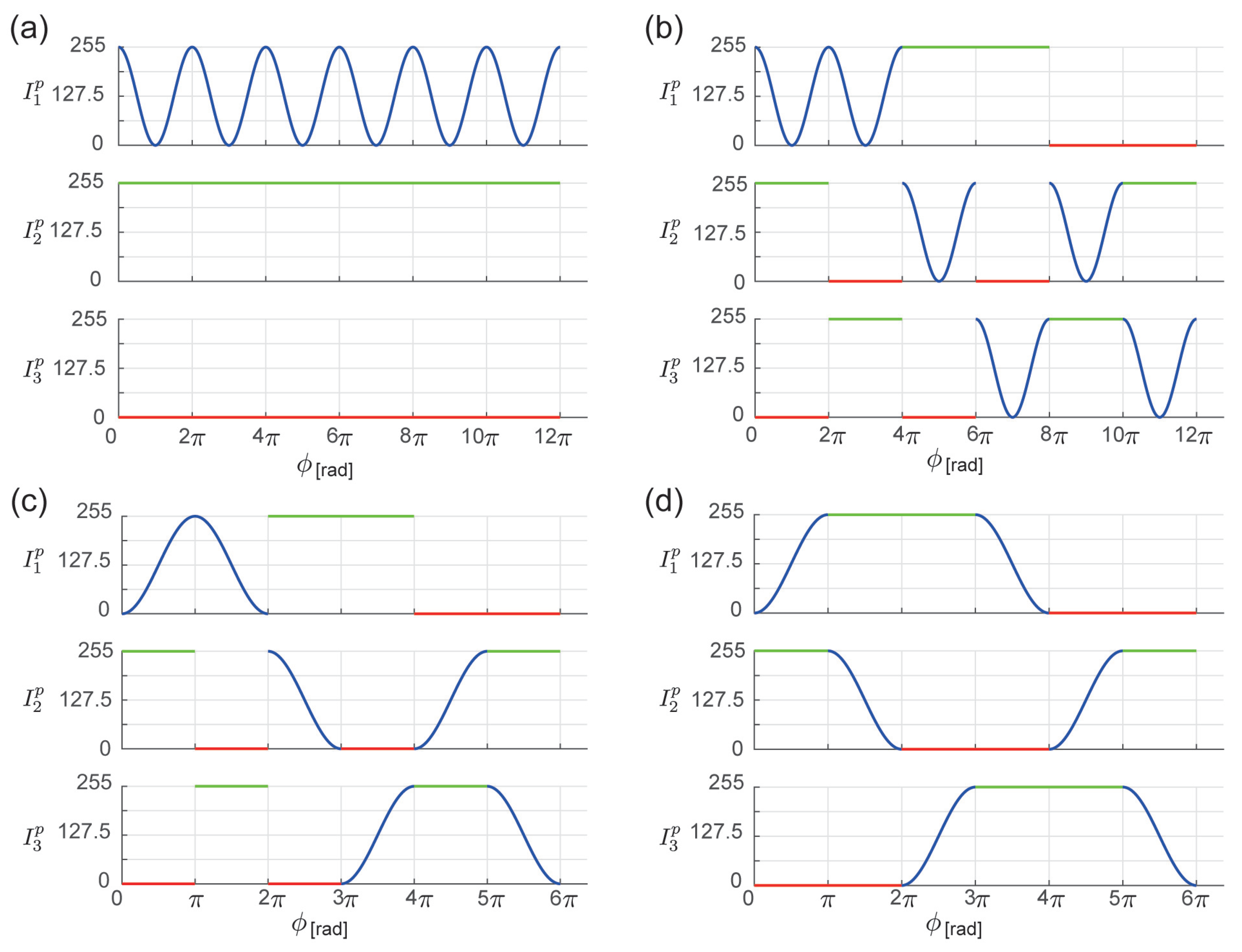
3.1. Ordered Periods Phase Shift (OPPS)
3.1.1. Basic Method
3.1.2. Realizing Unique Tuple Identification
3.1.3. Spatial Continuity of Patterns
3.1.4. Decoding Projected Patterns
3.1.5. Measurement Interpolation
3.1.6. Projection Period Limitations
3.2. Four-Step OPPS
3.2.1. Basic Method
3.2.2. Realizing Unique Tuple Identification
3.2.3. Spatial Continuity of Patterns
3.2.4. Decoding Projection Patterns
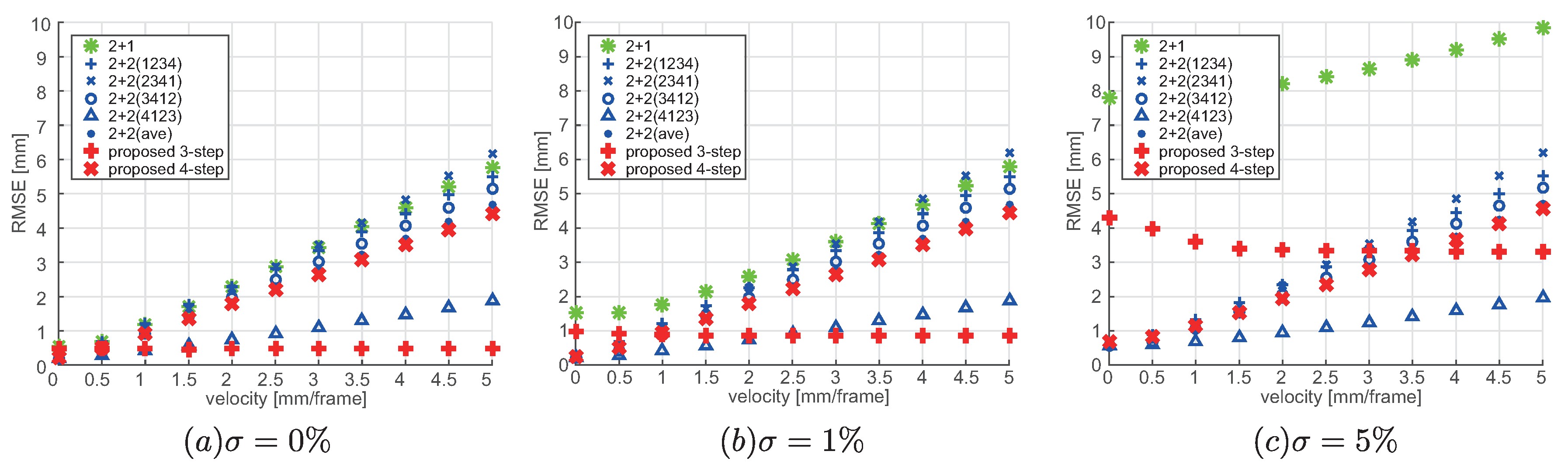
4. Experiments
4.1. Evaluation of Motion Error
4.2. Evaluation of Global Illumination
4.3. High-Speed OPPS
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Watanabe, Y. High-speed optical 3D sensing and its applications. Adv. Opt. Technol. 2016, 5, 367–376. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Van der Jeught, S.; Dirckx, J.J. Real-time structured light profilometry: A review. Opt. Lasers Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Watanabe, Y.; Komuro, T.; Ishikawa, M. 955-fps real-time shape measurement of a moving/deforming object using high-speed vision for numerous-point analysis. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3192–3197. [Google Scholar]
- Tabata, S.; Noguchi, S.; Watanabe, Y.; Ishikawa, M. High-speed 3D sensing with three-view geometry using a segmented pattern. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 3900–3907. [Google Scholar]
- Gao, H.; Takaki, T.; Ishii, I. GPU-based real-time structured light 3D scanner at 500 fps. Real-Time Image and Video Processing. In Proceedings of the International Society for Optics and Photonics, Brussels, Belgium, 16–19 April 2012; Volume 8437, p. 84370J. [Google Scholar]
- Maruyama, M.; Tabata, S.; Watanabe, Y. Multi-pattern Embedded Phase Shifting Using a High-Speed Projector for Fast and Accurate Dynamic 3D Measurement. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Lake Tahoe, NV, USA, 12–15 March 2018; pp. 921–929. [Google Scholar]
- Watanabe, Y.; Narita, G.; Tatsuno, S.; Yuasa, T.; Sumino, K.; Ishikawa, M. High-speed 8-bit image projector at 1,000 fps with 3 ms delay. In Proceedings of the 22nd International Display Workshops, Otsu, Japan, 9–11 December 2015; pp. 1064–1065. [Google Scholar]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Gupta, M.; Nayar, S.K. Micro phase shifting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 813–820. [Google Scholar]
- Weise, T.; Leibe, B.; Van Gool, L. Fast 3d scanning with automatic motion compensation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Boisvert, J.; Drouin, M.A.; Dicaire, L.G.; Picard, M.; Godin, G. Motion Compensation for Phase-Shift Structured-Light Systems Based on a Total-Variation Framework. In Proceedings of the IEEE International Conference on 3D Vision, Qingdao, China, 10–12 October 2017; pp. 658–666. [Google Scholar]
- Zhang, S.; Yau, S.T. High-speed three-dimensional shape measurement system using a modified two-plus-one phase-shifting algorithm. Opt. Eng. 2007, 46, 113603. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Gu, G.; Feng, S.; Feng, F. High-speed three-dimensional profilometry for multiple objects with complex shapes. Opt. Express 2012, 20, 19493–19510. [Google Scholar] [CrossRef]
- Jia, P.; Kofman, J.; English, C.E. Two-step triangular-pattern phase-shifting method for three-dimensional object-shape measurement. Opt. Eng. 2007, 46, 083201. [Google Scholar]
- Huang, P.S.; Zhang, S.; Chiang, F.P. Trapezoidal phase-shifting method for three-dimensional shape measurement. Opt. Eng. 2005, 44, 123601. [Google Scholar] [CrossRef]
- Zhang, S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 2010, 48, 149–158. [Google Scholar] [CrossRef]
- Chen, X.; Chen, S.; Luo, J.; Ma, M.; Wang, Y.; Wang, Y.; Chen, L. Modified Gray-Level Coding Method for Absolute Phase Retrieval. Sensors 2017, 17, 2383. [Google Scholar] [CrossRef]
- Chen, K.; Xi, J.; Yu, Y. Quality-guided spatial phase unwrapping algorithm for fast three-dimensional measurement. Opt. Commun. 2013, 294, 139–147. [Google Scholar] [CrossRef]
- Kemao, Q.; Gao, W.; Wang, H. Windowed Fourier-filtered and quality-guided phase-unwrapping algorithm. Appl. Opt. 2008, 47, 5420–5428. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.; Valadao, G. Phase unwrapping via graph cuts. IEEE Trans. Image Process. 2007, 15, 698–709. [Google Scholar] [CrossRef]
- Zheng, D.; Da, F. A novel algorithm for branch cut phase unwrapping. Opt. Lasers Eng. 2011, 49, 609–617. [Google Scholar] [CrossRef]
- Li, F.; Gao, S.; Shi, G.; Li, Q.; Yang, L.; Li, R.; Xie, X. Single Shot Dual-Frequency Structured Light Based Depth Sensing. IEEE J. Sel. Top. Signal Process. 2015, 9, 384–395. [Google Scholar] [CrossRef]
- Yang, L.; Li, F.; Xiong, Z.; Shi, G.; Niu, Y.; Li, R. Single-shot dense depth sensing with frequency-division multiplexing fringe projection. J. Vis. Commun. Image Represent. 2017, 46, 139–149. [Google Scholar] [CrossRef]
- Saldner, H.O.; Huntley, J.M. Temporal phase unwrapping: Application to surface profiling of discontinuous objects. Appl. Opt. 1997, 36, 2770–2775. [Google Scholar] [CrossRef]
- Chen, F.; Su, X. Phase-unwrapping algorithm for the measurement of 3D object. Opt.-Int. J. Light Electron Opt. 2012, 123, 2272–2275. [Google Scholar] [CrossRef]
- Song, L.; Dong, X.; Xi, J.; Yu, Y.; Yang, C. A new phase unwrapping algorithm based on Three Wavelength Phase Shift Profilometry method. Opt. Laser Technol. 2013, 45, 319–329. [Google Scholar] [CrossRef]
- Sansoni, G.; Corini, S.; Lazzari, S.; Rodella, R.; Docchio, F. Three-dimensional imaging based on Gray-code light projection: Characterization of the measuring algorithm and development of a measuring system for industrial applications. Appl. Opt. 1997, 36, 4463–4472. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Wang, Y.; Ma, M.; Zeng, C. Quantized phase coding and connected region labeling for absolute phase retrieval. Opt. Express 2016, 24, 28613–28624. [Google Scholar] [CrossRef]
- Moreno, D.; Hwang, W.Y.; Taubin, G. Rapid hand shape reconstruction with chebyshev phase shifting. In Proceedings of the 2016 IEEE Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 157–165. [Google Scholar]
- Cao, Y.; Su, X. RGB tricolor based fast phase measuring profilometry. In Advanced Materials and Devices for Sensing and Imaging, Proceedings of the International Society for Optics and Photonics, Shanghai, China, 14–18 October 2002; International Society for Optics and Photonics: Bellingham, WA, USA, 2002; Volume 4919, pp. 528–536. [Google Scholar]
- Schubert, E.; Rath, H.; Klicker, J. Fast 3D object recognition using a combination of color-coded phase-shift principle and color-coded triangulation. In Sensors and Control for Automation, Proceedings of the International Society for Optics and Photonics, Frankfurt, Germany, 19–24 June 1994; International Society for Optics and Photonics: Bellingham, WA, USA, 1994; Volume 2247, pp. 202–214. [Google Scholar]
- Zhang, Z.; Guo, T. Absolute Phase Measurement Based on Combining Binary Color-Code and Phase-Shift Light Projection. AIP Conf. Proc. 2010, 1236, 427–432. [Google Scholar]
- Tao, T.; Chen, Q.; Da, J.; Feng, S.; Hu, Y.; Zuo, C. Real-time 3-D shape measurement with composite phase-shifting fringes and multi-view system. Opt. Express 2016, 24, 20253–20269. [Google Scholar] [CrossRef]
- Hyun, J.S.; Chiu, G.T.C.; Zhang, S. High-speed and high-accuracy 3D surface measurement using a mechanical projector. Opt. Express 2018, 26, 1474–1487. [Google Scholar] [CrossRef]
- An, Y.; Hyun, J.S.; Zhang, S. Pixel-wise absolute phase unwrapping using geometric constraints of structured light system. Opt. Express 2016, 24, 18445–18459. [Google Scholar] [CrossRef]
- Chen, S.Y.; Cheng, N.J.; Su, W.H. Phase-shifting projected fringe profilometry using ternary-encoded patterns. In Photonic Fiber and Crystal Devices: Advances in Materials and Innovations in Device Applications XI, Proceedings of the International Society for Optics and Photonics, San Diego, CA, USA, 21–25 August 2011; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 10382, p. 103820U. [Google Scholar]
- Blender Online Community. Blender—A 3D Modelling and Rendering Package; Blender Foundation, Blender Institute: Amsterdam, The Netherlands, 2017. [Google Scholar]






| in Figure 2c | 1 | 2 | 3 | 4 | 5 | 6 |
| hash () | 1 | 4 | 2 | 3 | 5 | 6 |
| tuple | (1,2,3) | (1,3,2) | (2,1,3) | (2,3,1) | (3,1,2) | (3,2,1) |
| in Figure 2c | 1 | 2 | 3 | 4 | 5 | 6 |
| in Figure 3c | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| hash() in Figure 3d | 1 | 2 | 3 | 4 | 33 | 14 | 15 | 16 | 13 | 34 | 27 | 24 | 10 | 8 | 5 | 6 |
| in Figure 3c | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| hash() in Figure 3d | 7 | 11 | 12 | 9 | 21 | 22 | 23 | 28 | 25 | 46 | 47 | 20 | 17 | 30 | 31 | 44 |
| in Figure 3c | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| hash() in Figure 3d | 41 | 42 | 43 | 32 | 37 | 38 | 39 | 40 | 29 | 18 | 19 | 48 | 45 | 26 | 35 | 36 |
| tuple | (1,2,3,4) | (1,2,4,3) | (4,1,2,3) | (3,1,2,4) | (3,4,1,2) | (4,3,1,2) | (1,3,4,2) | (1,4,3,2) | (1,3,2,4) | (1,4,2,3) | (4,1,3,2) | (3,1,4,2) |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabata, S.; Maruyama, M.; Watanabe, Y.; Ishikawa, M. Pixelwise Phase Unwrapping Based on Ordered Periods Phase Shift. Sensors 2019, 19, 377. https://doi.org/10.3390/s19020377
Tabata S, Maruyama M, Watanabe Y, Ishikawa M. Pixelwise Phase Unwrapping Based on Ordered Periods Phase Shift. Sensors. 2019; 19(2):377. https://doi.org/10.3390/s19020377
Chicago/Turabian StyleTabata, Satoshi, Michika Maruyama, Yoshihiro Watanabe, and Masatoshi Ishikawa. 2019. "Pixelwise Phase Unwrapping Based on Ordered Periods Phase Shift" Sensors 19, no. 2: 377. https://doi.org/10.3390/s19020377
APA StyleTabata, S., Maruyama, M., Watanabe, Y., & Ishikawa, M. (2019). Pixelwise Phase Unwrapping Based on Ordered Periods Phase Shift. Sensors, 19(2), 377. https://doi.org/10.3390/s19020377




