Statistical Approach to Spectrogram Analysis for Radio-Frequency Interference Detection and Mitigation in an L-Band Microwave Radiometer
Abstract
:1. Introduction
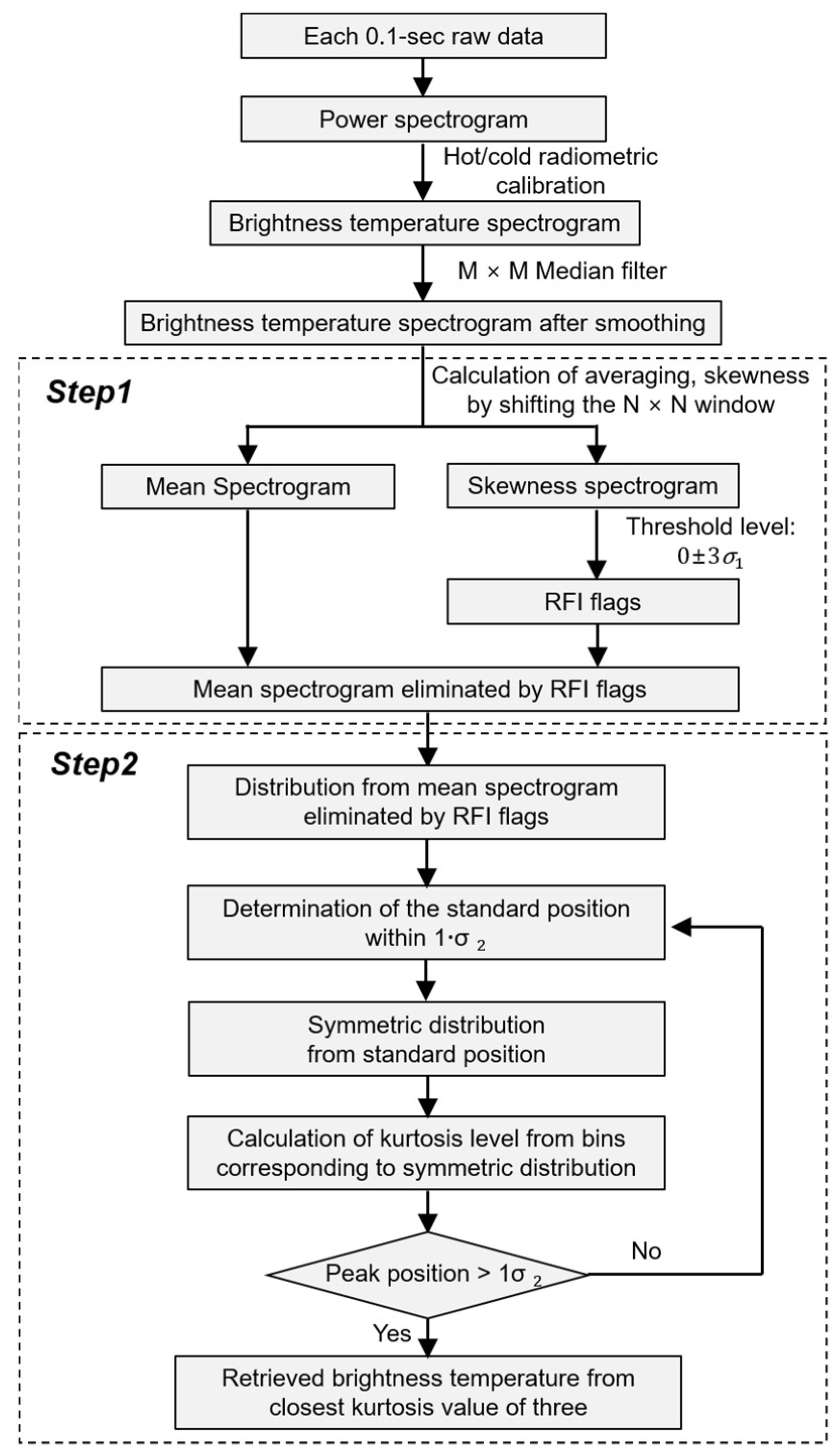
2. Proposed RFI Detection and Mitigation Algorithm
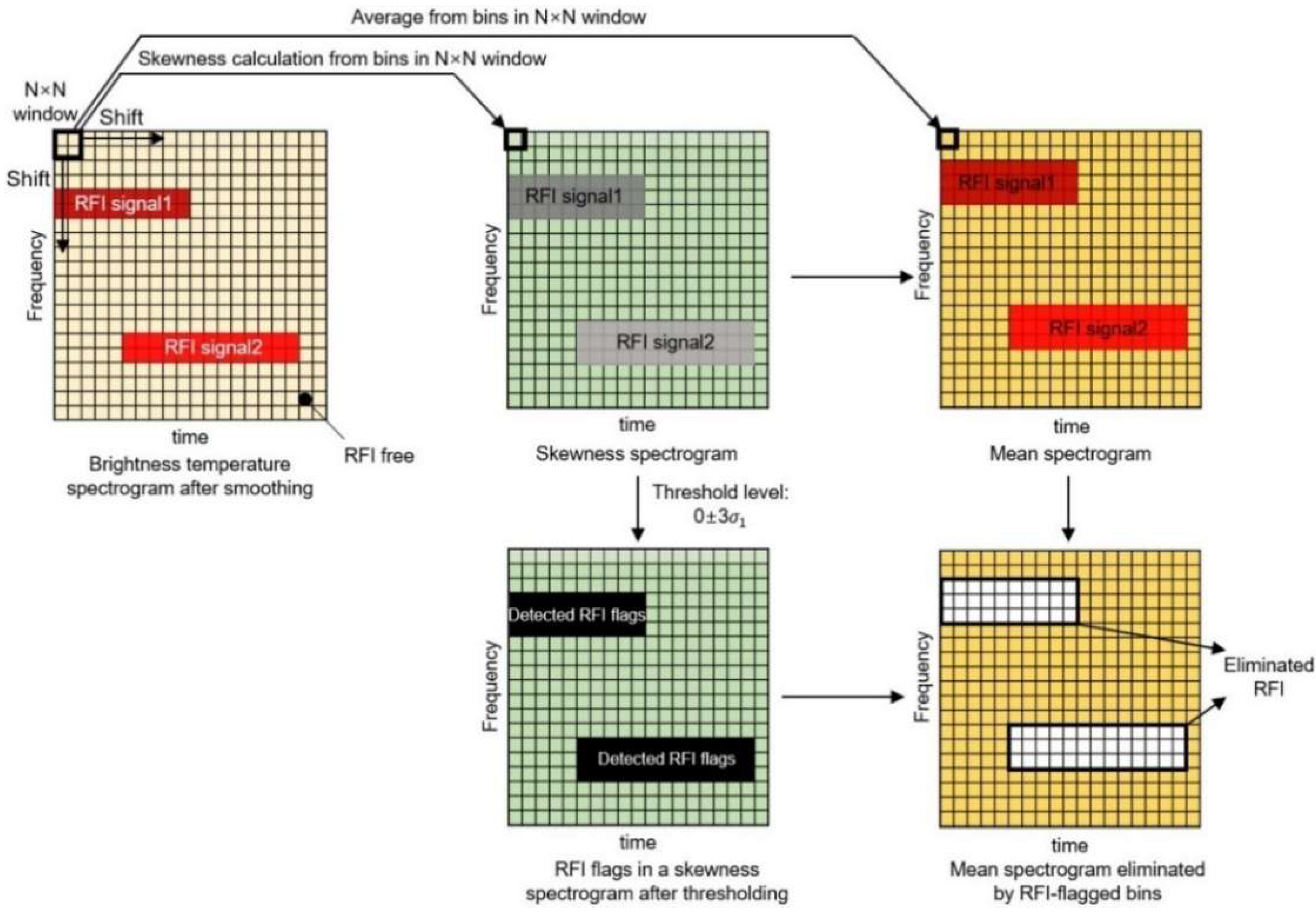
2.1. Step 1: Statistical Thresholding Using Skewness
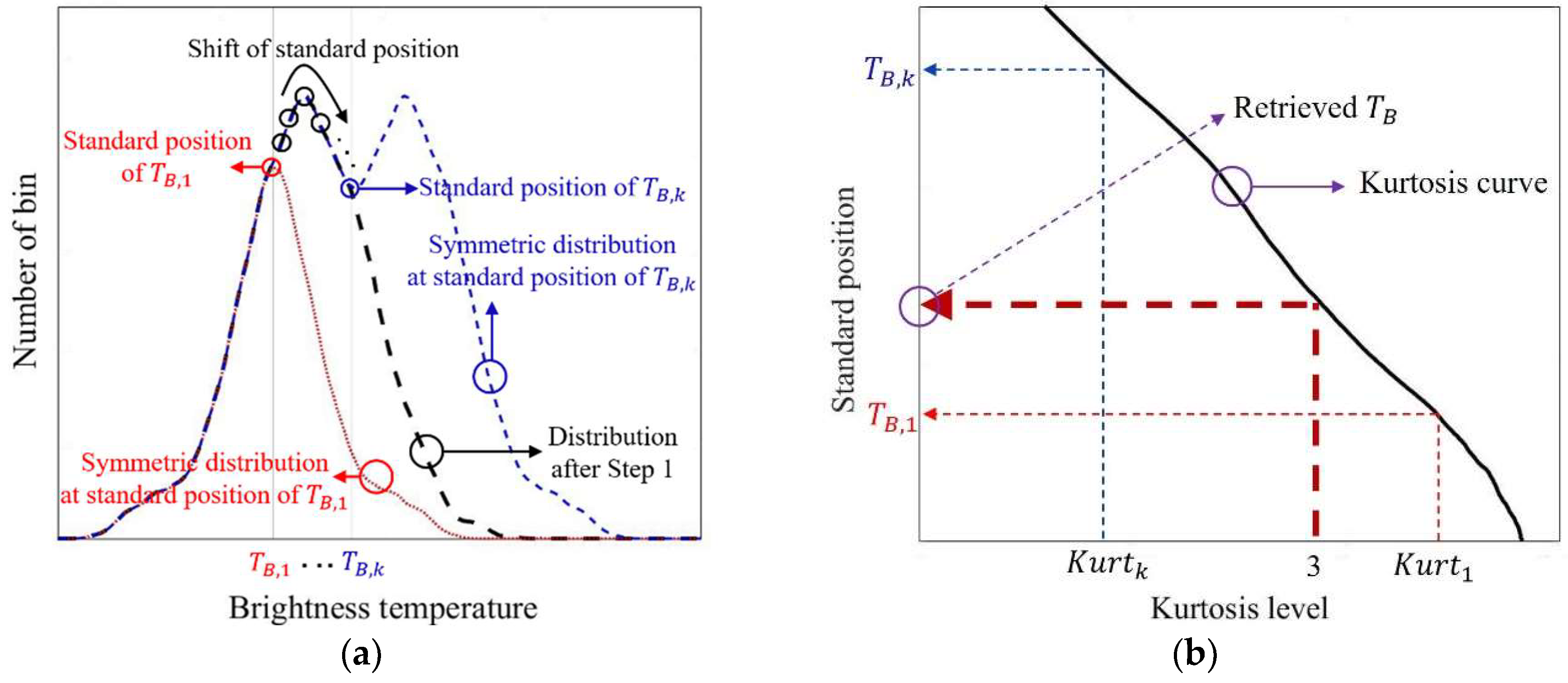
2.2. Step 2: Process of Obtaining the Retrieved Brightness Temperature Using Kurtosis
3. L-Band Microwave and Experimental Setup
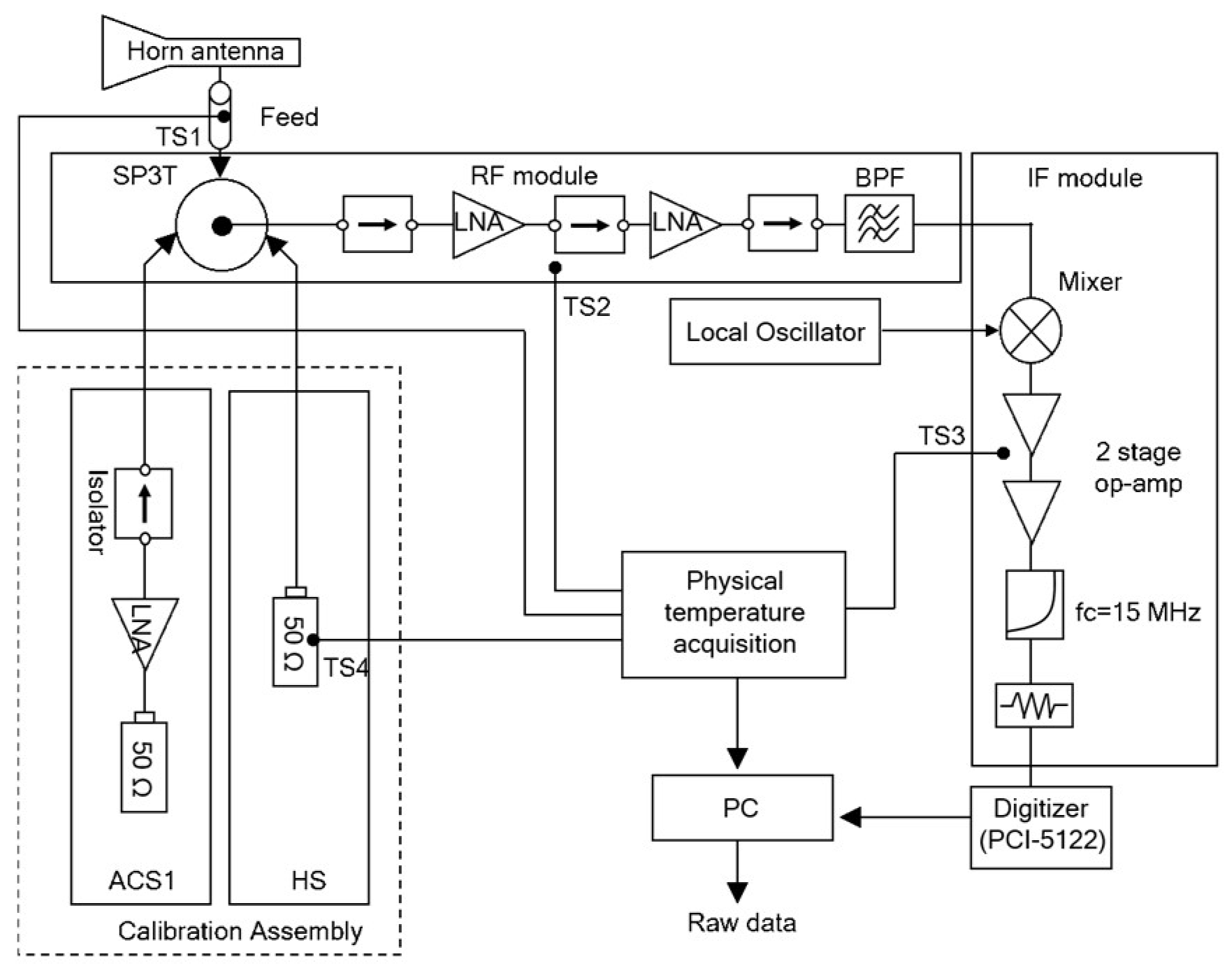
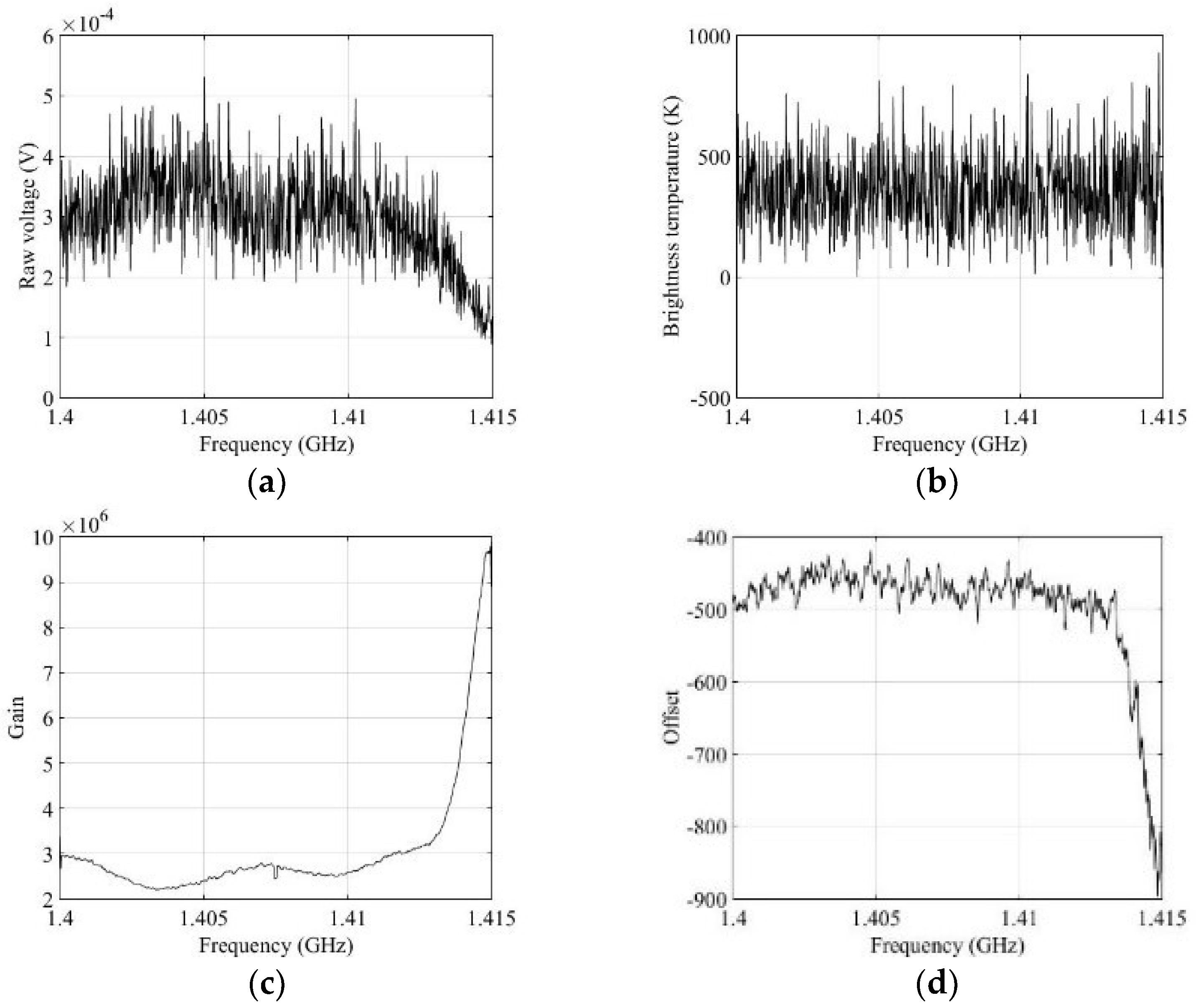
3.1. L-Band Radiometer Description
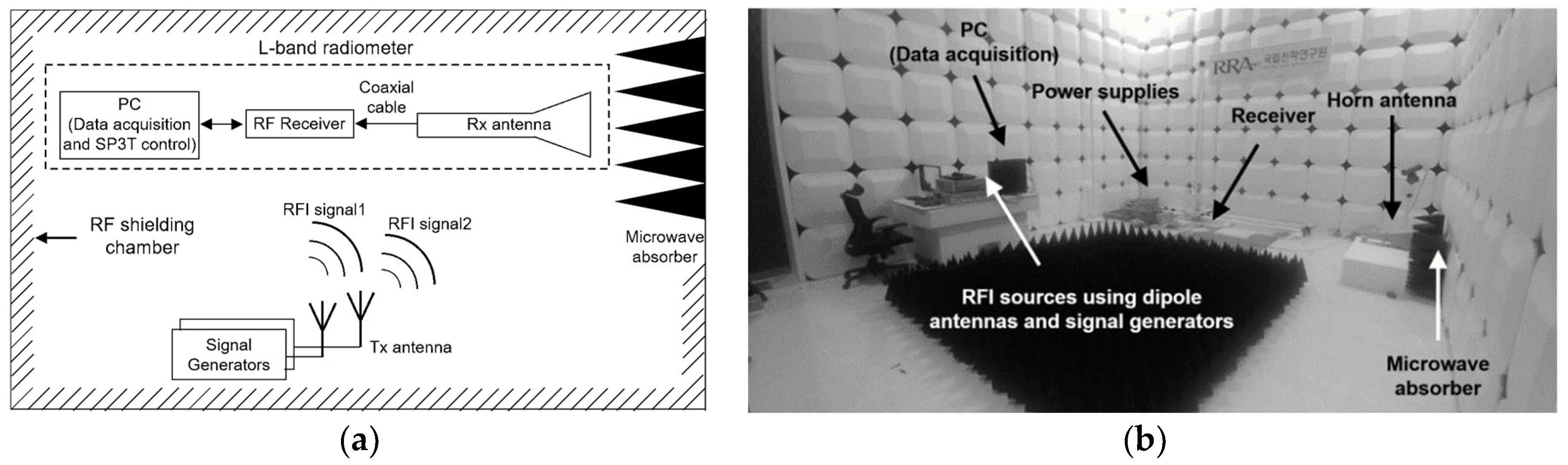
3.2. Experimental Setup
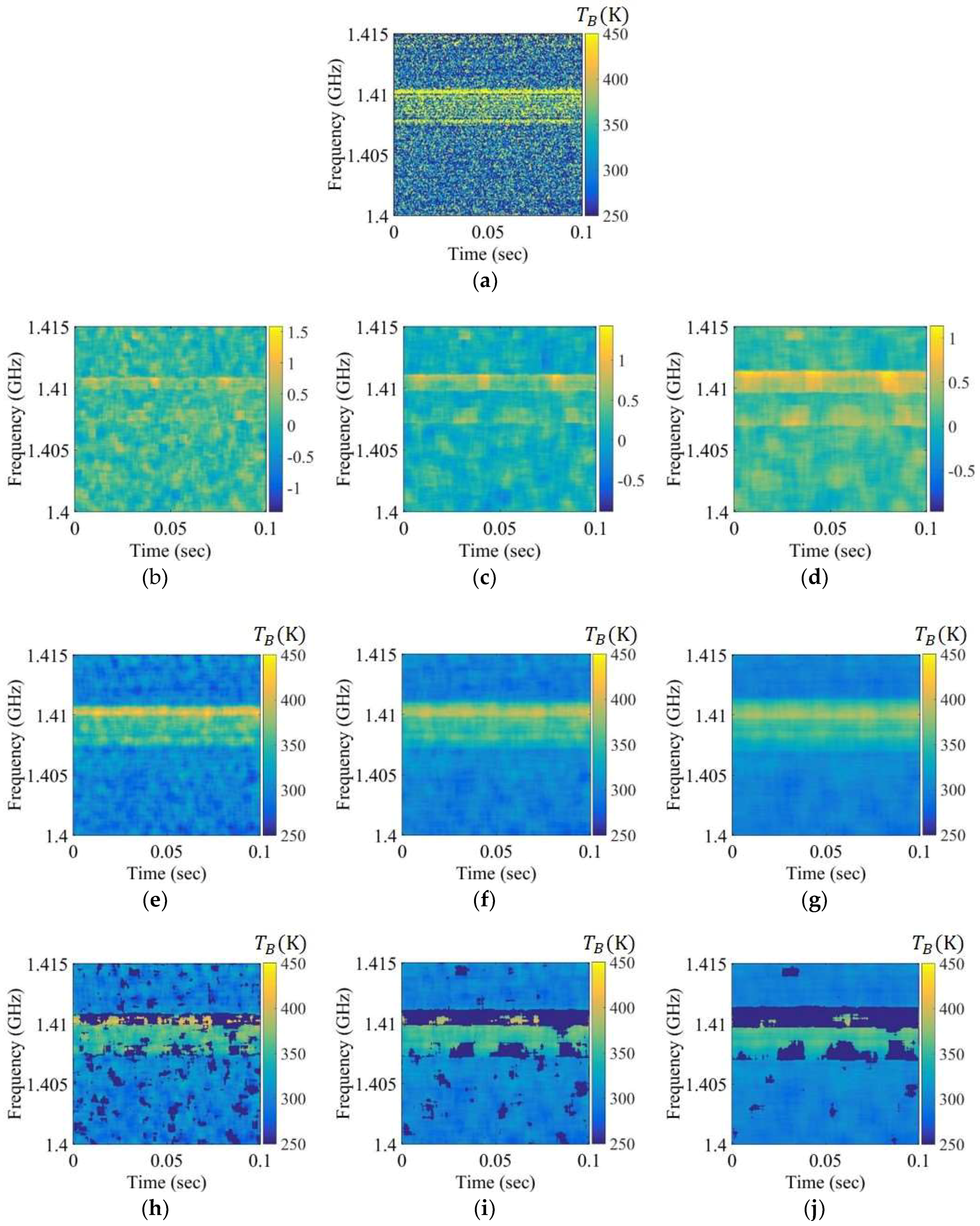
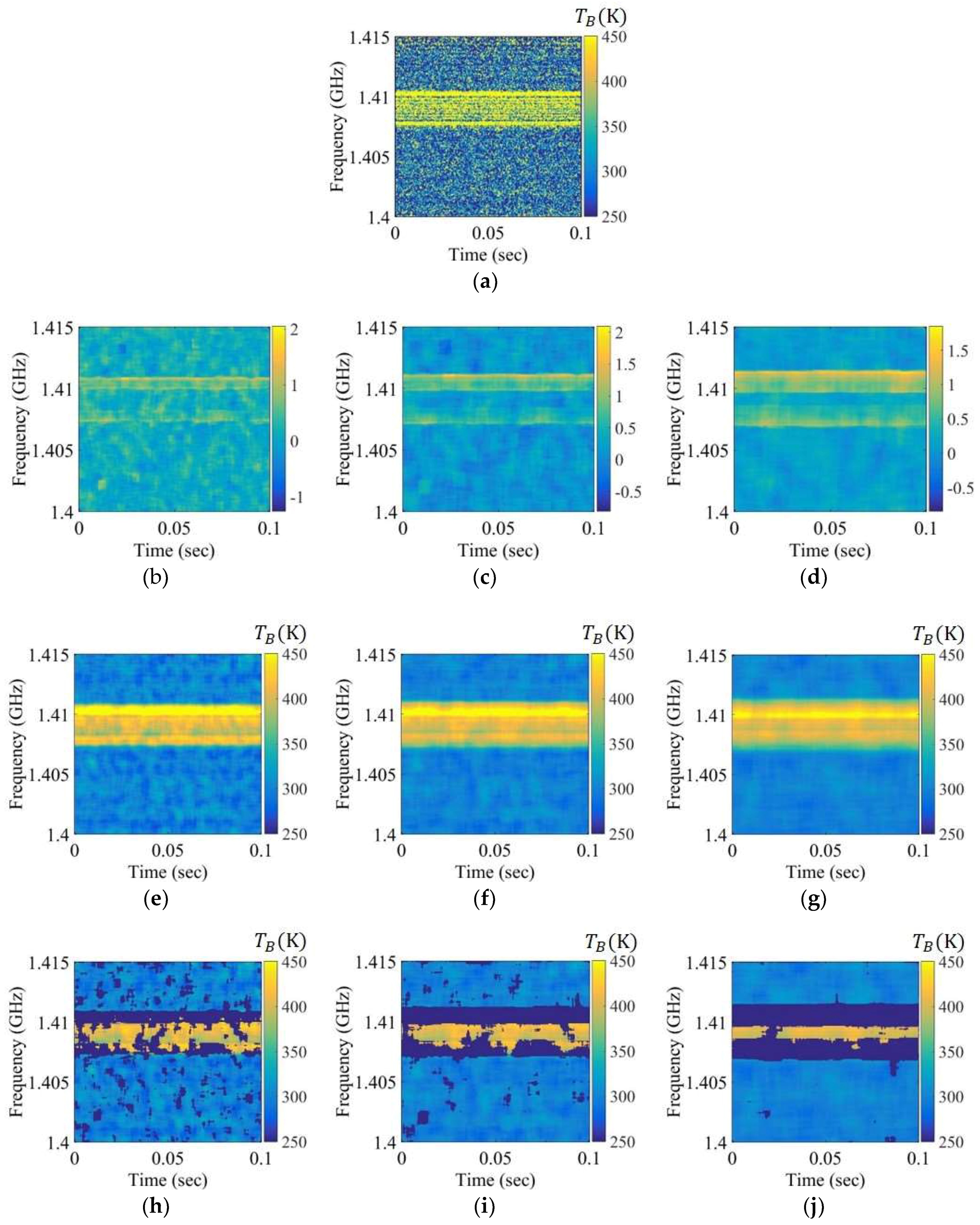
4. Experimental Results and Analysis
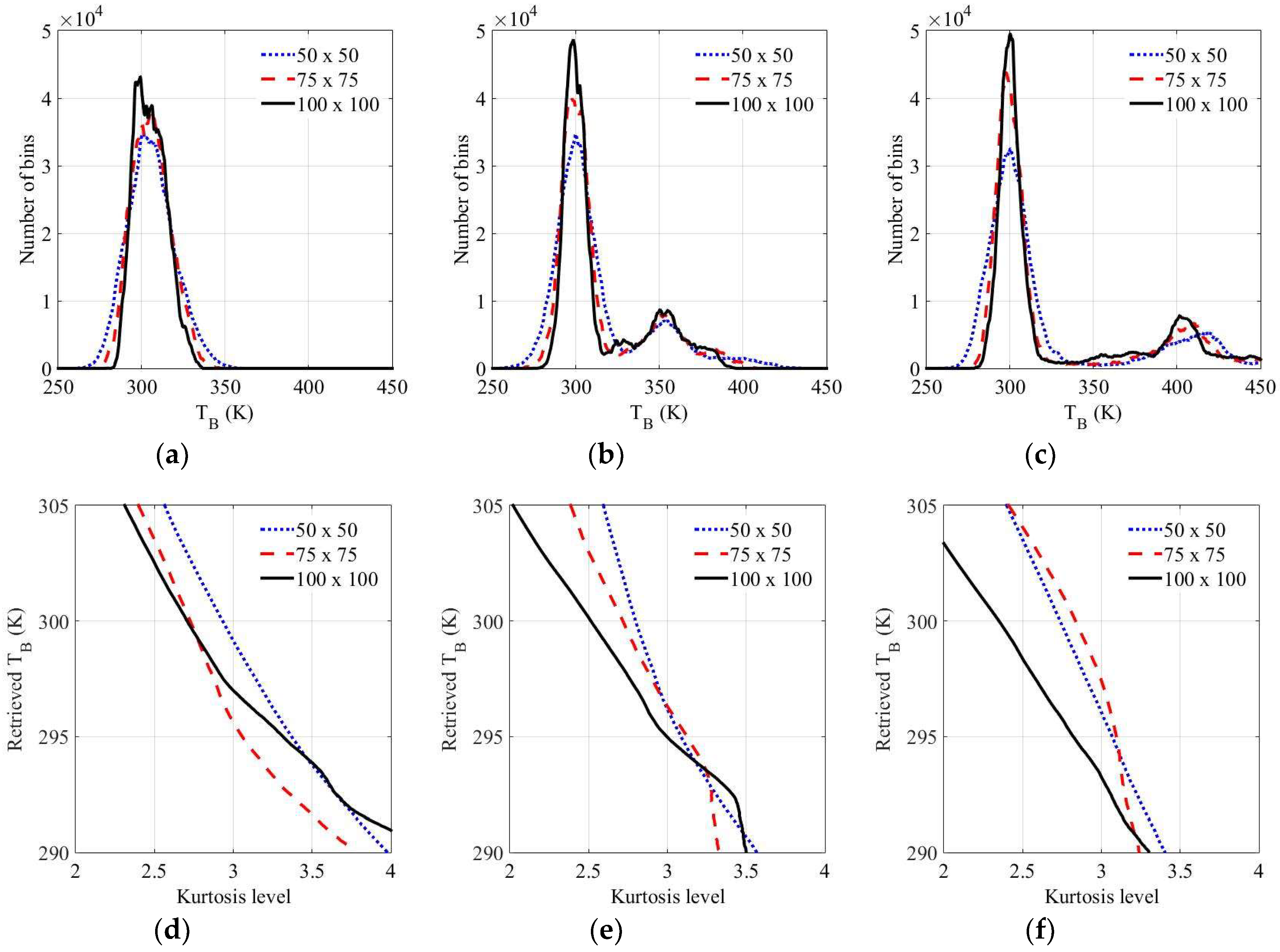
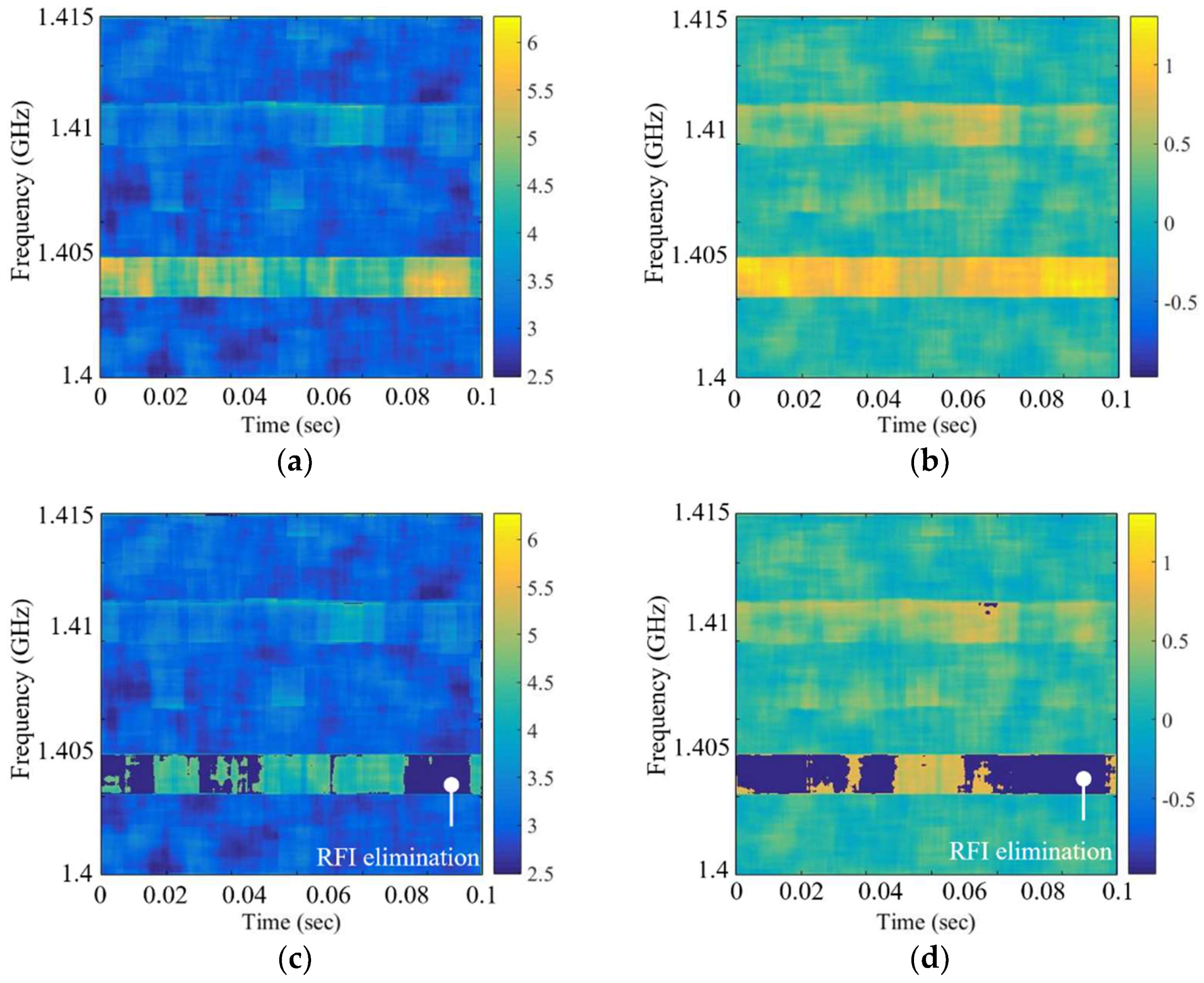
4.1. Experimental Results of Steps
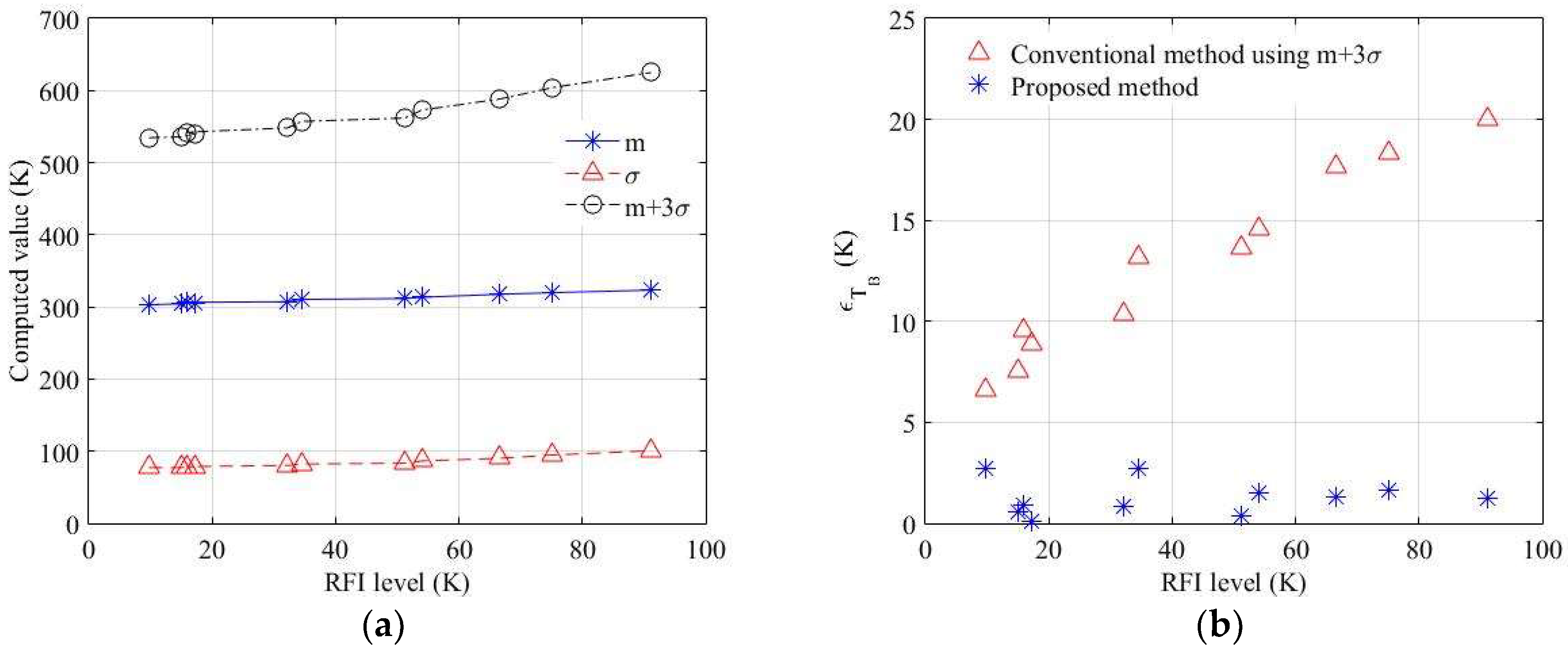
4.2. Error Analysis and Comparison between the Privious Method and Proposed Method
4.3. The Performance Comparison of the Skewness and Kurtosis in Step 1
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oliva, R.; Daganzo-Eusebio, E.; Kerr, Y.; Mecklenburg, S.; Nieto, S.; Richaume, P.; Gruhier, C. SMOS radio frequency interference scenario: Status and actions taken to improve the RFI environment in the 1400–1427-MHz passive band. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1427–1439. [Google Scholar] [CrossRef]
- Ruf, C.; Gross, S.; Misra, S. RFI detection and mitigation for microwave radiometry with an agile digital detector. IEEE Trans. Geosci. Remote Sens. 2006, 44, 694–706. [Google Scholar] [CrossRef]
- Querol, J.; Tarongí, J.; Forte, G.; Gómez, J.; Camps, A. MER-ITXELL: The multifrequency experimental radiometer with interference tracking for experiments over land and littoral—Instrument description, calibration and performance. Sensors 2017, 17, 1081. [Google Scholar] [CrossRef]
- Saleh, K.; Wigneron, J.; Waldteufel, P.; Rosnay, P.; Schwank, M.; Calvet, J.; Kerr, Y. Estimates of surface soil moisture under grass covers using L-band radiometry. Remote Sens. Environ. 2007, 109, 42–53. [Google Scholar] [CrossRef]
- Sawada, Y.; Tsutsui, H.; Koike, T.; Rasmy, M.; Seto, R.; Fujii, H. A field verification of an algorithm for retrieving vegetation water content from passive microwave observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2082–2095. [Google Scholar] [CrossRef]
- Tasselli, G.; Alimenti, F.; Bonafoni, S.; Basili, P.; Roselli, L. Fire detection by microwave radiometric sensors: Modeling a scenario in the presence of obstacles. IEEE Trans. Geosci. Remote Sens. 2010, 48, 314–324. [Google Scholar] [CrossRef]
- Aksoy, M. Evolution of the radio frequency interference environment faced by earth observing microwave radiometers in C and X bands over Europe. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1226–1229. [Google Scholar]
- Bonafoni, S.; Alimenti, F.; Roselli, L. An efficient gain estimation in the calibration of noise-adding total power radiometers for radiometric resolution improvement. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5289–5298. [Google Scholar] [CrossRef]
- Skou, N.; Lahtinen, J. Measured performance of improved cross frequency algorithm for detection of RFI from DTV. In Proceedings of the 2018 IEEE 15th specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment, Cambridge, MA, USA, 27–30 March 2018; pp. 62–66. [Google Scholar]
- Alimenti, F.; Bonafoni, S.; Roselli, L. A novel sensor based on a single-pixel microwave radiometer for warm object counting: Concept validation and IoT perspectives. Sensors 2017, 17, 1388. [Google Scholar] [CrossRef]
- Roo, R.; Misra, S.; Ruf, C. Sensitivity of the kurtosis statistic as a detector of pulsed sinusoidal RFI. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1938–1946. [Google Scholar] [CrossRef]
- Roo, R.; Misra, S. A demonstration of the effects of digitization on the calculation of kurtosis for the detection of RFI in microwave radiometry. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3129–3136. [Google Scholar] [CrossRef]
- Guner, B.; Frankford, M.; Johnson, J. A study of the Shapiro-Wilk test for the detection of pulsed sinusoidal radio frequency interference. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1745–1751. [Google Scholar] [CrossRef]
- Tarongi, J.; Camps, A. Normality analysis for RFI detection in microwave radiometry. Remote Sens. 2009, 2, 191–210. [Google Scholar] [CrossRef]
- Liang, Z.; Wei, J.; Zhao, J.; Liu, H.; Li, B.; Shen, J.; Zheng, C. The Statistical meaning of kurtosis and its new application to identification of persons based on seismic signals. Sensors 2008, 8, 5106–5119. [Google Scholar] [CrossRef]
- Ruf, C.; Misra, S.; Gross, S.; Roo, R. Detection of RFI by its amplitude probability distribution. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 2289–2291. [Google Scholar]
- Roo, R. A simplified calculation of the kurtosis for RFI detection. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. 327–330. [Google Scholar]
- Kurtosis. Available online: https://en.wikipedia.org/wiki/Kurtosis (accessed on 1 January 2019).
- Ellingson, S.; Hampson, G.; Johnson, J. Design of an L-band microwave radiometer with active mitigation of interference. In Proceedings of the International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 1751–1753. [Google Scholar]
- Niamsuwan, N.; Johnson, J.; Ellingson, S. Examination of a simple pulse blanking technique for RFI mitigation. Radio Sci. 2005, 40, 1–11. [Google Scholar] [CrossRef]
- Guner, B.; Johnson, J.; Niamsuwan, N. Time and frequency blanking for radio-frequency interference mitigation in microwave radiometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3672–3679. [Google Scholar] [CrossRef]
- Aksoy, M.; Johnson, J.; Misra, S.; Colliander, A.; O’Dwyer, I. L-Band radio-frequency interference observations during the SMAP validation experiment 2012. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1323–1335. [Google Scholar] [CrossRef]
- Fanise, P.; Pardé, M.; Zribi, M.; Dechambre, M.; Caudoux, C. Analysis of RFI identification and mitigation in CAROLS radiometer data using a hardware spectrum analyser. Sensors 2011, 11, 3037–3050. [Google Scholar] [CrossRef]
- Piepmeier, J.; Johnson, J.; Mohammed, P.; Bradley, D.; Ruf, C.; Aksoy, M.; Garcia, R.; Hudson, D.; Miles, L.; Wong, M. Radio-frequency interference mitigation for the soil moisture active passive microwave radiometer. IEEE Trans. Geosci. Remote Sens. 2014, 52, 761–775. [Google Scholar] [CrossRef]
- Tarongi, J.; Camps, A. Radio frequency interference detection and mitigation algorithms based on spectrogram analysis. Algorithms 2011, 4, 239–261. [Google Scholar] [CrossRef]
- Skewness. Available online: https://en.wikipedia.org/wiki/Skewness (accessed on 1 January 2019).
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing: Active and Passive, Volume I: Fundamentals and Radiometry; Artech House Publishers: Norwood, MA, USA, 1986; pp. 358–376. [Google Scholar]
- Frater, R.; Williams, D. An active ‘cold’ noise source. IEEE Trans. Microw. Theory Tech. 1981, 29, 344–347. [Google Scholar] [CrossRef]
- Schwank, M.; Wiesmann, A.; Werner, C.; Matzler, C.; Weber, D.; Murk, A.; Volksch, I.; Wegmuller, U. ELBARA II, an L-band radiometer system for soil moisture research. Sensors 2009, 10, 584–612. [Google Scholar] [CrossRef] [PubMed]
- Goodberlet, M.; Mead, J. Two-load radiometer precision and accuracy. IEEE Trans. Geosci. Remote Sens. 2006, 44, 58–67. [Google Scholar] [CrossRef]
- Kenney, J.; Keeping, E. Mathematics of Statistics; Van Nostrand Company Inc.: Washington, DC, USA, 1951; pp. 111–122. [Google Scholar]
- Sha’ameri, A.; Lynn, T. Spectrogram time-frequency analysis and classification of digital modulation signals. In Proceedings of the 2007 IEEE International Conference on Telecommunications and Malaysia International Conference on Communications, Penang, Malaysia, 14–17 May 2007; pp. 113–118. [Google Scholar]
- Gunther, J.; Moon, T. Burst mode synchronization of QPSK on AWGN channels using kurtosis. IEEE Trans. Commun. 2009, 57, 2453–2462. [Google Scholar] [CrossRef]
- Gupta, A.; Grossi, M. Effects of nonzero-centroid and skewness of fading spectrum on incoherent FSK and DPSK error probabilities. IEEE Trans. Commun. 1986, 32, 201–206. [Google Scholar] [CrossRef]
- Klein, L.; Swift, C. An improved model for the dielectric constant of sea water at microwave frequencies. IEEE J. Ocean. Eng. 1977, 2, 104–111. [Google Scholar] [CrossRef]

| Index | Parameter |
|---|---|
| Frequency range | 1.4–1.415 GHz |
| Antenna gain (dB) | 10 Typ. |
| Radiometry sensitivity | <0.13 K |
| Radiometry stability | <0.2 K over a period of 1 h |
| Radiometry accuracy | <1 K over a period of 1 h |
| Integration time | 1 s |
| RFI Signal Case | for Window Size | RMSE (K) for Window Size | ||||
|---|---|---|---|---|---|---|
| 50 × 50 | 75 × 75 | 100 × 100 | 50 × 50 | 75 × 75 | 100 × 100 | |
| Chirp signal | 4.53 | 3.10 | 2.71 | 2.06 | 1.92 | 1.50 |
| AM signal | 3.69 | 3.07 | 2.89 | 1.55 | 1.51 | 1.31 |
| Continuous signal | 3.58 | 3.66 | 2.54 | 1.71 | 1.42 | 1.46 |
| Pulsed signal | 3.78 | 3.15 | 2.87 | 2.06 | 1.70 | 1.62 |
| Continuous signal, pulsed signal | 2.31 | 3.23 | 2.57 | 1.24 | 1.21 | 1.22 |
| AM signal, pulsed signal | 2.81 | 2.41 | 2.24 | 1.32 | 1.15 | 1.13 |
| AM signal, continuous signal | 3.95 | 2.43 | 2.76 | 1.50 | 1.49 | 1.52 |
| Chirp signal, continuous signal | 4.57 | 3.43 | 2.78 | 1.66 | 1.63 | 1.70 |
| Chirp signal, pulsed signal | 4.67 | 3.66 | 2.81 | 1.61 | 1.42 | 1.24 |
| Chirp signal, AM signal, continuous signal | 4.28 | 3.28 | 2.82 | 2.10 | 1.63 | 1.53 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, M.; Kim, Y.-H. Statistical Approach to Spectrogram Analysis for Radio-Frequency Interference Detection and Mitigation in an L-Band Microwave Radiometer. Sensors 2019, 19, 306. https://doi.org/10.3390/s19020306
Oh M, Kim Y-H. Statistical Approach to Spectrogram Analysis for Radio-Frequency Interference Detection and Mitigation in an L-Band Microwave Radiometer. Sensors. 2019; 19(2):306. https://doi.org/10.3390/s19020306
Chicago/Turabian StyleOh, Myeonggeun, and Yong-Hoon Kim. 2019. "Statistical Approach to Spectrogram Analysis for Radio-Frequency Interference Detection and Mitigation in an L-Band Microwave Radiometer" Sensors 19, no. 2: 306. https://doi.org/10.3390/s19020306
APA StyleOh, M., & Kim, Y.-H. (2019). Statistical Approach to Spectrogram Analysis for Radio-Frequency Interference Detection and Mitigation in an L-Band Microwave Radiometer. Sensors, 19(2), 306. https://doi.org/10.3390/s19020306





