Genetic Optimization of Energy- and Failure-Aware Continuous Production Scheduling in Pasta Manufacturing
Abstract
1. Introduction
2. Literature Review
2.1. Energy-Aware Scheduling
2.2. Failure-Related Scheduling
3. Problem Formulation
3.1. Notation
3.1.1. Production Scheduling
- The machine is kept busy if there are remaining jobs to finish.
- The machine has a product-type-dependent production speed.
- The process of a job starts when it is charged on the machine and ends when it is unloaded.
- A new job is charged to the machine immediately after the end of the previous job.
- Each job has a specific product type and a target quantity.
- Preemption is not allowed, since changeover of jobs causes excessive waste.
3.1.2. Energy-Aware Scheduling
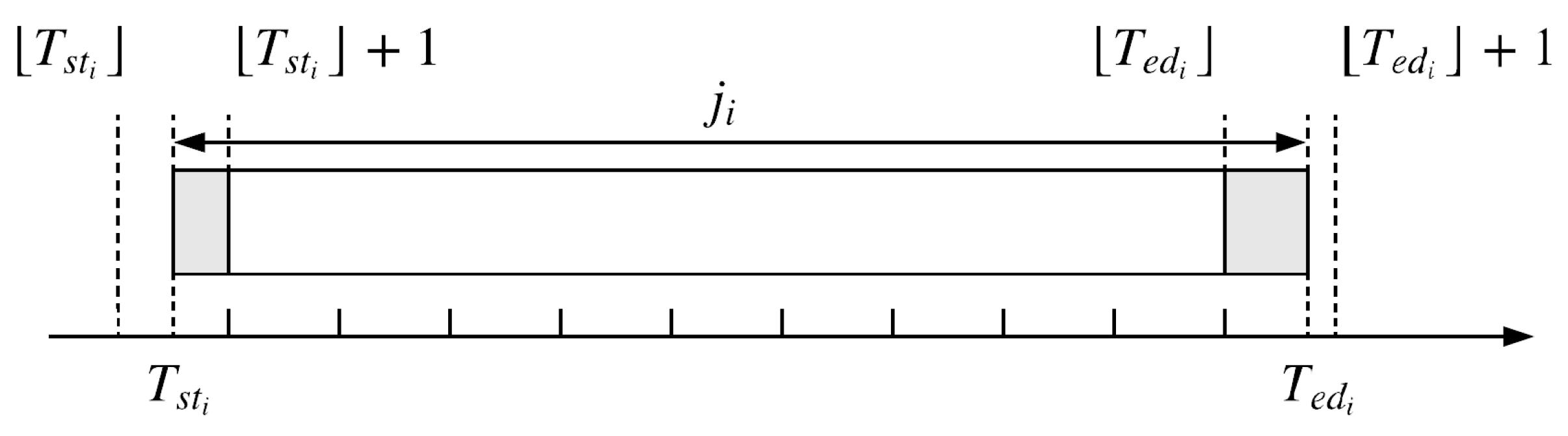
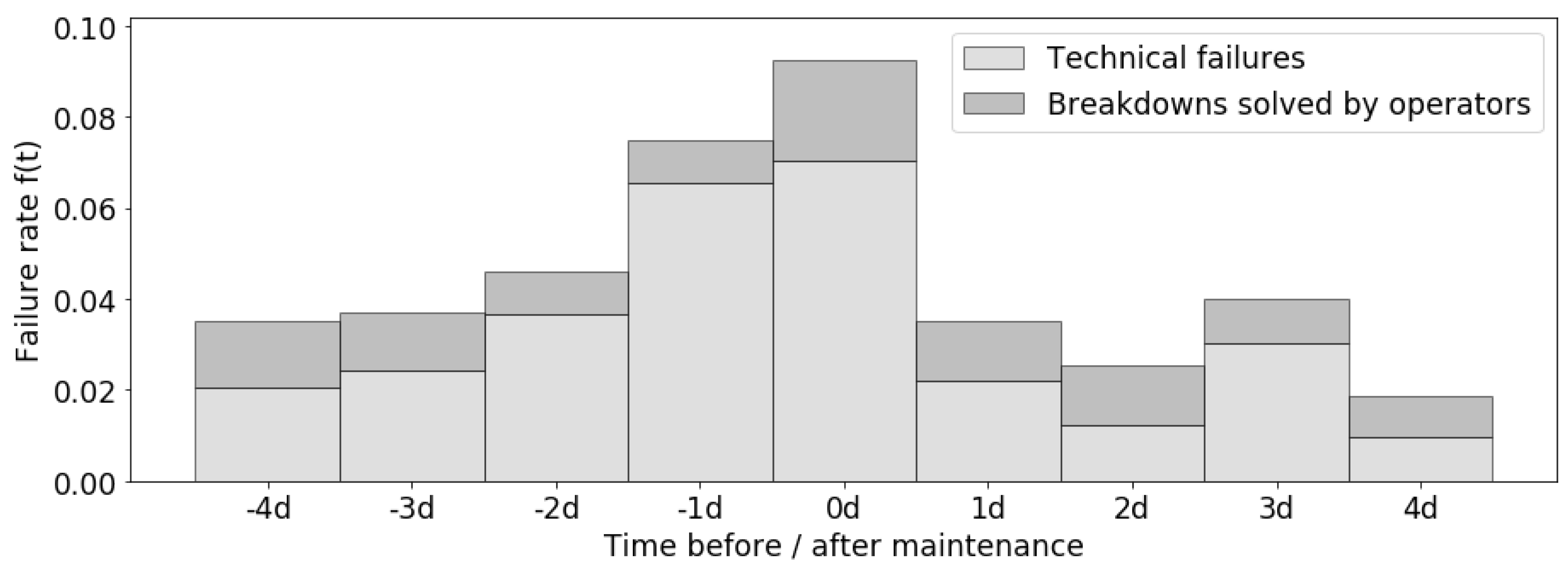
3.1.3. Failure-Aware Scheduling
3.2. Optimization Model
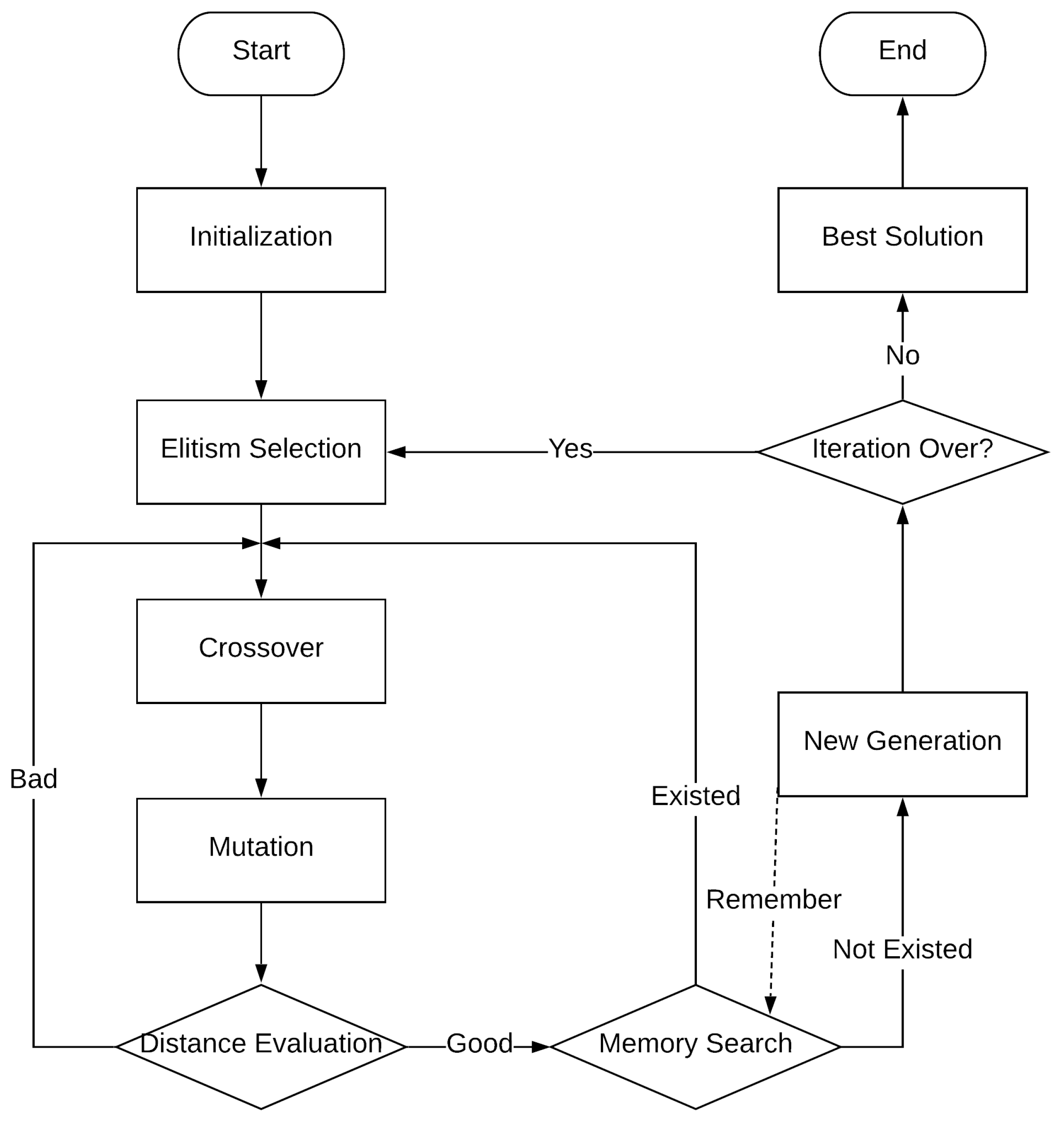
4. Method Description
4.1. Initialization
4.2. Elitism Selection
| Algorithm 1: Conventional genetic algorithm (CGA). |
 |
| Algorithm 2: Random choice algorithm (RCA). |
 |
4.3. Genetic Operators
| Algorithm 3: Improved genetic algorithm (IGA). |
 |
5. Case Study
5.1. Parameter Resolution
- Order information records (OIR) contain general attributes of orders processed in the job shop, including planning time, objective quantity, product type, and raw material cost.
- Order production records (OPR) contain processing details of orders, including effective time and production speed.
- Machine state records (MSR) contain runtime and downtime periods of the machine in the processing window of each order.
- Maintenance event records (MER) contain dates of maintenance events.
5.2. Simulation Settings
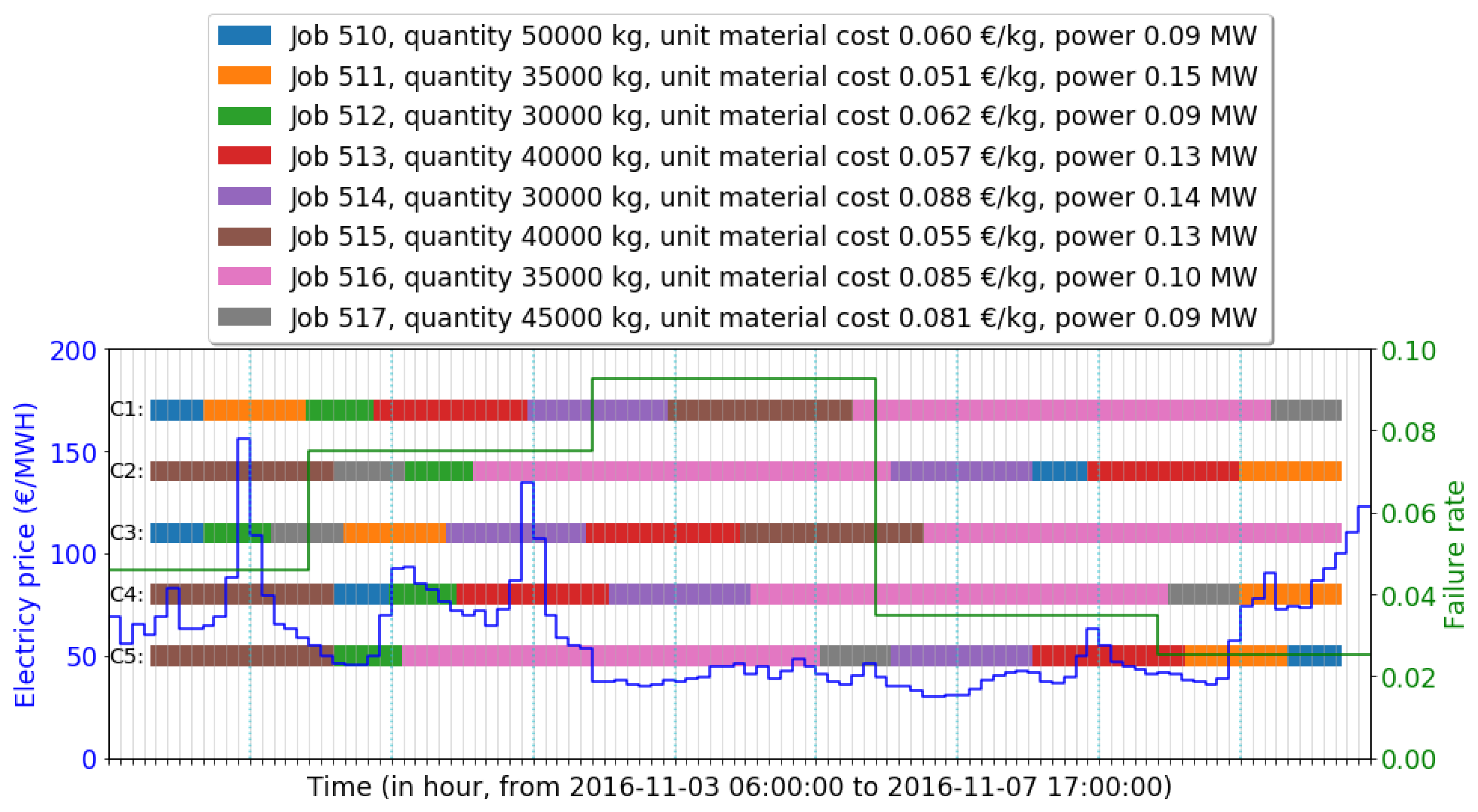
- The concerned waiting job set in the experiment is a subset of all finished jobs in MES records. Derived from a fixed date range (from 2016-11-03 06:00:00 to 2016-11-07 17:00:00), 8 jobs were investigated in the case study. Details are provided in Table 3.
- Corresponding Belpex RTP data have the same date range as the concerned waiting jobs.
- The time step in the schedule is one second.
- Maintenances are fixed on Saturdays.
- Randomly generated data are used instead of real production data for some job characteristics (raw material cost and power profile) according to the confidentiality agreement.
5.3. Results and Discussions
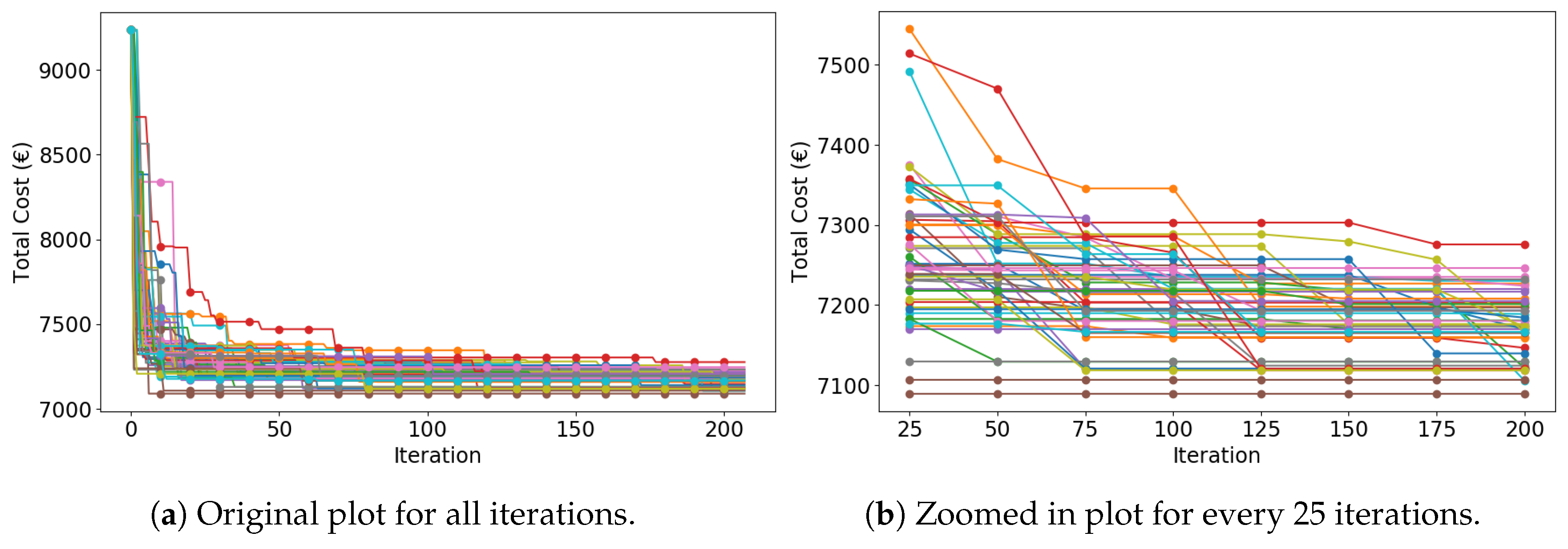
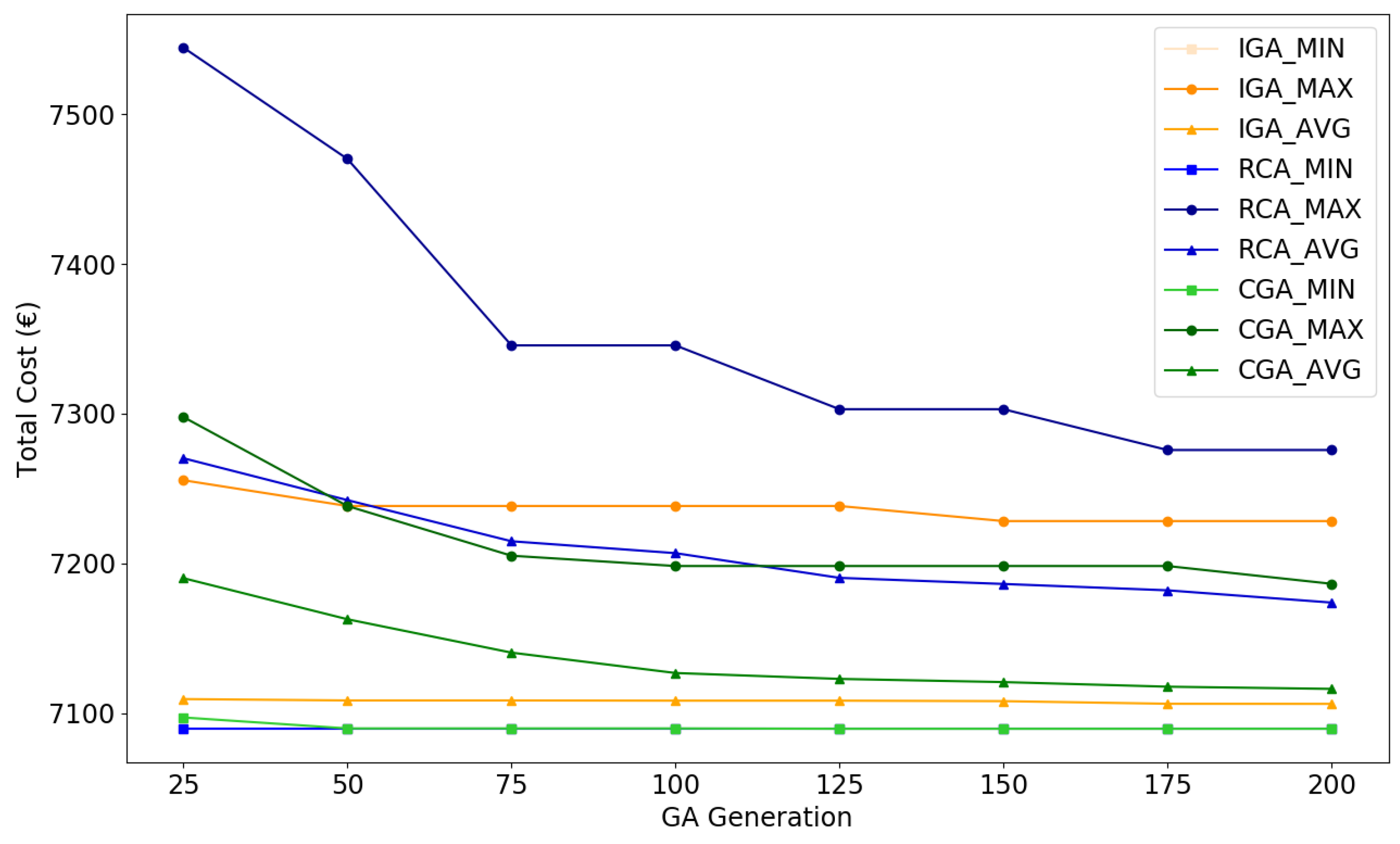
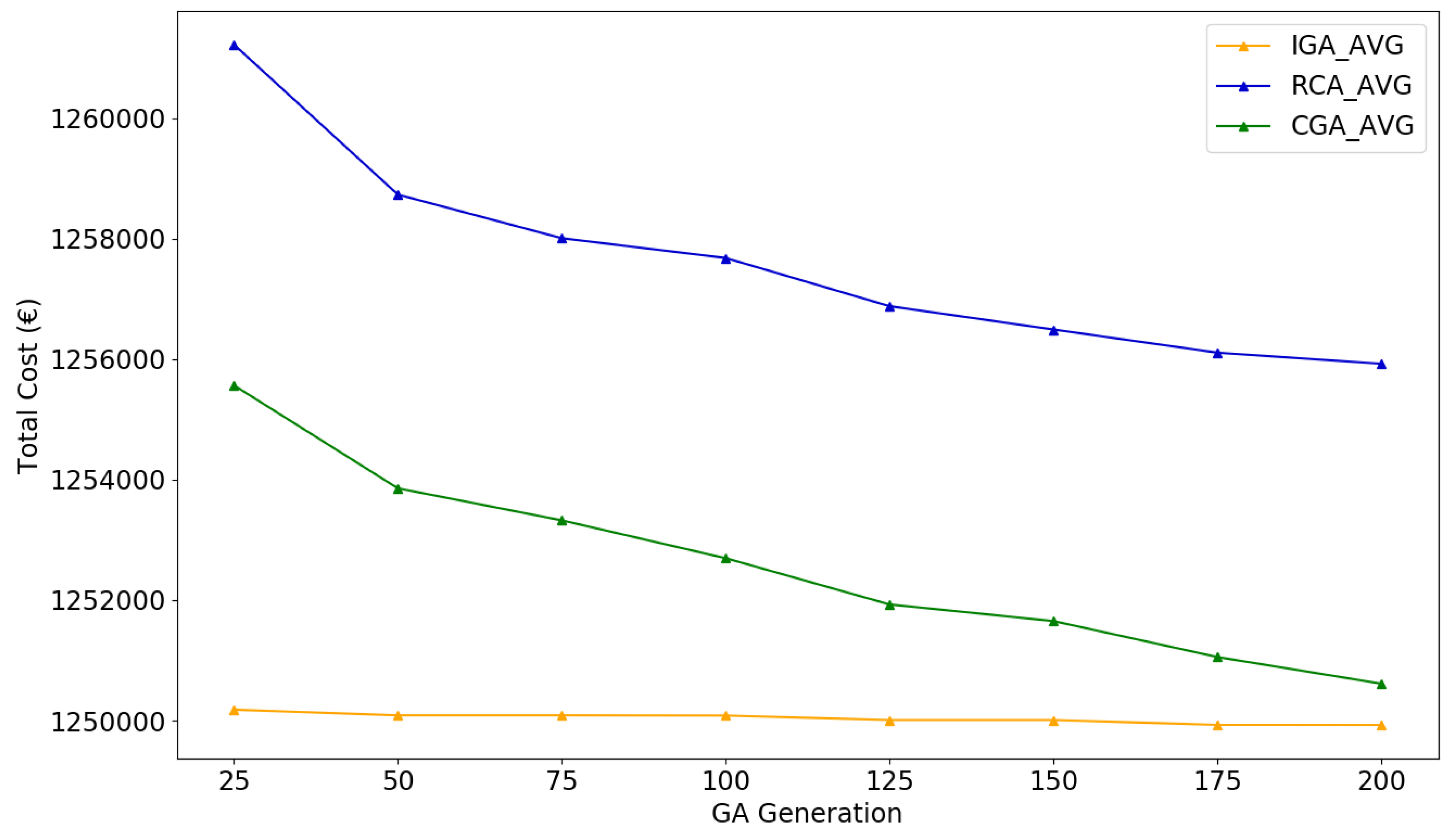
5.3.1. Convergence Analysis
5.3.2. Performance Evaluation
5.3.3. Complexity Analysis
5.4. Stress Test
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hadera, H.; Harjunkoski, I.; Sand, G.; Grossmann, I.E.; Engell, S. Optimization of steel production scheduling with complex time-sensitive electricity cost. Comput. Chem. Eng. 2015, 76, 117–136. [Google Scholar] [CrossRef]
- Cardenas, J.A.; Gemoets, L.; Ablanedo Rosas, J.H.; Sarfi, R. A literature survey on Smart Grid distribution: An analytical approach. J. Clean. Prod. 2014, 65, 202–216. [Google Scholar] [CrossRef]
- Aupy, G.; Benoit, A.; Robert, Y.T. Energy-aware scheduling under reliability and makespan constraints. In Proceedings of the 19th International Conference on High Performance Computing, Pune, India, 18–22 December 2012. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, L.; Arinez, J.; Biller, S. Energy-efficient production systems through schedule-based operations. IEEE Trans. Autom. Sci. Eng. 2013, 10, 27–37. [Google Scholar] [CrossRef]
- Liu, G.S.; Zhou, Y.; Yang, H.D.T. Minimizing energy consumption and tardiness penalty for fuzzy flow shop scheduling with state-dependent setup time. J. Clean. Prod. 2017, 147, 470–484. [Google Scholar] [CrossRef]
- Gong, X.; Van der Wee, M.; De Pessemier, T.; Verbrugge, S.; Colle, D.; Martens, L.; Joseph, W. Integrating labor awareness to energy-efficient production scheduling under real-time electricity pricing: An empirical study. J. Clean. Prod. 2017, 168, 239–253. [Google Scholar] [CrossRef]
- Ye, Y.; Li, J.; Li, Z.; Tang, Q.; Xiao, X.; Floudas, C.A. Robust optimization and stochastic programming approaches for medium-term production scheduling of a large-scale steelmaking continuous casting process under demand uncertainty. Comput. Chem. Eng. 2014, 66, 165–185. [Google Scholar] [CrossRef]
- Zhou, L.; Xu, K.; Cheng, X.; Xu, Y.; Jia, Q. Study on optimizing production scheduling for water-saving in textile dyeing industry. J. Clean. Prod. 2017, 141, 721–727. [Google Scholar] [CrossRef]
- Aytug, H.; Lawley, M.A.; McKay, K.; Mohan, S.; Uzsoy, R. Executing production schedules in the face of uncertainties: A review and some future directions. Eur. J. Oper. Res. 2005, 161, 86–110. [Google Scholar] [CrossRef]
- Francis, R.; Bekera, B. A metric and frameworks for resilience analysis of engineered and infrastructure systems. Reliab. Eng. Syst. Saf. 2014, 121, 90–103. [Google Scholar] [CrossRef]
- Gong, X.; De Pessemier, T.; Joseph, W.; Martens, L. A Stochasticity Handling Heuristic in Energy-cost-aware Scheduling for Sustainable Production. Procedia CIRP 2016, 48, 108–113. [Google Scholar] [CrossRef]
- O’Connor, P.; Kleyner, A. Practical Reliability Engineering, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002; ISBN 978-0-4708-4462-5. [Google Scholar]
- Pinedo, M.L. Chapter 2.1 Framework and Notation. In Scheduling: Theory, Algorithms, and Systems; Pinedo, M.L., Ed.; Springer: Berlin, Germany, 2016; pp. 13–19. ISBN 978-3-319-26580-3. [Google Scholar]
- Harvey, I. The microbial genetic algorithm. In Proceedings of the European Conference on Artificial Life, Budapest, Hungary, 13–16 September 2009; pp. 126–133. [Google Scholar]
- Gong, X.; De Pessemier, T.; Joseph, W.; Martens, L. A generic method for energy-efficient and energy-cost-effective production at the unit process level. J. Clean. Prod. 2016, 113, 508–522. [Google Scholar] [CrossRef]
- Veras, J.; Silva, I.; Pinheiro, P.; Rabêlo, R.; Veloso, A.; Borges, F.; Rodrigues, J. A Multi-Objective Demand Response Optimization Model for Scheduling Loads in a Home Energy Management System. Sensors 2018, 10, 3207. [Google Scholar] [CrossRef]
- Módos, I.; Šůcha, P.; Hanzálek, Z. Algorithms for robust production scheduling with energy consumption limits. Comput. Ind. Eng. 2017, 112, 391–408. [Google Scholar] [CrossRef]
- Ouyang, M. Review on modeling and simulation of interdependent critical infrastructure systems. Reliab. Eng. Syst. Saf. 2014, 121, 43–60. [Google Scholar] [CrossRef]
- Siedlak, D.J.L.; Pinon, O.J.; Robertson, B.E.; Mavris, D.N. Robust simulation-based scheduling methodology to reduce the impact of manual installation tasks on low-volume aerospace production flows. J. Manuf. Syst. 2018, 46, 193–207. [Google Scholar] [CrossRef]
- Li, Z.; Ierapetritou, M.T. Process scheduling under uncertainty: Review and challenges. Comput. Chem. Eng. 2008, 32, 715–727. [Google Scholar] [CrossRef]
- Li, X.; Jiang, X.; Garraghan, P.; Wu, Z. Holistic energy and failure aware workload scheduling in Cloud datacenters. Future Gener. Comput. Syst. 2018, 78, 887–900. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, M.; Hao, J. A two-phase soft optimization method for the uncertain scheduling problem in the steelmaking industry. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 416–431. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H.; Gong, J. Framework for modeling operational uncertainty to optimize offsite production scheduling of precast components. Autom. Constr. 2018, 86, 69–80. [Google Scholar] [CrossRef]
- Lu, Z.; Cui, W.; Han, X. Integrated production and preventive maintenance scheduling for a single machine with failure uncertainty. Comput. Ind. Eng. 2015, 80, 236–244. [Google Scholar] [CrossRef]
- Guo, Z.X.; Wong, W.K.; Leung, S.Y.S.; Fan, J.T.; Chan, S.F. Genetic optimization of order scheduling with multiple uncertainties. Expert Syst. Appl. 2008, 35, 1788–1801. [Google Scholar] [CrossRef]
- Drwal, M. Robust scheduling to minimize the weighted number of late jobs with interval due-date uncertainty. Comput. Oper. Res. 2018, 91, 13–20. [Google Scholar] [CrossRef]
- Ghezail, F.; Pierreval, H.; Hajri-Gabouj, S. Analysis of robustness in proactive scheduling: A graphical approach. Comput. Ind. Eng. 2010, 58, 193–198. [Google Scholar] [CrossRef]
- Lin, S.; Kernighan, B.W. An effective heuristic algorithm for the traveling-salesman problem. Oper. Res. 1973, 21, 498–516. [Google Scholar] [CrossRef]
- Abedinnia, H.; Glock, C.H.; Grosse, E.H.; Schneider, M. Machine scheduling problems in production: A tertiary study. Comput. Ind. Eng. 2017, 111, 403–416. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, M.; Chen, F.F. Single-machine-based joint optimization of predictive maintenance planning and production scheduling. Robot. Comput.-Integr. Manuf. 2018, 51, 238–247. [Google Scholar] [CrossRef]
- Zhou, S. Bayesian Modelling and Analysis of Utility-Based Maintenance for Repairable Systems. Ph.D. Thesis, Trinity College, Dublin, Ireland, 2017. Available online: http://hdl.handle.net/2262/83469 (accessed on 9 November 2018).
- Jiang, J.; Zhang, J.; Zhang, L.; Ran, X.; Tang, Y. Passive Location Resource Scheduling Based on an Improved Genetic Algorithm. Sensors 2018, 18, 2093. [Google Scholar] [CrossRef]
- Yang, S. Memory-based immigrants for genetic algorithms in dynamic environments. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, Washington, DC, USA, 25–29 June 2005; ACM: New York, NY, USA, 2005; pp. 1115–1122. [Google Scholar] [CrossRef]
- Hamming, R.W. Error Detecting and Error Correcting Codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Atlas.media.mit.edu. Pasta Product Trade, Exports and Importers. Available online: https://atlas.media.mit.edu/en/profile/hs92/1902/ (accessed on 14 September 2018).
- Internationalpasta.org. Pasta Statistics. Available online: http://www.internationalpasta.org/index.aspx?id=7 (accessed on 14 September 2018).
- Ruini, L.; Marino, M.; Pignatelli, S.; Laio, F.; Ridolfi, L. Water footprint of a large-sized food company: The case of Barilla pasta production. Water Resour. Ind. 2013, 1–2, 7–24. [Google Scholar] [CrossRef]
- Bruzzone, A.A.G.; Anghinolfi, D.; Paolucci, M.; Tonelli, F. Energy-aware scheduling for improving manufacturing process sustainability: A mathematical model for flexible flow shops. CIRP Ann. Manuf. Technol. 2012, 61, 459–462. [Google Scholar] [CrossRef]
- My.elexys.be. Markt Informatie. Available online: https://my.elexys.be/MarketInformation.aspx (accessed on 9 November 2018).
- Ukertechnofoods. Automatic Short-Cut Pasta Line with Capacity 750 kg/h. Available online: https://utf-group.com/pasta-equipment/pasta-line-750/ (accessed on 9 November 2018).
- Jacobson, L.; Kanber, B. Genetic Algorithms in Java Basics; Apress: New York, NY, USA, 2009; ISBN 978-1-4842-0328-6. [Google Scholar]
- Merkert, L.; Harjunkoski, I.; Isaksson, A.; Säynevirta, S.; Saarela, A.; Sand, G. Scheduling and energy—Industrial challenges and opportunities. Comput. Chem. Eng. 2015, 72, 183–198. [Google Scholar] [CrossRef]
- Janssen, H. Monte-Carlo based uncertainty analysis: Sampling efficiency and sampling convergence. Reliab. Eng. Syst. Saf. 2013, 109, 123–132. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Y.; Zheng, H.; Mi, S.; Tan, J. A framework of joint energy provisioning and manufacturing scheduling in smart industrial wireless rechargeable sensor networks. Sensors 2018, 18, 2591. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009; ISBN 978-0-2620-3384-8. [Google Scholar]





| Parameter | Description |
|---|---|
| J | set of waiting jobs with ID |
| job with index i | |
| N | number of waiting jobs |
| P | set of product types |
| M | number of possible product types |
| product type of | |
| objective quantity of | |
| unit production speed of product type p, where | |
| unit production speed of , whose product type is | |
| production duration of | |
| start time of | |
| end time of | |
| set of processing stages of | |
| set of durations of stages of | |
| duration of kth stage of | |
| power consumption of stage s | |
| energy consumption of processing | |
| energy cost of processing | |
| vector of energy price | |
| size of | |
| H | set of machine health states |
| kth state ranked with failure rate | |
| real-time response maintenance (maintenance type) | |
| replacement maintenance (maintenance type) | |
| a schedule | |
| machine failure rate changing over time t | |
| time stamp of a particular maintenance | |
| B | vector of failure rate after maintenance |
| failure rate of kth hour after maintenance | |
| vector of failure rate after raw material charged on the machine | |
| probability of failure occurrence during production of | |
| unit raw material cost of product type | |
| failure cost of |
| Record | Parameters |
|---|---|
| OIR | |
| OPR | |
| MSR | |
| MER | |
| BELPEX |
| ID | Product Type | Objectif Quantity | Start Time | End Time | Unit Material Cost | Power |
|---|---|---|---|---|---|---|
| 510 | FF011501 | 40,000 | 2016-11-03 09:30:51 | 2016-11-03 14:05:29 | 0.055 | 0.13 |
| 511 | FF082005 | 45,000 | 2016-11-03 14:05:33 | 2016-11-03 22:47:09 | 0.081 | 0.09 |
| 512 | FF025201 | 30,000 | 2016-11-03 22:47:15 | 2016-11-04 04:32:20 | 0.062 | 0.09 |
| 513 | FF027216 | 35,000 | 2016-11-04 04:32:23 | 2016-11-04 17:29:46 | 0.085 | 0.10 |
| 514 | FF049361 | 30,000 | 2016-11-04 17:29:50 | 2016-11-05 05:27:33 | 0.088 | 0.14 |
| 515 | FF049390 | 50,000 | 2016-11-05 05:27:41 | 2016-11-05 21:23:04 | 0.060 | 0.09 |
| 516 | FF174906 | 40,000 | 2016-11-05 21:23:07 | 2016-11-07 08:46:27 | 0.057 | 0.13 |
| 517 | FF044101 | 35,000 | 2016-11-07 08:46:35 | 2016-11-07 14:49:42 | 0.051 | 0.15 |
| ID | Case | Sequence | ||||
| C1 | Original schedule from historical record | [510, 511, 512, 513, 514, 515, 516, 517] | ||||
| C2 | Near-optimal schedule using IGA () | [515, 517, 512, 516, 514, 510, 513, 511] | ||||
| C3 | Schedule using shortest job first policy | [510, 512, 517, 511, 514, 513, 515, 516] | ||||
| C4 | Schedule minimizing energy cost | [515, 510, 512, 513, 514, 516, 517, 511] | ||||
| C5 | Schedule minimizing failure cost | [515, 512, 516, 517, 514, 513, 511, 510] | ||||
| ID | Energy Cost | Failure Cost | Overall Cost | Energy Saving | Material Saving | Total Saving |
| C1 | 655.69 | 8580.17 | 9235.86 | 0% | 0% | 0% |
| C2 | 641.17 | 6448.29 | 7089.46 | 2.21% | 24.85% | 23.24% |
| C3 | 666.53 | 8999.98 | 9666.51 | −1.65% | −4.89% | −4.66% |
| C4 | 622.30 | 8080.37 | 8702.67 | 5.09% | 5.83% | 5.77% |
| C5 | 648.42 | 6444.06 | 7092.48 | 1.11% | 24.90% | 23.21% |
| ID | Case | Sequence | ||||
| C6 | Original schedule from historical record | [510, 511, 512, 513, 514, 515, 516, 517] | ||||
| C7 | Near-optimal schedule using IGA () | [515, 517, 512, 516, 514, 510, 513, 511] | ||||
| C8 | Schedule using shortest job first policy | [510, 512, 517, 511, 514, 513, 515, 516] | ||||
| C9 | Schedule minimizing energy cost | [515, 510, 512, 513, 514, 516, 517, 511] | ||||
| C10 | Schedule minimizing failure cost | [515, 512, 516, 517, 514, 513, 511, 510] | ||||
| ID | Energy Cost | Failure Cost | Overall Cost | Energy Saving | Material Saving | Total Saving |
| C6 | 9835.40 | 8580.17 | 18,415.57 | 0% | 0% | 0% |
| C7 | 9527.27 | 6467.66 | 15,994.93 | 3.13% | 24.62% | 13.14% |
| C8 | 9997.90 | 8999.99 | 18,997.89 | −1.65% | −4.89% | −3.16% |
| C9 | 9334.48 | 8080.37 | 17,414.86 | 5.09% | 5.83% | 5.43% |
| C10 | 9726.34 | 6444.06 | 16,170.40 | 1.11% | 24.90% | 12.19% |
| Algorithm | Converge to Maximum | Converge to Minimum | Converge to Others | |
| IGA | 1 | 17 | 32 | |
| CGA | 1 | 4 | 45 | |
| RCA | 1 | 1 | 48 | |
| Algorithm | Maximum Cost | Minimum Cost | Average Cost | Standard Deviation |
| IGA | 7228.25 | 7089.46 | 7106.10 | 23.84 |
| CGA | 7186.35 | 7089.46 | 7116.11 | 22.23 |
| RCA | 7275.73 | 7089.69 | 7173.80 | 41.42 |
| Generation | C(IGA, CGA) | C(CGA, IGA) | C(IGA, RCA) | C(RCA, IGA) | C(CGA, RCA) | C(RCA, CGA) |
|---|---|---|---|---|---|---|
| 25 | 1 | 0.62 | 1 | 0.68 | 0.98 | 1 |
| 50 | 1 | 0.68 | 1 | 0.68 | 1 | 1 |
| 75 | 1 | 0.68 | 1 | 0.68 | 1 | 1 |
| 100 | 1 | 0.66 | 1 | 0.66 | 1 | 1 |
| 125 | 1 | 1 | 1 | 0.66 | 1 | 0.96 |
| 150 | 1 | 1 | 1 | 0.66 | 1 | 0.96 |
| 175 | 1 | 1 | 1 | 0.66 | 1 | 0.92 |
| 200 | 1 | 1 | 1 | 0.66 | 1 | 0.92 |
| Algorithm | Converge to Maximum | Converge to Minimum | Converge to Others | |
| IGA | 1 | 6 | 43 | |
| CGA | 1 | 1 | 48 | |
| RCA | 1 | 1 | 48 | |
| Algorithm | Maximum Cost | Minimum Cost | Average Cost | Standard Deviation |
| IGA | 1,258,670.98 | 1,248,039.40 | 1,249,926.71 | 2419.96 |
| CGA | 1,255,047.27 | 1,241,847.12 | 1,250,612.83 | 2698.97 |
| RCA | 1,261,961.80 | 1,251,042.40 | 1,255,922.92 | 2692.98 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, K.; De Pessemier, T.; Gong, X.; Martens, L.; Joseph, W. Genetic Optimization of Energy- and Failure-Aware Continuous Production Scheduling in Pasta Manufacturing. Sensors 2019, 19, 297. https://doi.org/10.3390/s19020297
Shen K, De Pessemier T, Gong X, Martens L, Joseph W. Genetic Optimization of Energy- and Failure-Aware Continuous Production Scheduling in Pasta Manufacturing. Sensors. 2019; 19(2):297. https://doi.org/10.3390/s19020297
Chicago/Turabian StyleShen, Ke, Toon De Pessemier, Xu Gong, Luc Martens, and Wout Joseph. 2019. "Genetic Optimization of Energy- and Failure-Aware Continuous Production Scheduling in Pasta Manufacturing" Sensors 19, no. 2: 297. https://doi.org/10.3390/s19020297
APA StyleShen, K., De Pessemier, T., Gong, X., Martens, L., & Joseph, W. (2019). Genetic Optimization of Energy- and Failure-Aware Continuous Production Scheduling in Pasta Manufacturing. Sensors, 19(2), 297. https://doi.org/10.3390/s19020297






