Building a Compact Convolutional Neural Network for Embedded Intelligent Sensor Systems Using Group Sparsity and Knowledge Distillation
Abstract
:1. Introduction
- The first strategy is determining the number of parameters of a student network automatically by utilizing group sparsity combined with knowledge transfer in the training process. It is already well known that a student network with a small number of parameters trained by using knowledge distillation (KD) loss leads to a better solution than those without KD. Our intuition at this point is that after the number of parameters of the student network is reduced based on a sparse loss, the resulting network can be regarded as a smaller network and the performance of such a compact network can be improved by the KD loss.
- The second strategy is to control the regularization parameter for balancing the accuracy and sparsity losses. For achieving this, we utilize a feedback control mechanism based on the proportional control theory [24,25,26,27], where the controller output is proportional to the difference between the desired setpoint and a measured value from a process (error signal). In our case, one of our goals is to make the student model mimic a cumbersome teacher model. Considering this goal in terms of control, the desired setpoint and measured process variable can be set to the accuracy losses of the teacher and student models, respectively. In addition, the feedback mechanism corresponds to adjusting the weight of the sparsity loss, i.e., the amount of emphasis put on the sparsity during the training.
2. Related Work
2.1. Knowledge Distillation
2.2. Parameter Reduction
2.3. Adaptive Regularization
3. Proposed Method
3.1. Review of Knowledge Distillation Based on a Soft Target Distribution
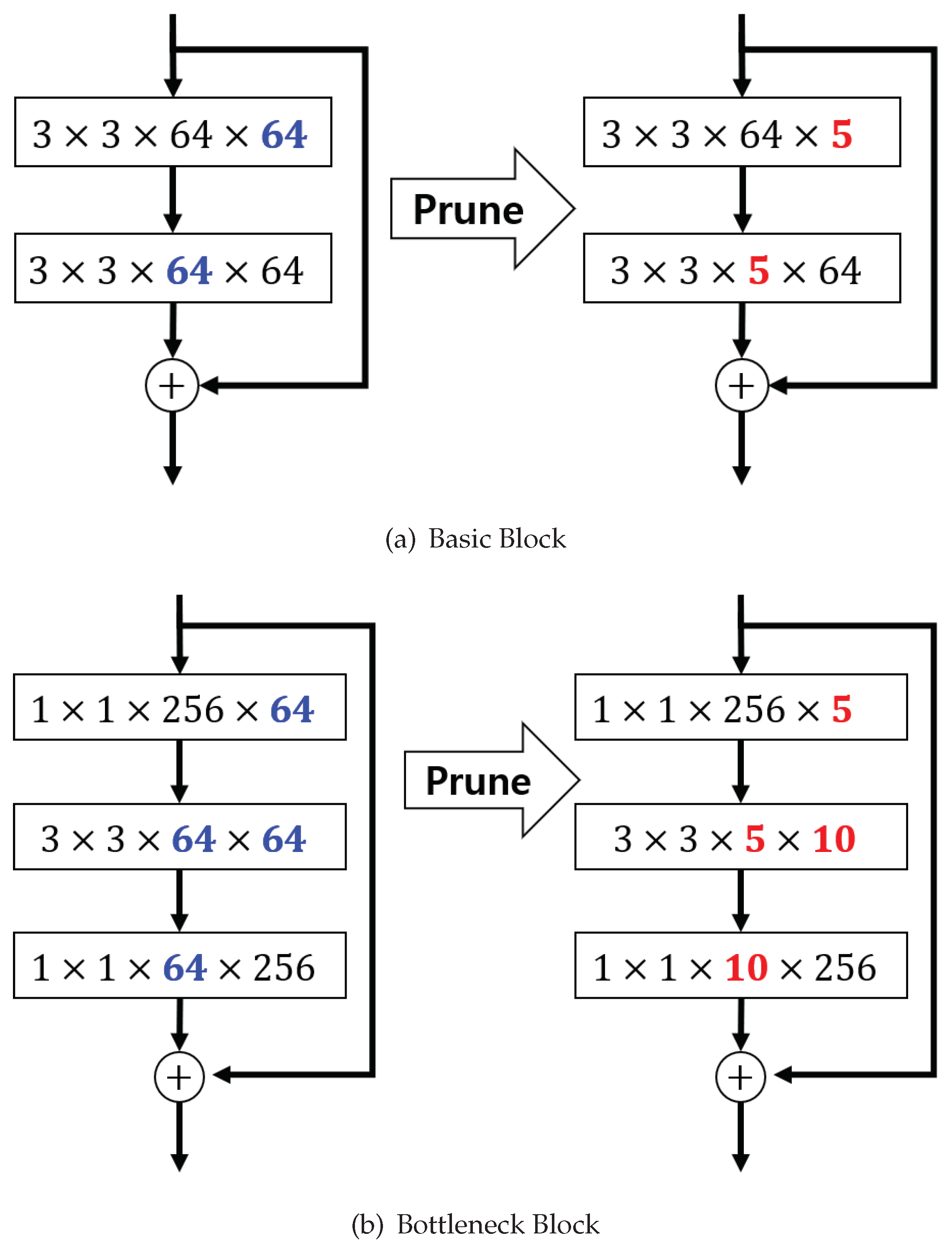
3.2. Knowledge Distillation With Group Sparse Regularization
3.3. Proportional Control of Group Sparsity Regularization
| Algorithm 1 Optimization with a closed-loop feedback controller. |
|
- At the start, k is set to zero, and the control value is set to one so that the regularization parameter is .
- If the performance of the student model is estimated to be worse than that of the teacher during the training, i.e., the cross-entropy value (the feedback value) from the student network is larger than that of the teacher, is reduced to focus more on performance enhancement.
- However, if the student’s performance is not bad compared with that of the teacher, i.e., is near zero, the value of is maintained at the same level, so that the relative strength for sparsity terms remains more or less the same. If the performance of the student is estimated to be better than that of the teacher, is controlled so that the overall sparsity is increased.
4. Experiments
4.1. Implementation and Environment Details
4.2. Evaluation of the Proposed Strategies
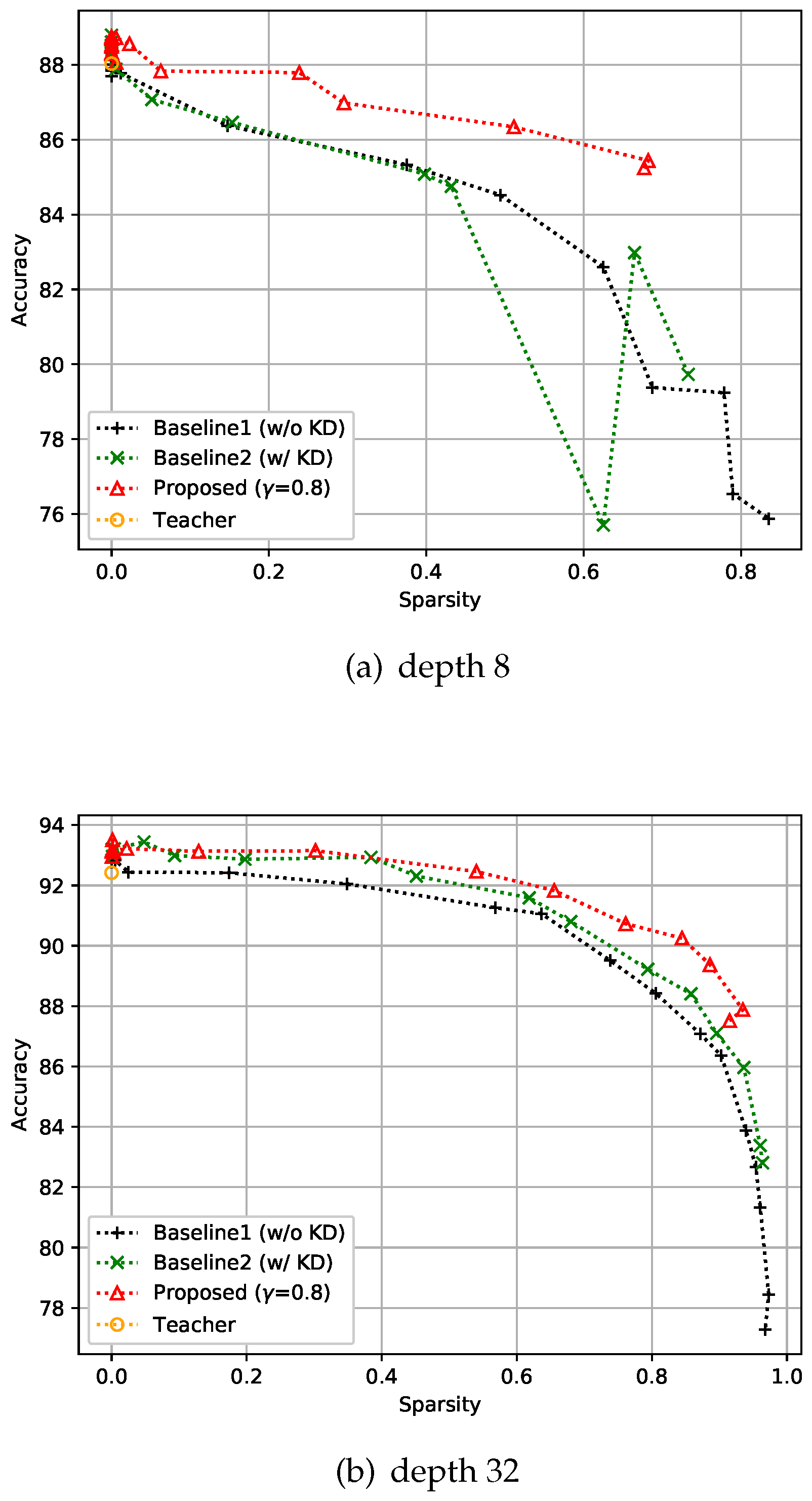
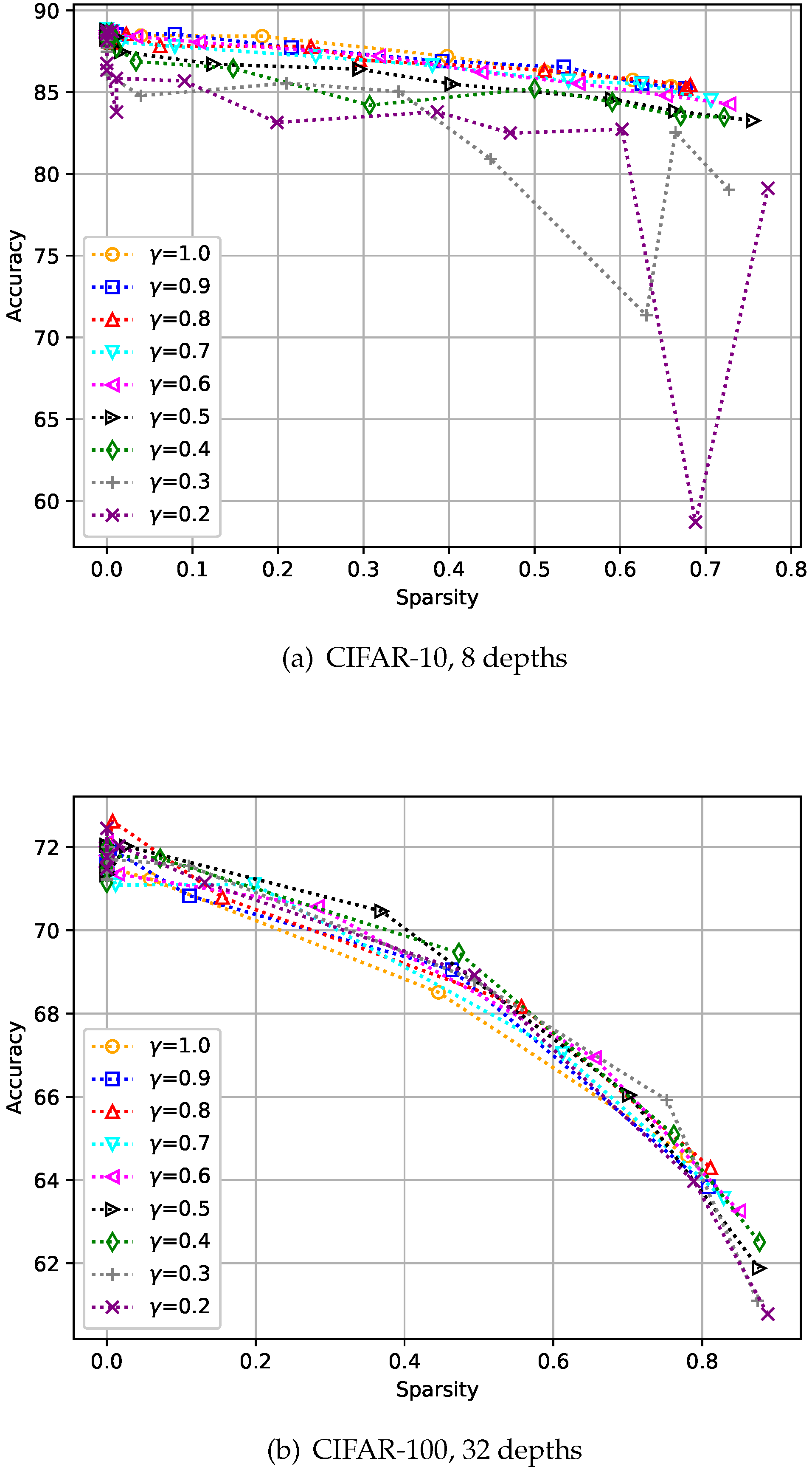
4.2.1. CIFAR-10 Dataset
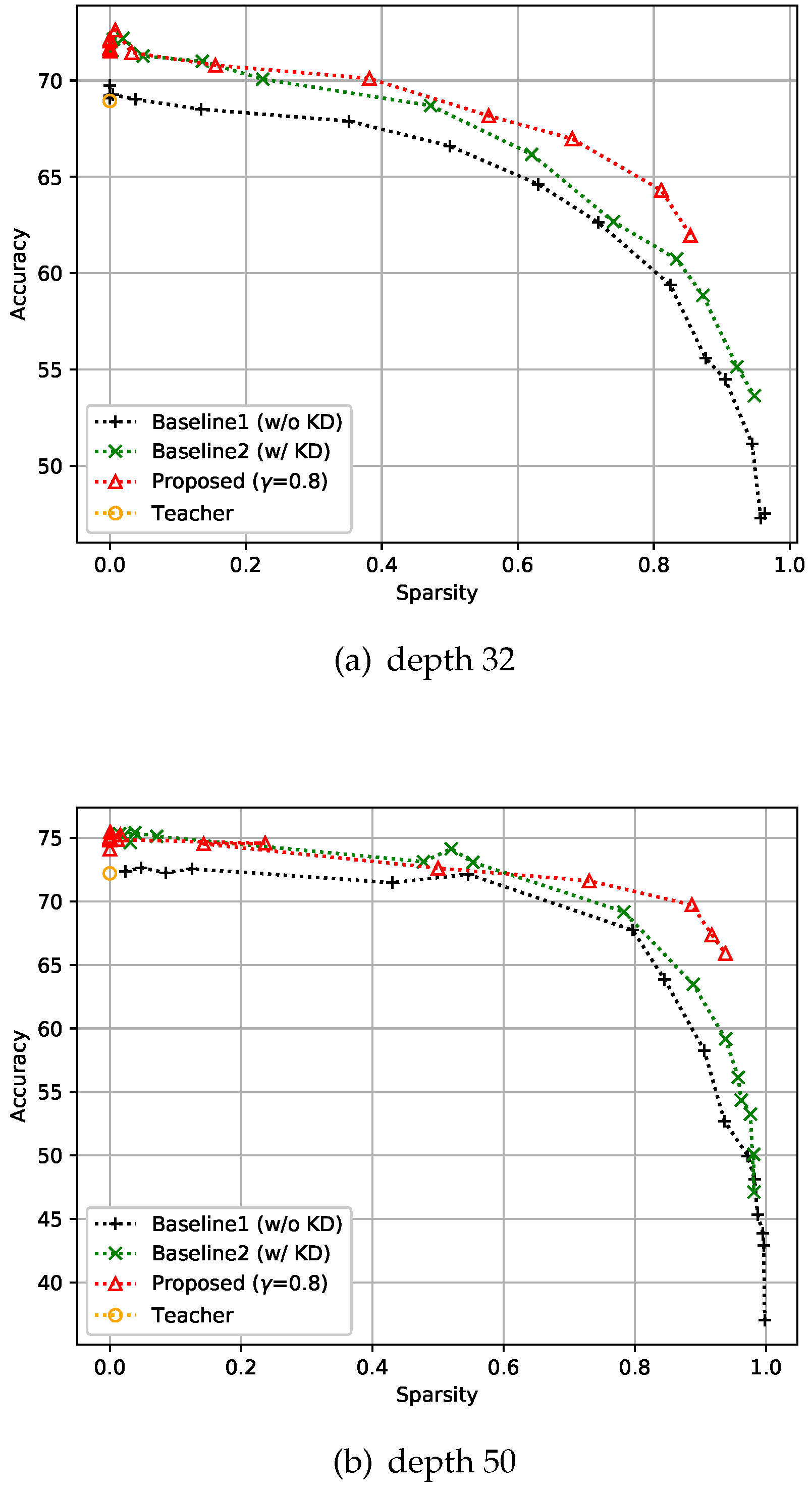
4.2.2. CIFAR-100 Dataset
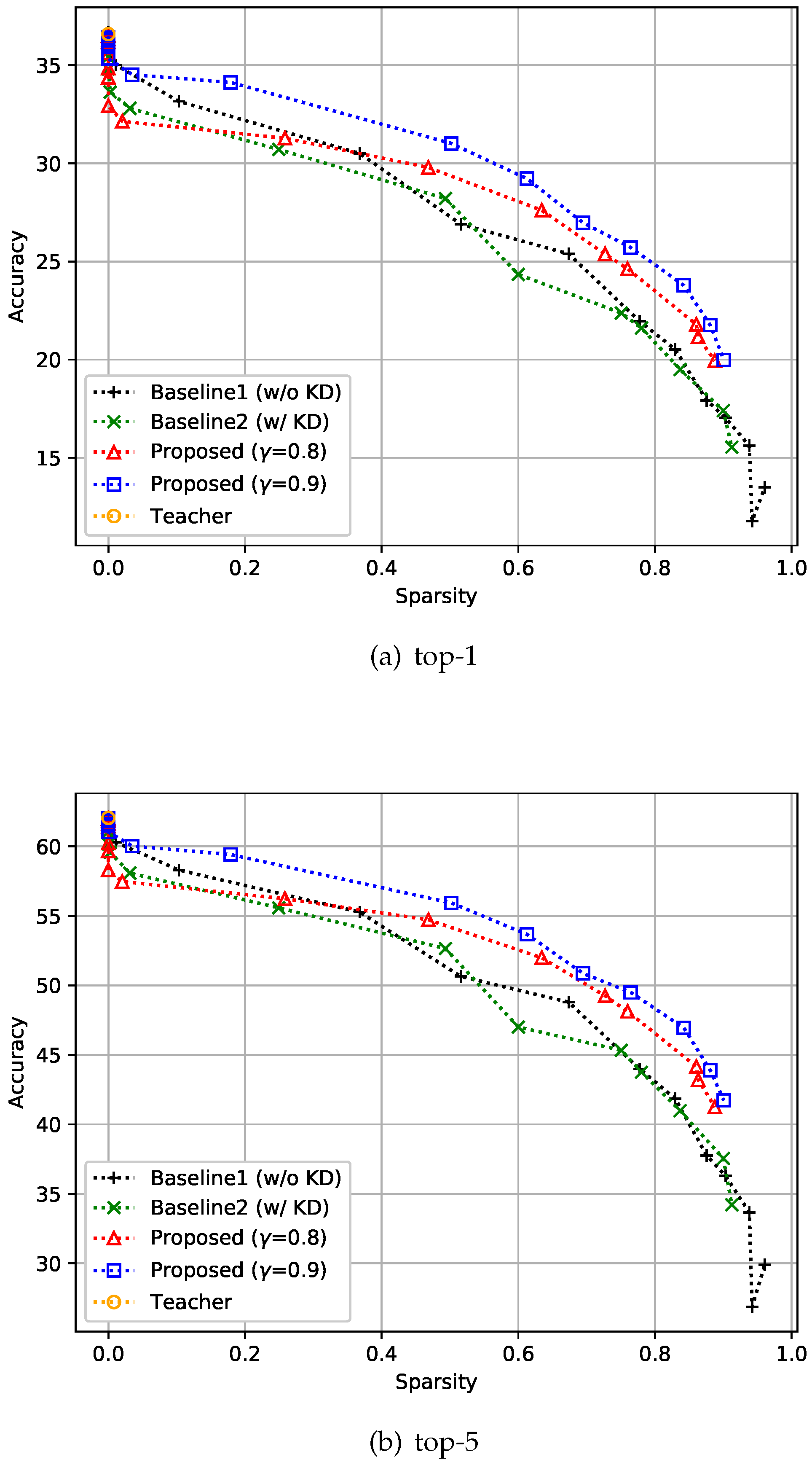
4.2.3. ImageNet3232 Dataset
4.3. Analysis of Hyper-Parameter
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, H.; Li, J.; Shen, S.; Xu, G. A Deep Convolutional Neural Network Inspired by Auditory Perception for Underwater Acoustic Target Recognition. Sensors 2019, 19, 1104. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Cho, B.; Hong, Y.W.; Byun, H. Contextual Action Cues from Camera Sensor for Multi-Stream Action Recognition. Sensors 2019, 19, 1382. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Tang, Q.; Jin, L.; Pan, Z. A Cascade Ensemble Learning Model for Human Activity Recognition with Smartphones. Sensors 2019, 19, 2307. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Tao, J.; Wang, J.; Chen, X.; Xie, J.; Xiong, J.; Yang, K. The Novel Sensor Network Structure for Classification Processing Based on the Machine Learning Method of the ACGAN. Sensors 2019, 19, 3145. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Wang, Y.; Zhao, L.; Fan, Z. An Event Recognition Method for Φ-OTDR Sensing System Based on Deep Learning. Sensors 2019, 19, 3421. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE conference on computer vision and pattern recognition, Madison, WI, USA, 26 June–1 July 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Madison, WI, USA, 26 June–1 July 2016. [Google Scholar]
- Yoon, J.; Hwang, S.J. Combined Group and Exclusive Sparsity for Deep Neural Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Han, S.; Liu, X.; Mao, H.; Pu, J.; Pedram, A.; Horowitz, M.A.; Dally, W.J. EIE: Efficient Inference Engine on Compressed Deep Neural Network. In Proceedings of the ACM/IEEE Annual International Symposium on Computer Architecture, Seoul, Korea, 18–22 June 2016. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-Level Accuracy with 50x Fewer Parameters and< 0.5 MB Model Size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Romero, A.; Ballas, N.; Kahou, S.E.; Chassang, A.; Gatta, C.; Bengio, Y. Fitnets: Hints for Thin Deep Nets. arXiv 2014, arXiv:1412.6550. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer. arXiv 2016, arXiv:1612.03928. [Google Scholar]
- Yim, J.; Joo, D.; Bae, J.; Kim, J. A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Wang, X.; Zhang, R.; Sun, Y.; Qi, J. KDGAN: Knowledge Distillation with Generative Adversarial Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Lan, X.; Zhu, X.; Gong, S. Knowledge Distillation by On-the-Fly Native Ensemble. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Zhou, H.; Alvarez, J.M.; Porikli, F. Less is More: Towards Compact CNNs. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Alvarez, J.M.; Salzmann, M. Learning the Number of Neurons in Deep Networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning Structured Sparsity in Deep Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Daubechies, I.; Defrise, M.; De Mol, C. An Iterative Thresholding Algorithm for Linear Inverse Problems with a Sparsity Constraint. Commun. Pure Appl. Math. A J. Issued Courant Inst. Math. Sci. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. A Sparse-Group Lasso. J. Comput. Graph. Stat. 2013, 22, 231–245. [Google Scholar] [CrossRef]
- DiStefano, J.J.; Stubberud, A.R.; Williams, I.J. Feedback and Control Systems; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Bequette, B.W. Process Control: Modeling, Design, and Simulation; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Control Theory—Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Control_theory (accessed on 18 June 2018).
- Proportional Control—Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Proportional_control (accessed on 18 June 2018).
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.222.9220&rep=rep1&type=pdf (accessed on 3 October 2019).
- Chrabaszcz, P.; Loshchilov, I.; Hutter, F. A Downsampled Variant of Imagenet as an Alternative to the Cifar Datasets. arXiv 2017, arXiv:1707.08819. [Google Scholar]
- Galatsanos, N.P.; Katsaggelos, A.K. Methods for Choosing the Regularization Parameter and Estimating the Noise Variance in Image Restoration and Their Relation. IEEE Trans. Image Process. 1992, 1, 322–336. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhe, S.; Cheng, C.; Wei, Z.; Chen, Z.; Chen, H.; Jiang, G.; Qi, Y.; Ye, J. Annealed Sparsity via Adaptive and Dynamic Shrinking. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Dong, W.; Zhang, L.; Shi, G.; Wu, X. Image Deblurring and Super-Resolution by Adaptive Sparse Domain Selection and Adaptive Regularization. IEEE Trans. Image Process. 2011, 20, 1838–1857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Larsen, J.; Svarer, C.; Andersen, L.N.; Hansen, L.K. Adaptive Regularization in Neural Network Modeling. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Leung, C.T.; Chow, T.W.S. Adaptive Regularization Parameter Selection Method for Enhancing Generalization Capability of Neural Networks. Artif. Intell. 1999, 107, 347–356. [Google Scholar] [CrossRef]
- Cho, J.; Kwon, J.; Hong, B.W. Adaptive Regularization via Residual Smoothing in Deep Learning Optimization. IEEE Access 2019, 7, 122889–122899. [Google Scholar] [CrossRef]
- Parikh, N.; Boyd, S. Proximal Algorithms. Found. Trends® Optim. 2014, 1, 127–239. [Google Scholar] [CrossRef]
- Cong, Y.; Yuan, J.; Liu, J. Sparse Reconstruction Cost for Abnormal Event Detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Berthelot, D.; Schumm, T.; Metz, L. Began: Boundary Equilibrium Generative Adversarial Networks. arXiv 2017, arXiv:1703.10717. [Google Scholar]
- Lin, S.; Ji, R.; Li, Y.; Deng, C.; Li, X. Towards Compact ConvNets via Structure-Sparsity Regularized Filter Pruning. arXiv 2019, arXiv:1901.07827. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A Large-Scale Hierarchical Image Database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.; Lee, M. Building a Compact Convolutional Neural Network for Embedded Intelligent Sensor Systems Using Group Sparsity and Knowledge Distillation. Sensors 2019, 19, 4307. https://doi.org/10.3390/s19194307
Cho J, Lee M. Building a Compact Convolutional Neural Network for Embedded Intelligent Sensor Systems Using Group Sparsity and Knowledge Distillation. Sensors. 2019; 19(19):4307. https://doi.org/10.3390/s19194307
Chicago/Turabian StyleCho, Jungchan, and Minsik Lee. 2019. "Building a Compact Convolutional Neural Network for Embedded Intelligent Sensor Systems Using Group Sparsity and Knowledge Distillation" Sensors 19, no. 19: 4307. https://doi.org/10.3390/s19194307




