Gunshot Airborne Surveillance with Rotary Wing UAV-Embedded Microphone Array
Abstract
1. Introduction
2. DoA Estimation and Shooter Localization
2.1. Preprocessing
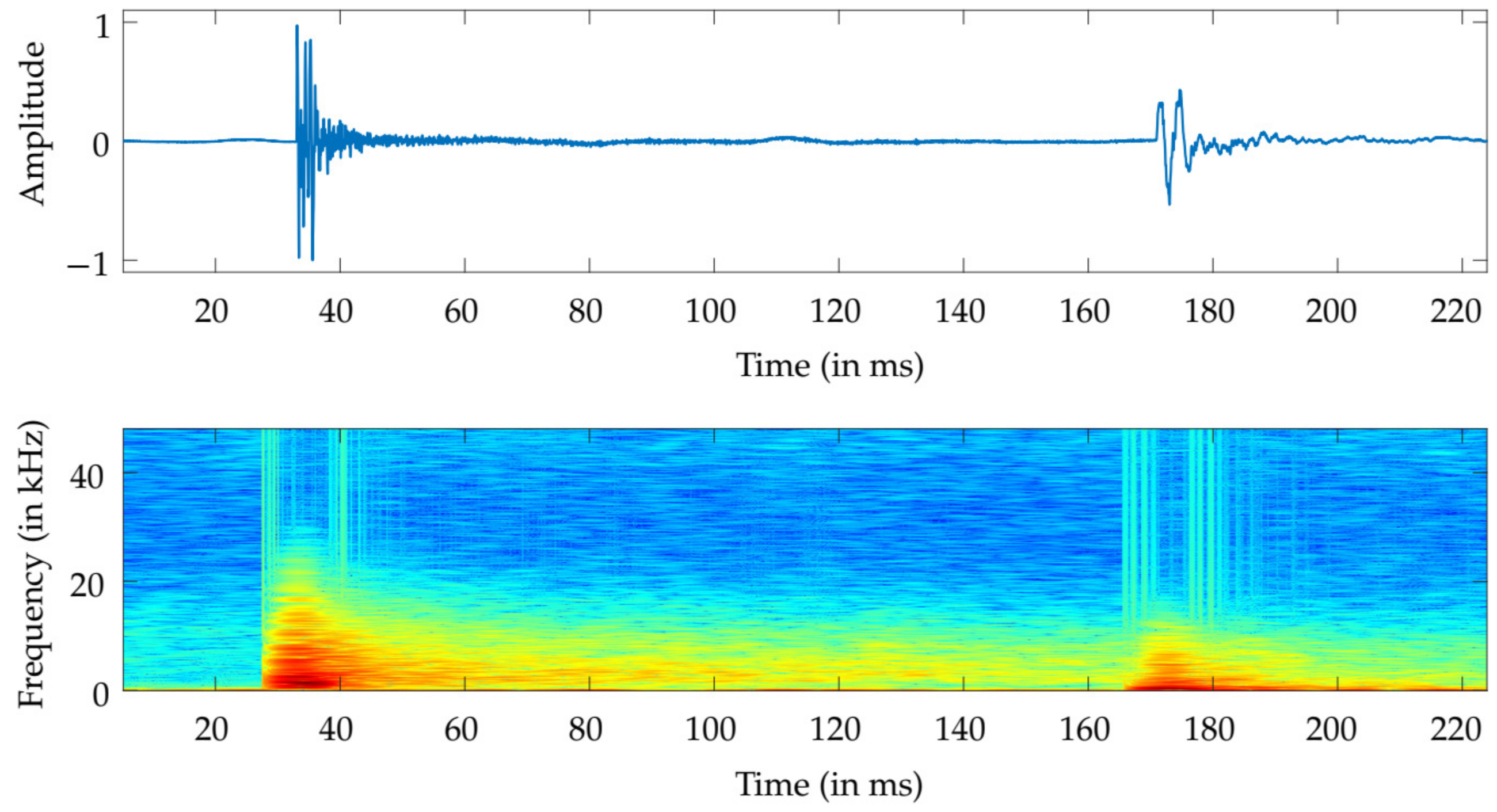
2.2. Gunshot Detection
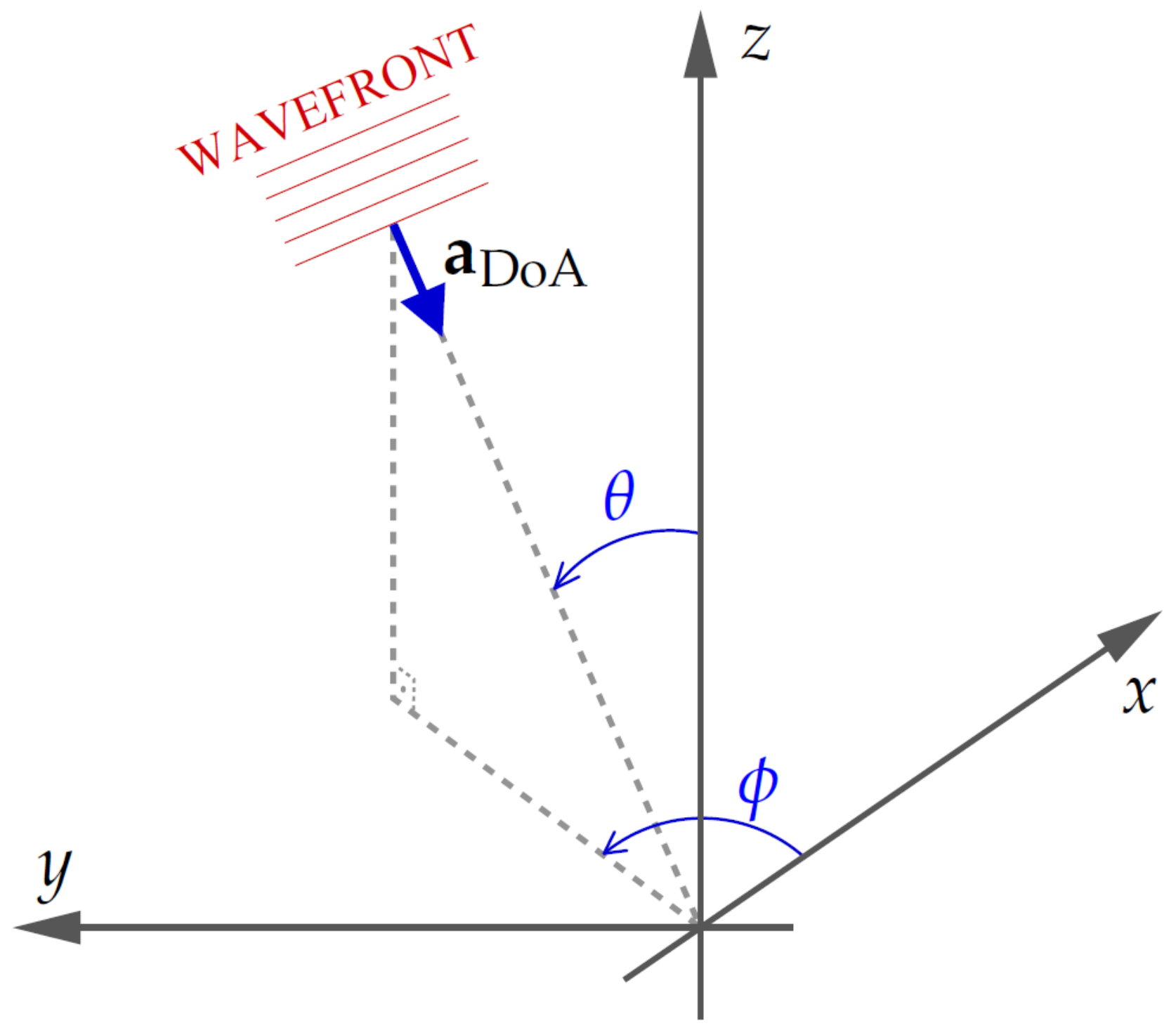
2.3. DoA Estimation Methods
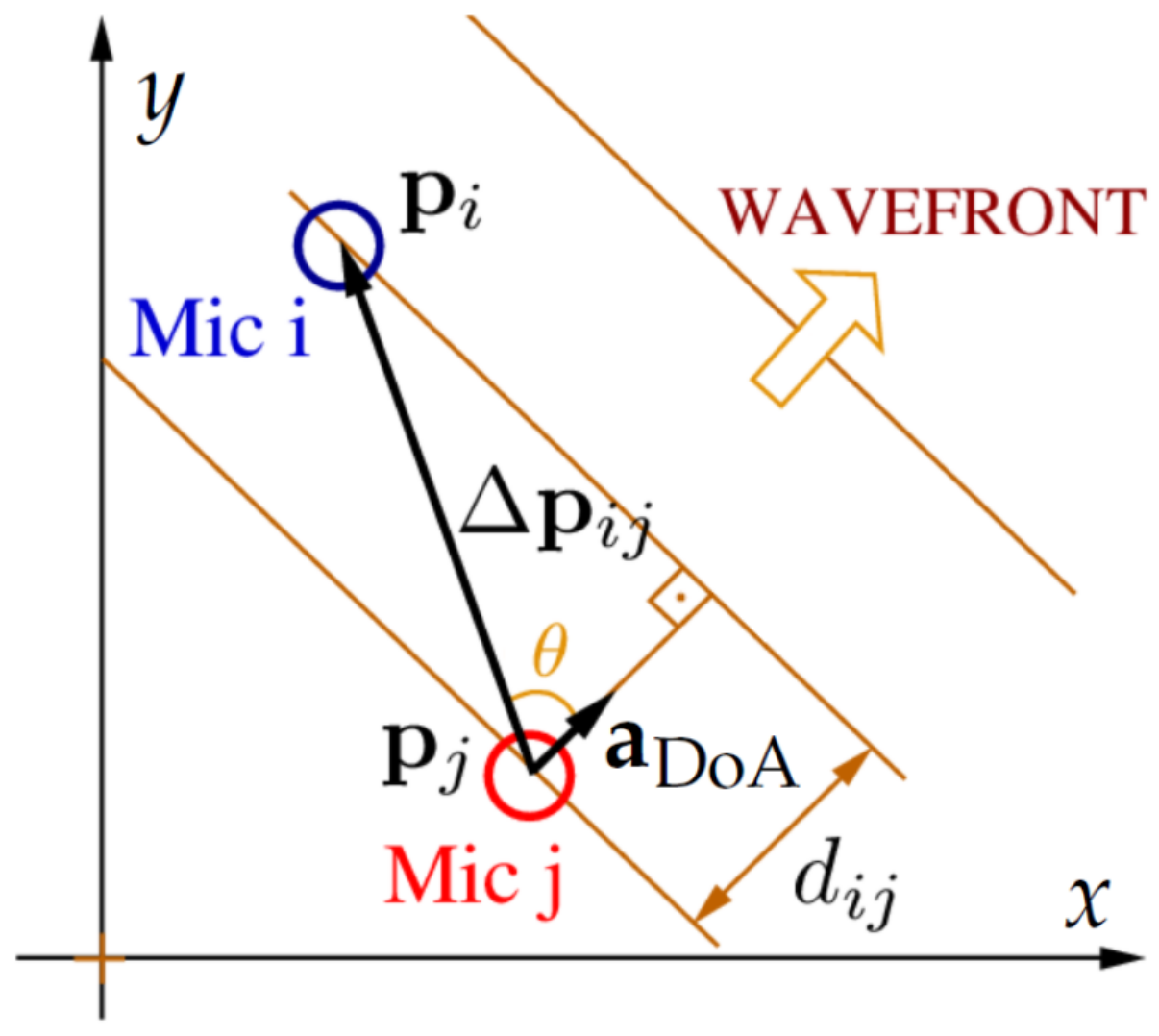
2.3.1. The Data Selection Least Squares DoA Estimation Algorithm
2.3.2. The MBSS Locate
2.4. Position Estimation
3. System Setup and Signal Acquisition
3.1. UAV and Avionics
3.2. Environmental Conditions and Shooting Site
3.3. Data Acquisition: Audio and Drone Position and Attitude
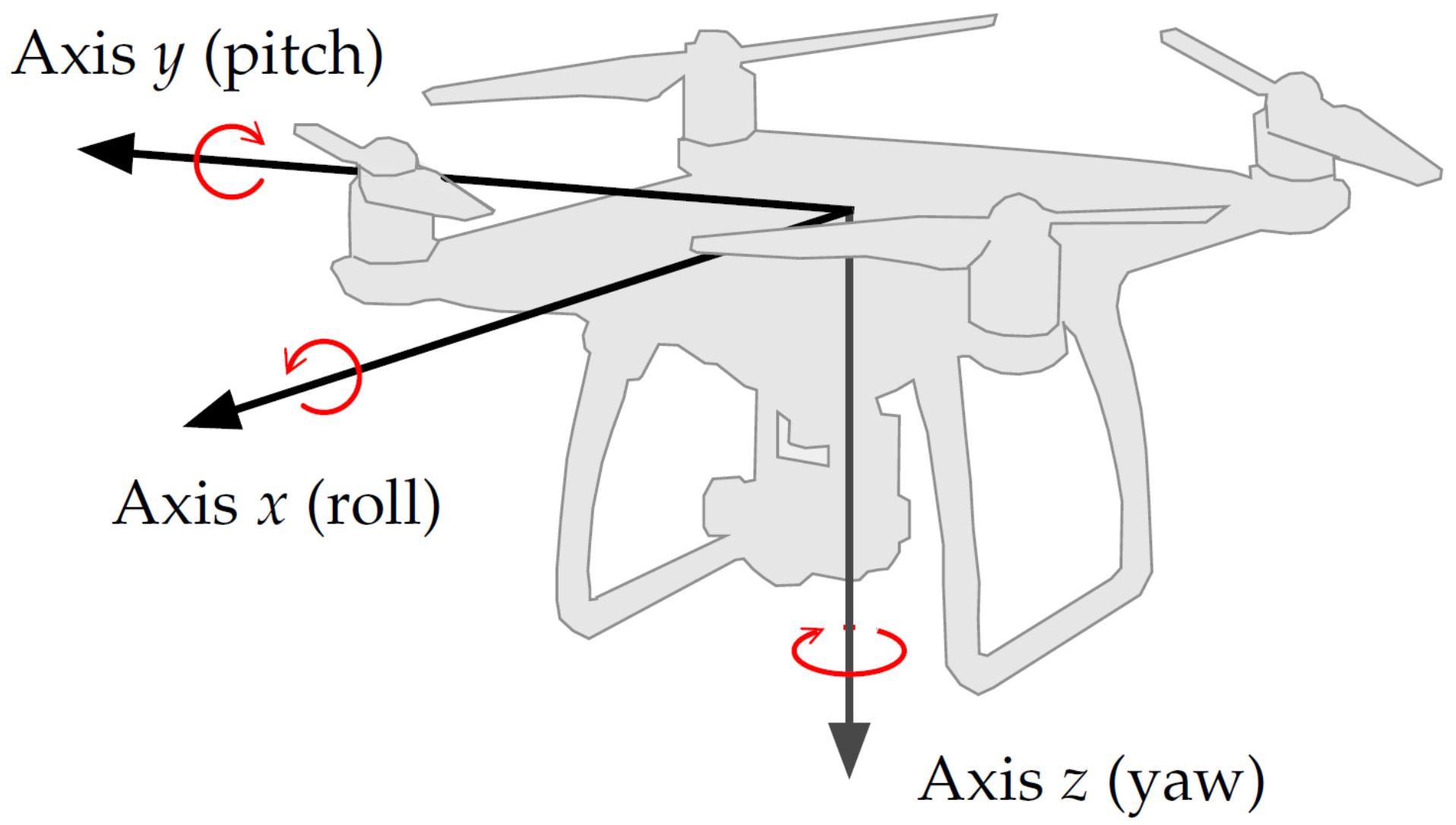
3.4. Axis Rotation
4. Experimental Results
4.1. Simulated Signals
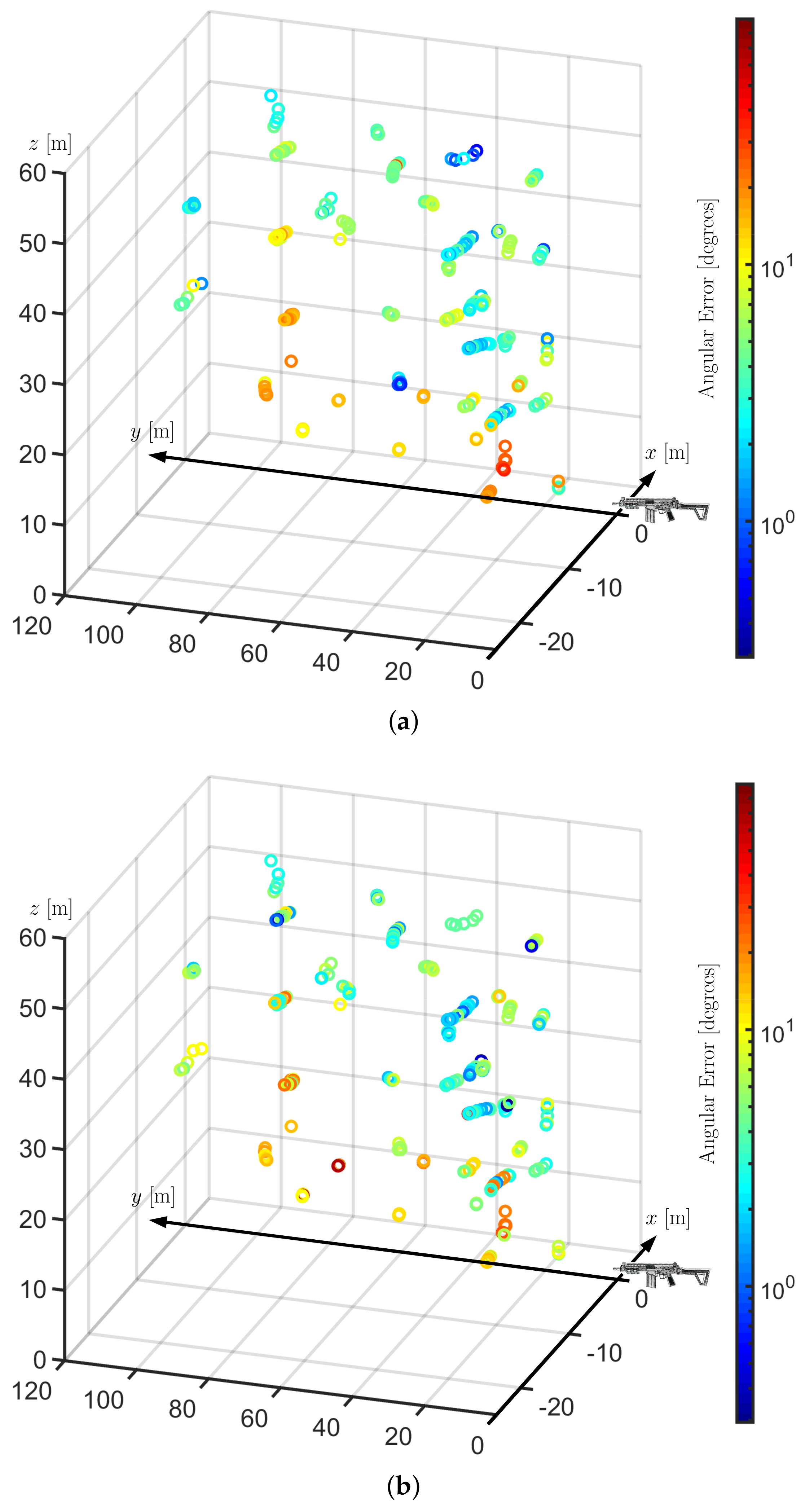
4.2. Field Recordings
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Complete Simulation Results
| Without Preprocessing | Median Filter | Wiener Filter | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SNR | n/Window Size (ms) | Mean Error () | Standard Deviation () | Error < | Mean Error () | Standard Deviation () | Error < | Mean Error () | Standard Deviation () | Error < |
| 10 | 3/20 | 0.5105 | 3.9269 | 99.1000 | 0.3259 | 0.5110 | 99.3000 | 19.4174 | 29.2600 | 63.9667 |
| 3/35 | 0.4113 | 2.9569 | 99.3333 | 0.3166 | 0.4897 | 99.2333 | 7.5168 | 19.8348 | 85.4667 | |
| 3/50 | 0.5498 | 4.3178 | 98.8000 | 0.3137 | 0.4720 | 99.3333 | 6.7859 | 18.8759 | 86.3667 | |
| 4/20 | 0.3577 | 2.5648 | 99.4333 | 0.2956 | 0.4566 | 99.4667 | 14.2784 | 25.6210 | 67.2667 | |
| 4/35 | 0.3456 | 2.5860 | 99.6000 | 0.2937 | 0.4598 | 99.3333 | 5.7116 | 17.1664 | 86.8000 | |
| 4/50 | 0.4492 | 3.7859 | 99.5333 | 0.2983 | 0.4652 | 99.4333 | 4.9097 | 15.8202 | 88.4333 | |
| 5/20 | 0.7266 | 4.2655 | 97.3333 | 0.2570 | 0.4065 | 99.6000 | 17.3627 | 23.8314 | 49.3333 | |
| 5/35 | 0.6415 | 4.0465 | 97.9000 | 0.2588 | 0.4150 | 99.6000 | 7.2962 | 17.0812 | 77.1333 | |
| 5/50 | 0.6343 | 4.1611 | 98.0333 | 0.2599 | 0.4206 | 99.6000 | 6.2528 | 15.9602 | 80.3000 | |
| 6/20 | 3.8631 | 9.2623 | 79.7000 | 0.2155 | 0.4113 | 99.7667 | 20.9030 | 21.0006 | 31.3000 | |
| 6/35 | 3.6364 | 8.7809 | 80.5667 | 0.2111 | 0.3641 | 99.8000 | 11.4076 | 17.0442 | 55.8333 | |
| 6/50 | 3.6197 | 8.7423 | 80.3000 | 0.2081 | 0.3555 | 99.8000 | 10.1562 | 16.0946 | 59.5667 | |
| 5 | 3/20 | 8.9438 | 21.7721 | 83.0333 | 0.4509 | 1.8724 | 98.7667 | 47.8794 | 27.9550 | 13.4000 |
| 3/35 | 9.0399 | 21.9193 | 82.9333 | 0.3980 | 0.6057 | 98.7667 | 35.8857 | 31.7066 | 33.7000 | |
| 3/50 | 9.2772 | 21.9742 | 82.3000 | 0.4750 | 1.9644 | 98.1333 | 33.3909 | 31.6343 | 37.4333 | |
| 4/20 | 6.3045 | 18.2118 | 85.9333 | 0.3558 | 0.5525 | 98.9000 | 43.6409 | 28.9848 | 15.2333 | |
| 4/35 | 6.7532 | 18.9762 | 85.2667 | 0.3634 | 0.5474 | 98.8667 | 32.8974 | 31.2853 | 34.8000 | |
| 4/50 | 6.6992 | 18.5737 | 84.9667 | 0.3960 | 1.0150 | 98.5000 | 30.4495 | 31.4588 | 39.6333 | |
| 5/20 | 9.0486 | 18.0645 | 68.8333 | 0.3576 | 1.0901 | 98.8867 | 43.5887 | 26.2580 | 7.9333 | |
| 5/35 | 8.9707 | 18.5345 | 69.1333 | 0.3306 | 0.7038 | 98.9000 | 33.1160 | 28.5151 | 23.4333 | |
| 5/50 | 8.7433 | 17.7275 | 69.2333 | 0.3717 | 1.4043 | 98.8333 | 31.2879 | 28.8127 | 26.4667 | |
| 6/20 | 16.3355 | 17.7956 | 34.0000 | 0.9664 | 4.5181 | 96.1667 | 42.2534 | 22.5981 | 3.1000 | |
| 6/35 | 16.1672 | 17.6804 | 33.6667 | 0.6625 | 2.9858 | 96.9667 | 33.7279 | 23.5199 | 11.7333 | |
| 6/50 | 15.8325 | 17.4014 | 34.9000 | 0.9330 | 4.5631 | 96.5667 | 32.1584 | 23.7626 | 13.8333 | |
| 2 | 3/20 | 25.0002 | 31.2690 | 54.2333 | 1.2066 | 6.5015 | 95.9667 | 54.8700 | 23.4266 | 2.7333 |
| 3/35 | 25.1071 | 31.2757 | 53.8667 | 1.2067 | 6.0516 | 96.0333 | 49.7629 | 27.4016 | 11.4333 | |
| 3/50 | 25.4807 | 31.2001 | 52.8667 | 1.3870 | 7.5824 | 95.3667 | 48.9076 | 27.9989 | 13.2667 | |
| 4/20 | 20.1555 | 28.8475 | 56.9667 | 0.8764 | 4.7645 | 96.7667 | 52.9217 | 23.9341 | 2.6333 | |
| 4/35 | 20.3873 | 29.0892 | 56.7333 | 0.8803 | 4.9494 | 96.7333 | 48.3238 | 28.1558 | 11.7333 | |
| 4/50 | 20.6283 | 29.0486 | 56.1000 | 0.9061 | 4.2183 | 96.2333 | 47.3459 | 28.5305 | 13.7667 | |
| 5/20 | 22.8296 | 25.8081 | 35.7667 | 1.4367 | 6.0686 | 93.6667 | 52.3569 | 22.8973 | 0.9667 | |
| 5/35 | 22.7192 | 26.2225 | 37.6000 | 1.4992 | 6.1723 | 93.4667 | 47.8062 | 26.4787 | 6.6000 | |
| 5/50 | 22.3695 | 25.7163 | 36.5000 | 1.8749 | 7.2668 | 92.2000 | 46.6417 | 27.0857 | 8.6667 | |
| 6/20 | 27.9808 | 20.9985 | 12.4000 | 4.6952 | 11.2968 | 80.1000 | 50.6875 | 21.5335 | 0.3667 | |
| 6/35 | 27.5228 | 21.0906 | 13.3000 | 4.4991 | 10.7498 | 79.8000 | 46.0894 | 23.3974 | 2.3000 | |
| 6/50 | 27.2111 | 20.6884 | 13.0667 | 5.6061 | 12.5749 | 77.4667 | 44.6994 | 23.9338 | 3.7000 | |
| 0 | 3/20 | 36.5372 | 31.9770 | 33.4000 | 3.8697 | 13.9666 | 89.8000 | 56.0114 | 22.1168 | 0.7667 |
| 3/35 | 36.5306 | 31.8651 | 33.2333 | 3.7284 | 13.1700 | 88.2333 | 54.1507 | 24.3032 | 4.6333 | |
| 3/50 | 36.6136 | 31.9203 | 33.6000 | 5.7540 | 17.5398 | 84.9667 | 52.7311 | 25.0567 | 6.1333 | |
| 4/20 | 31.5958 | 31.2282 | 35.3000 | 3.6497 | 13.9061 | 89.2000 | 54.8209 | 22.3306 | 0.9000 | |
| 4/35 | 32.0653 | 31.4251 | 35.3667 | 3.5862 | 12.6191 | 87.9667 | 53.1904 | 24.8787 | 5.0667 | |
| 4/50 | 32.1481 | 31.5255 | 35.2333 | 5.3396 | 16.2826 | 83.9333 | 51.8262 | 25.7706 | 6.8000 | |
| 5/20 | 32.7753 | 27.8043 | 20.3333 | 5.8269 | 14.5143 | 77.2333 | 54.4921 | 21.7418 | 0.1333 | |
| 5/35 | 32.9843 | 27.8264 | 18.7000 | 6.1626 | 14.3733 | 75.2000 | 52.8643 | 23.9831 | 2.4000 | |
| 5/50 | 33.8521 | 28.1587 | 19.3333 | 7.4859 | 16.4049 | 72.5333 | 51.4714 | 24.8103 | 3.5667 | |
| 6/20 | 34.9195 | 22.2685 | 6.1000 | 11.6739 | 17.7235 | 56.8000 | 53.4600 | 21.1648 | 0.2333 | |
| 6/35 | 35.2111 | 22.2109 | 5.6667 | 12.7202 | 18.1043 | 52.5667 | 50.6964 | 22.5240 | 0.7000 | |
| 6/50 | 35.5790 | 22.4075 | 5.9000 | 13.9468 | 19.1898 | 50.1667 | 49.6944 | 22.5882 | 0.9333 | |
| −2 | 3/20 | 45.1413 | 30.2568 | 19.2000 | 12.3675 | 26.0754 | 74.0333 | 56.6258 | 21.7486 | 0.1333 |
| 3/35 | 45.9091 | 29.6356 | 17.7333 | 14.7830 | 28.4758 | 68.8333 | 56.1857 | 22.8085 | 1.6667 | |
| 3/50 | 45.6604 | 29.8254 | 18.3667 | 17.2721 | 30.4772 | 63.3667 | 55.8175 | 23.0173 | 2.2333 | |
| 4/20 | 42.2719 | 30.5784 | 19.1667 | 12.4940 | 25.0592 | 67.9333 | 55.8804 | 21.4336 | 0.1000 | |
| 4/35 | 42.7540 | 30.2762 | 17.7667 | 14.9671 | 27.4779 | 63.3000 | 55.6017 | 23.0552 | 1.9667 | |
| 4/50 | 42.7118 | 30.1571 | 17.6000 | 17.0383 | 28.8422 | 58.1333 | 55.0972 | 23.3792 | 2.4667 | |
| 5/20 | 42.4860 | 27.6801 | 8.8667 | 15.7599 | 23.6227 | 51.5667 | 55.5419 | 21.4417 | 0.0667 | |
| 5/35 | 42.6461 | 27.3037 | 8.3667 | 17.8564 | 25.1710 | 46.1000 | 54.9616 | 22.8000 | 0.9000 | |
| 5/50 | 43.1371 | 27.2214 | 8.2000 | 19.7907 | 25.9766 | 41.5667 | 54.7407 | 23.0773 | 1.0667 | |
| 6/20 | 42.3165 | 23.0314 | 2.5333 | 22.9013 | 23.6372 | 30.6000 | 54.8717 | 21.0324 | 0.1333 | |
| 6/35 | 42.6043 | 23.0215 | 2.1333 | 24.5213 | 23.9388 | 26.7333 | 53.4221 | 22.0551 | 0.2333 | |
| 6/50 | 42.6747 | 23.0524 | 2.4333 | 26.4869 | 24.3458 | 24.3000 | 53.2176 | 22.3257 | 0.3000 | |
| −3 | 3/20 | 48.9503 | 28.0092 | 12.4667 | 20.0767 | 32.1463 | 59.5333 | 56.5733 | 21.7665 | 0.1667 |
| 3/35 | 49.2837 | 28.3516 | 13.0667 | 23.4632 | 34.2915 | 55.1000 | 56.6267 | 22.1172 | 1.0000 | |
| 3/50 | 49.3290 | 28.3126 | 12.6000 | 26.5068 | 35.6843 | 49.1000 | 56.1966 | 22.5202 | 1.4333 | |
| 4/20 | 47.1451 | 28.5781 | 11.9000 | 19.7724 | 31.0025 | 53.9333 | 56.2928 | 21.4432 | 0.1333 | |
| 4/35 | 46.7880 | 28.8198 | 12.6000 | 22.9690 | 32.6417 | 49.7000 | 56.4386 | 22.3254 | 1.1000 | |
| 4/50 | 47.4005 | 28.4842 | 11.5000 | 26.2416 | 33.8312 | 43.3667 | 55.9051 | 22.7439 | 1.3333 | |
| 5/20 | 46.7269 | 26.2793 | 5.2000 | 22.2956 | 27.3511 | 38.3000 | 56.0073 | 21.2151 | 0.1333 | |
| 5/35 | 46.3936 | 26.5745 | 5.7667 | 25.1084 | 29.1954 | 34.5667 | 56.1497 | 22.0678 | 0.5667 | |
| 5/50 | 46.9904 | 26.5622 | 5.7000 | 28.2202 | 30.0659 | 30.0667 | 55.4949 | 22.4393 | 0.6000 | |
| 6/20 | 45.9073 | 22.8674 | 1.1333 | 28.5282 | 24.7190 | 21.0667 | 55.4752 | 21.0532 | 0.1333 | |
| 6/35 | 45.7383 | 22.9903 | 1.3000 | 31.0702 | 25.8381 | 18.2333 | 54.8112 | 22.0272 | 0.2333 | |
| 6/50 | 46.3164 | 23.2109 | 1.1667 | 32.9346 | 25.6870 | 15.7667 | 54.2830 | 21.9627 | 0.2667 | |
| Without Preprocessing | Median Filter | Wiener Filter | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SNR | Window Size / Frame Size (ms) | Mean Error () | Standard Deviation () | Error < | Mean Error () | Standard Deviation () | Error < | Mean Error () | Standard Deviation () | Error < |
| 10 | 25/ 10 | 0.4531 | 0.4468 | 99.3000 | 0.5275 | 0.6029 | 98.4333 | 3.1767 | 10.7447 | 90.8000 |
| 35/10 | 0.4501 | 0.4328 | 99.3000 | 0.5220 | 0.5896 | 98.5333 | 8.9461 | 20.3771 | 80.2000 | |
| 35/12 | 0.4473 | 0.4259 | 99.3667 | 0.5094 | 0.5563 | 98.6667 | 2.2018 | 8.0205 | 92.9667 | |
| 50/10 | 0.4524 | 0.4338 | 99.3333 | 0.5354 | 0.6172 | 98.2333 | 11.4535 | 23.4741 | 77.0000 | |
| 50/12 | 0.4415 | 0.4084 | 99.4000 | 0.4956 | 0.5301 | 98.7333 | 3.3781 | 11.6631 | 91.3000 | |
| 50/15 | 0.4415 | 0.4084 | 99.4000 | 0.4956 | 0.5301 | 98.7333 | 3.3781 | 11.6631 | 91.3000 | |
| 50/20 | 0.4415 | 0.4084 | 99.4000 | 0.4956 | 0.5301 | 98.7333 | 3.3781 | 11.6631 | 91.3000 | |
| 5 | 25/ 10 | 0.5108 | 0.5392 | 98.9333 | 0.6013 | 0.7111 | 97.7333 | 20.9350 | 28.6107 | 55.7333 |
| 35/10 | 0.5069 | 0.5393 | 98.8667 | 0.6015 | 0.7019 | 97.8667 | 31.9753 | 31.9459 | 39.9667 | |
| 35/12 | 0.4865 | 0.4934 | 99.0667 | 0.5574 | 0.6240 | 98.2333 | 16.8103 | 26.6503 | 63.3667 | |
| 50/10 | 0.4985 | 0.5100 | 99.0333 | 0.5943 | 0.6907 | 97.7667 | 36.2389 | 31.7327 | 33.5667 | |
| 50/12 | 0.4608 | 0.4506 | 99.1667 | 0.5167 | 0.5624 | 98.6667 | 23.5154 | 29.7455 | 52.9000 | |
| 50/15 | 0.4608 | 0.4506 | 99.1667 | 0.5167 | 0.5624 | 98.6667 | 23.5154 | 29.7455 | 52.9000 | |
| 50/20 | 0.4608 | 0.4506 | 99.1667 | 0.5167 | 0.5624 | 98.6667 | 23.5154 | 29.7455 | 52.9000 | |
| 2 | 25/ 10 | 0.6587 | 1.0051 | 97.1000 | 0.7438 | 0.9689 | 96.1000 | 40.4421 | 31.5617 | 23.8333 |
| 35/10 | 0.6760 | 2.3588 | 97.2667 | 0.8466 | 3.2702 | 96.1333 | 46.9396 | 30.9384 | 16.6333 | |
| 35/12 | 0.5897 | 0.7246 | 97.9667 | 0.6831 | 0.8328 | 97.0333 | 36.6388 | 32.2888 | 29.8000 | |
| 50/10 | 0.6511 | 1.5885 | 97.5667 | 0.8426 | 3.2499 | 96.6000 | 50.0315 | 28.4052 | 11.7667 | |
| 50/12 | 0.5097 | 0.5408 | 98.7000 | 0.5769 | 0.6563 | 98.3000 | 42.3877 | 31.8309 | 22.3000 | |
| 50/15 | 0.5097 | 0.5408 | 98.7000 | 0.5769 | 0.6563 | 98.3000 | 42.3877 | 31.8309 | 22.3000 | |
| 50/20 | 0.5097 | 0.5408 | 98.7000 | 0.5769 | 0.6563 | 98.3000 | 42.3877 | 31.8309 | 22.3000 | |
| 0 | 25/ 10 | 0.8122 | 1.9544 | 95.9000 | 1.2682 | 5.4158 | 93.7333 | 48.3123 | 29.8138 | 12.0667 |
| 35/10 | 1.1827 | 5.8337 | 95.4000 | 1.6328 | 8.0185 | 93.4667 | 52.3492 | 27.8695 | 7.3000 | |
| 35/12 | 0.7021 | 0.8468 | 96.5000 | 0.8722 | 1.5264 | 95.1667 | 45.6052 | 30.6252 | 15.4000 | |
| 50/10 | 0.8504 | 2.5126 | 95.7667 | 1.1790 | 4.3650 | 93.7667 | 53.1432 | 26.8928 | 6.5000 | |
| 50/12 | 0.5871 | 0.7072 | 97.6667 | 0.8010 | 3.4158 | 96.5667 | 48.8692 | 30.1058 | 12.2333 | |
| 50/15 | 0.5871 | 0.7072 | 97.6667 | 0.8010 | 3.4158 | 96.5667 | 48.8692 | 30.1058 | 12.2333 | |
| 50/20 | 0.5871 | 0.7072 | 97.6667 | 0.8010 | 3.4158 | 96.5667 | 48.8692 | 30.1058 | 12.2333 | |
| −2 | 25/ 10 | 1.9049 | 9.1781 | 92.1000 | 3.6309 | 14.1082 | 88.3333 | 53.3834 | 27.6259 | 5.0333 |
| 35/10 | 2.2230 | 10.1234 | 91.9667 | 4.6370 | 16.5701 | 86.6667 | 55.5020 | 26.4814 | 3.5000 | |
| 35/12 | 0.9577 | 2.8586 | 94.5333 | 1.7432 | 7.3635 | 91.4000 | 51.7095 | 29.1208 | 7.5333 | |
| 50/10 | 1.8668 | 9.2858 | 93.4000 | 3.4592 | 14.0692 | 89.3000 | 55.2182 | 25.2605 | 2.9333 | |
| 50/12 | 0.6788 | 0.8690 | 96.7333 | 1.2045 | 5.6296 | 94.6667 | 53.4769 | 27.6794 | 5.8000 | |
| 50/15 | 0.6788 | 0.8690 | 96.7333 | 1.2045 | 5.6296 | 94.6667 | 53.4769 | 27.6794 | 5.8000 | |
| 50/20 | 0.6788 | 0.8690 | 96.7333 | 1.2045 | 5.6296 | 94.6667 | 53.4769 | 27.6794 | 5.8000 | |
| −3 | 25/ 10 | 2.7857 | 12.1656 | 90.6667 | 6.7664 | 20.3681 | 82.9667 | 54.2794 | 27.4513 | 4.6667 |
| 35/10 | 3.4863 | 13.8784 | 89.6667 | 8.3755 | 22.4228 | 80.2000 | 56.0700 | 25.9085 | 2.4000 | |
| 35/12 | 1.3376 | 5.6843 | 92.8667 | 3.5085 | 14.0162 | 87.4667 | 52.8001 | 28.5094 | 5.8333 | |
| 50/10 | 2.6344 | 11.6972 | 91.8000 | 6.2836 | 20.0453 | 84.7333 | 56.5674 | 24.8849 | 2.2333 | |
| 50/12 | 0.9751 | 4.4240 | 95.9333 | 2.0194 | 9.4220 | 92.3667 | 54.9000 | 27.0754 | 4.2667 | |
| 50/15 | 0.9751 | 4.4240 | 95.9333 | 2.0194 | 9.4220 | 92.3667 | 54.9000 | 27.0754 | 4.2667 | |
| 50/20 | 0.9751 | 4.4240 | 95.9333 | 2.0194 | 9.4220 | 92.3667 | 54.9000 | 27.0754 | 4.2667 | |
| −5 | 25/ 10 | 8.9995 | 23.7791 | 78.3000 | 17.8985 | 32.5969 | 62.9000 | 55.5686 | 26.8271 | 2.1333 |
| 35/10 | 12.1111 | 27.9742 | 74.6333 | 22.2779 | 35.4841 | 59.0333 | 57.1703 | 26.1266 | 1.1000 | |
| 35/12 | 4.4998 | 15.6668 | 84.3000 | 12.6640 | 28.4453 | 69.9000 | 54.9973 | 27.9755 | 3.2667 | |
| 50/10 | 8.5302 | 23.3745 | 80.3000 | 19.0307 | 33.8287 | 64.8667 | 56.8281 | 24.4191 | 0.9000 | |
| 50/12 | 3.0576 | 13.0383 | 90.7333 | 9.1981 | 24.1209 | 78.9333 | 56.3419 | 27.0353 | 1.8667 | |
| 50/15 | 3.0576 | 13.0383 | 90.7333 | 9.1981 | 24.1209 | 78.9333 | 56.3419 | 27.0353 | 1.8667 | |
| 50/20 | 3.0576 | 13.0383 | 90.7333 | 9.1981 | 24.1209 | 78.9333 | 56.3419 | 27.0353 | 1.8667 | |
| −8 | 25/ 10 | 33.5311 | 39.8177 | 41.2333 | 44.3035 | 40.9917 | 26.6333 | 57.2012 | 26.8990 | 1.8000 |
| 35/10 | 36.3345 | 39.9724 | 38.0667 | 46.8466 | 41.0956 | 26.0000 | 57.5182 | 25.5922 | 0.8667 | |
| 35/12 | 21.7416 | 34.7735 | 53.6667 | 35.2805 | 40.2148 | 35.5667 | 56.5289 | 27.8457 | 2.1667 | |
| 50/10 | 34.0082 | 39.6064 | 43.4000 | 46.5912 | 40.8337 | 25.9333 | 57.7520 | 24.7207 | 0.6667 | |
| 50/12 | 18.8424 | 33.5860 | 61.9000 | 34.4365 | 40.5661 | 40.2000 | 57.2580 | 26.3992 | 1.7000 | |
| 50/15 | 18.8424 | 33.5860 | 61.9000 | 34.4365 | 40.5661 | 40.2000 | 57.2580 | 26.3992 | 1.7000 | |
| 50/20 | 18.8424 | 33.5860 | 61.9000 | 34.4365 | 40.5661 | 40.2000 | 57.2580 | 26.3992 | 1.7000 | |
References
- Dong, J.; Wu, G.; Yang, T.; Jiang, Z. Battlefield situation awareness and networking based on agent distributed computing. Phys. Commun. 2019, 33, 178–186. [Google Scholar] [CrossRef]
- Astapov, S.; Berdnikova, J.; Ehala, J.; Kaugerand, J.; Preden, J.S. Gunshot acoustic event identification and shooter localization in a WSN of asynchronous multichannel acoustic ground sensors. Multidimens. Syst. Signal Process. 2018, 29, 563–595. [Google Scholar] [CrossRef]
- Ramos, A.L.L. Acoustic Sniper Positioning Systems. Ph.D. Thesis, University of Oslo, Oslo, Norway, 2015. [Google Scholar]
- Kastek, M.; Dulski, R.; Trzaskawka, P.; Piątkowski, T.; Polakowski, H. Spectral measurements of muzzle flash with multispectral and hyperspectral sensor. In International Symposium on Photoelectronic Detection and Imaging 2011: Advances in Infrared Imaging and Applications; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 8193, p. 81933Y. [Google Scholar]
- Borzino, A.M.C.R.; Apolinário, J.A., Jr.; de Campos, M.L.R.; Biscainho, L.W.P. Signal enhancement for gunshot DOA estimation with median filters. In Proceedings of the 6th Latin American Symposium on Circuits & Systems (LASCAS), Montevideo, Uruguay, 24–27 February 2015. [Google Scholar]
- Borzino, A.M.C.R.; Apolinário, J.A., Jr.; de Campos, M.L.R. Consistent DOA estimation of heavily noisy gunshot signals using a microphone array. IET Radar Sonar Navig. 2016, 10, 1519–1527. [Google Scholar] [CrossRef]
- Borzino, A.M.C.R.; Apolinário, J.A., Jr.; de Campos, M.L.R. Robust DOA estimation of heavily noisy gunshot signals. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 449–453. [Google Scholar]
- Ntalampiras, S. Moving vehicle classification using wireless acoustic sensor networks. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 129–138. [Google Scholar] [CrossRef]
- Prince, P.; Hill, A.; Piña Covarrubias, E.; Doncaster, P.; Snaddon, J.L.; Rogers, A. Deploying Acoustic Detection Algorithms on Low-Cost, Open-Source Acoustic Sensors for Environmental Monitoring. Sensors 2019, 19, 553. [Google Scholar] [CrossRef] [PubMed]
- Prasad, R. Alexa Everywhere: AI for Daily Convenience. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, VIC, Australia, 11–15 February 2019. [Google Scholar]
- Sibanyoni, S.V.; Ramotsoela, D.T.; Silva, B.J.; Hancke, G.P. A 2-D Acoustic Source Localization System for Drones in Search and Rescue Missions. IEEE Sens. J. 2019, 19, 332–341. [Google Scholar] [CrossRef]
- Hoshiba, K.; Washizaki, K.; Wakabayashi, M.; Ishiki, T.; Kumon, M.; Bando, Y.; Gabriel, D.; Nakadai, K.; Okuno, H. Design of UAV-embedded microphone array system for sound source localization in outdoor environments. Sensors 2017, 17, 2535. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Nakamura, K.; Nakadai, K.; Asano, F.; Hasegawa, Y.; Tsujino, H. Intelligent sound source localization for dynamic environments. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), St. Louis, MI, USA, 10–15 October 2009; pp. 664–669. [Google Scholar]
- Nakamura, K.; Nakadai, K.; Asano, F.; Ince, G. Intelligent sound source localization and its application to multimodal human tracking. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Francisco, CA, USA, 25–30 September 2011; pp. 143–148. [Google Scholar]
- Okutani, K.; Yoshida, T.; Nakamura, K.; Nakadai, K. Outdoor auditory scene analysis using a moving microphone array embedded in a quadrocopter. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Algarve, Portugal, 7–12 October 2012; pp. 3288–3293. [Google Scholar]
- Furukawa, K.; Okutani, K.; Nagira, K.; Otsuka, T.; Itoyama, K.; Nakadai, K.; Okuno, H.G. Noise correlation matrix estimation for improving sound source localization by multirotor UAV. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 3943–3948. [Google Scholar]
- Ohata, T.; Nakamura, K.; Mizumoto, T.; Taiki, T.; Nakadai, K. Improvement in outdoor sound source detection using a quadrotor-embedded microphone array. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2014; pp. 1902–1907. [Google Scholar]
- Wang, L.; Cavallaro, A. Time-frequency processing for sound source localization from a micro aerial vehicle. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 496–500. [Google Scholar]
- Wang, L.; Cavallaro, A. Acoustic sensing from a multi-rotor drone. Sens. J. 2018, 18, 4570–4582. [Google Scholar] [CrossRef]
- Wang, L.; Cavallaro, A. Ear in the sky: Ego-noise reduction for auditory micro aerial vehicles. In Proceedings of the 13th International Conference on Advanced Video and Signal Based Surveillance (AVSS), Colorado Springs, CO, USA, 23–26 August 2016; pp. 152–158. [Google Scholar]
- Basiri, M.; Schill, F.; Lima, P.; Floreano, D. On-board relative bearing estimation for teams of drones using sound. IEEE Robot. Autom. Lett. 2016, 1, 820–827. [Google Scholar] [CrossRef]
- Wang, L.; Sanchez-Matilla, R.; Cavallaro, A. Tracking a moving sound source from a multi-rotor drone. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2511–2516. [Google Scholar]
- Calderon, D.M.P.; Apolinário, J.A., Jr. Shooter localization based on DoA estimation of gunshot signals and digital map information. Lat. Am. Trans. 2015, 13, 441–447. [Google Scholar] [CrossRef]
- Fernandes, R.P.; Borzino, A.M.C.R.; Ramos, A.L.L.; Apolinário, J.A., Jr. Investigating the potential of UAV for gunshot DoA estimation and shooter localization. In Proceedings of the Simpósio Brasileiro de Telecomunicações e Processamento de Sinais, Belém, Brazil, 30 August–2 September 2016. [Google Scholar]
- Fernandes, R.P.; Ramos, A.L.L.; Apolinário, J.A., Jr. Airborne DoA estimation of gunshot acoustic signals using drones with application to sniper localization systems. In Proceedings of the SPIE Defense, Security, and Sensing, Anaheim, CA, USA, 9–13 April 2017. [Google Scholar]
- Beck, S.D.; Nakasone, H.; Marr, K.W. An introduction to forensic gunshot acoustics. In Proceedings of the 162nd Meeting of the Acoustical Society of America, San Diego, CA, USA, 31 October–4 November 2011. [Google Scholar]
- Brustad, B.M.; Freytag, J.C. A survey of audio forensic gunshot investigations. In Proceedings of the 26th International Conference: Audio Forensics in the Digital Age, Denver, CO, USA, 7–9 July 2005. [Google Scholar]
- Beck, S.D.; Nakasone, H.; Marr, K.W. Variations in recorded acoustic gunshot waveforms generated by small firearms. J. Acoust. Soc. Am. 2011, 129, 1748–1759. [Google Scholar] [CrossRef] [PubMed]
- Routh, T.K.; Maher, R.C. Recording anechoic gunshot waveforms of several firearms at 500 kilohertz sampling rate. In Proceedings of the 171st Meeting of the Acoustical Society of America, Salt Lake City, UT, USA, 23–27 May 2016. [Google Scholar]
- Maher, R.C. Modeling and Signal Processing of Acoustic Gunshot Recordings. In Proceedings of the IEEE 12th Digital Signal Processing Workshop & 4th IEEE Signal Processing Education Workshop, Teton National Park, WY, USA, 24–27 September 2006; pp. 257–261. [Google Scholar]
- Maher, R.C. Acoustical Characterization of Gunshots. In Proceedings of the IEEE Workshop on Signal Processing Applications for Public Security and Forensics, Washington, DC, USA, 11–13 April 2007. [Google Scholar]
- DuMond, J.W.; Cohen, E.R.; Panofsky, W.; Deeds, E. A determination of the wave forms and laws of propagation and dissipation of ballistic shock waves. J. Acoust. Soc. Am. 1946, 18, 97–118. [Google Scholar] [CrossRef]
- George, J.; Kaplan, L.M. Shooter Localization using a Wireless Sensor Network of Soldier-Worn Gunfire Detection Systems. J. Adv. Inf. Fusion 2013, 8, 15–32. [Google Scholar]
- Ishiki, T.; Kumon, M. A microphone array configuration for an auditory quadrotor helicopter system. In Proceedings of the International Symposium on Safety, Security, and Rescue Robotics, Hokkaido, Japan, 27–30 October 2014. [Google Scholar]
- Strauss, M.; Mordel, P.; Miguet, V.; Deleforge, A. DREGON: Dataset and Methods for UAV-Embedded Sound Source Localization. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Scalart, P.; Liu, M. Wiener Filter for Noise Reduction and Speech Enhancement. Available online: https://www.mathworks.com/matlabcentral/fileexchange/24462-wiener-filter-for-noise-reduction-and-speech-enhancement (accessed on 12 January 2019).
- Plapous, C.; Marro, C.; Scalart, P. Improved signal-to-noise ratio estimation for speech enhancement. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 2098–2108. [Google Scholar] [CrossRef]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 1109–1121. [Google Scholar] [CrossRef]
- Fitzgerald, D. Harmonic/percussive separation using median filtering. In Proceedings of the 13th International Conference on Digital Audio Effects (DAFX10), Graz, Austria, 6–10 September 2010. [Google Scholar]
- Mäkinen, T.; Pertilä, P. Shooter localization and bullet trajectory, caliber, and speed estimation based on detected firing sounds. Appl. Acoust. 2010, 71, 902–913. [Google Scholar] [CrossRef]
- Hainsworth, S. Beat tracking and musical metre analysis. In Signal Processing Methods for Music Transcription; Springer: Berlin/Heidelberg, Germany, 2006; pp. 101–129. [Google Scholar]
- Chacon-Rodriguez, A.; Julian, P.; Castro, L.; Alvarado, P.; Hernández, N. Evaluation of gunshot detection algorithms. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 58, 363–373. [Google Scholar] [CrossRef]
- Freire, I.L.; Apolinário, J.A., Jr. Gunshot detection in noisy environment. In Proceeding of the 7th International Telecommunications Symposium, Manaus, Brazil, 7–9 September 2010. [Google Scholar]
- Ahmed, T.; Uppal, M.; Muhammad, A. Improving efficiency and reliability of gunshot detection systems. In Proceeding of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–30 May 2013. [Google Scholar]
- Libal, U.; Spyra, K. Wavelet based shock wave and muzzle blast classification for different supersonic projectiles. Expert Syst. Appl. 2014, 41, 5097–5104. [Google Scholar] [CrossRef]
- Blandin, C.; Ozerov, A.; Vincent, E. Multi-source TDOA estimation in reverberant audio using angular spectra and clustering. Signal Process. 2012, 92, 1950–1960. [Google Scholar] [CrossRef]
- Van Trees, H.L. Optimum Array Processing—Part IV—Detection, Estimation, and Modulation Theory, Optimum Array Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Knapp, C.H.; Carter, G.C. The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- Van Den Broeck, B.; Bertrand, A.; Karsmakers, P.; Vanrumste, B.; Moonen, M. Time-domain generalized cross correlation phase transform sound source localization for small microphone arrays. In Proceeding of the 5th European DSP Education and Research Conference (EDERC), Amsterdam, The Netherlands, 13–14 September 2012; pp. 76–80. [Google Scholar]
- Ribeiro, J.G.; Serrenho, F.G.; Apolinário, J.A., Jr.; Ramos, A.L.L. Effective direction of arrival estimation of gunshot signals from an in-flight unmanned aerial vehicle. Autom. Target Recognit. XXVIII 2018, 10648, 106480H. [Google Scholar]
- Qin, B.; Zhang, H.; Fu, Q.; Yan, Y. Subsample time delay estimation via improved GCC PHAT algorithm. In Proceedings of the 9th International Conference on Signal Processing, Beijing, China, 26–29 October 2008; pp. 2579–2582. [Google Scholar]
- Brandstein, M.; Silverman, H. A robust method for speech signal time-delay estimation in reverberant rooms. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Munich, Germany, 21–24 April 1997. [Google Scholar]
- Freire, I.L.; Apolinário, J.A., Jr. DoA of gunshot signals in a spatial microphone array: Performance of the interpolated Generalized Cross-Correlation method. In Proceedings of the 6th Argentine School of Micro-Nanoelectronics, Technology and Applications (EAMTA), Buenos Aires, Argentina, 11–12 August 2011. [Google Scholar]
- Ribeiro, J.G.C.; Serrenho, F.G.; Apolinário, J.A., Jr.; Ramos, A.L.L. Improved DoA estimation with application to bearings-only acoustic source localization. In Proceedings of the International Symposium on Signal Processing and Information Technology (ISSPIT), Bilbao, Spain, 8–20 December 2017; pp. 100–105. [Google Scholar]
- Lebarbenchon, R.; Camberlein, E. Multi-Channel BSS Locate. Available online: http://bass-db.gforge.inria.fr/bss_locate/ (accessed on 20 February 2018).
- Loesch, B.; Yang, B. Adaptive segmentation and separation of determined convolutive mixtures under dynamic conditions. In International Conference on Latent Variable Analysis and Signal Separation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 41–48. [Google Scholar]
- Nesta, F.; Svaizer, P.; Omologo, M. Cumulative state coherence transform for a robust two-channel multiple source localization. In International Conference on Independent Component Analysis and Signal Separation; Springer: Berlin/Heidelberg, Germany, 2009; pp. 290–297. [Google Scholar]
- Yamaoka, K.; Ono, N.; Makino, S.; Yamada, T. Time-frequency-bin-wise Switching of Minimum Variance Distortionless Response Beamformer for Underdetermined Situations. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 7908–7912. [Google Scholar]
- McCowan, I.; Lincoln, M.; Himawan, I. Microphone array shape calibration in diffuse noise fields. Trans. Audio Speech Lang. Process. 2008, 16, 666–670. [Google Scholar] [CrossRef]
- Doğançay, K. Bearings-only target localization using total least squares. Signal Process. 2005, 85, 1695–1710. [Google Scholar] [CrossRef]
- Freire, I.L.; Apolinário, J.A., Jr. Localização de atirador por arranjo de microfones (in Portuguese). SBAI 2011, X, 1049–1053. [Google Scholar]
- Barger, J.E.; Milligan, S.D.; Brinn, M.S.; Mullen, R.J. Systems and Methods for Determining Shooter Locations with Weak Muzzle Detection. U.S. Patent 7710828B2, 4 May 2010. [Google Scholar]
- DJI. Phantom 4 Specs. Available online: https://www.dji.com/phantom-4/info#specs (accessed on 13 April 2019).
- Google. Google Maps, Map Data: Google. Available online: https://www.google.com/maps/ (accessed on 6 August 2019).
- TASCAM. Handheld Recorder DR-40. Available online: https://tascam.com/us/product/dr-40/spec (accessed on 13 April 2019).
- Airdata UAV. Available online: https://airdata.com (accessed on 20 June 2019).
- DJI. Flight Control. Available online: https://developer.dji.com/mobile-sdk/documentation/introduction/flightController_concepts.html (accessed on 14 April 2018).
- Rorres, C.; Anton, H. Elementary Linear Algebra: Applications Version, 10th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Indústria de Material Bélico do Brasil—IMBEL. Available online: http://www.imbel.gov.br/ (accessed on 7 July 2019).



| Microphone | x (cm) | y (cm) |
|---|---|---|
| 1 | 26.5 | |
| 2 | 26.5 | 27.0 |
| 3 | 26.0 | |
| 4 |
| Without Preprocessing | Median Filter | Wiener Filter | ||||
|---|---|---|---|---|---|---|
| SNR | n/Window Size (ms) | Error < 3 (%) | n/Window Size (ms) | Error < 3 (%) | n/Window Size (ms) | Error < 3 (%) |
| 10 | 4/35 | 99.6000 | 6/50 | 99.8000 | 4/50 | 88.4333 |
| 5 | 4/20 | 85.9333 | 4/20 | 98.9000 | 4/50 | 39.6333 |
| 2 | 4/20 | 56.9667 | 4/20 | 96.7667 | 4/50 | 13.7667 |
| 0 | 4/35 | 35.3667 | 3/20 | 89.8000 | 4/50 | 6.8000 |
| −2 | 3/20 | 19.2000 | 3/20 | 74.0333 | 4/50 | 2.4667 |
| −3 | 3/35 | 13.0667 | 3/20 | 59.5333 | 3/50 | 1.4333 |
| Without Preprocessing | Median Filter | Wiener Filter | ||||
|---|---|---|---|---|---|---|
| SNR | Window Size/ Frame Size (ms) | Error < 3 [%] | Window Size/ Frame Size (ms) | Error < 3 [%] | Window Size/ Frame Size (ms) | Error < 3 [%] |
| 10 | 50/12 50/15 50/20 | 99.4000 | 50/12 50/15 50/20 | 98.7333 | 35/12 | 92.9667 |
| 5 | 50/12 50/15 50/20 | 99.1667 | 50/12 50/15 50/20 | 98.6667 | 35/12 | 63.3667 |
| 2 | 50/12 50/15 50/20 | 98.7000 | 50/12 50/15 50/20 | 98.3000 | 35/12 | 29.8000 |
| 0 | 50/12 50/15 50/20 | 97.6667 | 50/12 50/15 50/20 | 96.5667 | 35/12 | 15.4000 |
| −2 | 50/12 50/15 50/20 | 96.7333 | 50/12 50/15 50/20 | 94.6667 | 35/12 | 7.5333 |
| −3 | 50/12 50/15 50/20 | 95.9333 | 50/12 50/15 50/20 | 92.3667 | 35/12 | 5.8333 |
| −5 | 50/12 50/15 50/20 | 90.7333 | 50/12 50/15 50/20 | 78.9333 | 35/12 | 3.2667 |
| −8 | 50/12 50/15 50/20 | 61.9000 | 50/12 50/15 50/20 | 40.2000 | 35/12 | 2.1667 |
| Mean Error () | Standard Deviaton () | Error < 10 (%) | |
|---|---|---|---|
| LS + MF | 8.3823 | 7.2215 | 70.4453 |
| MBSS | 9.6451 | 12.2113 | 72.8745 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serrenho, F.G.; Apolinário, J.A., Jr.; Ramos, A.L.L.; Fernandes, R.P. Gunshot Airborne Surveillance with Rotary Wing UAV-Embedded Microphone Array. Sensors 2019, 19, 4271. https://doi.org/10.3390/s19194271
Serrenho FG, Apolinário JA Jr., Ramos ALL, Fernandes RP. Gunshot Airborne Surveillance with Rotary Wing UAV-Embedded Microphone Array. Sensors. 2019; 19(19):4271. https://doi.org/10.3390/s19194271
Chicago/Turabian StyleSerrenho, Felipe Gonçalves, José Antonio Apolinário, Jr., António Luiz Lopes Ramos, and Rigel Procópio Fernandes. 2019. "Gunshot Airborne Surveillance with Rotary Wing UAV-Embedded Microphone Array" Sensors 19, no. 19: 4271. https://doi.org/10.3390/s19194271
APA StyleSerrenho, F. G., Apolinário, J. A., Jr., Ramos, A. L. L., & Fernandes, R. P. (2019). Gunshot Airborne Surveillance with Rotary Wing UAV-Embedded Microphone Array. Sensors, 19(19), 4271. https://doi.org/10.3390/s19194271






