1. Introduction
With the development of wireless communication technology, sensor network, microchip technology, and pervasive computing, the Internet of Things (IoT) has been applied in more and more areas, including smart home, smart health, wearable equipment, vehicular ad-hoc network, environmental monitoring, and smart grids, etc. [
1]. The IoT collects various information from the physical world through radio frequency identification (RFID) devices, infrared sensors, GPS, sensors, etc. It enables people-to-people, people-to-thing, thing-to-thing connection, and communication, which in turn realizes intelligent perception, recognition, decision-making, and control on the physical world [
2]. For example, wearable systems can effectively provide patients with seamless monitoring, remote surgery, telemedicine, timely assistance, and turn hospital-centered medical services into patient-centered care [
3]. However, while the Internet of Things provides people with more and more convenient services, its security issues are becoming increasingly prominent. Data security and privacy preservation are major challenges in the applications of the IoT. Integrity, non-repudiation and authenticity have become the key security requirements for the Internet of Things [
4].
In IoT applications, identity authentication, encryption, and integrity verification can be achieved by secure hash functions and digital signature algorithms which can ensure data privacy and rooting security [
2]. Many scholars have been working on this issue [
4,
5,
6]. Yeh et al. [
5] proposed a certificateless signature scheme based on elliptic curve cryptography (ECC). Since ECC is more efficient than bilinear mapping in terms of computational efficiency [
7], the scheme provides a safe and efficient interaction for IoT-based smart objects. When tackling the computational efficiency problem, Kumar et al. [
6] did not select bilinear pairing operations either. Instead, they proposed a lightweight digital signature scheme based on quadratic residual theory and proved the security of the scheme under the standard model. The solution, based on the intrusion detection system (IDS), authenticates the crowdsensing data acquired from IoT environment. Meanwhile, to meet security requirements of data integrity and authenticity in IoT environment, Yang et al. [
4] proposed a certificateless signature scheme. Based on the collision resistant hash function and computational Diffie-Hellman (CDH) assumption, Yang’s scheme was proved to be highly unforgeable under adaptive chosen message attacks in the standard model.
Computing power, battery capacity, and storage resources are the important factors that limit IoT capabilities [
2]. In IoT, such as SIoT [
8,
9,
10] and WIoT [
3], hundreds and thousands smart objects are connected. A large number of applications are many-to-one. That is, multiple data senders and one data receiver.
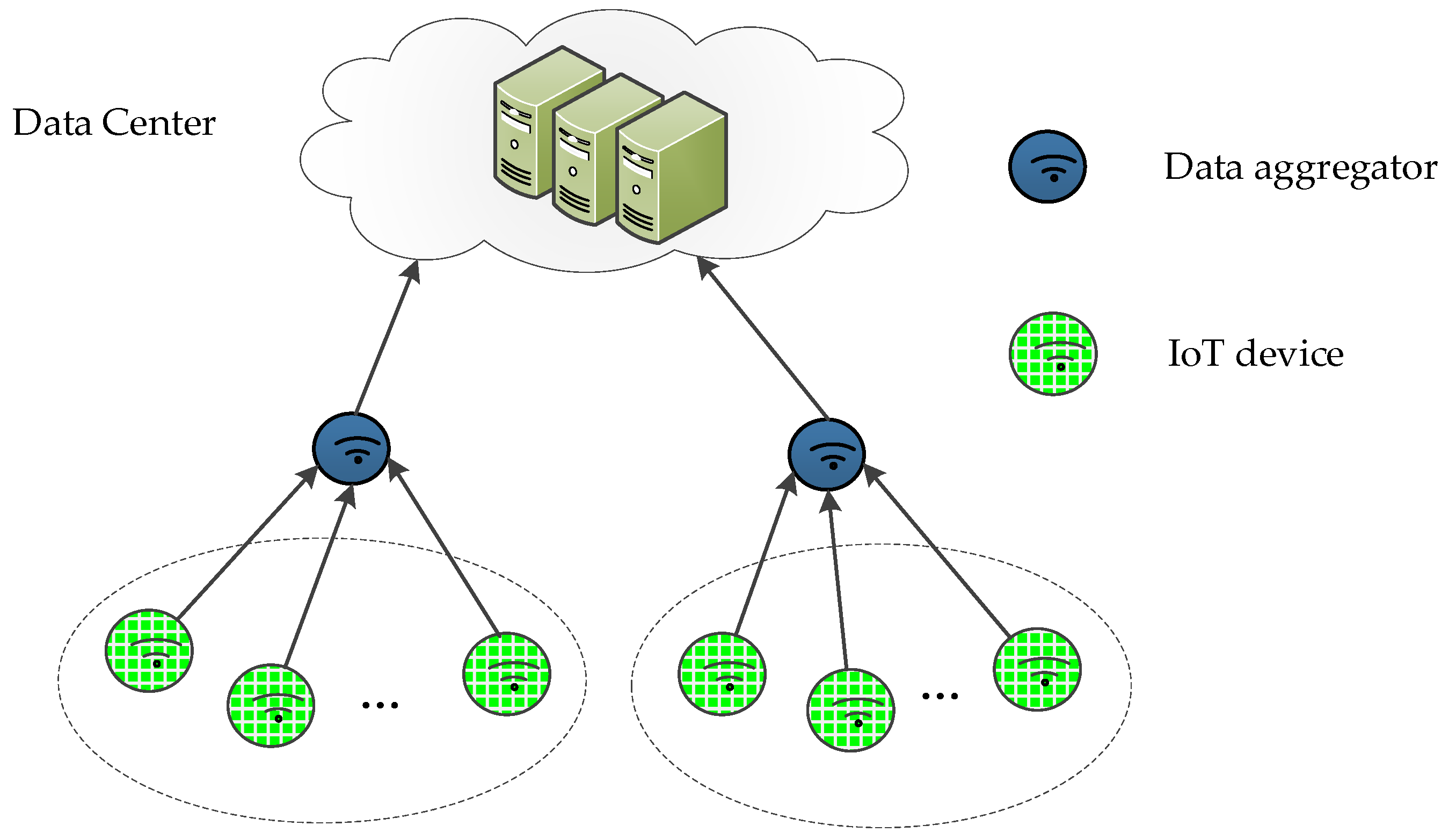
Figure 1 shows the many-to-one IoT scenario. In the scenario, smart objects generate or collect information from the physical world and pass data from one node to the other. Finally, the receiver aggregates IoT data and sends it to data center. In the case of smart health, a patient can generate multiple medical records. Some medical records, blood pressure, blood sugar, heart rate, etc., are generated from wearable devices. Other medical records such as medical orders and prescriptions, are from medical personnel. Considering the integrity and authenticity of medical data, each individual medical record should be signed by the corresponding responsible entity. Consequently the digital signatures on different medical data will map to one patient (many-to-one). Aggregate signature can compress the digital signatures of different messages into one short digital signature, thus saving storage space and improving computational efficiency. It is very suitable for IoT applications such as vehicular ad-hoc network, smart grid and wireless sensor network with limited bandwidth and computational resources. This nature of aggregate signatures has attracted interests of more and more scholars [
11,
12,
13]. Pankaj Kumar et al. [
11] proposed a certificateless aggregate signature scheme for medical wireless sensor networks. This scheme features certificateless cryptosystem and aggregate signature, and preserves privacy, non-repudiation and integrity of medical wireless sensor networks. In regard to vehicle-to-infrastructure (V2I) communication in vehicular ad hoc networks, Horng et al. [
12] proposed a certificateless aggregate signature. It implements conditional privacy preservation through pseudo identity. Another aggregate signature scheme was proposed by Shen et al. [
13] for wireless sensor networks based on identity-based cryptography. That solution has been proved resistant to coalition attacks, capable to reduce energy consumption and ensure security for data acquisition, processing and transmission in wireless sensor networks.
The motivation of our study is to find a solution to identity authentication and integrity verification in many-to-one IoT scenarios where device resources are limited, such as smart health, vehicular ad hoc networks and smart grid et al. In these applications, traditional encryption, authentication and cryptographic algorithms can severely reduce the efficiency of small embedded devices and increase their power consumption. However, secure hash function and lightweight aggregate signature algorithm can effectively solve the problem of battery capacity, computing power and storage capacity limitation while fulfilling security requirements. Therefore, we propose an aggregate signature scheme based on multi-trapdoor hash function in this paper.
The contributions of this paper are as follows:
Based on ECDLP, we constructed a double trapdoor hash function and a multi-trapdoor hash function respectively. Batch trapdoor collision computation of multi-trapdoor hash function can improve the efficiency of aggregate signature.
An aggregate signature scheme based on MTH is proposed. With Forking Lemma, the proposed scheme is proven to be secure against the existing unforgeability on adaptively chosen message attacks.
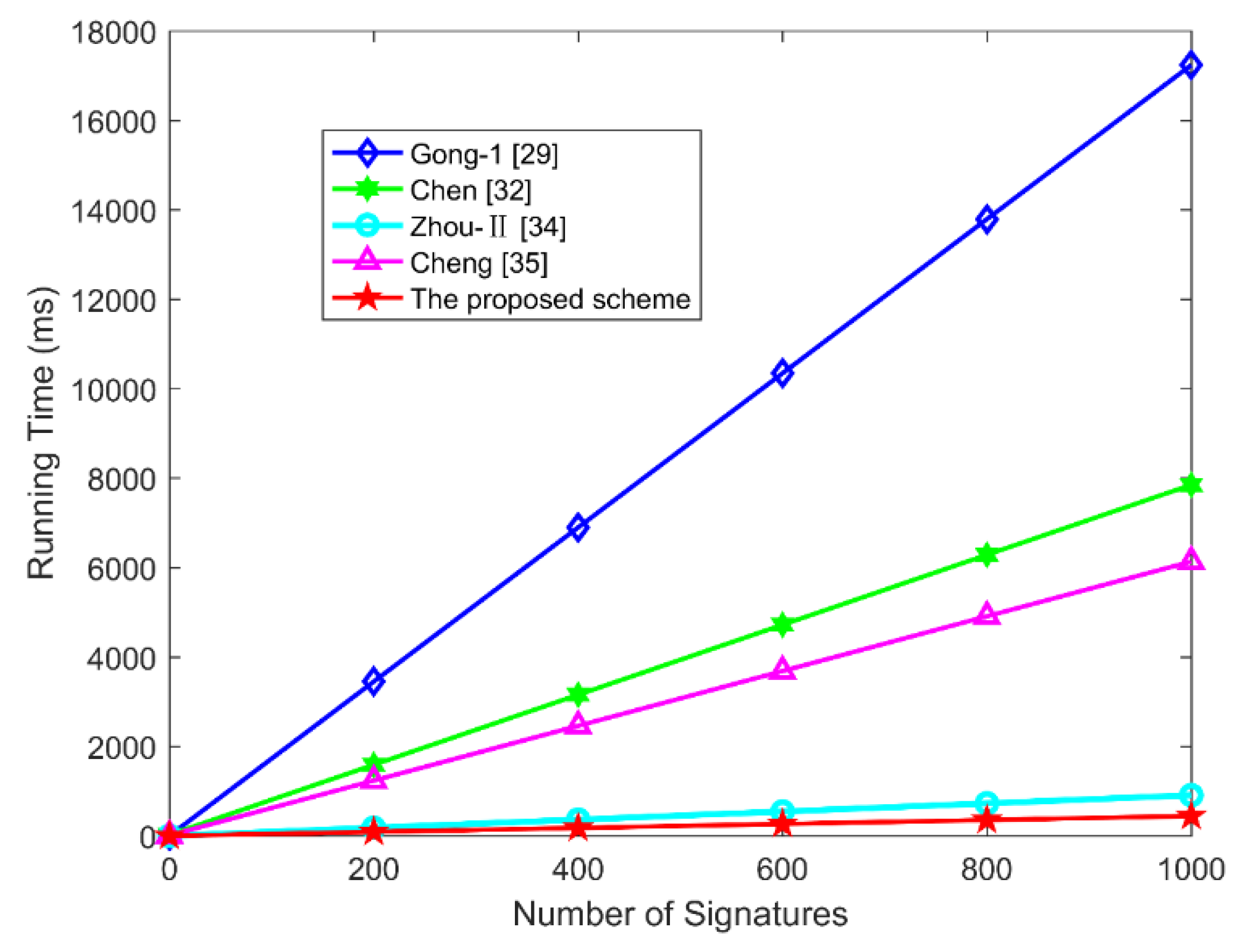
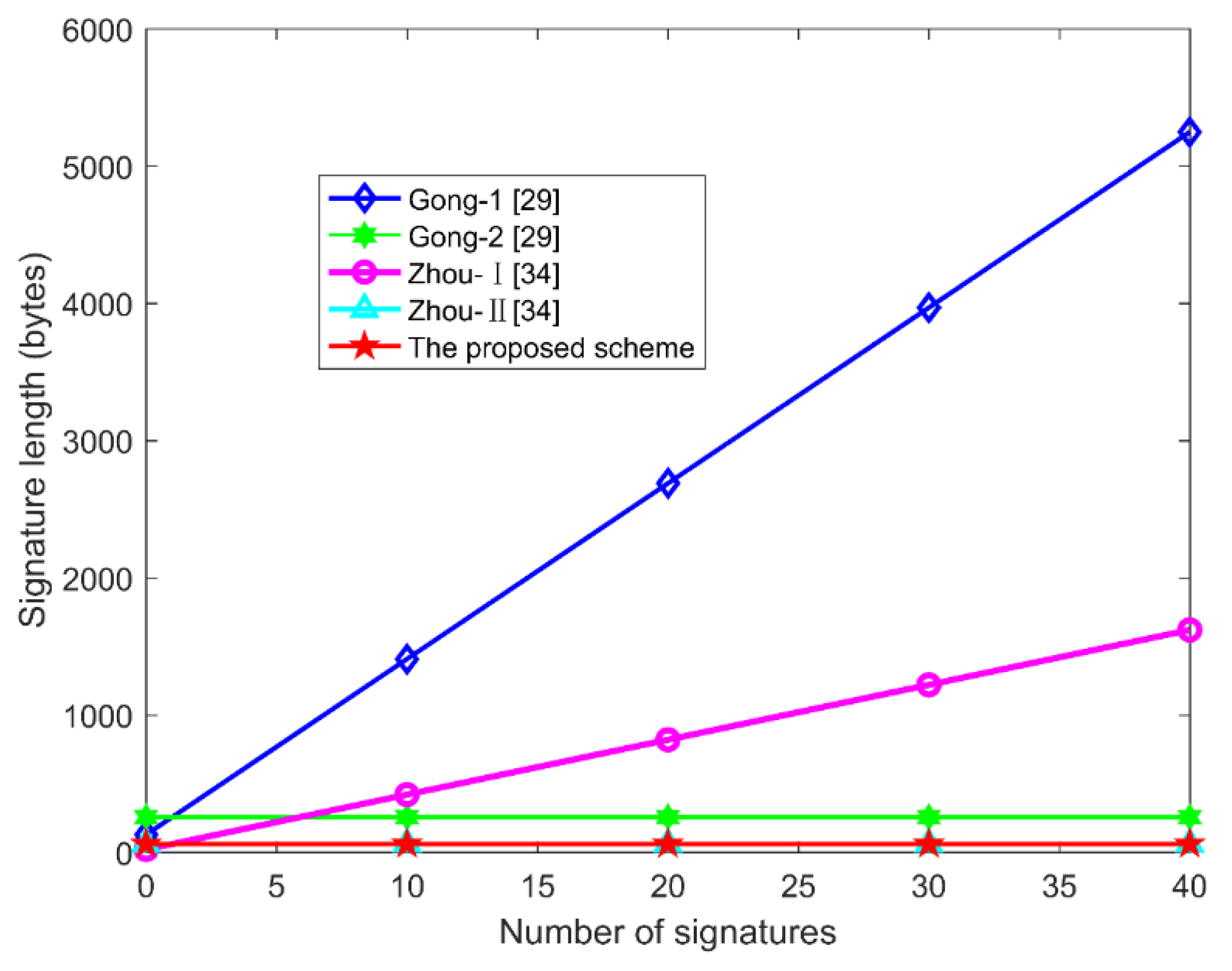
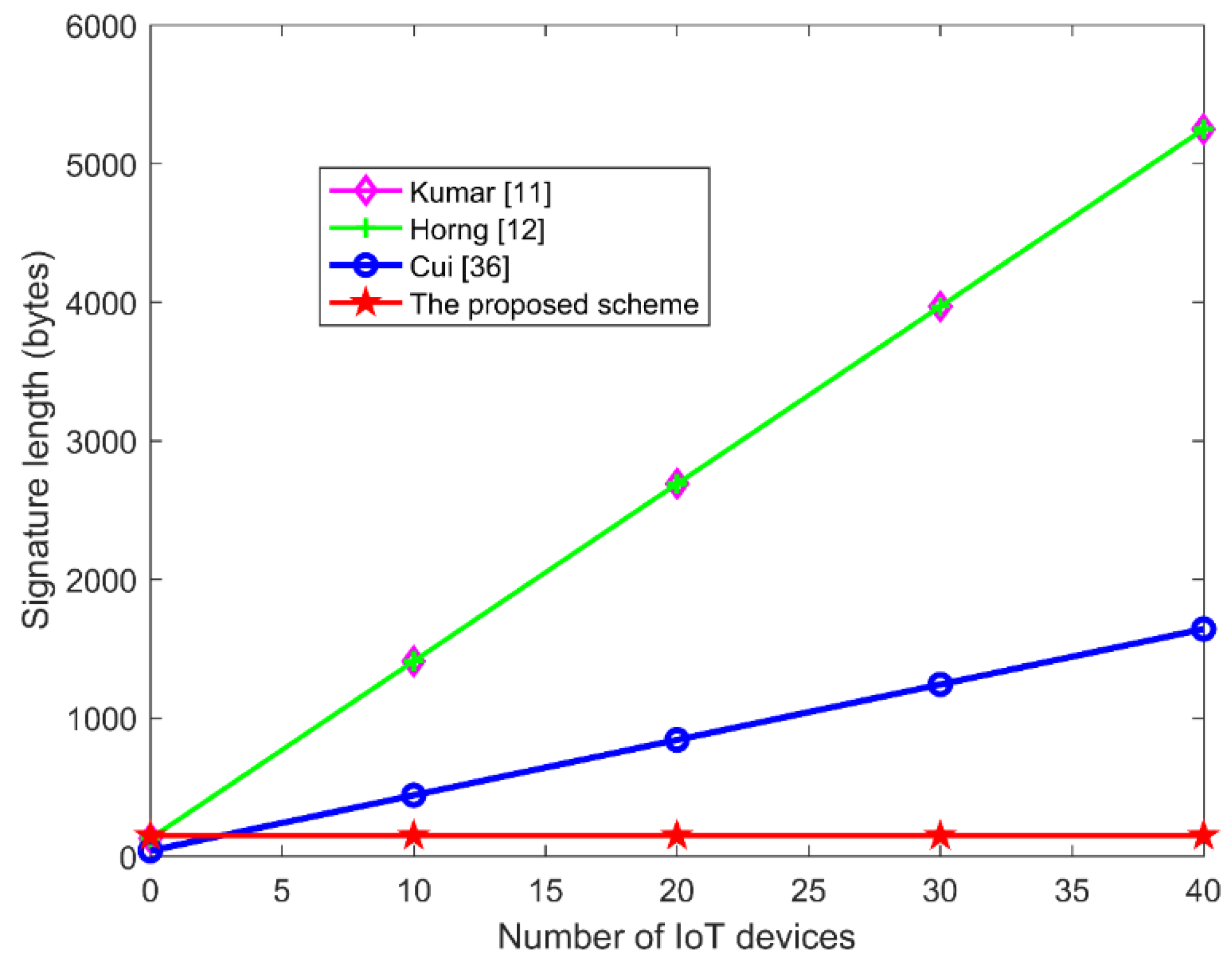
Compared with other bilinear pairings-based schemes, our ECC-based scheme is more efficient in terms of computational overhead. On the other hand, our MTH-AS scheme has the advantage in storage capacity because the length of the proposed aggregate signature is a constant.
Due to the above performance, our MTH-AS scheme is suitable for secure IoT applications with limited computing power, storage capacity, and bandwidth.
The rest of this paper is organized as follows.
Section 2 discusses the relevant works. The necessary preliminaries and system model are given in
Section 3.
Section 4 presents the ECDLP-based double trapdoor hash scheme DTH.
Section 5 describes the ECDLP-based multi-trapdoor hash function MTH. Thereafter, we demonstrate the MTH- based aggregate signature scheme for IoTs and carry out performance comparison in
Section 6. Finally, the conclusion is offered in
Section 7.
2. Related Work
Hash functions are one-way and collision resistant. Being a special type of hash function, trapdoor hash function [
14] is related to the concept of trapdoor commitment [
15]. The trapdoor hash function uses some special information (the trapdoor information) to produce a fixed hash value. People who know the trapdoor information open the trapdoor commitment in different ways, thus opening different collisions [
15]. That means, the owner of the trapdoor can calculate the trapdoor collision.
Krawczyk et al. [
14] first proposed the trapdoor hash function in order to construct chameleon signatures. Thereof, many digital signature schemes were developed based on chameleon signatures. One of the most representative schemes was a solution proposed by Shamir et al. [
16] for online/offline signatures. The scheme could resist the adaptive chosen message attacks. However, it encountered key exposure problems of the chameleon hash. That is because collision calculation would lead to exposure of trapdoor information. Focusing on solving this problem, Chen et al. [
17] and Atteniese et al. [
18] proposed trapdoor hash schemes without key exposure. In 2008, Chen et al. [
19] introduced a special double trapdoor hash scheme. This scheme features two trapdoors, long-term trapdoor and temporary trapdoor. It guarantees the safety of long-term trapdoor at the cost of temporary trapdoor leakage.
Chandrasekhar and Singhal et al. [
20,
21,
22,
23] carried out in-depth study on trapdoor hash function. Based on discrete logarithm, Chandrasekhar et al. [
20] proposed a multi-trapdoor hash function without key exposure. This scheme had multiple trapdoors corresponding to different entities. It was suitable for constructing multi-party digital signatures. Chandrasekhar et al. [
22] put forward the concept of aggregate signcryption. They proposed a new efficient scheme of aggregate signcryption which could generate the aggregate signcryption text of constant order. The new scheme combined multi-trapdoor hash function with decomposable multiplicative homomorphism ElGamal encryption while providing confidentiality, integrity and identity authentication for many-to-one communication scenarios.
The conception of aggregate signature was first proposed by Boneh et al. [
24] in 2003, which has played a significant role in promoting digital signature cryptography technology. Based on trapdoor permutations, sequential aggregate signature was proposed by Lysyanskaya et al. [
25] in 2004. In this scheme, before adding his own signature, every signer has to verify all the previously aggregated signatures. It is, however, not suitable for the situation where the signers operate independently of each other. Accordingly, Brogle et al. [
26] improved it with the idea of "lazy verification". Their scheme does not require the signer to know the public key of other signers, but the length of the signature grows linearly when the number of signers increases. In order to reduce the interaction between signers, a synchronous aggregation signature scheme with a synchronous clock was proposed by Ahn et al. [
27]. The scheme allows a signer to sign at most once in each period of time, and only the signatures in the same period can be aggregate. However, the computation cost is relatively high.
The identity-based aggregation signature scheme proposed by Gentry et al. [
28] does not require to store the public key of each signer. The purpose is to minimize the total amount of information for verification. However, it requires an additional trusted third party (e.g., key generation center).
Certificateless aggregation signature has the characteristics of keyless escrow in certificateless cryptosystem and relatively low computation and communication overhead in aggregation signatures. That’s why some relevant scholars have made in-depth research on it [
29,
30]. In 2007, Gong et al. [
29] firstly proposed two certificateless identity-based aggregation signature schemes. But there were shortcomings in respect of signature length and verification efficiency. Zhang et al. [
30] introduced a certain improvement in computation efficiency. In Zhang’s scheme, the verification process, not reliant on the number of aggregate signatures, requires a small set of a constant number of pairing computations. However, the generation of aggregate signatures requires assistance of a synchronous clock.
With the Forking Lemma [
31], the scheme proposed by Chen et al. [
32] was proven strong security based on the hardness of computational Diffie-Hellman problem (CDHP). It makes use of the bilinear pair and state information. However, the length of signature grew with the number of signers. The scheme proposed by Li et al. [
33] drew on the state information of Chen et al. [
32]. It was existentially unforgeable against adaptively chosen message attacks without the Forking Lemma. The scheme provides fixed-length aggregate signatures. Zhou et al. [
34] and Cheng et al. [
35] effectively compensated for the shortcomings of the above two schemes [
32,
33] by using elliptic curve discrete logarithm problem (ECLDP). Zhou et al. [
34] proposed two certificateless aggregate signatures CLAS-1 and CLAS-2, which were proven unforgeable by the discrete logarithm problem (DLP). Compared with CLAS-1, information sharing was used in CLAS-2 to aggregate partial signatures in advance. CLAS-2 provides shorter constant-level signature lengths than CLAS-1. Cui et al. [
36] applied the certificateless aggregation signature scheme to vehicle ad hoc network, and used pseudo-identity to provide privacy preservation for vehicle information. The scheme has high computation efficiency. However, the length of signature is related to the number of signers.
Among the above-mentioned schemes, the aggregate signature lengths of the schemes [
26,
32,
35,
36], CAS-1 [
29], and CLAS-II [
34] increase linearly with the number of signers and they are only suitable for low bandwidth network environments. Meanwhile, the schemes [
24,
29,
32] based on bilinear pairs having no advantage in the computational performance because the time overhead of bilinear pair operations is relatively high [
7]. The comparisons of relevant aggregate signatures are shown in
Table 1.
3. Preliminaries
3.1. Symbolic Representation
The symbols used in the proposed scheme are shown in
Table 2.
3.2. Double Trapdoor Hash Function
Different from other hash functions, trapdoor hash function is a probability function with the hash key and the trapdoor key <
HK,
TK >. The collision resistance of the trapdoor hash functions depends on the user’s knowledge state [
16]. When both
TK and
HK are known, it is easy to calculate the trapdoor collision. That is to say, when only
HK is known, it is difficult to find two different messages
M and
M′ in the message space, and two different auxiliary parameters
R and
R′, which satisfy
. However, when both
TK and
HK are known, it is easy to calculate
R′ based on
M,
M′ and
R such that
.
In trapdoor hash function, the calculation of the collision causes the trapdoor key to leak, which is called key exposure. In chameleon signature, the exposure of the trapdoor key affects its transitivity. In online/offline signature scheme, key exposure will result in anyone being able to forge the signature. A hash function without key exposure usually has two trapdoors, i.e., a long-term trapdoor and a temporary trapdoor. Collision calculations only expose the temporary trapdoor, thus preventing the long-term trapdoor key from leaking.
Different from the traditional trapdoor hash function family [
16], the trapdoor hash function [
20] proposed in this paper is a variant of the double trapdoor hash function family [
21], using the temporary key pair <
HK′,
TK′ > to generate trapdoor collisions.
Definition 1. Trapdoor hash function consists of four probability polynomial time (PPT) algorithms < ParGen, KeyGen, HashGen, TrapColGen >.
ParGen: Inputs security parameter k, outputs system parameters Params;
KeyGen: Inputs Params, outputs < HK, TK >;
HashGen: Inputs Params, message M, and auxiliary parameter R, and outputs the trapdoor hash value ;
TrapColGen: Inputs Params, < HK, TK >, M, R, and new message M′(≠M), and outputs new auxiliary parameter R′ and the temporary hash key HK′ such that:
When HK ≠ HK′, < HK′, TK′ > and < HK, TK > are called temporary hash/trapdoor key pair and long-term hash/trapdoor key pair respectively. The properties of double trapdoor hash functions are as follows:
- (1)
Validity: Given HK and (M, R), is calculated in polynomial time.
- (2)
Collision resistance: Given HK, there is no PPT algorithm that can find HK′ which satisfies: - (3)
Trapdoor collision: There is a PPT algorithm, given < HK, TK >, (M, R) and new message M′ ≠ M, output HK′ and R′ such that: - (4)
Key exposure freeness: Given the long-term hash key HK, temporary hash key HK′, and (M, R), (M′, R′), M′ ≠ M, there is no PPT algorithm to output long-term trapdoor key TK with non-negligible probability.
3.3. Elliptic Curve Discrete Logarithm
Definition 2. (Elliptic curve discrete logarithm problem (ECDLP) [37]). E(Fl) is an elliptic curve over the finite field Fl. And P is a q-order generator of E(Fl), when and Q = kP, find the integer k (0 ≤ k ≤ q−1). This definition is also known as the onewayness of ECDLP. The probability that algorithm successfully solves ECDLP is defined as: It is determined by the random selection of and .
3.4. Aggregate Signature
Aggregate signatures consist of PPT algorithms: AS = < Setup, KeyGen, Sign, Verify, Aggregate, Aggregate Verify >. And the tuple < Setup, KeyGen, Sign, Verify > constructs a standard system parameter establishment, key generation, signature, verification of the short signature process, called the standard signature of aggregate signature.
Setup: Inputs security parameter k, outputs system parameter Params.
KeyGen: For a particular (U is a user set), inputs system parameter Params, then outputs the private and public key < y, Y >.
Sign: For a message Mi to be signed, inputs private key , outputs individual signature .
Verify: Inputs public key Yi, message Mi, and individual short signature , if the verification algorithm is successful, it outputs ACCEPT, otherwise, it outputs REJECT.
Aggregate: Inputs , their signature messages and individual signatures , outputs aggregate signature .
Aggregate Verify: Inputs public keys , messages , and aggregate signature , if the aggregation validation algorithm is successful, it outputs ACCEPT, otherwise, it outputs REJECT.
3.5. Security Model
Assuming k is a security parameter, is a game between challenger and adversary . The attack model is shown below:
Setup
Inputs the security parameter k, runs the Setup algorithm and returns the system parameter to .
Query
adaptively performs the following oracle query.
- –
Hash queries: makes hash oracle queries to all hash functions in the proposed scheme, and challenger returns the corresponding value.
- –
Trapdoor hash queries: inputs < m, r > for trapdoor hash query and the oracle outputs .
- –
Key queries: inputs the message of user i to make key query, and the oracle returns the trapdoor key y of user i to the adversary .
- –
Signature queries: inputs the original message/random value pair , new message and hash key , the oracle outputs the signature.
Forge
Finally, outputs as a forged aggregate signature based on new message set .
The adversary wins the game if is a valid signature and does not make a key query on at least one user among n users.
3.6. System Model
In many-to-one IoT scenarios where bandwidth, computing power, and storage resources are limited, it is important to improve computational efficiency and storage capacity. Furthermore, it is also vital to protect data from modification and repudiation. Due to its natural compression properties, aggregate signatures are ideal for resource-constrained many-to-one IoT applications. As shown in
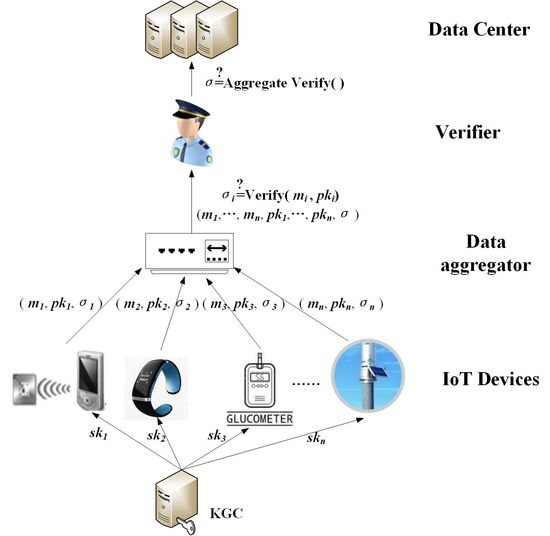
Figure 2, the system model of the aggregated signature in the IoT environment proposed in this paper consists of five components: the key generation center (KGC), IoT devices, data aggregator, verifier and data center.
• KGC
The KGC is responsible for system setup. It is regarded to be trusted in our proposed scheme. The KGC generates system parameters and sends them to all the entities, such as IoT devices, aggregator, verifier and data center. The private keys are computed by the KGC for each IoT device. Then these private keys are sent to each entity through a secure channel.
• IoT Devices
The IoT devices with limited computational and storage capacity are capable to collect real data from the physical world. In order to ensure data integrity, non-repudiation, privacy, and authenticity, with the system parameter and the private key, each IoT device makes individual signature on the original data they collect. Then the IoT devices send message , individual signature and public key to the data aggregator.
• Data aggregator
The data aggregator may be a node in the system model that verifies all the individual signatures it receives. It checks the validity of the individual signatures, if they are correct, then aggregates them into a single short signature. Finally, the data aggregator sends the aggregate signature to the verifier.
• Verifier
The verifier are responsible to check the correctness of the received aggregate signature. It can verify the correctness of all individual signatures by one operation. If the aggregation signature is verified correctly, all the messages and the aggregate signature are sent to the data center.
• Data Center
The data center has powerful storage space and computing power, which can store and share the validated aggregate signatures and original messages safely.