1. Introduction
Accurate determination of moisture content of grains is of great importance in grain trading, transportation, storage, and processing. Especially during storage, grain moisture plays an important role in the safe storage of grains [
1,
2]. Using the convection oven to dry the grain and measuring the loss of mass to determine the grain moisture is the standard method of grain moisture measurement in several countries because of its high precision and high reliability [
3,
4,
5], however, it has obvious disadvantages of being time-consuming and cumbersome. In order to achieve fast and precise moisture determination, many studies have been conducted to determine the moisture of grains by using near-infrared reflection methods [
6,
7,
8]. However, the penetration depth of infrared is shallow, and the measured result is easily affected by ambient light and impurities attached to the grain particles, therefore, the method is most often applied to grain moving on a conveyor belt in a processing plant, where the layer of grain is thin and the environment is relatively clean [
9].
With good penetrability, the microwave has been widely studied for measuring the moisture of grain [
10,
11,
12]. Microwave method indirectly calculates the moisture content of grain by measuring the complex permittivity, which is related to grain moisture. The complex permittivity is intrinsic properties of grain, and it is usually expressed as
. The real part
is called dielectric constant, and the negative number of the imaginary part
is called the loss factor. The complex permittivity of grain is the equivalent complex permittivity of a mixture of grain kernels and air. When the grain kernels’ size is much smaller than the wavelength, the mixture is an effective medium, which means grain can be regarded as a homogeneous medium. The size parameter can be used to evaluate the size of grains relating to the wavelength, which is defined as
, where
is the radius of particles and
is the wavelength [
13]. Taking wheat as an example, the maximum radius of the grain kernels is less than 4 mm [
14]. For electromagnetic waves with a frequency less than 4.8 GHz, the wavelength is greater than 62.5 mm. Consequently, the size parameters of grains were less than 0.4. It means that the grain kernels are small enough relative to the wavelength to gain as a homogeneous medium described by one complex permittivity. Besides, the influence of bulk density on measured results was a main problem faced by microwave grain moisture measuring technology. Fortunately, the dielectric constant and loss factor of grain were both related to the moisture content and the bulk density. Consequently, two equations can be established. One describes the relationship among the dielectric constant, the moisture content, and the bulk density. The other one describes the relationship among the loss factor, the moisture content, and the bulk density. Combining the two equations to eliminate the bulk density term, an equation can be obtained for calculating grain moisture from the dielectric constant and the loss factor. Based on the idea and many experimental data, Trabelsi et al. [
15,
16,
17] have proposed a density-independent calibration function as Equation (1) and a temperature compensation function as Equation (2):
where
is a density-independent calibration function, which is independent of the bulk density and is linearly related to the moisture content and temperature. At any given frequency, the value of
depends only on the grain complex permittivity.
is a frequency factor, which is related to the microwave frequency. It is a constant for a given grain sample at a given frequency. In the literature [
15], the linear relationship between expressions
and
was found.
is the bulk density. The parameter
was obtained from a complex plane consisting of
and
, and the parameter
equaled the slope of the linear regression function of
and
.
is temperature (°C),
is the percentage of moisture (wet basis).
,
and
are three undetermined coefficients. The model has been proven effective for the moisture determination of wheat, corn, soybeans, and peanuts (with a standard error of less than 0.97%) [
1]. In particular, a shelled peanut moisture determination device was developed by using free-space method (the standard error less than 0.55%), and successfully applied it in the peanut drying field [
18,
19,
20,
21]. The free space method can be used to calculate the complex permittivity of grain by measuring the attenuation and phase change of the microwave propagated through the grain. In this condition, only the microwave which transmits through the grain was related to the permittivity of grain. If the size of transverse of the sampler holder is not large enough, there will be great diffraction at the edges of the sample holder. A large part of the microwave energy will pass through the edges of the sample holder instead of penetrating it. To prevent the diffraction at the edges of the sample holder and the multiple reflections in the sample holder, the size of the cross-section and the thickness of the sampler holder must be large enough. The sizes of the sample holder in their studies [
20,
21] were 22.2 cm × 13.3 cm × 21.9 cm (4.5 L) and 4.4 cm × 4.4 cm × 12 cm (243 mL), respectively. This makes the measuring device bulky and difficult to carry, limiting its scope of application.
The open-ended waveguide technique is a type of microwave reflection method. Due to the different impedances between the sample and the waveguide, the discontinuous impedance at the interface between the waveguide and the measured object will cause microwave reflection. The intensity and phase of the reflected microwaves are related to the impedance of the sample, and the impedance of the sample is related to its complex permittivity. As a result, the measurement of the complex permittivity of the sample can be achieved by measuring the reflection coefficient of the microwaves at the interface between the waveguide and the sample. During the measuring process, no diffraction phenomenon exists, and only a small volume of sample can achieve the measurement. Consequently, compared to the free space method, the open-ended waveguide reflection method is very suitable for miniaturizing the sensor. The open-ended coaxial waveguide [
22], the open-ended circular waveguide [
23], the open-ended rectangular waveguide [
24], and the open-ended substrate integrated waveguide (SIW) [
25] are usually adopted. The SIW can be regarded as a rectangular waveguide, which has the advantage of small size. Compared to the open-ended circular waveguides, the open-ended rectangular waveguides, and the open-ended SIW, the open-ended coaxial waveguides have two outstanding advantages. First, the open-ended coaxial waveguide has no cut-off frequency, so it is especially suitable for wideband measurements. Secondly, the structure of the open-ended coaxial waveguide is the same as the coaxial cable. When the waveguide connects the coaxial cable, the connector is easy to be designed and manufactured. Using the circular waveguide or the rectangular waveguide needs to design the impedance matching structure and the electromagnetic field excitation structure for connecting the coaxial cable. Currently, the open-ended coaxial waveguide is widely used in liquid broadband complex permittivity measurement [
26,
27,
28].
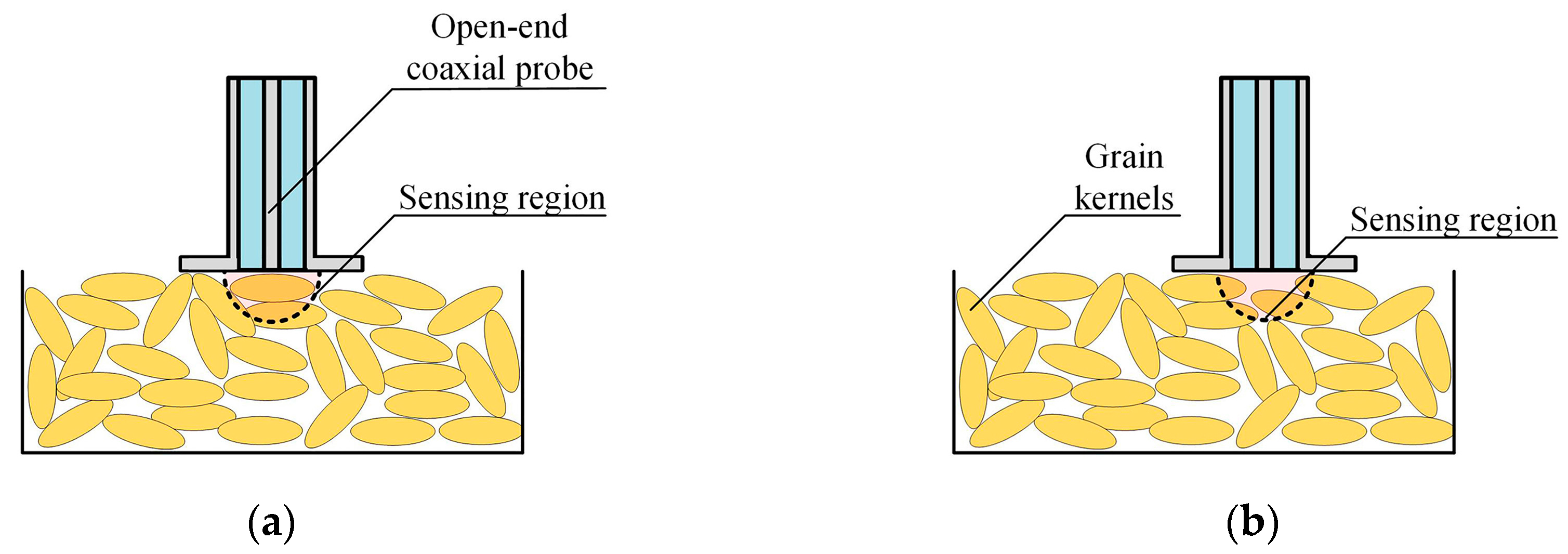
However, there are many problems in applying the open-ended coaxial waveguide directly to the grain moisture measurement field. Firstly, the existing open-ended coaxial waveguide can only be applied to small-sized particles. The size of the grain kernel is too large for the small sensing region of the open-ended coaxial probe. The complex permittivity of grain is the equivalent complex permittivity of a mixture of grain kernels and air. If the volume ratio of grain to air in the sensing region is different from the actual ratio, the measurement will have a large error. As shown in
Figure 1a, when the volume ratio of grain to air in the sensing region is larger than the actual ratio, the measured complex permittivity will be larger than its actual value. As shown in
Figure 1b, when the volume ratio of grain to air in the sensing region is smaller than the actual ratio, the measured complex permittivity will be smaller than its actual value. Since the volume ratio of grain to air in the sensing area is random, the measured complex permittivity is significantly unstable. This makes the method unusable for grain. Therefore, small size of the sensing region is the primary problem in applying the open-ended coaxial probe to the field of grain moisture measurement. The sensing region increases as the radius of the outer conductor increases [
29], so the sensing region can be expanded by adjusting the dimensions of the open-ended coaxial probe. In addition, another waveguide which connects with the coaxial waveguide can be designed to modify the impedance of the microwave in the grain. With proper dimensions, there will be more microwave energy entering the grain from the coaxial waveguide. Consequently, the depth of the sensing region can become larger. In this paper, by expanding the outer conductor radius of the coaxial waveguide and loading the grain sample in a circular waveguide, the expansion of the sensing region was realized. As a result, the improved open-ended coaxial probe can be suitable for the field of grain moisture measurement. Secondly, the environment (such as the ground, container) easily affects the measurement. Fortunately, the grain sample was loaded in a circular waveguide in this paper, and the metal boundary can prevent the measurement from the interference of the environment. Thirdly, the traditional coaxial probe models are not suitable. There are capacitive, quasi-static, and Taylor-series models to describe the relationship between the complex permittivity and the admittance of the coaxial end face [
30]. However, these models are proposed under two hypotheses. One is an infinitely large grain sample is filled in a half-space to avoid reflection signals affecting the measurement. This is impractical for the grains which have small dielectric constants and low loss factors. The other is that only one microwave mode—transverse electromagnetic mode (TEM)—exists in the open-ended coaxial probe. Although the open-ended coaxial probe is designed to fit single-mode transmission conditions, the high-order mode will be generated due to the discontinuity of impedance at the end face of the coaxial waveguide. These high-order modes have a great influence on the measurements. To solve this problem, the mode matching method [
31], an effective approach for analyzing the characteristics of microwaves in discontinuous waveguides, was adopted to build the model.
In this paper, a novel, portable, and fast grain moisture content measuring method is proposed, which overcomes the problems of the open-ended coaxial waveguide application in the grain moisture measurement field. Firstly, a grain moisture sensor was designed by combining the coaxial waveguide with a circular waveguide. The circular waveguide can be used as a sampler or the sample holder, and it can prevent the measurement from the environmental interference. Secondly, based on the mode matching method [
31], a new model was developed, which could precisely describe the relationship between the complex permittivity of grain and the reflection coefficient of the sensor. As the grain moisture increased, the real part and the absolute value of the imaginary part of the complex permittivity increased, and the magnitude of the corresponding reflection coefficient decreased and the phase decreased. Thirdly, a broadband reflection coefficient measuring method by using the ultra-wideband (UWB) radar module was proposed. Finally, taking wheat, rough rice, and barley as examples, the accuracy and stability of the method were verified. In addition, the paper discussed the influence of the pressure of the sensor on the accuracy of the proposed method.
2. Method
2.1. Design of the Grain Moisture Sensor
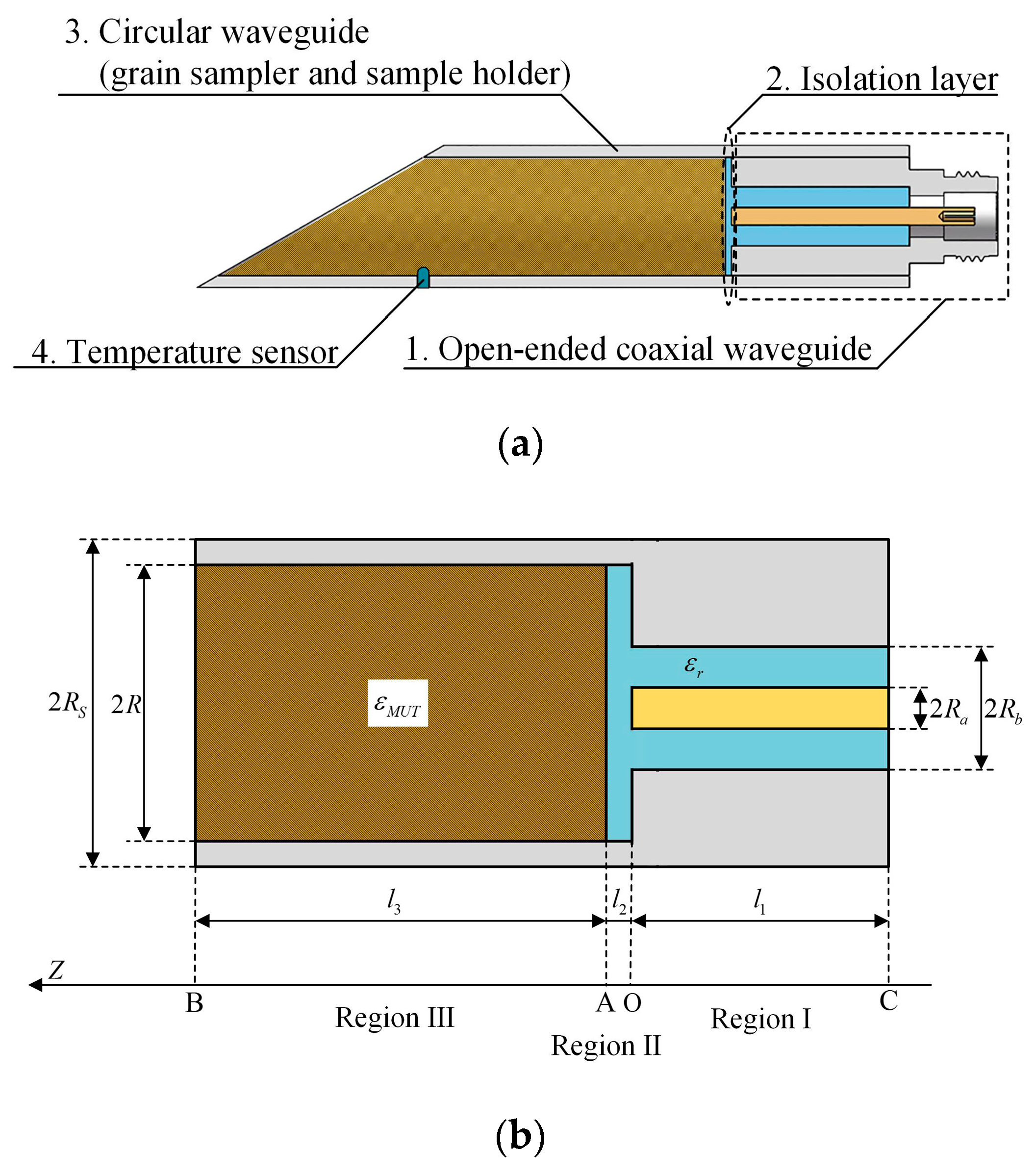
Due to the wide bandwidth, no diffraction and simple structure of the open-ended coaxial waveguide, a novel grain moisture sensor was designed. The sensor combined a circular waveguide (grain sampler and sample holder) with the open-ended coaxial waveguide in order to make the sensor suitable for grain moisture measurement in field condition. The schematic of the sensor is shown in
Figure 2 and the dimensions are shown in
Table 1. The sensor consisted of an open-ended coaxial waveguide, a circular waveguide, an isolation layer, a temperature sensor, and the type-N microwave connector. The sensor’s main features were as follows:
The open-ended coaxial waveguide. The type-N microwave connector was directly connected to the open-ended coaxial waveguide. The inner conductor was made of gold-plated brass, the outer conductor was made of 304 stainless steel, and the gap between inner and outer conductors was filled with Teflon. Since the dielectric constant of Teflon is approximately a constant (
) over wideband [
32], using Teflon to fill the gap can easily make the impedance of the coaxial waveguide be a constant over a wide range of frequency. The dimensions were chosen to make the characteristic impedance equal to 50 Ω and only TEM mode can transmit in the frequency range of 0-5 GHz.
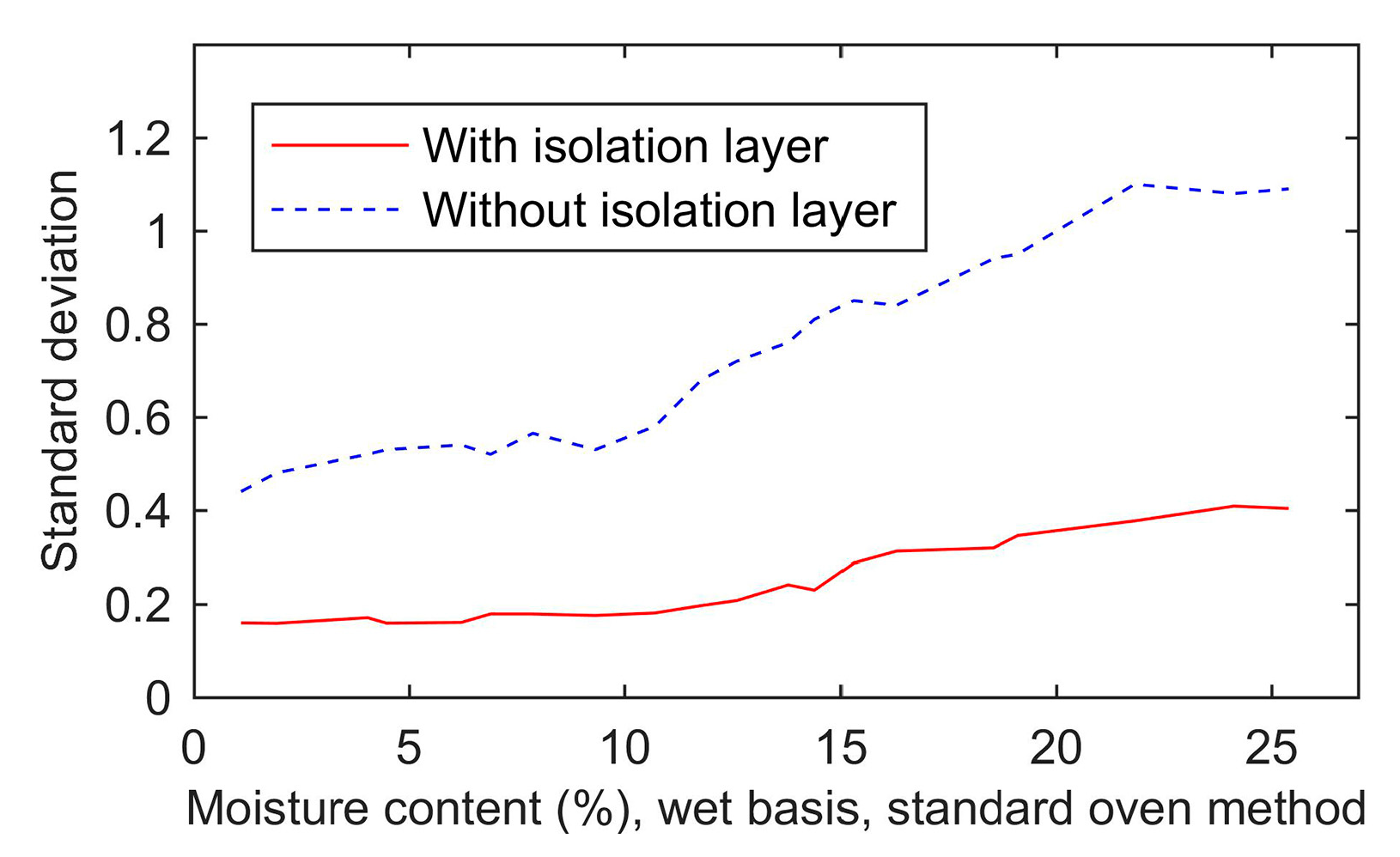
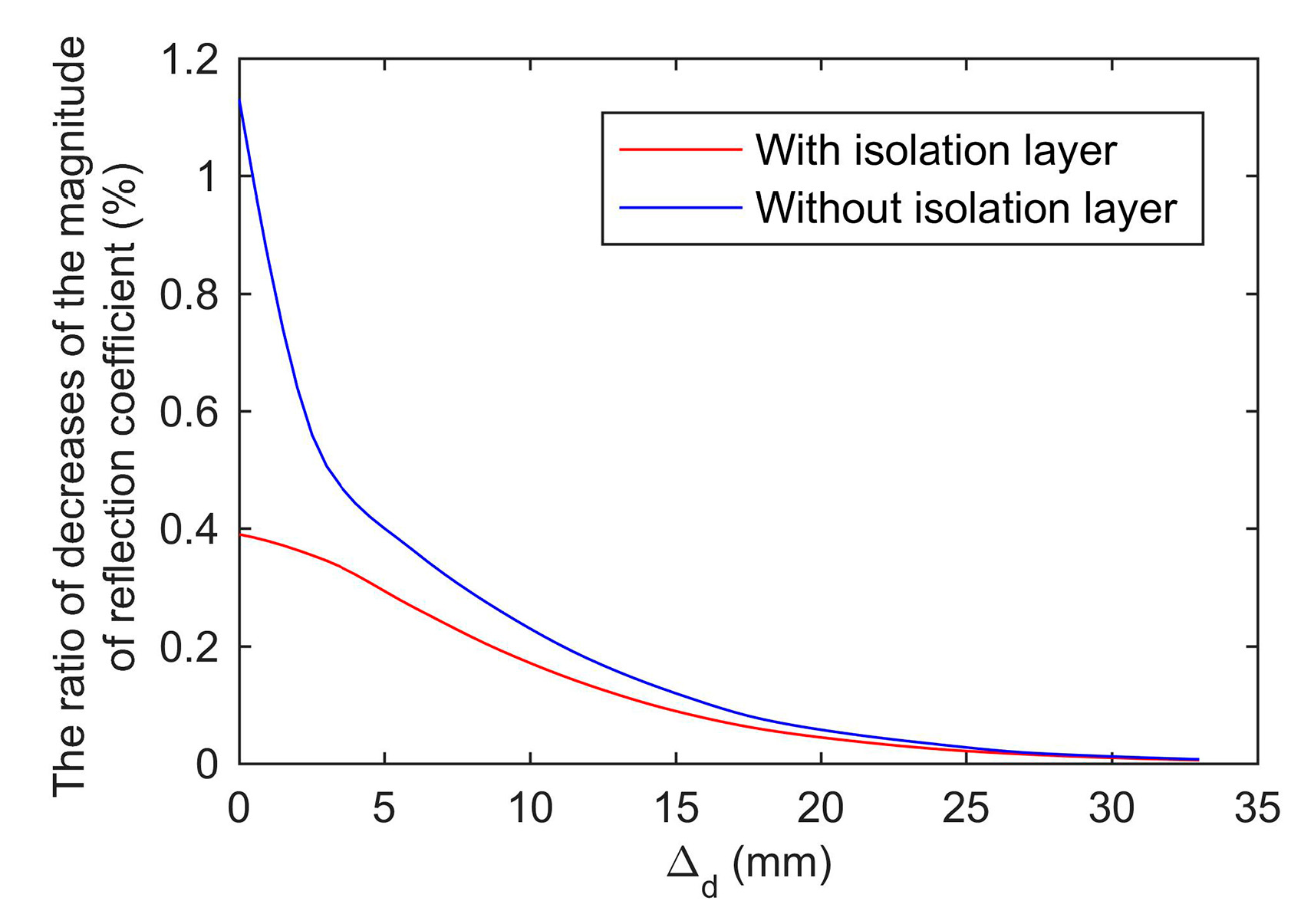
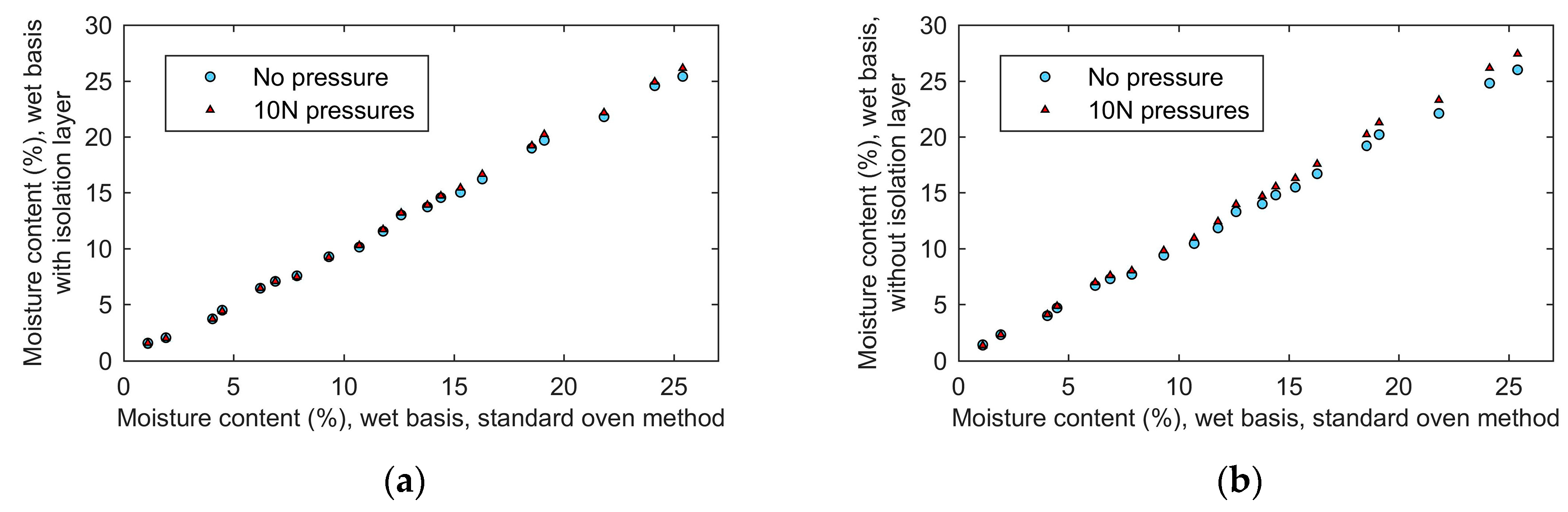
The isolation layer. The end face of the coaxial waveguide was covered with an isolation layer, which was made of Teflon. The isolation layer had two functions. First, it can protect the plating of the inner conductor. The conductivity changes can be avoided in long-term use thus improving the stability of the sensor. Second, it can improve the accuracy. Without the isolation layer, a conductive path will be formed between the inner and outer conductors through grain kernels. Unfortunately, the characteristic of the path is uncertain, because of the random distribution of grain kernels. As a result, without the isolation layer, there will be a large standard deviation in the measurement of the same sample.
The circular waveguide (grain sampler and sample holder). The circular waveguide was made of 304 stainless steel tubing, which was connected to the open-ended coaxial waveguide. The front of the circular waveguide was cut to 30 degrees, which made it easy to insert into the grain. The inner diameter was designed to make all microwave modes attenuate in the frequency range of 0-5 GHz. This allowed the electromagnetic field to exist in a limited region. Consequently, the measurement needs a small amount of grain sample, and the environment outside does not affect the test results. This can improve accuracy. The volume of the sampler was about 30 mL. Consequently, our proposed method only needs 30 mL grain to complete the measurement. Besides, the circular waveguide can be used as a sampler and the sample holder, since the inside of the circular waveguide was empty. This can make the sensor more convenient to use. Instead of sampling the grain and loading the grain sample into the sample holder, the proposed sensor can be inserted into the grain bulk, the measuring processes of sampling grain and loading the sample into the sample holder can be accomplished simultaneously. Therefore, the proposed sensor can simplify the measurement process and increasing the efficiency.
Temperature sensor. The PT100 platinum resistance thermometer (diameter: 2 mm, height: 5 mm) was placed far away from the isolation layer, which made the coaxial waveguide not be affected by the shell of the temperature sensor. In addition, the temperature sensor was isolated from the sampler by a 2 mm thick ABS plastic, which avoided the influence of the sampler’s temperature on measuring grain’s temperature.
2.2. Simulation and Measurement of the Proposed Sensor
Taking
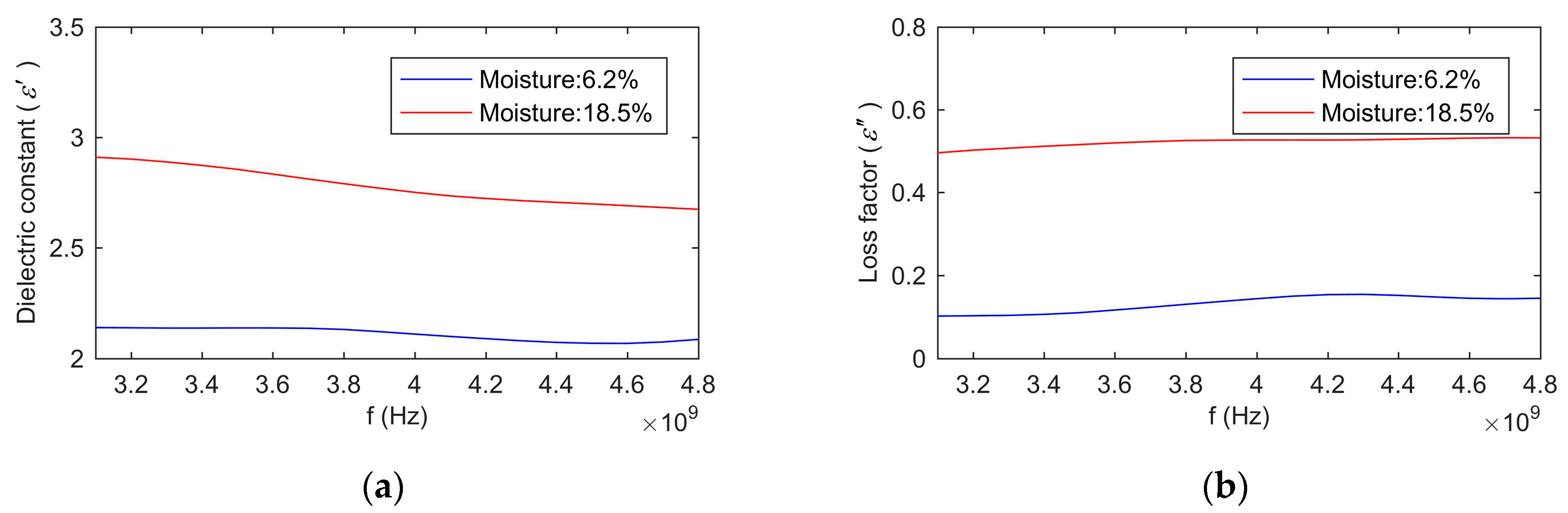
as the complex permittivity of the measured object, the electromagnetic field of the proposed sensor was simulated by CST (Dassault Systemes, Stuttgart, Germany). The complex permittivity was derived from the complex permittivity of white hard winter wheat at 4 GHz with a moisture content of 12.6%, which was adopted as a grain sample in this paper.
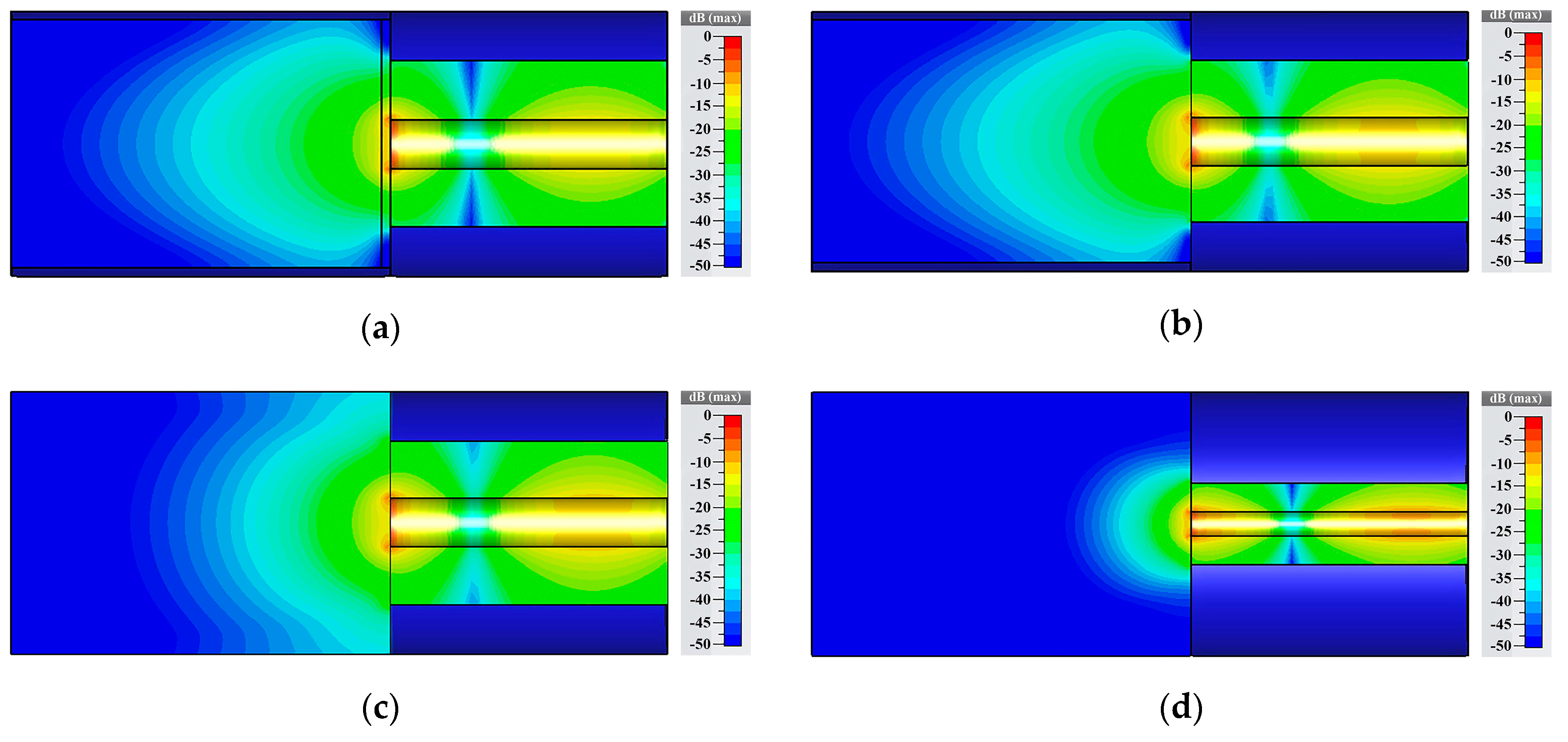
Figure 3 showed the electric field at 4 GHz.
Figure 3c,d shows conventional open-ended coaxial probes. The inner and outer conductor radii were 3 mm and 10 mm in
Figure 3c, respectively. The inner and outer conductor radii were 1.5 mm and 5 mm in
Figure 3d, respectively. The region where the electric field was greater than −30 dB was the sensor’s sensing region. The interference at the electric field above −30 dB can be detected by the UWB radar module with a dynamic range of 60 dB adopted in this paper. The depth of sensing region of
Figure 3c was 18 mm, and the depth of sensing region of
Figure 3d was 9 mm. Therefore, the sensing region of the open-ended coaxial probe can be increased by increasing the radii of the inner and outer conductors. However, there is a limit to the inner and outer conductor radii. Their radii are limited by the single mode transmission condition as shown in the following [
33]:
where
is the velocity of light, and
is the maximum frequency of sensor adopted. This indicates that the greater is the sum of the inner and outer conductor radii, the lower is the maximum frequency of the sensor used. In order to maximize the sensing region, we chose the maximum of the sum of inner and outer conductor radii, which met the single mode transmission condition in the frequency range of 0–5 GHz. Comparing to
Figure 3c,
Figure 3b added a circular waveguide with an inner radius of 15 mm connected to the coaxial waveguide. The circular waveguide could be seen as the sample holder. The wave impedance of the grain inside the circular waveguide was different from the wave impedance of the grain in free space. Choosing proper dimensions of the circular waveguide can change the wave impedance of the grain sample, which made more energy of electromagnetic wave enter into the grain sample. As a result, the sensing region of the sensor can be enlarged. In
Figure 3b, the depth of the sensing region was 26 mm, which was 13 mm more than the open-ended coaxial probe shown in
Figure 3c. In addition, since the grain sample was in free space in
Figure 3c, a part of the energy of electromagnetic wave leaked to the upper and lower space. If the environments interacted with this part of the energy, it would introduce environmental interference. In contrast, the electromagnetic wave in
Figure 3b was enclosed in the circular waveguide. Consequently, external interference was avoided.
Figure 3a was the proposed sensor in this paper. Comparing to
Figure 3b, the proposed sensor was added the isolation layer. The main function of the isolation layer was to prevent the coaxial inner conductor from direct contact with the grain kernels. This can protect the inner conductor’s plating. In addition, it can reduce the standard deviation of the measurement and improve the stability (the details were analyzed in the
Section 5.5). The depth of the sensing region of the proposed sensor was 25 mm, which was only 1 mm less than sensor without isolation layer. It indicated that the isolation layer hardly influenced the depth of the sensing region. This was mainly because Teflon had a small loss factor and its dielectric constant was close to grain. As a result, the isolation layer improved the stability and did not significantly affect the electromagnetic wave propagating into the grain sample.
The temperature sensor used in this paper was fixed on the edge of the opening of the circular waveguide. The electric field was less than −50 dB. The electric field intensity at the position of the temperature sensor was very small. In addition, the temperature sensor had a metal shell, which can produce electromagnetic shielding. Consequently, the electromagnetic field in the proposed sensor did not interfere with the temperature sensor.
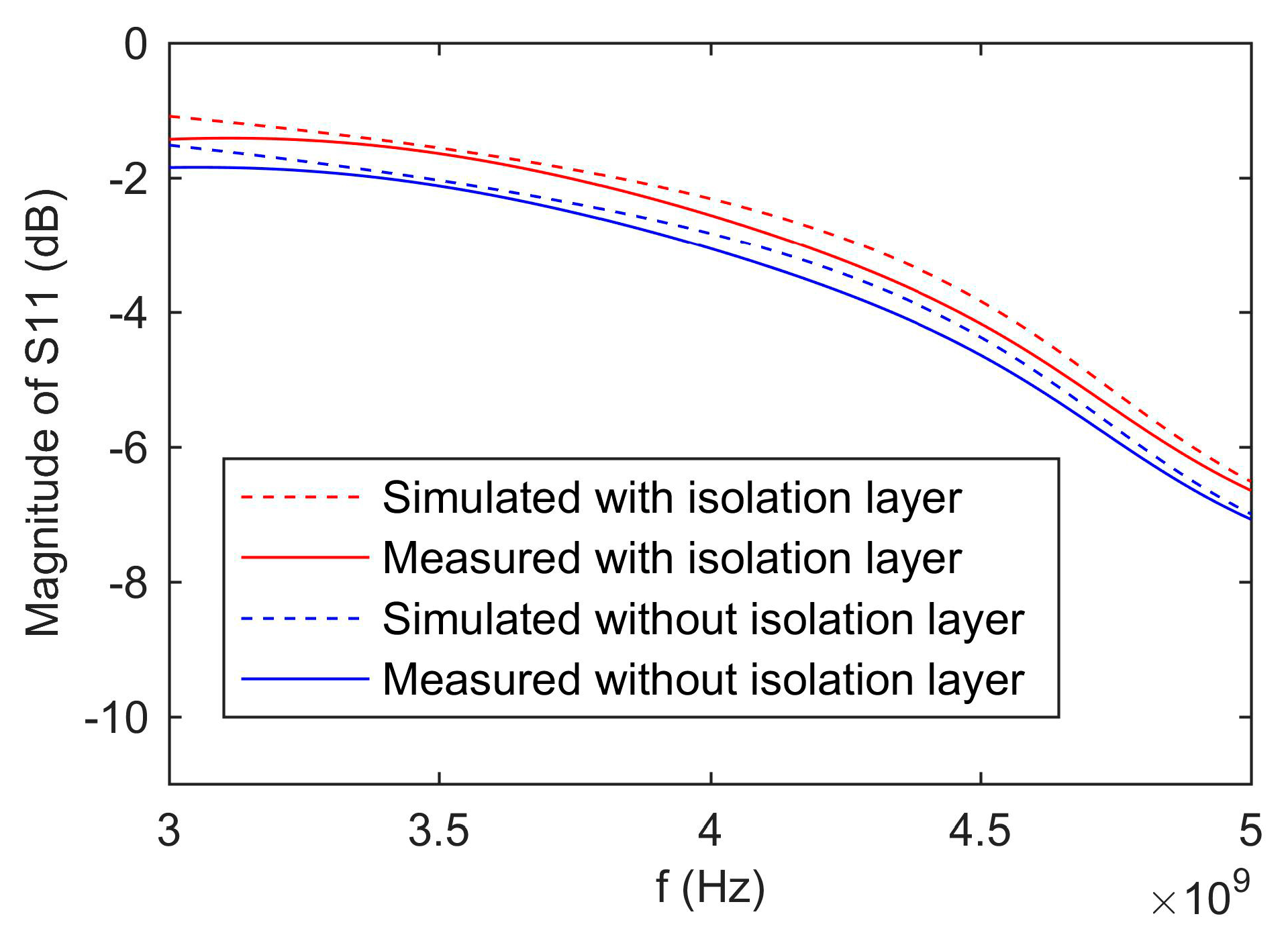
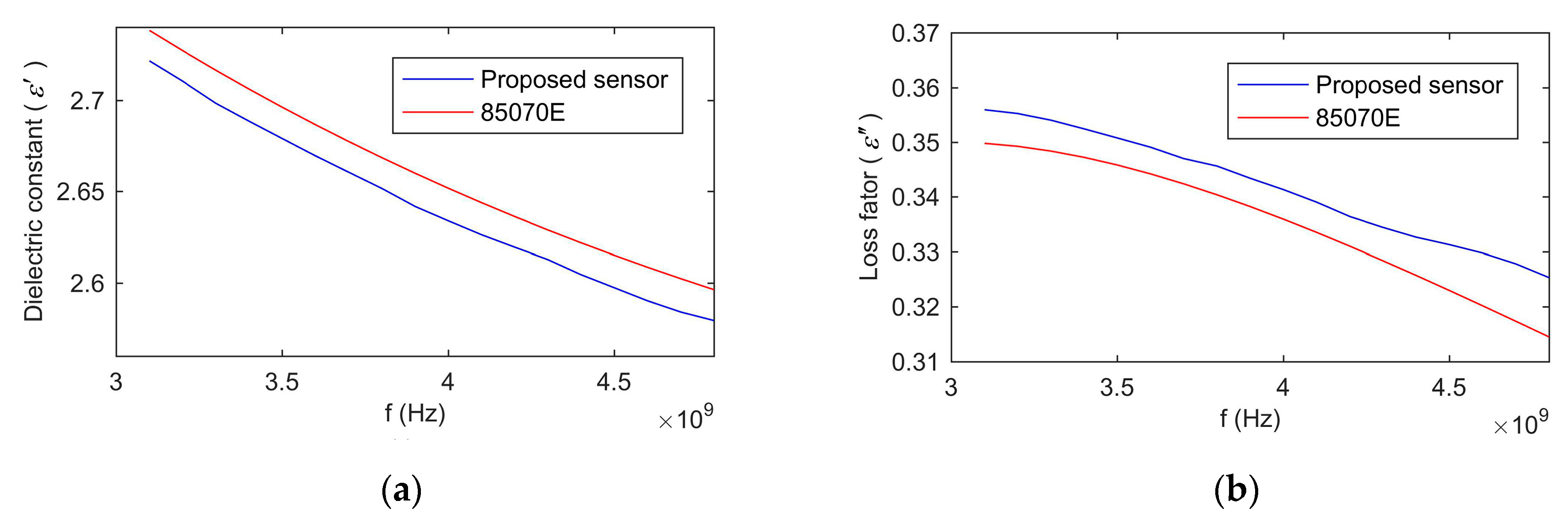
To compare simulation and measurement of the proposed sensor’s S-parameter, the decanol was adopted as standard material. Because the complex permittivity of decanol was very similar to grain and it can be measured by a 85070E dielectric probe (Keysight Technologies, Santa Rosa, CA, USA). Consequently, the decanol’s complex permittivity measured by the 85070E was brought into the simulation. The S-parameter of the sensor was measured by an E5071C vector network analyzer (VNA) (Keysight Technologies).
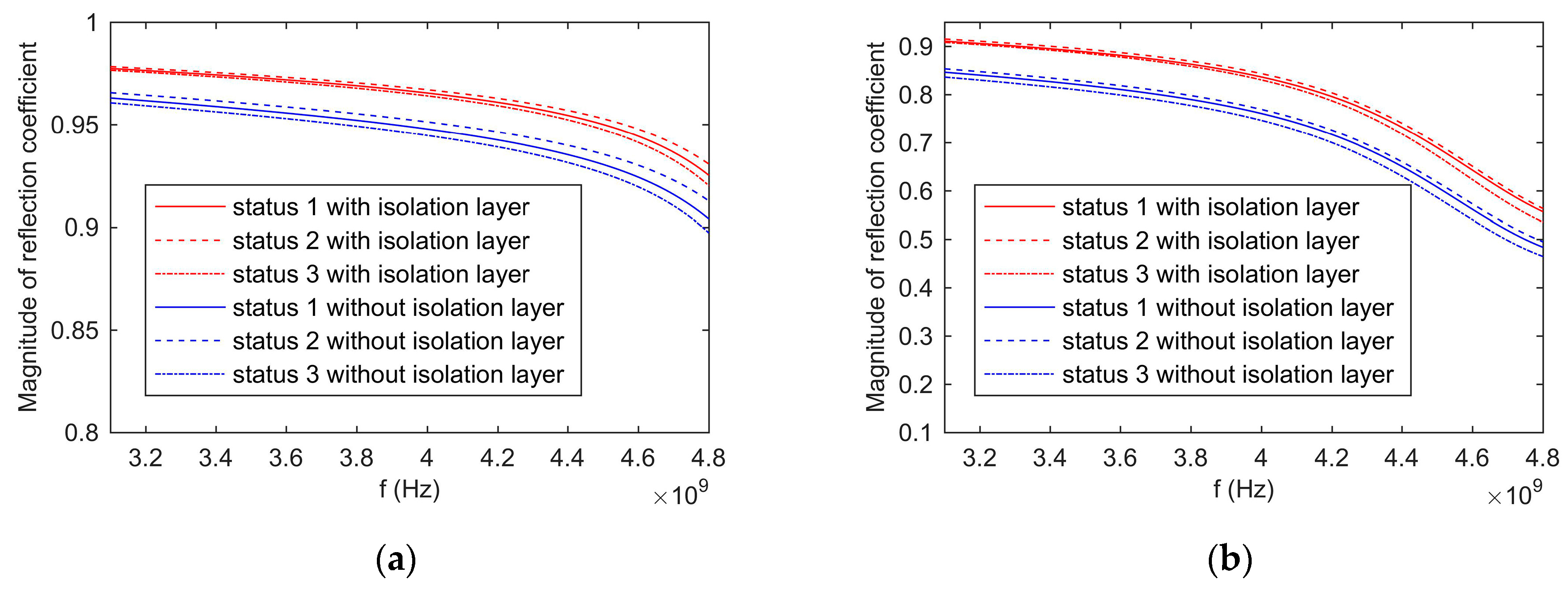
Figure 4 shows the simulated and measured values of S-parameter of the proposed sensor with isolation layer versus without isolation layer. The measured results were consistent with the simulation results. The differences between the measured and simulation results were caused by the error of the fabrication. Besides, the magnitude of S11 of the sensor with the isolation layer was larger than the sensor without the isolation layer. This was because the isolation layer reduced a part of the electromagnetic wave energy propagating into the sample holder. Consequently, more electromagnetic wave energy was reflected.
2.3. Modeling the Sensor Based on the Mode Matching Method
The mode matching method is an effective approach for analyzing the characteristics of microwaves in discontinuous waveguides [
31]. At both sides of the discontinuous interface, the transverse electric and magnetic fields can be expanded into combinations of transverse electromagnetic (TEM), transverse magnetic (TM) and transverse electric (TE) modes. The scattering coefficient at the discontinuous interface can be obtained by using boundary conditions and the orthogonality between different modes. In this paper, the electromagnetic field in the coaxial region was expanded into a combination of one TEM mode and
N TM
0n modes. The electromagnetic field in the isolation layer was expanded into a combination of
M TM
0n modes. Applying the mode matching method at the interface between the coaxial waveguide and the isolation layer in the circular waveguide, the model of the proposed sensor can be built as follows (details are given in
Appendix A):
where
denotes the reflection coefficient of the TEM mode in the region I,
denotes the
i-th TM mode electric field intensity coefficient in the region I.
and
are the admittances of the TEM mode and the
i-th TM mode in the region I, respectively.
indicates the coupling coefficient between the
i-th mode in region I and the
k-th mode in region II.
indicates input admittances of the
i-th TM mode at position O. Only the term
in the matrix
and the column vector
are related to the complex permittivity of the grain, and the other terms are constants determined by dimensions of the moisture sensor. The first element of the column vector is the TEM mode reflection coefficient at position O in the region I. As a result, Equation (4) can describe the relationship between the complex permittivity of the grain and the reflection coefficient of the coaxial waveguide (details about the methods for calculating admittances and coupling coefficients are given in
Appendix B).
When the complex permittivity of the substance filled in the sampler is known, it is easy to calculate the reflection coefficient by using Equation (4). However, the matrix
may be not a square matrix. In this paper, we solved this problem by the least squares method as follows:
When the reflection coefficient is known, it is very difficult to calculate the complex permittivity of the grain, because the analytical equation for calculating the complex permittivity from the reflection coefficient cannot be obtained. Fortunately, in 3.1–4.8 GHz range, the ranges of complex permittivity of wheat, barley, and rough rice are bounded (
,
) [
1]. For bounded problems that cannot be solved analytically, the look-up table method can quickly give an approximate solution. Low time consumption is the advantage of the method, while large memory consumption is a disadvantage. Its accuracy depends on the step size of the discretization. The smaller the step, the higher the accuracy. Since the range of the complex permittivity is limited, the problem can be solved by the look-up table method. In this paper, the range of complex permittivity was discretized in steps of 0.001, and reflection coefficients corresponding to each complex permittivity was calculated. We created a table containing all complex dielectric constant values and corresponding reflection coefficients. When the reflection coefficient was known, its corresponding complex permittivity could be obtained by looking up the table to find the closest item.
Determining
N and
M in Equation (4) is very significant. If these are infinity, Equation (4) is an accurate model describing the proposed sensor. However, considering the computational complexity and precision, the appropriate values should be chosen. Since the radius of the isolation layer is much larger than the distance between the inner and outer conductors of the coaxial waveguide, the intensity of high-order modes in isolation layer is larger than that in the coaxial waveguide at the same frequency. Consequently,
M should be greater than
N. To determine the values of
N and
M, we took
(the data from white hard winter wheat adopted in this paper) as an example to study the influence of
N and
M on the reflection coefficient at 4 GHz. The result is shown in
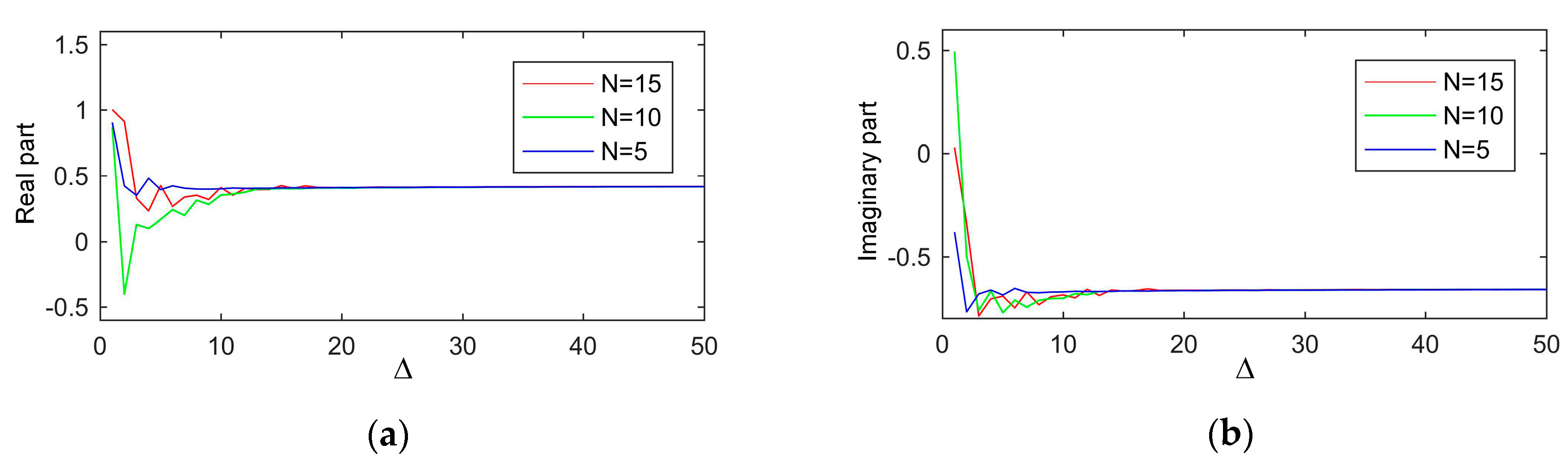
Figure 5. The
denotes for
M-N. First of all, the reflection coefficient became stable when
was large enough. Secondly, the larger the value of
N, the larger the value of
was needed. Thirdly, regardless of
N, the reflection coefficient converged to the same value as
increased. Considering the computational complexity and precision,
N equaled 5 and
equaled 20 (
M equaled 25) in this paper.
2.4. The Reflection Coefficient Measuring Method Based on the UWB Radar Module
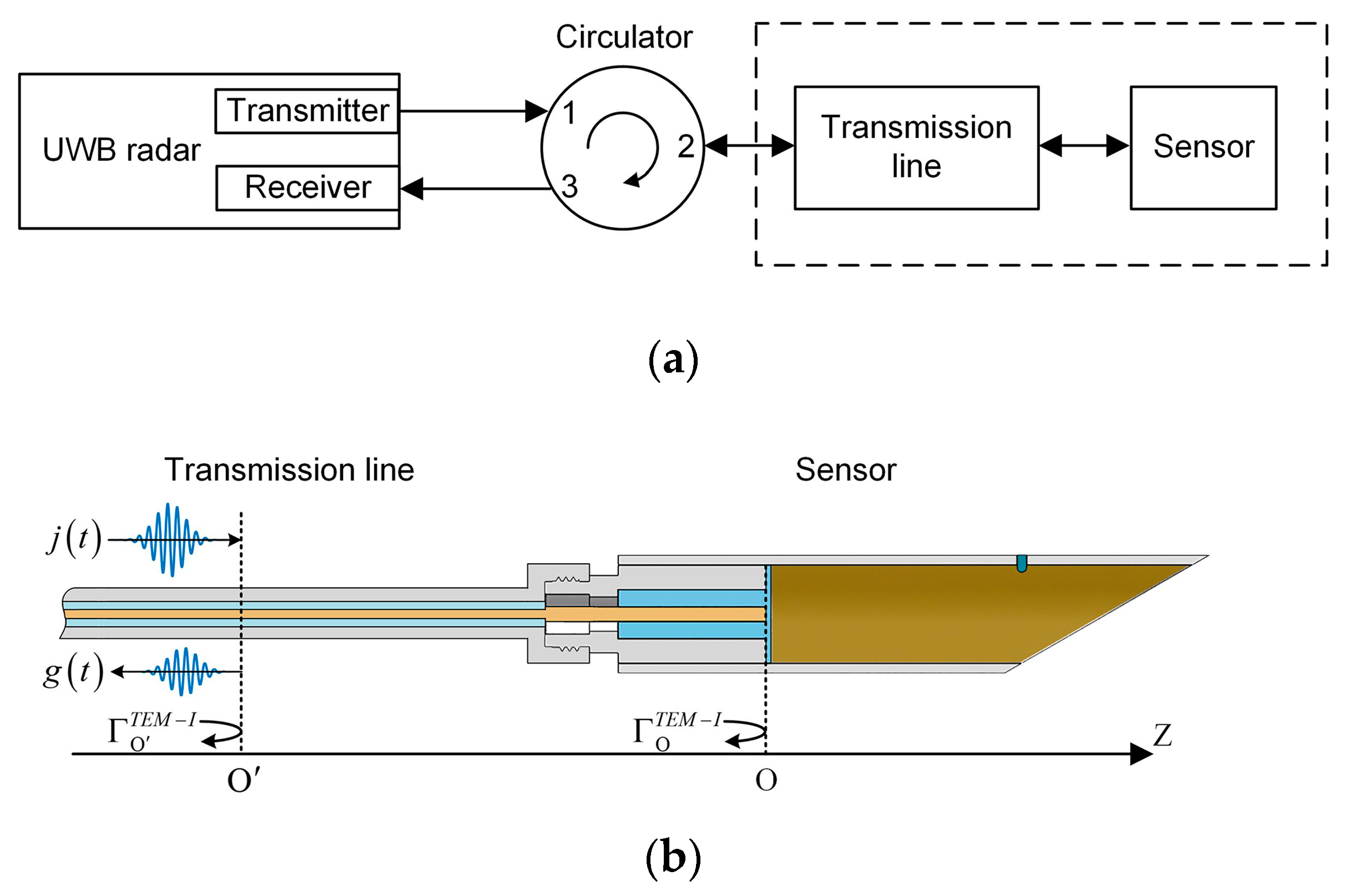
To achieve a portable device to measure wideband reflection coefficient, a new approach based on a UWB radar module was proposed in this paper. The diagram is shown in
Figure 6a. It consisted of a UWB radar module, a circulator, and a 4 m long transmission line. The radar module (P440, Humatics Inc., Waltham, MA, USA) used in this paper can generate 3.1–4.8 GHz UWB signals, and the sampling interval of the receiver was 61 ps (matching the Nyquist sampling theorem). The circulator (UIYCC2528A, UIY Inc., Shenzhen, China) used in this paper had a 0.5 dB insertion loss and a 24 dB isolation, which could separate the transmitted signal and the reflected signal. The transmission line (RG316, Kingsignal Inc., Shenzhen, China) had a path loss of 1.65 dB·m
−1 and a path delay of 4.7 ns·m
−1. Its main function was delaying the reflected signal to avoid aliasing with the leaked signal from the transmitter to the receiver. During the measuring process, the UWB module generated a UWB signal to be transmitted to the circulator port 1, and the circulator sent the signal from the port 2 (isolated port 3) through the transmission line to the moisture sensor. After that, the signal was reflected at the end face of the coaxial waveguide, and the reflected signal transmitted to the circulator port 2 through the transmission line, and the circulator sent the reflected signal from the port 3 to the receiver.
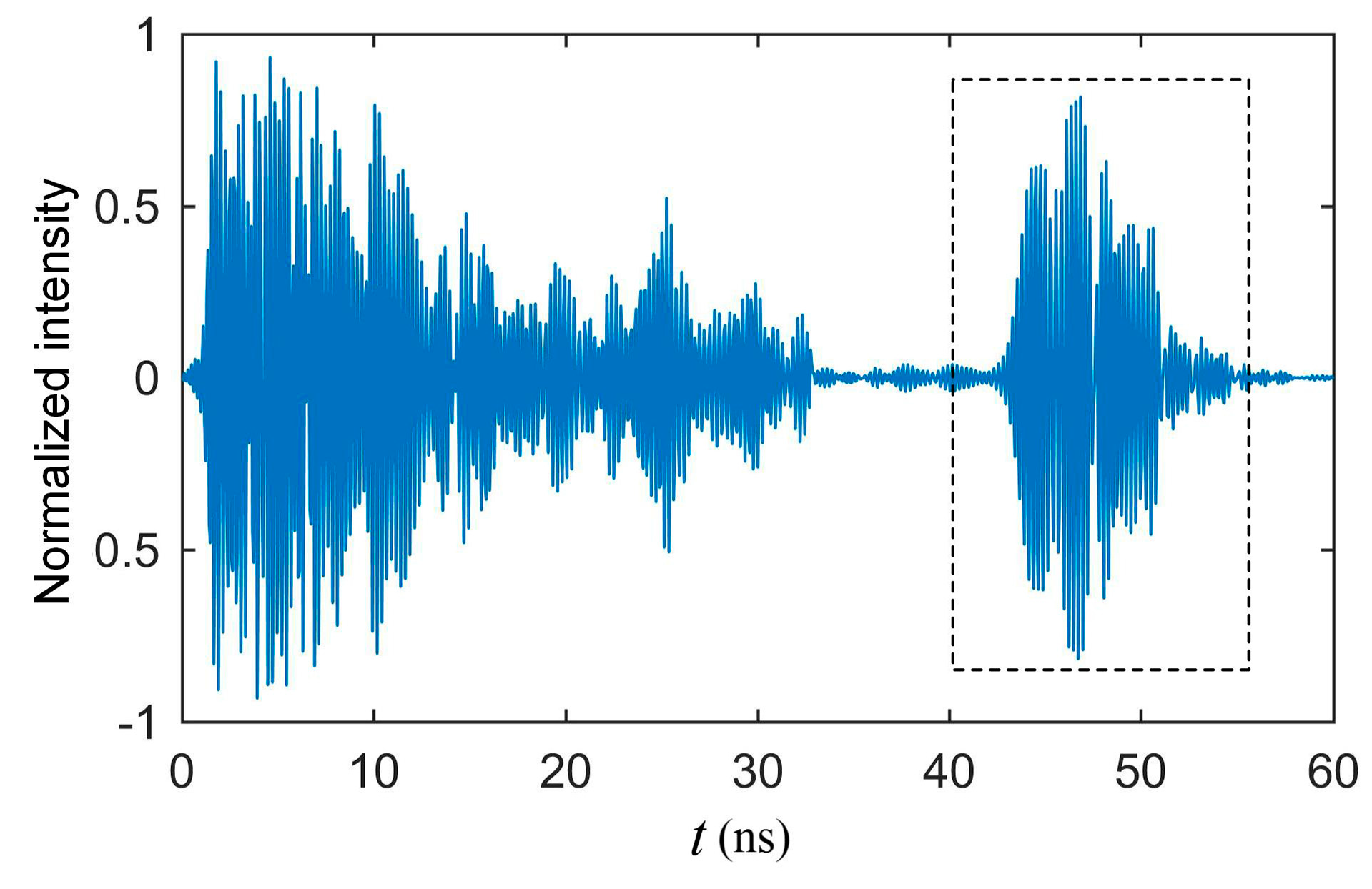
Figure 7 shows an example of a received signal when there was no grain in the sampler. The signal between 0 and 35 ns is the leaked signal from the transmitter to the receiver. The signal inside the dashed line box is the reflection signal from the proposed sensor, which is separated from the leaked signal. This represents that the time delay generated by the transmission line successfully avoid aliasing.
Only the signal in the dashed line box was useful to the measurement, so we extracted the signal between 40 ns and 55 ns as the reflected signal
g(t) in this paper. A virtual origin position
in the transmission line shown in
Figure 6b was created, which corresponded to the reflected signal at 40 ns.
G was the Fast Fourier Transform of
g(t). Assuming the incident signal at the position
was
j(t), and its Fast Fourier Transform was
J, the reflection coefficient at the position
can be expressed as follows:
If the waveguide between position
and position
was seen as a two-port network, the reflection coefficient at the position
can be calculated from the reflection coefficient at the position
by following equation [
33].
where
,
,
and
are S-parameters of the two-port network between position
and position
. By bringing Equation (9) into Equation (10), we get the following equations:
Except for and , , , and in Equation (11) are not dependent on the measured object. For a certain frequency, they are constants. After the constants are determined, the reflection coefficient of the end of the coaxial waveguide () can be calculated from by using Equation (11).
2.5. The Method of Calculating the Moisture Content from the Complex Permittivity
In this paper, the density-independent calibration function (1) was adopted to calculate the moisture content. The calibration function is a general method for calculating the moisture content of grain from the complex coefficient, which can eliminate the influence of the bulk density. In addition, it had no relationship with how the complex permittivity was measured. In general, if the complex permittivity of grain can be measured by any method, the calibration function can be used to calculate the grain moisture content from the complex permittivity. We formed Equation (15) by bring Equation (1) into Equation (2). It can be used for calculating the moisture content of grain from its corresponding complex permittivity:
where
is a frequency factor, which is related to the microwave frequency. It is a constant for a given variety of grain at a given frequency.
is temperature (°C),
is the percentage of moisture (wet basis).
,
and
are three undetermined coefficients. As Equation (1), the expression
can be denoted by
, which is called the density-independent calibration function. Although the complex permittivity of grain in the frequency range of 3.1–4.8 GHz was measured, Equation (15) adopted only the complex permittivity of a single frequency to calculate the moisture content. The performance of Equation (15) is related to the frequency and the grain type. The optimal frequency for different grain types is different. To improve the accuracy, the optimal frequency for each grain type should be determined through the calibration process. Since the UWB radar module measures the wideband reflection coefficient, the complex permittivity of grain obtained is a spectrum from 3.1 to 4.8 GHz. The moisture determination method described in this paper thus has a good performance for multiple types of grains.
2.6. Summary of the Proposed Method
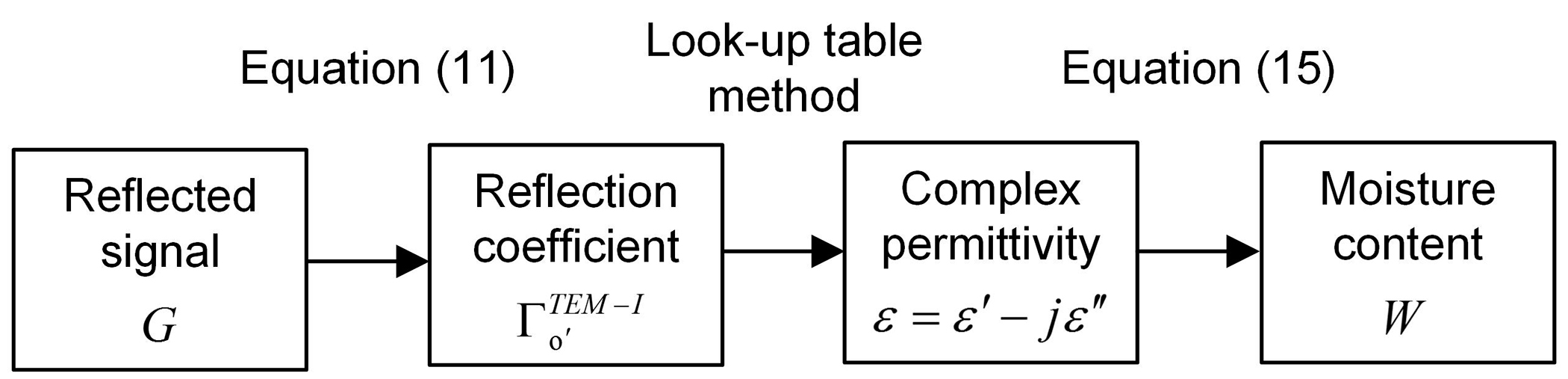
As shown in
Figure 8, the proposed moisture content measuring method can be summarized as follows.
- (1)
Load the sample. 30 mL grain sample can be easily sampled and loaded in the sensor just by inserting the proposed sensor into the grain bulk. Because the circular waveguide designed can be used as the grain sampler and the sample holder.
- (2)
Collect the reflected signal g(t) by using the UWB radar module and calculate G by the Fast Fourier Transform.
- (3)
Calculate the reflection coefficient from the reflected signal in the frequency domain by using Equation (11).
- (4)
Calculate the complex permittivity of grain from the reflection coefficient by look-up table method proposed in
Section 2.3.
- (5)
Calculate the moisture content from the complex permittivity by using Equation (15).
Based on the proposed method, a photograph of the developed measuring device is shown in
Figure 9.
3. Calibration Method
There are two equations that must be calibrated. Therefore, the calibration consists of two steps. The first step is calibrating Equation (11). There are three parameters
,
, and
. Therefore, three standard materials with known complex permittivity can be used to achieve the calibration. In this paper, we firstly fixed the proposed sensor vertically and made the sample holder up. Then filled the sampler with air, methanol at 20 °C, or ethanol at 20 °C. Their corresponding reflected signals in the frequency domain (
,
, and
) were obtained, and their corresponding reflection coefficients of the end of coaxial waveguide (
,
, and
) were calculated by using Equation (8). The complex permittivity of air equals one, and the complex permittivity of methanol and ethanol can be obtained from the tables of dielectric dispersion data for pure liquids [
34]. The three sets of data were brought into Equation (11), and the three functions were expressed in matrix form as follows:
The three parameters , , and can be determined by solving Equation (16). This calibration step was only needed to be done one time after the proposed moisture measuring device was manufactured.
The second step is calibrating Equation (15). There is the optimal frequency (
), the frequency factor
, and three coefficients (
,
,
) that need to be determined. Firstly, we created a calibration data set. For a certain type of grain, four samples with different moisture contents were prepared. Their standard moisture content (
,
,
,
) was determined by oven method (ISO 712-2009), and their complex permittivity spectra at 20 °C (
,
,
,
) were measured, and their complex permittivity spectra at 30 °C (
,
,
,
) were measured.
denoted a vector
, and
denoted a vector
, and
denoted a column vector
. The linear relationship between
and
can be used to determine
and
. We formed an objective function as follows:
where
is the optimal value of
at optimal frequency
.
denotes the vector
at the frequency
.
denotes the vector of
, which obtained by bringing
and
into Equation (1).
represents the linear correlation coefficient of
and
of calibration data set. The objective function aims to find the best combination of
and
to make the linear correlation coefficient take the maximum value. In this paper, the range of
was discretized from zero to one in steps of 0.0001, and the range of
was discretized from 3.1 to 4.8 GHz in the steps of 0.1 GHz. The calibration data set
and
were brought into the objective function (17), and tried every combination of
and
to find the optimal values (
and
) which made the linear correlation coefficient take the maximum. Finally, other parameters (
,
,
) can be obtained by bringing every calibration data into Equation (15) and a matrix function can be formed as follows:
where
equals 20, and
equals 30.
,
,
,
,
,
and
denote the value
by bringing
,
,
,
,
,
,
, and
into Equation (1), respectively. The matrix function can be solved by the least squares method as follows:
For each type of grain, this calibration step was needed to be done one by one.
4. Sample Preparation and Measurement
For this study, about 2 kg of hard white winter wheat (cultivar: Hemai-20) with initial moisture of 11.0% (wet basis) were obtained from Keyuan Seed Industry Co., Ltd. (Shandong, China). About 2 kg of winter barley (cultivar: Xiyin-2) with initial moisture of 10.2% (wet basis) were obtained from Ruifeng Seed Industry Co., Ltd. (Gansu, China). About 2 kg of rough rice (cultivar: Liangyou-3218) with initial moisture of 11.0% (wet basis) were obtained from Kelongyu Seed Industry Co., Ltd., (Hunan, China). Each type of grain was divided into 20 samples of 100 g each and these were conditioned to 20 different moisture contents using the method described by Trabelsi [
19] and Nelson [
35]. The samples with moisture contents above their initial values were prepared by spraying grains with distilled water and storing in plastic bags for 72 h at 4 °C to equilibrate. The samples with moisture contents below their initial values were prepared by drying at 80 °C in a convection oven for 2 h to 72 h. All samples were manually mixed regularly to ensure even distribution of moisture and were equilibrated to room temperature (25 °C) overnight before measurements. The moisture contents were determined by grinding and drying in triplicate, 5 g samples in a convection oven at 130 °C for 90 min (ISO 712-2009) [
4]. The standard deviations of each moisture were less than 0.17. The moisture contents determined by the oven drying method were considered true values.
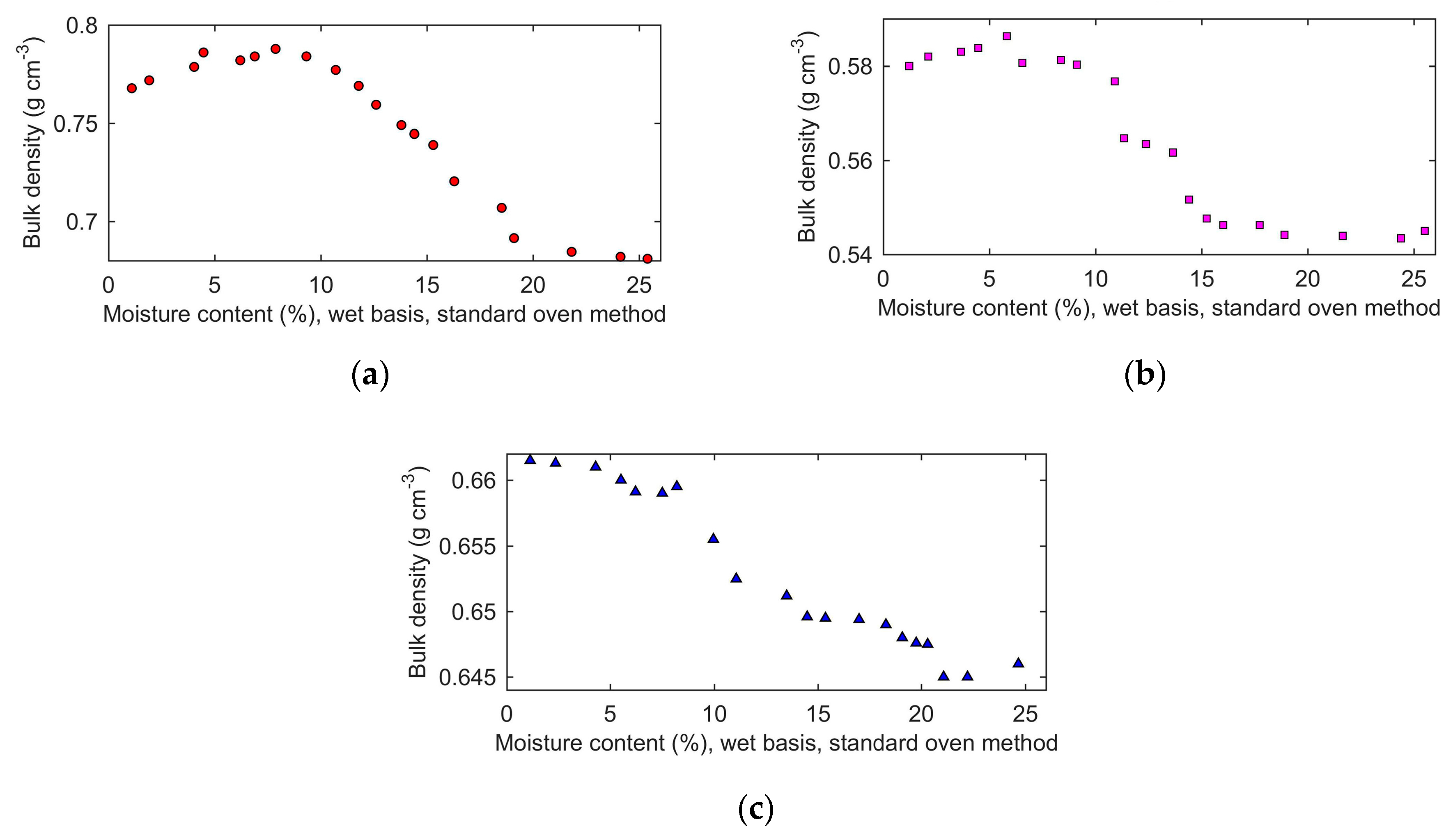
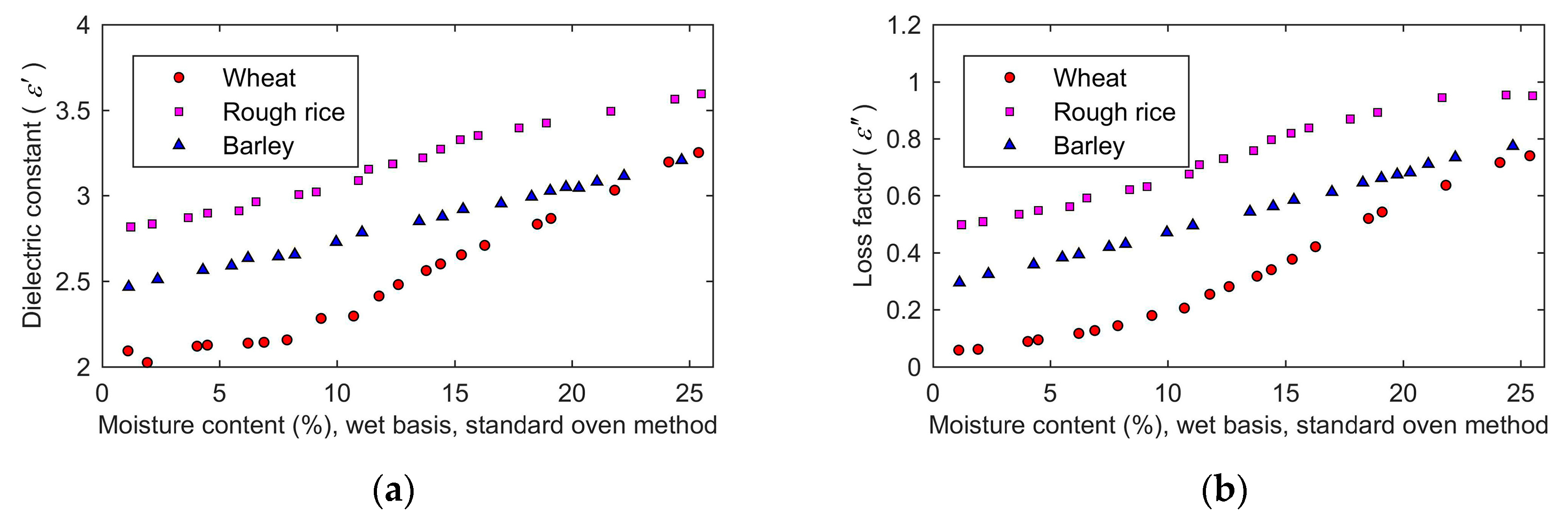
Bulk densities of all prepared samples were measured, and the results are shown in
Figure 10. When the moisture content was less than 8%, wet basis, the bulk density of wheat and rough rice increased slightly with the increase of moisture. When the moisture content was more than 8%, wet basis, the bulk density of wheat and rough rice decreased sharply at first and then decreased slightly.
The bulk density of barley decreased with increasing moisture content. At the same moisture content, the bulk density of wheat was larger than that of rough rice, and the bulk density of rough rice was larger than that of barley.
In addition, the length of wheat kernel, rough rice kernel, and barley kernel were measured. The average length increased with the increase of moisture content. The length of wheat was from 6.1 mm to 6.7 mm, and the length rough rice was from 7.4 mm to 8.2 mm, the length of barley was from 8.7 mm to 9.6 mm.
Based on the proposed calibration method, four samples with moisture contents approximately 5%, 10%, 15%, and 20% were selected from the prepared samples as calibration samples for each type of grain (wheat, rough rice, and barley).
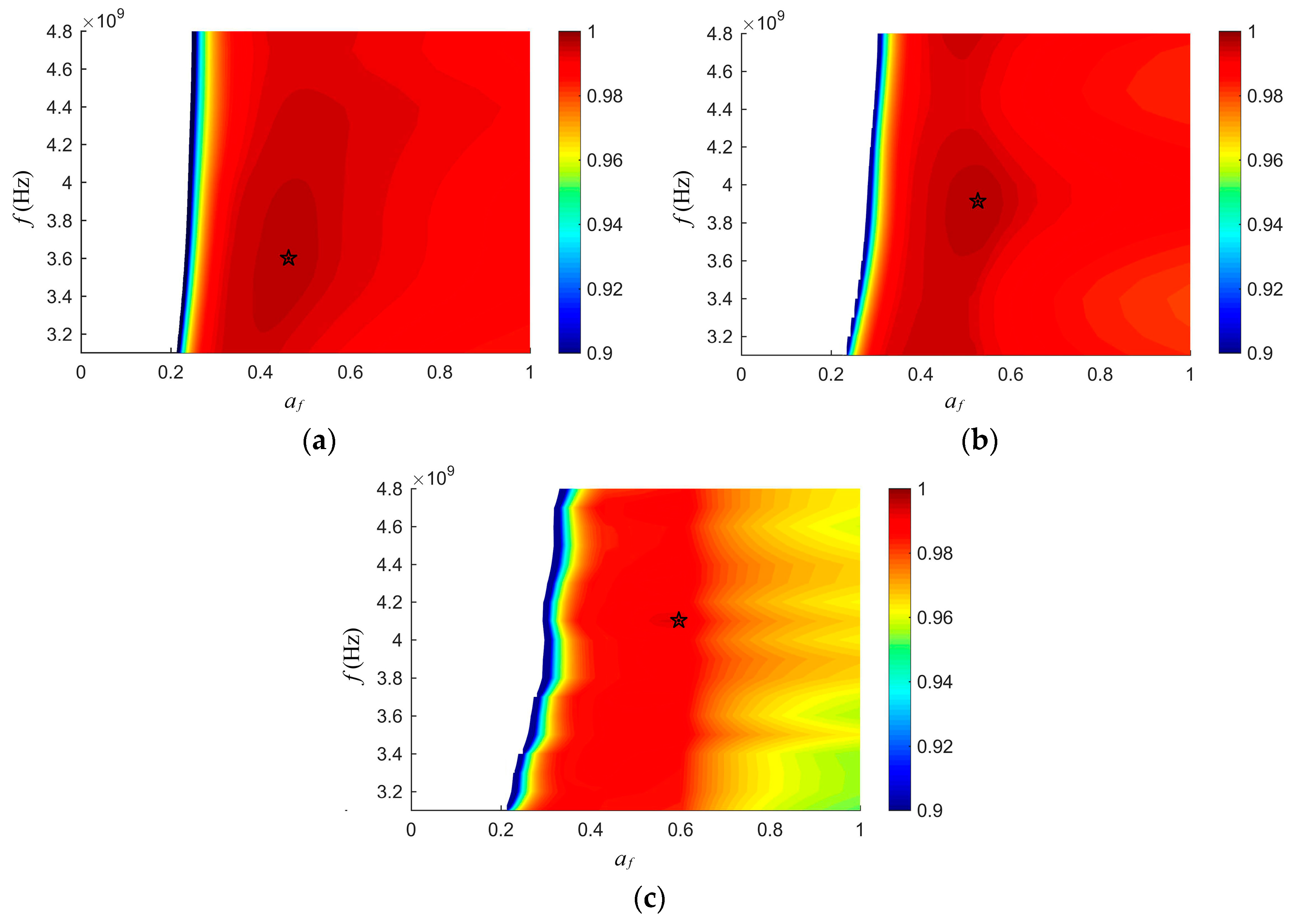
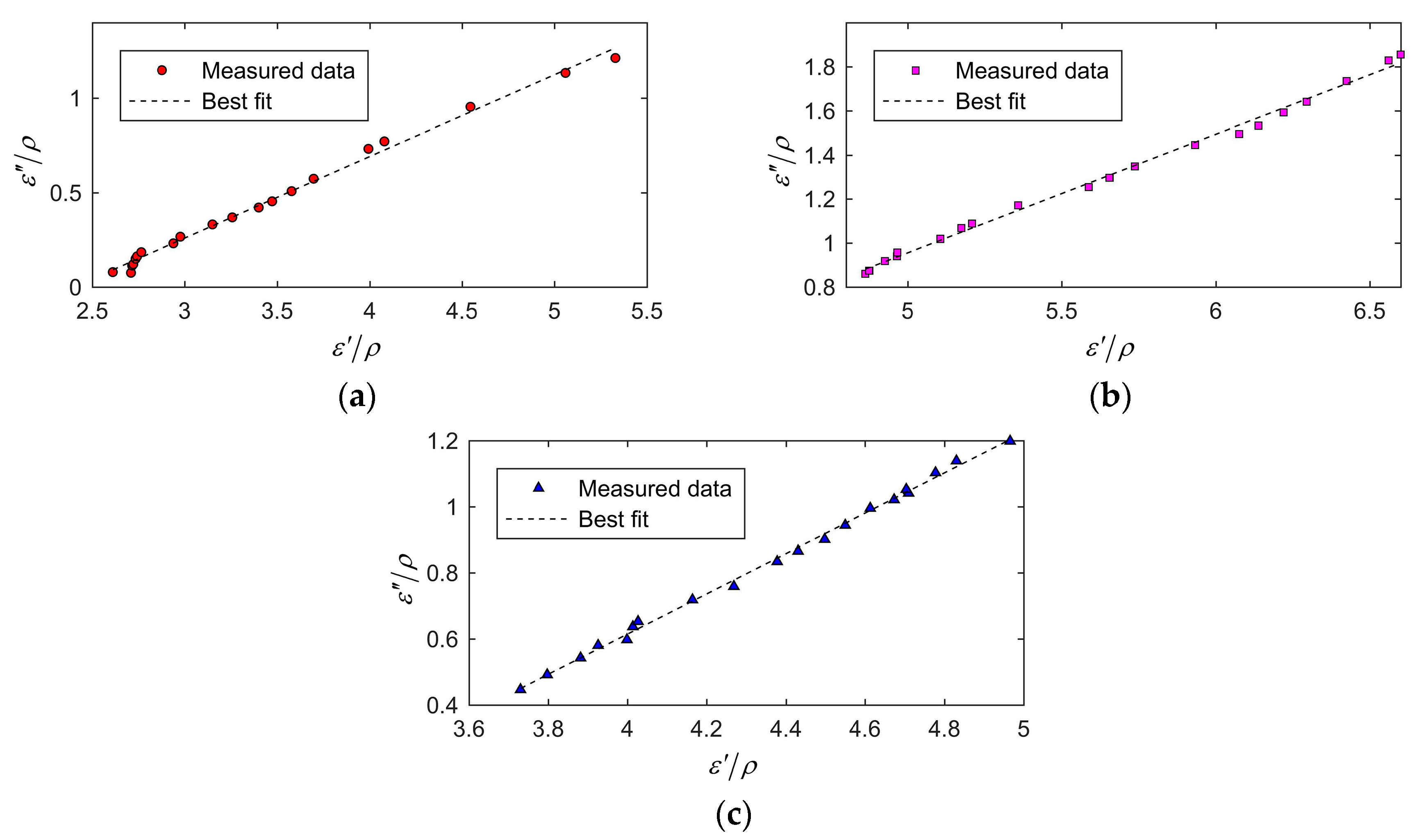
Figure 11a,b,c illustrate the frequency factor
and
dependence of the value of the objective function (17) for wheat, rough rice, and barley, respectively.
The blank region on the left side of the figure was the forbidden region. When
was too small, the expression
was smaller than zero, which made
an imaginary number. It was meaningless that
was an imaginary number, so the blank region on the left side of the figures indicated the forbidden region. The pentagram in each figure denotes the optimal combination of
and
. It can be seen there is the best combination for each type of grain, and the optimal values are shown in
Table 2.
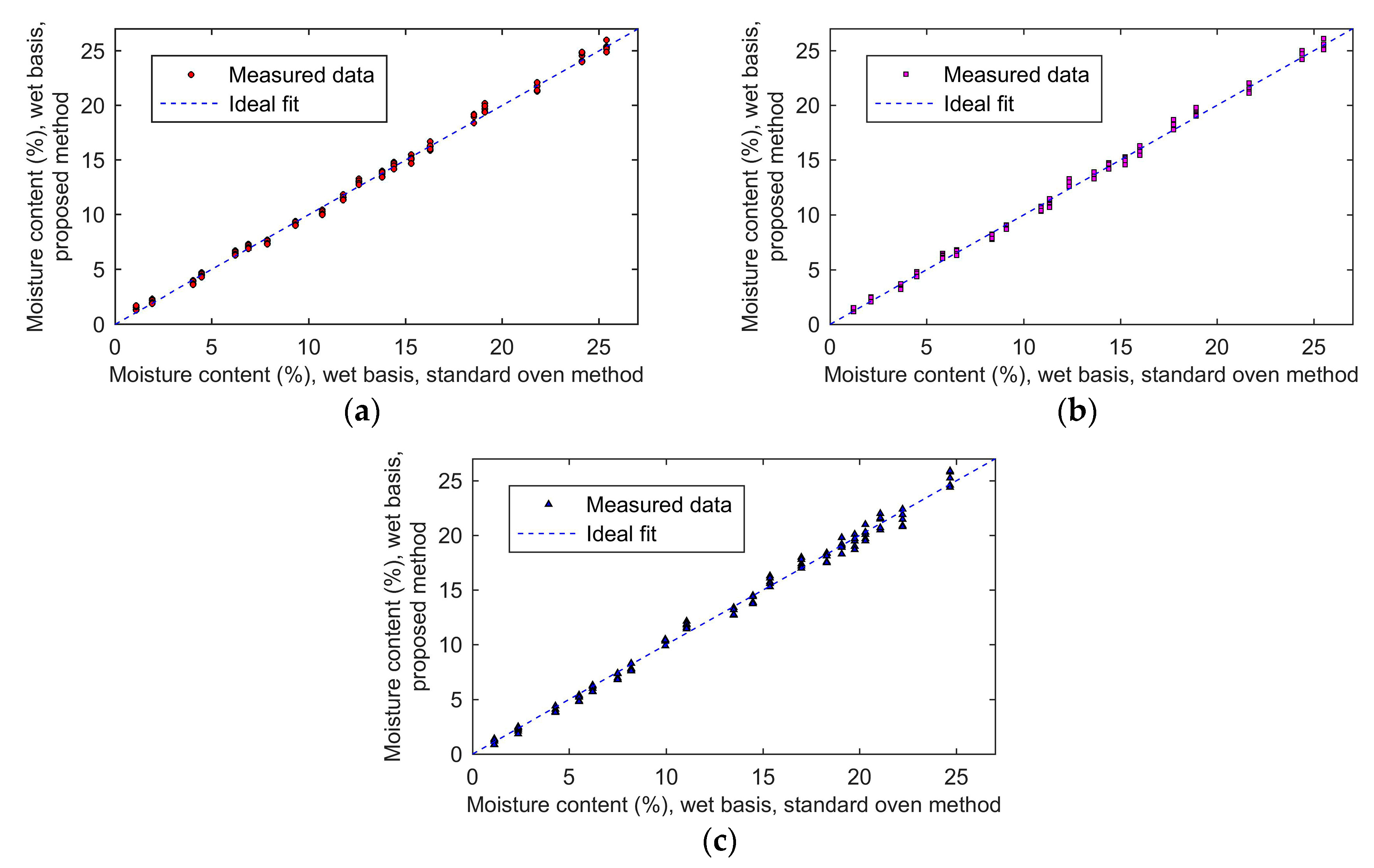
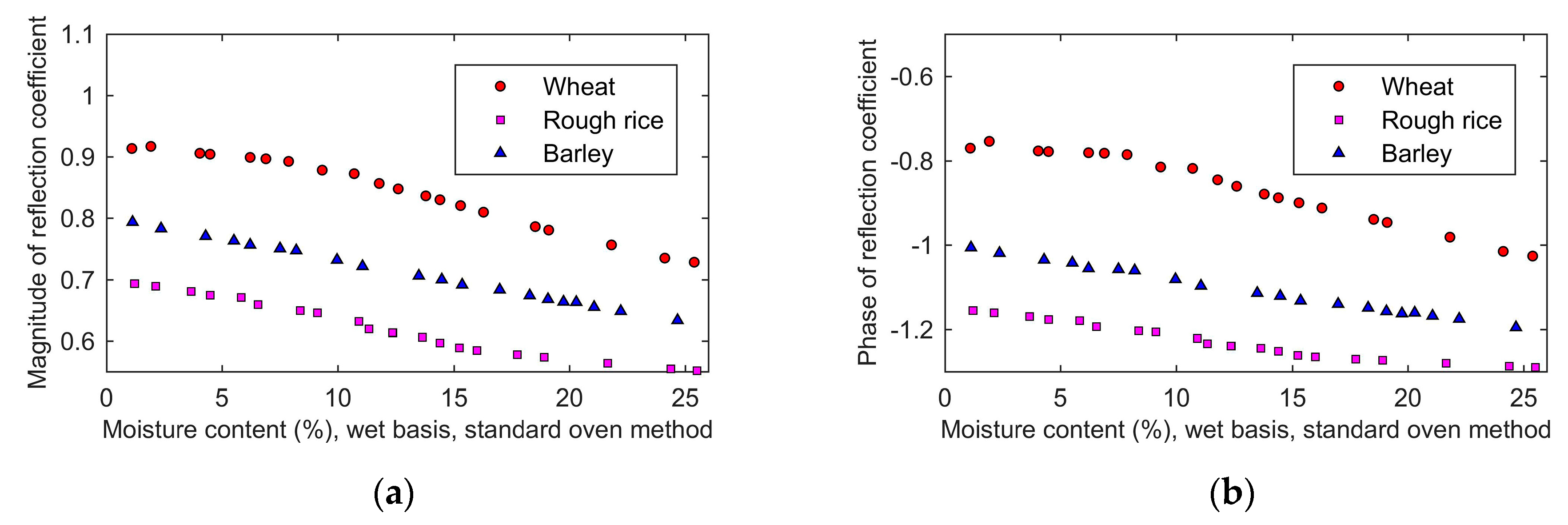
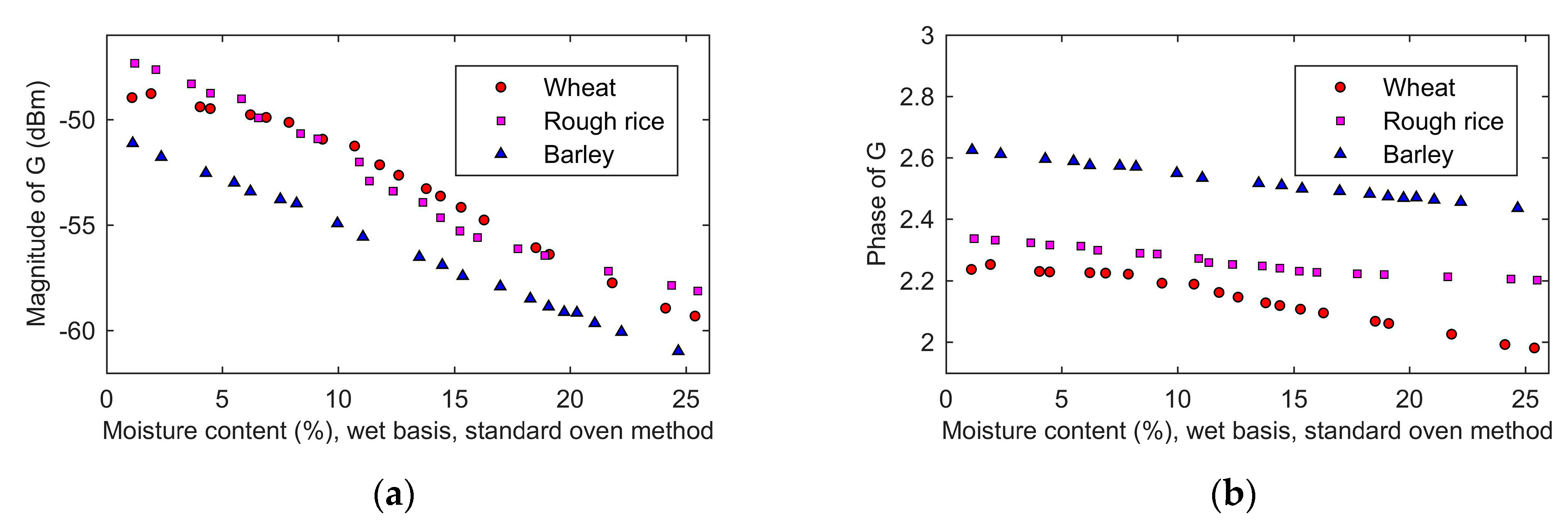
After calibration, 20 wheat samples, 20 barley samples, and 20 rough rice samples were sequentially measured by using the developed moisture measuring device. The measurements were carried out at the room temperature (25 °C). The grain samples were placed in many plastic cups, and the sensor was inserted vertically into the grain, and each sample was measured five times.