Design and Implementation of a Novel Measuring Scheme for Fiber Interferometer Based Sensors
Abstract
:1. Introduction
2. Polymer Micro Cavity Fiber Fizeau Interferometer
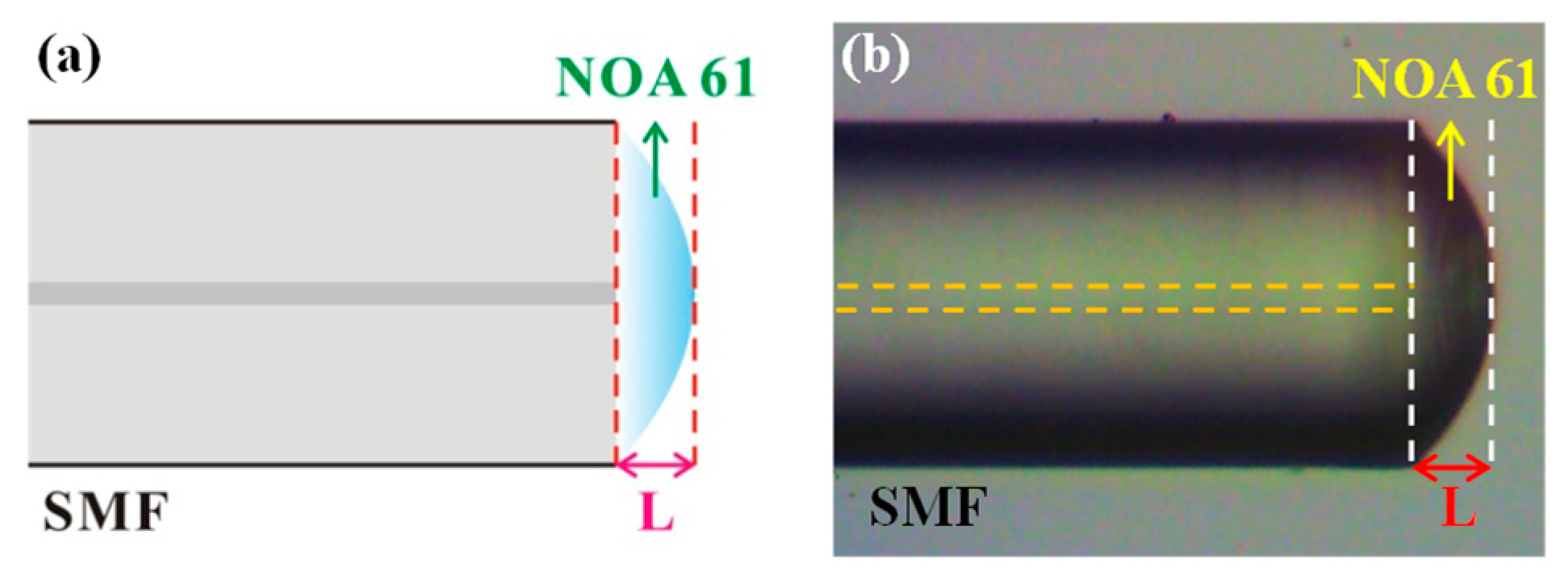
2.1. PMCFFI Manufacturing Steps
2.2. PMCFFI Interference Principle
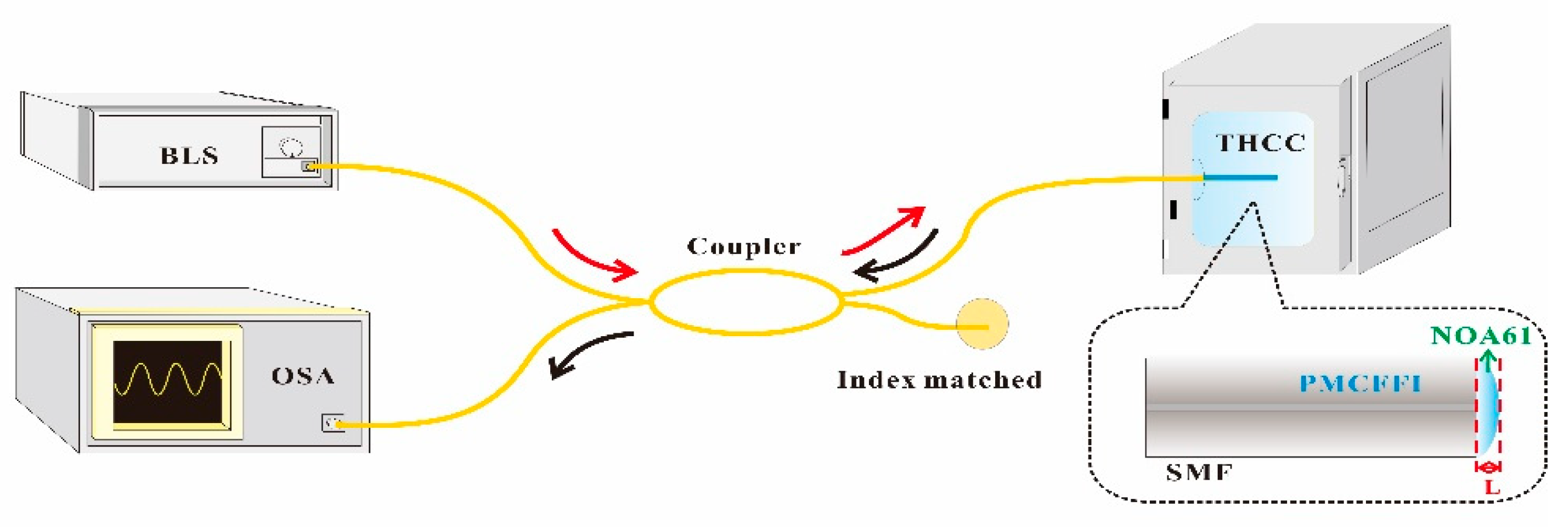
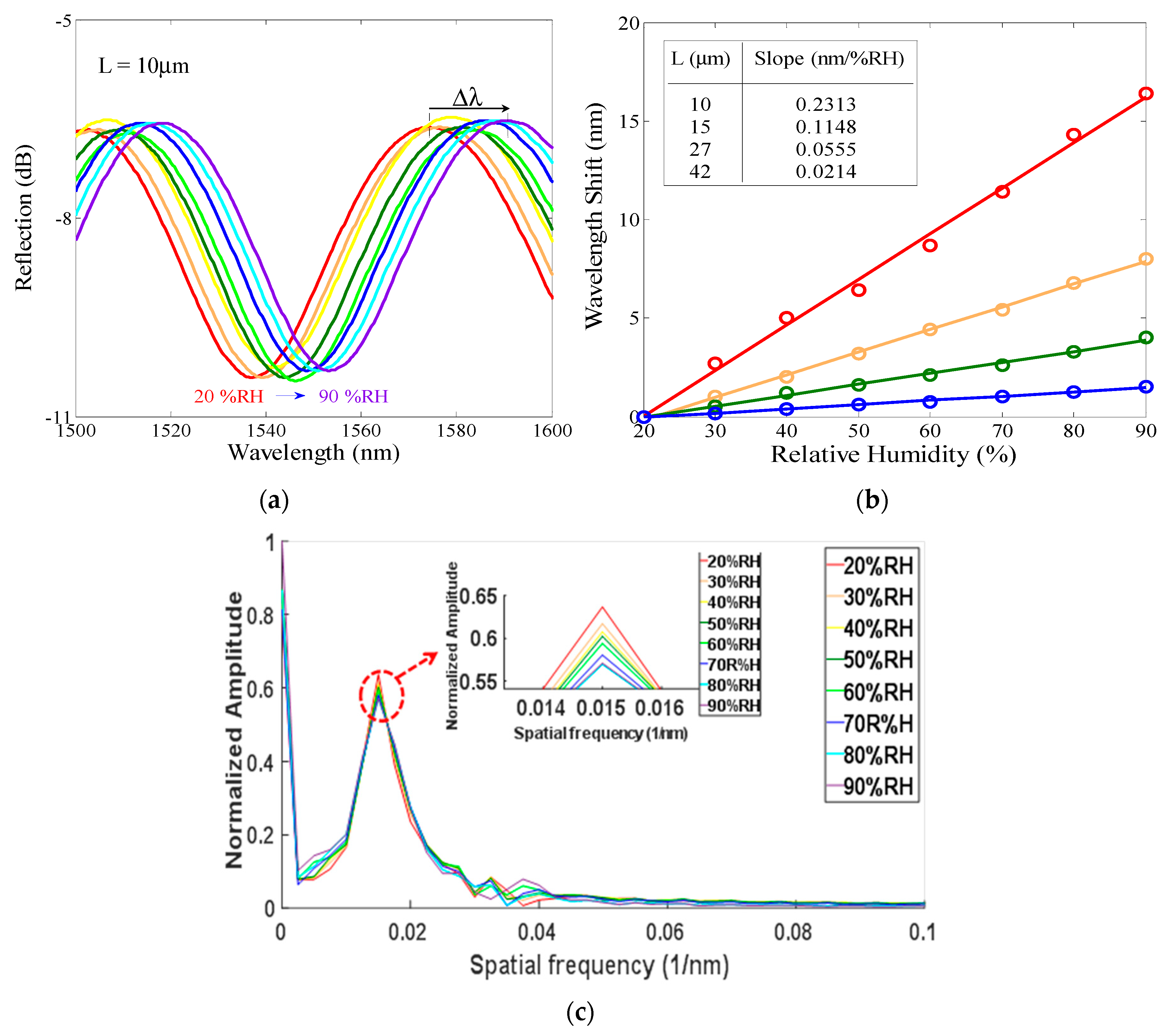
2.3. Experimental Measurement Configuration and Results
3. Development of the Proposed Measurement System Based on PMCFFI Sensing Device
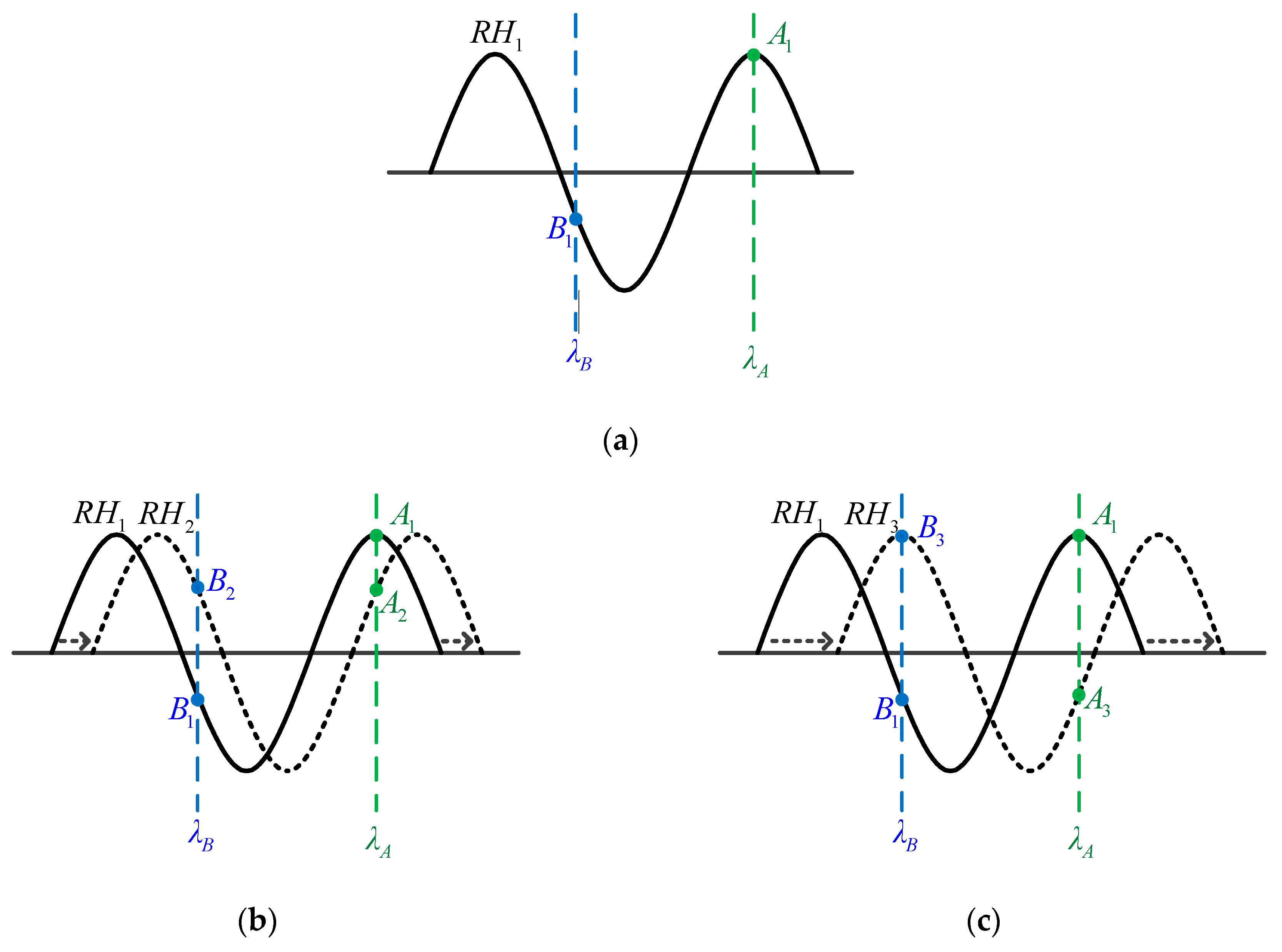
3.1. Measurement Principle and Implementation
3.2. System Prototype
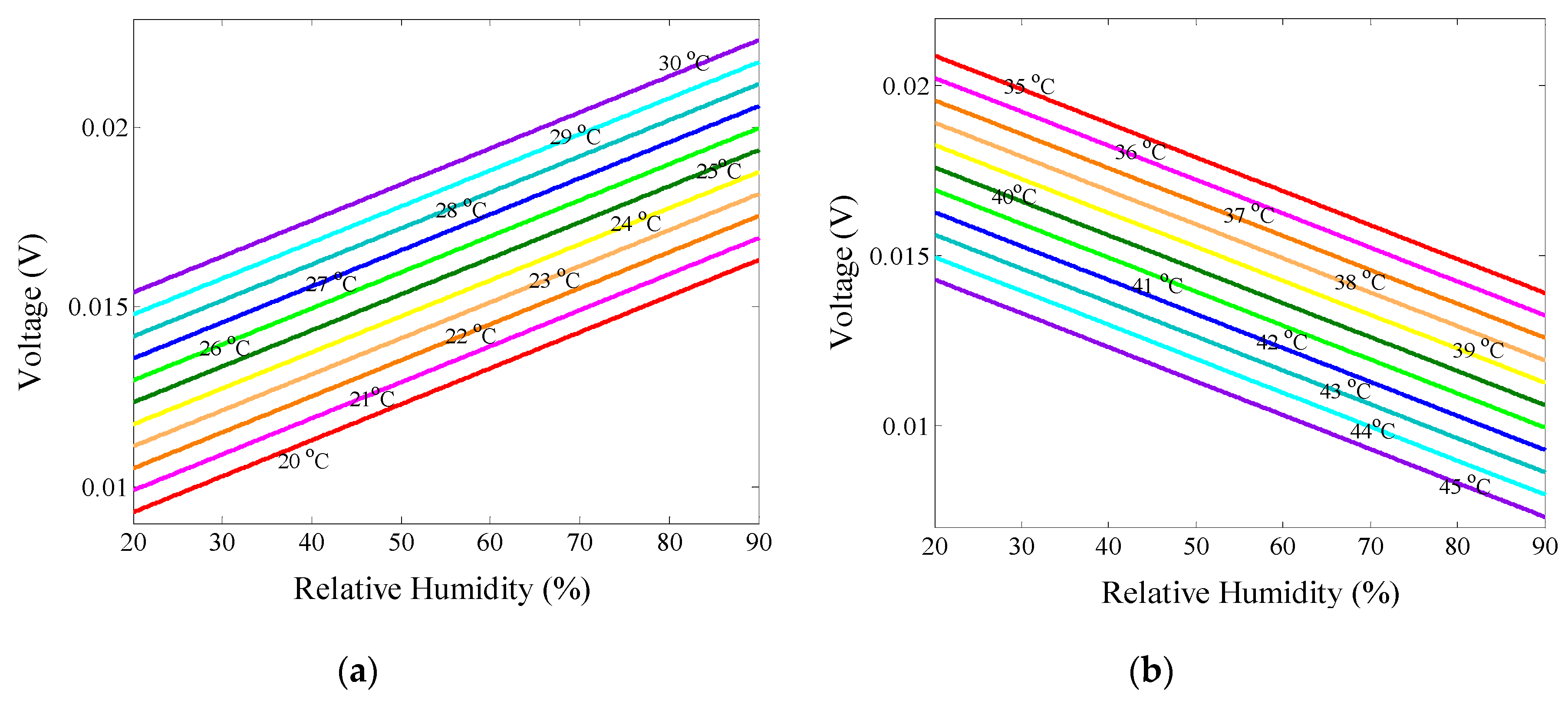
3.3. Measurement Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Jiang, L.; Wang, S.; Li, B.; Lu, Y. High-temperature sensor based on an abrupt-taper Michelson interferometer in single-mode fiber. Appl. Opt. 2013, 52, 2038–2041. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.; Sun, X.; Han, M.; Li, D. Compact magnetic-field sensor based on optical microfiber Michelson interferometer and Fe3O4 nanofluid. Appl. Opt. 2013, 52, 734–741. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-L.; Lee, C.-F.; Li, C.-M.; Chiang, T.-C.; Hsiao, Y.-L. Directional anemometer based on an anisotropic flat-clad tapered fiber Michelson interferometer. Appl. Phys. Lett. 2012, 101, 23502. [Google Scholar] [CrossRef]
- Zhang, X.; Bai, H.; Pan, H.; Wang, J.; Yan, M.; Xiao, H.; Wang, T. In-Line Fiber Michelson Interferometer for Enhancing the Q Factor of Cone-Shaped In wall Capillary Coupled Resonators. IEEE Photon. J. 2018, 10, 6801808. [Google Scholar]
- Tan, Y.; Sun, L.-P.; Jin, L.; Li, J.; Guan, B.-O. Microfiber Mach-Zehnder interferometer based on long period grating for sensing applications. Opt. Express 2013, 21, 154–164. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Qin, Z.; Harris, J.; Baset, F.; Lu, P.; Bhardwaj, V.R.; Bao, X. Vibration sensing using a tapered bend-insensitive fiber based Mach-Zehnder interferometer. Opt. Express 2013, 21, 3031–3042. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.-M.; Lee, C.-L.; Chang, H.-P.; Shih, W.C.; Li, C.-M. Highly Sensitive Tapered Fiber Mach–Zehnder Interferometer for Liquid Level Sensing. IEEE Photon. Technol. Lett. 2013, 25, 1354–1357. [Google Scholar] [CrossRef]
- Zhang, R.; Pu, S.; Li, Y.; Zhao, Y.; Jia, Z.; Yao, J.; Li, Y. Mach-Zehnder Interferometer Cascaded with FBG for Simultaneous Measurement of Magnetic Field and Temperature. IEEE Photon. J. 2019, 19, 4079–4083. [Google Scholar] [CrossRef]
- Tian, J.; Lu, Y.; Zhang, Q.; Han, M. Microfluidic refractive index sensor based on an all-silica in-line Fabry-Perot interferometer fabricated with microstructured fibers. Opt. Express 2013, 21, 6633–6639. [Google Scholar] [CrossRef]
- Jiang, M.; Li, Q.-S.; Wang, J.-N.; Jin, Z.; Sui, Q.; Ma, Y.; Shi, J.; Zhang, F.; Jia, L.; Yao, W.-G.; et al. TiO2 nanoparticle thin film-coated optical fiber Fabry-Perot sensor. Opt. Express 2013, 21, 3083–3090. [Google Scholar] [CrossRef]
- Wu, X.; Solgaard, O. Short-cavity multimode fiber-tip Fabry-Pérot sensors. Opt. Express 2013, 21, 14487–14499. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.N.; Wang, C.; Hu, T. Compressible fiber optic micro-Fabry-Pérot cavity with ultra-high pressure sensitivity. Opt. Express 2013, 21, 14084–14089. [Google Scholar] [CrossRef]
- Lee, C.L.; Lee, L.H.; Hwang, H.E.; Hsu, J.M. Highly sensitive air-gap fiber Fabry–Pérot interferometers based on polymer-filled hollow core fibers. IEEE Photon. Technol. Lett. 2012, 24, 149–151. [Google Scholar] [CrossRef]
- Lee, C.L.; Zheng, Y.C.; Ma, C.L.; Chang, H.J.; Lee, C.F. Dynamic micro-air-bubble drifted in a liquid core fiber Fabry-Pérot interferometer for directional fiber-optic level meter. Appl. Phys. Lett 2013, 102, 193504. [Google Scholar] [CrossRef]
- Lee, C.-L.; Hsu, J.-M.; Horng, J.-S.; Sung, W.-Y.; Li, C.-M. Microcavity Fiber Fabry–Pérot Interferometer with an Embedded Golden Thin Film. IEEE Photon. Technol. Lett. 2013, 25, 833–836. [Google Scholar] [CrossRef]
- Lee, C.-L.; Hung, C.-H.; Li, C.-M.; You, Y.-W. Simple air-gap fiber Fabry–Perot interferometers based on a fiber endface with Sn-microsphere overlay. Opt. Commun. 2012, 285, 4395–4399. [Google Scholar] [CrossRef]
- Wang, B.; Tian, J.; Hu, L.; Yao, Y. High Sensitivity Humidity Fiber-Optic Sensor Based on All-Agar Fabry–Perot Interferometer. IEEE Photon. J. 2018, 18, 4879–4885. [Google Scholar] [CrossRef]
- Li, E.; Peng, G.-D.; Ding, X. High spatial resolution fiber-optic Fizeau interferometric strain sensor based on an in-fiber spherical microcavity. Appl. Phys. Lett. 2008, 92, 101117. [Google Scholar] [CrossRef] [Green Version]
- Chan, J.Y.; Le, C.L.; Ha, P. Dynamic mitigation of EV charging stations impact on active Distribution Networks with Distributed BESSs. In Proceedings of the 2018 23rd Opto-Electronics and Communications Conference (OECC), Jeju Island, Korea, 2–6 July 2018. [Google Scholar]
- Li, Z.; Tian, J.; Jiao, Y.; Sun, Y.; Yao, Y. Simultaneous Measurement of Air Pressure and Temperature Using Fiber-Optic Cascaded Fabry–Perot Interferometer. IEEE Photon. J. 2019, 11, 7100410. [Google Scholar] [CrossRef]
- Huang, B.; Xiong, S.; Chen, Z.; Zhu, S.; Zhang, H.; Huang, X.; Feng, Y.; Gao, S.; Chen, S.; Liu, W.; et al. In-Fiber Mach-Zehnder Interferometer Exploiting a Micro-Cavity for Strain and Temperature Simultaneous Measurement. IEEE Photon. J. 2019, 19, 5632–5638. [Google Scholar] [CrossRef]
- Wu, S.; Wang, L.; Chen, X.; Zhou, B. Flexible Optical Fiber Fabry–Perot Interferometer Based Acoustic and Mechanical Vibration Sensor. J. Light. Technol. 2018, 36, 2216–2221. [Google Scholar] [CrossRef]
- Leandro, D.; Lopez-Amo, M. All-PM Fiber Loop Mirror Interferometer Analysis and Simultaneous Measurement of Temperature and Mechanical Vibration. J. Light. Technol. 2018, 36, 1105–1111. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, K.; Zhou, X.; Yang, Y.; Zhao, Z.; Zou, H.; Yu, Q. High-Sensitivity Fabry-Perot Interferometric Acoustic Sensor for Low-Frequency Acoustic Pressure Detections. J. Light. Technol. 2017, 35, 5276–5279. [Google Scholar] [CrossRef]
- Gao, R.; Lu, D.; Cheng, J.; Qi, Z. Ultrasonic Detection of High-Intensity Focused Ultrasound Field using Quadrature Point Phase Step in a Fiber Optic Interferometric Sensor. J. Light. Technol. 2019, 37, 2694–2699. [Google Scholar] [CrossRef]
- Zhang, W.; Qiao, X.; Shao, Z.; Wang, R.; Rong, Q.; Guo, T.; Li, J.; Ma, W. An optical fiber Fabry-Perot interferometric sensor based on functionalized diaphragm for ultrasound detection and imaging. IEEE Photon. J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Chen, X.; He, S.; Li, D.; Wang, K.; Fan, Y.; Wu, S. Optical fiber voltage sensor based on Michelson interferometer using phase generated carrier demodulation algorithm. IEEE Photon. J. 2016, 16, 1. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, W.; Zhu, T.; Liu, M. High Voltage Sensing Based on Fiber Fabry–Perot Interferometer Driven by Electric Field Forces. J. Light. Technol. 2014, 32, 3337–3343. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Zeng, Y.; Zhou, B.; Wang, L.; Liu, L.; He, S. Elastic Optical Fiber Fabry–Perot Interferometer for Highly Sensitive AC Magnetic Field Measurement. IEEE Photon. J. 2018, 18, 5799–5804. [Google Scholar] [CrossRef]
- Wu, W.; Cao, Y.; Zhang, H.; Liu, B.; Zhang, X.; Duan, S.; Liu, Y. Compact Magnetic Field Sensor Based on a Magnetic-Fluid-Integrated Fiber Interferometer. IEEE Magn. Lett. 2019, 10, 1–5. [Google Scholar] [CrossRef]
- Ghildiyal, S.; Ranjan, P.; Mishra, S.; Balasubramaniam, R.; John, J. Fabry–Perot Interferometer-Based Absolute Pressure Sensor with Stainless Steel Diaphragm. IEEE Sens. J. 2019, 19, 6093–6101. [Google Scholar] [CrossRef]
- Tang, Z.; Lou, S.; Wang, X.; Zhang, W.; Yan, S.; Xing, Z. High-Performance Bending Vector and Strain Sensor Using a Dual-Tapered Photonic Crystal Fiber Mach–Zehnder Interferometer. IEEE Photon. J. 2019, 19, 4062–4068. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, D.; Wang, L.; Zhao, Y.; Zhao, C.; Kang, J. F-P Interferometer for Low Liquid Velocity Measurement with Non-contact and High Sensitivity. In Proceedings of the 2018 Asia Communications and Photonics Conference (ACP), Hangzhou, China, 26–29 October 2018. [Google Scholar]
- Zhou, B.; Jiang, H.; Lu, C.; He, S. Hot Cavity Optical Fiber Fabry–Perot Interferometer as a Flow Sensor with Temperature Self-Calibrated. J. Light. Technol. 2016, 34, 5044–5048. [Google Scholar] [CrossRef]
- Liu, S.; Meng, H.; Deng, S.; Wei, Z.; Wang, F.; Tan, C. Fiber Humidity Sensor Based on a Graphene-Coated Core-Offset Mach–Zehnder Interferometer. IEEE Sens. J. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, A.; Yuan, L. Gelatin-Coated Michelson Interferometric Humidity Sensor Based on a Multicore Fiber with Helical Structure. J. Light. Technol. 2019, 37, 2452–2457. [Google Scholar] [CrossRef]
- Singh, M.; Raghuwanshi, S.K.; Prakash, O. Ultra-Sensitive Fiber Optic Gas Sensor Using Graphene Oxide Coated Long Period Gratings. IEEE Photon. Technol. Lett. 2019, 31, 1473–1476. [Google Scholar] [CrossRef]
- Feng, W.; Deng, D.; Yang, X.; Liu, W.; Wang, M.; Yuan, M.; Peng, J.; Chen, R. Trace Carbon Monoxide Gas Sensor Based on PANI/Co3O4/CuO Composite Membrane-Coated Thin-Core Fiber Modal Interferometer. IEEE Sens. J. 2018, 18, 8762–8766. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, W.; Wang, S.; Jiang, J.; Liu, K.; Wang, X.; Zhang, J. Temperature Insensitive and Integrated Differential Pressure Sensor for Liquid Level Sensing Based on an Optical Fiber Fabry–Perot Interferometer. IEEE Photon- J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Dong, Y.; Xiao, S.; Xiao, H.; Liu, J.; Sun, C.; Jian, S. An Optical Liquid-Level Sensor Based on D-Shape Fiber Modal Interferometer. IEEE Photon. Technol. Lett. 2017, 29, 1067–1070. [Google Scholar] [CrossRef]
- Li, X.; Warren-Smith, S.C.; Ebendorff-Heidepriem, H.; Zhang, Y.-N.; Nguyen, L.V. Optical fiber refractive index sensor with low detection limit and large dynamic range using a hybrid fiber interferometer. J. Light. Technol. 2019, 37, 1. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Zhang, T.; Yang, D.; Wang, Y.; Yu, D. Integrated Fiber-Optic Fabry-Pérot Interferometer Sensor for Simultaneous Measurement of Liquid Refractive Index and Temperature. IEEE Sens. J. 2019, 19, 5007–5013. [Google Scholar] [CrossRef]
- Lee, C.-L.; You, Y.-W.; Dai, J.-H.; Hsu, J.-M.; Horng, J.-S. Hygroscopic polymer microcavity fiber Fizeau interferometer incorporating a fiber Bragg grating for simultaneously sensing humidity and temperature. Sens. Actuators B Chem. 2016, 222, 339–346. [Google Scholar] [CrossRef]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.-T.; Lee, C.-L.; You, Y.-W. Design and Implementation of a Novel Measuring Scheme for Fiber Interferometer Based Sensors. Sensors 2019, 19, 4080. https://doi.org/10.3390/s19194080
Ma C-T, Lee C-L, You Y-W. Design and Implementation of a Novel Measuring Scheme for Fiber Interferometer Based Sensors. Sensors. 2019; 19(19):4080. https://doi.org/10.3390/s19194080
Chicago/Turabian StyleMa, Chao-Tsung, Cheng-Ling Lee, and Yan-Wun You. 2019. "Design and Implementation of a Novel Measuring Scheme for Fiber Interferometer Based Sensors" Sensors 19, no. 19: 4080. https://doi.org/10.3390/s19194080
APA StyleMa, C.-T., Lee, C.-L., & You, Y.-W. (2019). Design and Implementation of a Novel Measuring Scheme for Fiber Interferometer Based Sensors. Sensors, 19(19), 4080. https://doi.org/10.3390/s19194080





