StarNAV: Autonomous Optical Navigation of a Spacecraft by the Relativistic Perturbation of Starlight
Abstract
:1. Introduction
2. Background
2.1. Need for Autonomous Spacecraft Navigation
2.2. Remarks on the History of Star-Based Navigation
3. Mathematical Models for the Observation of Starlight by a Moving Spacecraft
3.1. Reference Star Models
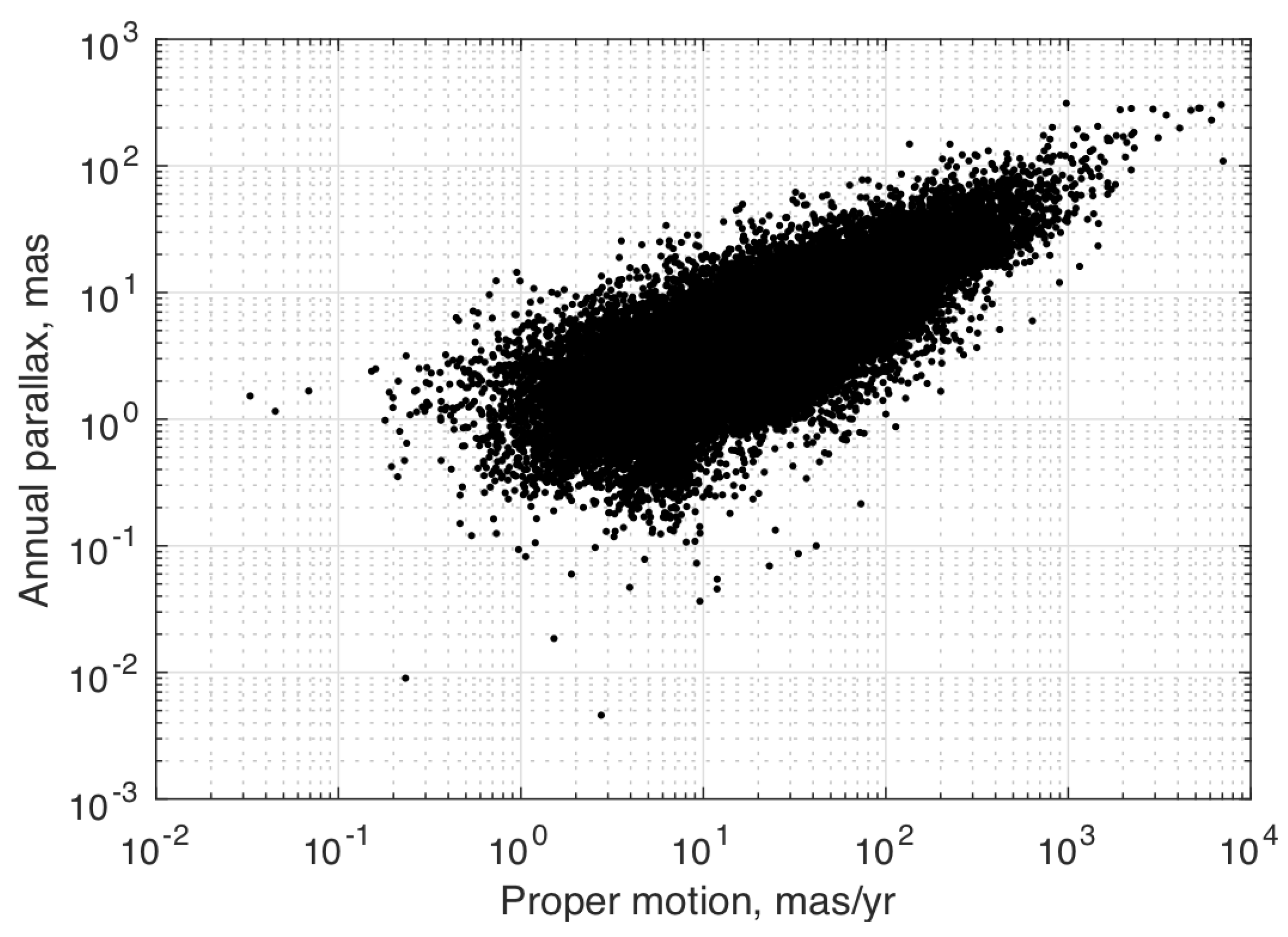
3.1.1. Star Catalogs and Astrometric Models
3.1.2. Models for Reference Stellar Spectra
3.1.3. Models for Stellar Photon Flux
3.2. Perturbations in Apparent Direction of Starlight
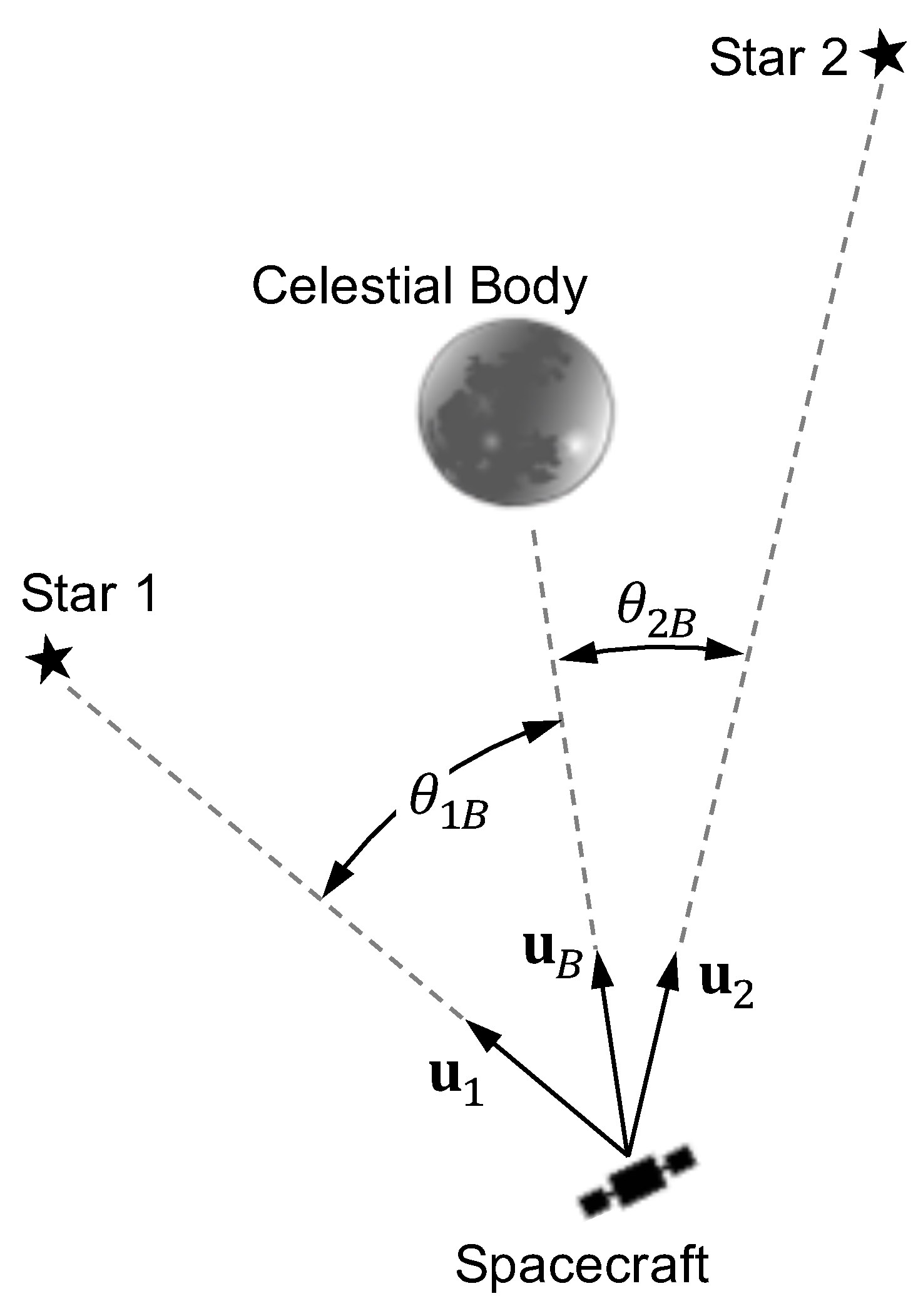
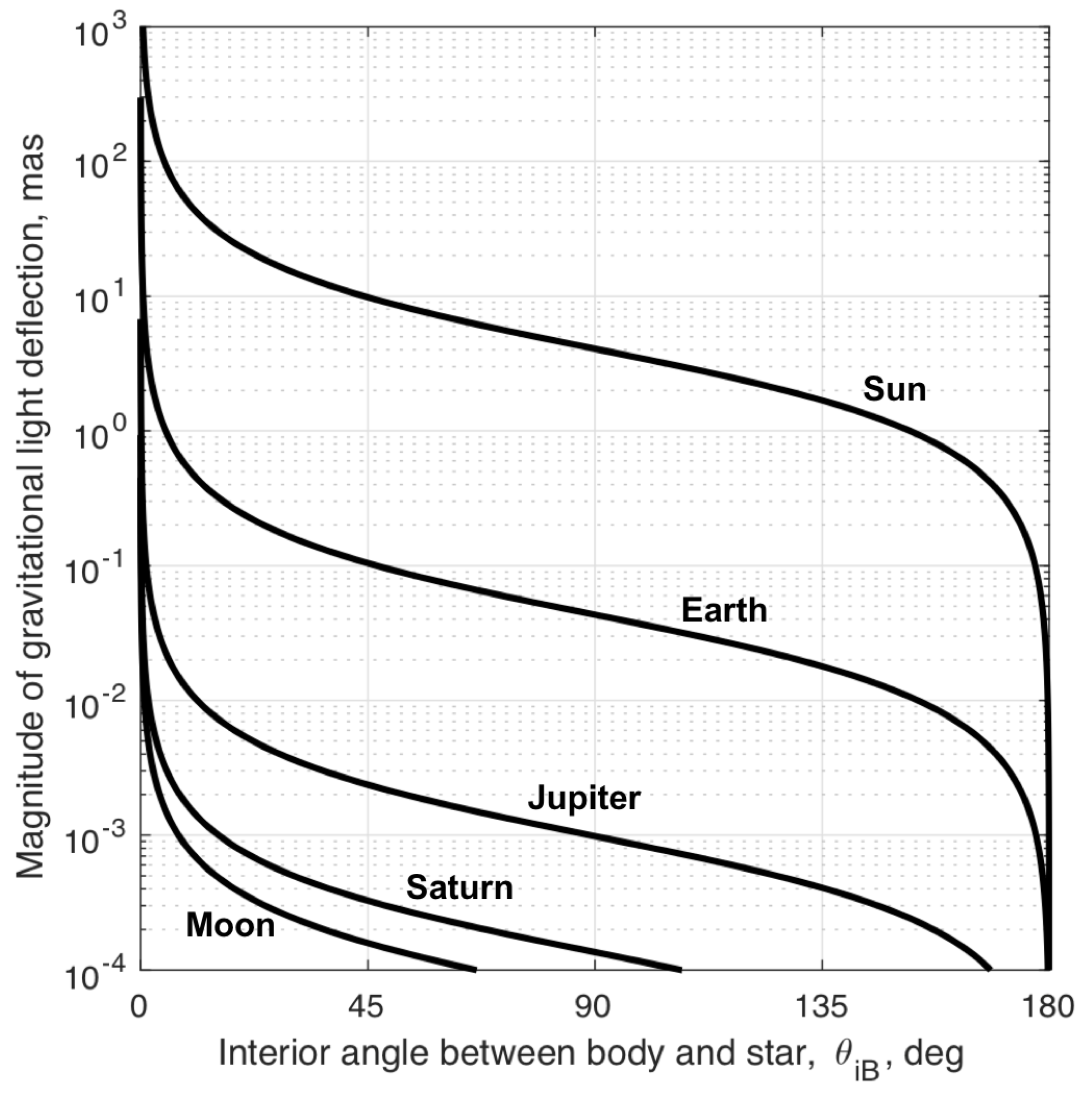
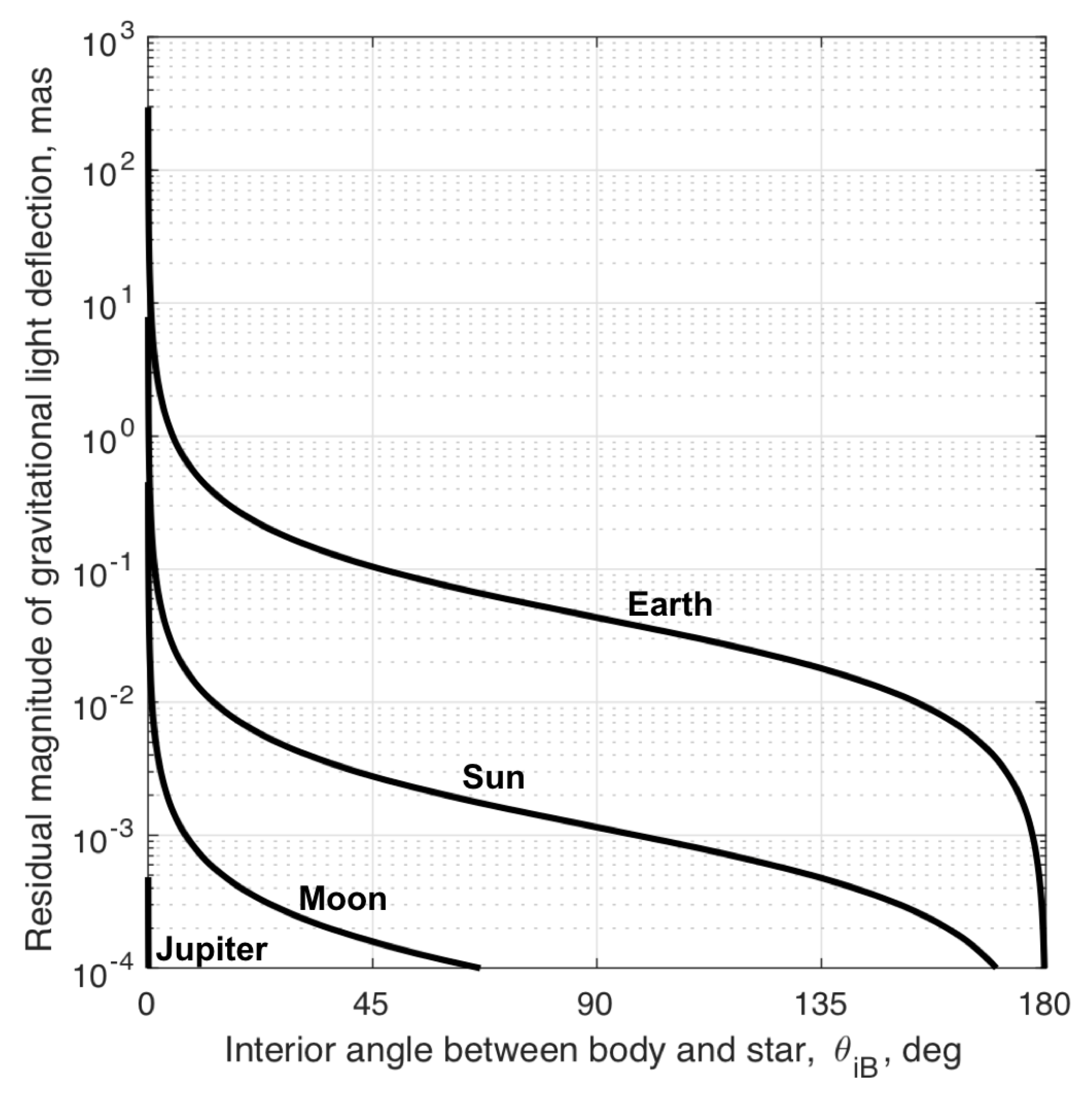
3.2.1. Gravitational Deflection of Starlight in the Solar System
3.2.2. Stellar Aberration
Effect of Stellar Aberration on Observed Direction to a Single Star
Effect of Stellar Aberration on Inter-Star Angle
3.3. Perturbations in Frequency of Stellar Spectra
3.3.1. Gravitational Blueshift/Redshift
3.3.2. Relativistic Doppler Effect
3.3.3. Remarks on the Combination of Gravitational Blueshift and Relativistic Doppler Effect
4. Preliminary Feasibility Assessment of StarNAV Measurements
4.1. Feasibility of StarNAV-SA Measurements
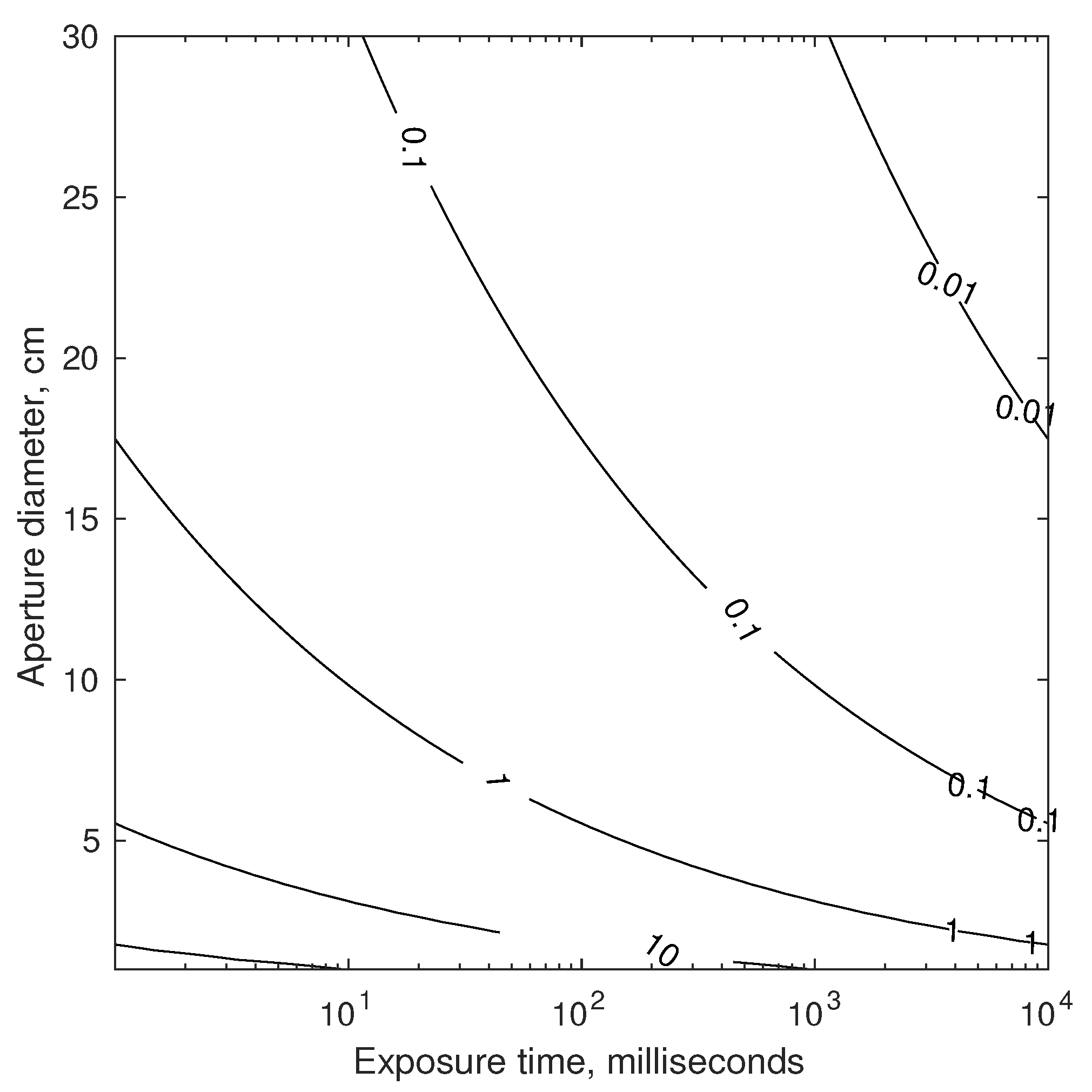
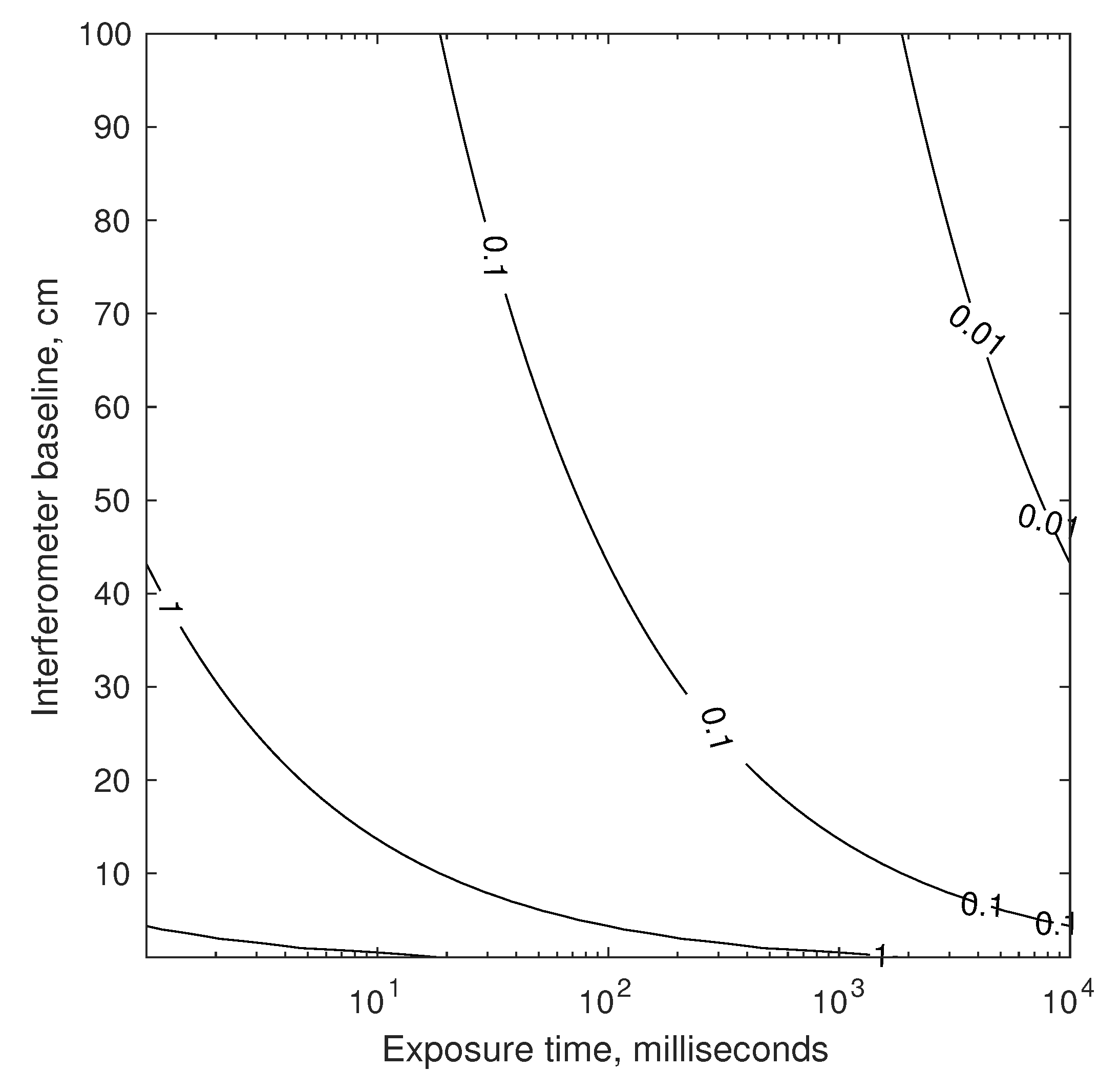
4.1.1. Performance of Candidate StarNAV-SA Optical Instruments
Telescopes
Interferometers
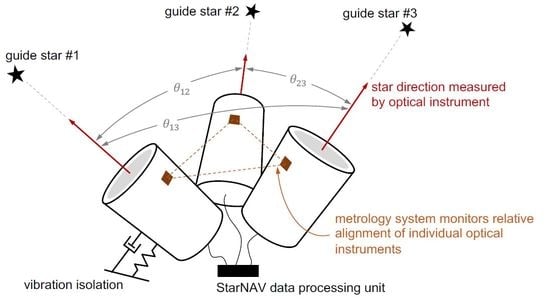
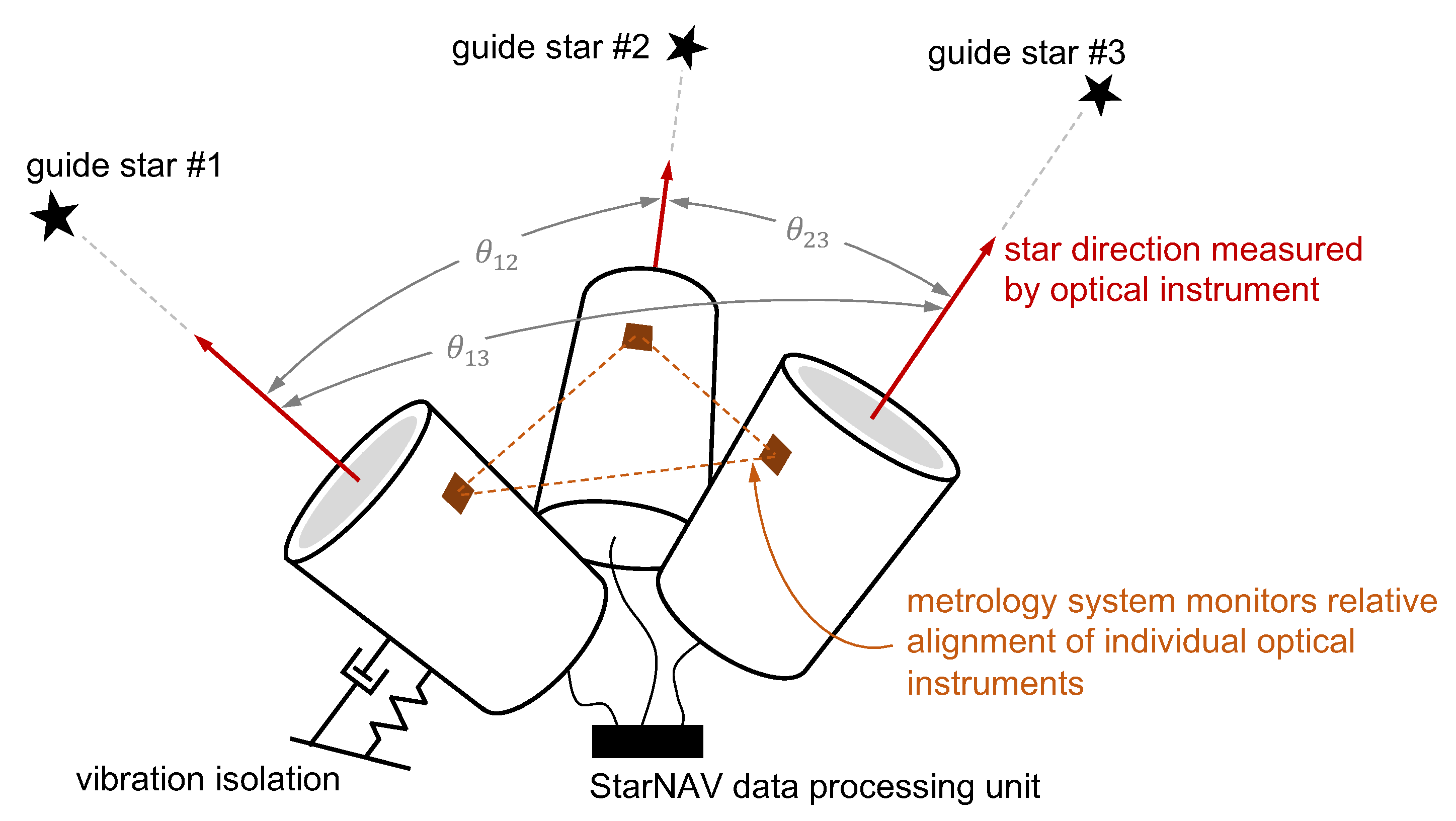
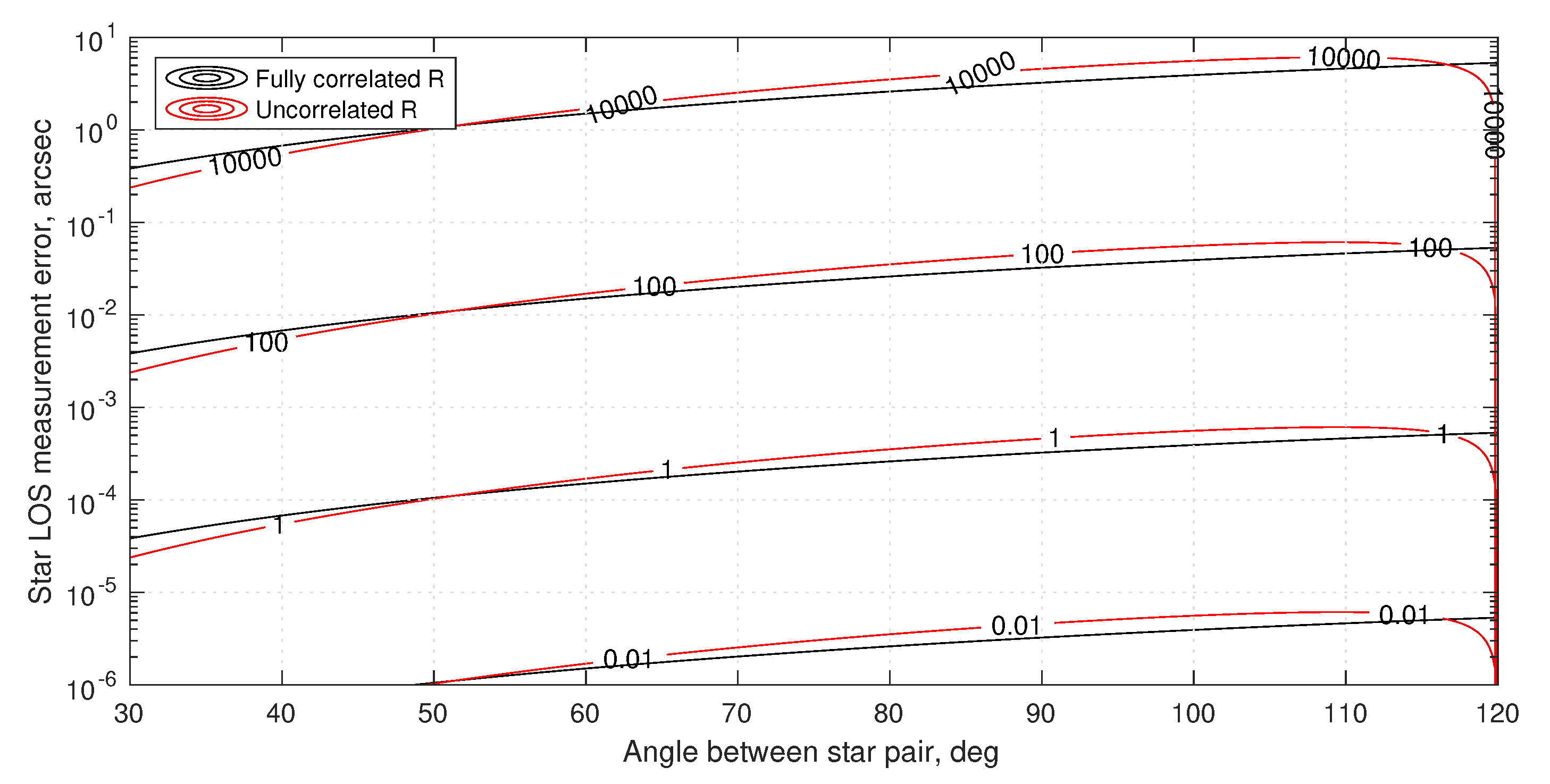
4.1.2. Instrument Alignment and Metrology
4.1.3. Instrument Platform Pointing and Vibration
4.2. Feasibility of StarNAV-DE Measurements
4.2.1. Stability of Stellar Spectra for Radial Velocity Estimation
4.2.2. Suitable Source for Frequency Calibration
4.2.3. Measuring Spectral Shift with a Navigation Instrument
5. Instantaneous Estimation of Velocity from Simultaneous Star Sightings
5.1. Representation of Spacecraft Velocity in Different Reference Frames
5.2. Instantaneous Velocity Fix from Perturbation in Absolute Star Directions
5.3. Instantaneous Velocity Fix from Perturbation of Inter-Star Angle
6. Initial Orbit Determination (IOD) using StarNAV
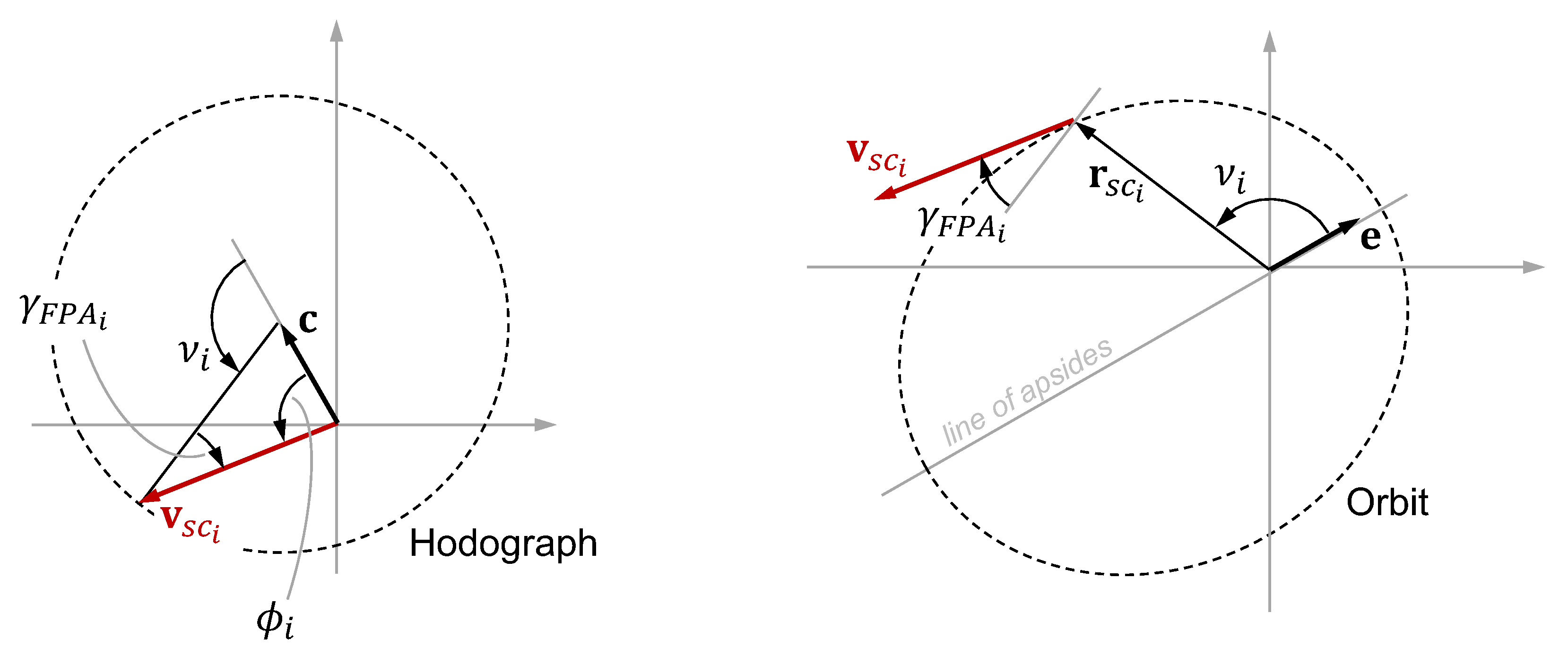
6.1. Analytic Velocity-Only IOD Solution using Geometry of the Orbital Hodograph
6.2. Improved IOD using Many Velocity Vectors Collected at Known Times
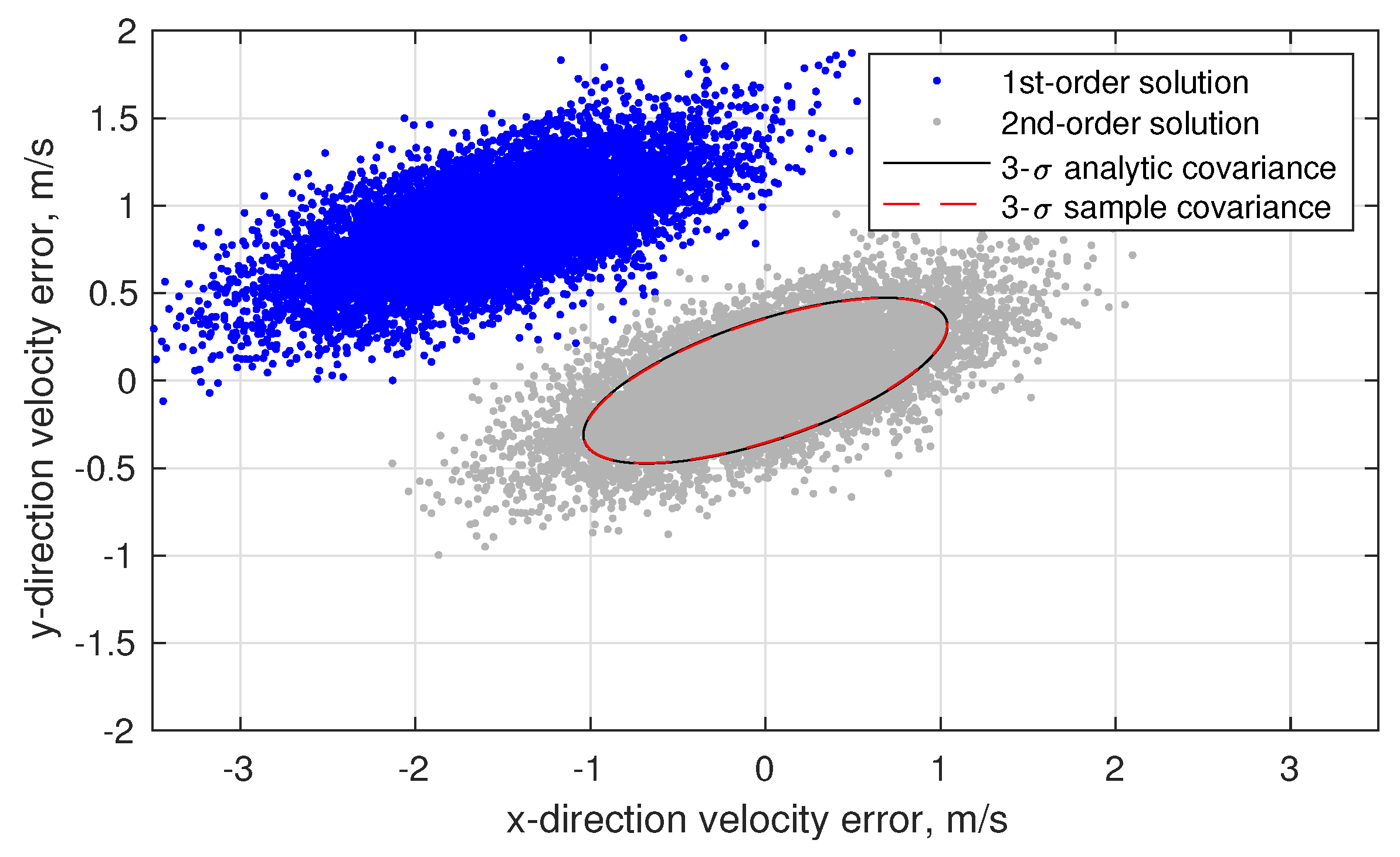
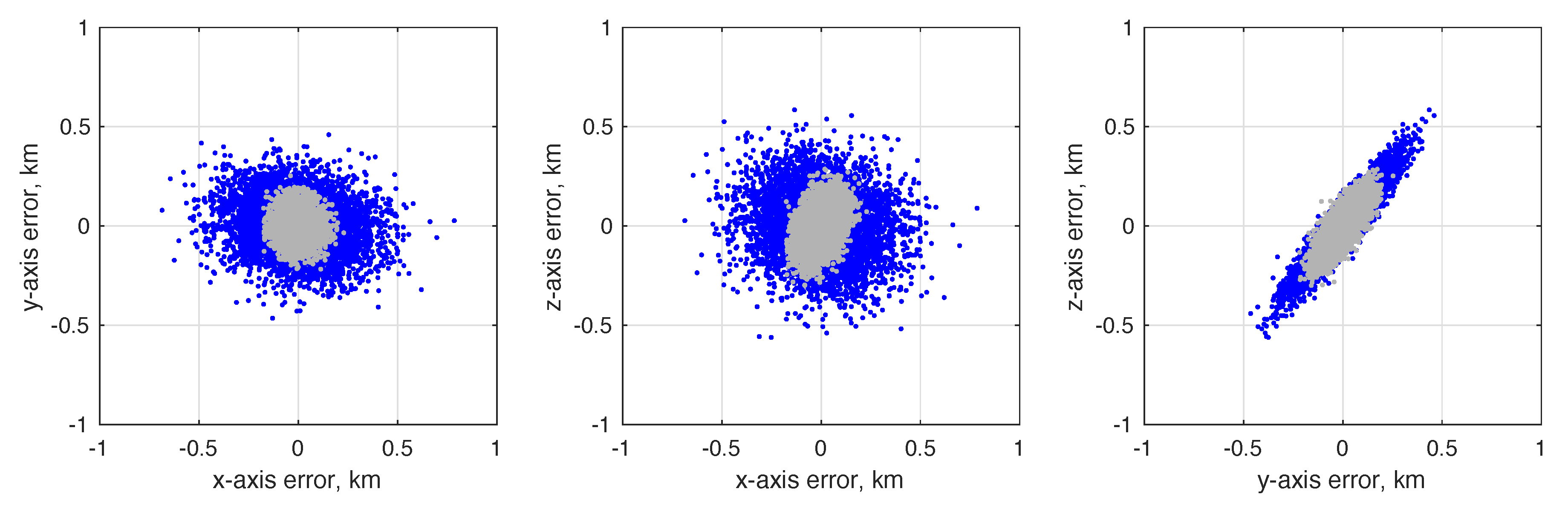
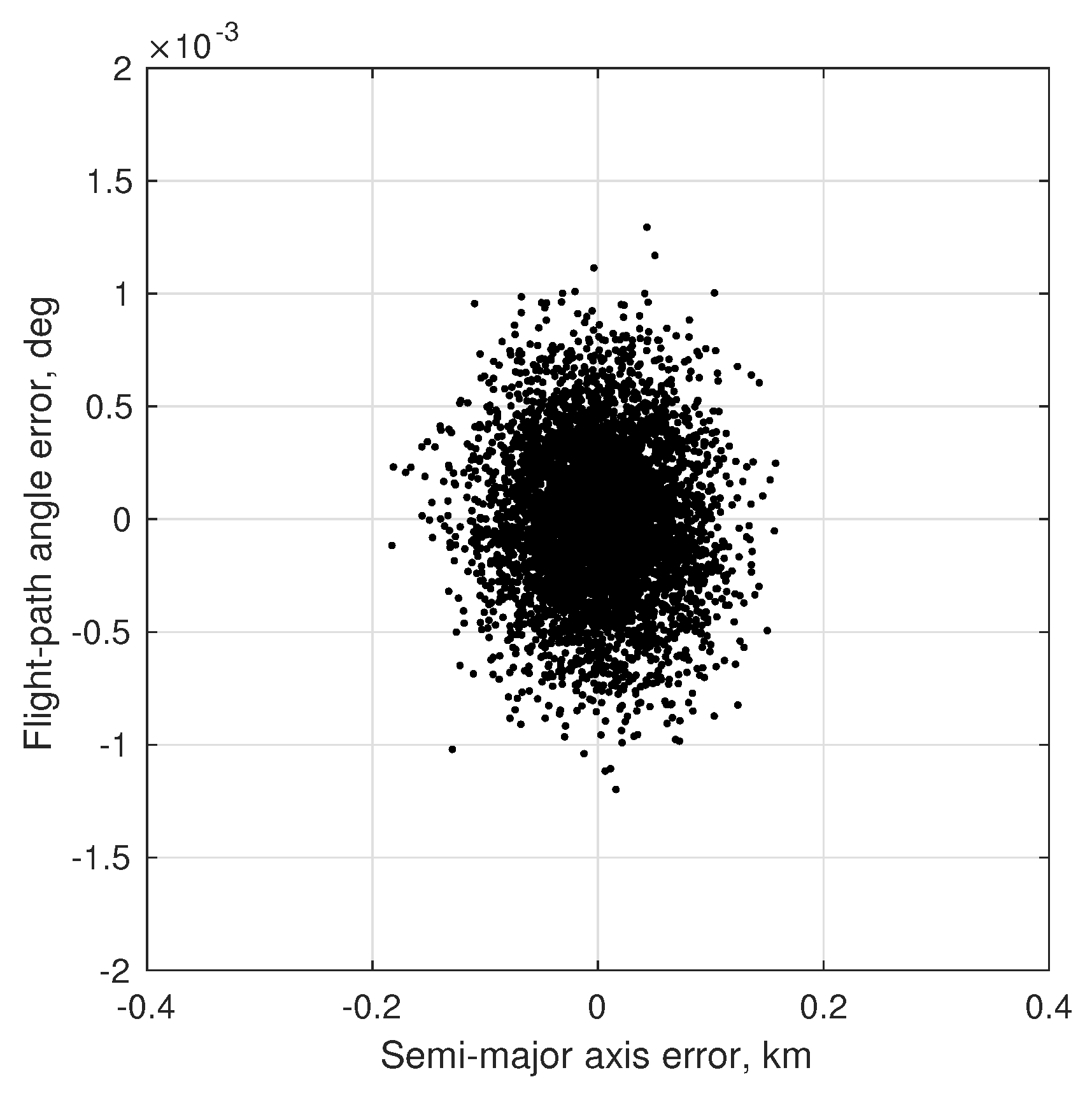
6.3. Numerical Results
7. Sequential Processing of StarNAV Observables with an Extended Kalman Filter
7.1. EKF Framework
7.1.1. State Vector Selection
7.1.2. State and Covariance Propagation
7.1.3. Measurement Update
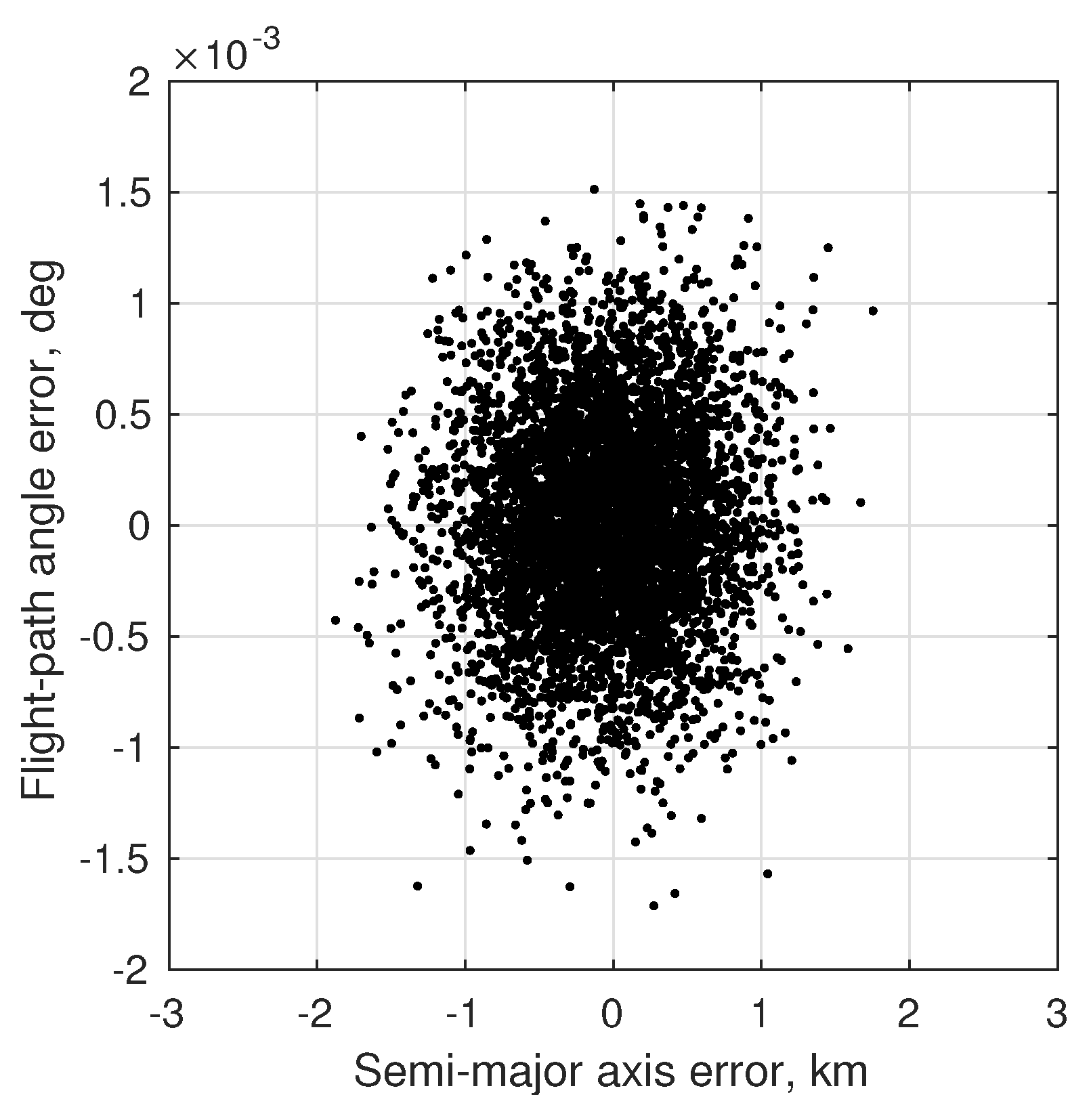
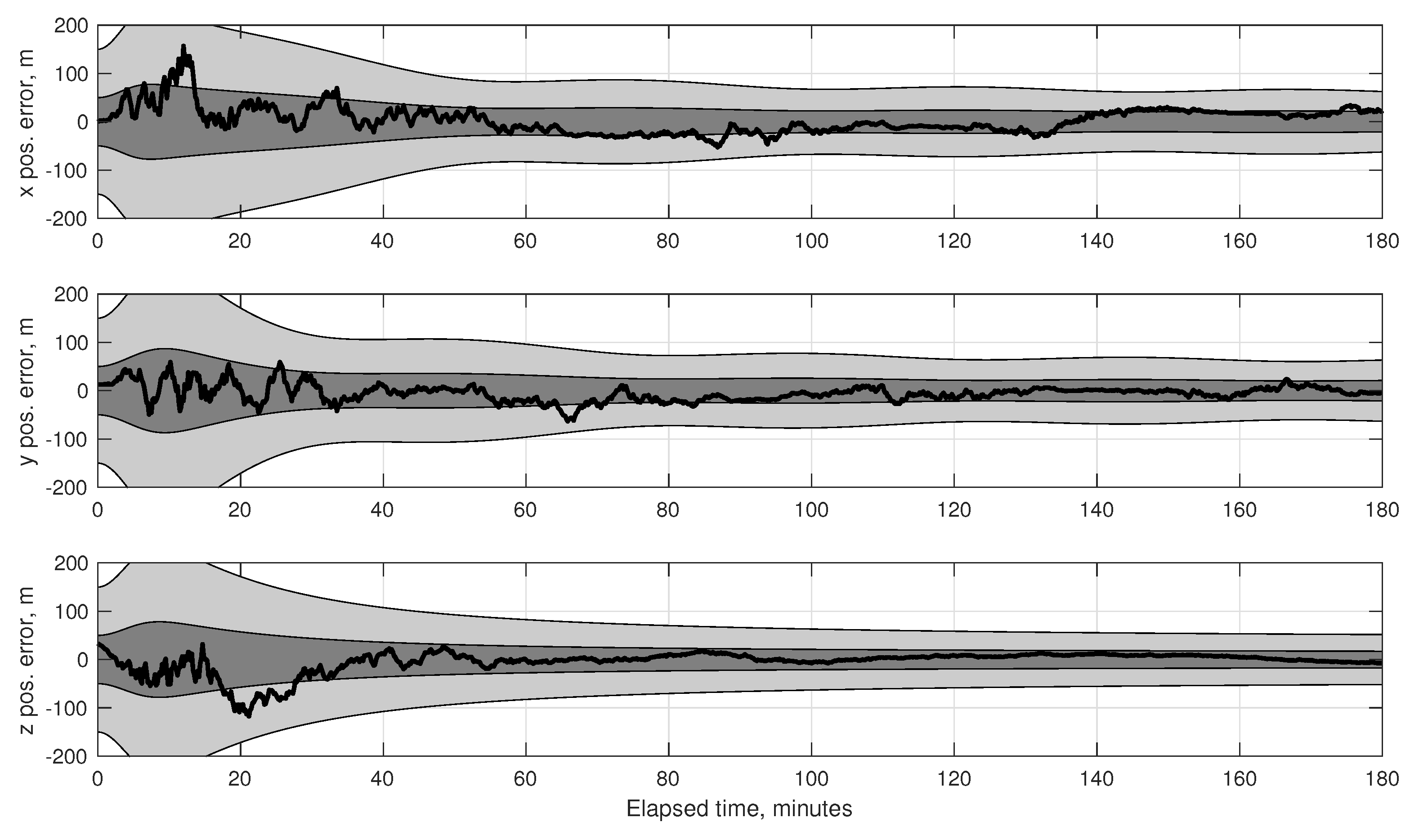
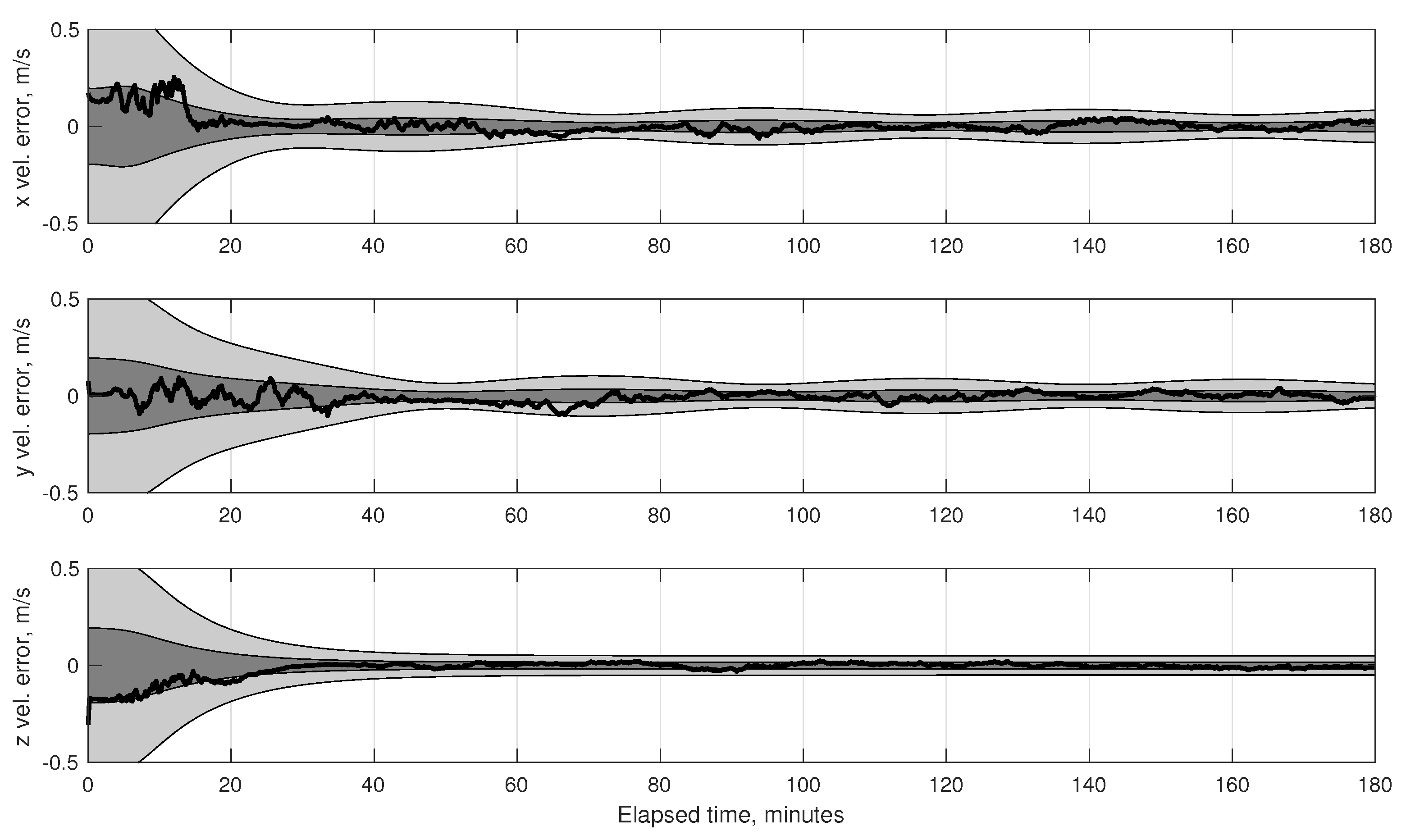
7.2. Numerical Results
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BCRF | Barycentric Celestial Reference Frame |
| CCD | Charged Couple Device |
| DSAC | Deep Space Atomic Clock |
| DSN | Deep Space Network |
| EKF | Extended Kalman Filter |
| FOGM | First Order Gauss-Markov |
| FPA | Flight Path Angle |
| GEO | Geostationary Orbit |
| GNSS | Global Navigation Satellite Systems |
| IOD | Initial Orbit Determination |
| LEO | Low Earth Orbit |
| LOS | Line of Sight |
| OPD | Optical Path Delay |
| OPNAV | Optical Navigation |
| PPN | Parameterized Post-Newtonian |
| SNR | Signal-to-Noise Ratio |
| SSB | Solar System Barycenter |
| STM | State Transition Matrix |
| XNAV | X-ray Pulsar Navigation |
Appendix A. Historical Remarks on the Lorentz Transformation and Stellar Aberration
References
- Christian, J.; Hollenberg, C. Initial Orbit Determination from Three Velocity Vectors. J. Guid. Control. Dyn. 2019, 42, 894–899. [Google Scholar] [CrossRef]
- Hollenberg, C.; Christian, J. Geometric Solutions for Problems in Velocity-Based Orbit Determination. J. Astronaut. Sci. 2019. [Google Scholar] [CrossRef]
- Christian, J. Accurate Planetary Limb Localization for Image-Based Spacecraft Navigation. J. Spacecr. Rocket. 2017, 54, 708–730. [Google Scholar] [CrossRef]
- Franklin, R.; Birx, D. A Study of Natural Electromagnetic Phenomena for Space Navigation. Proc. IRE 1960, 48, 532–541. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Z.; Zhang, W.; Xu, J. A Novel Autonomous Celestial Integrated Navigation for Deep Space Exploration Based on Angle and Stellar Spectra Shift Velocity Measurement. Sensors 2019, 19, 2555. [Google Scholar] [CrossRef] [PubMed]
- Hoag, D.; Wrigley, W. Navigation and guidance in interstellar space. Acta Astronaut. 1975, 2, 513–533. [Google Scholar] [CrossRef]
- Yucalan, D.; Peck, M. A Static Estimation Method for Autonomous Navigation of Relativistic Spacecraft. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019. [Google Scholar]
- Norton, R.; Wildey, R. Fundamental Limitations to Optical Doppler Measurements for Space Navigation. Proc. IRE 1961, 49, 1655–1659. [Google Scholar] [CrossRef]
- Melvin, P. A Kalman Filter for Orbit Determination with Applications to GPS and Stellar Navigation. Number AAS 96-145. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Austin, TX, USA, 11–15 February 1996. [Google Scholar]
- Klioner, S. A Practical Relativistic Model for Microarcsecond Astrometry in Space. Astron. J. 2003, 125, 1580–1597. [Google Scholar] [CrossRef] [Green Version]
- Lindegren, L.; Hernandez, J.; Bombrun, A.; Klioner, S.; Bastian, U.; Ramos-Lerate, M.; De Torres, A.; Steidelmüller, H.; Stephenson, C.; Hobbs, D.; et al. Gaia Data Release 2: The astrometric solution. Astron. Astrophys. 2018, 616, A2. [Google Scholar] [CrossRef]
- Sheikh, S.; Pines, D.; Ray, P.; Wood, K.; Lovelette, M.; Wolff, M. Spacecraft Navigation using X-ray Pulsars. J. Guid. Control. Dyn. 2006, 29, 49–63. [Google Scholar] [CrossRef]
- Emadzadeh, A.; Speyer, J. Navigation in Space by X-ray Pulsars; Springer: New York, NY, USA, 2011. [Google Scholar]
- Sazhin, M.; Zharov, V.; Milyukov, V.; Pshirkov, M.; Sementsov, V.; Sazhina, O. Space Navigation by X-ray Pulsars. Mosc. Univ. Phys. Bull. 2018, 73, 141–153. [Google Scholar] [CrossRef]
- Winternitz, L.; Mitchell, J.; Hassouneh, M.; Valdez, J.; Price, S.; Ray, P.; Wood, K.; Arzoumanian, Z.; Gendreau, K. SEXTANT X-ray Pulsar Navigation demonstration: Flight system and test results. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016. [Google Scholar]
- Winternitz, L.; Mitchell, J.; Hassouneh, M.; Price, S.; Semper, S.; Yu, W.; Ray, P.; Wolff, M.; Kerr, M.; Wood, K.; et al. SEXTANT X-ray Pulsar Navigation Demonstration: Additional On-Orbit Results. In Proceedings of the 15th International Conference on Space Operations, SpaceOps 2018, Marseille, France, 28 May–1 June 2018. [Google Scholar]
- Holt, G.; D’Souza, C.; Saley, D. Orion Optical Navigation Progress Toward Exploration Mission 1. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Broschart, S.; Bradley, N.; Bhaskaran, S. Optical-Based Kinematic Positioning for Deep-Space Navigation. Number AAS 17-599. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Columbia River Gorge, Stevenson, WA, USA, 20–24 August 2017. [Google Scholar]
- Broschart, S.; Bradley, N.; Bhaskaran, S. Kinematic Approximations of Position Accuracy Achieved Using Optical Observations of Distant Asteroids. J. Spacecr. Rocket. 2019. [Google Scholar] [CrossRef]
- Bradley, N.; Bhaskaran, S.; Olikara, Z.; Broschart, S. Navigation Accuracy at Jupiter and Saturn using Optical Observations of Planetary Satellites. Number AAS 19-231. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Ka’anapali, Maui, HI, USA, 13–17 January 2019. [Google Scholar]
- Bhaskaran, S.; Riedel, J.; Synnott, S.; Wang, T. The Deep Space 1 Autonomous Navigation System: A Post-Flight Analysis. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Denver, CO, USA, 14–17 August 2000. [Google Scholar]
- Ely, T.; Seubert, J.; Bell, J. Advancing Navigation, Timing, and Science with the Deep Space Atomic Clock. In Proceedings of the SpaceOps 2014 Conference, Pasadena, CA, USA, 5–9 May 2014. [Google Scholar]
- Ely, T.; Seubert, J. One-Way Radiometric Navigation with the Deep Space Atomic Clock. Number AAS 15-384. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Williamsburg, VA, USA, 11–15 January 2015. [Google Scholar]
- Ely, T.; Seubert, J.; Prestage, J.; Tjoelker, R.; Burt, E.; Dorsey, A.; Enzer, D.; Herrera, R.; Kuang, D.; Murpht, D.; et al. Overview of the Deep Space Atomic Clock Technology Demonstration Mission. Number AAS 19-796. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Kayton, M. Navigation: Ships to Space. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 474–519. [Google Scholar] [CrossRef]
- Pimenta, F. Astronomy and Navigation. In Handbook of Archaeoastronomy and Ethnoastronomy; Ruggles, C.L.N., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 43–65. [Google Scholar]
- Mörzer Bruyns, W. Sextants at Greenwich: A Catalogue of the Mariner’s Quadrants, Mariner’s Astrolabes, Cross-Staffs, Backstaffs, Octants, Sextants, Quintants, Reflecting Circles, and Artificial Horizons in the National Maritime Museum, Greenwich; Oxford University Press: New York, NY, USA, 2009; pp. 7–15. [Google Scholar]
- Tibbetts, G. Arab Navigation in the Red Sea. Geogr. J. 1961, 127, 322–334. [Google Scholar] [CrossRef]
- Levathes, L. When China Ruled the Seas: The Treasure Fleet of the Dragon Throne, 1405–1433; Open Road Distribution: New York, NY, USA, 1994; pp. 67–69. [Google Scholar]
- Lewis, D. We, the Navigators: The Ancient Art of Landfinding in the Pacific; University of Hawaii Press: Honolulu, HI, USA, 1994; pp. 82–122. [Google Scholar]
- Kanas, N. Star Maps: History, Artistry and Cartography; Praxis Publishing: Chichester, UK, 2009. [Google Scholar]
- Neugebauer, O. The Early History of the Astrolabe. Studies in Ancient Astronomy IX. ISIS 1949, 40, 240–256. [Google Scholar] [CrossRef]
- North, J. The Astrolabe. Sci. Am. 1974, 230, 96–107. [Google Scholar] [CrossRef]
- Brainard, F. The Sextant and Other Reflecting Mathematical Instruments; D. Van Nostrand Company: New York, NY, USA, 1891; pp. 7–15. [Google Scholar]
- Kaplan, G. Determining the Position and Motion of a Vessel from Celestial Observations. Navigation 1995, 42, 631–648. [Google Scholar] [CrossRef]
- Janiczek, P. STELLA: Toward Automated Celestial Navigation. Surf. Warf. 1996, 21, 34–37. [Google Scholar]
- Kaplan, G. A Navigation Solution Involving Changes to Course and Speed. Navigation 1996, 43, 470–482. [Google Scholar] [CrossRef]
- Kaplan, G. New Technology for Celestial Navigation. In Nautical Almanac Office Sesquicentennial Symposium; U.S. Naval Observatory: Washington, DC, USA, 1999. [Google Scholar]
- Parish, J.; Parish, A.; Swanzy, M.; Woodbury, D.; Mortari, D.; Junkins, J. Stellar Positioning System (Part I): An Autonomous Position Determination Solution. Navigation 2010, 57, 1–12. [Google Scholar] [CrossRef]
- Lampkin, B. Sextant Sighting Performance for Space Navigation Using Simulated and Real Celestial Targets. Navigation 1965, 12, 312–320. [Google Scholar] [CrossRef]
- Jorris, T.; Barth, A. The USAF Manned Space Navigation Experiment on Apollo and Its Implications on Advanced Manned Spacecraft. In ION National Space Meeting on Simplified Manned Guidance, Navigation and Control; United States Institute of Navigation: Cocoa Beach, FL, USA, 1968. [Google Scholar]
- Smith, D.; Lampkin, B. Sextant Sighting Measurements from On Board the Gemini XII Spacecraft; Technical Report NASA TN D-4952; National Aeronautics and Space Administration: Washington, DC, USA, 1968. [Google Scholar]
- Powers, S. Preliminary Results from Skylab Experiment T002, Manual Navigation. Navigation 1974, 21, 279–287. [Google Scholar] [CrossRef]
- Hoag, D. The History of Apollo On-board Guidance, Navigation, and Control. J. Guid. Control. Dyn. 1983, 6, 4–13. [Google Scholar] [CrossRef]
- Holt, G.; Wood, B. Sextant Navigation on the International Space Station: A Human Space Exploration Demo. Number AAS 19-064. In Proceedings of the AAS Guidance, Navigation and Control Conference, Breckenridge, CO, USA, 1–6 February 2019. [Google Scholar]
- Owen, W. Methods of Optical Navigation. Number AAS 11-215. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, New Orleans, LA, USA, 13–17 February 2011. [Google Scholar]
- Owen, W.; Duxbury, T.; Action, C.; Synnott, S.; Riedel, J.; Bhaskaran, S. A Brief History of Optical Navigation at JPL. Number AAS 08-053. In Proceedings of the AAS Guidance and Control Conference, Breckenridge, CO, USA, 1–6 February 2008. [Google Scholar]
- Campbell, J.; Synnott, S.; Bierman, G. Voyager Orbit Determination at Jupiter. IEEE Trans. Autom. Control. 1983, AC-28, 256–268. [Google Scholar] [CrossRef]
- Synnott, S.; Donegan, A.; Riedel, J.; Stuve, J. Interplanetary Optical Navigation: Voyager Uranus Encounter. In Proceedings of the AIAA/AAS Astrodynamics Conference, Williamsburg, VA, USA, 18–20 August 1986. [Google Scholar]
- Riedel, J.; Owen, W.; Stuve, J. Optical Navigation During the Voyager Neptune Encounter. In Proceedings of the AIAA/AAS Astrodynamics Conference, Portland, OR, USA, 20–22 August 1990. [Google Scholar]
- Gillam, S.; Owen, W.; Vaughan, A.; Wang, T.; Costello, J.; Jacobson, R.; Bluhm, D.; Pojman, J.; Ionasescu, R. Optical Navigation for the Cassini/Huygens Mission. Number AAS 07-252. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Mackinac Island, MI, USA, 19–23 August 2007. [Google Scholar]
- Owen, W.; Dumont, P.; Jackman, C. Optical Navigation Preparations for New Horizons Pluto Flyby. In Proceedings of the 23rd International Symposium on Space Flight Dynamics (ISSFD), Pasadena, CA, USA, 29 October–2 November 2012. [Google Scholar]
- Liebe, C.C. Star Trackers for Attitude Determination. IEEE Aerosp. Electron. Syst. Mag. 1995, 10, 10–16. [Google Scholar] [CrossRef]
- Liebe, C.C. Accuracy Performance of Star Trackers—A Tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Markley, F.; Crassidis, J. Fundamentals of Spacecraft Attitude Determination and Control; Springer: New York, NY, USA, 2014. [Google Scholar]
- Blue Canyon Technologies. Star Trackers. Specification Sheet; Blue Canyon Technologies: Boulder, CO, USA, 2019. [Google Scholar]
- Ball Aerospace. CT-2020. Specification Sheet; Ball Aerospace: Boulder, CO, USA, 2018. [Google Scholar]
- Sodern Ariane Group. Hydra-M Two Heads Star Tracker. Specification Sheet; Sodern Ariane Group: Limeil-Brevannes, France, 2017. [Google Scholar]
- Shuster, M. Stellar Aberration and Parallax: A Tutorial. J. Astronaut. Sci. 2003, 51, 477–494. [Google Scholar]
- Yim, J.; Crassidis, J.; Junkins, J. Autonomous Navigation of an Interplanetary Spacecraft. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Denver, CO, USA, 14–17 August 2000. [Google Scholar]
- Sinclair, A.; Henderson, T.; Hurtado, J.; Junkins, J. Development of Spacecraft Orbit Determination and Navigation using Solar Doppler Shift. Number AAS 03-159. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Big Sky, MT, USA, 3–7 August 2003. [Google Scholar]
- Henderson, T.; Pollock, T.; Sinclair, A.; Theisinger, J.; Hurtado, J.; Junkins, J. Hardware Development and Measurements of Solar Doppler Shift for Spacecraft Orbit Determination. Number AAS 03-613. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Big Sky, MT, USA, 3–7 August 2003. [Google Scholar]
- Hindman, G. Apparatus, System and Method for Spacecraft Navigation Using Extrasolar Planetary Systems. U.S. Patent Application Publication US 2013/0006449 A1, 3 January 2013. [Google Scholar]
- Liu, J.; Fang, J.C.; Liu, G. Solar Frequency Shift-Based Radial Velocity Difference Measurement for Formation Flight and Its Integrated Navigation. J. Aerosp. Eng. 2017, 30. [Google Scholar] [CrossRef]
- Ning, X.; Gui, M.; Zhang, J.; Fang, J.; Liu, F. Solar oscillation time delay measurement assisted celestial navigation method. Acta Astronaut. 2017, 134, 152–158. [Google Scholar] [CrossRef]
- Ning, X.; Gui, M.; Fang, J.; Liu, G.; Wu, W. A Novel Autonomous Celestial Navigation Method Using Solar Oscillation Time Delay Measurement. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1392–1403. [Google Scholar] [CrossRef]
- Pantalone, B.; Kudenov, M. Initial orbit determination using Doppler shift of Fraunhofer lines. Celest. Mech. Dyn. Astron. 2018, 130, 80. [Google Scholar] [CrossRef]
- Oliver, B. The view from the starship bridge and other observations. IEEE Spectr. 1964, 1, 86–92. [Google Scholar] [CrossRef]
- Moskowitz, S.; Devereux, W. Trans-Stellar Space Navigation. AIAA J. 1968, 6, 1021–1029. [Google Scholar] [CrossRef]
- McMaster, D. Navigational Techniques for Interstellar Relativistic Flight. Master’s Thesis, Air Force Institute of Technology, Wright-Patterson AFB, Dayton, OH, USA, 1971. [Google Scholar]
- Wertz, J. Insterstellar Navigation. Spaceflight 1972, 14, 206–216. [Google Scholar]
- Calabro’, E. Relativistic aberrational interstellar navigation. Acta Astronaut. 2011, 69, 360–364. [Google Scholar] [CrossRef]
- Perryman, M. The history of astrometry. Eur. Phys. J. H 2012, 37, 745–792. [Google Scholar] [CrossRef] [Green Version]
- Seidelmann, K. Explanatory Supplement to the Astronomical Almanac; University Science Books: Sausalito, CA, USA, 2006; pp. 128–130, 609–664. [Google Scholar]
- Perryman, M.; Lindegren, L.; Kovalevsky, J.; Hoeg, E.; Bastian, U.; Bernacca, P.; Crézé, M.; Donati, F.; Grenon, M.; Grewing, M.; et al. The Hipparcos Catalogue. Astron. Astrophys. 1997, 323, L49–L52. [Google Scholar]
- van Leeuwen, F. Validation of the new Hipparcos reduction. Astron. Astrophys. 2007, 474, 653–664. [Google Scholar] [CrossRef] [Green Version]
- Gaia Collaboration. Gaia Data Release 2: Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef]
- van Leeuwen, F. The Hipparcos Mission. Space Sci. Rev. 1997, 81, 201–409. [Google Scholar] [CrossRef]
- Gaia Collaboration. The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar] [CrossRef]
- Feissel, M.; Mignard, F. The adoption of ICRS on 1 January 1998: Meaning and consequences. Astron. Astrophys. 1998, 331, L33–L36. [Google Scholar]
- Ma, C.; Arias, E.; Eubanks, T.; Fey, A.; Gontier, A.; Jacobs, C.; Sovers, O.; Archinal, B.; Charlot, P. The International Celestial Reference Frame as Realized by Very Long Baseline Interferometry. Astron. J. 1998, 116, 516–546. [Google Scholar] [CrossRef]
- Fey, A.; Gordon, D.; Jacobs, C.S.; Ma, C.; Gaume, R.A.; Arias, E.F.; Bianco, G.; Boboltz, D.A.; Böckmann, S.; Bolotin, S.; et al. The Second International Celestial Reference Frame by Very Long Baseline Interferometry. Astron. J. 2015, 150. [Google Scholar] [CrossRef]
- Gordon, D. ICRF3: A New Realization of the International Celestial Reference Frame. Number G42A-01. In Proceedings of the American Geophysical Union, Fall Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Lindegren, L.; Lammers, U.; Hobbs, D.; O’Mullane, W.; Bastian, U.; Hernández, J. The astrometric core solution for the Gaia mission: Overview of models, algorithms, and software implementation. Astron. Astrophys. 2012, 538, A78. [Google Scholar] [CrossRef]
- Karimi, R.; Mortari, D. Interplanetary Autonomous Navigation Using Visible Planets. J. Guid. Control. Dyn. 2015, 38, 1151–1156. [Google Scholar] [CrossRef]
- Morgan, W.; Keenan, P.; Kellman, E. An Atlas of Stellar Spectra with an Outline of Spectral Classification; University of Chicago Press: Chicago, IL, USA, 1943. [Google Scholar]
- Lindegren, L.; Dravins, D. The fundamental definition of “radial velocity”. Astron. Astrophys. 2003, 401, 1185–1201. [Google Scholar] [CrossRef]
- Bessell, M. Standard Photometric Systems. Annu. Rev. Astron. Astrophys. 2005, 43, 293–336. [Google Scholar] [CrossRef] [Green Version]
- Johnson, H.; Morgan, W. Fundamental Stellar Photometry for Standards of Spectral Type on the Revised System of the Yerkes Spectral Atlas. Astrophys. J. 1953, 117, 313–352. [Google Scholar] [CrossRef]
- Cousins, A. VRI Standards in the E Regions. Mem. R. Astron. Soc. 1976, 81, 25–36. [Google Scholar]
- Smith, J.; Tucker, D.L.; Kent, S.; Richmond, M.W.; Fukugita, M.; Ichikawa, T.; Ichikawa, S.I.; Jorgensen, A.M.; Uomoto, A.; Gunn, J.E.; et al. The u′g′r′i′z′ Standard-Star System. Astron. J. 2002, 123, 2121–2144. [Google Scholar] [CrossRef]
- Jordi, C.; Gebran, M.; Carrasco, J.; Bruijne, J.; Voss, H.; Fabricius, C.; Kunde, J.; Vallenari, A.; Kohley, R.; Mora, A. Gaia broad band photometry. Astron. Astrophys. 2010, 523, A48. [Google Scholar] [CrossRef]
- Schumaker, B. Apparent Brightness of Stars and Lasers. Telecommun. Data Acquis. Prog. Rep. 1988, 42–93, 111–130. [Google Scholar]
- Bessell, M. UBVRI Photometry II: The Cousins VRI System, its Temperature and Absolute Flux Calibration, and Relevance for Two-Dimensional Photometry. Publ. Astron. Soc. Pac. 1979, 91, 589–607. [Google Scholar] [CrossRef]
- Planck, M. Über eine Verbesserung der Wien’schen Spectralgleichung. Verhandlungen der Deutschen Physikalischen Gesellschaft 1900, 2, 202–204. [Google Scholar]
- Holst, G.; Lomheim, T. CMOS/CCD Sensors and Camera Systems; JCD Publishing and SPIE Press: Winter Park, FL, USA, 2007. [Google Scholar]
- Turon, C.; Crézé, M.; Egret, D.; Gomez, A.; Grenon, M.; Jahreiß, H.; Réquième, Y.; Argue, A.N.; Bec-Borsenberger, A.; Dommanget, J.; et al. Version 2 of the HIPPARCOS Input Catalogue. Bulletin d’Information du Centre de Données Stellaires 1993, 43, 5–6. [Google Scholar]
- Brumberg, V.; Klioner, S.; Kopeikin, S. Relativistic reduction of astrometric observations at POINTS level of accuracy. In Proceedings of the 141st IAU Symposium on Inertial Coordinate System on the Sky, Leningrad, Russia, 17–21 October 1990. [Google Scholar]
- Will, C. Theoretical Frameworks for Testing Relativistic Gravity. II. Parametrized Post-Newtonian Hydrodynamics, and the Nordtvedt Effect. Astrophys. J. 1971, 163, 611. [Google Scholar] [CrossRef]
- Will, C. Theory and Experiment in Gravitational Physics; Cambridge University Press: New York, NY, USA, 1981; pp. 86–115, 167–173. [Google Scholar]
- Will, C. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef]
- Bradley, J. IV. A letter from the Reverend Mr. James Bradley Savilian Professor of Astronomy at Oxford, and F. R. S. to Dr. Edmond Halley Astronom. Reg. & c. giving an account of a new discovered motion of the fix’d stars. Philos. Trans. R. Soc. 1728, 34, 637–661. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Annalen der Physik 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Norton, J. Einstein’s Investigations of Galilean Covariant Electrodynamics Prior to 1905. Arch. Hist. Exact Sci. 2004, 59, 45–105. [Google Scholar] [CrossRef]
- Linet, B.; Teyssandier, P. Time transfer and frequency shift to the order 1/c4 in the field of an axisymmetric rotating body. Phys. Rev. D 2002, 66, 024045. [Google Scholar] [CrossRef]
- Kopeikin, S.; Ozernoy, L. Post-Newtonian Theory for Precision Doppler Measurements of Binary Star Orbits. Astrophys. J. 1999, 523, 771–785. [Google Scholar] [CrossRef]
- Moskowitz, S.; Devereux, W. Navigational Aspects of Transstellar Space Flight. Adv. Space Sci. Technol. 1970, 10, 75–126. [Google Scholar] [CrossRef]
- Benhacine, L. Optical Aberrations and their Effect on the Centroid Location of Unresolved Objects. Master’s Thesis, West Virginia University, Morgantown, VA, USA, 2017. [Google Scholar]
- Lindegren, L.; Bastian, U. Basic Principles of Scanning Space Astrometry. Eur. Astron. Soc. Publ. Ser. 2010, 45, 109–114. [Google Scholar] [CrossRef]
- Falconi, O. Maximum Sensitivities of Optical Direction and Twist Measuring Instruments. J. Opt. Soc. Am. 1964, 54, 1315–1320. [Google Scholar] [CrossRef]
- Lindegren, L. Photoelectric Astrometry—A Comparison of Methods for Precise Image Location. In Proceedings of the International Astronomical Union Colloquium No. 48, Vienna, Austria, 12–14 September 1978; pp. 197–217. [Google Scholar]
- Lindegren, L. High-accuracy positioning: Astrometry. In Observing Photons in Space: A Guide to Experimental Space Astronomy; Springer: New York, NY, USA, 2013; pp. 299–311. [Google Scholar]
- Kirchhoff, G. Zur Theorie der Lichtstrahlen. Annalen der Physik 1883, 254, 663–695. [Google Scholar] [CrossRef] [Green Version]
- Fowles, G. Introduction to Modern Optics, 2nd ed.; Dover: New York, NY, USA, 1989; pp. 108–111, 114–125. [Google Scholar]
- Airy, G. On the Diffraction of an Object-glass with Circular Aperture. Trans. Camb. Philos. Soc. 1835, 5, 283–291. [Google Scholar]
- Rayleigh, L. XXXI. Investigations in optics, with special reference to the spectroscope. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1879, 8, 261–274. [Google Scholar] [CrossRef]
- Monnier, J. Optical interferometry in astronomy. Rep. Prog. Phys. 2003, 66, 789–857. [Google Scholar] [CrossRef] [Green Version]
- Quirrenbach, A. Optical Interferometry. Annu. Rev. Astron. Astrophys. 2001, 39, 353–401. [Google Scholar] [CrossRef]
- Celestron. Astro Fi Instruction Manual, Model # 22201, 22202, 22203; Celestron: Torrance, CA, USA, 2018. [Google Scholar]
- Arnoix, J. Star sensor baffle optimization: Some helpful practical design rules. Proc. SPIE 1996, 2864, 333–338. [Google Scholar] [CrossRef]
- Reasenberg, R.; Babcock, R.; Murison, M.; Noecker, M.; Phillips, J.; Schumaker, B.; Ulvestad, J. POINTS: An astrometric spacecraft with multifarious applications. Proc. SPIE 1994, 2200, 2–17. [Google Scholar] [CrossRef]
- Loiseau, S.; Shaklan, S. Optical design, modelling and tolerancing of a Fizeau interferometer dedicated to astrometry. Astron. Astrophys. Suppl. Ser. 1996, 117, 167–178. [Google Scholar] [CrossRef] [Green Version]
- Shao, M. SIM: The space interferometry mission. Proc. SPIE 1998, 3350, 536–540. [Google Scholar] [CrossRef]
- Loreggia, D.; Gardiol, D.; Gai, M.; Lattanzi, M.; Busonero, D. Fizeau interferometer for global astrometry in space. Appl. Opt. 2004, 42, 721–728. [Google Scholar] [CrossRef] [PubMed]
- Michelson, A.; Pease, F. Measurement of the Diameter of α Orionis with the Interferometer. Astrophys. J. 1920, 53, 249–259. [Google Scholar] [CrossRef]
- Tango, W.; Twiss, R. Michelson Stellar Interferometry. Prog. Opt. 1980, 17, 239–277. [Google Scholar] [CrossRef]
- Halverson, S.; Kuhnert, A.; Logan, J.; Regehr, M.; Shaklan, S.; Spero, R.; Zhao, F.; Chang, T.; Schmidtlin, E.; Gutierrez, R.; et al. Progress towards picometer accuracy laser metrology for the space interferometry mission. Proc. SPIE 2000, 10569, 1056919. [Google Scholar] [CrossRef]
- Halverson, S.; Alvarez-Salazar, O.; Azizi, A.; Dekens, F.; Nemati, B.; Zhao, F. Progress towards picometer accuracy laser metrology for the space interferometry mission: Update. Proc. SPIE 2004, 10569, 1056919. [Google Scholar] [CrossRef]
- Grogan, R.; Blackwood, G.; Calvet, R. Optical delay line nanometer-level pathlength control law design for space-based interferometry. Proc. SPIE 1998, 3350, 14–25. [Google Scholar] [CrossRef]
- Laskin, R. Space Interferometry Mission (SIM): Technology completion and transition to flight. Proc. SPIE 2004, 5491, 334–352. [Google Scholar] [CrossRef]
- Reasenberg, R.; Babcock, R.; Phillips, J.D.; Johnston, K.J.; Simon, R. Newcomb: A POINTS precursor mission with scientific capacity. Proc. SPIE 1993, 1947, 272–281. [Google Scholar] [CrossRef]
- Reasenberg, R.; Babcock, R.; Phillips, J.; Johnston, K.; Simon, R. Newcomb: A scientific interferometry mission at low cost. Proc. SPIE 1994, 2200, 18–26. [Google Scholar] [CrossRef]
- Jamieson, T. Athermalization of optical instruments from the optomechanical viewpoint. Proc. SPIE 1992, 10265, 1026508. [Google Scholar] [CrossRef]
- Wingate, C.; Coughlin, T.; Sullivan, R. An ultra stable optical bench for the magnetic survey satellite. Acta Astronaut. 1980, 7, 1389–1401. [Google Scholar] [CrossRef]
- Robertson, D.; Fitzsimons, E.; Killow, C.; Perreur-Lloyd, M.; Ward, H.; Bryant, J.; Cruise, A.; Dixon, G.; Hoyland, D.; Smith, D.; et al. Construction and testing of the optical bench for LISA Pathfinder. Class. Quantum Gravity 2013, 30, 085006. [Google Scholar] [CrossRef] [Green Version]
- Shao, M.; Colavita, M.; Hines, B.; Staelin, D.; Hutter, D.; Johnston, K.; Mozurkewich, D.; Simon, R.; Hershey, J.; Hughes, A.; et al. The Mark III stellar interferometer. Astron. Astrophys. 1988, 193, 357–371. [Google Scholar]
- Shao, M.; Colavita, M.; Hines, B.; Hershey, J.; Hughes, J.; Hutter, D.; Kaplan, G.; Johnston, K.; Mozurkwich, D.; Simon, R.; et al. Wide-Angle Astrometry with the Mark III Stellar Interferometer. Astron. J. 1990, 100, 1701–1711. [Google Scholar] [CrossRef]
- Hutter, D.; Elias, N. Array metrology system for an optical long-baseline interferometer. Proc. SPIE 2003, 4838, 1234–1245. [Google Scholar] [CrossRef]
- Gai, M.; Busonero, D.; Riva, A. A metrology concept for multiple telescope astrometry. Proc. SPIE 2012, 8442, 84421O. [Google Scholar] [CrossRef]
- Gielesen, W.; de Bruijn, D.; van den Dool, T.; Kamphues, F.; Mekking, J.; Calvel, B.; Laborie, A.; Coatantiec, C.; Touzeau, S.; Erdmann, M.; et al. Gaia basic angle monitoring system. Proc. SPIE 2013, 8863, 88630G. [Google Scholar] [CrossRef]
- Mora, A.; Bastian, U.; Biermann, M.; Chassat, F.; Lindegren, L.; Serraller, I.; Serpell, E.; van Reeven, W. The Gaia Basic angle: Measurement and variations. Eur. Astron. Soc. Publ. Ser. 2014, 68, 65–68. [Google Scholar] [CrossRef]
- Beals, G.; Crum, R.; Dougherty, H.; Hegel, D.; Kelley, J.; Rodden, J. Hubble Space Telescope Precision Pointing Control System. J. Guid. Control. Dyn. 1988, 11, 119–123. [Google Scholar] [CrossRef]
- Lee, A.; Yu, J.; Kahn, P.; Stoller, R. Space Interferometry Mission Spacecraft Pointing Error Budgets. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 502–514. [Google Scholar] [CrossRef]
- Brugarolas, P.; Kang, B. Instrument pointing control system for the Stellar Interferometry Mission: Planet Quest. Proc. SPIE 2006, 6268, 626825. [Google Scholar] [CrossRef]
- Pong, C.; Smith, M.; Knutson, M.; Lim, S.; Miller, D.; Seager, S.; Villaseñor, J.; Murphy, D. One-Arcsecond Line-of-Sight Pointing Control on ExoplanetSat, A Three-Unit CubeSat. Number AAS 11-035. In Proceedings of the AAS Guidance and Control Conference, Breckenridge, CO, USA, 4–9 February 2011. [Google Scholar]
- Nguyen, T.; Morgan, E.; Vanderspek, R.; Levine, A.; Kephart, M.; Francis, J.; Zapetis, J.; Cahoy, K.; Ricker, G. Fine-pointing performance and corresponding photometric precision of the Transiting Exoplanet Survey Satellite. J. Astron. Telesc. Instrum. Syst. 2018, 4, 047001. [Google Scholar] [CrossRef]
- Masterson, R.; Miller, D.; Grogan, R. Development and Validation of Reaction Wheel Disturbance Models: Empirical Model. J. Sound Vib. 2002, 249, 575–598. [Google Scholar] [CrossRef]
- Oaida, B.; Bayard, D.; Abrahamson, M. On-orbit measurements of ISS vibrations during OPALS extended mission operations. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar] [CrossRef]
- Cobb, R.; Sullivan, J.; Das, A.; Davis, L.; Hyde, T.; Davis, T.; Rahman, Z.; Spanos, J. Vibration isolation and suppression system for precision payloads in space. Smart Mater. Struct. 1999, 8, 798–812. [Google Scholar] [CrossRef]
- Bronowicki, A.; MacDonald, R.; Gursel, Y.; Goullioud, R.; Neville, T.; Platus, D. Dual Stage Passive Vibration Isolation for Optical Interferometer Missions. Proc. SPIE 2002, 4852, 753–763. [Google Scholar] [CrossRef]
- Winthrop, M.; Cobb, R. Survey of state-of-the-art vibration isolation research and technology for space applications. Proc. SPIE 2003, 5052, 13–26. [Google Scholar] [CrossRef]
- Cropper, M.; Katz, D.; Sartoretti, P.; Prusti, T.; De Bruijne, J.H.J.; Chassat, F.; Charvet, P.; Boyadjian, J.; Perryman, M.; Sarri, G.; et al. Gaia Data Release 2: Gaia Radial Velocity Spectrometer. Astron. Astrophys. 2018, 616, A5. [Google Scholar] [CrossRef]
- Dumusque, X.; Udry, S.; Lovis, C.; Santos, N.; Monteiro, M. Planetary detection limits taking into account stellar noise I. Observational strategies to reduce stellar oscillation and granulation effects. Astron. Astrophys. 2011, 525, A140. [Google Scholar] [CrossRef]
- Kjeldsen, H.; Bedding, T.; Arentoft, T.; Butler, P.; Dall, T.; Karoff, C.; Kiss, L.; Tinney, C.; Chaplin, W. The Amplitude of Solar Oscillations using Stellar Techniques. Astrophys. J. 2008, 682, 1370–1375. [Google Scholar] [CrossRef]
- Schrijver, C.; Zwaan, C. Solar and Stellar Magnetic Activity; Cambridge University Press: Cambridge, UK, 2000; pp. 45–59. [Google Scholar]
- Schmidt, W.; Grossmann-Doerth, U.; Schröter, E. The solar granulation in the vicinity of sunspots. Astron. Astrophys. 1988, 197, 306–310. [Google Scholar]
- Smith, M.; Huang, Y.; Livingston, W. The Amplification of Solar-Line Asymmetries by Rotation. Publ. Astron. Soc. Pac. 1987, 98, 297–302. [Google Scholar] [CrossRef]
- Lagrange, A.; Meunier, N.; Desort, M. Using the Sun to estimate Earth-like planets detection capabilities I. Impacts of cold spots. Astron. Astrophys. 2010, 512, A38. [Google Scholar] [CrossRef]
- Meunier, N.; Desort, M.; Lagrange, A. Using the Sun to estimate Earth-like planets detection capabilities II. Impacts of plages. Astron. Astrophys. 2010, 512, A39. [Google Scholar] [CrossRef]
- Busse, F. Differential Rotation in Stellar Convection Zones. Astrophys. J. 1970, 159, 629. [Google Scholar] [CrossRef]
- Pepe, F.; Ehrenreich, D.; Meyer, M. Instrumentation for the detection and characterization of exoplanets. Nature 2014, 513, 358–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaplin, W.; Cegla, H.; Watson, C.; Davies, G.; Ball, W. Filtering Solar-Like Oscillations for Exoplanet Detection in Radial Velocity Observations. Astron. J. 2019, 157, 163. [Google Scholar] [CrossRef] [Green Version]
- Chaplin, W.; Elsworth, Y.; Howe, R.; Isaak, G.; McLeod, C.; Miller, B.; van der Raay, H.; Wheeler, S. BiSON Performance. Sol. Phys. 1996, 168, 1–18. [Google Scholar] [CrossRef]
- Gabriel, A.; the GOLF Team. Global Oscillations at Low Frequency from the SOHO Mission (GOLF). Adv. Space Res. 1991, 11, 103–112. [Google Scholar] [CrossRef]
- Katz, D.; Munari, U.; Cropper, M.; Zwitter, T.; Thévenin, F.; David, M.; Viala, Y.; Crifo, F.; Gomboc, A.; Royer, F.; et al. Spectroscopic survey of the Galaxy with Gaia—I. Design and performance of the Radial Velocity Spectrometer. Mon. Not. R. Astron. Soc. 2004, 354, 1223–1238. [Google Scholar] [CrossRef]
- Lovis, C.; Pepe, F.; Bouchy, F.; Lo Curto, G.; Mayor, M.; Pasquini, L.; Queloz, D.; Rupprecht, G.; Udry, S.; Zucker, S. The exoplanet hunter HARPS: unequalled accuracy and perspectives toward 1 cm s-1 precision. Proc. SPIE 2006, 6269, 62690P. [Google Scholar] [CrossRef]
- Pantalone, B.; Kudenov, M. Fraunhofer line optical correlator for improvement of initial orbit determination. Proc. SPIE 2017, 10407, 104070K. [Google Scholar] [CrossRef]
- Fischer, D.; Anglada-Escude, G.; Arriagada, P.; Baluev, R.V.; Bean, J.L.; Bouchy, F.; Buchhave, L.A.; Carroll, T.; Chakraborty, A.; Crepp, J.R.; et al. State of the Field: Extreme Precision Radial Velocities. Publ. Astron. Soc. Pac. 2016, 128, 066001. [Google Scholar] [CrossRef]
- Lovis, C.; Pepe, F. A new list of thorium and argon spectral lines in the visible. Astron. Astrophys. 2007, 468, 1115–1121. [Google Scholar] [CrossRef] [Green Version]
- Marcy, G.; Butler, P. Precision Radial Velocities with an Iodine Absorption Cell. Publ. Astron. Soc. Pac. 1992, 104, 270–277. [Google Scholar] [CrossRef]
- Butler, R.; Marcy, G.; Williams, E.; McCarthy, C.; Dosanjh, P. Attaining Doppler Precision of 3 cm s-1. Publ. Astron. Soc. Pac. 1996, 108, 500–509. [Google Scholar] [CrossRef]
- Schwab, C.; Stürmer, J.; Gurevich, Y.; Führer, T.; Lamoreaux, S.; Walther, T.; Quirrenbach, A. Stabilizing a Fabry–Perot Etalon Peak to 3 cm s-1 for Spectrograph Calibration. Publ. Astron. Soc. Pac. 2015, 127, 880–889. [Google Scholar] [CrossRef]
- Murphy, M.; Udem, T.; Holzwarth, R.; Sizmann, A.; Pasquini, L.; Araujo-Hauck, C.; Dekker, H.; D’Odorico, S.; Fischer, M.; Hänsch, T.W.; et al. High-precision wavelength calibration of astronomical spectrographs with laser frequency combs. Mon. Not. R. Astron. Soc. 2007, 380, 839–847. [Google Scholar] [CrossRef]
- McCracken, R.; Charsley, J.; Reid, D. A decade of astrocombs: Recent advances in frequency combs for astronomy. Opt. Express 2017, 25, 15058–15078. [Google Scholar] [CrossRef] [PubMed]
- Suh, M.; Yi, X.; Lai, Y.H.; Leifer, S.; Grudinin, I.S.; Vasisht, G.; Martin, E.C.; Fitzgerald, M.P.; Doppmann, G.; Wang, J.; et al. Searching for exoplanets using a microresonator astrocomb. Nat. Photonics 2019, 13, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Halverson, S.; Terrien, R.; Mahadevan, S.; Roy, A.; Bender, C.; Stefánsson, G.K.; Monson, A.; Levi, E.; Hearty, F.; Blake, C.; et al. A comprehensive radial velocity error budget for next generation Doppler spectrometers. Proc. SPIE 2016, 9908, 99086P. [Google Scholar] [CrossRef]
- Bechter, A.; Bechter, E.; Crepp, J.; King, D.; Crass, J. A radial velocity error budget for single-mode Doppler spectrographs. Proc. SPIE 2018, 10702, 107026T. [Google Scholar] [CrossRef] [Green Version]
- Hatzes, A.; Cochran, W. Spectrograph Requirements for Precise Radial Velocity Measurements. In ESO Workshop on High Resolution Spectroscopy with the VLT; European Southern Observatory: Munich, Germany, 1992. [Google Scholar]
- Huang, C.; Ries, J.; Tapley, B.; Watkins, M. Relativistic Effects for Near-Earth Satellite Orbit Determination. Celest. Mech. Dyn. Astron. 1990, 48, 167–185. [Google Scholar] [CrossRef]
- Moyer, T. Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003; pp. 55–101. [Google Scholar]
- Action, C.; Bachman, N.; Semenov, B.; Wright, E. A look towards the future in the handling of space science mission geometry. Planet. Space Sci. 2018, 150, 9–12. [Google Scholar] [CrossRef]
- Wertz, J. (Ed.) Spacecraft Attitude Determination and Control; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1986; pp. 166–180. [Google Scholar]
- Shuster, M.; Oh, S. Three-Axis Attitude Determination from Vector Observations. J. Guid. Control. Dyn. 1981, 4, 70–77. [Google Scholar] [CrossRef]
- Shuster, M. Kalman Filtering of Spacecraft Attitude and the QUEST Model. J. Astronaut. Sci. 1990, 38, 377–393. [Google Scholar]
- Gibbs, J. On the Determination of Elliptic Orbits from Three Complete Observations. Mem. Natl. Acad. Sci. 1889, 4, 79–104. [Google Scholar]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications, 3rd ed.; Microcosm Press: Hawthorne, CA, USA, 2007; pp. 20–23, 51–56, 451–457, 794–796. [Google Scholar]
- Escobal, P.R. Methods of Orbit Determination; Robert E. Krieger Publishing Company: Malabar, FL, USA, 1976; pp. 306–307. [Google Scholar]
- Hamilton, W.R. The Hodograph, or a New Method of Expressing in Symbolical Language the Newtonian Law of Attraction. Proc. R. Ir. Acad. 1847, 3, 344–353. [Google Scholar]
- Altman, S.P. Orbital Hodograph Analysis; American Astronautical Society: Baltimore, MD, USA, 1965. [Google Scholar]
- Eades, J.B. Orbit Information Derived from its Hodograph; NASA TM X-63307; Number X-643-68-264; Goddard Space Flight Center: Greenbelt, MD, USA, 1968. [Google Scholar]
- Thompson, B.F.; Choi, K.K.; Piggott, S.W.; Beaver, S.R. Orbital Targeting Based on Hodograph Theory for Improved Rendezvous Safety. J. Guid. Control. Dyn. 2010, 33, 1566–1576. [Google Scholar] [CrossRef]
- Gondelach, D.; Noomen, R. Hodographic-Shaping Method for Low-Thrust Interplanetary Trajectory Design. J. Spacecr. Rocket. 2015, 52, 728–738. [Google Scholar] [CrossRef]
- Markovsky, I.; Van Huffel, S. Overview of Total Least Squares Methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Al-Sharadqah, A.; Chernov, N. Error analysis for circle fitting algorithms. Electron. J. Stat. 2009, 3, 886–911. [Google Scholar] [CrossRef]
- Kalman, R. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–54. [Google Scholar] [CrossRef]
- Kalman, R.; Bucy, R. New Results in Linear Filtering and Prediction. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974; pp. 81–82. [Google Scholar]
- Maybeck, P. Stochastic Models: Estimation and Control: Volume 2; Academic Press: New York, NY, USA, 1982; pp. 39–59. [Google Scholar]
- Carpenter, J.; D’Souza, C. Navigation Filter Best Practices; Technical Report NASA/TP-2018-219822; NASA Langley Research Center: Hampton, VA, USA, 2018. [Google Scholar]
- Lear, W. Kalman Filtering Techniques; Technical Report JSC-20688; NASA Johnson Space Center: Houston, TX, USA, 1985.
- Markley, F. Approximate Cartesian State Transition Matrix. J. Astronaut. Sci. 1986, 34, 161–169. [Google Scholar]
- Tapley, B.; Schutz, B.; Born, G. Statistical Orbit Determination; Elsevier Academic Press: Amsterdam, The Netherlands, 2004; pp. 162–164, 267–268, 501–509. [Google Scholar]
- Crassidis, J.; Junkins, J. Optical Estimation of Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2004; pp. 205–207, 256–258. [Google Scholar]
- Bucy, R.; Joseph, P. Filtering for Stochastic Processes with Applications to Guidance; Interscience Publishers: New York, NY, USA, 1968; pp. 174–176. [Google Scholar]
- Action, C. Ancillary data services of NASA’s Navigation and Ancillary Information Facility. Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Ochsenbein, F.; Bauer, P.; Marcout, J. The VizieR database of astronomical catalogues. Astron. Astrophys. Suppl. Ser. 2000, 143, 23–32. [Google Scholar] [CrossRef] [Green Version]
- Lorentz, H. La Théorie electromagnétique de Maxwell et son application aux corps mouvants; E.J. Brill: Leiden, The Netherlands, 1892. [Google Scholar]
- Lorentz, H. De relatieve beweging van de aarde en den aether. Koninklijke Nederlandsche Akademie van Wetenschappen Proc. 1893, 74–79. [Google Scholar]
- Lorentz, H. Versuch einer Theorie der Elektrischen und Optischen Erscheinungen in Bewegten Körpern; E.J. Brill: Leiden, The Netherlands, 1895. [Google Scholar]
- FitzGerald, G. The Ether and the Earth’s Atmosphere. Science 1889, 13, 390. [Google Scholar] [CrossRef]
- Lorentz, H. Simplified Theory of Electrical and Optical Phenomena in Moving Systems. Koninklijke Akademie van Wetenschappen Proc. 1899, 51, 427–442. [Google Scholar]
- Larmor, J. Aether and Matter; Cambridge University Press: Cambridge, UK, 1900. [Google Scholar]
- Poincaré, H. Sur la dynamique de l’électron. C. R. Acad. Sci. Paris 1905, 140, 1504–1508. [Google Scholar] [CrossRef]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics Extended, 5th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1997; pp. 968–972. [Google Scholar]
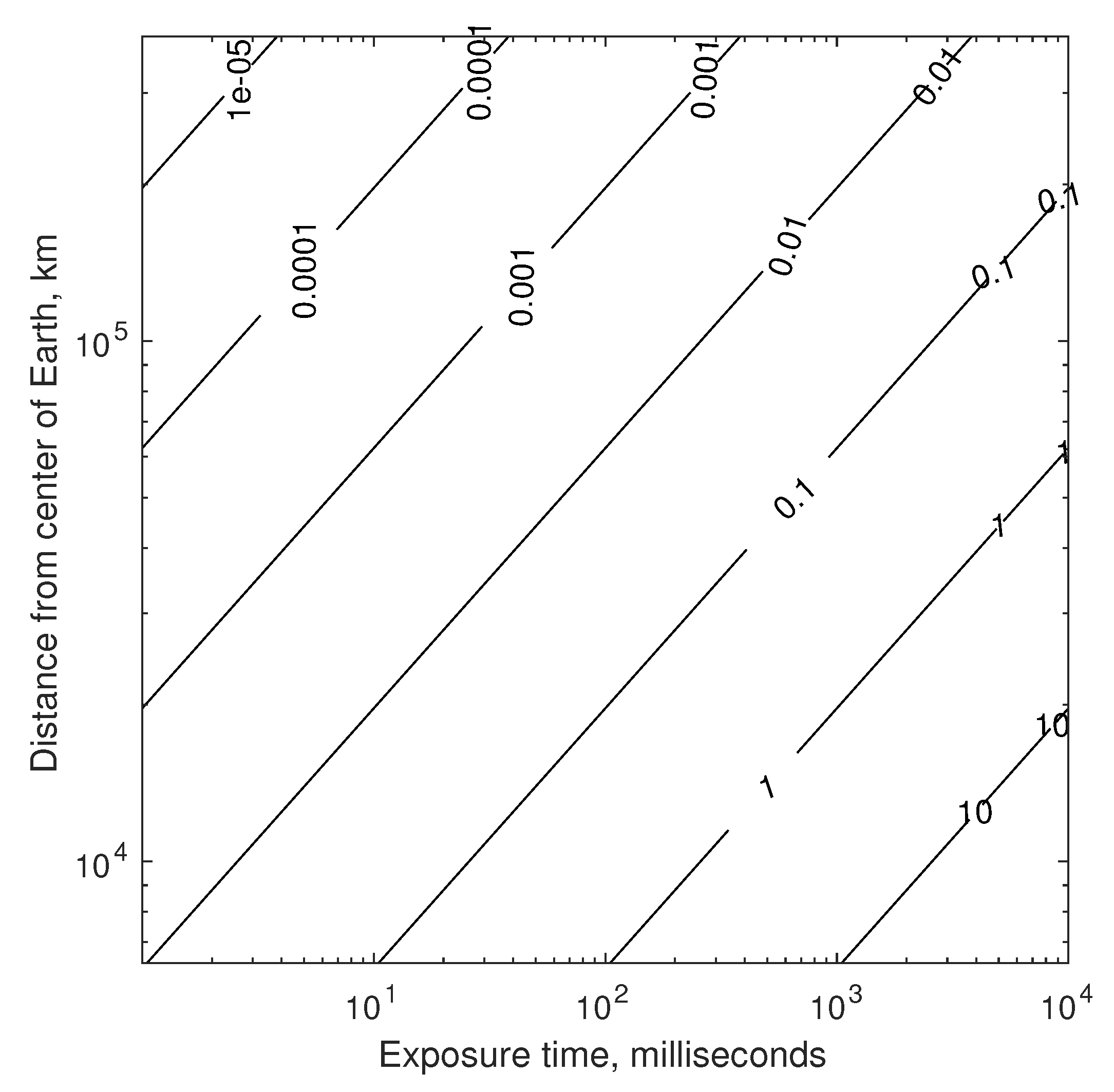
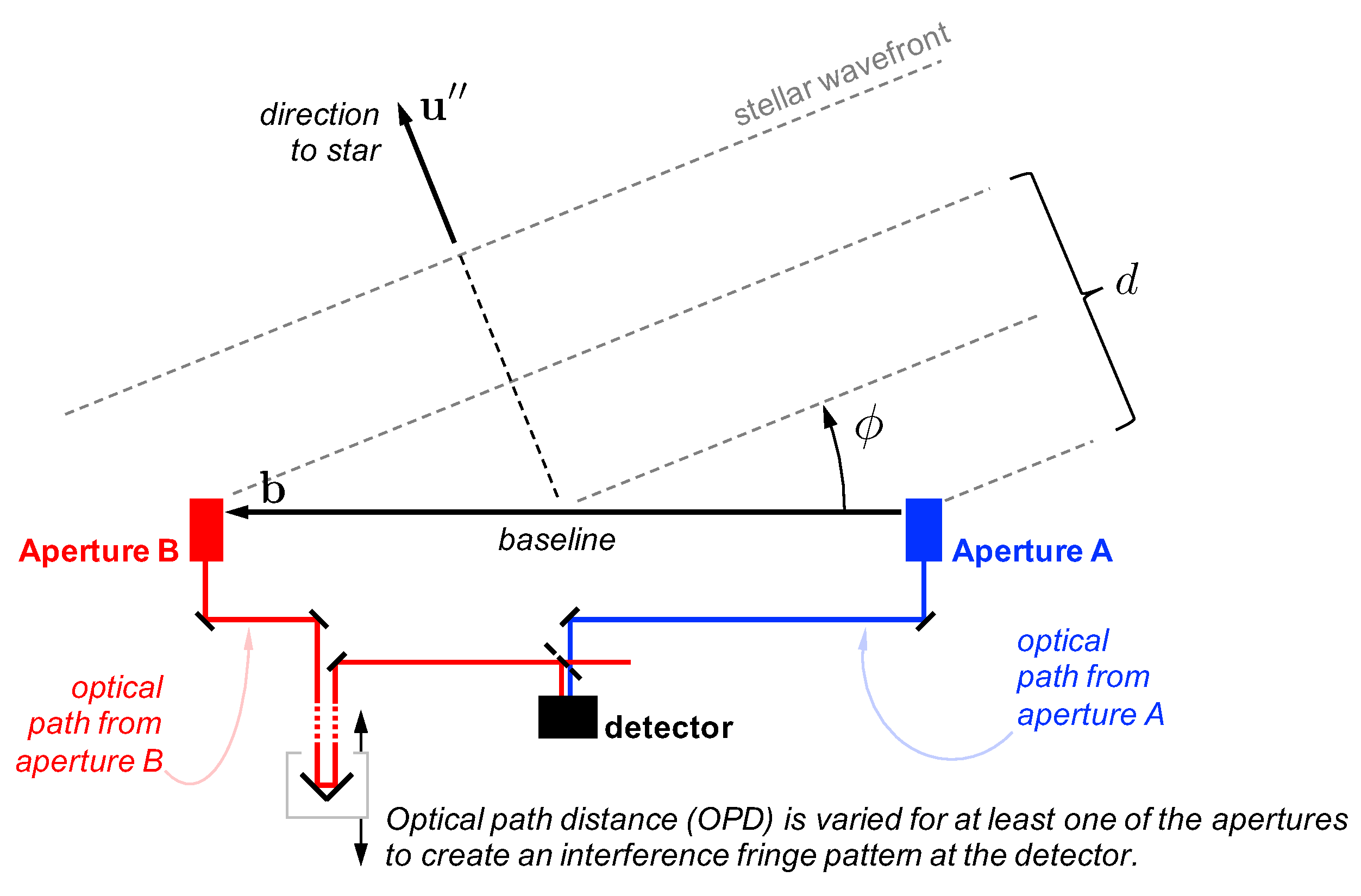
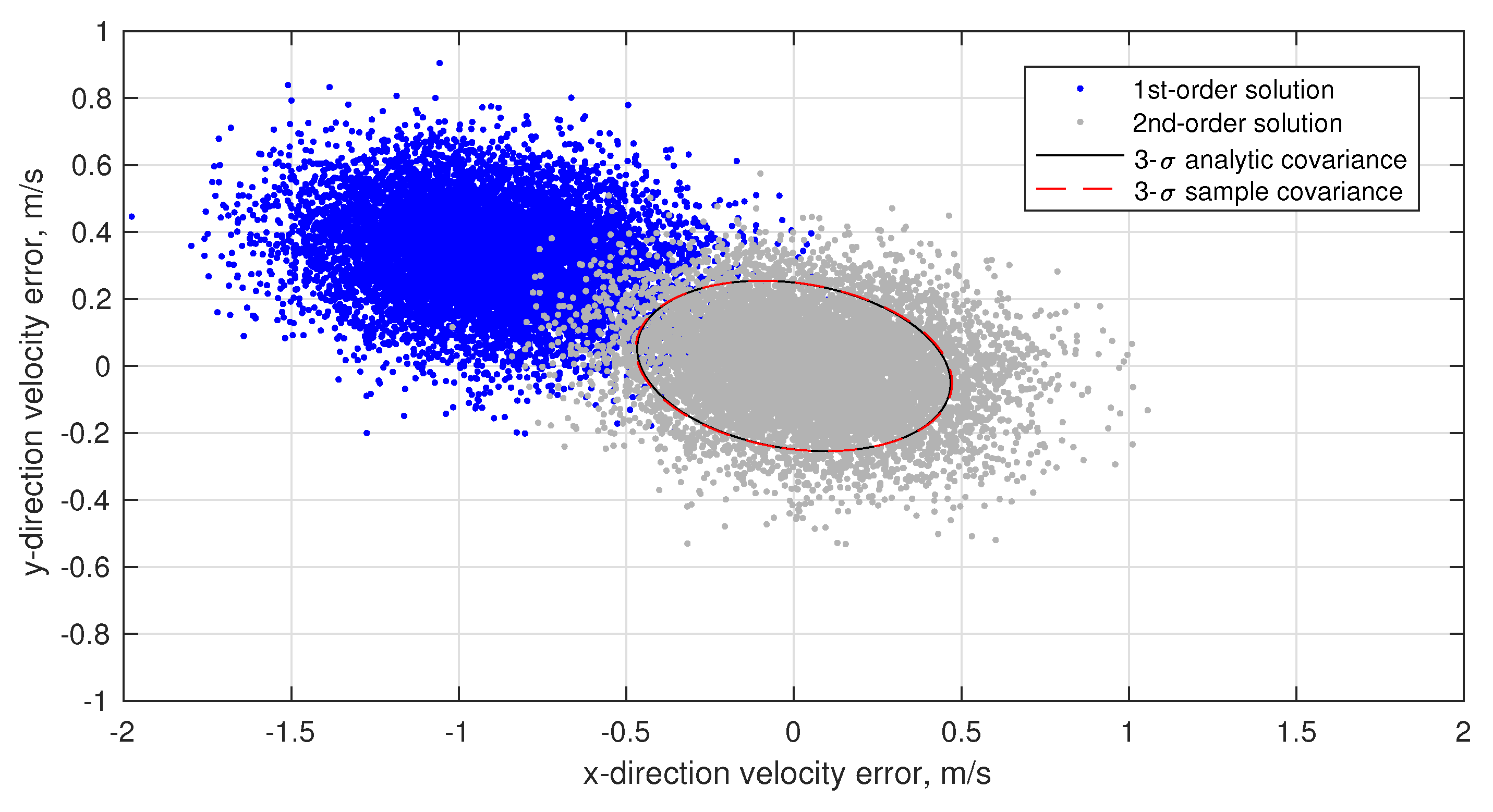
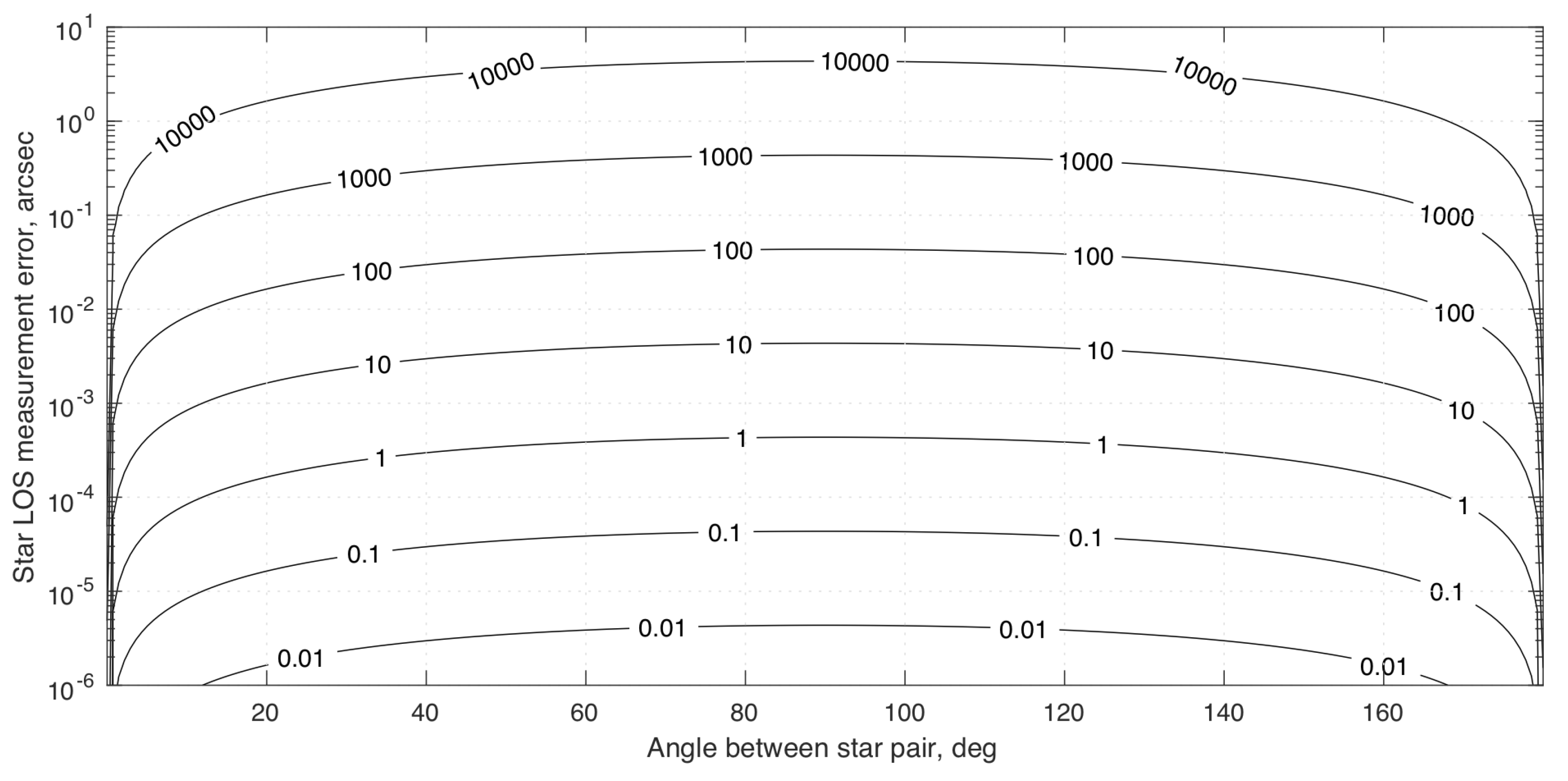

| Apparent Visual Magnitude, | Number of Stars * Brighter than | Photon Flux photons/m/second |
|---|---|---|
| 0 | 4 | |
| 1 | 15 | |
| 2 | 49 | |
| 3 | 170 | |
| 4 | 512 | |
| 5 | 1601 | |
| 6 | 5011 |
| Celestial Body | ||
|---|---|---|
| Sun | 179.7 deg | 13.1 deg |
| Earth | 154.0 deg | 154.0 deg |
| Moon | 0.75 deg | 0.75 deg |
| Jupiter | 11.2 deg | 2.90 arcsec |
| Saturn | 1.55 deg | 0.18 arcsec |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christian, J.A. StarNAV: Autonomous Optical Navigation of a Spacecraft by the Relativistic Perturbation of Starlight. Sensors 2019, 19, 4064. https://doi.org/10.3390/s19194064
Christian JA. StarNAV: Autonomous Optical Navigation of a Spacecraft by the Relativistic Perturbation of Starlight. Sensors. 2019; 19(19):4064. https://doi.org/10.3390/s19194064
Chicago/Turabian StyleChristian, John A. 2019. "StarNAV: Autonomous Optical Navigation of a Spacecraft by the Relativistic Perturbation of Starlight" Sensors 19, no. 19: 4064. https://doi.org/10.3390/s19194064
APA StyleChristian, J. A. (2019). StarNAV: Autonomous Optical Navigation of a Spacecraft by the Relativistic Perturbation of Starlight. Sensors, 19(19), 4064. https://doi.org/10.3390/s19194064