Wayside Detection of Wheel Minor Defects in High-Speed Trains by a Bayesian Blind Source Separation Method
Abstract
1. Introduction
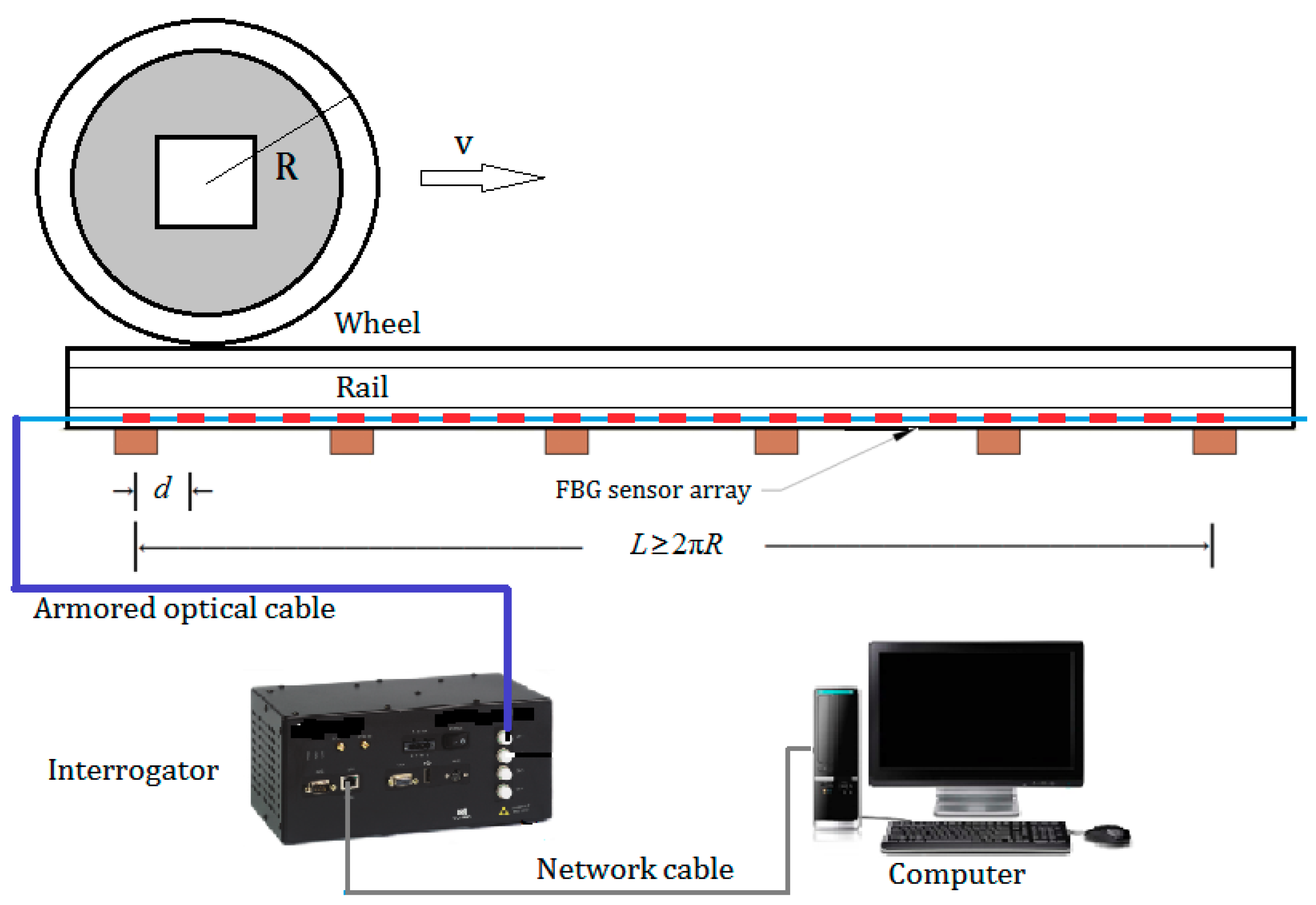
2. FBG-Based Wayside Wheel Defect Detection System
2.1. FBG Sensing System in Wayside Detection
- Assurance of immunity to electromagnetic field: most of the conventional wheel condition monitoring systems, either resistance strain gauge- or accelerometer-based, are vulnerable to EMI induced by high voltage power supply system of modern HSR [23];
- Massive multiplexing capability: HSR always has strict requirements on clearance, which can be problematic for conventional sensing systems when considerable measuring points are needed. In contrast, FBG-based sensing system allows the use of hundreds of sensing points (FBGs) in a single fiber cable. This ability facilitates easy installation on HSR tracks with light-weight trackside equipment;
- High reliability and durability: the FBG-based sensing system can operate for more than 20 years without losses in performance even in extreme climate, such as heavy rains and snows, strong winds, or extremely hot summer days, and corrosion environment and large shocks caused by track maintenance work [22];
- Long conduction distance: the FBG-based sensing system can offer up to 100 km distant detection [23], because the optical fiber has a salient advantage in long-distance transmission with much lower signal attenuation. This allows the monitoring equipment to be installed far away from the instrumented rail section where the sensors are deployed and both the sensors and connecting fibers at the instrumented zone require no power supply.
2.2. FBG-Based Wayside Wheel Defect Detector
3. Wheel Defect Identification
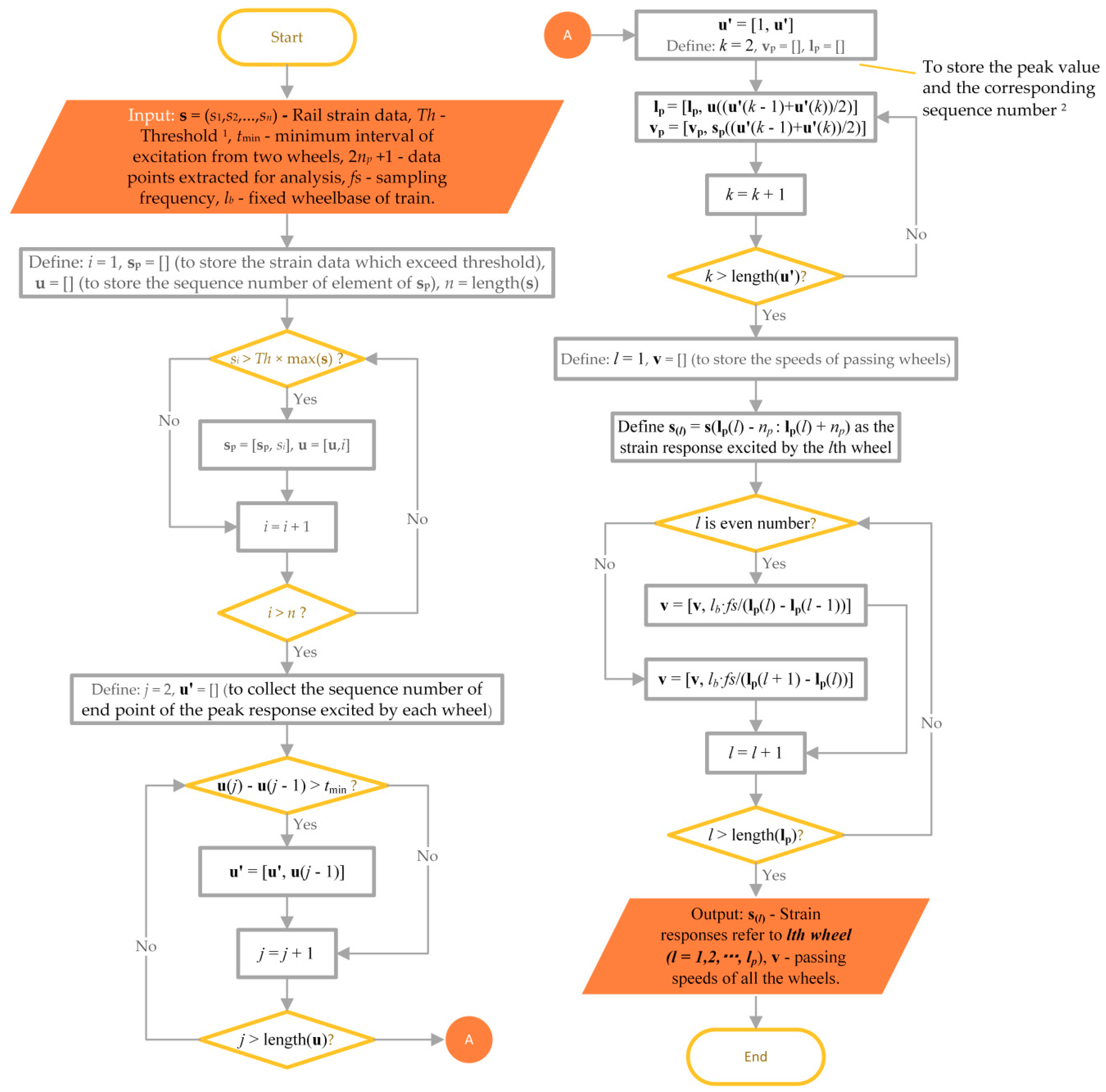
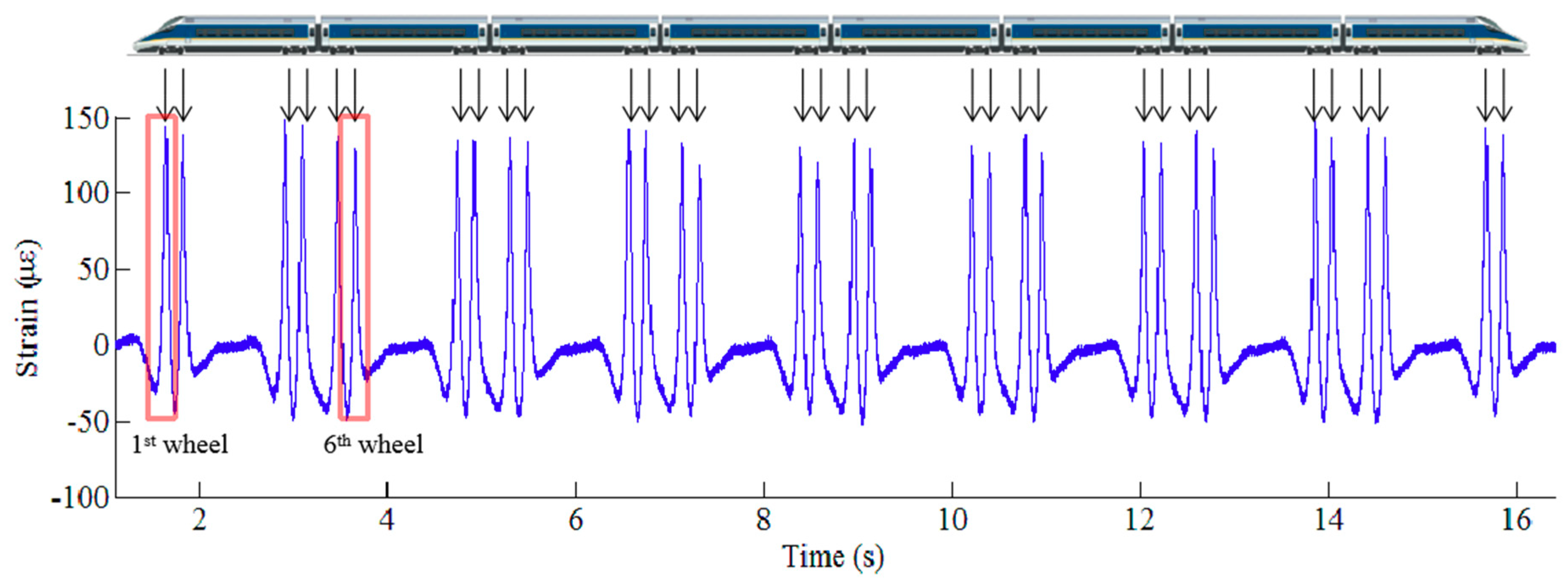
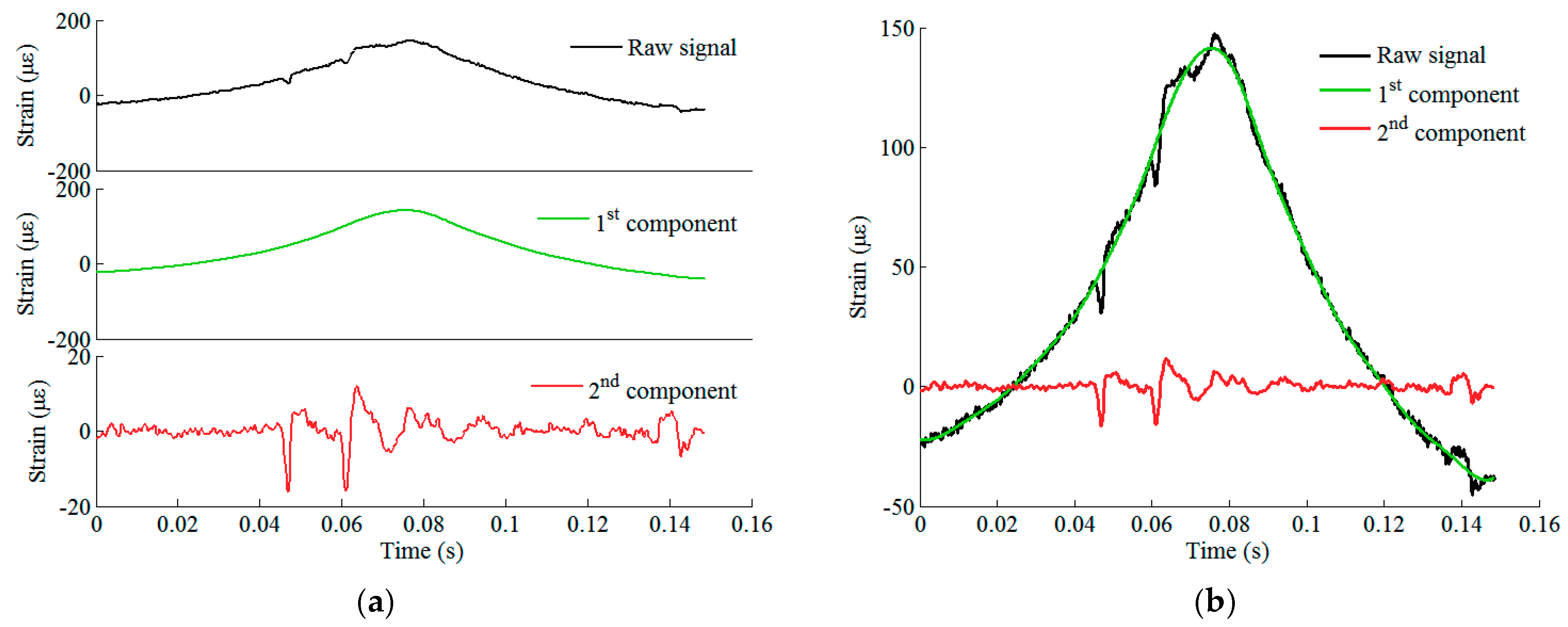
3.1. Strain Response Extraction
3.2. Defect-Sensitive Feature Extraction Based on Bayesian BSS
3.2.1. Bayesian BSS
3.2.2. Assumptions and Model Establishment
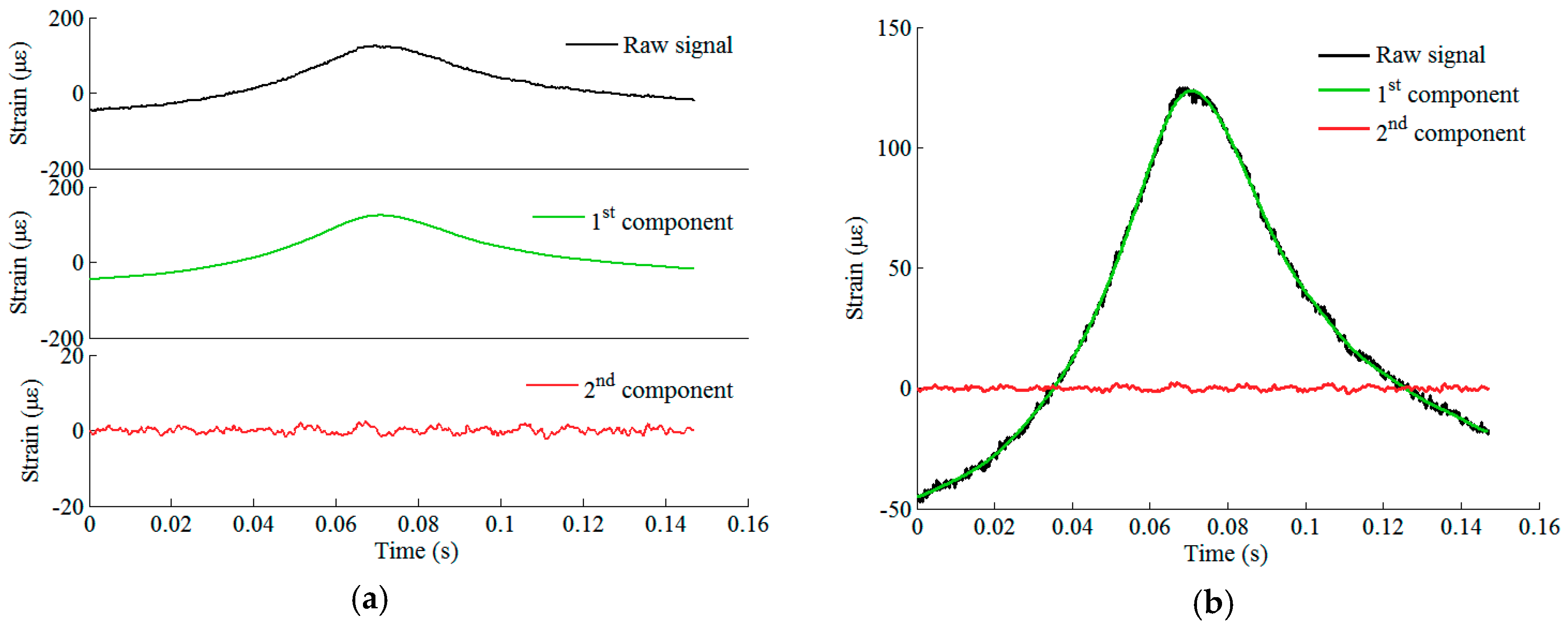
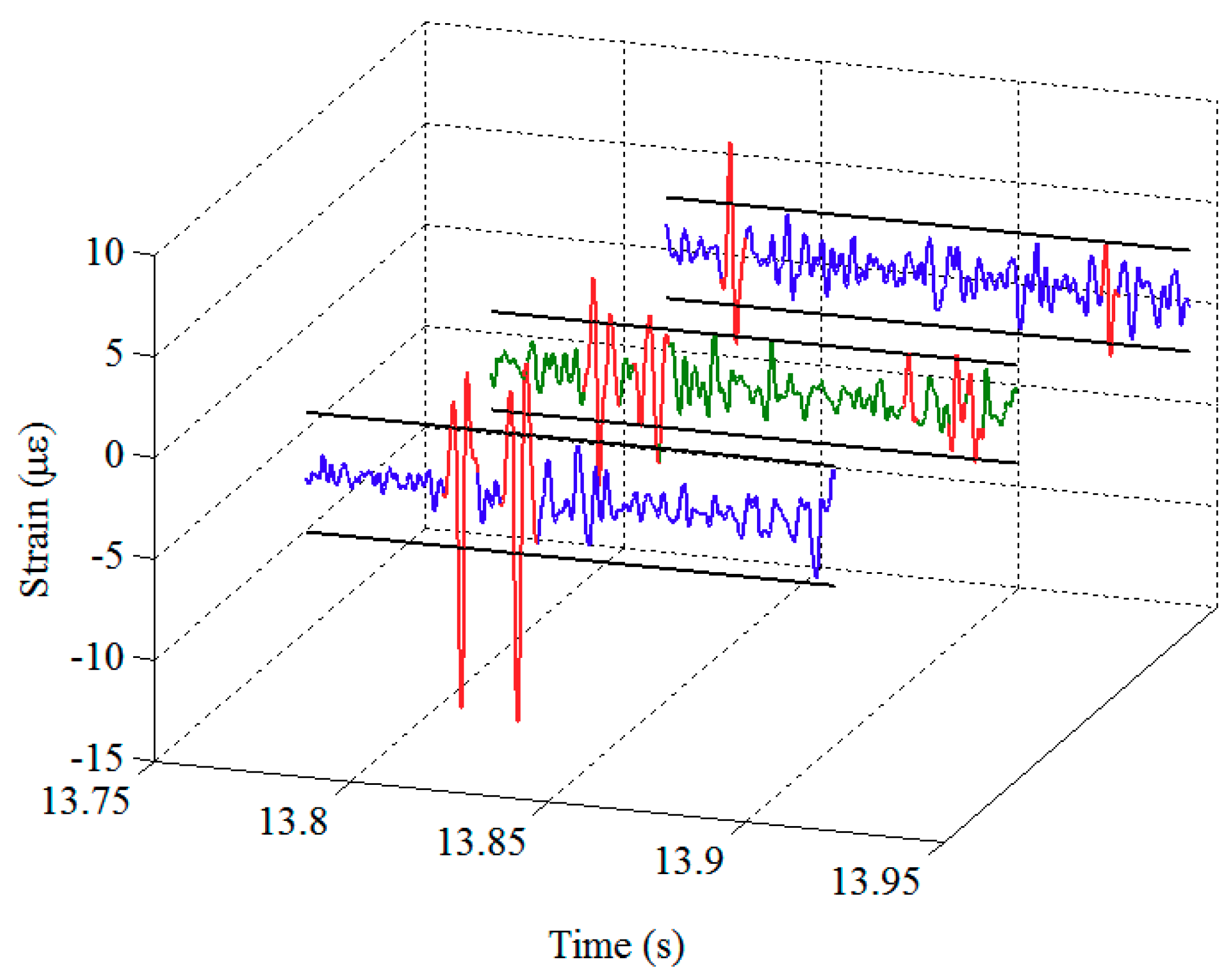
3.2.3. Defect-Sensitive Feature Extraction
3.3. Defect Identification
- The speed variation of passing trains: The process of train passage lasts from seconds to dozens of seconds, so it is possible that the train is speeding up or slowing down during this process and the speed is not constant. However, as described in the proposed method, the condition of wheels is assessed individually, that is, the detection of each wheel is free from the interference of other wheels. Since the instrumented rail section with FBG array is only about 3 m long, the speed of each wheel is unlikely to change dramatically during its passage across the instrumented section. In addition, it has been proven that the dynamic strain monitoring data of rail obtained under different constant running speeds of a train give rise to consistent wheel defect detection results as long as the running speed is instantly measured and enough large dynamic strain of the rail is excited by the passing wheel. It is observed that when the train’s running speed is lower than 20 km/h, the anomaly stemming from minor wheel defect is difficult to perceive in the measured rail dynamic strain response.
- The temperature effect on strain measurement: For strain measurement using FBG sensors, the temperature effect usually should not be ignored, since the output wavelength of FBG sensors can shift with temperature variation. However, temperature-induced wavelength change would not influence the performance of the proposed method. This is because the wavelength change caused by temperature variation mainly results in the change of baseline of the output signal. The influence of temperature can be easily eliminated by deducting the mean value of wavelength before or after train passage. Particularly in the proposed method, after pursuing BSS, the change of temperature will be reflected in the first component (source) rather than the second component (source), the latter being used for wheel defect detection. Also, the temperature variation during the short time of the wheel’s passage across the instrumented section is ignorable.
- Different locations of FBGs with respect to sleepers: In this study, the FBG sensors on the array have different locations with respect to sleepers. These FBGs measure the rail strain due to bending, and the measurement result may be influenced by the distance of the sensor from the sleeper. Therefore, it is necessary to compare the signals generated by different FBGs on the array. As shown in Figure 4, under the excitation of the same wheel, the waveforms of the rail strain responses at different locations are similar. Even if there are slight differences in the amplitude of response peak, this kind of difference is mainly reflected in the first component after signal processing using BSS, rather than in the second component. Therefore, the detection results would not be affected by this issue.
4. In-Situ Verification
4.1. Implementation of Online Detector
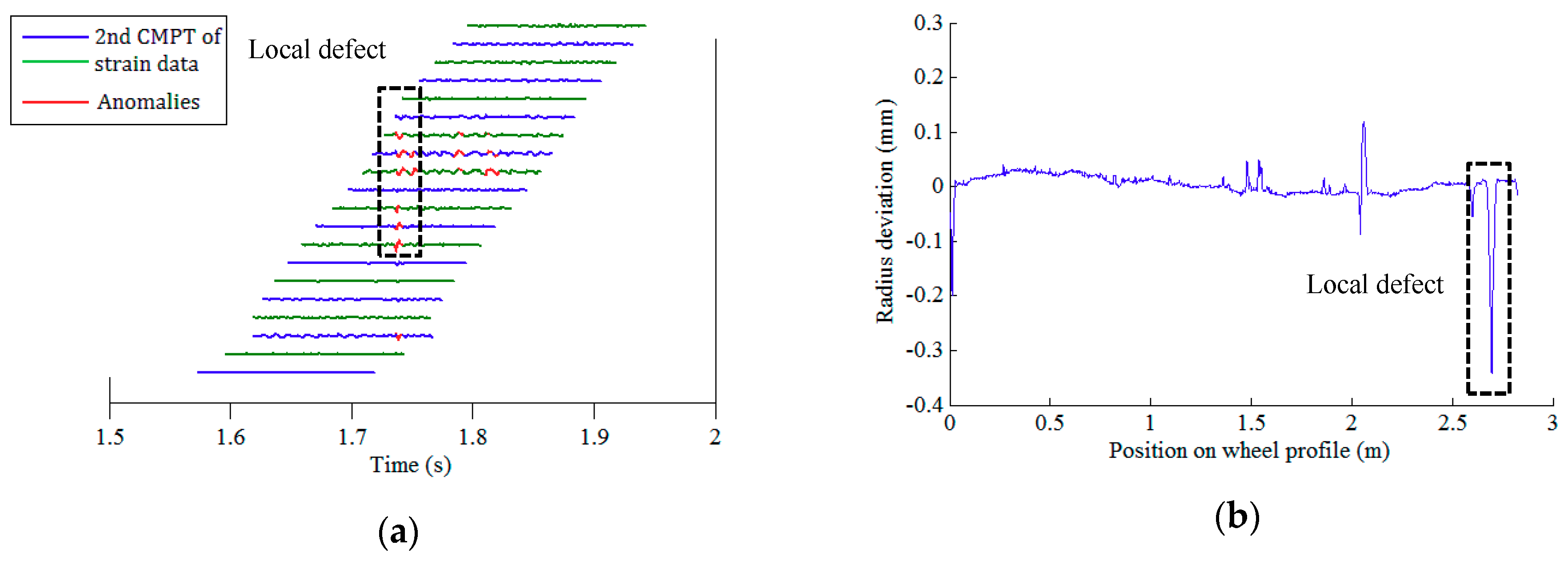
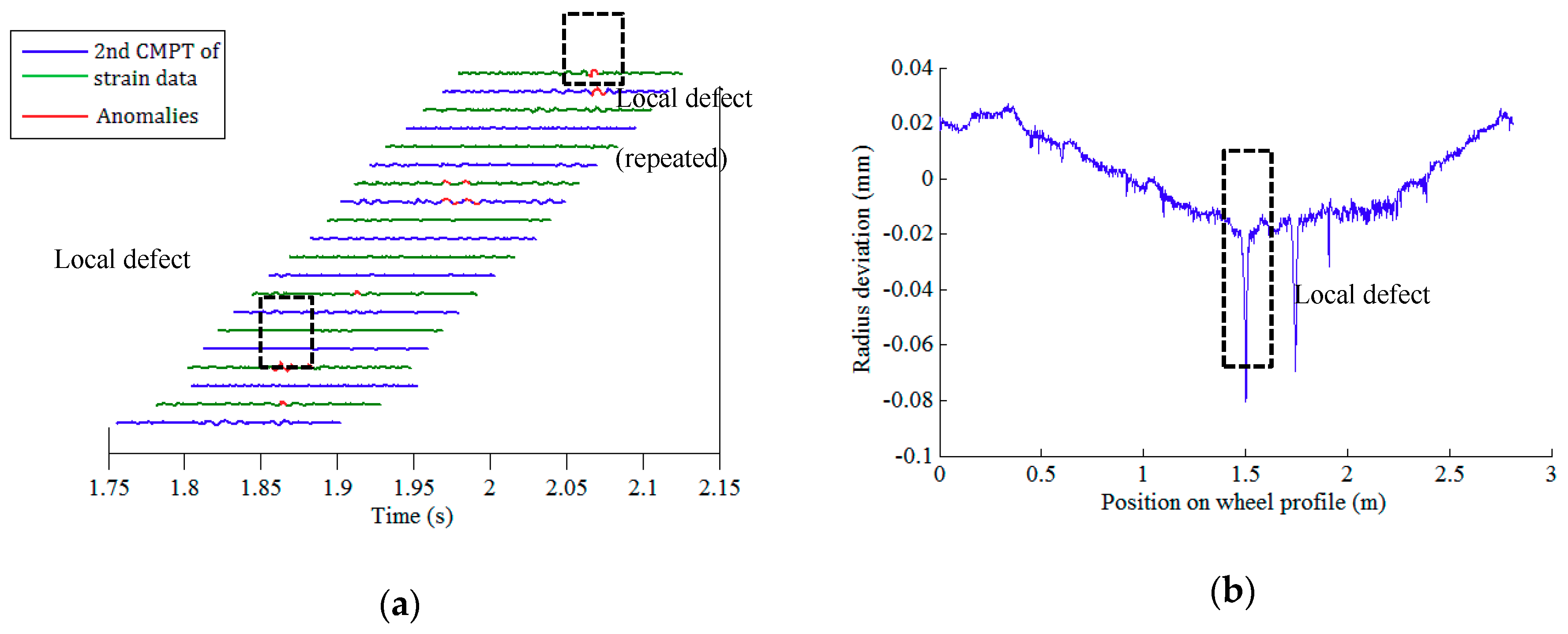
4.2. Blind Test
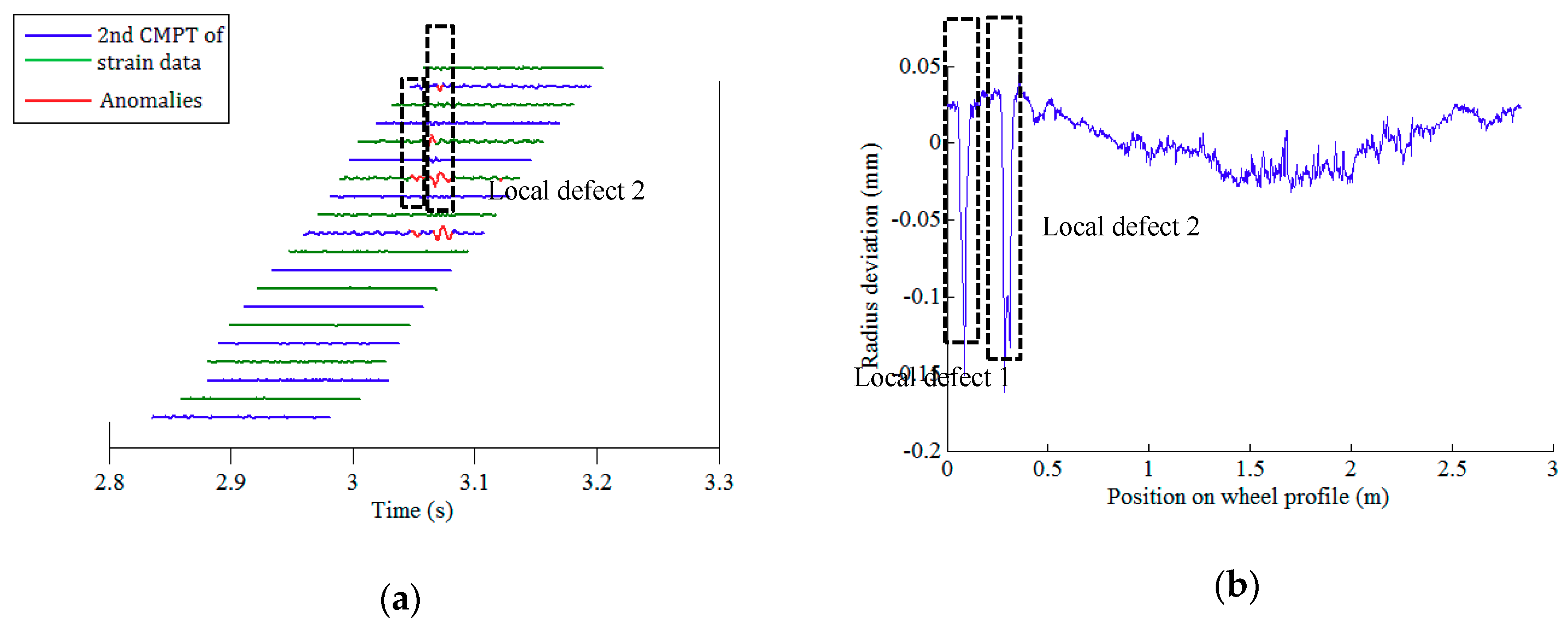
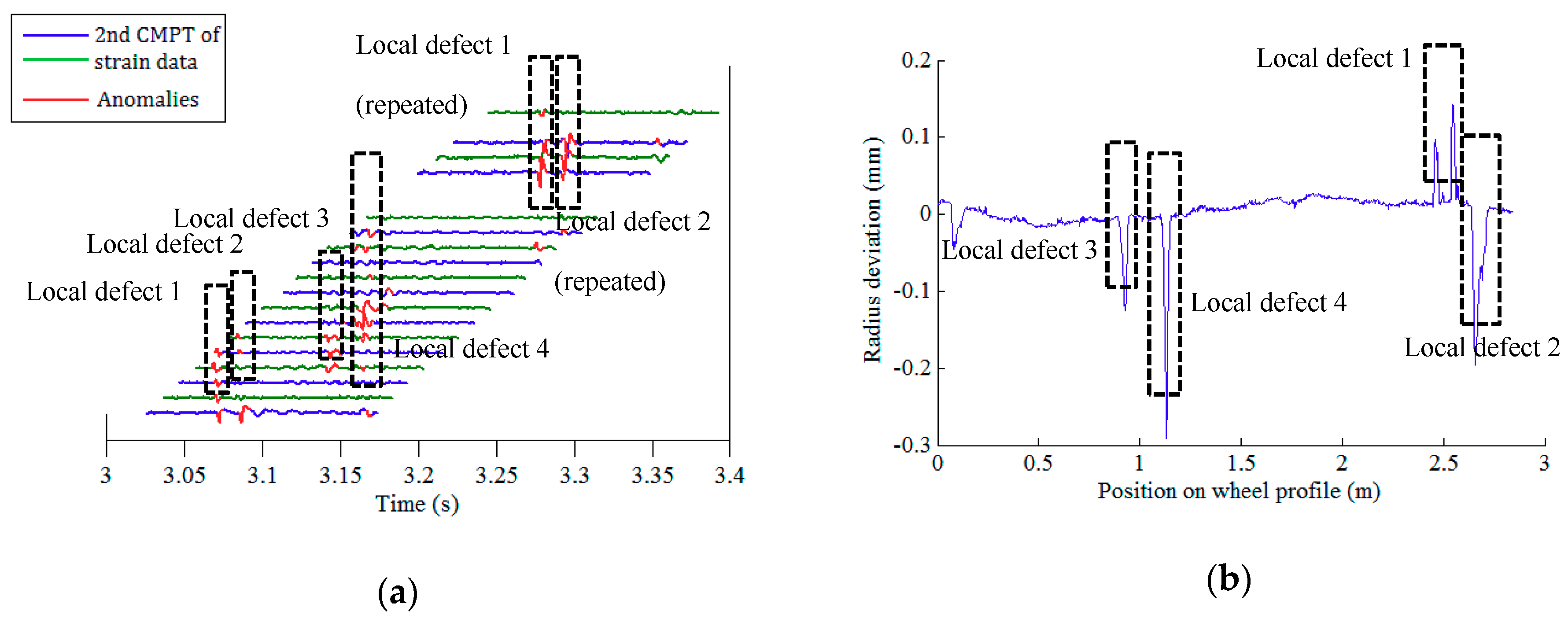
4.3. Test Results and Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johansson, A.; Nielsen, J.C. Out-of-round railway wheels—Wheel-rail contact forces and track response derived from field tests and numerical simulations. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2003, 217, 135–146. [Google Scholar] [CrossRef]
- Jin, X.; Wu, L.; Fang, J.; Zhong, S.; Ling, L. An investigation into the mechanism of the polygonal wear of metro train wheels and its effect on the dynamic behaviour of a wheel/rail system. Veh. Syst. Dyn. 2012, 50, 1817–1834. [Google Scholar] [CrossRef]
- Kouroussis, G.; Connolly, D.P.; Verlinden, O. Railway-induced ground vibrations—A review of vehicle effects. Int. J. Rail Transp. 2014, 2, 69–110. [Google Scholar] [CrossRef]
- Wu, T.X.; Thompson, D.J. A hybrid model for the noise generation due to railway wheel flats. J. Sound Vib. 2002, 251, 115–139. [Google Scholar] [CrossRef]
- Nielsen, J. Out-of-round railway wheels. In Wheel–Rail Interface Handbook; Lewis, R., Olofsson, U., Eds.; Woodhead Publishing: Sawston, UK, 2009; pp. 245–279. [Google Scholar]
- Barke, D.W.; Chiu, W.K. A review of the effects of out-of-round wheels on track and vehicle components. Proc. Inst. Mech. Eng. Part F: J. Rail Rapid Transit 2005, 219, 151–175. [Google Scholar] [CrossRef]
- Dukkipati, R.V.; Dong, R. Impact loads due to wheel flats and shells. Veh. Syst. Dyn. 1999, 31, 1–22. [Google Scholar] [CrossRef]
- Morys, B. Enlargement of out-of-round wheel profiles on high speed trains. J. Sound Vib. 1999, 227, 965–978. [Google Scholar] [CrossRef]
- Wu, X.; Chi, M. Study on stress states of a wheelset axle due to a defective wheel. J. Mech. Sci. Technol. 2016, 30, 4845–4857. [Google Scholar] [CrossRef]
- Braghin, F.; Lewis, R.; Dwyer-Joyce, R.S.; Bruni, S. A mathematical model to predict railway wheel profile evolution due to wear. Wear 2006, 261, 1253–1264. [Google Scholar] [CrossRef]
- Liu, Y.; Stratman, B.; Mahadevan, S. Fatigue crack initiation life prediction of railroad wheels. Int. J. Fatigue 2006, 28, 747–756. [Google Scholar] [CrossRef]
- Enblom, R. Deterioration mechanisms in the wheel–rail interface with focus on wear prediction: A literature review. Veh. Syst. Dyn. 2009, 47, 661–700. [Google Scholar] [CrossRef]
- Wu, Y.; Du, X.; Zhang, H.J.; Wen, Z.F.; Jin, X.S. Experimental analysis of the mechanism of high-order polygonal wear of wheels of a high-speed train. J. Zhejiang Univ. Sci. A 2017, 18, 579–592. [Google Scholar] [CrossRef]
- Baeza, L.; Fayos, J.; Roda, A.; Insa, R. High frequency railway vehicle-track dynamics through flexible rotating wheelsets. Veh. Syst. Dyn. 2008, 46, 647–659. [Google Scholar] [CrossRef]
- Nielsen, J.C.; Lombaert, G.; François, S. A hybrid model for prediction of ground-borne vibration due to discrete wheel/rail irregularities. J. Sound Vib. 2015, 345, 103–120. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.; Liu, J. Wheel-rail impact and the dynamic forces at discrete supports of rails in the presence of singular rail surface defects. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 124–139. [Google Scholar] [CrossRef]
- Bian, J.; Gu, Y.; Murray, M.H. A dynamic wheel–rail impact analysis of railway track under wheel flat by finite element analysis. Veh. Syst. Dyn. 2013, 51, 784–797. [Google Scholar] [CrossRef]
- Liu, X.; Zhai, W. Analysis of vertical dynamic wheel/rail interaction caused by polygonal wheels on high-speed trains. Wear 2014, 314, 282–290. [Google Scholar] [CrossRef]
- Smith, R.A. Hatfield memorial lecture 2007 railways and materials: Synergetic progress. Ironmak. Steelmak. 2008, 35, 505–513. [Google Scholar] [CrossRef]
- Papaelias, M.; Amini, A.; Huang, Z.; Vallely, P.; Dias, D.C.; Kerkyras, S. Online condition monitoring of rolling stock wheels and axle bearings. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 709–723. [Google Scholar] [CrossRef]
- Stratman, B.; Liu, Y.; Mahadevan, S. Structural health monitoring of railroad wheels using wheel impact load detectors. J. Fail. Anal. Prev. 2007, 7, 218–225. [Google Scholar] [CrossRef]
- Filograno, M.L.; Corredera, P.; Rodríguez-Plaza, M.; Andrés-Alguacil, A.; González-Herráez, M. Wheel flat detection in high-speed railway systems using fiber Bragg gratings. IEEE Sens. J. 2013, 13, 4808–4816. [Google Scholar] [CrossRef]
- Tam, H.Y.; Lee, T.; Ho, S.L.; Haber, T.; Graver, T.; Méndez, A. Utilization of fiber optic bragg grating sensing systems for health monitoring in railway applications. Struct. Health Monit. Quantif. Valid. Implement. 2007, 1, 1824–1831. [Google Scholar]
- Wei, C.; Xin, Q.; Chung, W.H.; Liu, S.Y.; Tam, H.Y.; Ho, S.L. Real-time train wheel condition monitoring by fiber Bragg grating sensors. Int. J. Distrib. Sens. Netw. 2011, 8, 409048. [Google Scholar] [CrossRef]
- Kouroussis, G.; Connolly, D.P.; Alexandrou, G.; Vogiatzis, K. Railway ground vibrations induced by wheel and rail singular defects. Veh. Syst. Dyn. 2015, 53, 1500–1519. [Google Scholar] [CrossRef]
- Skarlatos, D.; Karakasis, K.; Trochidis, A. Railway wheel fault diagnosis using a fuzzy-logic method. Appl. Acoust. 2004, 65, 951–966. [Google Scholar] [CrossRef]
- Belotti, V.; Crenna, F.; Michelini, R.C.; Rossi, G.B. Wheel-flat diagnostic tool via wavelet transform. Mech. Syst. Signal Process. 2006, 20, 1953–1966. [Google Scholar] [CrossRef]
- Dybała, J.; Radkowski, S. Reduction of doppler effect for the needs of wayside condition monitoring system of railway vehicles. Mech. Syst. Signal Process. 2013, 38, 125–136. [Google Scholar] [CrossRef]
- Zhang, D.; Entezami, M.; Stewart, E.; Roberts, C.; Yu, D. A novel doppler effect reduction method for wayside acoustic train bearing fault detection systems. Appl. Acoust. 2019, 145, 112–124. [Google Scholar] [CrossRef]
- Asplund, M.; Lin, J. Evaluating the measurement capability of a wheel profile measurement system by using GR&R. Measurement 2016, 92, 19–27. [Google Scholar]
- Zhang, Z.F.; Gao, Z.; Liu, Y.Y.; Jiang, F.C.; Yang, Y.L.; Ren, Y.F.; Yang, H.J.; Yang, K.; Zhang, X.D. Computer vision based method and system for online measurement of geometric parameters of train wheel sets. Sensors 2011, 12, 334–346. [Google Scholar] [CrossRef]
- Liu, X.Z.; Ni, Y.Q.; Zhou, L. Condition-based maintenance of high-speed railway vehicle wheels through trackside monitoring. In Proceedings of the second International Workshop on Structural Health Monitoring for Railway System, Qingdao, China, 17–19 October 2018. [Google Scholar]
- Milković, D.; Simić, G.; Jakovljević, Ž.; Tanasković, J.; Lučanin, V. Wayside system for wheel–rail contact forces measurements. Measurement 2013, 46, 3308–3318. [Google Scholar] [CrossRef]
- Asplund, M.; Famurewa, S.; Rantatalo, M. Condition monitoring and e-maintenance solution of railway wheels. J. Qual. Maint. Eng. 2014, 20, 216–232. [Google Scholar] [CrossRef]
- Liu, X.Z.; Ni, Y.Q. Wheel tread defect detection for high-speed trains using FBG-based online monitoring techniques. Smart Struct. Syst. 2018, 21, 687–694. [Google Scholar]
- Ni, Y.Q.; Ying, Z.G.; Liu, X.Z. Online detection of wheel defect by extracting anomaly response features on rail: Analytical modelling, monitoring system design, and in-situ verification. In Proceedings of the 14th International Conference on Railway Engineering, Edinburgh, UK, 21–22 June 2017. [Google Scholar]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Belouchrani, A.; Abed-Meraim, K.; Cardoso, J.F.; Moulines, E. A blind source separation technique using second-order statistics. IEEE Trans. Signal Process. 1997, 45, 434–444. [Google Scholar] [CrossRef]
- Xu, C.; Ni, Y.Q. A Bayesian source separation method for noisy observations by embedding Gaussian process prior. In Proceedings of the 7th World Conference on Structural Control and Monitoring, Qingdao, China, 22–25 July 2018. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.-Z.; Xu, C.; Ni, Y.-Q. Wayside Detection of Wheel Minor Defects in High-Speed Trains by a Bayesian Blind Source Separation Method. Sensors 2019, 19, 3981. https://doi.org/10.3390/s19183981
Liu X-Z, Xu C, Ni Y-Q. Wayside Detection of Wheel Minor Defects in High-Speed Trains by a Bayesian Blind Source Separation Method. Sensors. 2019; 19(18):3981. https://doi.org/10.3390/s19183981
Chicago/Turabian StyleLiu, Xiao-Zhou, Chi Xu, and Yi-Qing Ni. 2019. "Wayside Detection of Wheel Minor Defects in High-Speed Trains by a Bayesian Blind Source Separation Method" Sensors 19, no. 18: 3981. https://doi.org/10.3390/s19183981
APA StyleLiu, X.-Z., Xu, C., & Ni, Y.-Q. (2019). Wayside Detection of Wheel Minor Defects in High-Speed Trains by a Bayesian Blind Source Separation Method. Sensors, 19(18), 3981. https://doi.org/10.3390/s19183981





