Three-Dimensional Mapping of Clay and Cation Exchange Capacity of Sandy and Infertile Soil Using EM38 and Inversion Software
Abstract
1. Introduction
2. Materials and Methods
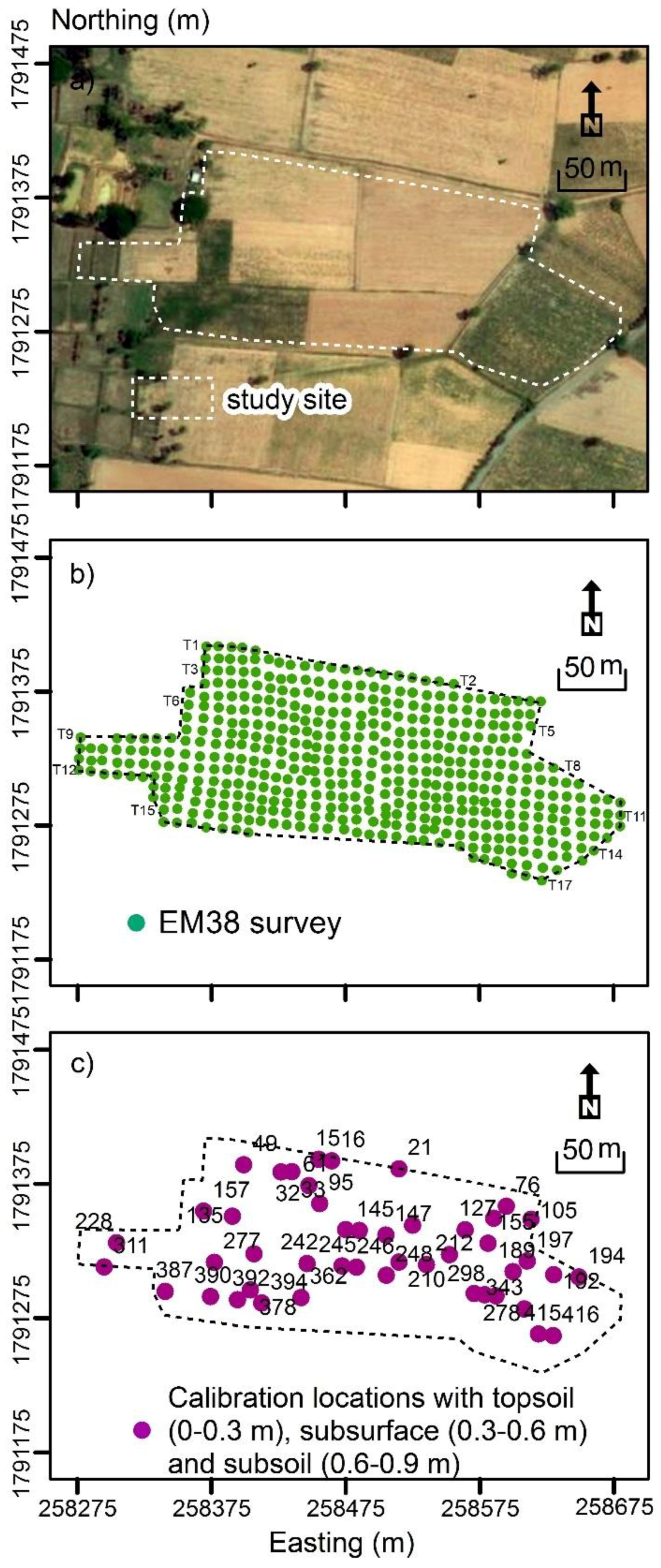
2.1. Study Area
2.2. Data Collection and Interpolation
2.3. Soil Sampling and Laboratory Analysis
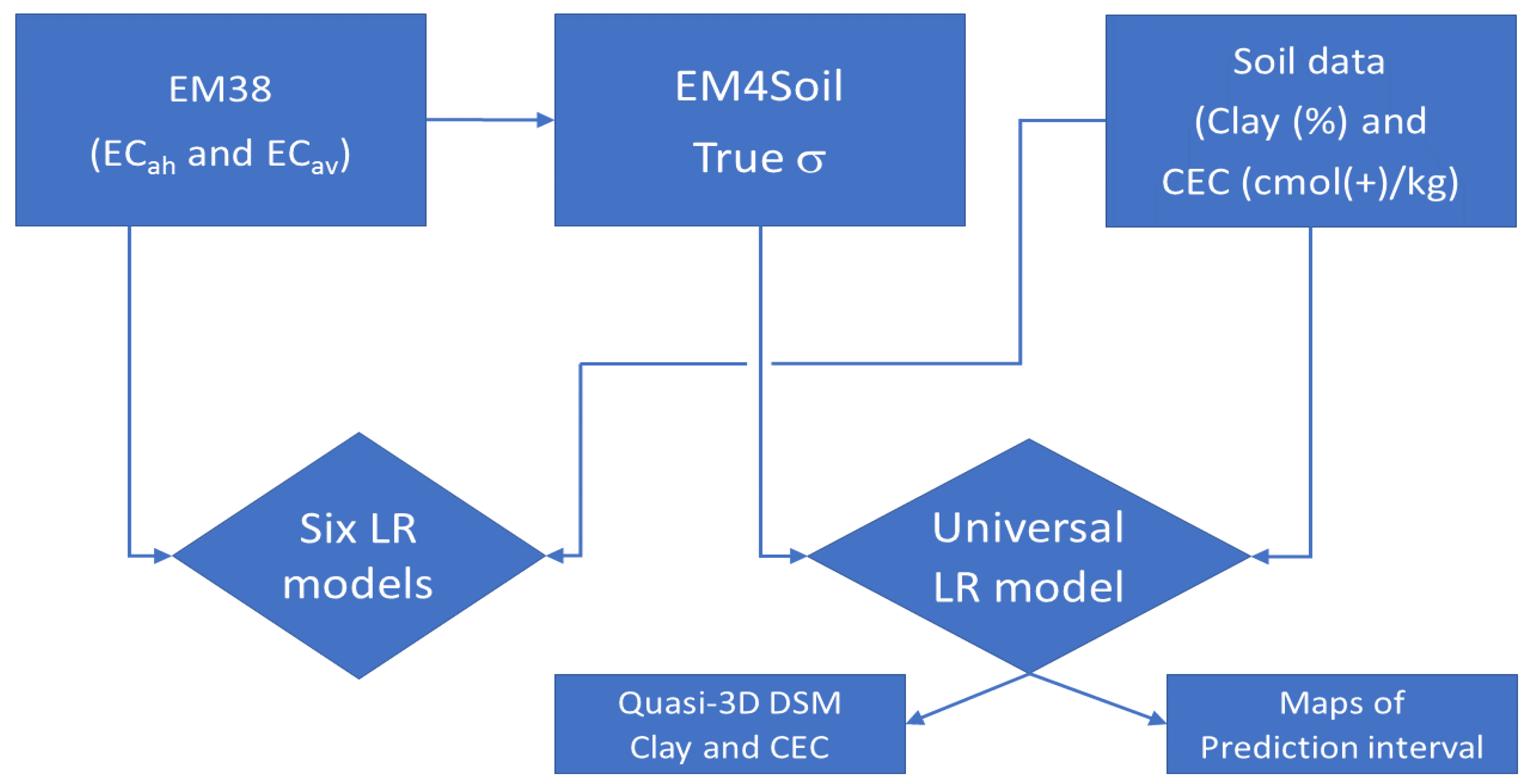
2.4. Quasi-3D Inversion of EM38
2.5. Validation and Comparison with LR
2.6. Prediction Interval (PI)
3. Results and Discussion
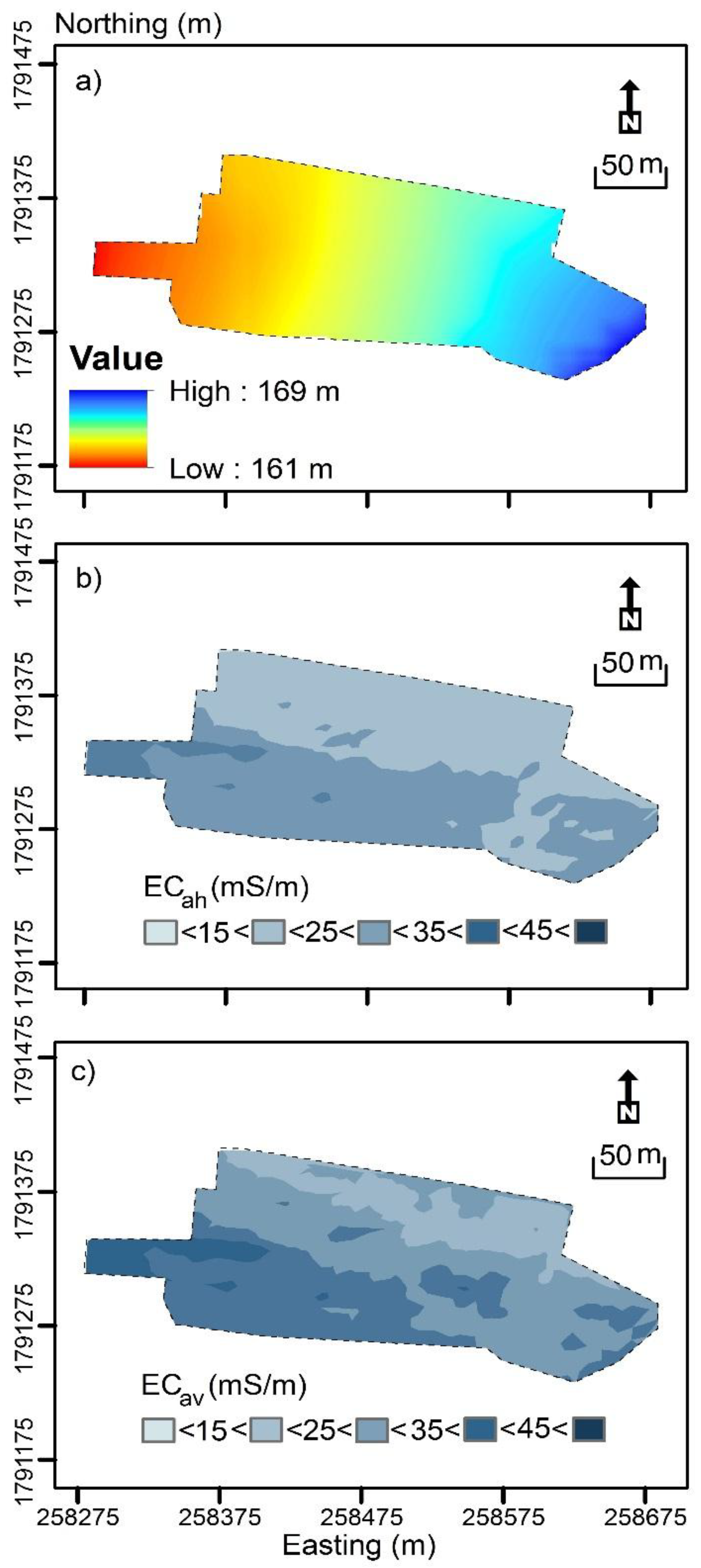
3.1. Preliminary ECah and ECav Data Analysis
3.2. Preliminary Clay and CEC Data Analysis
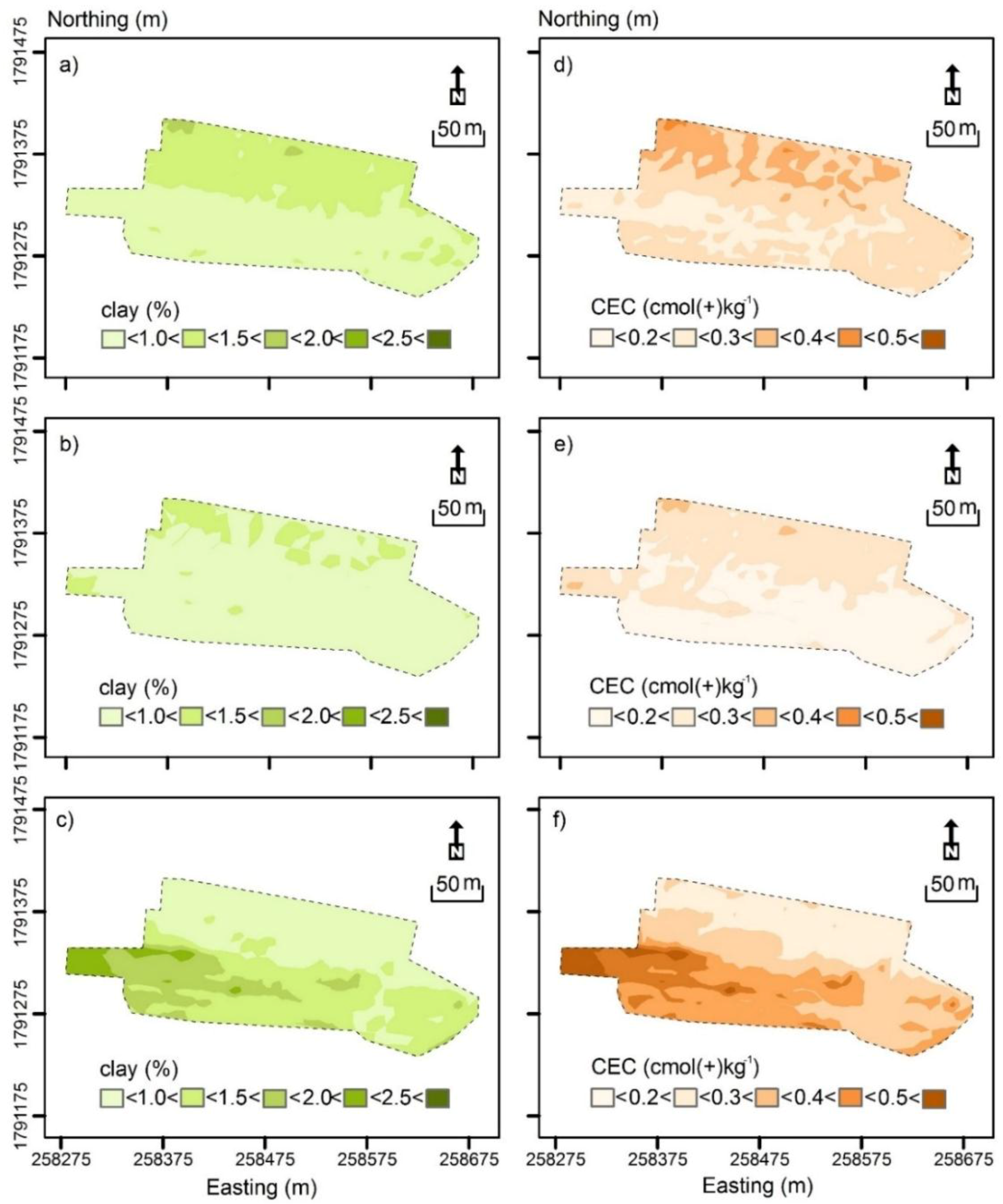
3.3. Spatial Distribution of Clay and CEC Data
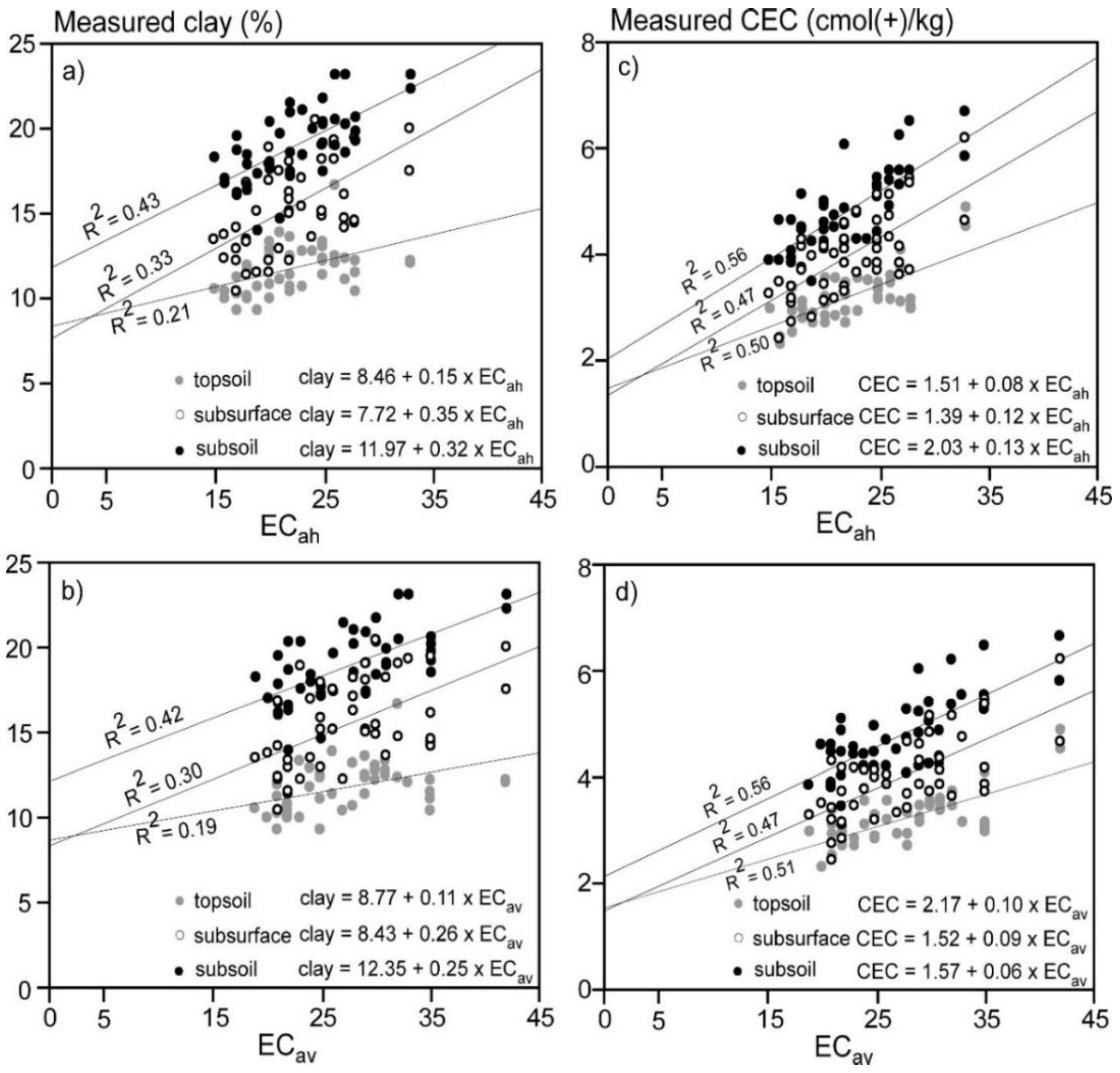
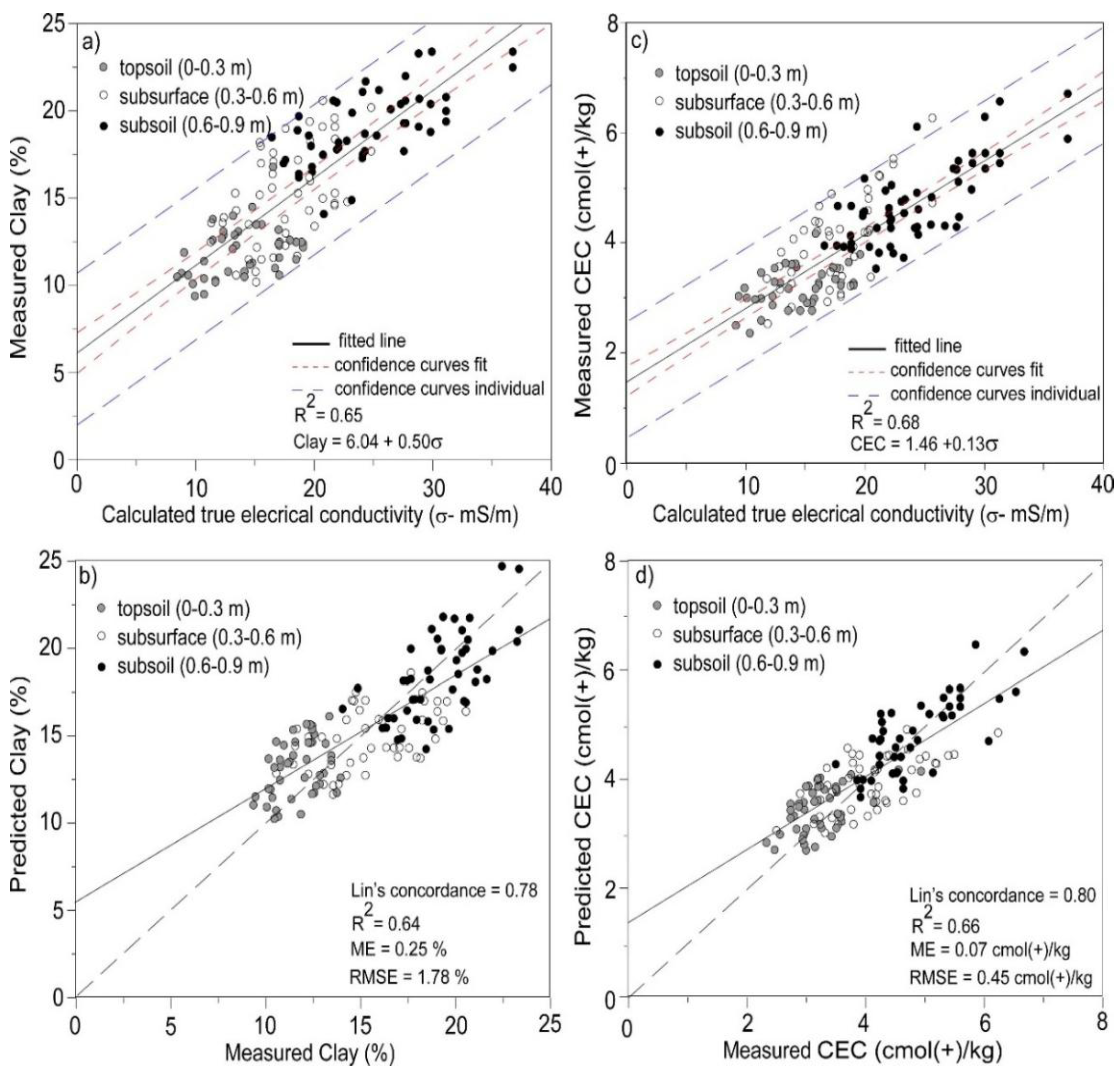
3.4. Linear Regression of Clay and CEC of Individual Depth Increment and ECa
3.5. Linear Regression of Clay for All Depth Increment and σ
3.6. Linear Regression of CEC for All Depth Increments and σ
3.7. Digital Soil Maps of Clay and CEC
3.8. Mapping the Prediction Interval (PI) of Predicted Clay and CEC
3.9. Soil Improvement Guidelines Based on Clay and CEC Maps
4. Conclusions and Discussion
Author Contributions
Acknowledgements
Conflicts of Interests
References and Notes
- FAO. Management of Tropical Sandy Soils for Sustainable Agriculture “A Holistic Approach for Sustainable Development of Problem Soils in the Tropics” 27th November–2nd December 2005, Khon Kaen Thailand; FAO: Bangkok, Thailand, 2005; 24p. [Google Scholar]
- Chiu, Y.C.; Huang, L.N.; Uang, C.M.; Huang, J.F. Determination of cation exchange capacity of clay minerals by potentiometric titration using divalent cation electrodes. Colloid Surf. 1990, 46, 327–337. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, X.; Khongnawang, T.; Arshad, M.; Triantafilis, J. A Vis-NIR spectral library to predict clay in Australian cotton growing soil. Soil Sci. Soc. Am. J. 2018, 82, 1347–1357. [Google Scholar] [CrossRef]
- Xu, R.; Zhao, A.; Yuan, J.; Jiang, J. pH buffering capacity of acid soils from tropical and subtropical regions of China as influenced by incorporation of crop straw biochars. Soils Sediments 2012, 12, 494–502. [Google Scholar] [CrossRef]
- Vaught, R.; Brye, K.R.; Miller, D.M. Relationships among Coefficient of Linear Extensibility and Clay Fractions in Expansive, Stoney Soils. Soil Sci. Soc. Am. J. 2006, 70, 1983–1990. [Google Scholar] [CrossRef]
- Castrignanò, A.; Giugliarini, L.; Risaliti, R.; Martinelli, N. Study of spatial relationships among some soil physico-chemical properties of a field in central Italy using multivariate geostatistics. Geoderma 2000, 97, 39–60. [Google Scholar] [CrossRef]
- Asadzadeh, F.; Akbarzadeh, A.; Zolfaghari, A.; Taghizadeh-Mehrjardi, R.; Mehrabanian, M.; Rahimi-Lake, H.; Sabeti-Amirhandeh, M. Study and comparison of some geostatistical methods for mapping cation exchange capacity (CEC) in soils of northern Iran. Ann. Fac. Eng. Hunedoara 2012, 10, 59–66. [Google Scholar]
- Burgess, T.M.; Webster, R. Optimal interpolation and isarithmic mapping of soil properties, I the semi-variogram and punctual kriging. J. Soil Sci. 1980, 31, 315–331. [Google Scholar] [CrossRef]
- Wu, J.; Norvell, W.A.; Hopkins, D.G.; Smith, D.B.; Ulmer, M.G.; Welch, R.M. Improved Prediction and Mapping of Soil Copper by Kriging with Auxiliary Data for Cation-Exchange Capacity. Soil Sci. Soc. Am. J. 2003, 67, 919–927. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Sample adequately to estimate variograms of soil properties. Eur. J. Soil Sci. 1992, 43, 177–192. [Google Scholar] [CrossRef]
- Jung, W.K.; Kitchen, N.R.; Sudduth, K.A.; Anderson, S.H. Spatial characteristics of claypan soil properties in an agricultural field. Soil Sci. Soc. Am. 2006, 70, 1387–1397. [Google Scholar] [CrossRef]
- Khaledian, Y.; Brevik, E.C.; Pereira, P.; Cerdà, A.; Fattah, M.A.; Tazikeh, H. Modeling soil cation exchange capacity in multiple countries. Catena 2017, 158, 194–200. [Google Scholar] [CrossRef]
- Sulieman, M.; Saeed, I.; Hassaballa, A.; Rodrigo-Comino, J. Modeling cation exchange capacity in multi geochronological-derived alluvium soils: An approach based on soil depth intervals. Catena 2017, 167, 327–339. [Google Scholar] [CrossRef]
- Williams, B.G.; Hoey, D. The use of electromagnetic induction to detect the spatial variability of the salt and clays of soils. Aust. J. Soil Res. 1987, 25, 21–27. [Google Scholar] [CrossRef]
- Triantafilis, J.; Huckel, A.I.; Odeh, I.O.A. Comparison of statistical prediction methods for estimating field-scale clay using different combinations of ancillary variables. Soil Sci. 2001, 66, 415–427. [Google Scholar] [CrossRef]
- Mertens, F.M.; Patzold, S.; Welp, G. Spatial heterogeneity of soil properties and its mapping with apparent electrical conductivity. Plant Nutr. Soil Sci. 2008, 171, 146–154. [Google Scholar] [CrossRef]
- Heil, K.; Schmidhalter, U. The Application of EM38: Determination of Soil Parameters, Selection of Soil Sampling Points and Use in Agriculture and Archaeology. Sensors 2017, 17, 2540. [Google Scholar] [CrossRef]
- Bishop, T.F.A.; McBratney, A.B. A comparison of prediction methods for the creation of fieldextent soil property maps. Geoderma 2001, 103, 149–160. [Google Scholar] [CrossRef]
- Sudduth, K.A.; Kitchen, N.R.; Bollero, G.A.; Bullock, D.G.; Wiebold, W.J. Comparison of Electromagnetic Induction and Direct Sensing of Soil Electrical Conductivity. Agron. J. 2003, 95, 472–482. [Google Scholar] [CrossRef]
- Triantafilis, J.; Lesch, S.M.; La Lau, K.; Buchanan, S.M. Field level digital soil mapping of cation exchange capacity using electromagnetic induction and a hierarchical spatial regression model. Soil Res. 2009, 47, 651–663. [Google Scholar] [CrossRef]
- Paisanchareon, K. Research and Development on Soil Water and Fertilizers for Sugarcane; Department of Agriculture, Ministry of Agriculture and Cooperatives: Krung Thep Maha Nakhon, Thailand, 2015. [Google Scholar]
- Office of Soil Survey and Land Use Planning. Miracle of Soils: Soil Groups for Cash Crops Cultivation in Thailand; Land Development Department, Ministry of Agriculture and Cooperatives: Krung Thep Maha Nakhon, Thailand, 2005. [Google Scholar]
- Zare, E.; Huang, J.; Monteiro Santos, F.A.; Triantafilis, J. Mapping salinity in three dimensions using a DUALEM-421 and electromagnetic inversion software. Soil Sci. Soc. Am. J. 2015, 79, 1729–1740. [Google Scholar] [CrossRef]
- Huang, J.; Scudiero, E.; Clary, W.; Corwin, D.L.; Triantafilis, J. Time-lapse monitoring of soil water content using electromagnetic conductivity imaging. Soil Use Manag. 2017, 33, 191–204. [Google Scholar] [CrossRef]
- Koganti, T.; Moral, F.J.; Rebollo, F.J.; Huang, J.; Triantafilis, J. Mapping cation exchange capacity using a Veris-3100 instrument and invVERIS modelling software. Sci. Total Environ. 2017, 599–600, 2156–2165. [Google Scholar] [CrossRef]
- Khedari, J.; Sanprajak, A.; Hirunlarbh, J. Thailand climatic zones. Renew Energ. 2002, 25, 267–280. [Google Scholar] [CrossRef]
- Thai Meteorological Department Website. 2017. Available online: https://www.tmd.go.th/en/ (accessed on 25 April 2017).
- Sugar Research Australia. Nutrient Management Guidelines for Sugarcane in New South Wales. 2017. Available online: http://www.sugarresearch.com.au/icms_docs/194337_SIX_EASY_STEPS_Nutrient_Guidelines_for_NSW.pdf (accessed on 28 February 2017).
- Geonics. Ltd. 1745 Meyerside Drive, Unit 8, Mississauga, Ontario L5T 1C6, Canada.
- Garmin International, Inc. 1200 East 151st Street, Olathe, KS 66062-3426, USA.
- Beretta, A.N.; Silbermann, A.V.; Paladino, L.; Torres, D.; Bassahun, D.; Musselli, R.; García-Lamohte, A. Soil texture analyses using a hydrometer: Modification of the Bouyoucos method. Cien. Investig. Agrar. 2014, 41, 263–271. [Google Scholar] [CrossRef]
- Chapman, H.D. Cation Exchange Capacity. In Methods of Soil Analysis; Black, C.A., Ed.; American Society of Agronomy: Madison, WI, USA, 1965; pp. 891–901. [Google Scholar]
- EMTOMO. EM4Soil v304; EMTOMO: Lisboa, Portugal, 2017. [Google Scholar]
- Monteiro Santos, F.A.; Triantafilis, J.; Bruzgulis, K. A spatially constrained 1D inversion algorithm for quasi-3D conductivity imaging: Application to DUALEM-421 data collected in a riverine plain. Geophysics 2011, 76, B43–B53. [Google Scholar] [CrossRef]
- Constable, S.C.; Parker, R.L.; Constable, C.G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics 1987, 52, 289–300. [Google Scholar] [CrossRef]
- McNeill, J.D. Electromagnetic Terrain Conductivity Measurement at Low Induction Numbers; Geonics Ltd.: Mississauga, ON, Canada, 1980. [Google Scholar]
- Kaufman, A.A.; Keller, G.V. Frequency and Transient Sounding Methods in Geochemistry and Geophysics. Geophys. J. Int. 1983, 77, 935–937. [Google Scholar]
- Lawrence, I.; Lin, K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar]
- Curran-Everett, D. Explorations in statistics: Confidence intervals. Adv. Physiol. Educ. 2009, 33, 87–90. [Google Scholar] [CrossRef]
- SAS Institute. JMP Version 13; SAS Institute Inc.: Cary, NC, USA, 2017. [Google Scholar]
- Triantafilis, J.; Wong, V.; Monteiro Santos, F.A.; Page, D.; Wege, R. Modeling the electrical conductivity of hydrogeological strata using joint-inversion of loop-loop electromagnetic data. Geophysics 2012, 77, 285–294. [Google Scholar] [CrossRef]
- Triantafilis, J.; Monteiro Santos, F.A. Resolving the spatial distribution of the true electrical conductivity with depth using EM38 and EM31 signal data and a laterally constrained inversion model. Aust. J. Soil Res. 2010, 48, 434–446. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, J.; Zhao, D.; Li, N.; Zare, E.; Triantafilis, J. Digital regolith mapping of clay across the Ashley irrigation area using electromagnetic induction data and inversion modelling. Geoderma 2019, 346, 18–29. [Google Scholar] [CrossRef]
- Davies, G.B.; Huang, J.; Monteiro Santos, F.A.; Triantafilis, J. Modeling coastal salinity in quasi 2D and 3D using a DUALEM-421 and inversion software. Groundwater 2015, 53, 424–431. [Google Scholar] [CrossRef]
- Triantafilis, J.; Roe, J.A.E.; Monteiro Santos, F.A. Detecting a leachate-plume in an aeolian sand landscape using a DUALEM-421 induction probe to measure electrical conductivity followed by inversion modelling. Soil Use Manag 2011, 27, 357–366. [Google Scholar] [CrossRef]



| Clay (%) | Chemical Fertilizer Rates (kg/ha) | Compost Fertilizer Rates (t/ha) | ||
|---|---|---|---|---|
| N | P2O5 | K2O | ||
| <15 | 113 | 38 | 113 | 25 |
| 15–18 | 113 | 38 | 75 | 19 |
| 18–35 | 75 | 19 | 75 | 18 |
| >35 | 72 | 38 | 38 | 18 |
| CEC (cmol(+)/kg) | Lime Application (t/ha) |
|---|---|
| <4 | 1.25 |
| 4–8 | 2.5 |
| 8–16 | 4 |
| >16 | 5 |
| ECa (mS/m) | |||||||
|---|---|---|---|---|---|---|---|
| Data Source | n | Min | Mean | Median | Max | Skewness | CV (%) |
| Survey data | |||||||
| ECah | 467 | 14 | 23.1 | 23 | 35 | 0.2 | 19.4 |
| ECav | 467 | 18 | 28.8 | 29 | 45 | 0.3 | 20.5 |
| Calibration data | |||||||
| ECah | 46 | 15 | 22.3 | 22 | 33 | 0.4 | 19.5 |
| ECav | 46 | 19 | 27.5 | 27.5 | 42 | 0.67 | 19.5 |
| Property/Depth | n | Min | Mean | Median | Max | Skewness | CV (%) |
|---|---|---|---|---|---|---|---|
| clay (%) | |||||||
| topsoil (0–0.3 m) | 46 | 9.4 | 11.9 | 12 | 16.8 | 0.8 | 12.2 |
| subsurface (0.3–0.6 m) | 46 | 10.6 | 15.6 | 15.3 | 20.6 | 0.1 | 17 |
| subsoil (0.6–0.9 m) | 46 | 14.1 | 19.1 | 19 | 23.4 | 0.1 | 11.2 |
| CEC (cmol(+)/kg) | |||||||
| topsoil (0–0.3 m) | 46 | 2.3 | 3.3 | 3.2 | 5 | 1.3 | 14.8 |
| subsurface (0.3–0.6 m) | 46 | 2.5 | 4.1 | 4 | 6.3 | 0.6 | 18.5 |
| subsoil (0.6–0.9 m) | 46 | 3.5 | 4.9 | 4.7 | 6.7 | 0.7 | 15.1 |
| Clay | λ | S1, CF | S1, FS | S2, CF | S2, FS |
| 0.07 | 0.631 | 0.648 | 0.596 | 0.616 | |
| 0.3 | 0.625 | 0.643 | 0.537 | 0.559 | |
| 0.6 | 0.622 | 0.643 | 0.465 | 0.487 | |
| 0.9 | 0.619 | 0.637 | 0.409 | 0.430 | |
| CEC | |||||
| 0.07 | 0.666 | 0.674 | 0.656 | 0.666 | |
| 0.3 | 0.666 | 0.674 | 0.641 | 0.655 | |
| 0.6 | 0.667 | 0.672 | 0.599 | 0.617 | |
| 0.9 | 0.668 | 0.676 | 0.559 | 0.577 |
| Clay | Parameter | Estimate | SE | t-ratio | Prob > |t| | R2 |
| Intercept | 6.04 | 0.63 | 9.62 | <0.0001* | 0.65 | |
| 0.07, S1, FS | 0.50 | 0.03 | 15.84 | <0.0001* | ||
| CEC | ||||||
| Intercept | 1.46 | 0.16 | 9.09 | <0.0001* | 0.68 | |
| 0.9, S1, FS | 0.13 | 0.01 | 16.85 | <0.0001* |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khongnawang, T.; Zare, E.; Zhao, D.; Srihabun, P.; Triantafilis, J. Three-Dimensional Mapping of Clay and Cation Exchange Capacity of Sandy and Infertile Soil Using EM38 and Inversion Software. Sensors 2019, 19, 3936. https://doi.org/10.3390/s19183936
Khongnawang T, Zare E, Zhao D, Srihabun P, Triantafilis J. Three-Dimensional Mapping of Clay and Cation Exchange Capacity of Sandy and Infertile Soil Using EM38 and Inversion Software. Sensors. 2019; 19(18):3936. https://doi.org/10.3390/s19183936
Chicago/Turabian StyleKhongnawang, Tibet, Ehsan Zare, Dongxue Zhao, Pranee Srihabun, and John Triantafilis. 2019. "Three-Dimensional Mapping of Clay and Cation Exchange Capacity of Sandy and Infertile Soil Using EM38 and Inversion Software" Sensors 19, no. 18: 3936. https://doi.org/10.3390/s19183936
APA StyleKhongnawang, T., Zare, E., Zhao, D., Srihabun, P., & Triantafilis, J. (2019). Three-Dimensional Mapping of Clay and Cation Exchange Capacity of Sandy and Infertile Soil Using EM38 and Inversion Software. Sensors, 19(18), 3936. https://doi.org/10.3390/s19183936






