Navigation Algorithm Based on the Boundary Line of Tillage Soil Combined with Guided Filtering and Improved Anti-Noise Morphology
Abstract
1. Introduction
2. Materials and Methods
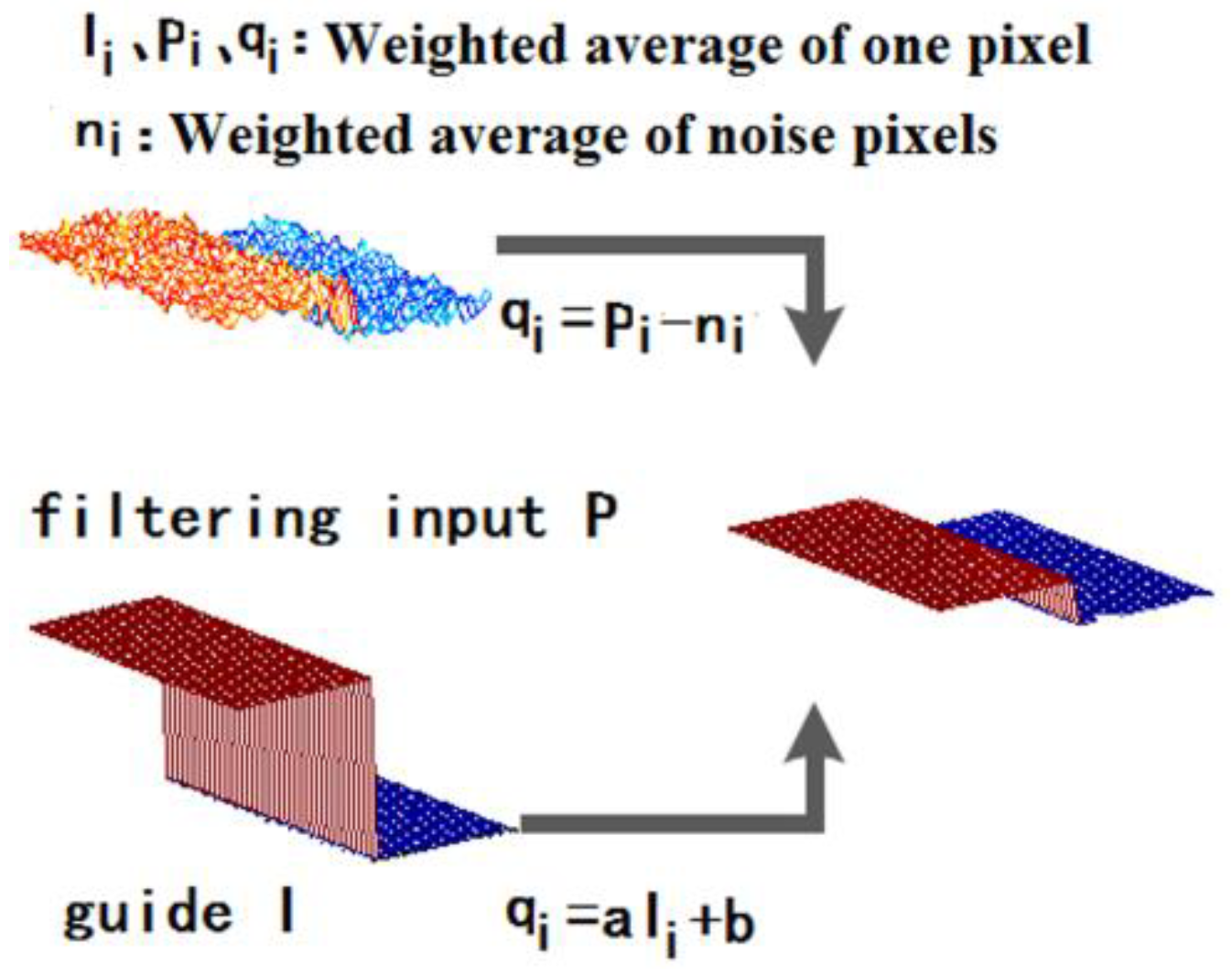
2.1. Guided Filtering
2.1.1. Local Linear Model
2.1.2. Local Linear Model Solution
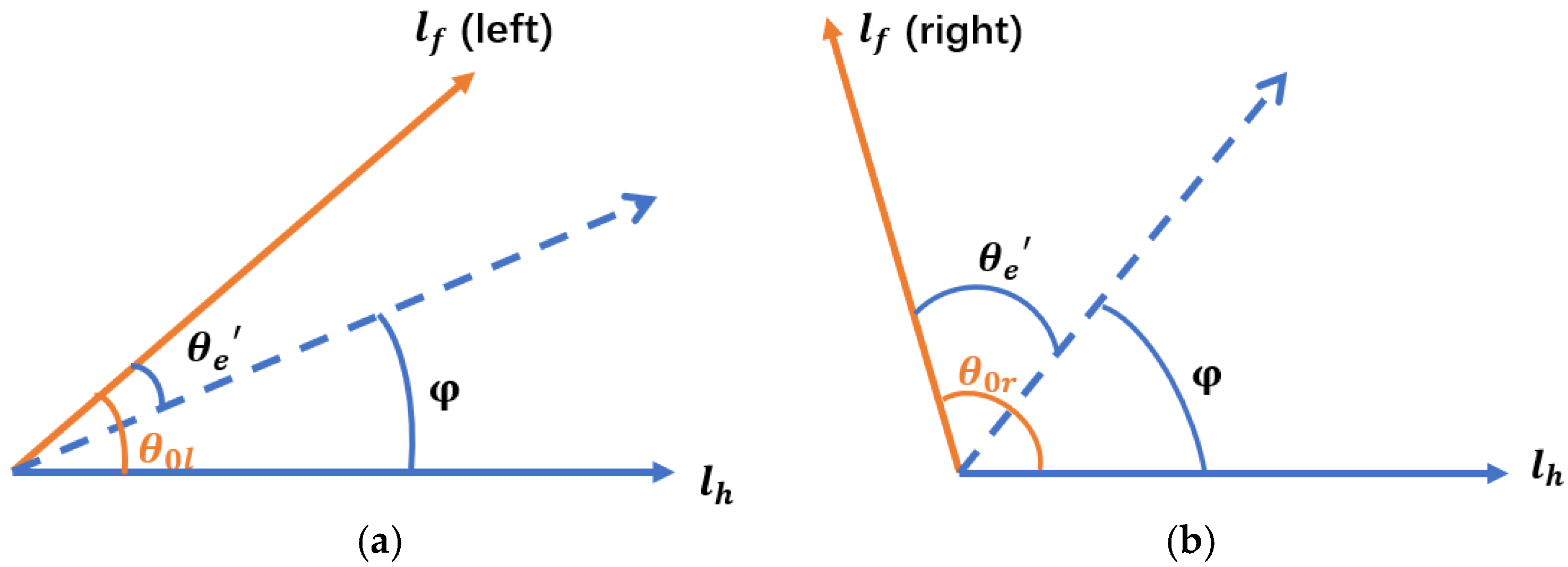
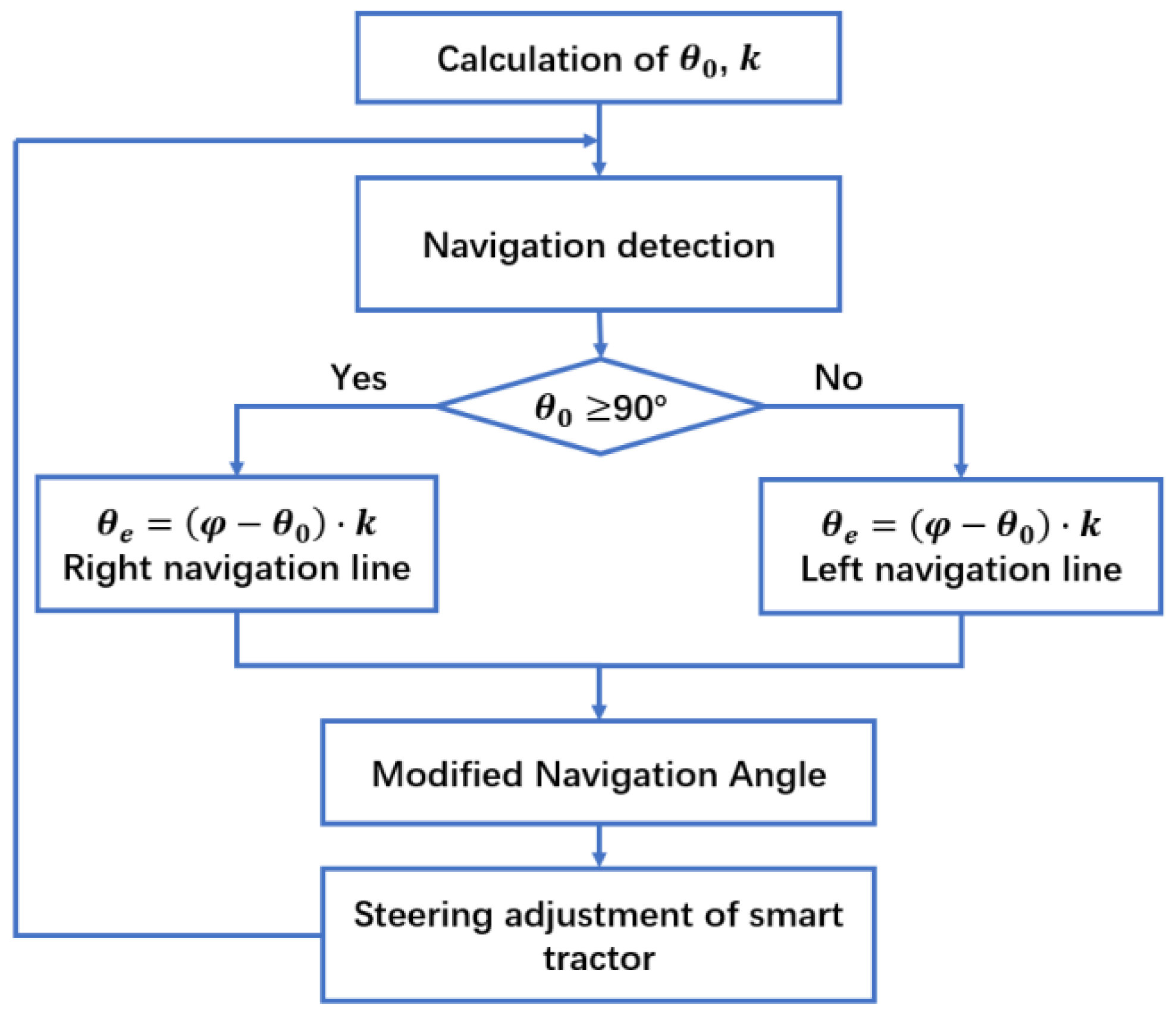
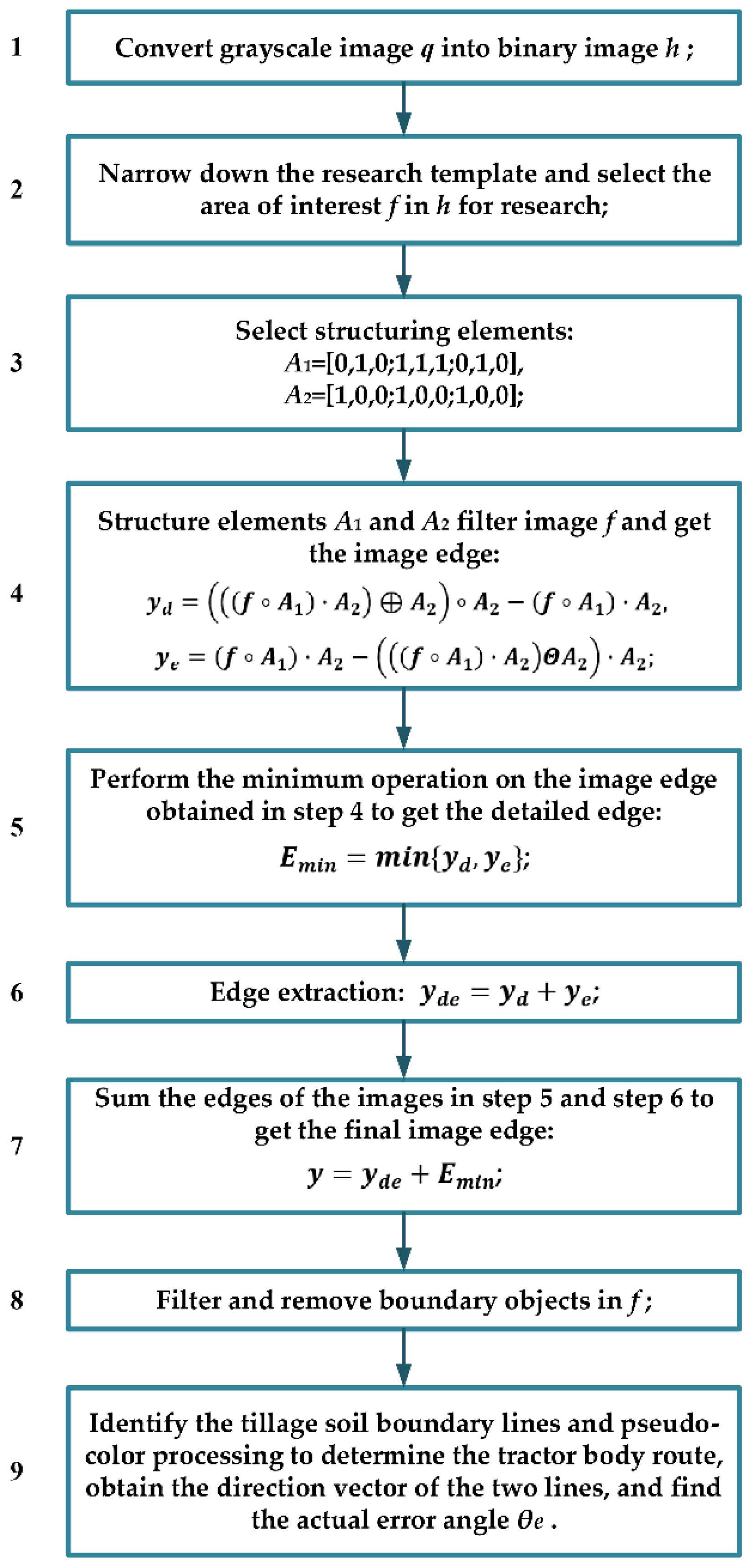
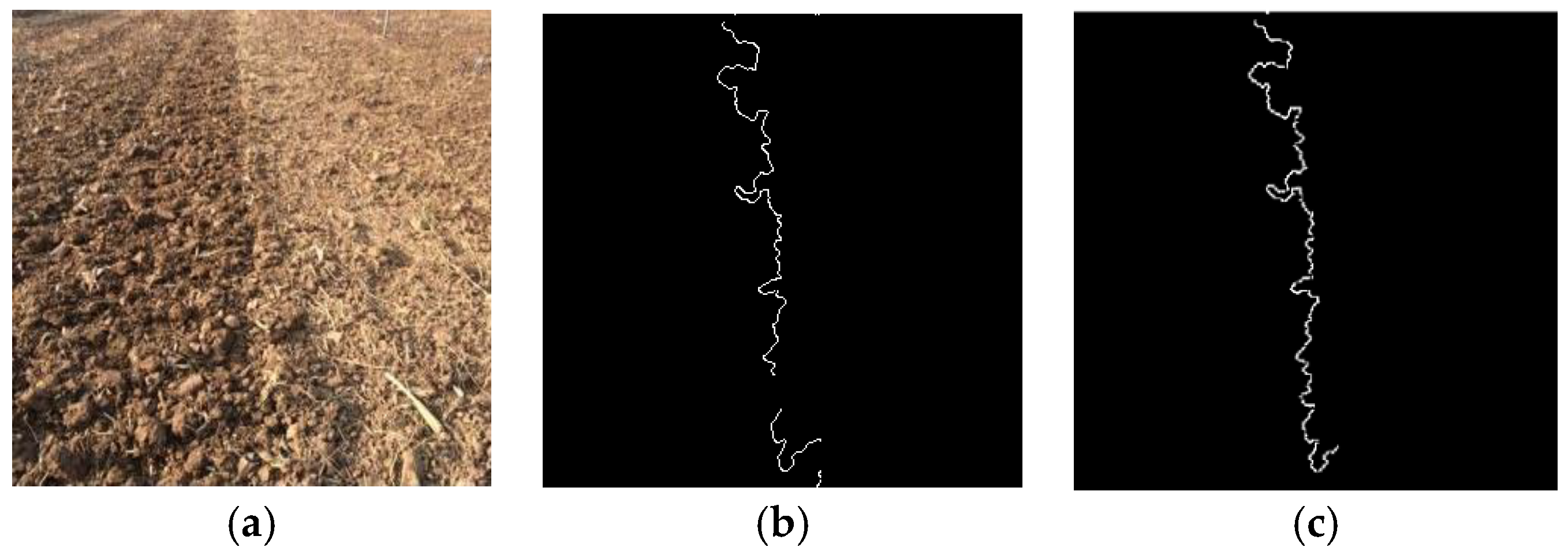
2.2. Improved Anti-Noise Morphology Algorithm for Image Navigation Line Extraction
3. Experiment
3.1. Effectiveness Verification of the Algorithm
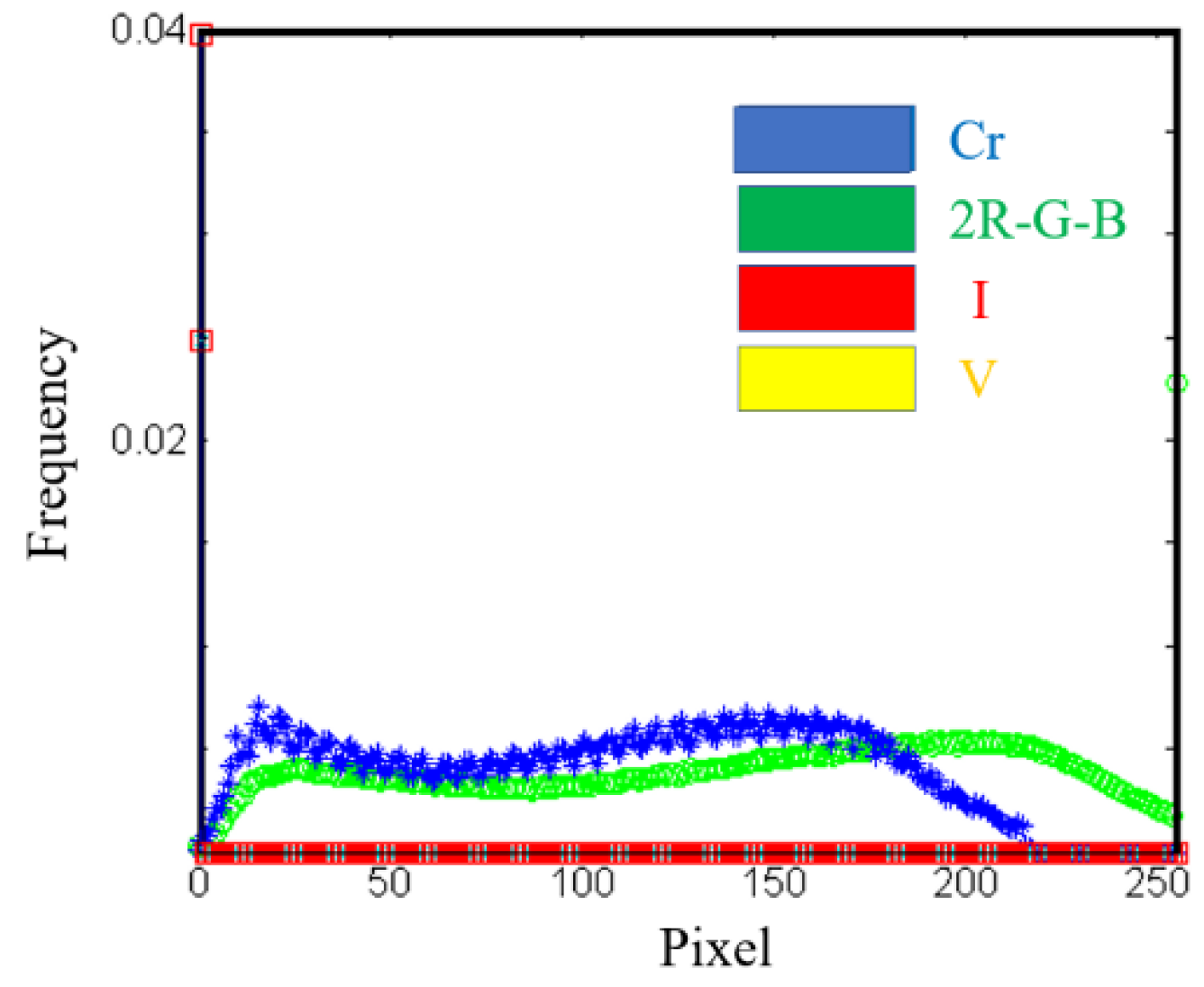
3.1.1. Color Space Selection
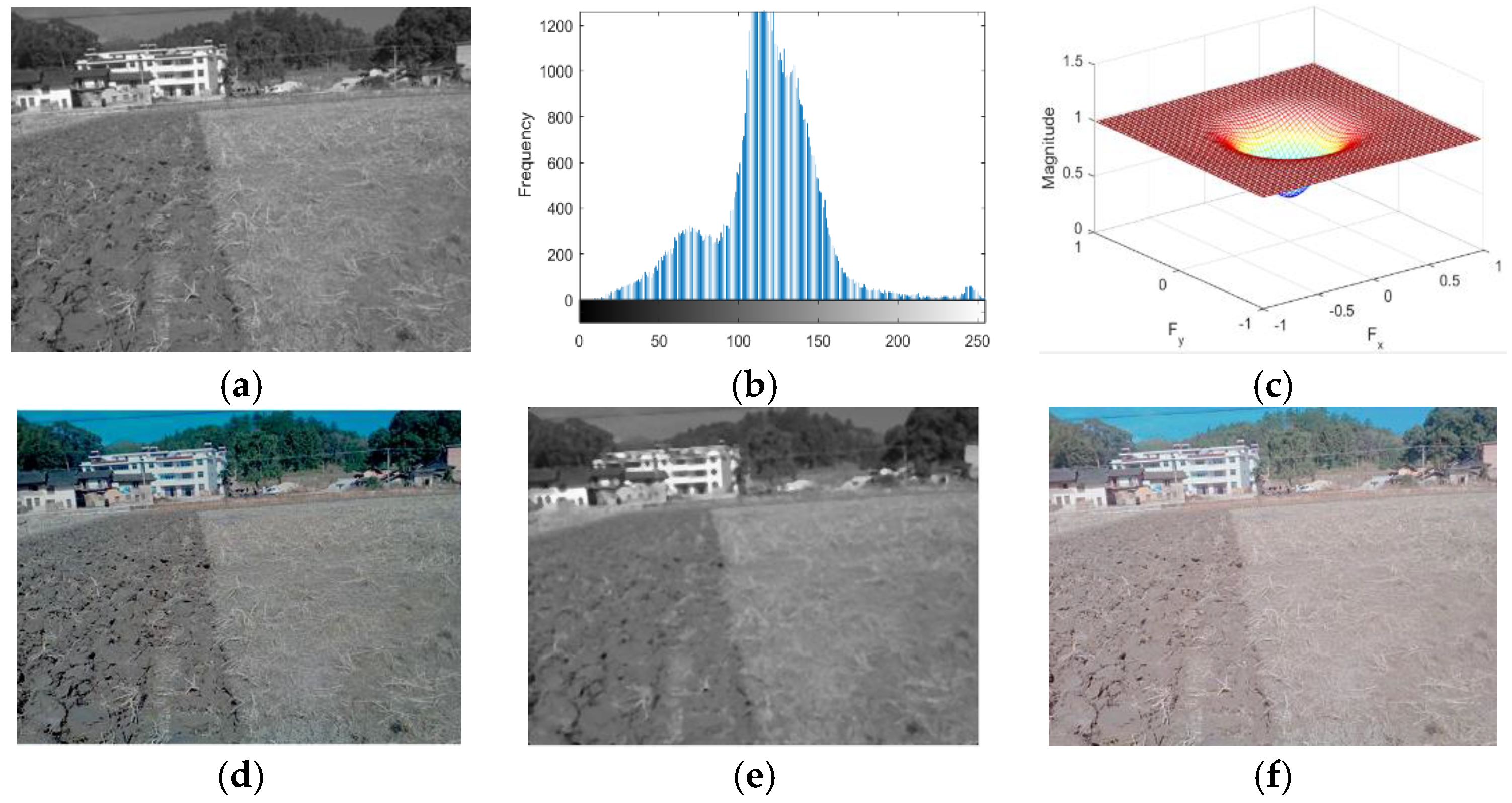
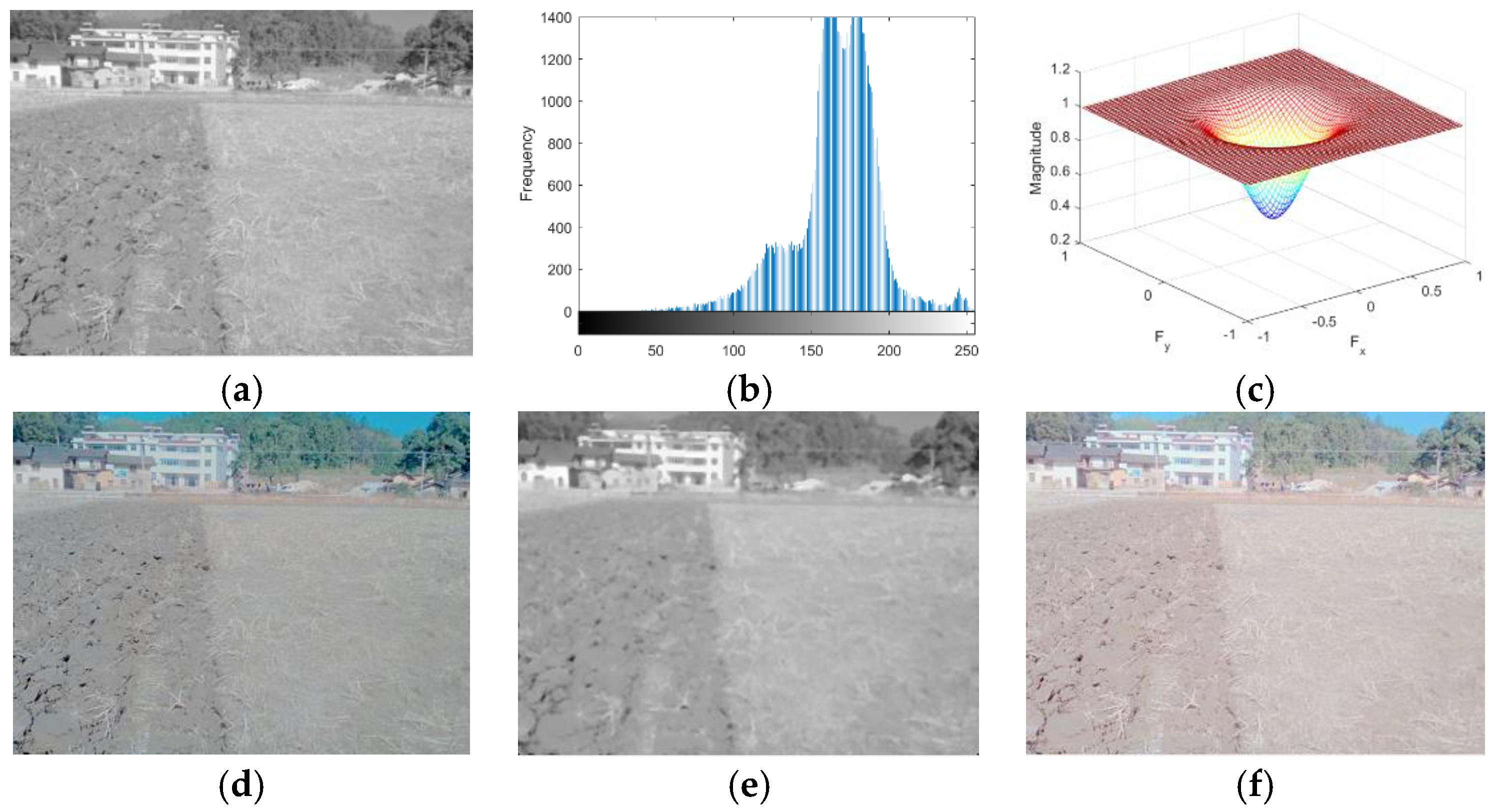
3.1.2. Filtering Method Selection
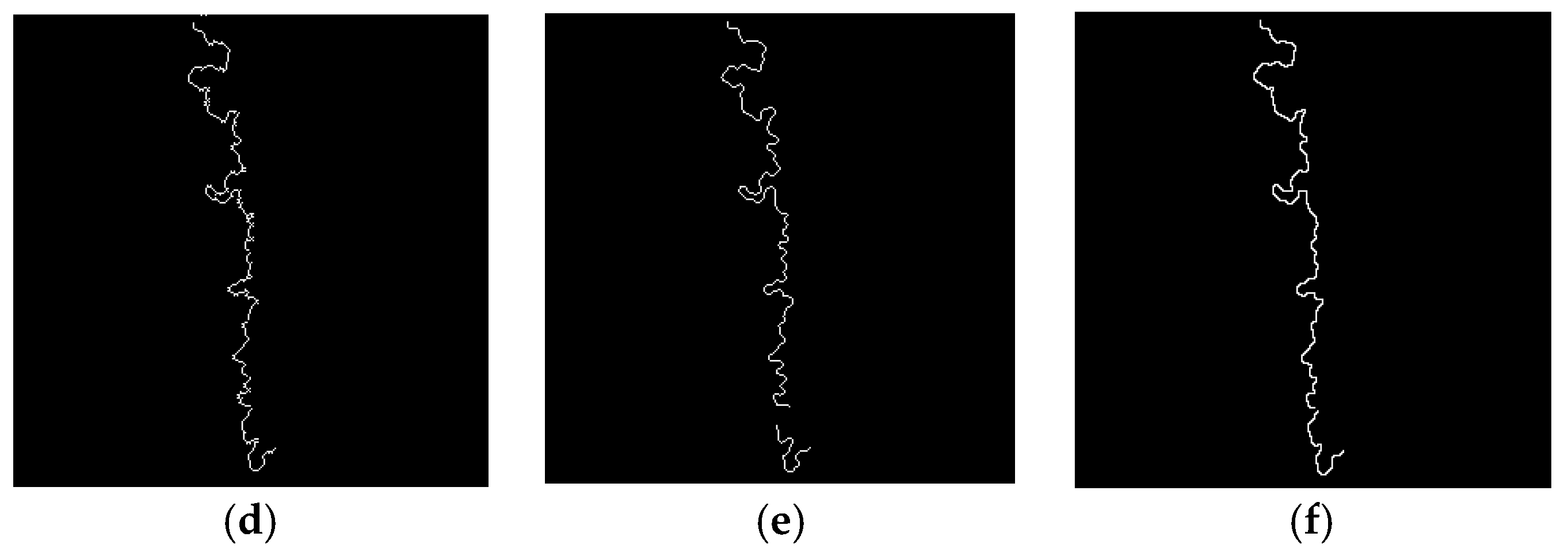
3.1.3. Navigation Line Extraction Using Improved Anti-Noise Morphology Algorithm
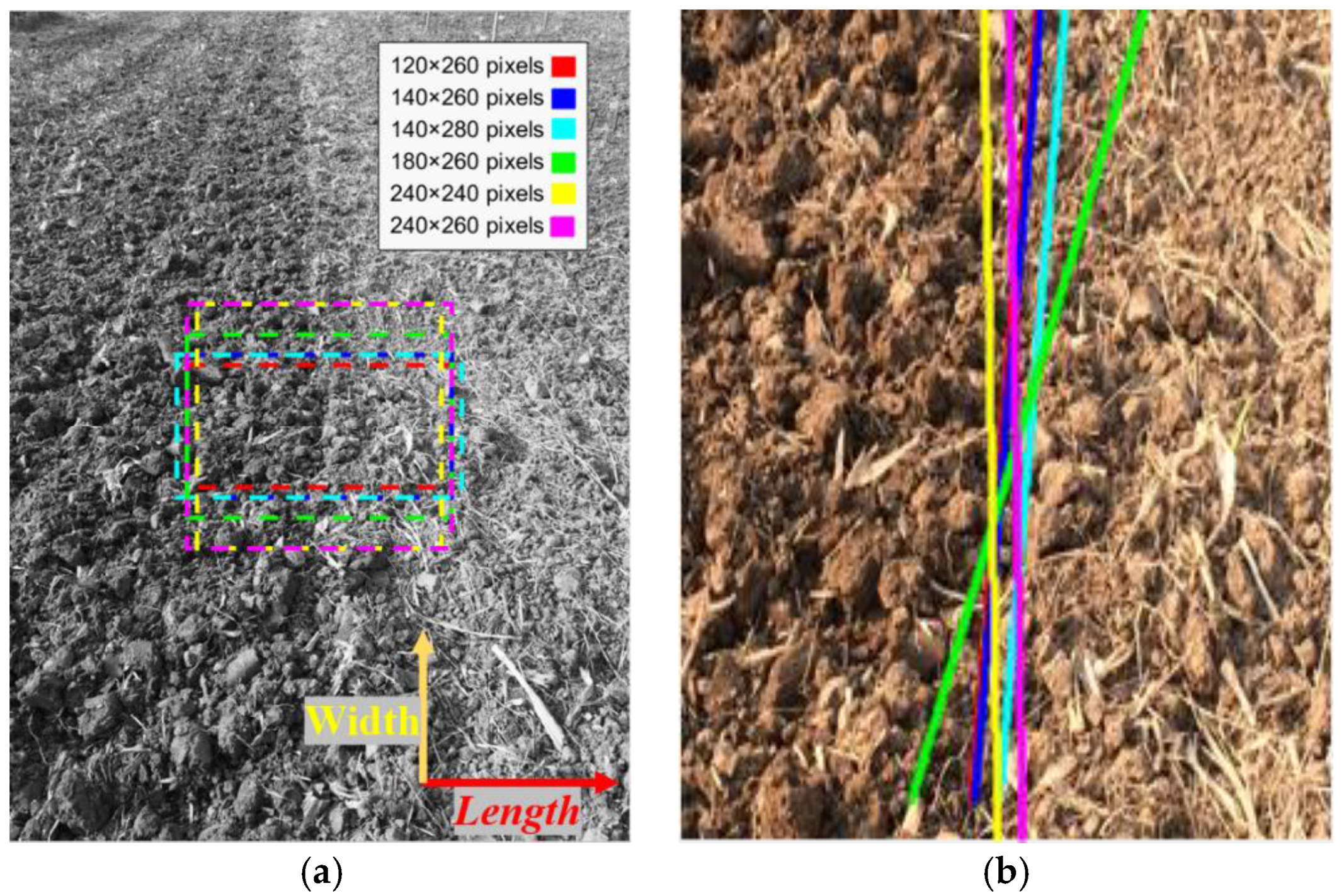
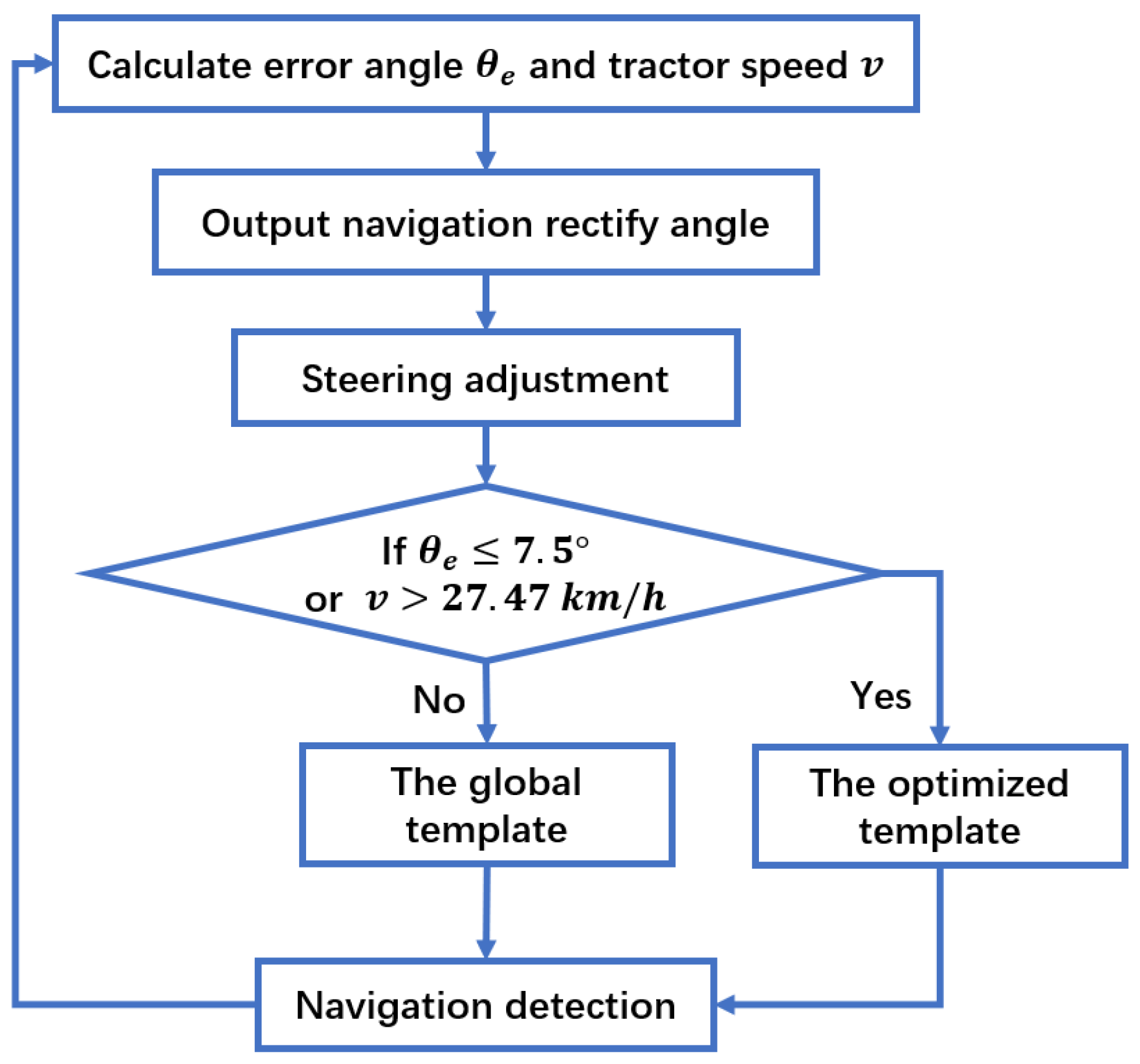
3.1.4. Image Template Optimization
- (1)
- The original image is transformed to grayscale and uniformly scaled to pixels.
- (2)
- The middle of the longest line is used as a reference point.
- (3)
- Different size rectangles centered at the reference point are used for navigation precision comparation, as shown in Figure 17a.
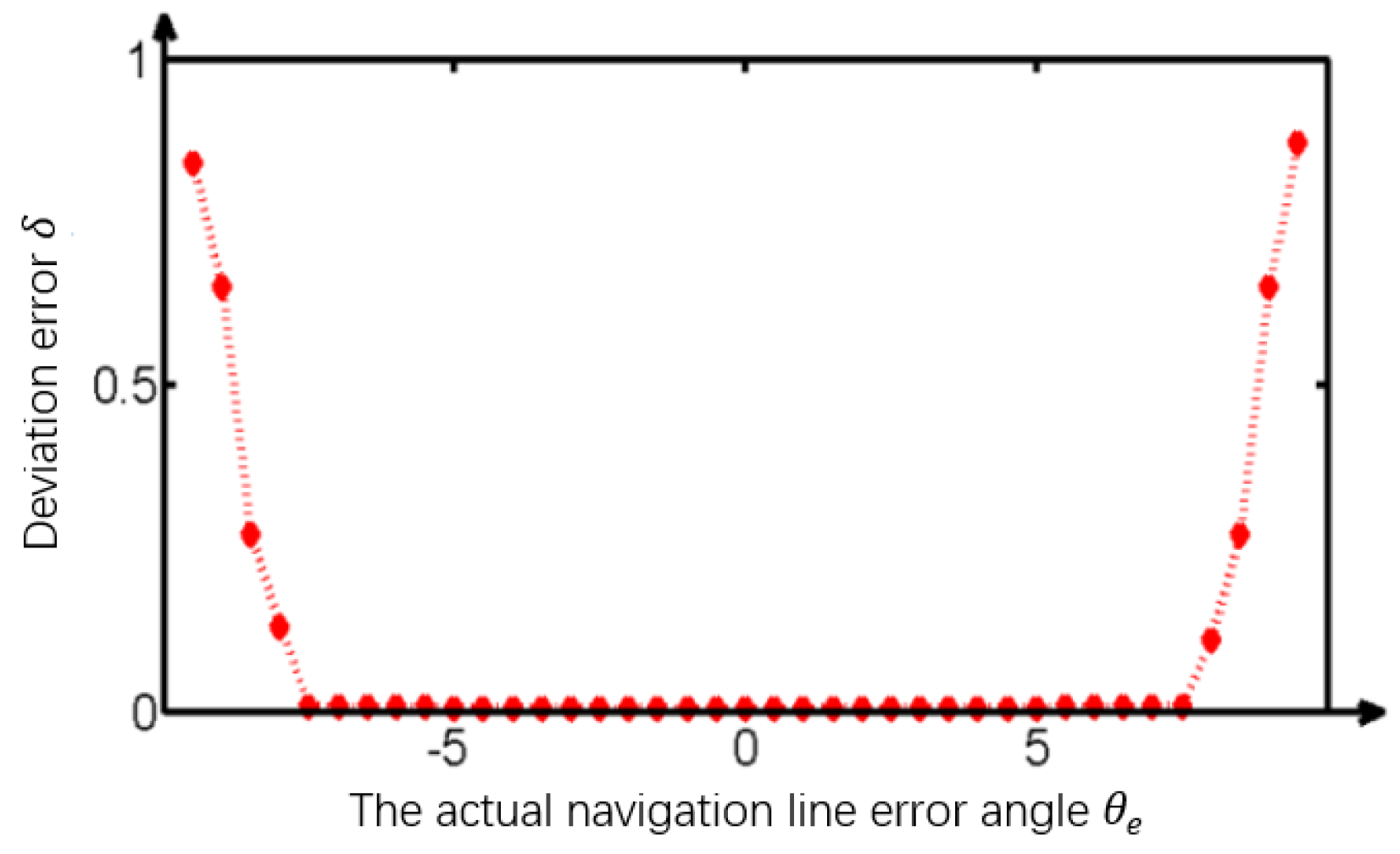
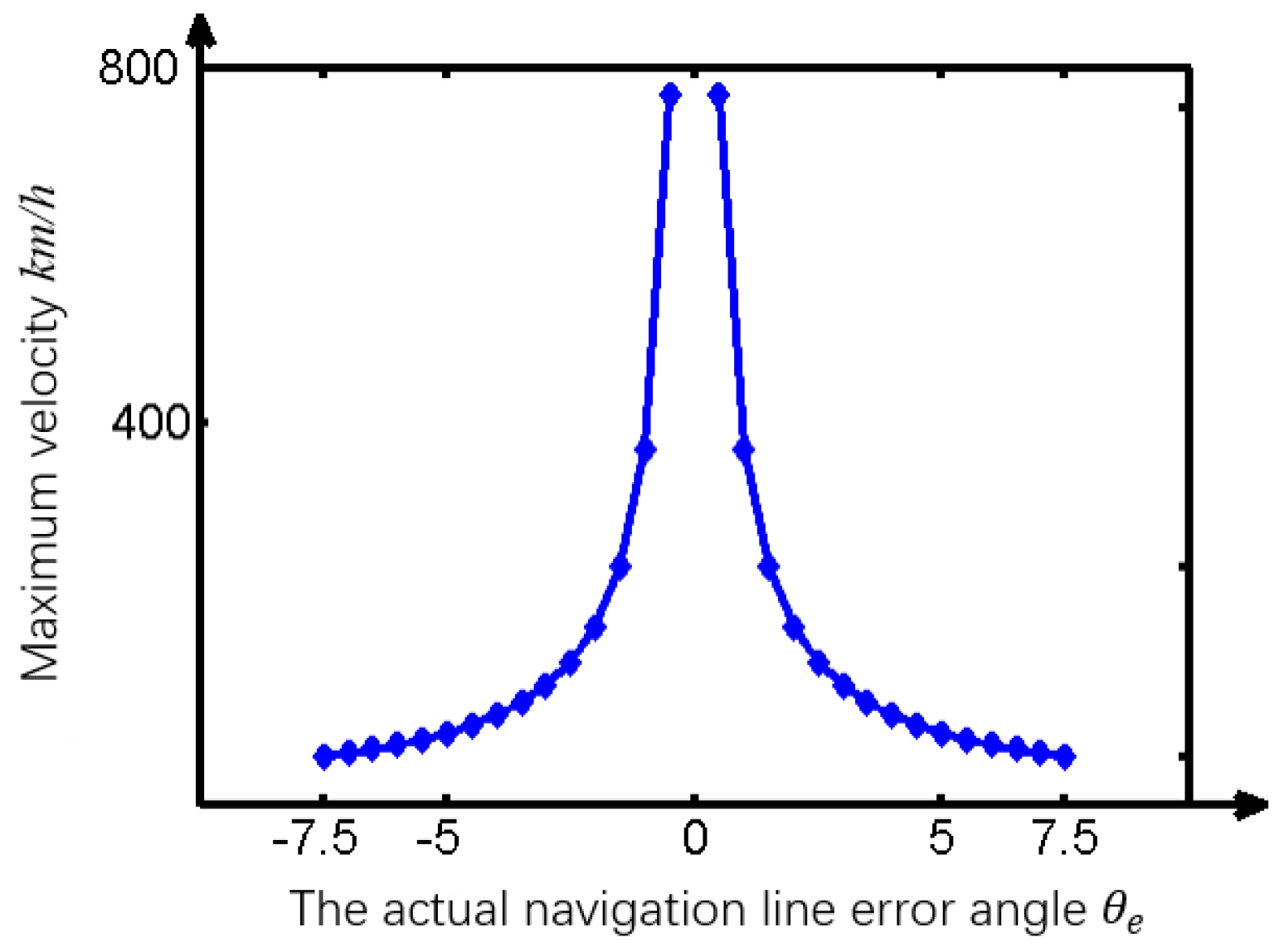
3.2. Navigation Experiment in the Field
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khutaevich, A.B. A Laboratory Study of the Pneumatic Sowing Device for Dotted and Combined Crops. Ama Agric. Mech. Asia Afr. Latin Am. 2019, 50, 57–59. [Google Scholar]
- Paraforos, D.S.; Hübner, R.; Griepentrog, H.W. Automatic determination of headland turning from auto-steering position data for minimising the infield non-working time. Comput. Electron. Agric. 2018, 152, 393–400. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Liu, W.; Su, D.; Yan, X. A Novel Tangential Electric-Field Sensor Based on Electric Dipole and Integrated Balun for the Near-Field Measurement Covering GPS Band. Sensors 2019, 19, 1970. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhao, X.; Pang, C.; Zhang, L.; Feng, B. The Influence of Satellite Configuration and Fault Duration Time on the Performance of Fault Detection in GNSS/INS Integration. Sensors 2019, 19, 2147. [Google Scholar] [CrossRef] [PubMed]
- Mitterer, T.; Gietler, H.; Faller, L.-M.; Zangl, H. Artificial Landmarks for Trusted Localization of Autonomous Vehicles Based on Magnetic Sensors. Sensors 2019, 19, 813. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, M.; Kharrati, H.; Seyedarabi, H.; Baradarannia, M.; Seyedarabi, M. The Correcting Approach of Gyroscope-Free Inertial Navigation Based on the Applicable Topological Map. J. Comput. Inf. Sci. Eng. 2019, 19, 021001. [Google Scholar] [CrossRef]
- He, S.; Cha, J.; Park, C.G. EKF-Based Visual Inertial Navigation Using Sliding Window Nonlinear Optimization. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2470–2479. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, D. 3D Autonomous Navigation Line Extraction for Field Roads Based on Binocular Vision. J. Sens. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Majeeth, S.S.; Babu, C.N.K. Gaussian Noise Removal in an Image using Fast Guided Filter and its Method Noise Thresholding in Medical Healthcare Application. J. Med. Syst. 2019, 43, 280. [Google Scholar] [CrossRef]
- Xie, W.; Jiang, T.; Li, Y.; Jia, X.; Lei, J. Structure Tensor and Guided Filtering-Based Algorithm for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4218–4230. [Google Scholar] [CrossRef]
- Han, Y.; Yang, J.; He, X.; Yu, Y.; Chen, D.; Huang, J.; Zhang, Z.; Zhang, J.; Xu, S. Multiband notch filter based guided-mode resonance for mid-infrared spectroscopy. Opt. Commun. 2019, 445, 64–68. [Google Scholar] [CrossRef]
- Babashakoori, S.; Ezoji, M. Average fiber diameter measurement in Scanning Electron Microscopy images based on Gabor filtering and Hough transform. Measurement 2019, 141, 364–370. [Google Scholar] [CrossRef]
- Guan, J.; An, F.; Zhang, X.; Chen, L.; Mattausch, H.J. Energy-Efficient Hardware Implementation of Road-Lane Detection Based on Hough Transform with Parallelized Voting Procedure and Local Maximum Algorithm. IEICE Trans. Inf. Syst. 2019, E102D, 1171–1182. [Google Scholar] [CrossRef]
- Nachtegael, M.; Kerre, E.E. Connections between binary, gray-scale and fuzzy mathematical morphologies. Fuzzy Sets Syst. 2001, 124, 73–85. [Google Scholar] [CrossRef]
- Yang, J.; Li, X. Boundary detection using mathematical morphology. Pattern Recognit. Lett. 1995, 16, 1277–1286. [Google Scholar] [CrossRef]
- Andrade, A.O.; Prado Trindade, R.M.; Maia, D.S.; Nunes Santiago, R.H.; Guimaraes Guerreiro, A.M. Analysing some R-Implications and its application in fuzzy mathematical morphology. J. Intell. Fuzzy Syst. 2014, 27, 201–209. [Google Scholar] [CrossRef]
- Zhang, J. Research on Image Processing Based on Mathematical Morphology. Agro Food Ind. Hi-Tech 2017, 28, 2738–2742. [Google Scholar]
- Sussner, P.; Valle, M.E. Classification of Fuzzy Mathematical Morphologies Based on Concepts of Inclusion Measure and Duality. J. Math. Imaging Vis. 2008, 32, 139–159. [Google Scholar] [CrossRef]
- Fan, P.; Zhou, R.-G.; Hu, W.W.; Jing, N. Quantum image edge extraction based on Laplacian operator and zero-cross method. Quantum Inf. Process. 2019, 18. [Google Scholar] [CrossRef]
- Kaisserli, Z.; Laleg-Kirati, T.M.; Lahmar-Benbernou, A. A novel algorithm for image representation using discrete spectrum of the Schrödinger operator. Digit. Signal. Process. 2015, 40, 80–87. [Google Scholar] [CrossRef]
- He, Q.; Zhang, Z. A new edge detection algorithm for image corrupted by White-Gaussian noise. AEU Int. J. Electron. Commun. 2007, 61, 546–550. [Google Scholar] [CrossRef]
- Kamiyama, M.; Taguchi, A. HSI Color Space with Same Gamut of RGB Color Space. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, E100, 341–344. [Google Scholar] [CrossRef]
- Pérez, M.A.A.; Rojas, J.J.B. Conversion from n bands color space to HSI n color space. Opt. Rev. 2009, 16, 91–98. [Google Scholar] [CrossRef]
- Lissner, I.; Urban, P. Toward a Unified Color Space for Perception-Based Image Processing. IEEE Trans. Image Process. 2012, 21, 1153–1168. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Shi, Y. Skin Color Detecting Unite YCgCb Color Space with YCgCr Color Space. In Proceedings of the 2009 International Conference on Image Analysis and Signal Processing, Taizhou, China, 11–12 April 2009; pp. 221–225. [Google Scholar]
- Adelmann, H.G. Butterworth equations for homomorphic filtering of images. Comput. Biol. Med. 1998, 28, 169–181. [Google Scholar] [CrossRef]
- Voicu, L.I.; Myler, H.R.; Weeks, A.R. Practical considerations on color image enhancement using homomorphic filtering. J. Electron. Imaging 1997, 6, 108. [Google Scholar] [CrossRef]
- Yoon, J.H.; Ro, Y.M. Enhancement of the contrast in mammographic images using the homomorphic filter method. Ieice Trans. Inf. Syst. 2002, E85D, 298–303. [Google Scholar]
- Highnam, R.; Brady, M. Model-based image enhancement of far infrared images. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 410–415. [Google Scholar] [CrossRef]
- Kumari, A.; Sahoo, S.K. Fast single image and video deweathering using look-up-table approach. AEU Int. J. Electron. Commun. 2015, 69, 1773–1782. [Google Scholar] [CrossRef]
- Zhu, M.; Su, F.; Li, W. Improved Multi-scale Retinex Approaches for Color Image Enhancement. Quantum Nano Micro Inf. Technol. 2011, 39, 32–37. [Google Scholar] [CrossRef]
- Yao, L.; Lin, Y.; Muhammad, S. An Improved Multi-Scale Image Enhancement Method Based on Retinex Theory. J. Med. Imaging Health Inform. 2018, 8, 122–126. [Google Scholar] [CrossRef]
- Herscovitz, M.; Yadid-Pecht, O. A modified Multi Scale Retinex algorithm with an improved global impressionof brightness for wide dynamic range pictures. Mach. Vis. Appl. 2004, 15, 220–228. [Google Scholar] [CrossRef]
- Rising, H.K. Analysis and generalization of Retinex by recasting the algorithm in wavelets. J. Electron. Imaging 2004, 13, 93. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, X.; Zhang, H.; Zhao, L. Edge detection algorithm of image fusion based on improved Sobel operator. In Proceedings of the 2017 IEEE 3rd Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 3–5 October 2017; pp. 457–461. [Google Scholar]
- Zhang, C.-C.; Fang, J.-D.; Atlantis, P. Edge Detection Based on Improved Sobel Operator. In Proceedings of the 2016 International Conference on Computer Engineering and Information Systems, Shanghai, China, 12–13 November 2016; pp. 129–132. [Google Scholar]
- Wang, K.F. Edge Detection of Inner Crack Defects Based on Improved Sobel Operator and Clustering Algorithm. Appl. Mech. Mater. 2011, 55, 467–471. [Google Scholar] [CrossRef]
- Qu, Y.D.; Cui, C.S.; Chen, S.B.; Li, J.Q. A fast subpixel edge detection method using Sobel-Zernike moments operator. Image Vis. Comput. 2005, 23, 11–17. [Google Scholar] [CrossRef]
- Kutty, S.B.; Saaidin, S.; Yunus, P.N.A.M.; Abu Hassan, S. Evaluation of canny and sobel operator for logo edge detection. In Proceedings of the 2014 International Symposium on Technology Management and Emerging Technologies, Bandung, Indonesia, 27–29 May 2014; pp. 153–156. [Google Scholar]
- Tao, J.; Cai, J.; Xie, H.; Ma, X. Based on Otsu thresholding Roberts edge detection algorithm research. In Proceedings of the 2nd International Conference on Information, Electronics and Computer, Wuhan, China, 7–9 March 2014; pp. 121–124. [Google Scholar]
- Wang, A.; Liu, X. Vehicle License Plate Location Based on Improved Roberts Operator and Mathematical Morphology. In Proceedings of the 2012 Second International Conference on Instrumentation, Measurement, Computer, Communication and Control, Harbin, China, 8–10 December 2012; pp. 995–998. [Google Scholar]
- Ye, H.; Shen, B.; Yan, S. Prewitt edge detection based on BM3D image denoising. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control. Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 1593–1597. [Google Scholar]
- Yu, K.; Xie, Z. A fusion edge detection method based on improved Prewitt operator and wavelet transform. In Proceedings of the International Conference on Engineering Technology and Applications (ICETA), Tsingtao, China, 29–30 April 2014; pp. 289–294. [Google Scholar]
- Ando, T.; Hiai, F. Operator log-convex functions and operator means. Math. Ann. 2011, 350, 611–630. [Google Scholar] [CrossRef][Green Version]
- Han, X.; Kim, H.-J.; Jeon, C.W.; Moon, H.C.; Kim, J.H.; Yi, S.Y. Application of a 3D tractor-driving simulator for slip estimation-based path-tracking control of auto-guided tillage operation. Biosyst. Eng. 2019, 178, 70–85. [Google Scholar] [CrossRef]
- Malavazi, F.B.; Guyonneau, R.; Fasquel, J.-B.; Lagrange, S.; Mercier, F. LiDAR-only based navigation algorithm for an autonomous agricultural robot. Comput. Electron. Agric. 2018, 154, 71–79. [Google Scholar] [CrossRef]
- Higuti, V.A.H.; Velasquez, A.E.B.; Magalhaes, D.V.; Becker, M.; Chowdhary, G. Under canopy light detection and ranging-based autonomous navigation. J. Field Robot. 2019, 36, 547–567. [Google Scholar] [CrossRef]
- Li, J.B.; Zhu, R.G.; Chen, B.Q. Image detection and verification of visual navigation route during cotton field management period. Int. J. Agric. Biol. Eng. 2018, 11, 159–165. [Google Scholar] [CrossRef]
- Garcia-Santillan, I.; Guerrero, J.M.; Montalvo, M.; Pajares, G. Curved and straight crop row detection by accumulation of green pixels from images in maize fields. Precis. Agric. 2018, 19, 18–41. [Google Scholar] [CrossRef]
- Yang, L.; Gao, D.; Hoshino, Y.; Suzuki, S.; Cao, Y.; Yang, S. Evaluation of the accuracy of an auto-navigation system for a tractor in mountain areas. In Proceedings of the 2017 IEEE/SICE International Symposium on System Integration (SII), Taipei, Taiwan, 11–14 December 2017; pp. 133–138. [Google Scholar]
- Menesatti, P.; Angelini, C.; Pallottino, F.; Antonucci, F.; Aguzzi, J.; Costa, C. RGB Color Calibration for Quantitative Image Analysis: The “3D Thin-Plate Spline”. Warping Approach Sens. 2012, 12, 7063–7079. [Google Scholar] [CrossRef] [PubMed]
- Tripicchio, P.; Satler, M.; Dabisias, G.; Ruffaldi, E.; Avizzano, C.A. Towards Smart Farming and Sustainable Agriculture with Drones. In Proceedings of the 2015 International Conference on Intelligent Environments, Prague, Czech Republic, 15–17 July 2015; pp. 140–143. [Google Scholar]
- Bauer, A.; Bostrom, A.G.; Ball, J.; Applegate, C.; Cheng, T.; Laycock, S.; Rojas, S.M.; Kirwan, J.; Zhou, J. Combining computer vision and deep learning to enable ultra-scale aerial phenotyping and precision agriculture: A case study of lettuce production. Hortic. Res. 2019, 6, 70. [Google Scholar] [CrossRef] [PubMed]
- Barth, R.; Ijsselmuiden, J.; Hemming, J.; Van Henten, E. Data synthesis methods for semantic segmentation in agriculture: A Capsicum annuum dataset. Comput. Electron. Agric. 2018, 144, 284–296. [Google Scholar] [CrossRef]











| Color Space | Time Consumption (s) |
|---|---|
| YCbCr | 0.094 |
| HSV | 1.541 |
| HIS | 1.639 |
| RGB | 0.126 |
| Filtering Method | Highlighting | Time Consumption (s) |
|---|---|---|
| Tarel | − | 0.902 |
| Multi-scale retinex | + | 0.552 |
| Wavelet-based retinex | + | 1.008 |
| Homomorphic filtering (HF) | − | 0.867 |
| Guided | + | 0.113 |
| Edge Operators | Time Consumption (s) |
|---|---|
| Sobel | 0.089 |
| Roberts | 0.090 |
| Prewitt | 0.090 |
| Log | 0.096 |
| Improved anti-noise morphology | 0.073 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Zeng, M.; Wang, L.; Luo, H.; Mukherjee, S.; Huang, X.; Deng, Y. Navigation Algorithm Based on the Boundary Line of Tillage Soil Combined with Guided Filtering and Improved Anti-Noise Morphology. Sensors 2019, 19, 3918. https://doi.org/10.3390/s19183918
Lu W, Zeng M, Wang L, Luo H, Mukherjee S, Huang X, Deng Y. Navigation Algorithm Based on the Boundary Line of Tillage Soil Combined with Guided Filtering and Improved Anti-Noise Morphology. Sensors. 2019; 19(18):3918. https://doi.org/10.3390/s19183918
Chicago/Turabian StyleLu, Wei, Mengjie Zeng, Ling Wang, Hui Luo, Subrata Mukherjee, Xuhui Huang, and Yiming Deng. 2019. "Navigation Algorithm Based on the Boundary Line of Tillage Soil Combined with Guided Filtering and Improved Anti-Noise Morphology" Sensors 19, no. 18: 3918. https://doi.org/10.3390/s19183918
APA StyleLu, W., Zeng, M., Wang, L., Luo, H., Mukherjee, S., Huang, X., & Deng, Y. (2019). Navigation Algorithm Based on the Boundary Line of Tillage Soil Combined with Guided Filtering and Improved Anti-Noise Morphology. Sensors, 19(18), 3918. https://doi.org/10.3390/s19183918





