A Time–Frequency Acoustic Emission-Based Technique to Assess Workpiece Surface Quality in Ceramic Grinding with PZT Transducer
Abstract
1. Introduction
2. Ceramic Grinding Overview
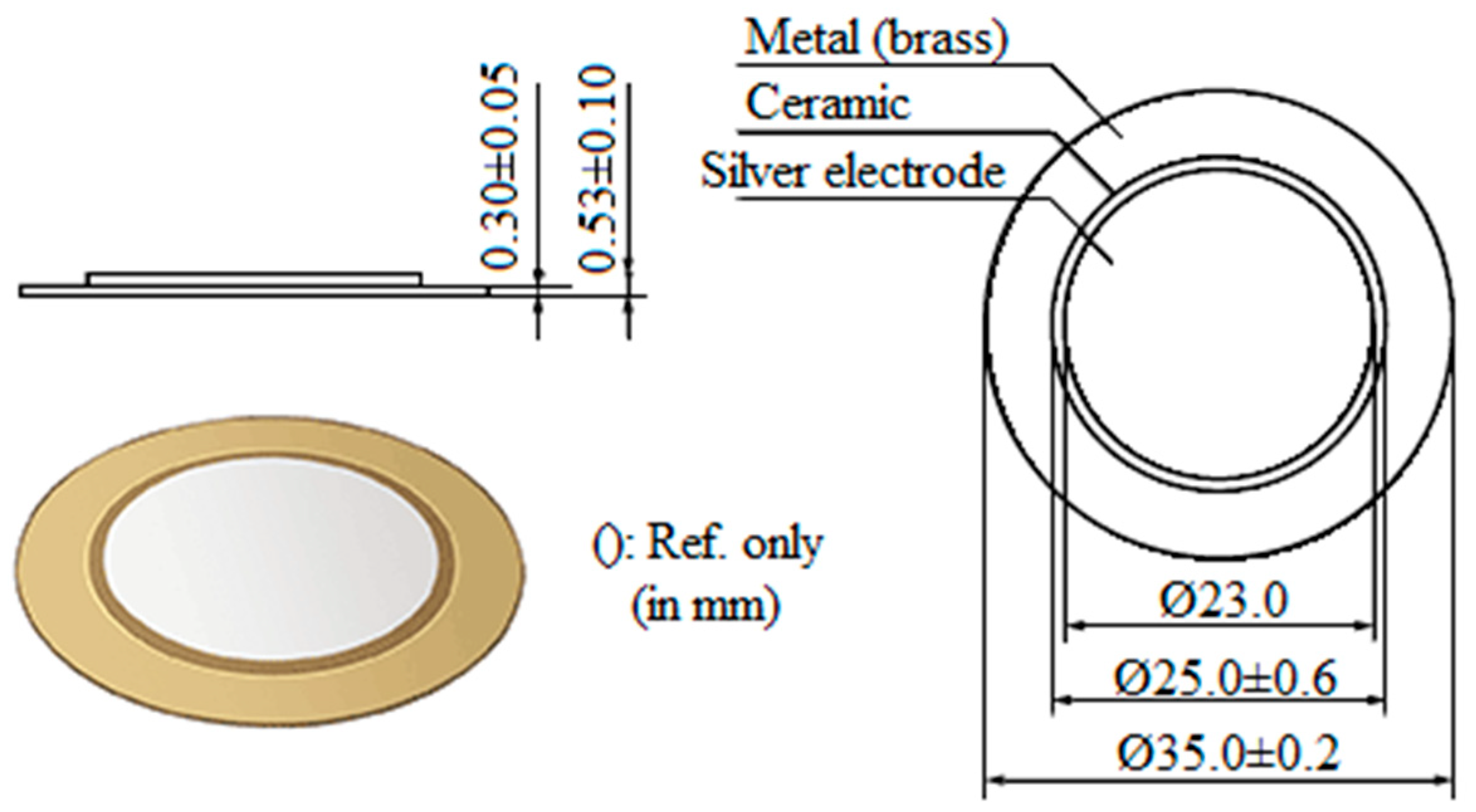
3. Piezoelectric Diaphragms
4. Signal Processing
5. Materials and Methods
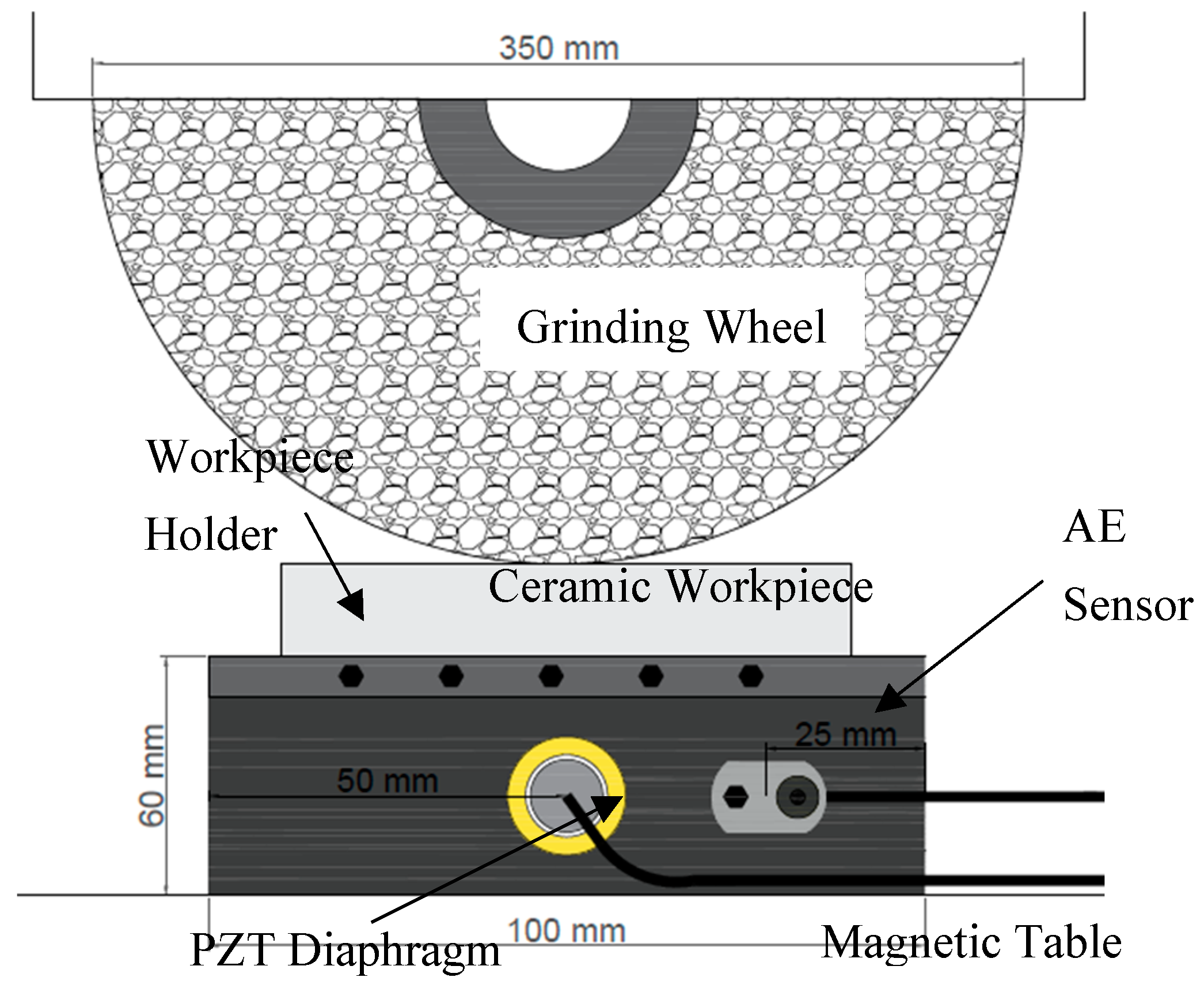
5.1. Experimental Setup
5.2. Workpiece Surface Assessment
5.3. Data Acquisition
5.4. Signal Processing
6. Results and Discussion
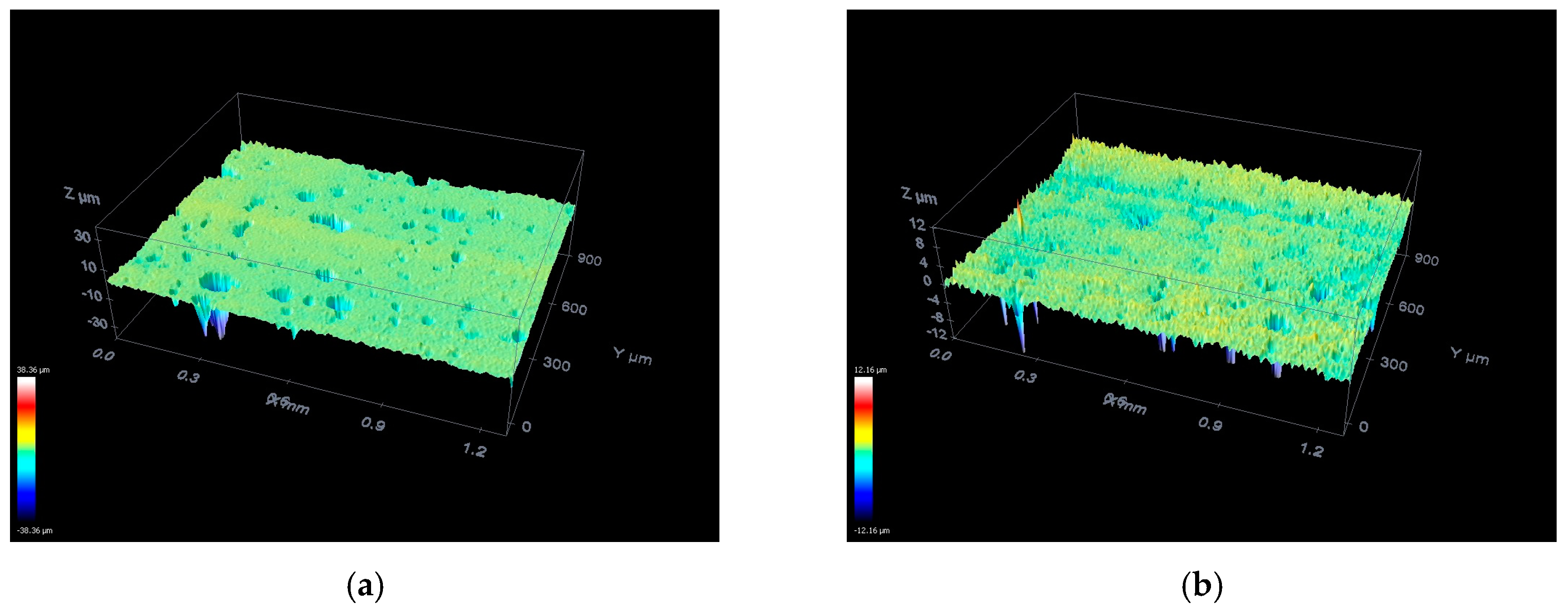
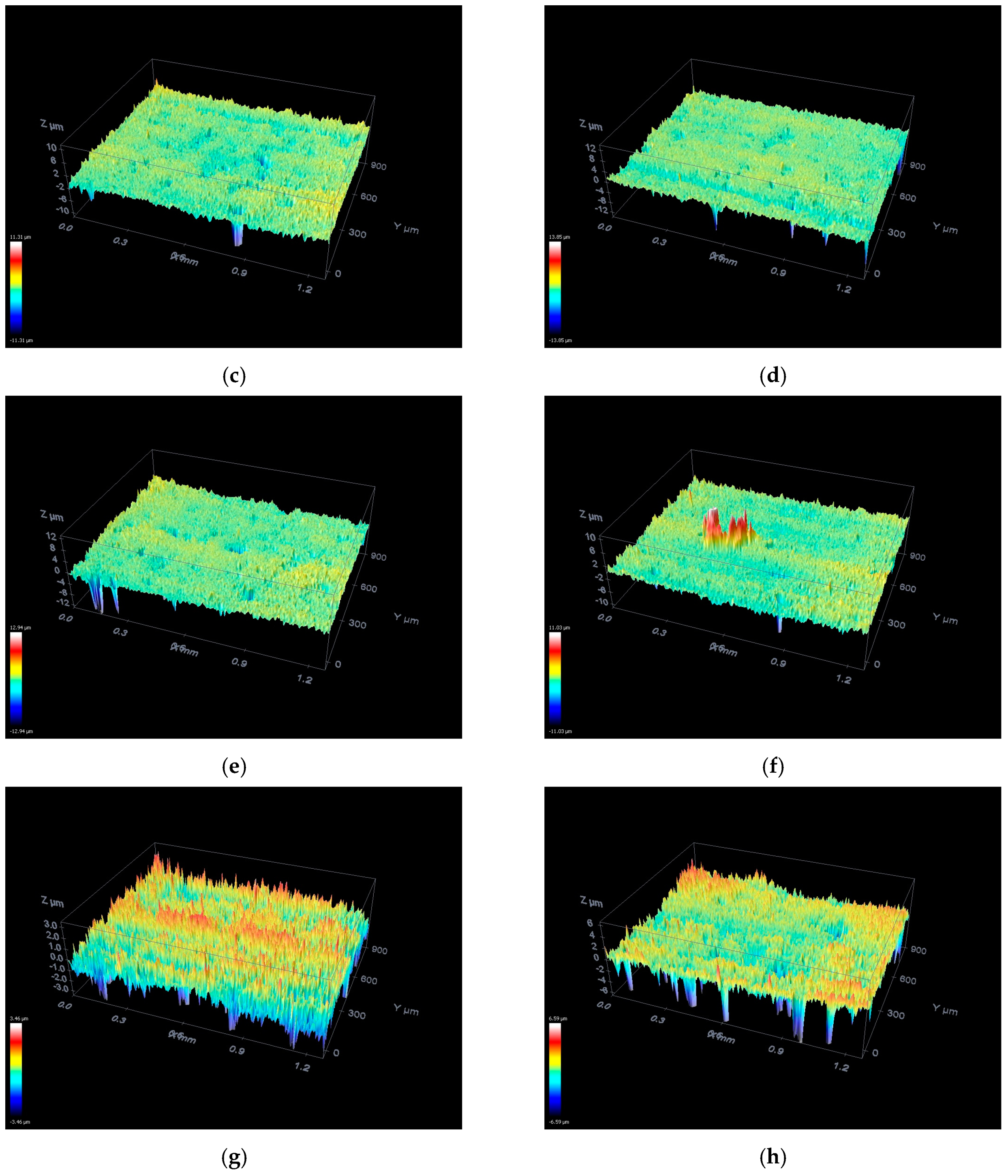
6.1. Workpiece Surface Assessment
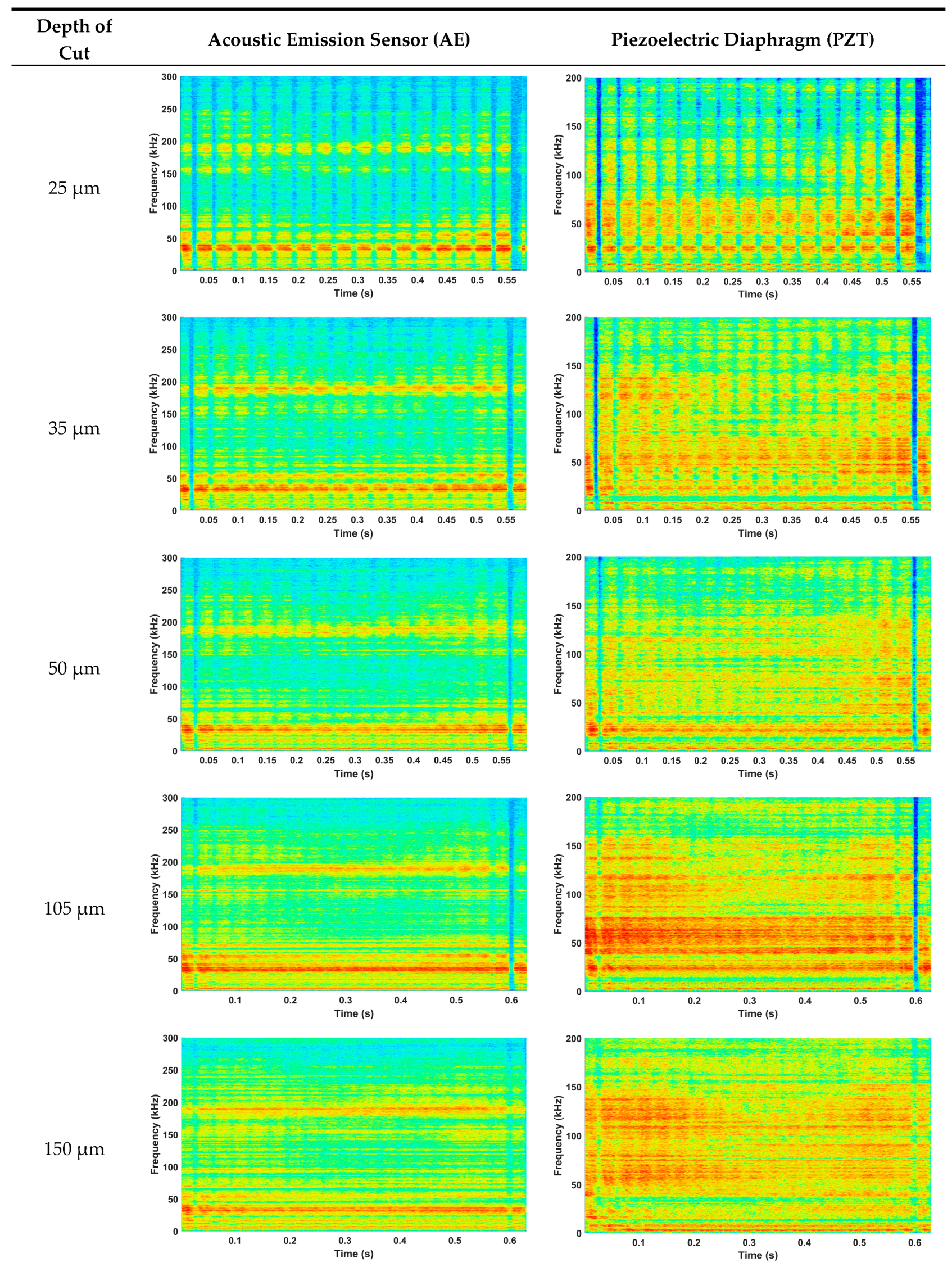
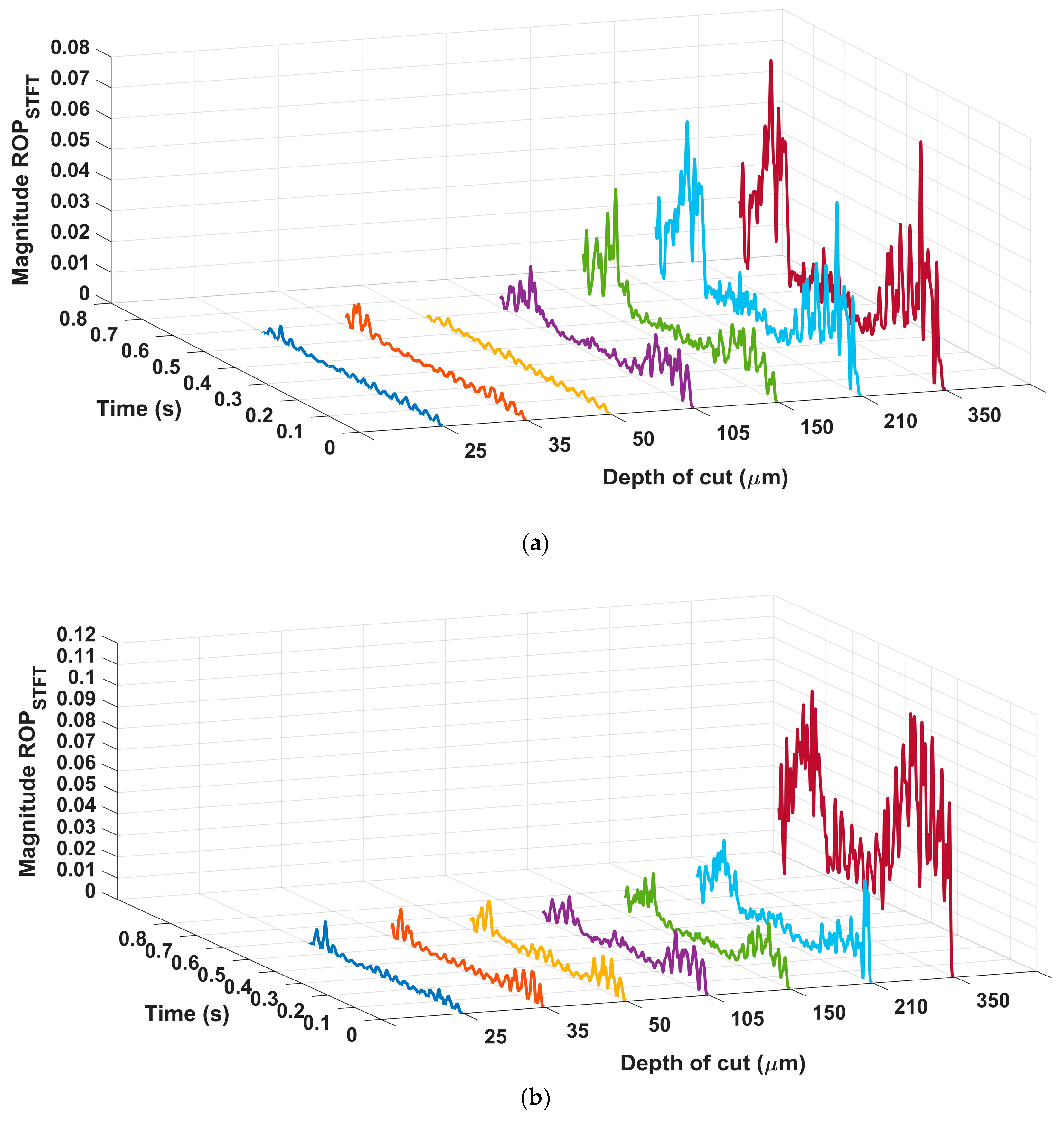
6.2. Signal Processing
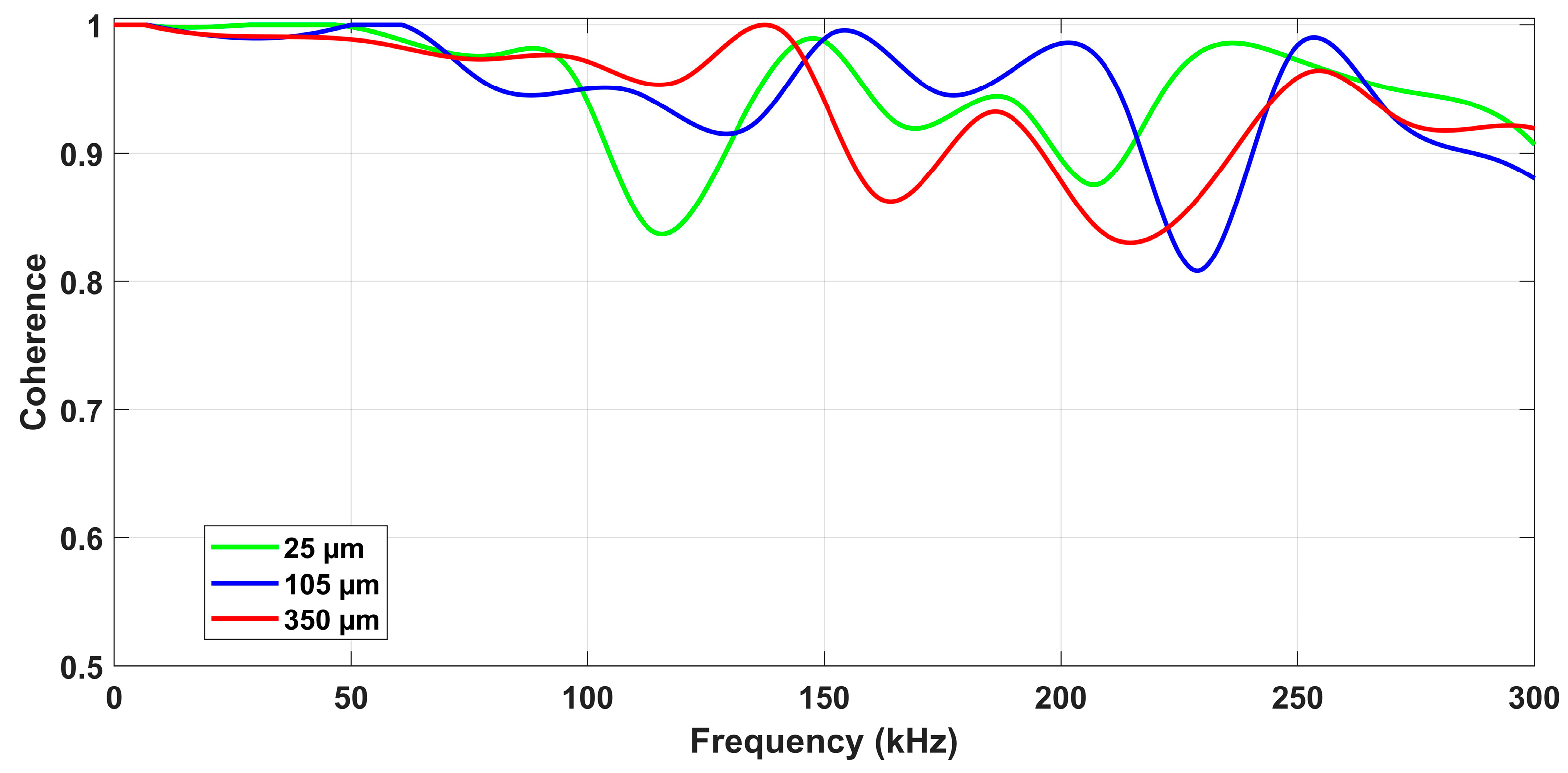
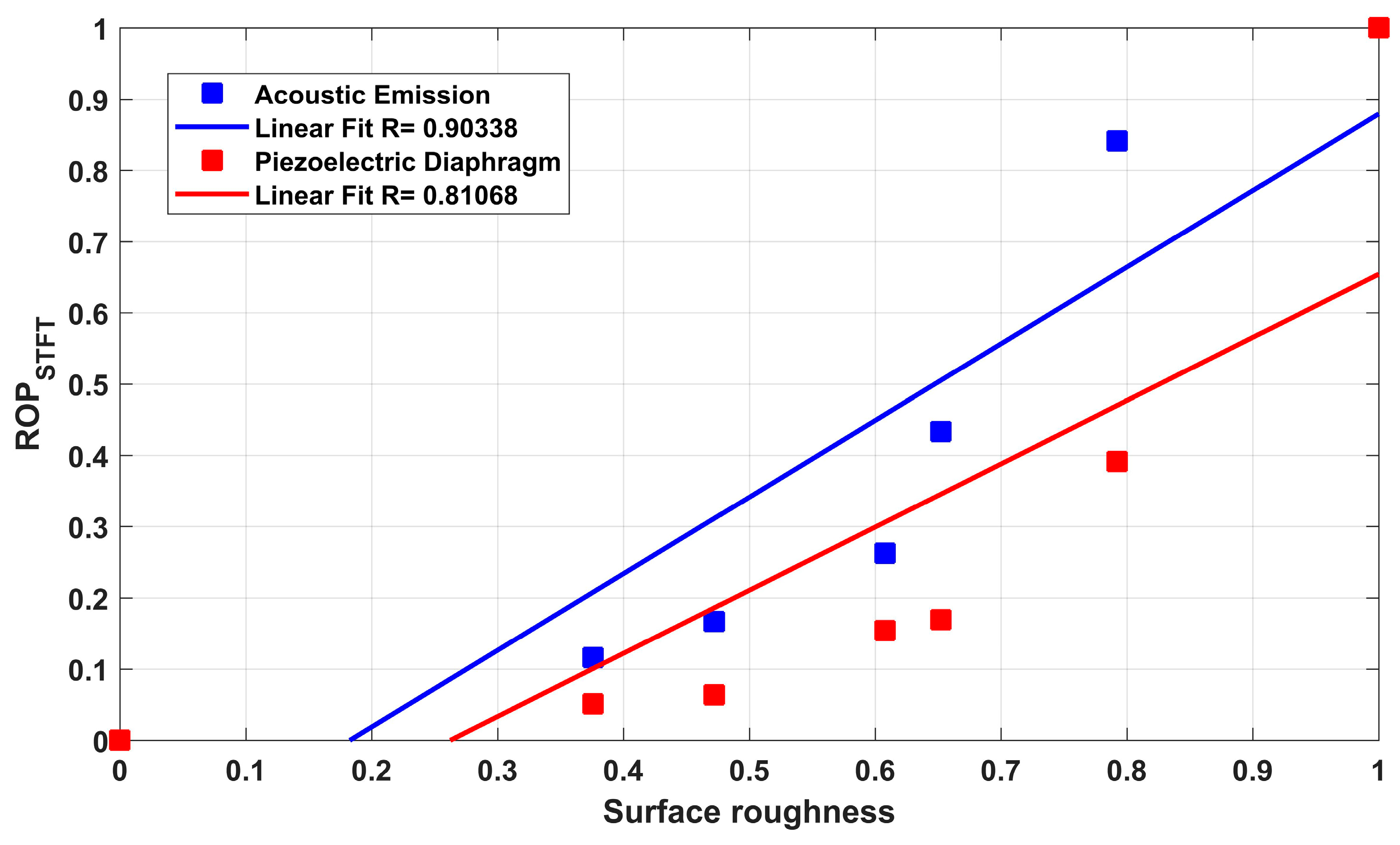
6.3. Correlation Analysis
7. Conclusions
- A grinding process performed at a high depth of cut results in increased mean surface roughness and acoustic activity levels;
- Machining under severe conditions caused greater irregularities in the ceramic surfaces;
- The increase in ROP values was directly related to the increase in surface roughness, which was caused by the increase in process severity;
- The PZT diaphragm responded satisfactorily to the process stimuli; the results were supported by the behavior of the AE sensor;
- The coherence analysis between the responses of the low-cost PZT diaphragm and the AE sensor reinforced the results obtained, proving the viability of using the PZT diaphragm in the monitoring of the grinding process; all coherence values were higher than 80%;
- The results demonstrated the feasibility of applying the low-cost PZT diaphragms for the tested machining conditions and can be extended to other low-cost sensors and materials.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chakule, R.R.; Chaudhari, S.S.; Talmale, P.S. Evaluation of the effects of machining parameters on MQL based surface grinding process using response surface methodology. J. Mech. Sci. Technol. 2017, 31, 3907–3916. [Google Scholar] [CrossRef]
- Onwuka, G.; Abou-El-Hossein, K. Surface Roughness in Ultra-high Precision Grinding of BK7. Procedia CIRP 2016, 45, 143–146. [Google Scholar] [CrossRef][Green Version]
- D’Addona, D.M.; Matarazzo, D.; Teti, R.; De Aguiar, P.R.; Bianchi, E.C.; Fornaro, A. Prediction of Dressing in Grinding Operation via Neural Networks. Procedia CIRP 2017, 62, 305–310. [Google Scholar] [CrossRef]
- Karpuschewski, B.; Wehmeier, M.; Inasaki, I. Grinding monitoring system based on power and acoustic emission sensors. CIRP Ann.-Manuf. Technol. 2000, 49, 235–240. [Google Scholar] [CrossRef]
- Teti, R.; Jemielniak, K.; O’Donnell, G.; Dornfeld, D. Advanced monitoring of machining operations. CIRP Ann.-Manuf. Technol. 2010, 59, 717–739. [Google Scholar] [CrossRef]
- Kim, H.Y.; Kim, S.R.; Ahn, J.H. Process monitoring of centerless grinding using acoustic emission. J. Mater. Process. Technol. 2001, 111, 273–278. [Google Scholar] [CrossRef]
- Lopes, W.N.; Ferreira, F.I.; Alexandre, F.A.; Ribeiro, D.M.S.; Junior, P.D.O.C.; de Aguiar, P.R.; Bianchi, E.C. Digital signal processing of acoustic emission signals using power spectral density and counts statistic applied to single-point dressing operation. IET Sci. Meas. Technol. 2017, 11, 631–636. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Shen, N.; Gao, H.; Zhao, C.; Wang, Y. Modeling of acoustic emission based on the experimental and theoretical methods and its application in face grinding. Int. J. Adv. Manuf. Technol. 2018, 98, 2335–2346. [Google Scholar] [CrossRef]
- Boaron, A.; Weingaertner, W.L. Dynamic in-process characterization method based on acoustic emission for topographic assessment of conventional grinding wheels. Wear 2018, 406–407, 218–229. [Google Scholar] [CrossRef]
- Holford, K.M.; Eaton, M.J.; Hensman, J.J.; Pullin, R.; Evans, S.L.; Dervilis, N.; Worden, K. A new methodology for automating acoustic emission detection of metallic fatigue fractures in highly demanding aerospace environments: An overview. Prog. Aerosp. Sci. 2017, 90, 1–11. [Google Scholar] [CrossRef]
- Sikdar, S.; Kundu, A.; Jurek, M.; Ostachowicz, W. Nondestructive Analysis of Debonds in a Composite Structure under Variable Temperature Conditions. Sensors 2019, 19, 3454. [Google Scholar] [CrossRef] [PubMed]
- Dias, E.A.; Pereira, F.B.; Ribeiro Filho, S.L.M.; Brandão, L.C. Monitoring of through-feed centreless grinding processes with acoustic emission signals. Measurement 2016, 94, 71–79. [Google Scholar] [CrossRef]
- He, B.; Wei, C.; Ding, S.; Shi, Z. A survey of methods for detecting metallic grinding burn. Measurement 2019, 134, 426–439. [Google Scholar] [CrossRef]
- Lopes, B.G.; Alexandre, F.A.; Lopes, W.N.; de Aguiar, P.R.; Bianchi, E.C.; Viera, M.A.A. Study on the effect of the temperature in Acoustic Emission Sensor by the Pencil Lead Break Test. In Proceedings of the 2018 13th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 12–14 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1226–1229. [Google Scholar]
- Badger, J.; Murphy, S.; O’Donnell, G.E. Acoustic emission in dressing of grinding wheels: AE intensity, dressing energy, and quantification of dressing sharpness and increase in diamond wear-flat size. Int. J. Mach. Tools Manuf. 2018, 125, 11–19. [Google Scholar] [CrossRef]
- Viera, M.A.; Alexandre, F.; Lopes, W.; de Aguiar, P.; da Silva, R.B.; D’addona, D.; Andreoli, A.; Bianchi, E.; da Silva, R.; D’addona, D.; et al. A contribution to the monitoring of ceramic surface quality using a low-cost piezoelectric transducer in the grinding operation. In Proceedings of the 5th International Electronic Conference on Sensors and Applications, 15–30 November 2018; MDPI: Basel, Switzerland, 2018; Volume 4, p. 16. Available online: https://ecsa-5.sciforum.net/ (accessed on 10 September 2019).
- Oliveira Junior, P.O.; Ferreira, F.I.; Aguiar, P.R.; Batista, F.G.; Bianchi, E.C.; Daddona, D.M. Time-domain Analysis Based on the Electromechanical Impedance Method for Monitoring of the Dressing Operation. Procedia CIRP 2018, 67, 319–324. [Google Scholar] [CrossRef]
- De Freitas, E.S.; Baptista, F.G. Experimental analysis of the feasibility of low-cost piezoelectric diaphragms in impedance-based SHM applications. Sens. Actuators A Phys. 2016, 238, 220–228. [Google Scholar] [CrossRef]
- Budoya, D.E.; Baptista, F.G. A Comparative Study of Impedance Measurement Techniques for Structural Health Monitoring Applications. IEEE Trans. Instrum. Meas. 2018, 67, 912–924. [Google Scholar] [CrossRef]
- Chang, K.T.; Chiang, H.C.; Lee, C.W. Design and implementation of a piezoelectric clutch mechanism using piezoelectric buzzers. Sens. Actuators A Phys. 2008, 141, 515–522. [Google Scholar] [CrossRef]
- Lamberti, N.; Caliano, G.; Savoia, A.S. ACUPAD: A track-pad device based on a piezoelectric bimorph. Sens. Actuators A Phys. 2015, 222, 130–139. [Google Scholar] [CrossRef]
- Castro, B.; Clerice, G.; Ramos, C.; Andreoli, A.; Baptista, F.; Campos, F.; Ulson, J. Partial Discharge Monitoring in Power Transformers Using Low-Cost Piezoelectric Sensors. Sensors 2016, 16, 1266. [Google Scholar] [CrossRef]
- Junior, P.; D’Addona, D.M.; Aguiar, P.R. Dressing Tool Condition Monitoring through Impedance-Based Sensors: Part 1—PZT Diaphragm Transducer Response and EMI Sensing Technique. Sensors 2018, 18, 4455. [Google Scholar] [CrossRef] [PubMed]
- De Freitas, E.S.; Baptista, F.G.; Budoya, D.E.; De Castro, B.A. Equivalent Circuit of Piezoelectric Diaphragms for Impedance-Based Structural Health Monitoring Applications. IEEE Sens. J. 2017, 17, 5537–5546. [Google Scholar] [CrossRef]
- Da Silva, R.B.; Ferreira, F.I.; Baptista, F.G.; de Aguiar, P.R.; de Souza Ruzzi, R.; Hubner, H.B.; Fonseca, M.D.P.C.; Bianchi, E.C. Electromechanical impedance (EMI) technique as alternative to monitor workpiece surface damages after the grinding operation. Int. J. Adv. Manuf. Technol. 2018, 98, 2429–2438. [Google Scholar] [CrossRef]
- Marchi, M.; Baptista, F.G.; De Aguiar, P.R.; Bianchi, E.C. Grinding process monitoring based on electromechanical impedance measurements. Meas. Sci. Technol. 2015, 26, 045601. [Google Scholar] [CrossRef]
- Ribeiro, D.M.S.; Aguiar, P.R.; Fabiano, L.F.G.; D’Addona, D.M.; Baptista, F.G.; Bianchi, E.C. Spectra Measurements Using Piezoelectric Diaphragms to Detect Burn in Grinding Process. IEEE Trans. Instrum. Meas. 2017, 66, 3052–3063. [Google Scholar] [CrossRef]
- Junior, P.; D’Addona, D.; Aguiar, P.; Teti, R. Dressing Tool Condition Monitoring through Impedance-Based Sensors: Part 2—Neural Networks and K-Nearest Neighbor Classifier Approach. Sensors 2018, 18, 4453. [Google Scholar] [CrossRef] [PubMed]
- Viera, M.A.A.; de Aguiar, P.R.; Junior, P.O.; da Silva, R.B.; Jackson, M.J.; Alexandre, F.A.; Bianchi, E.C. Low-Cost Piezoelectric Transducer for Ceramic Grinding Monitoring. IEEE Sens. J. 2019, 19, 7605–7612. [Google Scholar] [CrossRef]
- Thomazella, R.; Lopes, W.N.; Aguiar, P.R.; Alexandre, F.A.; Fiocchi, A.A.; Bianchi, E.C. Digital signal processing for self-vibration monitoring in grinding: A new approach based on the time-frequency analysis of vibration signals. Measurement 2019, 145, 71–836. [Google Scholar] [CrossRef]
- Zhang, G.; Zeng, Y.; Zhang, W. Scratching of SiC ceramics at two dimensional pre-stressing. Int. J. Nanomanuf. 2017, 13, 270. [Google Scholar] [CrossRef]
- Sanchez, L.E.A.; Bukvic, G.; Fiocchi, A.A.; Fortulan, C.A. Allowance removal from green pieces as a method for improvement surface quality of advanced ceramics. J. Clean. Prod. 2018, 186, 10–21. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Tonshoff, H.K.; Czenkusch, C.; Heinzel, C. Modelling and optimization of grinding processes. J. Intell. Manuf. 1998, 9, 303–314. [Google Scholar] [CrossRef]
- Do Nascimento, W.R.; Yamamoto, A.A.; de Mello, H.J.; Canarim, R.C.; de Aguiar, P.R.; Bianchi, E.C. A study on the viability of minimum quantity lubrication with water in grinding of ceramics using a hybrid-bonded diamond wheel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 1630–1638. [Google Scholar] [CrossRef]
- Thomas, B.; David, E.; Manu, R. Empirical modelling and parametric optimisation of surface roughness of silicon carbide advanced ceramics in surface grinding. Int. J. Precis. Technol. 2015, 5, 277–293. [Google Scholar] [CrossRef]
- Liu, W.; Deng, Z.; Shang, Y.; Wan, L. Effects of grinding parameters on surface quality in silicon nitride grinding. Ceram. Int. 2017, 43, 1571–1577. [Google Scholar] [CrossRef]
- Wu, C.; Li, B.; Liu, Y.; Liang, S.Y. Surface roughness modeling for grinding of Silicon Carbide ceramics considering co-existence of brittleness and ductility. Int. J. Mech. Sci. 2017, 133, 167–177. [Google Scholar] [CrossRef]
- Khare, S.K.; Agarwal, S. Predictive Modeling of Surface Roughness in Grinding. Procedia CIRP 2015, 31, 375–380. [Google Scholar] [CrossRef]
- Park, J.-B.; Jeon, Y.; Ko, Y. Effects of titanium brush on machined and sand-blasted/acid-etched titanium disc using confocal microscopy and contact profilometry. Clin. Oral Implants Res. 2015, 26, 130–136. [Google Scholar] [CrossRef]
- Liao, D.; Shao, W.; Tang, J.; Li, J.; Tao, X. Numerical generation of grinding wheel surfaces based on time series method. Int. J. Adv. Manuf. Technol. 2018, 94, 561–569. [Google Scholar] [CrossRef]
- Anand, P.S.P.; Arunachalam, N.; Vijayaraghavan, L. Study on grinding of pre-sintered zirconia using diamond wheel. Mater. Manuf. Process. 2018, 33, 634–643. [Google Scholar] [CrossRef]
- Nakai, M.E.; Junior, H.G.; Aguiar, P.R.; Bianchi, E.C.; Spatti, D.H. Neural tool condition estimation in the grinding of advanced ceramics. IEEE Lat. Am. Trans. 2015, 13, 62–68. [Google Scholar] [CrossRef]
- Feng, J.; Kim, B.S.; Shih, A.; Ni, J. Tool wear monitoring for micro-end grinding of ceramic materials. J. Mater. Process. Technol. 2009, 209, 5110–5116. [Google Scholar] [CrossRef]
- Junior, P.O.C.; Aguiar, P.R.; Foschini, C.R.; França, T.V.; Ribeiro, D.M.S.; Ferreira, F.I.; Lopes, W.N.; Bianchi, E.C. Feature extraction using frequency spectrum and time domain analysis of vibration signals to monitoring advanced ceramic in grinding process. IET Sci. Meas. Technol. 2019, 13, 1–8. [Google Scholar] [CrossRef]
- Conceicao, P.O.; Marchi, M.; Aguiar, P.R.; Bianchi, E.C.; Franca, T.V. The correlation of vibration signal features in grinding of advanced ceramics. IEEE Lat. Am. Trans. 2016, 14, 4006–4012. [Google Scholar] [CrossRef]
- Junior, M.M.D.S.; Ulson, J.A.C.; Castro, B.A.D.; Ardila-Rey, J.A.; Campos, F.D.S.; Ferreira, L.T. Analysis of Piezoelectric Sensors in Adulteration of Bovine Milk Using the Chromatic Technique. Proceedings 2018, 4, 38. [Google Scholar] [CrossRef]
- Castro, B.A.; Clerice, G.A.M.; Andreoli, A.L.; de Souza Campos, F.; Ulson, J.A.C. A low cost system for acoustic monitoring of partial discharge in power transformer by Piezoelectric Sensor. IEEE Lat. Am. Trans. 2016, 14, 3225–3231. [Google Scholar] [CrossRef]
- De Almeida, V.A.D.; Baptista, F.G.; De Aguiar, P.R. Piezoelectric transducers assessed by the pencil lead break for impedance-based structural health monitoring. IEEE Sens. J. 2015, 15, 693–702. [Google Scholar] [CrossRef]
- De Castro, B.A.; De Melo Brunini, D.; Baptista, F.G.; Andreoli, A.L.; Ulson, J.A.C. Assessment of Macro Fiber Composite Sensors for Measurement of Acoustic Partial Discharge Signals in Power Transformers. IEEE Sens. J. 2017, 17, 6090–6099. [Google Scholar] [CrossRef]
- Yang, Z.; Yu, Z. Grinding wheel wear monitoring based on wavelet analysis and support vector machine. Int. J. Adv. Manuf. Technol. 2012, 62, 107–121. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, D.; Sheng, S. A discrete STFT processor for real-time spectrum analysis. In Proceedings of the IEEE Asia-Pacific Conference Circuits Systems (APCCAS), Singapore, 4–7 December 2006; pp. 1943–1946. [Google Scholar] [CrossRef]
- Kim, B.S.; Lee, S.H.; Lee, M.G.; Ni, J.; Song, J.Y.; Lee, C.W. A comparative study on damage detection in speed-up and coast-down process of grinding spindle-typed rotor-bearing system. J. Mater. Process. Technol. 2007, 187–188, 30–36. [Google Scholar] [CrossRef]
- Mangueira Lima, É.; Brito, N.S.D.; de Souza, B.A.; dos Santos, W.C.; de Andrade Fortunato, L.M. Analysis of the influence of the window used in the Short-Time Fourier Transform for High Impedance Fault detection. In Proceedings of the 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 350–355. [Google Scholar]
- Martins, C.H.R.; Aguiar, P.R.; Frech, A.; Bianchi, E.C. Tool condition monitoring of single-point dresser using acoustic emission and neural networks models. IEEE Trans. Instrum. Meas. 2014, 63, 667–679. [Google Scholar] [CrossRef]
- Aguiar, P.R.; Bianchi, E.C.; Oliveira, J.F.G. A method for burning detection in grinding process using acoustic emission and effective electric power signals. Manuf. Syst. 2002, 31, 253–257. [Google Scholar]
- Alexandre, F.A.; Lopes, W.N.; Lofrano Dotto, F.R.; Ferreira, F.I.; Aguiar, P.R.; Bianchi, E.C.; Lopes, J.C. Tool condition monitoring of aluminum oxide grinding wheel using AE and fuzzy model. Int. J. Adv. Manuf. Technol. 2018, 96, 67–79. [Google Scholar] [CrossRef]
- Lin, Y.-K.; Wu, B.-F.; Chen, C.-M. Characterization of Grinding Wheel Condition by Acoustic Emission Signals. In Proceedings of the 2018 International Conference on System Science and Engineering (ICSSE), New Taipei, Taiwan, 28–30 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Aguiar, P.R.; Serni, P.J.A.; Bianchi, E.C.; Dotto, F.R.L. In-process grinding monitoring by acoustic emission. In Proceedings of the 2004 IEEE International Conference Acoustics Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; Volume 5, pp. 1–4. [Google Scholar] [CrossRef]
- Guo, S.; Li, C.; Zhang, Y.; Wang, Y.; Li, B.; Yang, M.; Zhang, X.; Liu, G. Experimental evaluation of the lubrication performance of mixtures of castor oil with other vegetable oils in MQL grinding of nickel-based alloy. J. Clean. Prod. 2017, 140, 1060–1076. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Lin, J.; Zhao, W. Correlation analysis of motor current and chatter vibration in grinding using complex continuous wavelet coherence. Meas. Sci. Technol. 2016, 27, 115106. [Google Scholar] [CrossRef]
- Gish, H.; Cochran, D. Generalized coherence (signal detection). In Proceedings of the ICASSP-88, International Conference on Acoustics, Speech, and Signal Processing, New York, NY, USA, 11–14 April 1988; IEEE: Piscataway, NJ, USA, 1988; pp. 2745–2748. [Google Scholar]
- Scannell, E.; Carter, G. Confidence bounds for magnitude-squared coherence estimates. IEEE Trans. Acoust. 1978, 26, 475–477. [Google Scholar] [CrossRef]
- Moia, D.F.G.; Thomazella, I.H.; Aguiar, P.R.; Bianchi, E.C.; Martins, C.H.R.; Marchi, M. Tool condition monitoring of aluminum oxide grinding wheel in dressing operation using acoustic emission and neural networks. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 627–640. [Google Scholar] [CrossRef]
- Marinescu, I.D.; Rowe, W.B.; Dimitrov, B.; Ohmori, H. Tribology of Abrasive Machining Processes; Elsevier: Atlanta, GA, USA, 2013; ISBN 978-1-4377-3467-6. [Google Scholar]
| Grinding Speed | |
| Cutting speed () | 33 m/s |
| Worktable speed () | 58 mm/s |
| Depth of cut (µm) | 25–35–50–105–150–210–350 |
| Lubri-Cooling Specification | |
| Fluid | Shell–DMS 3200 F-1 |
| Flow rate | 27.5 L/min |
| Pressure | <0.7 MPa |
| Concentration | 4% oil-water |
| Depth of Cut (a-µm) | Surface Roughness (Ra-µm) |
|---|---|
| 25 | 0.516 ± 0.027 |
| 35 | 0.620 ± 0.033 |
| 50 | 0.647 ± 0.037 |
| 105 | 0.684 ± 0.040 |
| 150 | 0.697 ± 0.042 |
| 210 | 0.736 ± 0.051 |
| 350 | 0.793 ± 0.055 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aulestia Viera, M.A.; Aguiar, P.R.; Oliveira Junior, P.; Alexandre, F.A.; Lopes, W.N.; Bianchi, E.C.; da Silva, R.B.; D’addona, D.; Andreoli, A. A Time–Frequency Acoustic Emission-Based Technique to Assess Workpiece Surface Quality in Ceramic Grinding with PZT Transducer. Sensors 2019, 19, 3913. https://doi.org/10.3390/s19183913
Aulestia Viera MA, Aguiar PR, Oliveira Junior P, Alexandre FA, Lopes WN, Bianchi EC, da Silva RB, D’addona D, Andreoli A. A Time–Frequency Acoustic Emission-Based Technique to Assess Workpiece Surface Quality in Ceramic Grinding with PZT Transducer. Sensors. 2019; 19(18):3913. https://doi.org/10.3390/s19183913
Chicago/Turabian StyleAulestia Viera, Martin A., Paulo R. Aguiar, Pedro Oliveira Junior, Felipe A. Alexandre, Wenderson N. Lopes, Eduardo C. Bianchi, Rosemar Batista da Silva, Doriana D’addona, and Andre Andreoli. 2019. "A Time–Frequency Acoustic Emission-Based Technique to Assess Workpiece Surface Quality in Ceramic Grinding with PZT Transducer" Sensors 19, no. 18: 3913. https://doi.org/10.3390/s19183913
APA StyleAulestia Viera, M. A., Aguiar, P. R., Oliveira Junior, P., Alexandre, F. A., Lopes, W. N., Bianchi, E. C., da Silva, R. B., D’addona, D., & Andreoli, A. (2019). A Time–Frequency Acoustic Emission-Based Technique to Assess Workpiece Surface Quality in Ceramic Grinding with PZT Transducer. Sensors, 19(18), 3913. https://doi.org/10.3390/s19183913









