Focusing Bistatic Forward-Looking Synthetic Aperture Radar Based on an Improved Hyperbolic Range Model and a Modified Omega-K Algorithm
Abstract
:1. Introduction
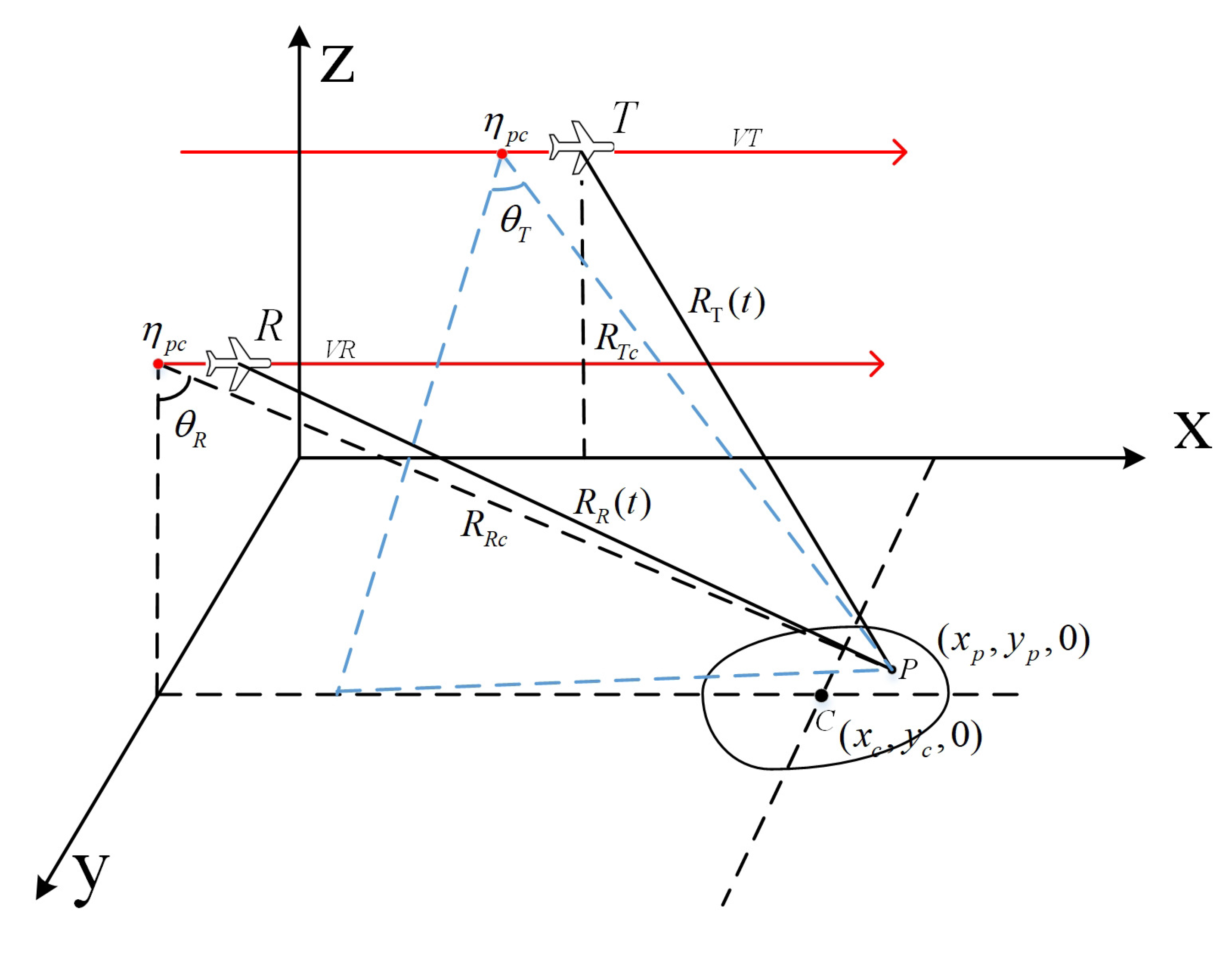
2. Geometry and Equivalent Slant Range Model
2.1. Equivalent Slant Range Model
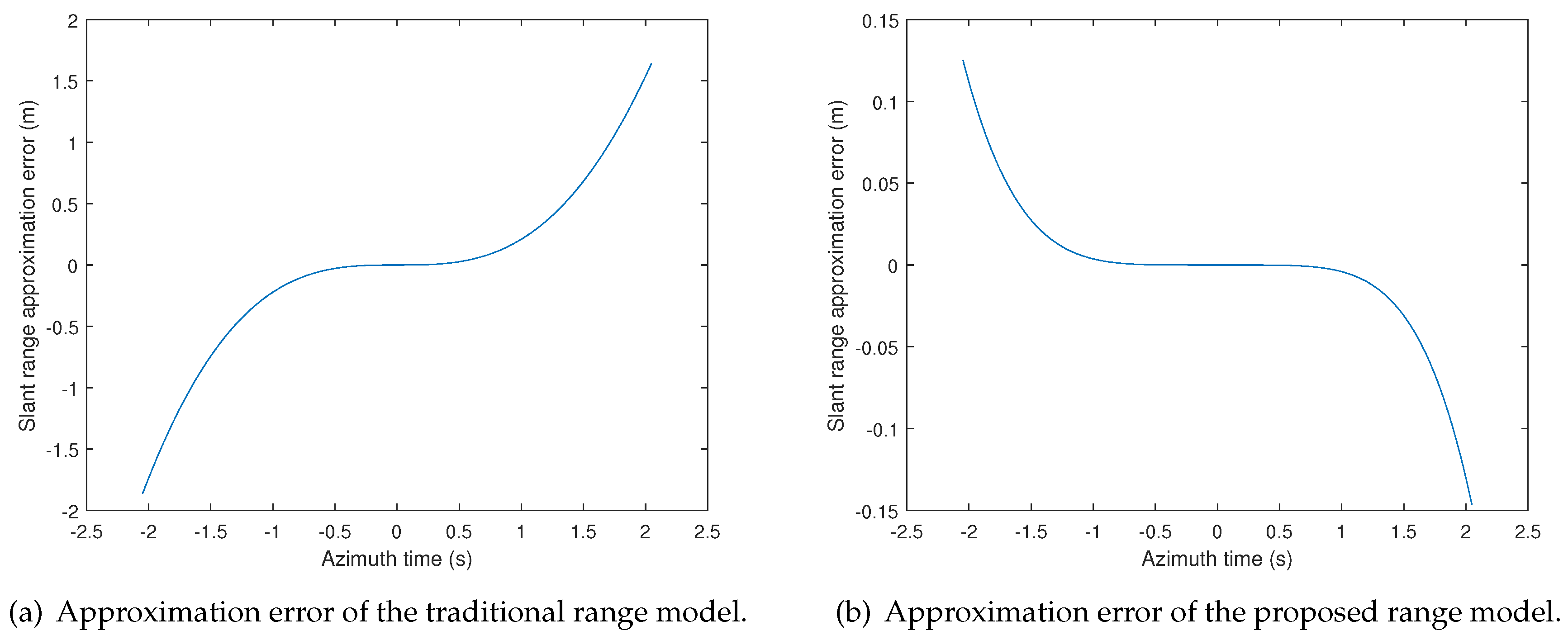
2.2. Range Error Analysis
3. Imaging Algorithm
3.1. Signal Model
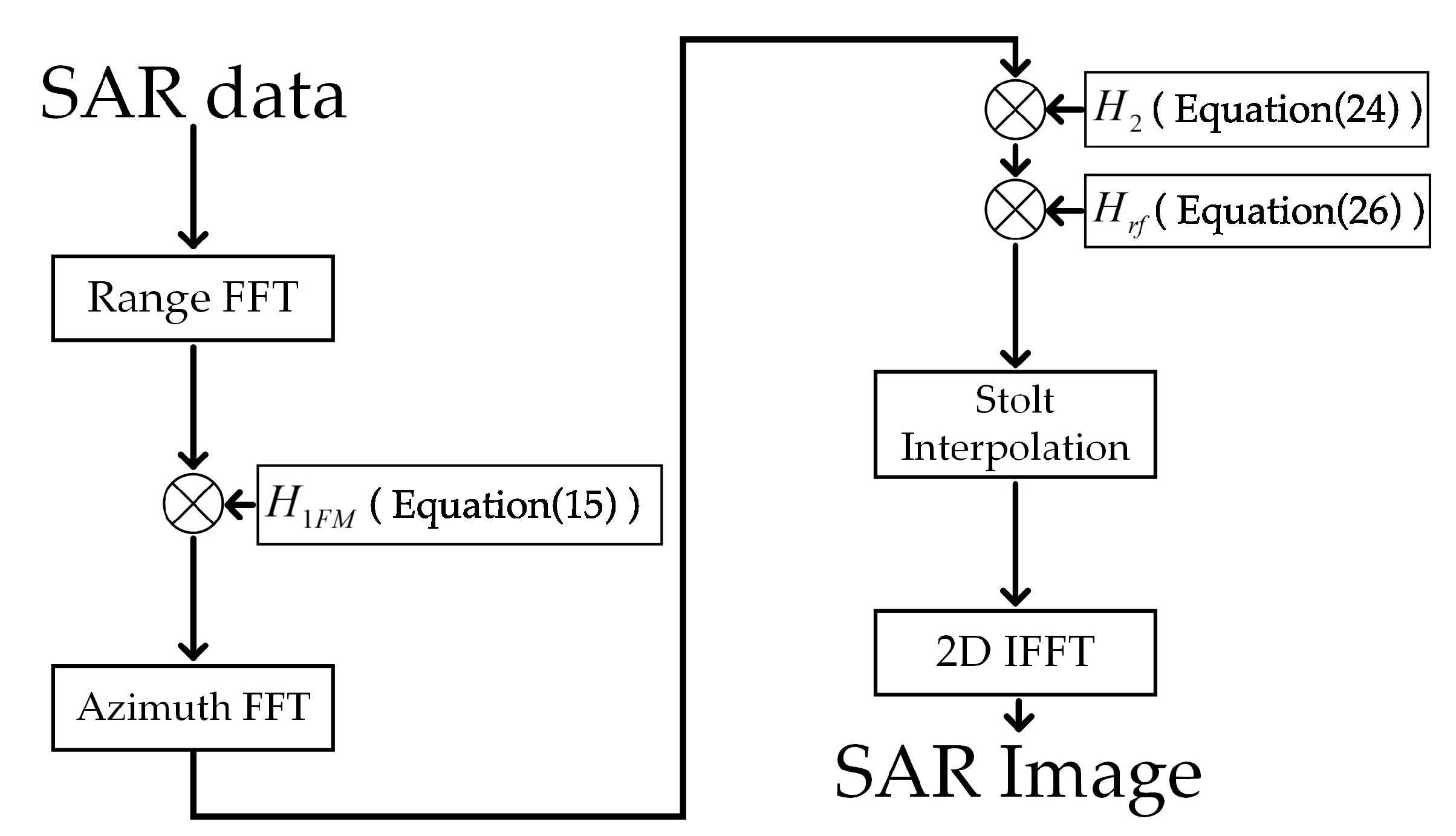
3.2. Modified Omega-K Imaging Algorithm
- (1)
- Performing range fast Fourier transform (FFT) on SAR data gets .
- (2)
- Multiplying Equation (15) and gets .
- (3)
- Performing azimuth fast Fourier transform (FFT) on gets .
- (4)
- Multiplying Equation (24) and gets .
- (5)
- Multiplying Equation (26) and gets .
- (6)
- Performing Stolt interpolation on gets .
- (7)
- Performing 2D-IFFT on gets output SAR focusing results.
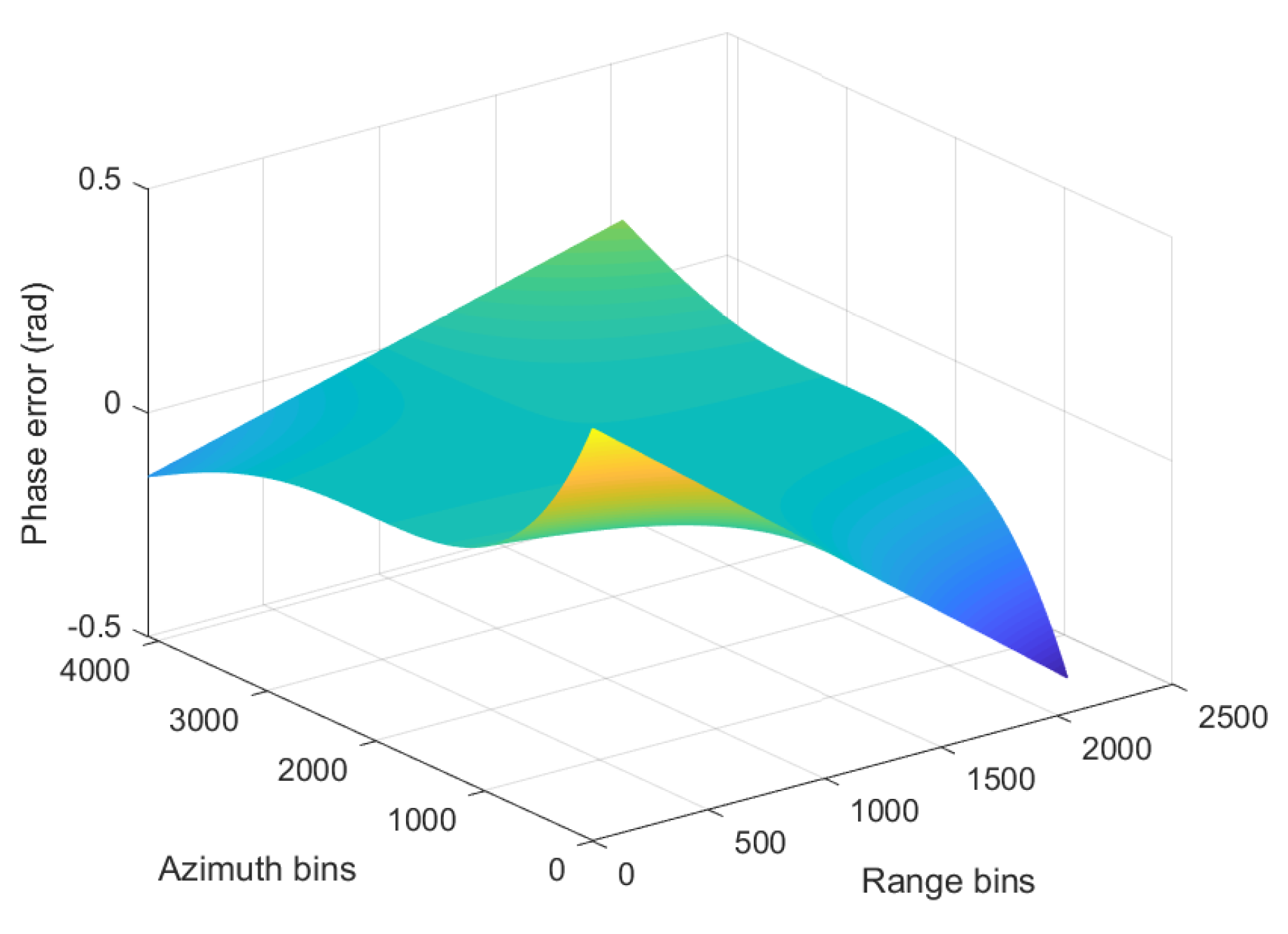
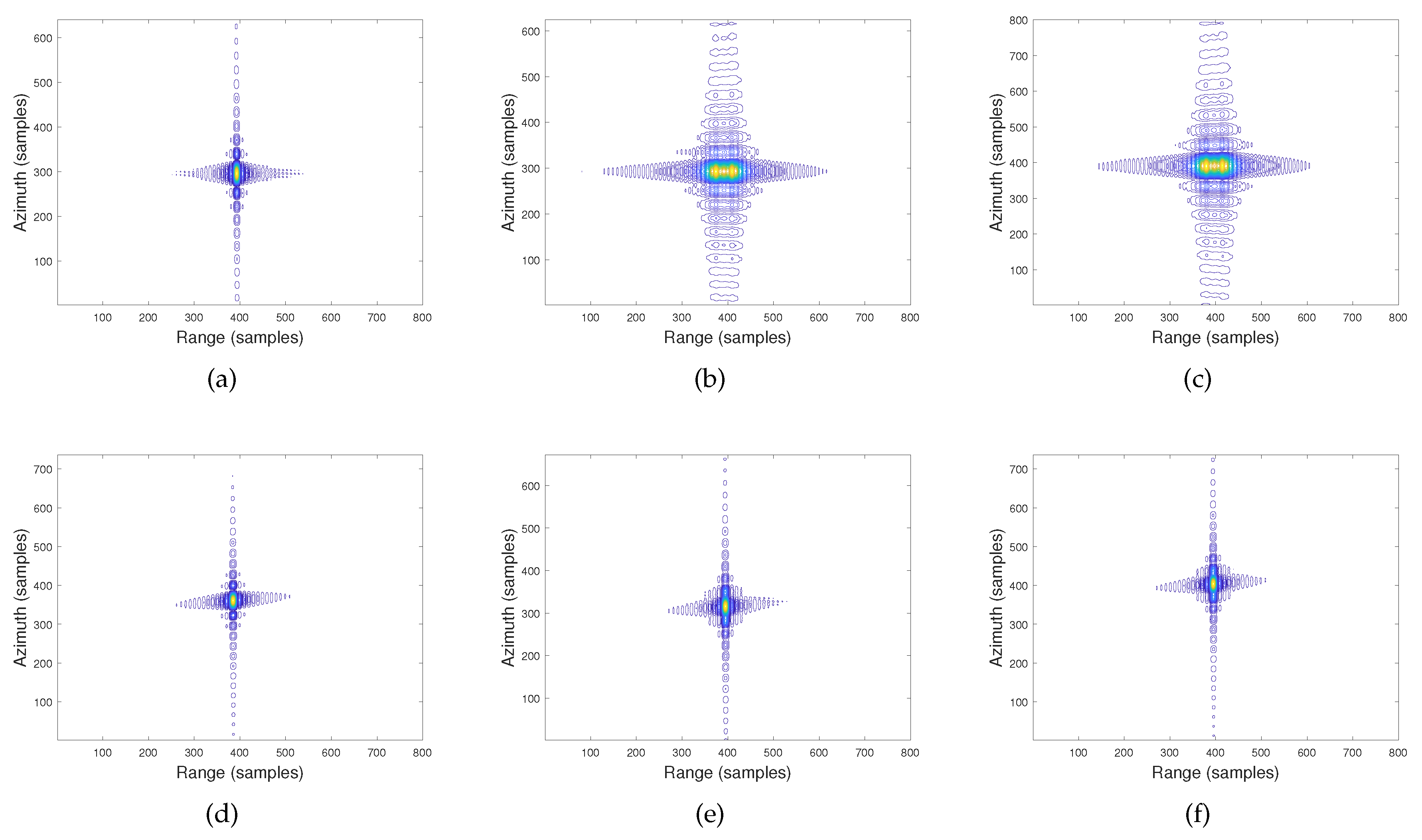
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Zhong, H.; Yan, A.; Sun, M.; Zhang, X.; Zhang, J. An improved ENLCS algorithm based on a quadratic ellipse model for high-resolution one-stationary bistatic SAR. Remote. Sens. Lett. 2018, 9, 867–876. [Google Scholar] [CrossRef]
- Ma, C.; Gu, H.; Su, W.; Zhang, X.; Li, C. Focusing one-stationary bistatic forward-looking synthetic aperture radar with squint minimisation method. IET Radar Sonar Navig. 2015, 9, 927–932. [Google Scholar] [CrossRef]
- Liang, M.; Su, W.; Ma, C.; Gu, H.; Yang, J. Focusing one-stationary bistatic forward-looking synthetic aperture radar based on squint minimization and modified nonlinear chirp scaling algorithm. Int. J. Remote Sens. 2018, 39, 7830–7845. [Google Scholar] [CrossRef]
- Wu, J.; Li, Z.; Huang, Y.; Yang, J.; Yang, H.; Liu, Q.H. Focusing Bistatic Forward-Looking SAR with Stationary Transmitter Based on Keystone Transform and Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2014, 11, 148–152. [Google Scholar] [CrossRef]
- Loffeld, O.; Nies, H.; Peters, V.; Knedlik, S. Models and useful relations for bistatic SAR processing. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2031–2038. [Google Scholar] [CrossRef]
- Walterscheid, I.; Ender, J.H.G.; Brenner, A.R.; Loffeld, O. Bistatic SAR Processing and Experiments. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2710–2717. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Ul-Ann, Q.; Nies, H.; Ortiz, A.M.; Samarah, A. A Bistatic Point Target Reference Spectrum for General Bistatic SAR Processing. IEEE Geosci. Remote Sens. Lett. 2008, 5, 517–521. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Neo, Y.L.; Nies, H.; Dai, Z. Extending Loffeld’s bistatic formula for the general bistatic SAR configuration. IET Radar Sonar Navig. 2010, 4, 74–84. [Google Scholar] [CrossRef]
- Ma, C.; Gu, H.; Su, W.; Li, C.; Chen, J. Focusing bistatic forward-looking synthetic aperture radar based on modified Loffeld’s bistatic formula and chirp scaling algorithm. J. Appl. Remote Sens. 2014, 8, 083586. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.; Cumming, I.G. A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion. IEEE Geosci. Remote Sens. Lett. 2007, 4, 93–96. [Google Scholar] [CrossRef]
- Bamler, R.; Boerner, E. On the use of numerically computed transfer functions for processing of data from bistatic SARs and high squint orbital SARs. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005. [Google Scholar]
- Qiu, X.; Hu, D.; Ding, C. Focusing Bistaitc Images use RDA based on Hyperbolic Approximating. In Proceedings of the CIE International Conference on Radar, Shanghai, China, 16–19 October 2006. [Google Scholar]
- Ma, C.; Gu, H.; Su, W.; Li, C. Focusing bistatic forward-looking synthetic aperture radar based on modified hyperbolic approximating. Acta Phys. Sin. 2014, 63, 028403. [Google Scholar]
- Chen, S.; Yuan, Y.; Zhang, S.; Zhao, H.; Chen, Y. A New Imaging Algorithm for Forward-Looking Missile-Borne Bistatic SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 543–1552. [Google Scholar] [CrossRef]
- Feng, D.; An, D.; Huang, X. An Extended Fast Factorized Back Projection Algorithm for Missile-Borne Bistatic Forward-Looking SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2724–2734. [Google Scholar] [CrossRef]


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Carrier frequency | 9 GHz | Transmitter center slant range | 4300 m |
| Pulse duration | 2 | Transmitter squint angle | |
| Bandwidth | 200 MHz | Receiver center slant range | 3600 m |
| Sampling frequency | 300 MHz | Receiver forward-looking angle | |
| Pulse repetition frequency | 1 kHz | Sensor speed | 200 m/s |
| Targets | PSLR (dB) | ISLR (dB) | ||
|---|---|---|---|---|
| Azimuth | Range | Azimuth | Range | |
| Traditional omega-K algorithm | −1.705 | - | - | - |
| Proposed omega-K algorithm | −12.87 | −13.33 | −8.86 | −9.9558 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Su, W.; Gu, H.; Yang, J. Focusing Bistatic Forward-Looking Synthetic Aperture Radar Based on an Improved Hyperbolic Range Model and a Modified Omega-K Algorithm. Sensors 2019, 19, 3792. https://doi.org/10.3390/s19173792
Wang C, Su W, Gu H, Yang J. Focusing Bistatic Forward-Looking Synthetic Aperture Radar Based on an Improved Hyperbolic Range Model and a Modified Omega-K Algorithm. Sensors. 2019; 19(17):3792. https://doi.org/10.3390/s19173792
Chicago/Turabian StyleWang, Chenchen, Weimin Su, Hong Gu, and Jianchao Yang. 2019. "Focusing Bistatic Forward-Looking Synthetic Aperture Radar Based on an Improved Hyperbolic Range Model and a Modified Omega-K Algorithm" Sensors 19, no. 17: 3792. https://doi.org/10.3390/s19173792
APA StyleWang, C., Su, W., Gu, H., & Yang, J. (2019). Focusing Bistatic Forward-Looking Synthetic Aperture Radar Based on an Improved Hyperbolic Range Model and a Modified Omega-K Algorithm. Sensors, 19(17), 3792. https://doi.org/10.3390/s19173792





