DMS-SLAM: A General Visual SLAM System for Dynamic Scenes with Multiple Sensors
Abstract
1. Introduction
- A novel method for VSLAM initialization is proposed to set up static initialization 3D map points.
- Static 3D points are included in the local map through GMS feature matching algorithm between keyframes, and static global 3D map is constructed.
- High accuracy and real-time monocular, stereo and RGB-D positioning and mapping system for dynamic scenarios.
2. Related Works
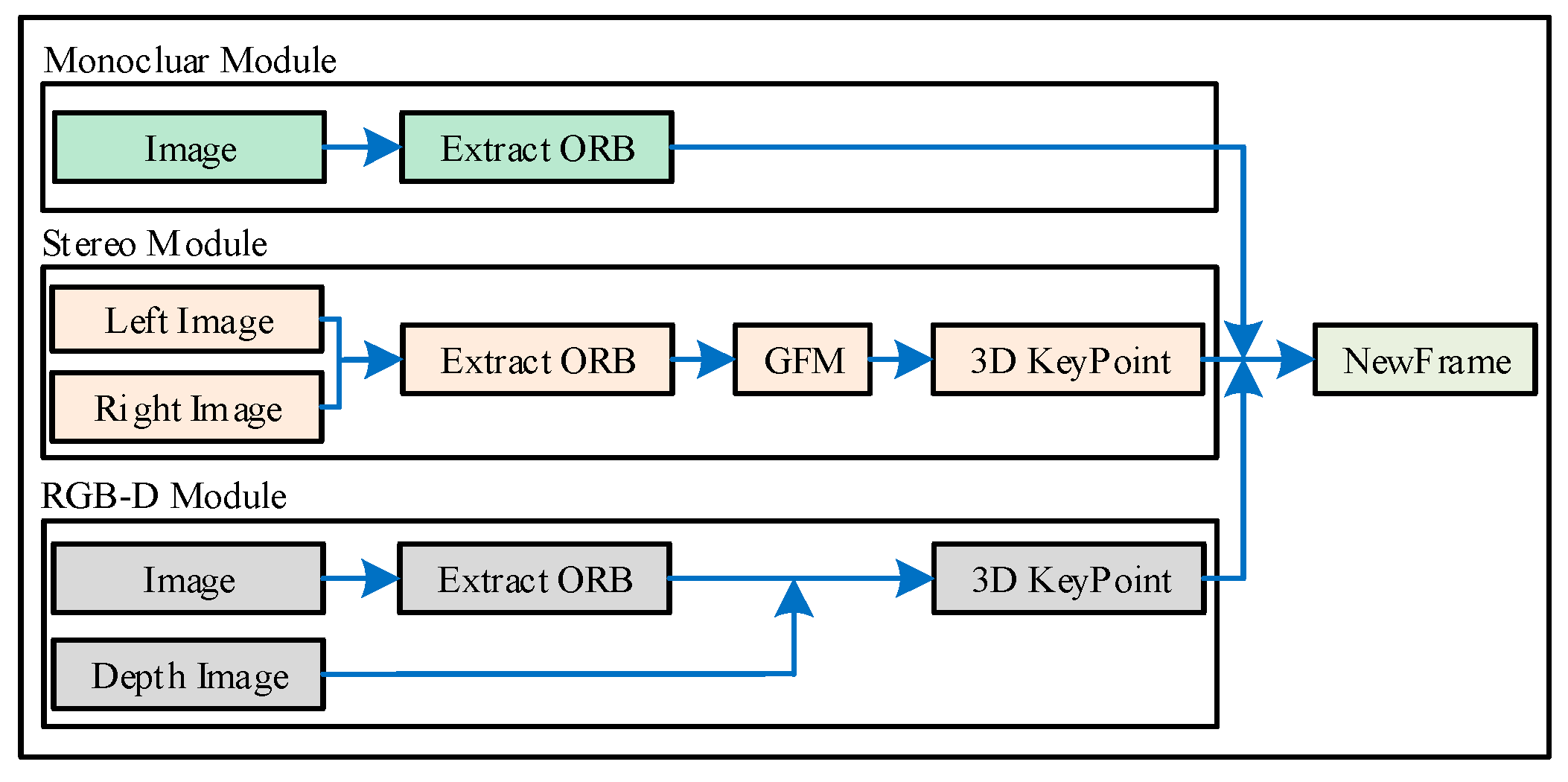
3. System Overview
4. Methodology
4.1. Feature Matching
4.2. Construct NewFrame
4.3. System Intialization
4.4. Tracking
4.5. Local Mapping
4.6. Relocalization and Loop Detection
5. Evaluation
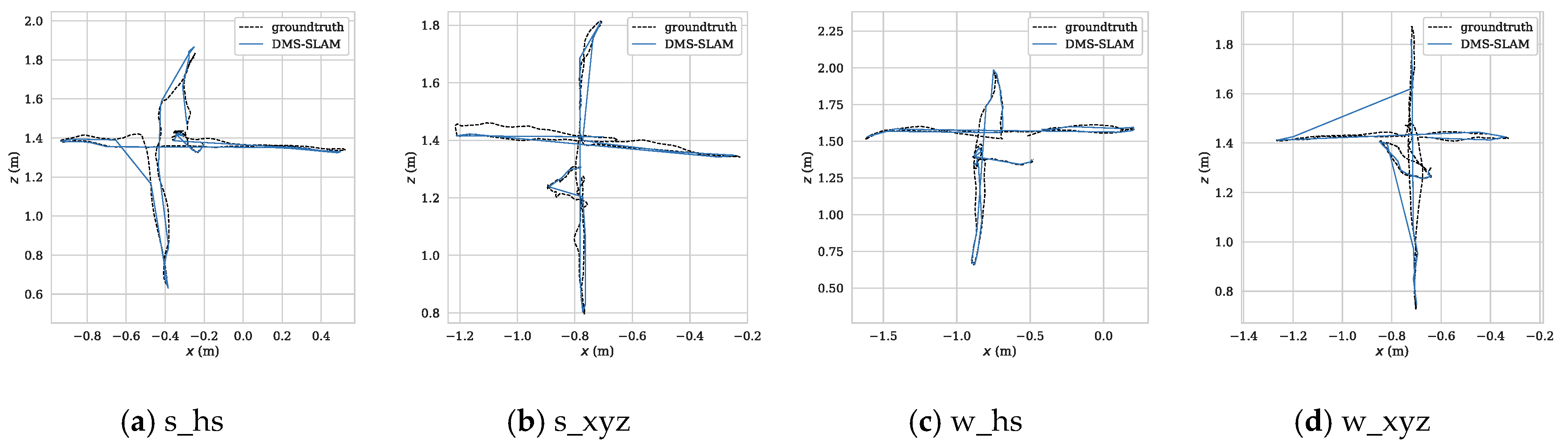
- In this paper, our RGB-D and monocular camera experiments were performed on the fr3 series of datasets with ground truth in TUM. s refers to sitting, w to walking and hs to halfsphere.
- The available information is reduced due to the elimination of the effects of dynamic objects in the scene. Therefore, in the following experiments, we extract 1500 ORB feature points for analysis and comparison of accuracy and speed.
- In the TUM dataset, the camera’s frame rate is 30, and the sliding window size is set to 7 determined by the experiment. However, in the KITTI dataset, the camera’s frame rate is 10, so setting the sliding window size to 3 to eliminate the effects of dynamic objects.
- In contrast to the semantic segmentation method which is used to eliminate the effects of dynamic objects through GPU acceleration, e.g., DynaSLAM, DS-SLAM, all our experimental results are only run on the CPU (Intel i5 2.2 GHz 8 GB).
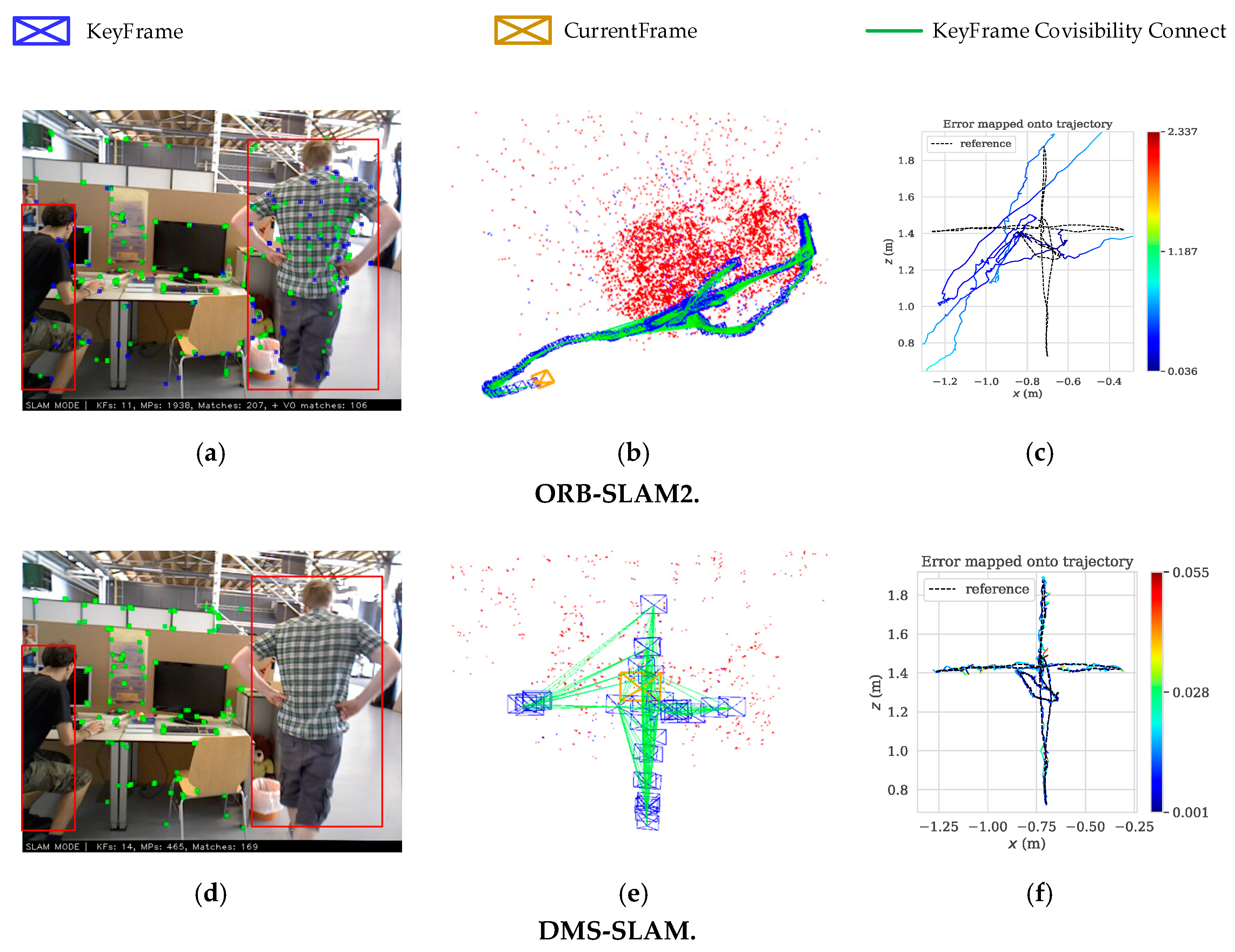
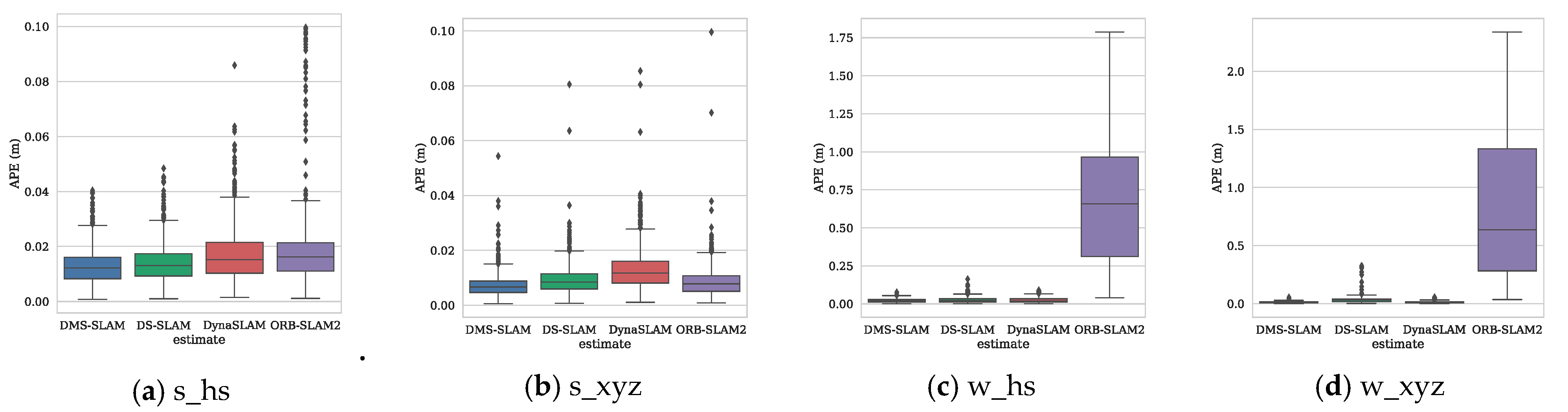
5.1. RGB-D
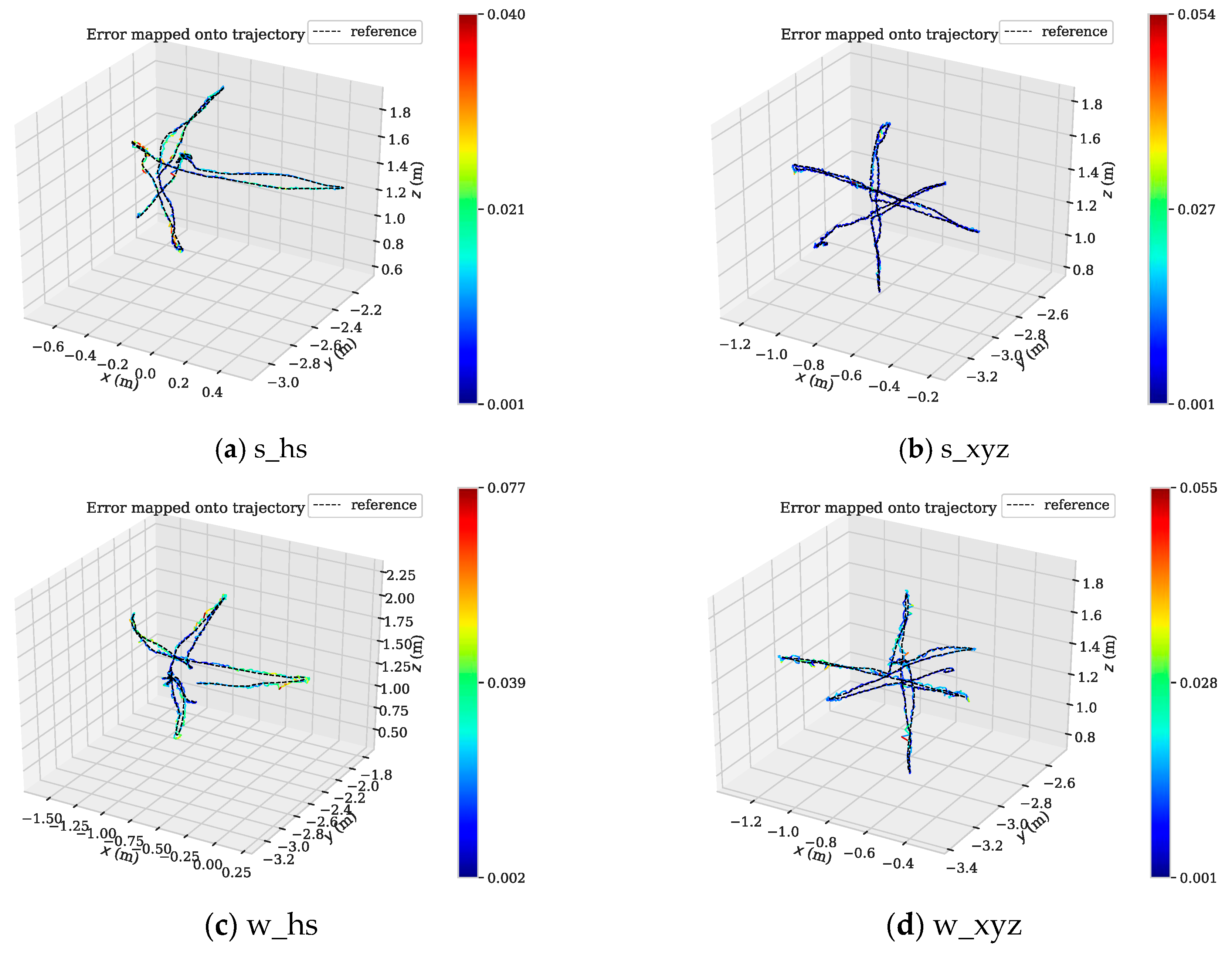
5.2. Monocular
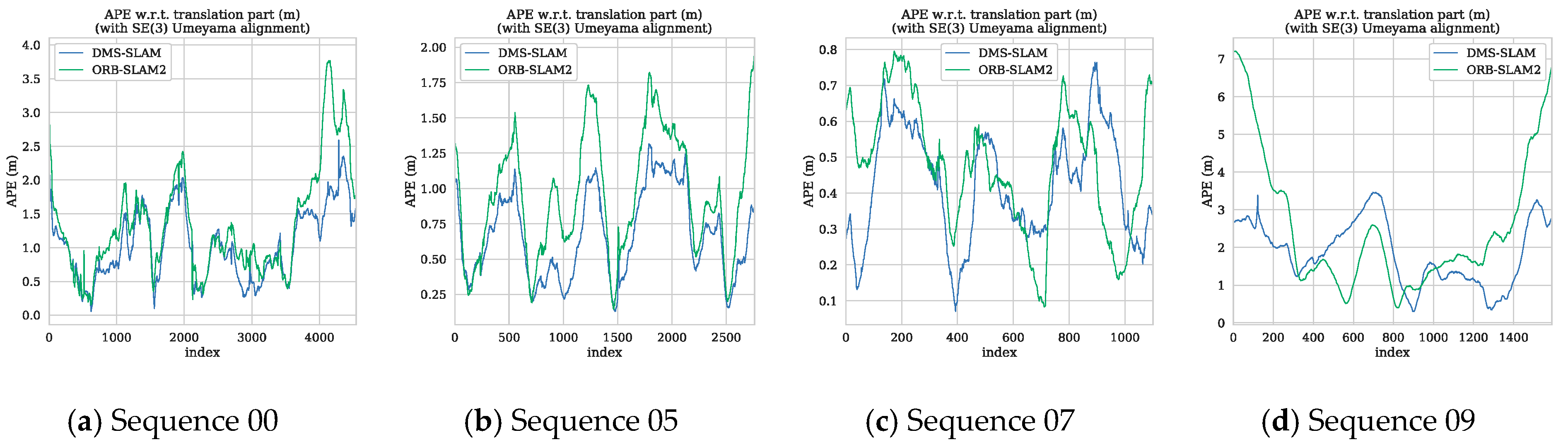
5.3. Stereo
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Nistér, D.; Naroditsky, O.; Bergen, J.R. Visual odometry for ground vehicle applications. J. Field Robot. 2006, 23, 3–20. [Google Scholar] [CrossRef]
- Lee, S.H.; Croon, G.D. Stability-based scale estimation for monocular SLAM. IEEE Robot. Autom. Lett. 2018, 3, 780–787. [Google Scholar] [CrossRef]
- Klein, G.; Murray, D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 6th IEEE and ACM International Symposium on Mixed and Augmented Reality (ISMAR), Nara, Japan, 13–16 November 2007; pp. 1–10. [Google Scholar]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kuala Lumpur, Malaysia, 20–22 October 2014; pp. 15–22. [Google Scholar]
- Engel, J.; Schoeps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Murartal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An open-source SLAM system for monocular, stereo and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Wang, R.; Demmel, N.; Cremers, D. LDSO: Direct sparse odometry with loop closure. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2198–2204. [Google Scholar]
- Lee, S.H.; Civera, J. Loosely-Coupled semi-direct monocular SLAM. IEEE Robot. Autom. Lett. 2018, 4, 399–406. [Google Scholar] [CrossRef]
- Agudo, A.; Moreno-Noguer, F.; Calvo, B.; Montiel, J.M.M. Sequential non-rigid structure from motion using physical priors. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 979–994. [Google Scholar] [CrossRef] [PubMed]
- Agudo, A.; Moreno-Noguer, F.; Calvo, B.; Montiel, J. Real-time 3D reconstruction of non-rigid shapes with a single moving camera. Comput. Vis. Image Underst. 2016, 153, 37–54. [Google Scholar] [CrossRef]
- Bian, J.; Lin, W.Y.; Matsushita, Y.; Yeung, S.K.; Nguyen, T.D.; Cheng, M.M. Gms: Grid-based motion statistics for fast, ultra-robust feature correspondence. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 25–30 June 2017; pp. 4181–4190. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura (IROS), Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 1052–1067. [Google Scholar] [CrossRef] [PubMed]
- Civera, J.; Davison, A.J.; Montiel, J.M. Inverse depth parametrization for monocular SLAM. IEEE Trans. Robot. 2008, 24, 932–945. [Google Scholar] [CrossRef]
- Eade, E.; Drummond, T. Scalable monocular SLAM. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 17–22 June 2006; pp. 469–476. [Google Scholar]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In Proceedings of the International Workshop on Vision Algorithms, London, UK, 21–22 September 1999; pp. 298–372. [Google Scholar]
- Engel, J.; Stückler, J.; Cremers, D. Large-scale direct SLAM with stereo cameras. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1935–1942. [Google Scholar]
- Wang, R.; Schworer, M.; Cremers, D. Stereo DSO: Large-scale direct sparse visual odometry with stereo cameras. In Proceedings of the IEEE International Conference on Computer Visionm, Venice, Italy, 22–29 October 2017; pp. 3903–3911. [Google Scholar]
- Mourikis, A.I.; Roumeliotis, S.I. A multi-state constraint Kalman filter for vision-aided inertial navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Roma, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar]
- Li, M.; Mourikis, A.I. High-precision, consistent EKF-based visual-inertial odometry. Int. J. Robot. Res. 2013, 32, 690–711. [Google Scholar] [CrossRef]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual–inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2015, 34, 314–334. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Visual-inertial monocular SLAM with map reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Tong, Q.; Li, P.; Shen, S. VINS-Mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2017, 34, 1004–1020. [Google Scholar]
- Shi, J.; Tomasi, C. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 21–23 June 1994. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the 2006 European Conference on Computer Vision (ECCV), Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G.R. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Raguram, R.; Frahm, J.M.; Pollefeys, M. A comparative analysis of RANSAC techniques leading to adaptive real-time random sample consensus. In Proceedings of the 2008 European Conference on Computer Vision, Marseille, France, 12–18 October 2008; pp. 500–513. [Google Scholar]
- Fang, Y.; Dai, B. An improved moving target detecting and tracking based on optical flow technique and Kalman filter. In Proceedings of the 4th International Conference on Computer Science and Education (ICCSE), Nanning, China, 25 July 2009; pp. 1197–1202. [Google Scholar]
- Wang, Y.; Huang, S. Motion segmentation based robust RGB-D SLAM. In Proceedings of the 11th World Congress on Intelligent Control and Automation (WCICA), Shenyang, China, 29 June–4 July 2014; pp. 3122–3127. [Google Scholar]
- Alcantarilla, P.F.; Yebes, J.J.; Almazán, J.; Bergasa, L.M. On combining visual SLAM and dense scene flow to increase the robustness of localization and mapping in dynamic environments. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–19 May 2012; pp. 1290–1297. [Google Scholar]
- Yu, C.; Liu, Z.; Liu, X.J.; Xie, F.; Yang, Y.; Wei, Q.; Fei, Q. DS-SLAM: A semantic visual slam towards dynamic environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1168–1174. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Bescos, B.; Fácil, J.M.; Civera, J.; Neira, J. DynaSLAM: Tracking, mapping, and inpainting in dynamic scenes. IEEE Robot. Autom. Lett. 2018, 3, 4076–4083. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the 2017 IEEE international conference on computer vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Bârsan, I.A.; Liu, P.; Pollefeys, M.; Geiger, A. Robust dense mapping for large-scale dynamic environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–26 May 2018; pp. 7510–7517. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. Epnp: An accurate on solution to the pnp problem. Int. J. Comput. Vis. 2009, 81, 155. [Google Scholar] [CrossRef]
- Gálvez-López, D.; Tardos, J.D. Bags of binary words for fast place recognition in image sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, Rhode Island, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Qin, T.; Cao, S.; Pan, J.; Shen, S. A general optimization-based framework for global pose estimation with multiple Sensors. arXiv 2019, arXiv:1901.03642. [Google Scholar]












| Methods | No Sliding Window | With Sliding Window | ||
|---|---|---|---|---|
| Times (ms) | Matches | Times (ms) | Matches | |
| BF | 5.23 | 627 | 5.40 | 401 |
| FLANN2 | 20.93 | 124 | 13.21 | 65 |
| GMS | 6.01 | 650 | 6.27 | 318 |
| Datasets | ATE RMSE (cm) | Tracking Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|
| DMS-SLAM | Dyna SLAM | DS-SLAM | ORB-SLAM2 | DMS-SLAM | Dyna SLAM | DS-SLAM | ORB-SLAM2 | |
| s_hs | 1.406 | 1.913 | 1.481 | 2.307 | 0.051 | 1.242 | 0.172 | 0.098 |
| s_rpy | 1.757 | 3.017 | 1.868 | 1.775 | 0.046 | 1.565 | 0.124 | 0.077 |
| s_static | 0.687 | 0.636 | 0.610 | 0.960 | 0.041 | 1.294 | 0.142 | 0.079 |
| s_xyz | 0.800 | 1.354 | 0.979 | 0.817 | 0.052 | 1.557 | 0.135 | 0.078 |
| w_hs | 2.270 | 2.674 | 2.821 | 35.176 | 0.047 | 1.244 | 0.152 | 0.092 |
| w_ rpy | 3.875 | 4.020 | 37.370 | 66.203 | 0.048 | 1.273 | 0.146 | 0.081 |
| w_ static | 0.746 | 0.800 | 0.810 | 44.131 | 0.045 | 1.134 | 0.115 | 0.072 |
| w_ xyz | 1.283 | 1.574 | 2.407 | 45.972 | 0.046 | 1.184 | 0.136 | 0.079 |
| Datasets | ATE RMSE (cm) | Tracking Time (s) | TCR (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DMS-SLAM | Dyna SLAM | ORB-SLAM2 | DMS-SLAM | Dyna SLAM | ORB-SLAM2 | DMS-SLAM | Dyna SLAM | ORB-SLAM2 | |
| s_hs | 1.729 | 1.964 | 1.954 | 0.052 | 0.763 | 0.055 | 99.19 | 94.68 | 98.92 |
| s_rpy | 1.661 | 2.160 | 1.251 | 0.046 | 0.820 | 0.046 | 91.83 | 54.39 | 73.66 |
| s_static | 0.621 | 0.379 | 0.882 | 0.040 | 0.770 | 0.043 | 98.02 | 41.30 | 48.23 |
| s_xyz | 0.928 | 1.058 | 0.974 | 0.054 | 0.810 | 0.053 | 95.64 | 94.77 | 95.96 |
| w_hs | 1.859 | 1.965 | 1.931 | 0.047 | 0.754 | 0.049 | 97.75 | 97.00 | 89.22 |
| w_ rpy | 4.086 | 5.023 | 6.593 | 0.041 | 0.792 | 0.041 | 89.45 | 84.29 | 88.68 |
| w_ static | 0.204 | 0.342 | 0.498 | 0.039 | 0.761 | 0.039 | 86.81 | 84.79 | 86.54 |
| w_ xyz | 1.090 | 1.370 | 1.368 | 0.044 | 0.807 | 0.049 | 99.07 | 97.02 | 88.24 |
| Datasets | ATE RMSE (m) | Tracking Time (s) | |||
|---|---|---|---|---|---|
| DMS-SLAM | DynaSLAM | ORB-SLAM2 | DMS-SLAM | ORB-SLAM2 | |
| KITTI00 | 1.1 | 1.4 | 1.3 | 0.082 | 0.132 |
| KITTI01 | 9.7 | 9.4 | 10.4 | 0.081 | 0.141 |
| KITTI02 | 6.0 | 6.7 | 5.7 | 0.080 | 0.125 |
| KITTI03 | 0.5 | 0.6 | 0.6 | 0.080 | 0.135 |
| KITTI04 | 0.2 | 0.2 | 0.2 | 0.077 | 0.132 |
| KITTI05 | 0.7 | 0.8 | 0.8 | 0.083 | 0.130 |
| KITTI06 | 0.6 | 0.8 | 0.8 | 0.082 | 0.140 |
| KITTI07 | 0.4 | 0.5 | 0.5 | 0.080 | 0.128 |
| KITTI08 | 3.2 | 3.5 | 3.6 | 0.084 | 0.127 |
| KITTI09 | 2.1 | 1.6 | 3.2 | 0.079 | 0.133 |
| KITTI10 | 1.0 | 1.2 | 1.0 | 0.081 | 0.121 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zeng, W.; Feng, B.; Xu, F. DMS-SLAM: A General Visual SLAM System for Dynamic Scenes with Multiple Sensors. Sensors 2019, 19, 3714. https://doi.org/10.3390/s19173714
Liu G, Zeng W, Feng B, Xu F. DMS-SLAM: A General Visual SLAM System for Dynamic Scenes with Multiple Sensors. Sensors. 2019; 19(17):3714. https://doi.org/10.3390/s19173714
Chicago/Turabian StyleLiu, Guihua, Weilin Zeng, Bo Feng, and Feng Xu. 2019. "DMS-SLAM: A General Visual SLAM System for Dynamic Scenes with Multiple Sensors" Sensors 19, no. 17: 3714. https://doi.org/10.3390/s19173714
APA StyleLiu, G., Zeng, W., Feng, B., & Xu, F. (2019). DMS-SLAM: A General Visual SLAM System for Dynamic Scenes with Multiple Sensors. Sensors, 19(17), 3714. https://doi.org/10.3390/s19173714





