Real-Time Photometric Calibrated Monocular Direct Visual SLAM
Abstract
1. Introduction
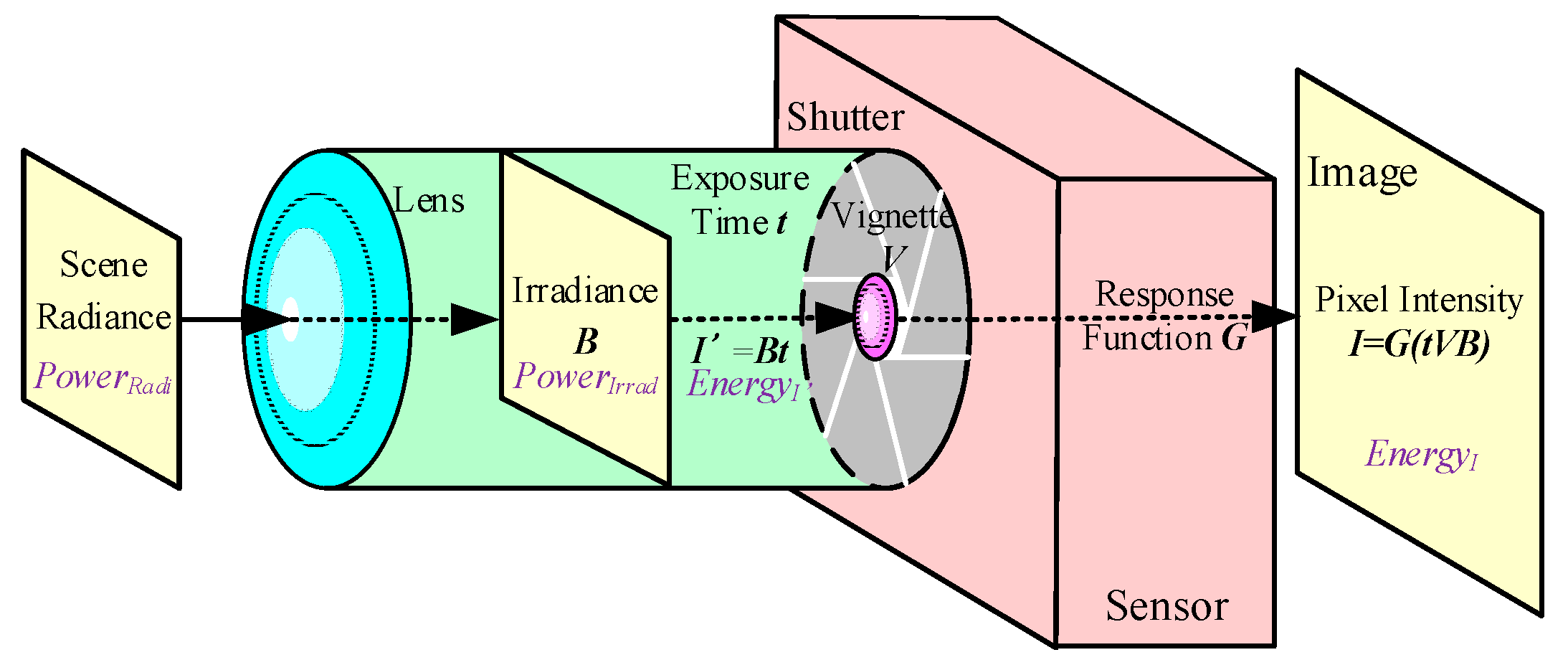
2. Photometric Calibration Model
2.1. Vignetting and Response Function
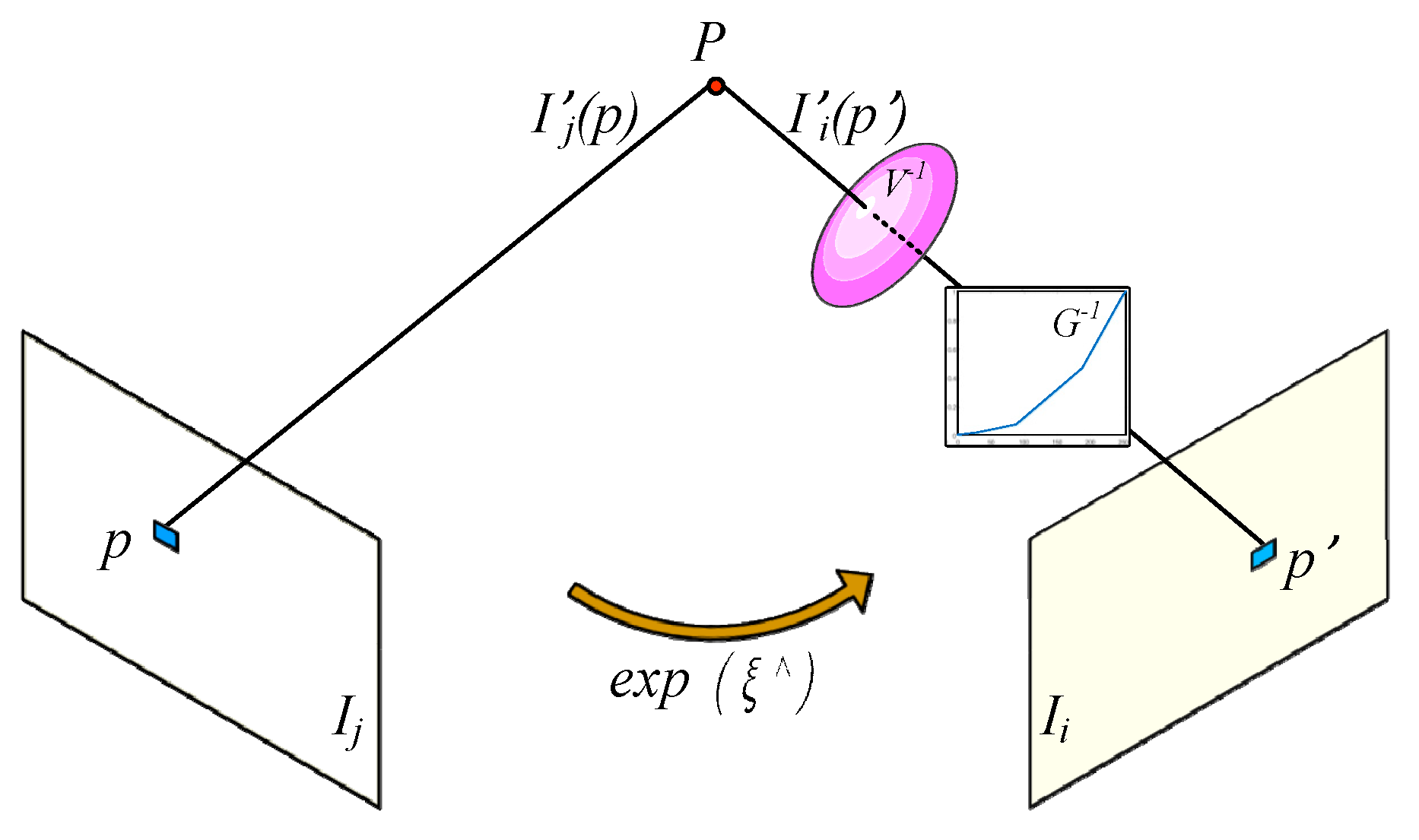
2.2. Photometric Calibration Equation
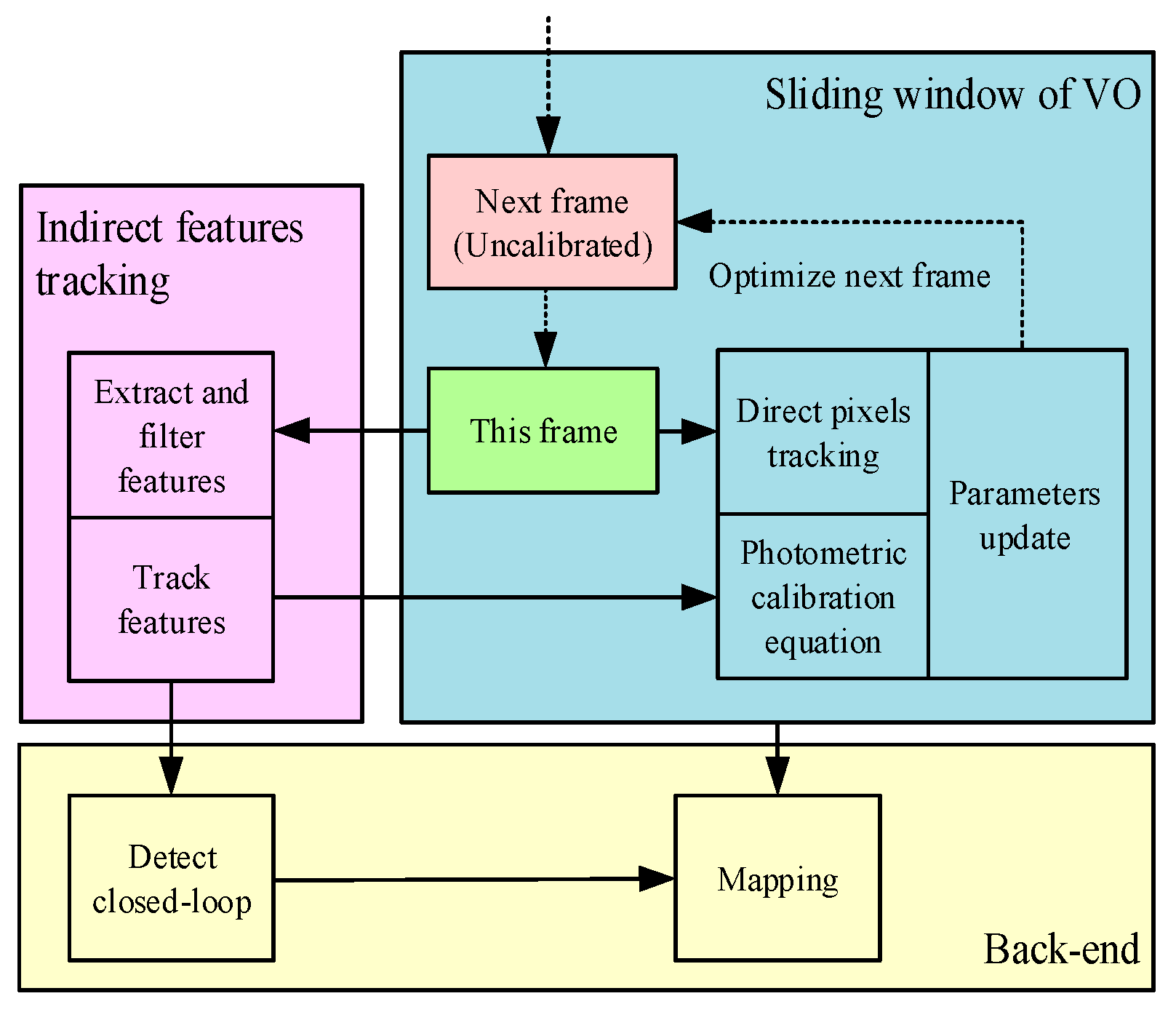
3. The Combination of Photometric Calibration and Direct SLAM
3.1. Direct Sparse Model
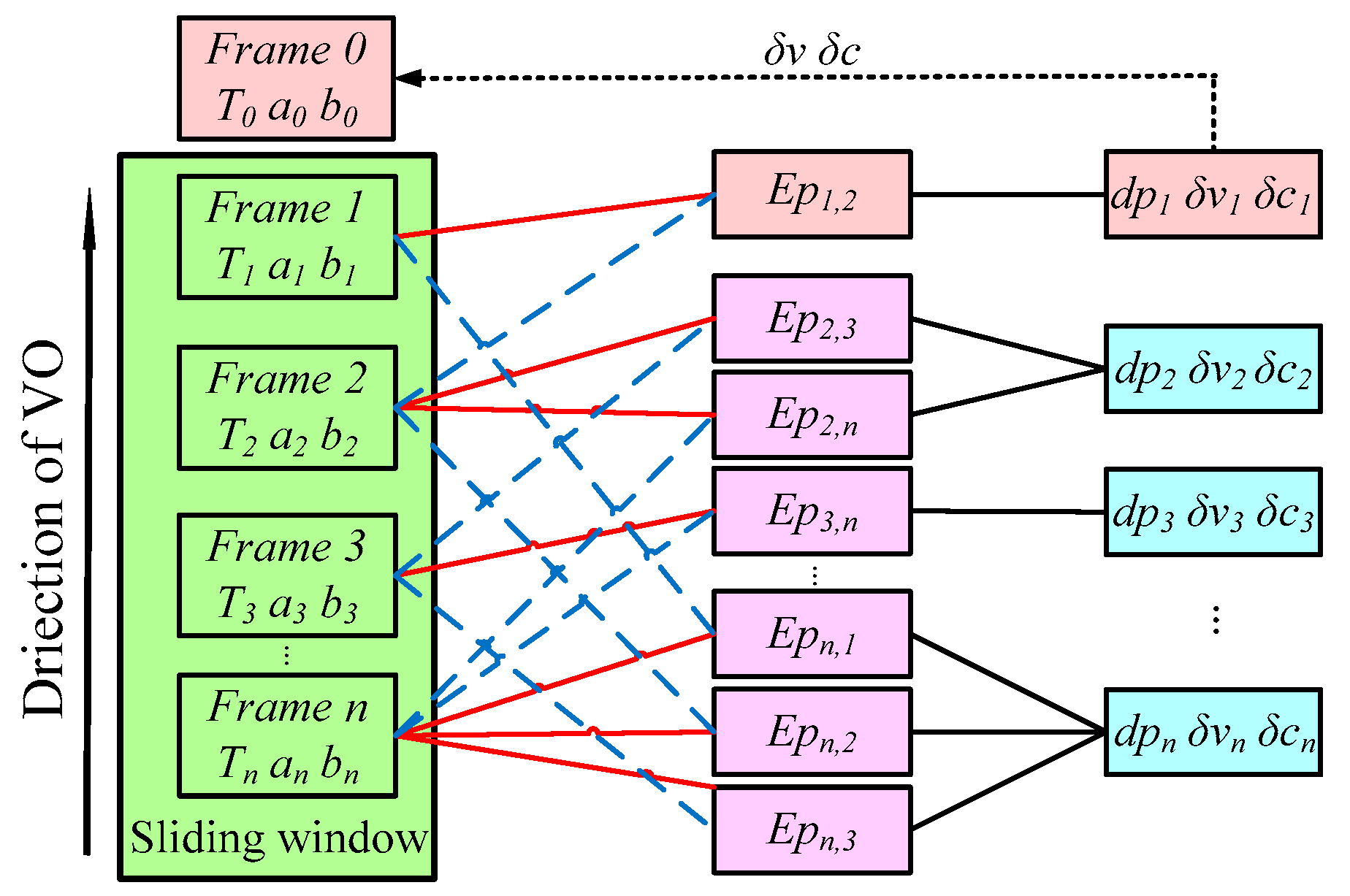
3.2. Parameters Update
3.3. Window Optimization
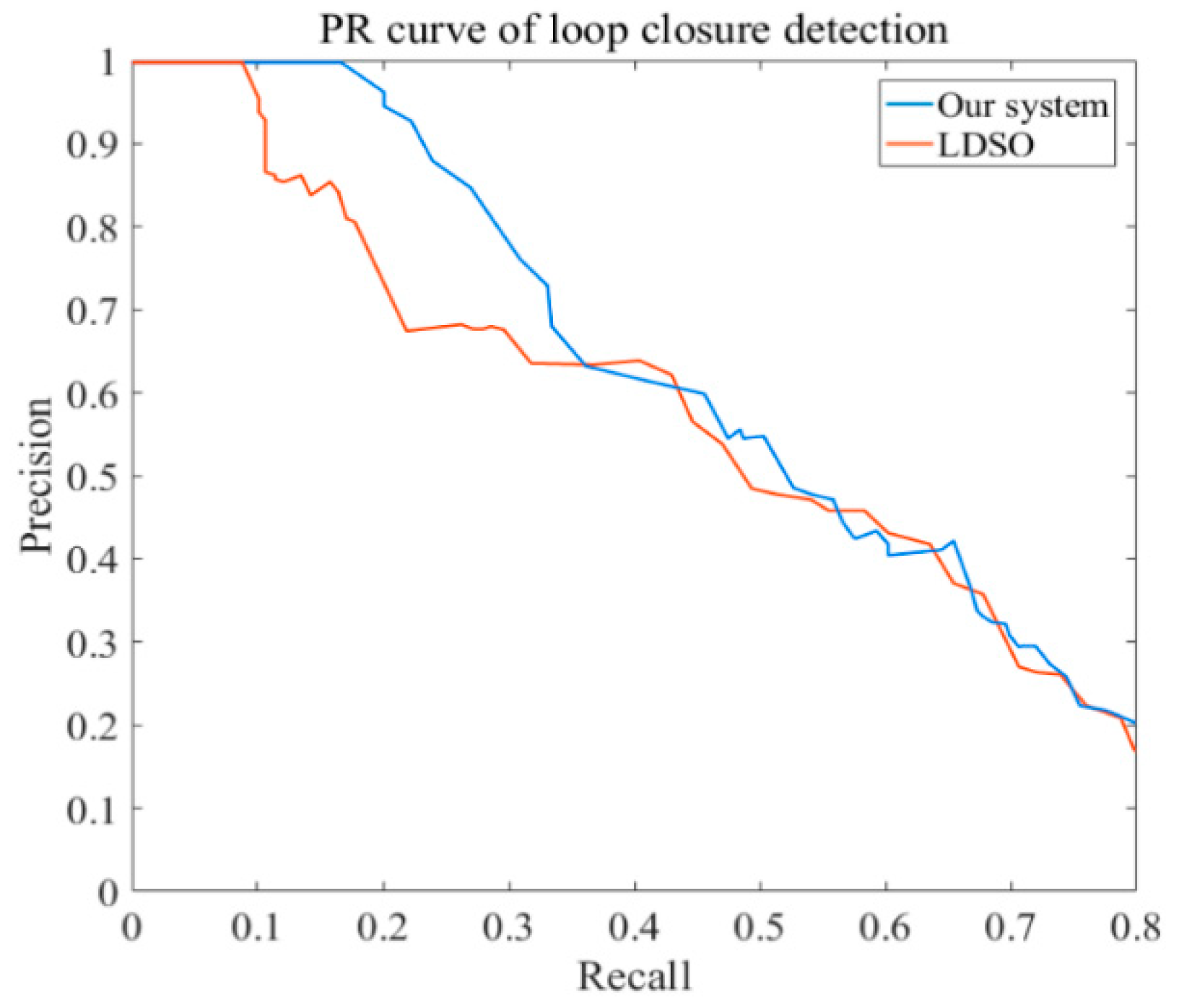
3.4. Loop Closure Detection
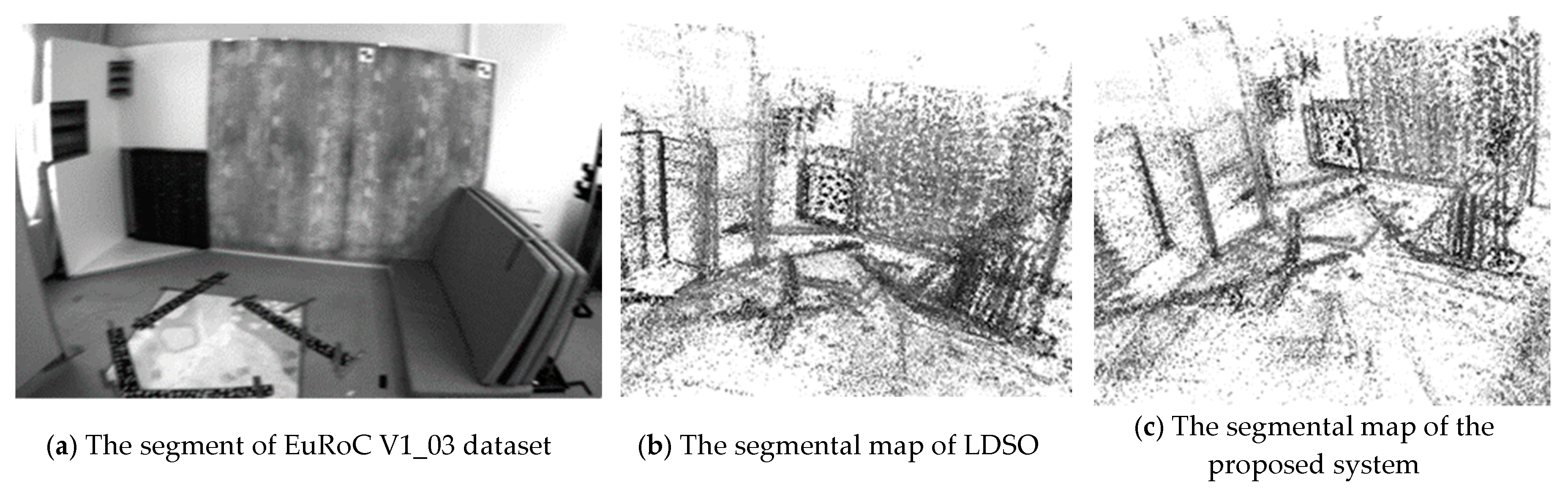
4. Experiments
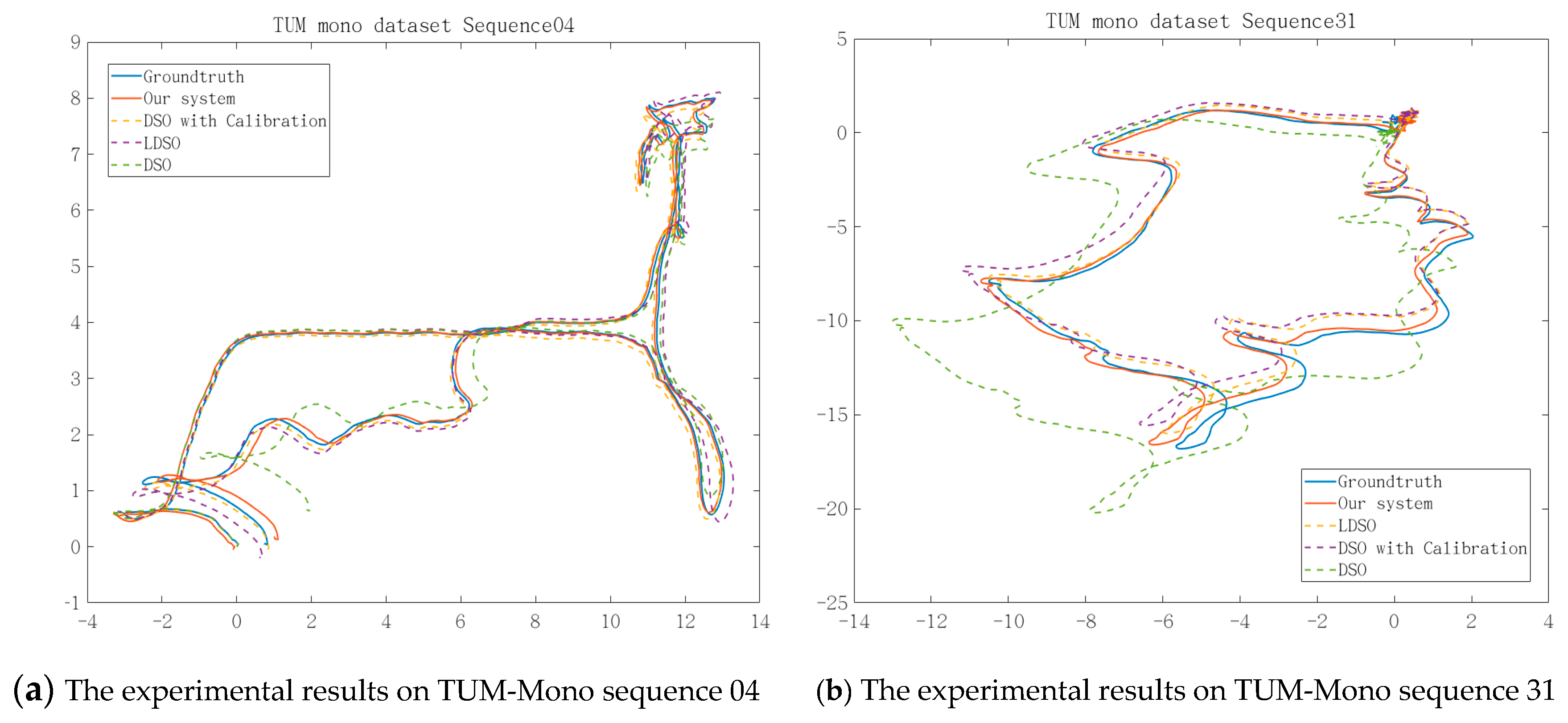
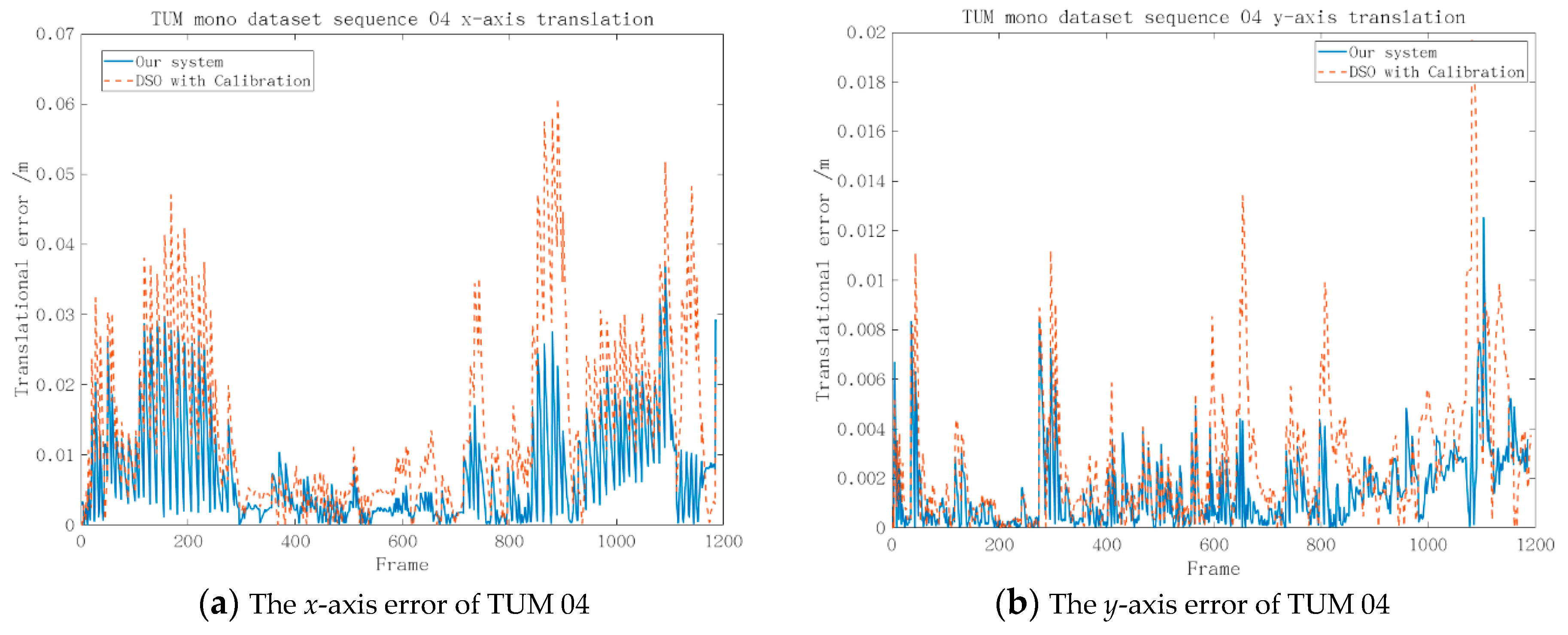
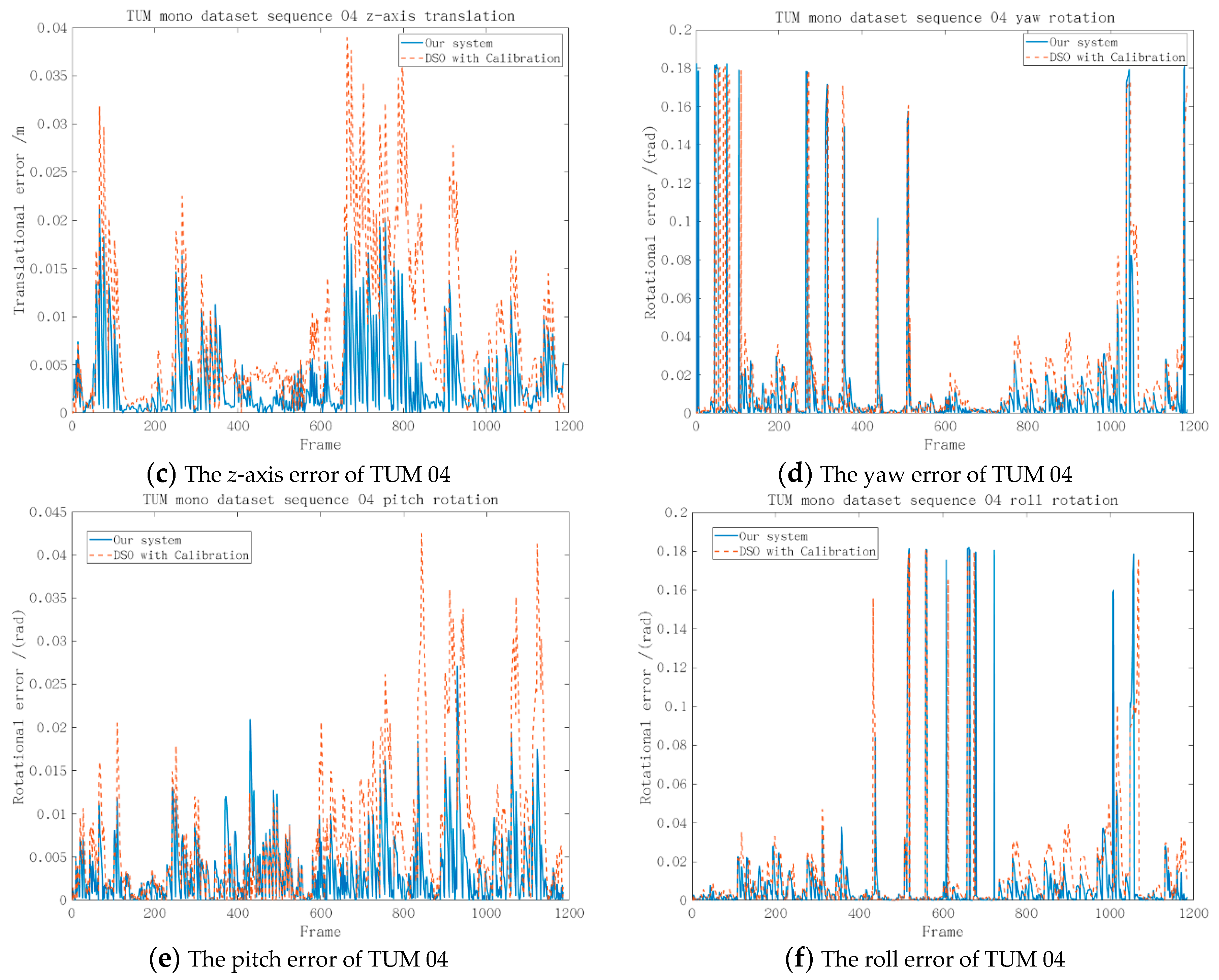
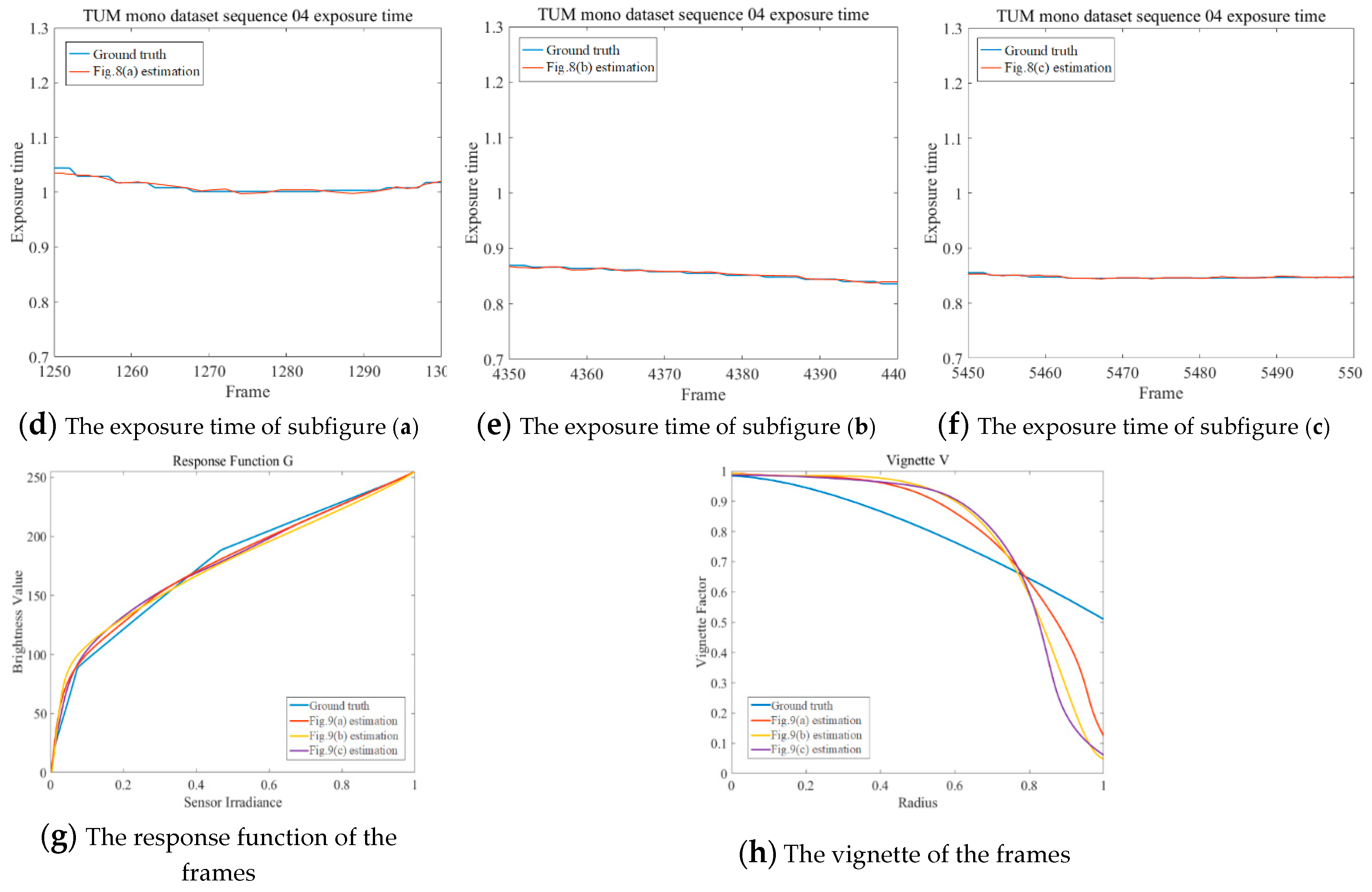
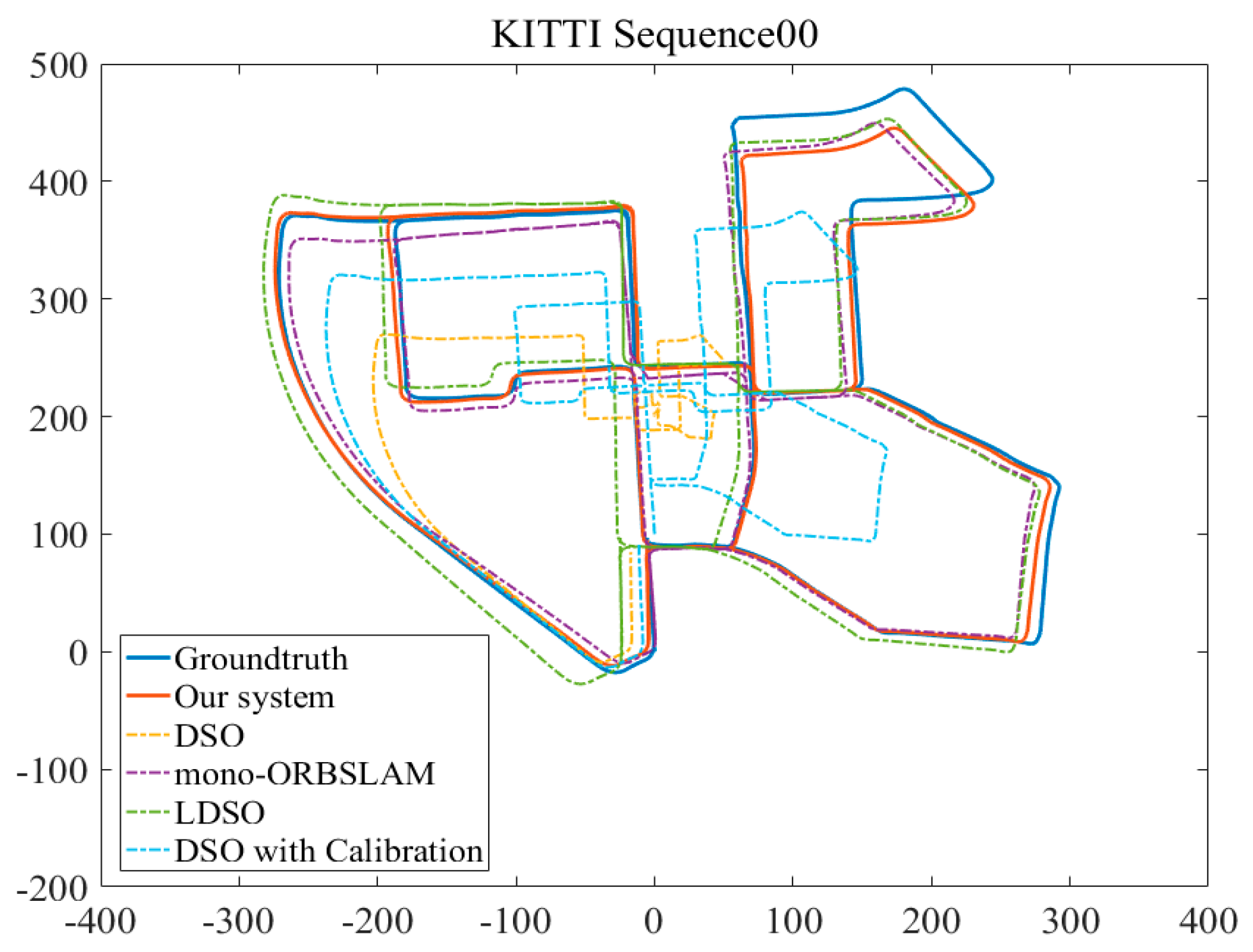
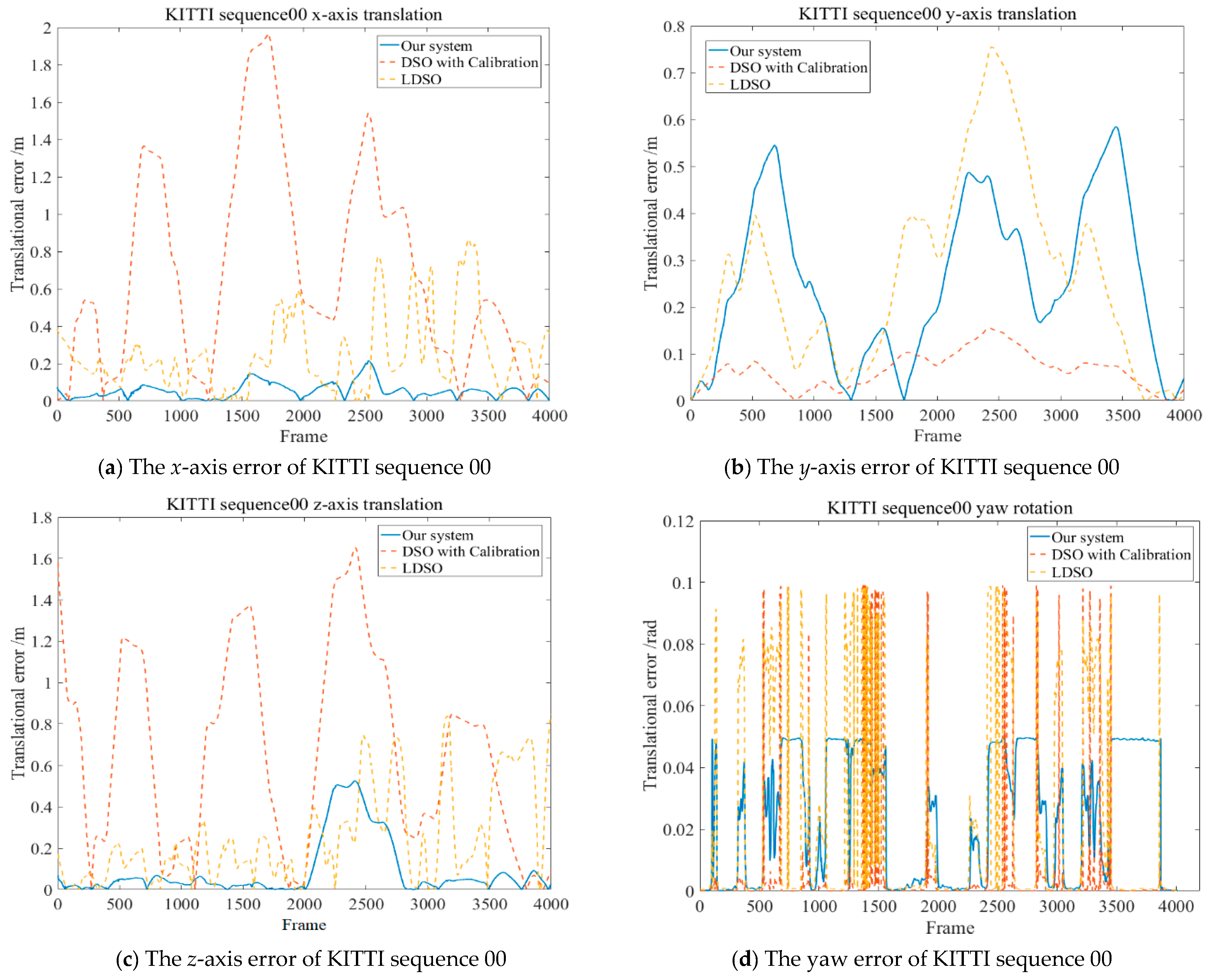
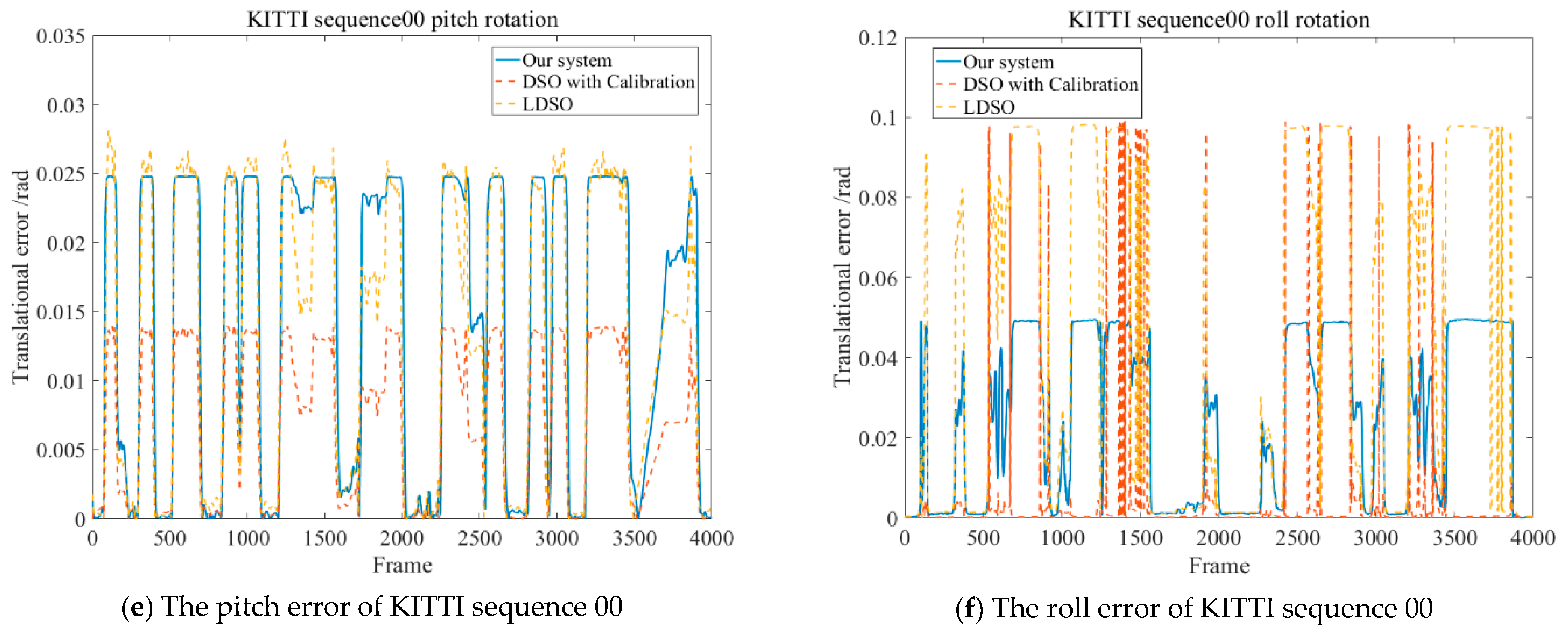
4.1. Experiments Based on Different Datasets
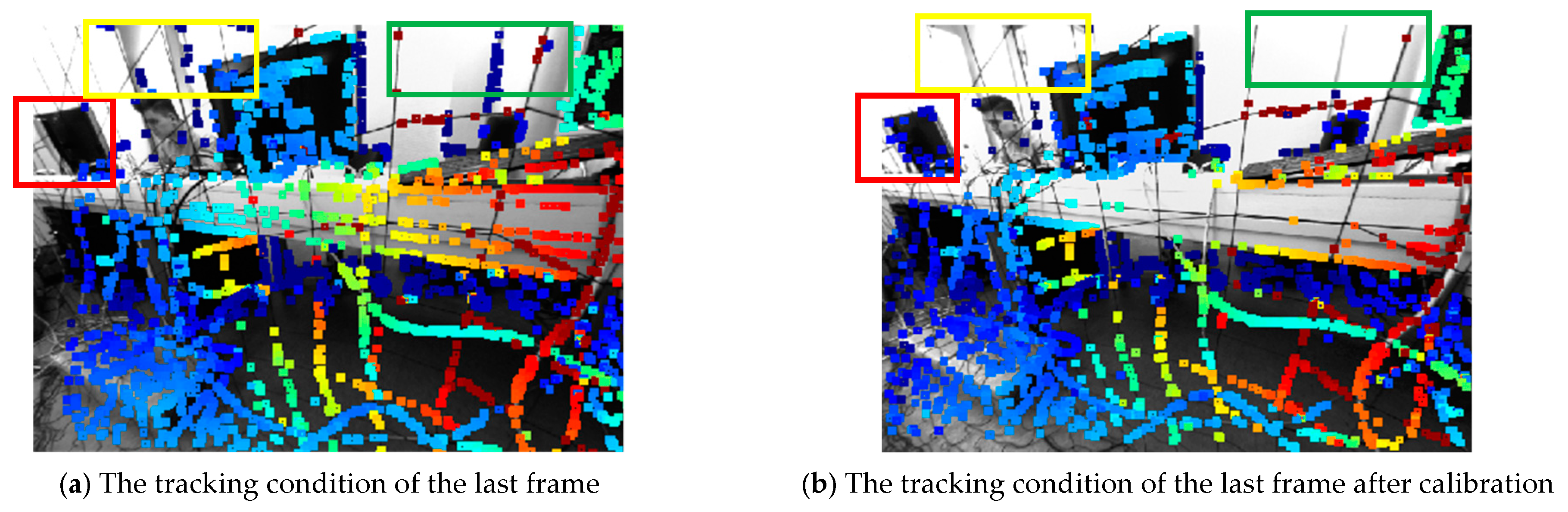
4.2. Actual Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Engel, J.; Usenko, V.; Cremers, D. A photometrically calibrated benchmark for monocular visual odometry. arXiv 2016, arXiv:1607.02555. [Google Scholar]
- Gostar, A.K.; Fu, C.; Chuah, W.; Hossain, M.I.; Tennakoon, R.; Bab-Hadiashar, A.; Hoseinnezhad, R. State Transition for Statistical SLAM Using Planar Features in 3D Point Clouds. Sensors 2019, 19, 1614. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wu, Z. RGB-D SLAM with Manhattan Frame Estimation Using Orientation Relevance. Sensors 2019, 19, 1050. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.B.; Wang, S.R.; Xu, C. Monocular semidirect visual odometry for large-scale outdoor localization. IEEE Access 2019, 7, 57927–57942. [Google Scholar]
- Jiang, L.; Zhao, P.; Dong, W.; Li, J.; Ai, M.; Wu, X.; Hu, Q. An Eight-Direction Scanning Detection Algorithm for the Mapping Robot Pathfinding in Unknown Indoor Environment. Sensors 2018, 18, 4254. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Civera, J. Loosely-Coupled Semi-Direct Monocular SLAM. IEEE Robot. Autom. Lett. 2019, 4, 399–406. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, T.; Liu, Y.; Yan, Q.R. Visual SLAM XIV: From Theory to Practice; Electronic Industry Press: Beijing, China, 2017; pp. 184–188, 203–204, 245–255. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. SVO: Semidirect Visual Odometry for Monocular and Multicamera Systems. IEEE Trans. Robot. 2017, 33, 249–265. [Google Scholar] [CrossRef]
- Kim, P.; Lim, H.; Jin, K.H. Robust visual odometry to irregular illumination changes with RGB-D camera. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 3688–3694. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef]
- Kim, C.; Kim, P.; Lee, S.; Kim, H.J. Edge-Based Robust RGB-D Visual Odometry Using 2-D Edge Divergence Minimization. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar]
- Bergmann, P.; Cremers, D.; Wang, R. Online Photometric Calibration of Auto Exposure Video for Realtime Visual Odometry and SLAM. IEEE Robot. Autom. Lett. 2018, 3, 627–634. [Google Scholar] [CrossRef]
- Schwörer, M.; Cremers, D.; Wang, R. Stereo DSO: Large-Scale Direct Sparse Visual Odometry with Stereo Cameras. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1–6. [Google Scholar]
- Yang, N.; Wang, R.; Stückler, J.; Cremers, D. Deep Virtual Stereo Odometry: Leveraging Deep Depth Prediction for Monocular Direct Sparse Odometry. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 835–852. [Google Scholar]
- Gao, X.; Wang, R.; Demmel, N.; Cremers, D. LDSO: Direct Sparse Odometry with Loop Closure. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2198–2204. [Google Scholar]
- Sloan, P.; Kautz, J.; Snyder, J. Precomputed radiance transfer for real-time rendering in dynamic, low-frequency lighting environments. ACM Trans. Graphy. 2017, 21, 527–536. [Google Scholar]
- Huo, Y.; Zhang, X. Single image-based HDR image generation with camera response function estimation. IET Image Process. 2017, 11, 1317–1324. [Google Scholar] [CrossRef]
- Dan, B.G.; Chen, J.H. Vignette and exposure calibration and compensation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2276–2288. [Google Scholar]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Forward-Backward Error: Automatic Detection of Tracking Failures. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 1–4. [Google Scholar]
- Park, S.; Pollefeys, M.; Schops, T. Illumination change robustness in direct visual SLAM. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4523–4530. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.; Tardós, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2017, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Wu, Y.X.; Wang, C.; Xian, Y.X. SLAM based on sparse direct method and graph optimization for mobile robot. Chin. J. Sci. Instrum. 2018, 39, 257–263. [Google Scholar]
- Zhou, S.-C.; Yan, R.; Li, J.-X.; Chen, Y.-K.; Tang, H. A brain-inspired SLAM system based on ORB features. Int. J. Autom. Comput. 2017, 14, 564–575. [Google Scholar] [CrossRef]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.W.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 1157–1163. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, H.; Cho, S. Bag-of-concepts: Comprehending document representation through clustering words in distributed representation. Neurocomputing 2017, 266, 336–352. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1–8. [Google Scholar]





| Sequence | DSO [17] | LDSO [17] | ORBSLAM [17] | Our System |
|---|---|---|---|---|
| 00 | 126.7 | 9.322 | 8.27 | 7.48 |
| 01 | 165.03 | 11.68 | - | 20.15 |
| 02 | 138.7 | 31.98 | 26.86 | 12.14 |
| 03 | 4.77 | 2.85 | 1.21 | 2.04 |
| 04 | 1.08 | 1.22 | 0.77 | 0.13 |
| 05 | 49.85 | 5.1 | 7.91 | 5.09 |
| 06 | 113.57 | 13.552 | 12.54 | 11.08 |
| 07 | 27.99 | 2.96 | 3.44 | 0.56 |
| 08 | 120.17 | 129.02 | 46.81 | 105.4 |
| 09 | 74.29 | 21.64 | 76.54 | 26.90 |
| 10 | 16.32 | 17.36 | 6.61 | 17.45 |
| System | Sections | Time |
|---|---|---|
| LDSO | Total | 894.43ms |
| Our system | Filtering and tracking feature | 40.21 ms |
| Exposure time estimation | 3.24 ms | |
| Parameters v and c update | 193.15 ms | |
| Input frame I optimization | 135.23 ms | |
| Back-end | 564.51 ms | |
| Total | 936.34 ms |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Yuan, X.; Zhang, C.; Song, Y.; Liu, C.; Li, Z. Real-Time Photometric Calibrated Monocular Direct Visual SLAM. Sensors 2019, 19, 3604. https://doi.org/10.3390/s19163604
Liu P, Yuan X, Zhang C, Song Y, Liu C, Li Z. Real-Time Photometric Calibrated Monocular Direct Visual SLAM. Sensors. 2019; 19(16):3604. https://doi.org/10.3390/s19163604
Chicago/Turabian StyleLiu, Peixin, Xianfeng Yuan, Chengjin Zhang, Yong Song, Chuanzheng Liu, and Ziyan Li. 2019. "Real-Time Photometric Calibrated Monocular Direct Visual SLAM" Sensors 19, no. 16: 3604. https://doi.org/10.3390/s19163604
APA StyleLiu, P., Yuan, X., Zhang, C., Song, Y., Liu, C., & Li, Z. (2019). Real-Time Photometric Calibrated Monocular Direct Visual SLAM. Sensors, 19(16), 3604. https://doi.org/10.3390/s19163604





