Maize Silage Kernel Fragment Estimation Using Deep Learning-Based Object Recognition in Non-Separated Kernel/Stover RGB Images
Abstract
1. Introduction
2. Materials and Methods
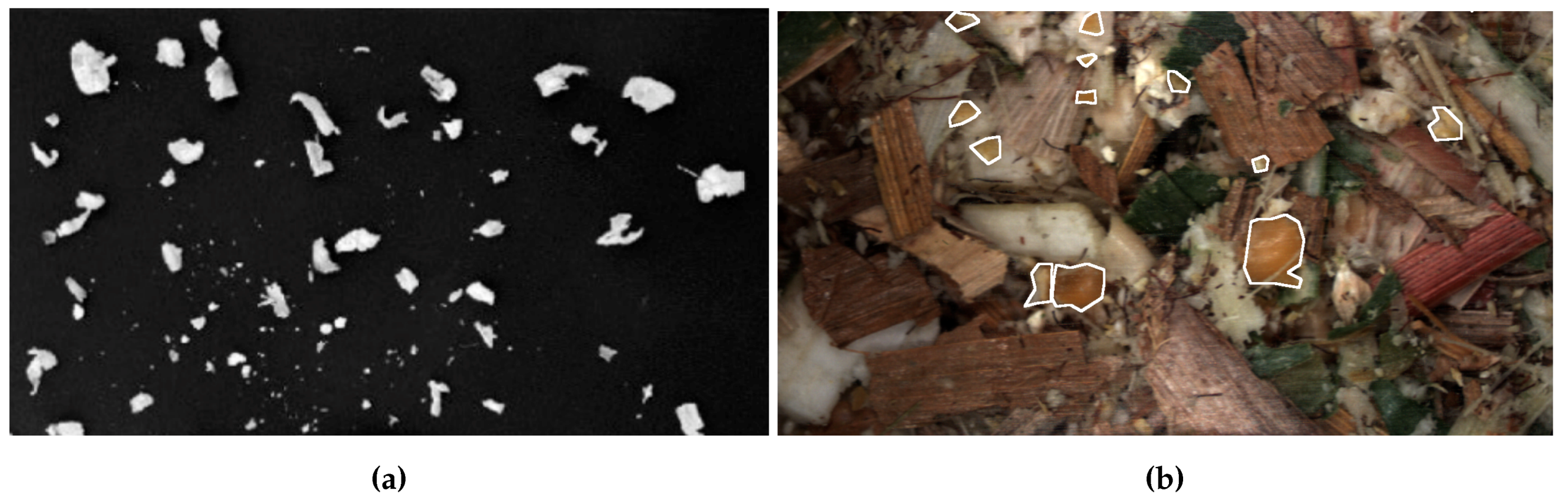
2.1. Images
2.2. Datasets
2.3. Deep Learning Models
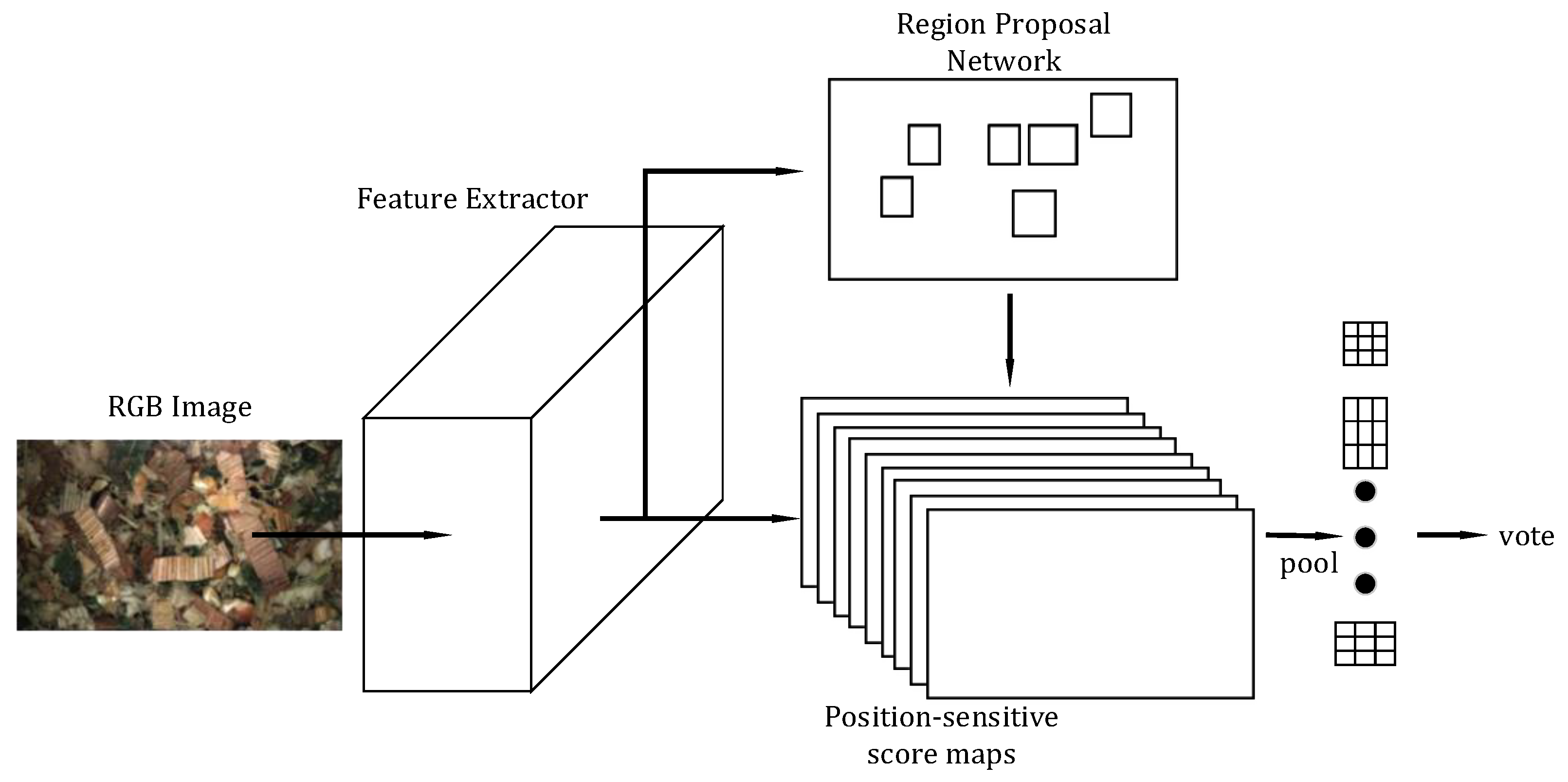
2.3.1. Region-Based Fully Convolutional Networks (R-FCN)
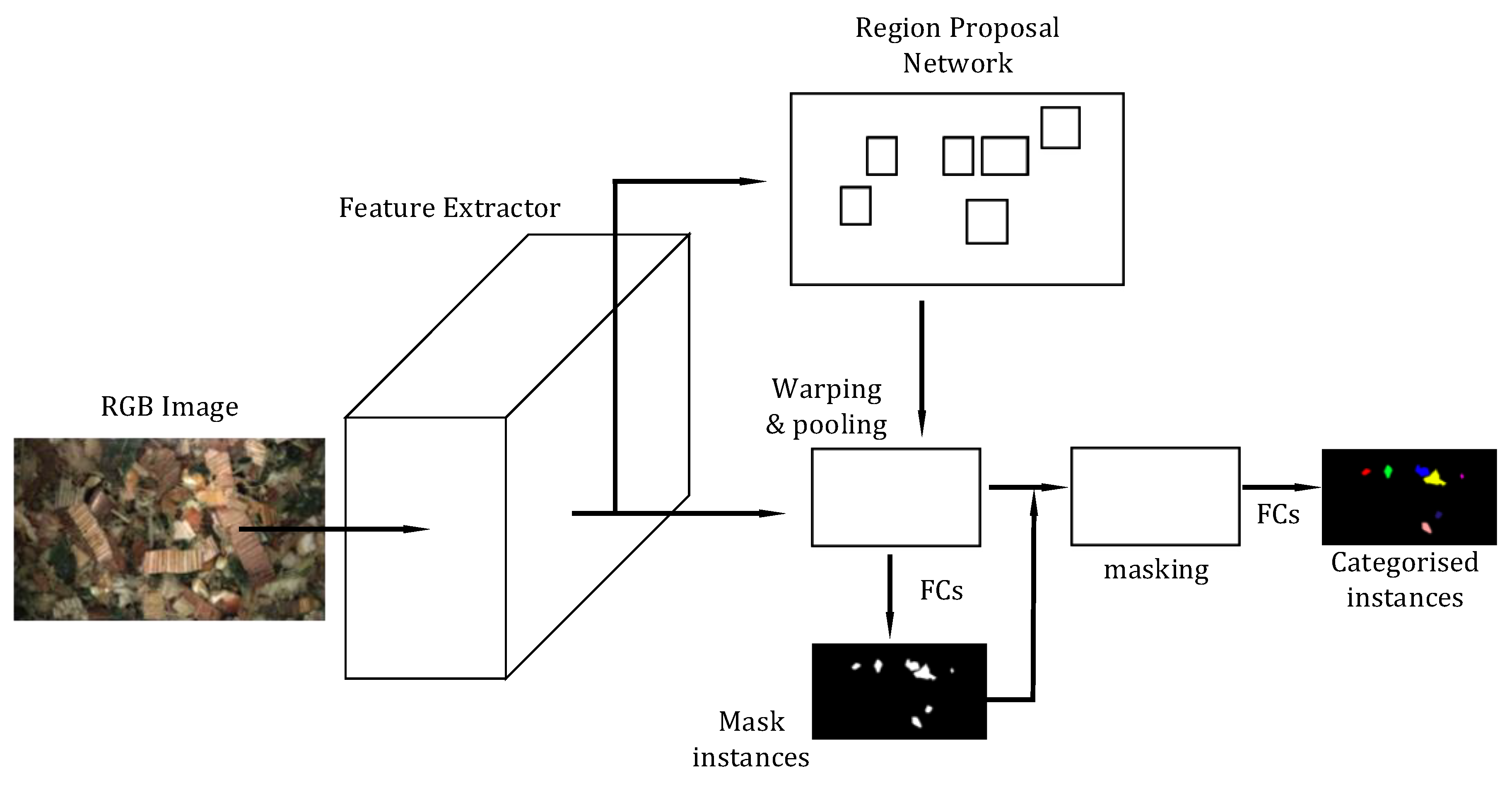
2.3.2. Instance-Aware Semantic Segmentation via Multi-Task Network Cascades (MNC)
2.4. Hardware
2.5. Computer Vision Metrics
3. Results
3.1. Computer Vision Results
3.2. Kernel Processing
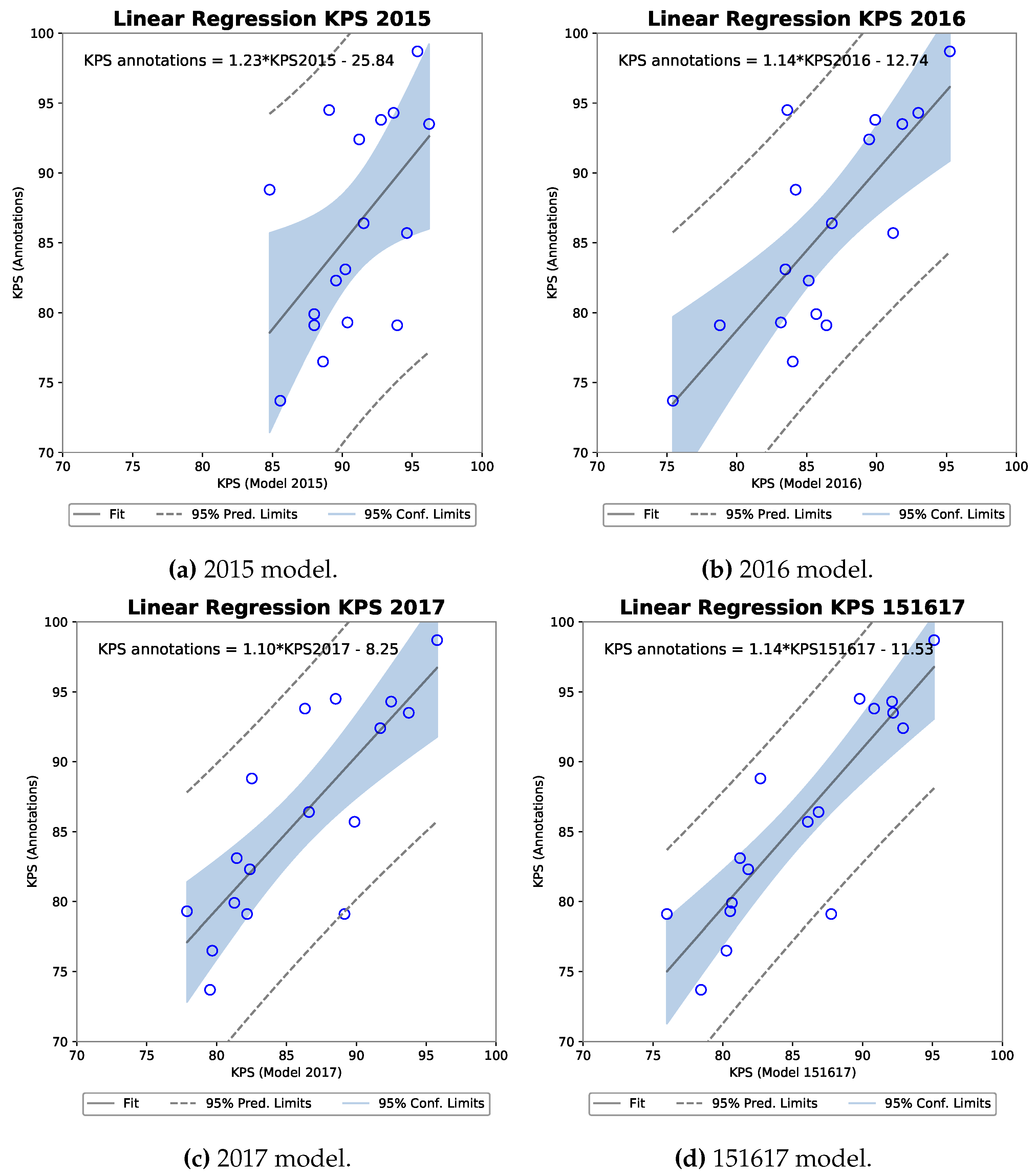
3.3. Correlation Analysis
3.3.1. R-FCN
3.3.2. MNC
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| RGB | Red, Green, and Blue |
| PG | Processor Gap |
| CSPS | Corn Silage Processing Score |
| PSPS | Penn State Particle Separator |
| CNN | Convolutional Neural Network |
| CL | Cutting Length |
| R-FCN | Region-based Fully Convolutional Network |
| MNC | Multi-task Network Cascades |
| FCN | Fully Convolutional Network |
| RoI | Region of Interest |
| RPN | Region Proposal Network |
| SGD | Stochastic Gradient Descent |
| FC | Fully-Connected |
| GPU | Graphics Processing Unit |
| KPS | Kernel Processing Score |
| IoU | Intersection-over-Union |
| AP | Average Precision |
References
- Johnson, L.M.; Harrison, J.H.; Davidson, D.; Mahanna, W.C.; Shinners, K. Corn Silage Mangement: Effects of Hybrid, Chop Length, and Mechanical Processing on Digestion and Energy Content. J. Dairy Sci. 2003, 86, 208–231. [Google Scholar] [CrossRef]
- Marsh, B.A. Comparison of Fuel Usage and Harvest Capacity in Self-propelled Forage Harvesters. World Acad. Sci. Eng. Technol. 2013, 7, 649–654. [Google Scholar]
- Mertens, D.R. Particle size, fragmentation index, and effective fiber: Tools for evaluating the physical attributes of corn silages. In Proceedings of the Four-State Dairy Nutrition and Management Conference, Dubuque, IA, USA, 15 June 2005; pp. 211–220. [Google Scholar]
- Heinrichs, J. The Penn State Particle Separator. Penn State Extension. 2013. Available online: https://extension.psu.edu/penn-state-particle-separator (accessed on 24 July 2018).
- Shinners, K.J.; Holmes, B.J. Making Sure Your Kernel Processor Is Doing Its Job. Focus Forage 2014, 15, 1–3. [Google Scholar]
- Drewry, J.L.; Luck, B.D.; Willett, R.M.; Rocha, E.M.C.; Harmon, J.D. Predicting kernel processing score of harvested and processed corn silage via image processing techniques. Comput. Electron. Agric. 2019, 160, 144–152. [Google Scholar] [CrossRef]
- Kaur, H.; Singh, B. Classification and grading rice using multi-class SVM. Int. J. Sci. Res. 2013, 3, 1–5. [Google Scholar]
- Aggarwal, A.K.; Mohan, R. Aspect ratio analysis using image processing for rice grain quality. Int. J. Food Eng. 2010, 5. [Google Scholar] [CrossRef]
- Antonucci, F.; Figorilli, S.; Costa, C.; Pallottino, F.; Spanu, A.; Menesatti, P. An Open Source Conveyor Belt Prototype for Image Analysis-Based Rice Yield Determination. Food Bioprocess Technol. 2017, 10, 1257–1264. [Google Scholar] [CrossRef]
- Van Dalen, G. Determination of the size distribution and percentage of broken kernels of rice using flatbed scanning and image analysis. Food Res. Int. 2004, 37, 51–58. [Google Scholar] [CrossRef]
- Dubosclard, P.; Larnier, S.; Konik, H.; Herbulot, A.; Devy, M. Automatic visual grading of grain products by machine vision. J. Electron. Imaging 2015, 24, 1–13. [Google Scholar] [CrossRef]
- Visen, N.S.; Paliwal, J.; Jayas, D.S.; White, N.D.G. Image analysis of bulk grain samples using neural networks. Can. Biosyst. Eng. 2004, 46, 11–15. [Google Scholar]
- Anami, B.S.; Savakar, D. Effect of foreign bodies on recognition and classification of bulk food grains image samples. J. Appl. Comput. Sci. 2009, 6, 77–83. [Google Scholar]
- Lee, C.Y.; Yan, L.; Wang, T.; Lee, S.R.; Park, C.W. Intelligent classification methods of grain kernels using computer vision analysis. Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef]
- Guevara-Hernandez, F.; Gomez-Gil, J. A machine vision system for classification of wheat and barley grain kernels. Spanish. J. Agr. Res. 2011, 9, 672–680. [Google Scholar] [CrossRef]
- Patil, N.K.; Malemath, V.S.; Yadahalli, R.M. Color and texture based identification and classification of food grains using different color models and haralick features. Int. J. Comput. Sci. Eng. 2011, 3, 3669. [Google Scholar]
- Miao, A.; Zhuang, J.; Tang, Y.; He, Y.; Chu, X.; Luo, S. Hyperspectral Image-Based Variety Classification of Waxy Maize Seeds by the t-SNE Model and Procrustes Analysis. Sensors 2018, 18, 2022. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Skovsen, S.; Dyrmann, M.; Mortensen, A.K.; Steen, K.A.; Green, O.; Eriksen, J.; Gislum, R.; Jørgensen, R.N. Estimation of the Botanical Composition of Clover-Grass Leys from RGB Images Using Data Simulation and Fully Convolutional Neural Networks. Sensors 2017, 17, 2930. [Google Scholar] [CrossRef]
- Fuentes, A.; Yoon, S.; Kim, S.C.; Park, D.S. A Robust Deep-Learning-Based Detector for Real-Time Tomato Plant Diseases and Pests Recognition. Sensors 2017, 17, 2022. [Google Scholar] [CrossRef]
- Hall, D.; McCool, C.; Dayoub, F.; Sunderhauf, N.; Upcroft, B. Evaluation of Features for Leaf Classification in Challenging Conditions. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Waikola, HI, USA, 5–9 January 2015; pp. 797–804. [Google Scholar]
- Mohanty, S.P.; Hughes, D.P.; Marcel, S. Using Deep Learning for Image-based Plant Disease Detection. Front. Plant Sci. 2016, 7, 1419. [Google Scholar] [CrossRef]
- Milioto, A.; Lottes, P.; Stachniss, C. Real-time Blob-wise Sugar Beets vs Weeds Classification for Monitoring Fields using Convolutional Neural Networks. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2017, V-2/W3, 41–48. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Dai, J.; He, K.; Sun, J. R-FCN: Object Detection via Region-based Fully Convolutional Networks. In Proceedings of the Conference on Neural Information Processing (NIPS), Barcelona, Spain, 4–9 December 2016; pp. 379–387. [Google Scholar]
- Dai, J.; He, K.; Sun, J. Instance-Aware Semantic Segmentation via Multi-task Network Cascades. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Las Vegas, NV, USA, 26 June 2016; pp. 3150–3158. [Google Scholar]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The PASCAL Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Lin, T.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Computer Vision—ECCV 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Ren, S.; He, K.; Girschick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the NIPS’15 Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556v6. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Las Vegas, NV, USA, 26 June 2016; pp. 770–778. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girschick, R.; Guadarrama, S.; Darrel, T. Caffe: Convolutional Architecture for Fast Feature Embedding. arXiv 2014, arXiv:1408.5093. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 2013. [Google Scholar]






| 2015 | 2016 | 2017 | 151617 | |
|---|---|---|---|---|
| Train Images | 111 | 115 | 1167 | 1393 |
| Train Kernel Instances | 1388 | 675 | 4844 | 6907 |
| Test Images | 76 | 85 | 884 | 1045 |
| Test Kernel Instances | 836 | 433 | 3425 | 4694 |
| Train Memory (MB) | Test Memory (MB) | Inference Time per Image (s) | |
|---|---|---|---|
| R-FCN (ResNet-101) | 6877 | 3251 | 0.101 |
| MNC (AlexNet) | 3439 | 2369 | 0.087 |
| R-FCN | MNC | |||||||
|---|---|---|---|---|---|---|---|---|
| Train Dataset | AP | Prec | Recall | F1-Score | AP | Prec | Recall | F1-Score |
| 2015 Test | ||||||||
| 2015 | 34.0 | 55.5 | 53.0 | 54.2 | 27.7 | 44.5 | 31.8 | 37.1 |
| 2016 | 19.0 | 80.0 | 21.0 | 33.3 | 16.8 | 60.5 | 16.5 | 25.9 |
| 2017 | 28.5 | 51.1 | 40.2 | 45.0 | 27.7 | 50.0 | 32.1 | 39.1 |
| 151617 | 65.9 | 70.0 | 76.0 | 73.9 | 40.4 | 50.3 | 46.3 | 48.2 |
| 2016 Test | ||||||||
| 2015 | 25.3 | 23.3 | 87.1 | 36.8 | 40.7 | 30.1 | 61.0 | 40.3 |
| 2016 | 41.8 | 52.1 | 73.2 | 60.9 | 52.1 | 54.4 | 62.8 | 58.3 |
| 2017 | 34.2 | 41.7 | 63.1 | 50.2 | 53.0 | 45.7 | 67.9 | 54.6 |
| 151617 | 66.9 | 56.9 | 90.8 | 70.0 | 71.8 | 47.6 | 80.8 | 59.9 |
| 2017 Test | ||||||||
| 2015 | 15.3 | 19.0 | 70.5 | 29.9 | 18.6 | 20.2 | 36.4 | 25.8 |
| 2016 | 19.2 | 43.4 | 44.1 | 43.7 | 24.3 | 39.8 | 32.8 | 36.0 |
| 2017 | 31.0 | 36.4 | 66.9 | 47.2 | 36.3 | 32.9 | 53.3 | 40.7 |
| 151617 | 33.4 | 37.6 | 67.2 | 48.2 | 35.9 | 31.9 | 53.7 | 40.0 |
| 151617 Test | ||||||||
| 2015 | 19.6 | 23.4 | 73.6 | 35.6 | 26.1 | 26.2 | 42.9 | 32.5 |
| 2016 | 22.3 | 50.1 | 44.7 | 47.2 | 28.4 | 46.7 | 34.2 | 39.5 |
| 2017 | 30.2 | 39.2 | 62.5 | 48.2 | 35.8 | 36.0 | 51.0 | 42.2 |
| 151617 | 34.0 | 40.7 | 66.0 | 50.4 | 36.1 | 34.2 | 52.2 | 41.4 |
| %(<4.75 mm) | 2015 | 2016 | 2017 | 151617 | |||||
|---|---|---|---|---|---|---|---|---|---|
| PG | R-FCN | MNC | R-FCN | MNC | R-FCN | MNC | R-FCN | MNC | Annotation |
| 1 | 96.2 | 97.7 | 91.8 | 94.7 | 93.8 | 95.5 | 92.2 | 97.3 | 93.5 |
| 1 | 95.4 | 95.4 | 95.2 | 96.1 | 95.8 | 98.8 | 95.1 | 97.7 | 98.7 |
| 1 | 88.0 | 76.4 | 85.7 | 86.5 | 81.3 | 87.2 | 80.7 | 88.9 | 79.9 |
| 1 | 93.7 | 94.8 | 93.0 | 91.1 | 92.5 | 95.7 | 92.1 | 96.1 | 94.3 |
| 2 | 93.9 | 94.8 | 78.8 | 75.2 | 89.2 | 95.8 | 87.8 | 97.3 | 79.1 |
| 2 | 92.8 | 97.7 | 89.9 | 92.6 | 86.3 | 95.7 | 90.8 | 95.7 | 93.8 |
| 2 | 84.8 | 71.5 | 84.2 | 100.0 | 82.5 | 85.8 | 82.7 | 87.7 | 88.8 |
| 2 | 88.0 | 86.1 | 86.4 | 85.6 | 82.2 | 90.6 | 76.0 | 92.6 | 79.1 |
| 3 | 89.6 | 80.7 | 85.1 | 83.5 | 82.4 | 89.3 | 81.8 | 90.4 | 82.3 |
| 3 | 94.6 | 95.2 | 91.2 | 95.7 | 89.9 | 94.1 | 86.1 | 93.8 | 85.7 |
| 3 | 90.4 | 85.9 | 83.2 | 83.1 | 77.9 | 90.3 | 80.5 | 90.0 | 79.3 |
| 3 | 89.1 | 86.3 | 83.6 | 84.5 | 88.5 | 93.0 | 89.8 | 91.8 | 94.5 |
| 3.5 | 90.2 | 80.8 | 83.5 | 88.0 | 81.4 | 89.5 | 81.2 | 91.2 | 83.1 |
| 3.5 | 88.6 | 75.5 | 84.0 | 81.6 | 79.7 | 89.0 | 80.3 | 90.2 | 76.6 |
| 3.5 | 91.2 | 93.0 | 89.5 | 92.6 | 91.7 | 93.2 | 92.9 | 94.6 | 92.4 |
| 3.5 | 85.6 | 75.9 | 75.4 | 72.5 | 79.5 | 84.7 | 78.4 | 86.1 | 73.7 |
| 3.5 | 91.5 | 89.8 | 86.8 | 91.3 | 86.6 | 91.5 | 86.9 | 92.9 | 86.4 |
| Avg. abs. error | 6.7 | 5.3 | 3.8 | 4.6 | 3.3 | 6.3 | 2.7 | 7.2 |
| Shapiro-Wilk | Pearson’s Correlation | ||||
|---|---|---|---|---|---|
| KPS | W | p-value | r(15) | p-value | (%) |
| Annotations | 0.94 | 0.32 | NA | NA | NA |
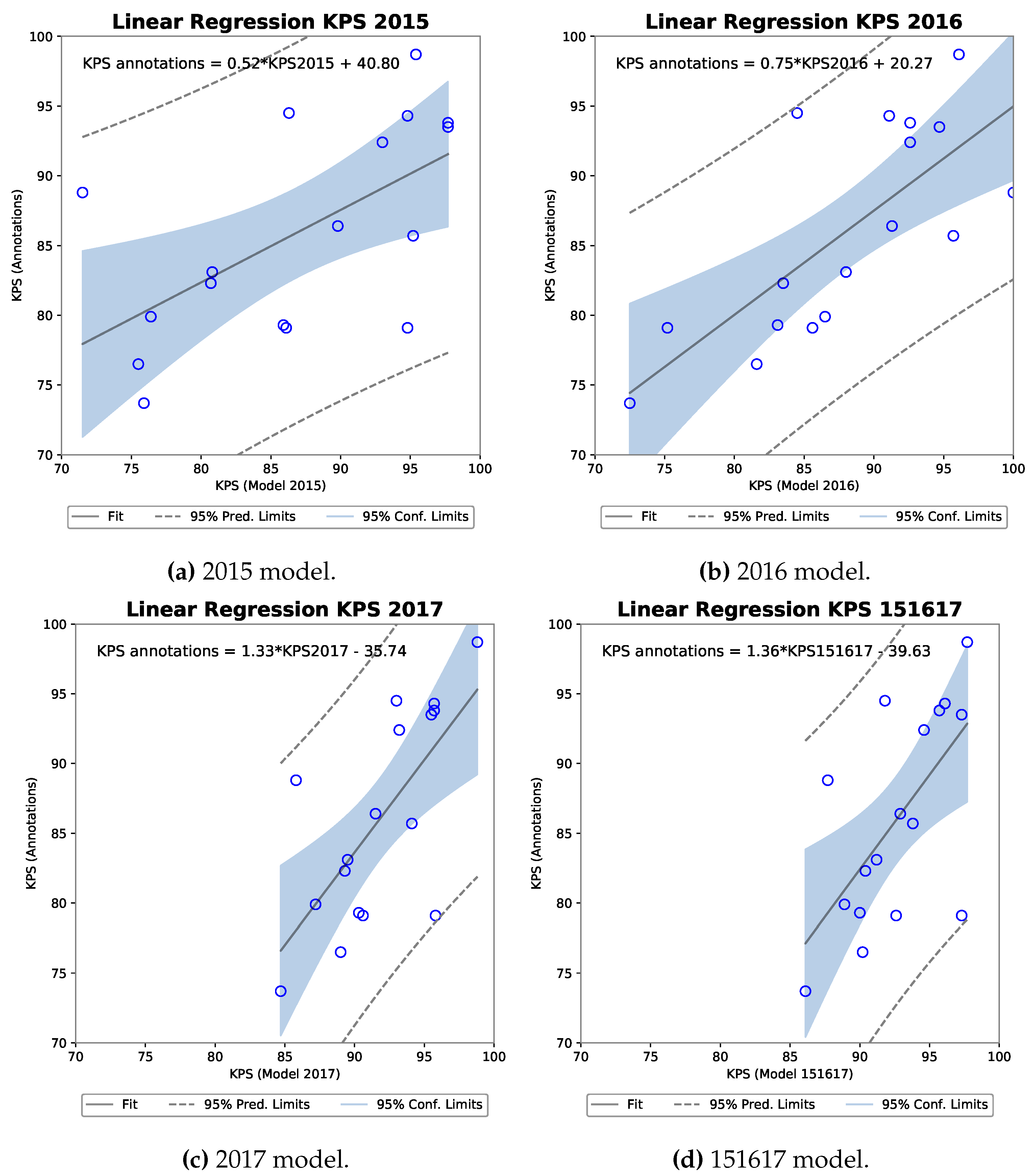
| 2015 | 0.973 | 0.870 | 0.54 | 0.0244 | 29.4 |
| 2016 | 0.97 | 0.816 | 0.77 | 0.0003 | 59.5 |
| 2017 | 0.94 | 0.320 | 0.81 | 0.00009 | 65.1 |
| 151617 | 0.94 | 0.327 | 0.88 | 0.000003 | 77.7 |
| Shapiro-Wilk | Pearson’s Correlation | ||||
|---|---|---|---|---|---|
| KPS | W | p-Value | r(15) | p-Value | (%) |
| Annotations | 0.94 | 0.32 | |||
| 2015 | 0.91 | 0.098 | 0.60 | 0.0106 | 36.2 |
| 2016 | 0.97 | 0.743 | 0.74 | 0.0007 | 54.4 |
| 2017 | 0.97 | 0.806 | 0.69 | 0.002 | 48.1 |
| 151617 | 0.97 | 0.666 | 0.63 | 0.0065 | 39.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasmussen, C.B.; Moeslund, T.B. Maize Silage Kernel Fragment Estimation Using Deep Learning-Based Object Recognition in Non-Separated Kernel/Stover RGB Images. Sensors 2019, 19, 3506. https://doi.org/10.3390/s19163506
Rasmussen CB, Moeslund TB. Maize Silage Kernel Fragment Estimation Using Deep Learning-Based Object Recognition in Non-Separated Kernel/Stover RGB Images. Sensors. 2019; 19(16):3506. https://doi.org/10.3390/s19163506
Chicago/Turabian StyleRasmussen, Christoffer Bøgelund, and Thomas B. Moeslund. 2019. "Maize Silage Kernel Fragment Estimation Using Deep Learning-Based Object Recognition in Non-Separated Kernel/Stover RGB Images" Sensors 19, no. 16: 3506. https://doi.org/10.3390/s19163506
APA StyleRasmussen, C. B., & Moeslund, T. B. (2019). Maize Silage Kernel Fragment Estimation Using Deep Learning-Based Object Recognition in Non-Separated Kernel/Stover RGB Images. Sensors, 19(16), 3506. https://doi.org/10.3390/s19163506






