1. Introduction
Recently, the studies of transport dynamics in complex systems which exhibit the subdiffusion property have attracted increasing attention. Typical examples include the water in membranes for fuel cells [
1], charge transport in amorphous semiconductors [
2] or heating processes of the heterogeneous rod [
3]. It is worth mentioning that the mean squared displacement of subdiffusion process is a power-law function of fractional exponent, which is smaller than that of the Gaussian diffusion process [
4,
5]. Due to the strong interactions between components in these processes, a rather complex dynamical behavior would emerge. Note that a fractional order derivative itself is a kind of convolution and naturally links to subdiffusion processes, time fractional diffusion system is confirmed in [
5,
6,
7,
8] to be used to efficiently describe these subdiffusion processes. Then, some model-based investigations are needed to deal with their rather complex dynamical behaviors.
Source seeking is a fundamental issue in nature and, currently, different approaches have been developed to study it for the non-fractional diffusion systems (see monographs [
9,
10] and the survey [
11] for example). This is motivated by the fact that, in some practical applications, such as the pollution problems, the danger may increase if the source remains unknown [
12]. However, from a practical point of view, engineers are more interested in the sensing problem that, if a source is detectable, how can it be identified based on a limited number of sensor measurements. Then, in this paper, we consider this source sensing problem for the subdiffusion processes governed by time fractional diffusion systems.
Motivated by these above considerations, in this paper, we deal with the following time fractional diffusion systems with a Riemann–Liouville fractional order derivative:
where
is an open bounded subset with a smooth boundary
,
and
represent the Riemann–Liouville fractional order derivative and integral, respectively. Here,
denotes the unknown source to be specified later and
A is the infinitesimal generator of a strongly continuous semigroup
in
. It is supposed that
is a self-adjoint uniformly elliptic operator and, in addition,
, where
V is a Hilbert space such that
with continuous injections (
is the dual of
V).
It is worth noting that, although the initial condition for Riemann–Liouville type time fractional diffusion system does not take the same form as that of non-fractional differential equations, expressions like
in system (1) make sense. The reason is that it does not require a direct experimental evaluation of these fractional integrals. Instead, one can get it by measuring the initial values of its “inseparable twin”, which is obtained based on some basic physical law for the particular field of science. That is, the physical meaning for the Riemann–Liouville fractional integral of a function is equivalent to the initial value of its “inseparable twin”. For example, in the fractional Voigt model (a spring and a spring-pot in parallel) of viscoelasticity, the physical meaning of a Riemann–Liouville fractional integral of the unknown strain
is in fact identical to the initial condition of its “inseparable twin”—the stress [
13]. This is also consistent with the known fact that the spring in the Voigt model only affects long-term behavior. For more “inseparable twins”, we refer the reader to e.g., monographs [
14,
15] for more information on the pair of current and voltage in electrical circuits or the pair of temperature difference and heat flux in heat conduction, etc.
The applications of system (1) are rich in the real world. As stated in [
16], system (1) is usually used to describe the dynamic process in spatially inhomogeneous environments. Typical examples include the flow through porous media with a source or sensing the source of groundwater flow, etc. The corresponding sensing techniques cited in this paper can also be used to enable more complex tasks such as landmine clearing, the disease spreading control in agriculture lands or the crowd evacuation in the case of emergencies.
Let the limited number of sensor measurements be given by
where
depends on the structure of sensors and
Z is a Hilbert space. Then, the source sensing problem can be stated as follows:
Given the measurements
, find a source
S such that the solution of system (1) satisfies
Several questions arise in such problems: can the available measurements
z uniquely determine
S? If so, how does
S depend on
z and is there an approach to determine it (sensing)?
In the past two decades, several numerical algorithm approaches have been proposed for the source sensing problem of non-fractional diffusion systems. In [
17], fast algorithms to solve the source sensing problem for elliptic partial differential equations (PDEs) were presented, in which the solution was approximated by using the Fourier–Galerkin truncated method. By using the multidimensional frequency estimation techniques, a new framework for solving the source sensing problems for systems governed by linear PDEs was presented in [
18,
19]. In addition, if the source is assumed to be a sum of a finite number of Dirac delta functions at unknown locations, numerical algorithms for the source identification problem of linear heat equations and time-dependent advection-diffusion systems with a nonlinear reaction were considered in [
20,
21], respectively. For an overview of the optimisation approaches for pollution source sensing in groundwater, we refer the reader to [
22] and the references cited therein, although it was confirmed in [
23,
24] that the transport phenomena under the ground should be a subdiffusion process governed by time fractional diffusion systems.
However, the investigations for the source sensing problem of time fractional diffusion systems are still very limited. This is due to the fact that there is a need for further studies on the optimization variant theory and gradient theory of fractional order systems. As a result, the above optimisation numerical methods seem to be inapplicable for system (1). Furthermore, a source detection method has been proposed by El Jai and Afifi [
25], in which the source is characterized by three parameters according to its properties. Here, we adopt these concepts and introduce the notion of regional detection of unknown sources, where we are interested in the sensing of unknown source only in a subregion of the whole domain. As it will be shown, the idea of regional detection can surely save energy resources. In addition, it is easier to be implemented even for some cases where we have a possibility to detect it in the whole domain.
After the introduction, the mathematical concepts of source and detection are given in the next section. The third section is focused on the regional strategic sensors, regional spy sensors and their relationships. In
Section 4, an approach on solving the source sensing problem is presented. Two applications are worked out in the end.
2. Preliminary Results
The purpose of this section is to introduce the notions of sources, detection and some basic results to be used thereafter.
2.1. Sources
Let . The definition of a source S is as follows:
Definition 1. [25] A source S is characterized by a triplet , where - 1.
represents the support of source that varies in time t;
- 2.
defines the intensity of source in x at time t;
- 3.
denotes the support of g and represents the life duration of source
Here, the support , which describes the moving trajectory of the source, is usually determined by the evolution of some dynamic systems. With this, S is said to be a
moving pointwise source if is reduced to a single point of for all ;
moving zone source if is reduced to a region of for all ;
boundary source if , and, in this case, we can define the similar pointwise/zone boundary sources;
fixed source if is independent of t, which may be pointwise, zone or boundary.
In addition, it is worth noting that, when discussing the sensing problem, the pointwise fixed source defined as , is always used. In this case, is independent of t, which is used to describe a single point of .
2.2. Regional Detection
Since the detection of a source can be done by neglecting its life duration, we consider the source as a couple
. Let the set of such sources be
. One has
Here,
represents the set of parts of
and
denotes the space of functions
. With this,
can be a vector space with convenient scalar product operations.
Definition 2. A source S is said to be detectable on I if the knowledge of system (1)
, together with the output function (2)
, is sufficient to guarantee that the operatoris injective. However, in many cases, it is impossible or too costly to reconstruct all parameters of a source. Let be a non-empty, not necessarily connected subregion of In what follows, we introduce the concepts of regional detection.
Assume that the source is located in
such that
Considering the subspace
and defining the operator
we obtain the following definition.
Definition 3. A source S is called to be detectable on I if (1), (2) is sufficient to ensure that is injective.
Note that a source, which is detectable, is called to be detectable if
2.3. Some Basic Results
To obtain our results, in this part, we present some basic results on fractional calculus.
Definition 4 ([
26])
. The Riemann–Liouville fractional integral of order for a function y is given bywhere represents the Euler gamma function defined by and the right side is pointwise defined on . Definition 5 ([
26])
. The Riemann–Liouville fractional derivative of order for a function y is defined asprovided that the right side is pointwise defined on . Consider system (1); without loss of generality, suppose that and when .
Let
be the Laplace transforms of functions
y and
S. Based on
system (1) is equivalent to
which yields
Then, if there exists a function
such that its Laplace transform is
let
, El-Borai has shown in [
27,
28] that the unique solution of system (1) satisfies
Here,
can, for example, be [
29],
In addition, for the sake of simplicity, let
Equation (13) yields that
For more knowledge on the expression of solutions to system (1), we refer the reader to [
7,
30,
31] and the references cited therein.
4. Source Sensing Approach
In this section, we show how to identify the source under the hypothesis that are spy sensors.
Theorem 3. If are spy sensors, then the source in system (1) can be uniquely identified by the observation z as the unique solution of the following equationThat is, given any , the equality could imply . Proof. Let
be the solution of system
Then, the difference
satisfies
In what follows, we divide the proof into three steps.
Step 1, we consider the following semi-norm
and show that
defines a norm for the space
. For this, we only need to prove that any
with
could yield
[
36]. Indeed, by Definitions 3 and 8, since
are
spy sensors, we get that
is injective, i.e.,
could imply
. With this, we conclude that
is a Hilbert space endowed with the norm
and the inner product
Step 2, we prove that the operator
given by
is an isomorphism from space
into its dual
Here,
denotes the adjoint operator of
Indeed, given any
, by (
15), one has
Then, the duality relationship
and (
28) yield that
It follows from (40) that
Then, if we consider the linear mapping
given by
it leads to
Therefore,
is a continuous operator and has a unique extension to
such that
Moreover, we obtain that the linear operator
is continuous. Then,
is an isomorphism from
to
, which is following from (
45) and (
47).
Step 3, based on Theorem 1.1 of [
37], to complete the proof, we only need to show that
is a coercive operator. That is, there exists a positive constant
such that
In fact, with these above preliminaries, if
is injective,
is Hilbert space endowed with the norm
and the inner product
For any
one has
Then, (36) has a unique solution. This means that any satisfying the equality could yield . Consequently, the unknown source S is uniquely identified and the proof is finished. □
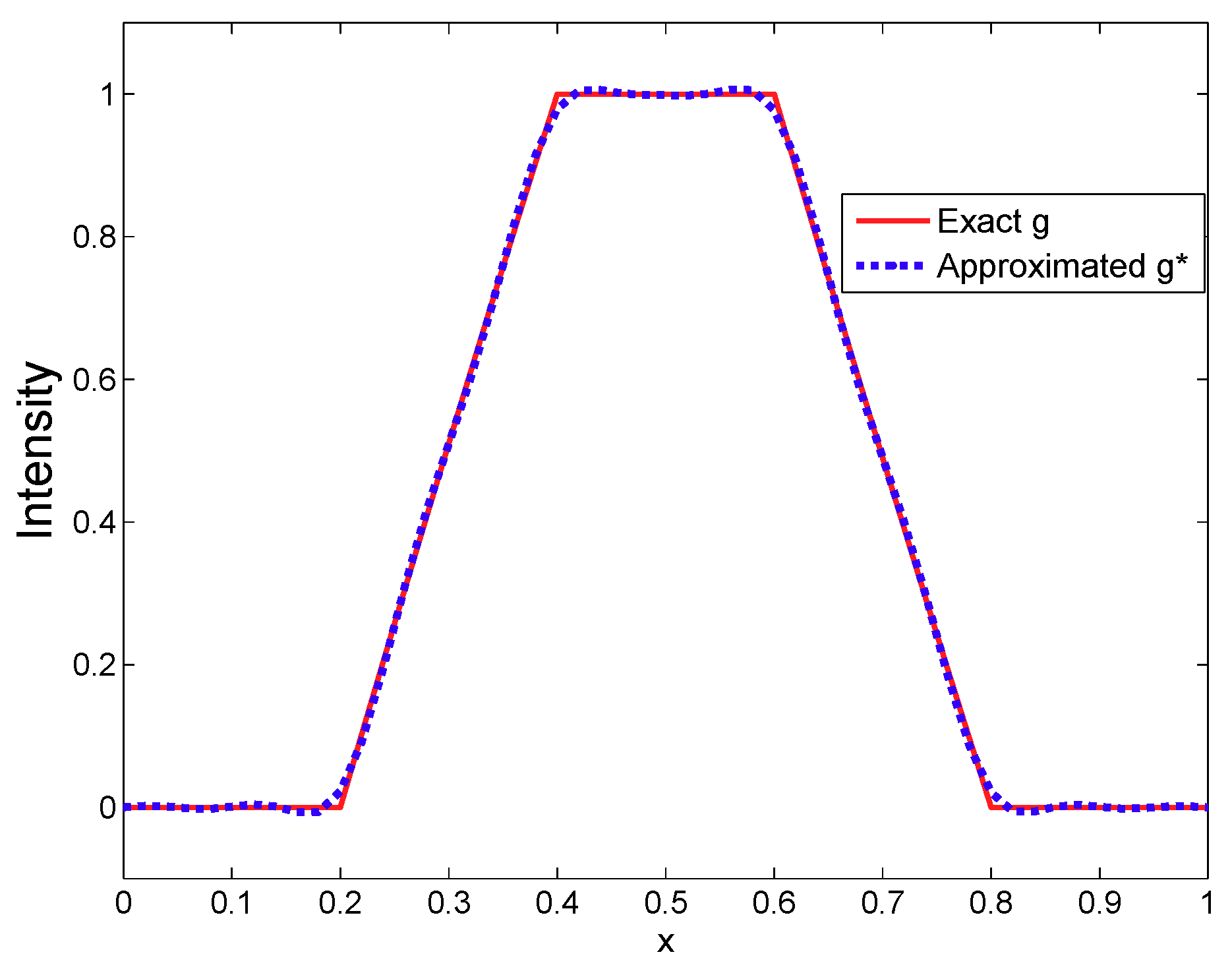
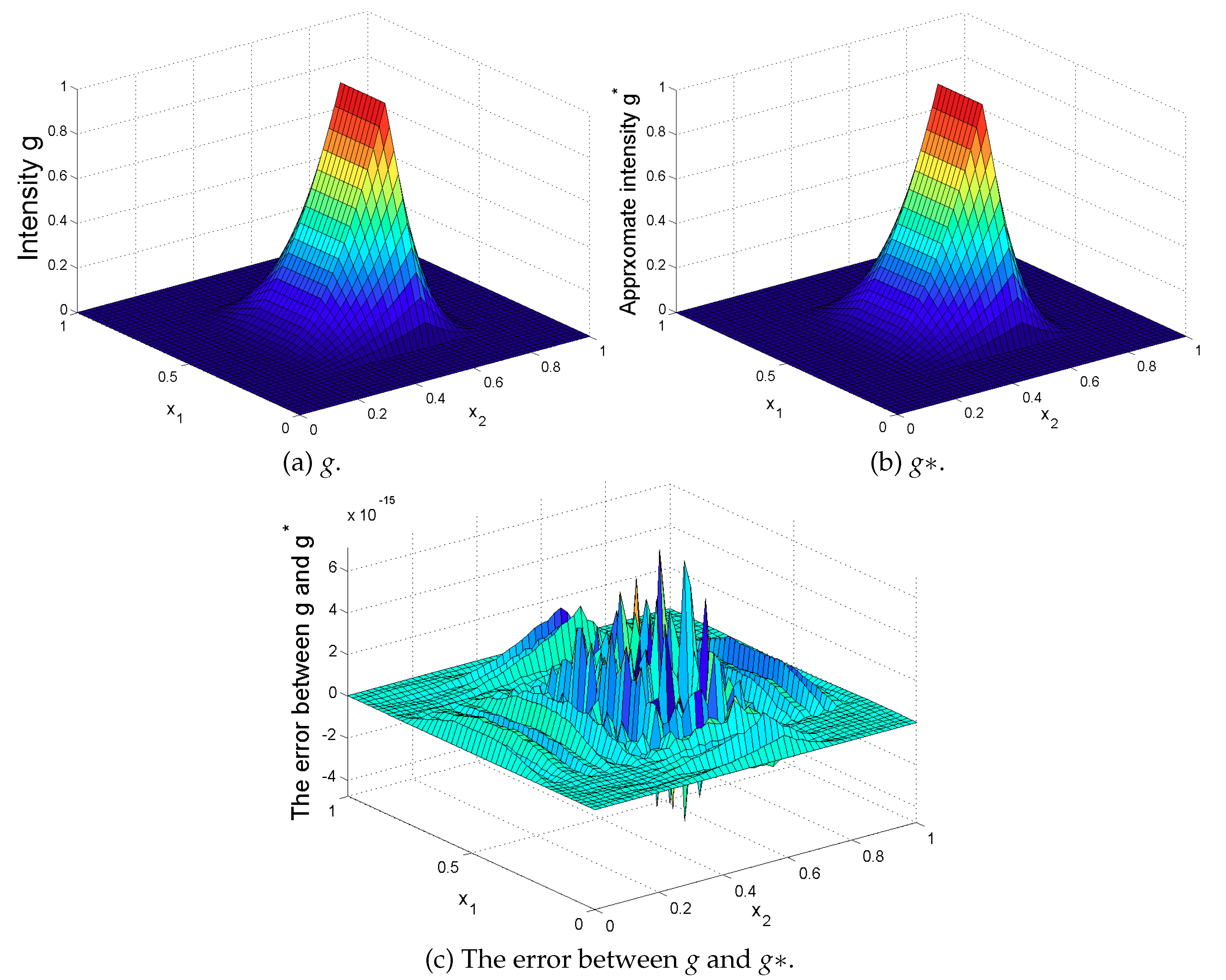
Remark 1. From Theorem 3, if are spy sensors, we get that the operator is injective by using the knowledge of the considered time fractional diffusion system and the sensor measurements. The main tool used in the above proof is the duality theory and our results could be used for sensing both the bounded time-varying space-dependence source (the zone source) and the unbounded time-varying space-dependence source (the pointwise source). With this, we see that the obtained results can be considered as a generalization of that in [38]. In particular, if and in the integral (15) is uniformly bounded with respect to all , i.e., , holds for some constant , we have [7]which is convergent and is consistent with the conditional stability results in Theorem 3.1 of [38]. Remark 2. Note that Theorem 3 is obtained by assuming that the measurement doesn’t contain noise and the considered domain is regular so that the eigenvalue pairing of operator A satisfying Equations (21) and (22) is obtained. However, these assumptions may fail in some practical applications. For this, due to the memory effect of the fractional derivative, more new properties on fractional derivatives (or on Mittag–Leffler functions) and more constraints on a system operator are required. While interesting, we conclude that source sensing problems for time fractional diffusion systems under uncertain measurements of an irregular bounded domain and their robust analysis are of great interest. Next, we give a concrete algorithm to recover the unknown fixed zone source . Here, denotes the support of the source and represents its intensity.
Since
forms a complete and orthonormal basis in
,
can be rewritten as follows:
Then, the source sensing problem is converted to identify the value of coefficients
By (
36), one has
Multiplying both sides of (
53) with
yields that
With this, set
and
. For a big enough integer
J,
can then be approximated by solving the following equation:
It is worth mentioning that the matrix of (
55) is positive. Consequently, we have
5. Further Remarks
Realize that the Caputo fractional order derivative is another widely used derivative in fractional order systems; in this section, we consider the source sensing problem for the following time fractional diffusion system with a Caputo fractional derivative:
where
denotes the Caputo fractional derivative.
Taking a Laplace transform on both sides of system (
57), it yields that
Observing that
and
the unique solution of system (
57) satisfies [
7]
For the approach on identifying the source
governed by system (
57), however, the conclusions obtained in previous sections will never hold if the measurements are defined as in (
19). This is due to the fact that
is usually not equal to
if
. Then, some new revised definition of the measurements should be introduced.
Observing that
for any
,
following from (
59), if the sensor measurements are revised to be given by
p sensors
as follows:
Consider system (
57) with
, define
, and we obtain the following result.
Definition 9. System (57), (61) with is said weakly observable if Theorem 4. Define matrices aswhere , and . Then, the sensors are strategic for system (57) with if and only if Since the proof of Theorem 4 is very similar to that of Theorem 1, we omit it.
Consider system (
57), let the operator
be given by
where
The source sensing problem is stated as follows:
Given the measurements
defined by (
61), find a source
S such that the solution of system (
57) satisfies
Theorem 5. Assume that are spy sensors. Then, the source in system (57) can be uniquely identified by the observation z in (61) as the unique solution of the following equation Proof. For any two solutions
,
of system (57), their difference
satisfies
Then, we divide the proof into three steps.
Step 1, if
are
spy sensors, we get that
is injective. Then, the semi-norm
defines a norm for the space
. Therefore,
is a Hilbert space endowed with the norm
and the inner product
Step 2, given any
, since
The duality relationship
leads to
Define
as
Similar to Step 2 of Theorem 3, we get that the operator is an isomorphism from to its dual
Step 3, for any
one has
Then, Theorem 1.1 of [
37] yields that (67) has a unique solution. As a result, the unknown source
S in system (57) is uniquely identified by the observation (61). The proof is finished. □
Similarly, for any unknown fixed zone source
, by (52) and (67), we have
For big enough integer
J, then
can be approximated by multiplying both sides of (74) with
as follows:
where
and
. With this, we obtain that