Practical Considerations for Accuracy Evaluation in Sensor-Based Machine Learning and Deep Learning
Abstract
1. Introduction
2. Background on the Proposed Practical Accuracy Tests
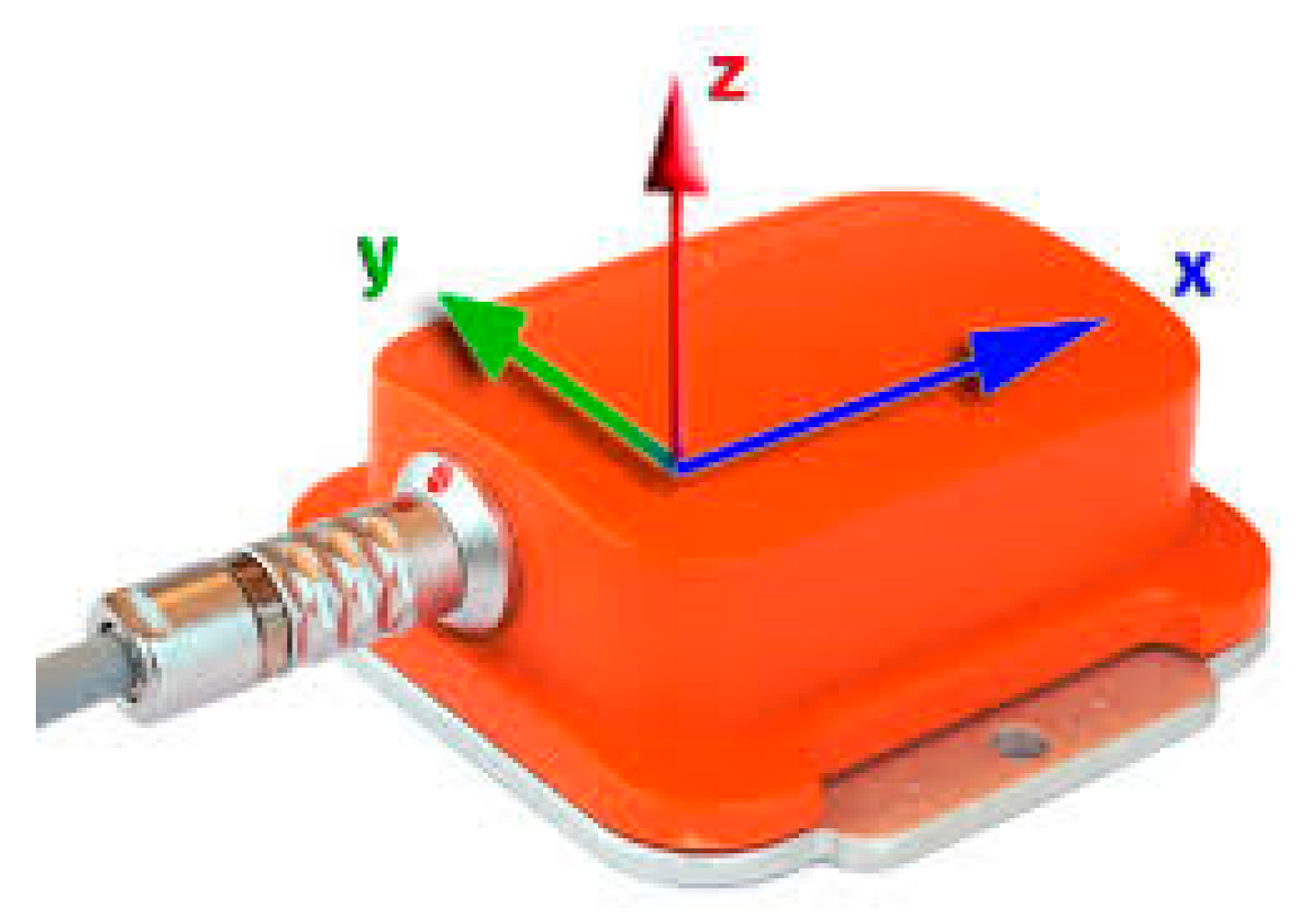
3. Dataset Details and Simulation Tools
4. Baseline Accuracy
5. Experimental Results
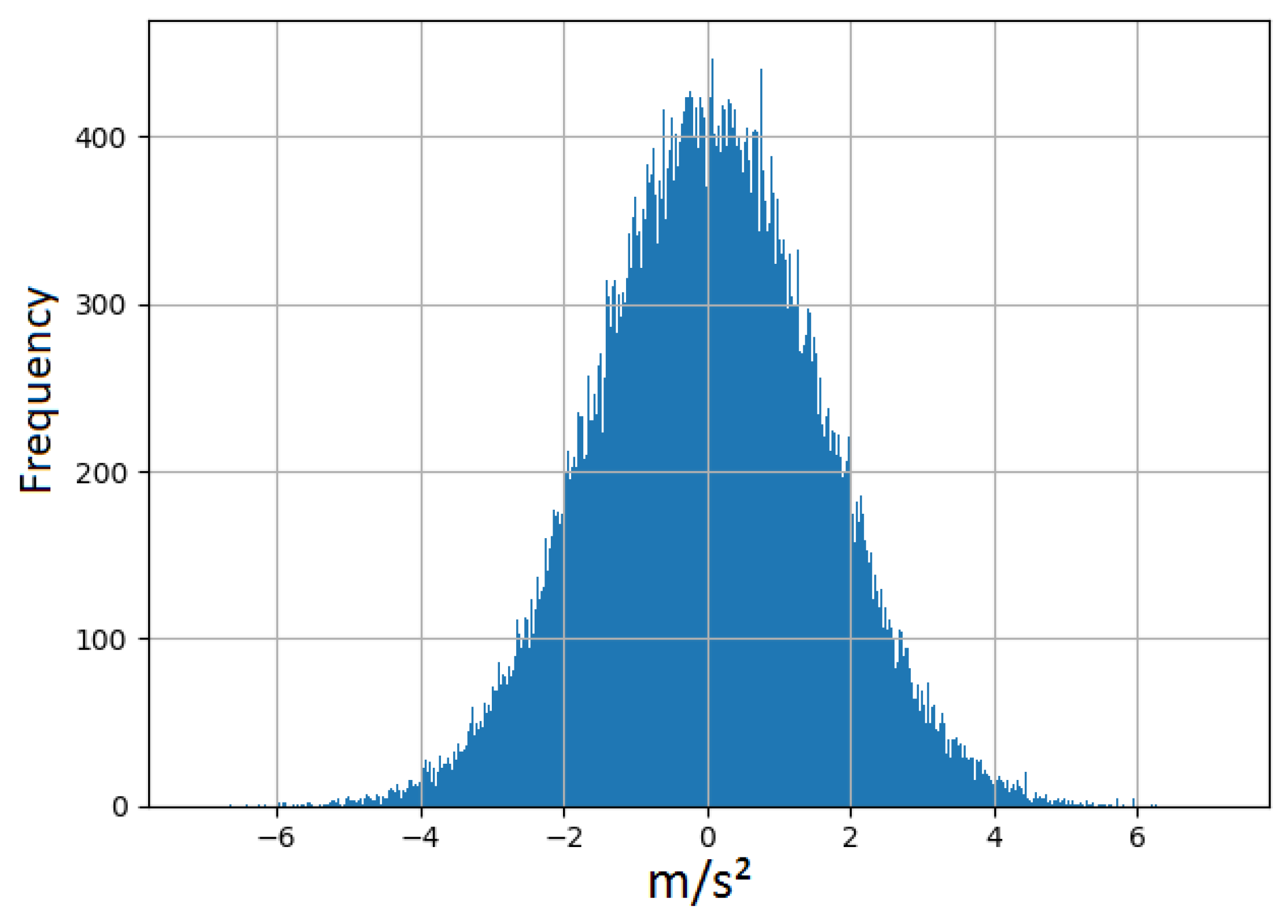
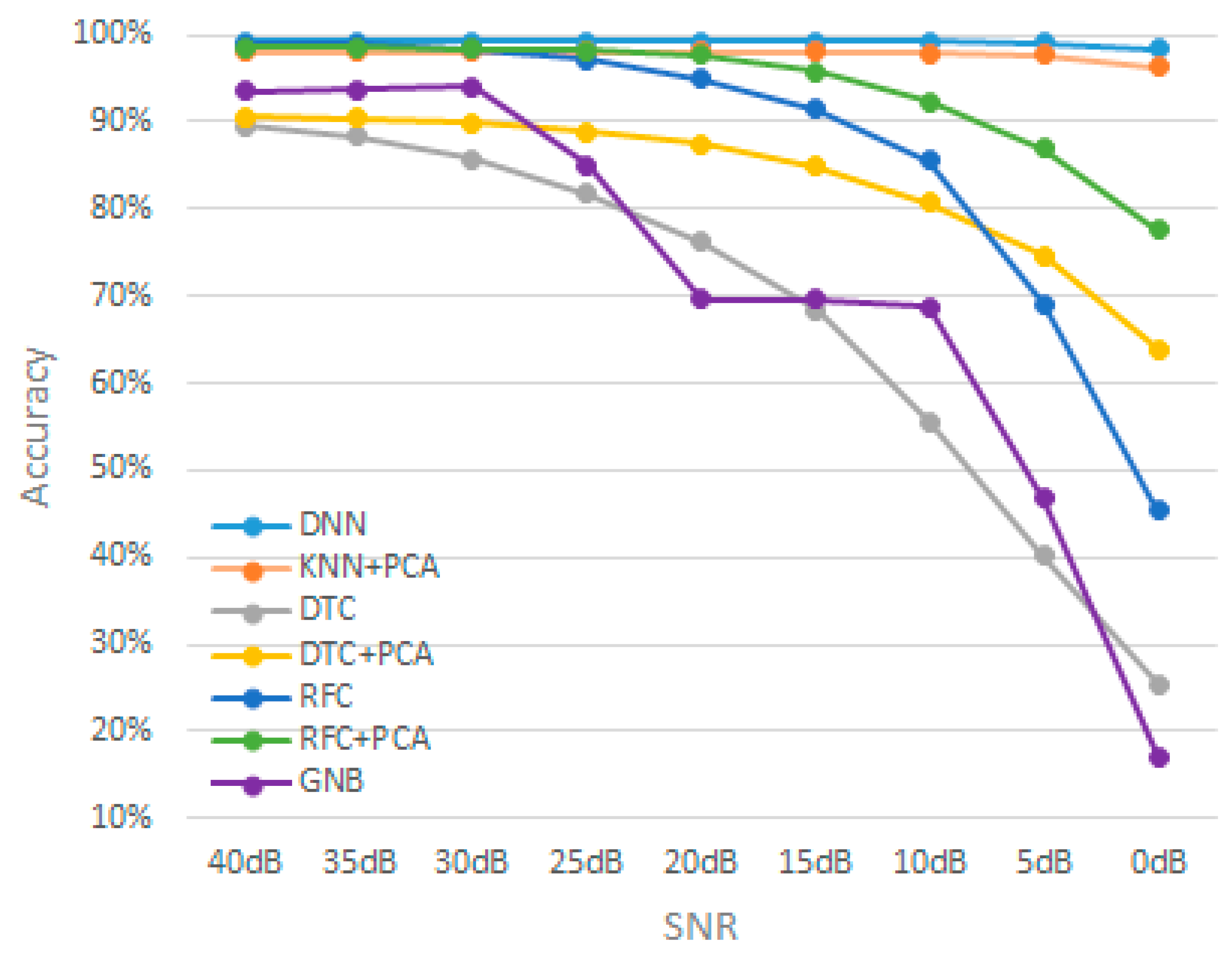
5.1. Thermal Noise Simulation
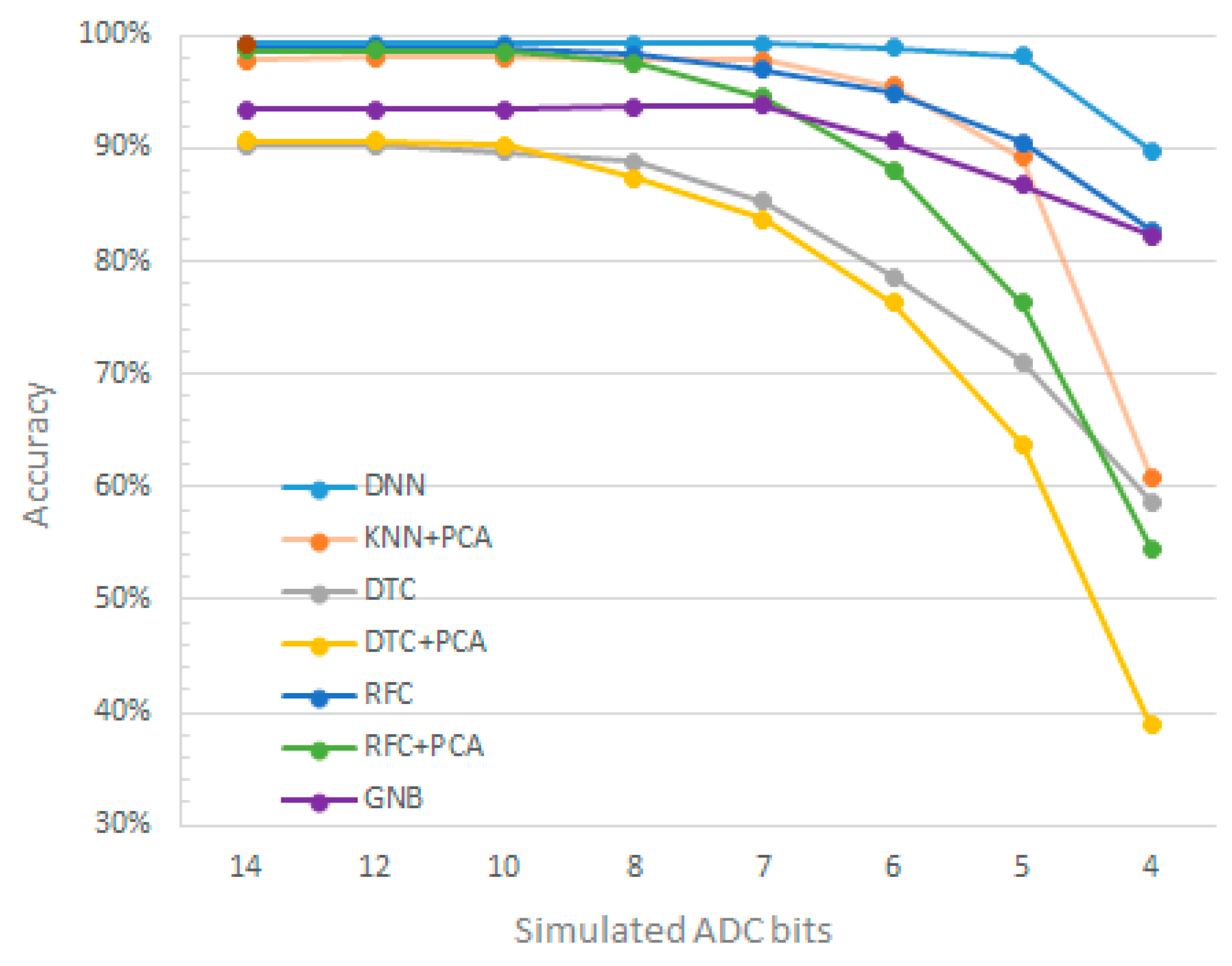
5.2. Quantization Levels Simulation
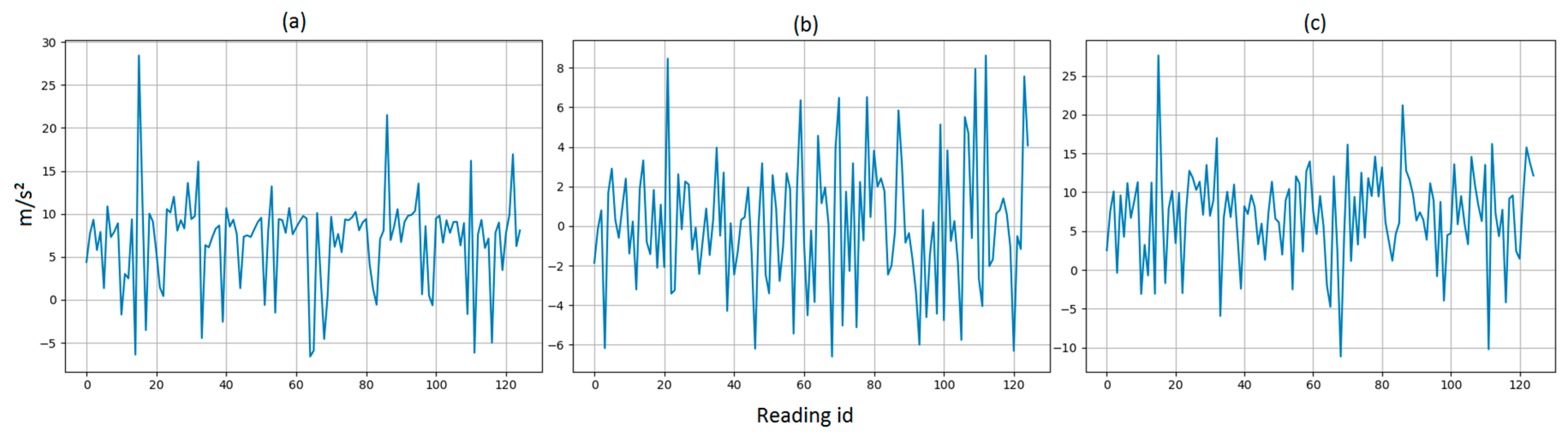
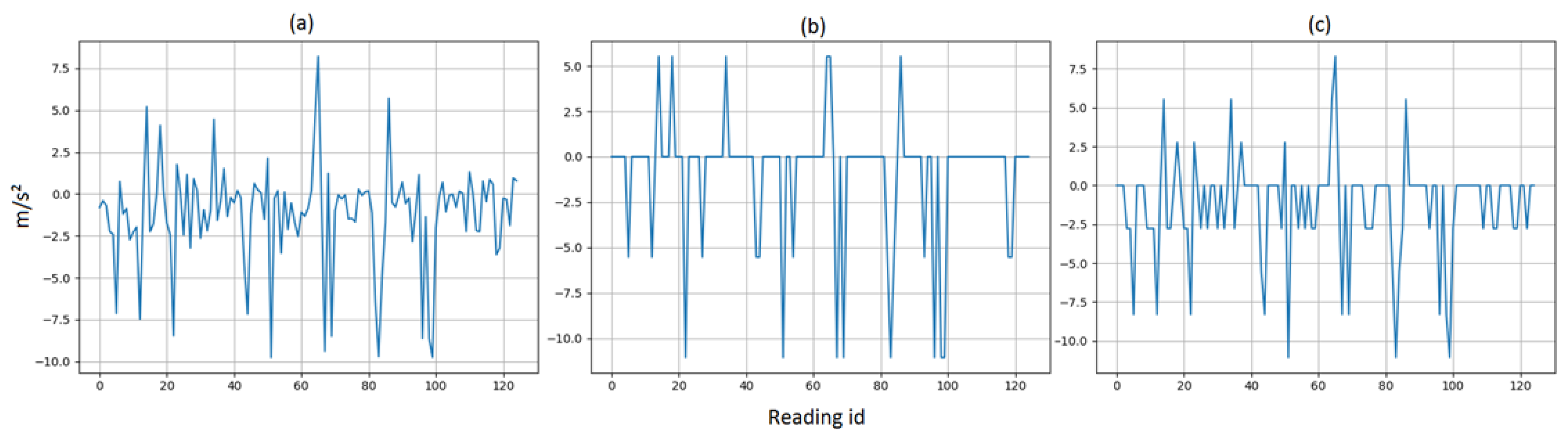
5.3. Impact of Sensor Failure on the Accuracy
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Emmert-Streib, F.; Matthias, D. Evaluation of Regression Models: Model Assessment, Model Selection and Generalization Error. Mach. Learn. Knowl. Extr. 2019, 1, 521–551. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Salisou, M.; Matthias, D. A comprehensive survey of error measures for evaluating binary decision making in data science. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, e1303. [Google Scholar] [CrossRef]
- Karystinos, G.N.; Dimitrios, P.A. On overfitting, generalization, and randomly expanded training sets. IEEE Trans. Neural Netw. 2000, 11, 1050–1057. [Google Scholar] [CrossRef] [PubMed]
- Altun, K.; Billur, B.; Orkun, T. Comparative study on classifying human activities with miniature inertial and magnetic sensors. Pattern Recognit. 2010, 43, 3605–3620. [Google Scholar] [CrossRef]
- Barshan, B.; Murat, C.Y. Recognizing daily and sports activities in two open source machine learning environments using body-worn sensor units. Comput. J. 2014, 57, 1649–1667. [Google Scholar] [CrossRef]
- Chung, S. Sensor Data Acquisition and Multimodal Sensor Fusion for Human Activity Recognition Using Deep Learning. Sensors 2019, 19, 1716. [Google Scholar] [CrossRef]
- Miao, F. A Wearable Sensor for Arterial Stiffness Monitoring Based on Machine Learning Algorithms. IEEE Sens. J. 2018, 19, 1426–1434. [Google Scholar] [CrossRef]
- Yeh, C. Machine Learning for Long Cycle Maintenance Prediction of Wind Turbine. Sensors 2019, 19, 1671. [Google Scholar] [CrossRef]
- University of Califonia Irvine Machine Learning Repository, Daily and Sports Activities Data Set. 2013. Available online: https://archive.ics.uci.edu/ml/datasets/daily+and+sports+activities (accessed on 1 March 2019).
- Villeneuve, E. Signal quality and compactness of a dual-accelerometer system for gyro-free human motion analysis. IEEE Sens. J. 2016, 16, 6261–6269. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Sharkey, P.M.; Vaidyanathan, R.; Harwin, W.S. Measuring motion with kinematically redundant accelerometer arrays: Theory, simulation and implementation. Mechatronics 2013, 23, 518–529. [Google Scholar] [CrossRef]
- Uyttenhove, K.; Michel, S.; Steyaert, J. Speed-power-accuracy tradeoff in high-speed CMOS ADCs. IEEE Trans. Circuits Syst. Analog Digit. Signal Proc. 2002, 49, 280–287. [Google Scholar] [CrossRef]
- Belcher, R.A. ADC standard IEC 60748-4-3: Precision measurement of alternative ENOB without a sine wave. IEEE Trans. Instrum. Meas. 2015, 64, 3183–3200. [Google Scholar] [CrossRef]
- Technologies, X.; MTi, B.V. MTx User Manual. Document MT0100P, Revision N. 27 May 2009. Available online: http://www.xsens.com (accessed on 2 April 2019).
- Attal, F. Physical human activity recognition using wearable sensors. Sensors 2015, 15, 31314–31338. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. An incremental learning method based on probabilistic neural networks and adjustable fuzzy clustering for human activity recognition by using wearable sensors. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 691–699. [Google Scholar] [CrossRef] [PubMed]
- Trabelsi, D. An unsupervised approach for automatic activity recognition based on hidden Markov model regression. IEEE Trans. Autom. Sci. Eng. 2013, 10, 829–835. [Google Scholar] [CrossRef]
- Chollet, F. 2015 Keras. Available online: https://github.com/fchollet/keras (accessed on 12 October 2018).
- Pedregosa, F. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Jeong, B.G. Simplified noise model parameter estimation for signal-dependent noise. Signal Process. 2014, 96, 266–273. [Google Scholar] [CrossRef]
- Robert, L.P. Mechanical-thermal noise in MEMS gyroscopes. IEEE Sens. J. 2005, 5, 493–500. [Google Scholar]
- Lent, B. Practical Considerations of Accelerometers Noise. Available online: https://www.endevco.com/news/archivednews/2009/2009_12/TP324.pdf (accessed on 1 May 2019).
- Abolghasem, N. A generalized study of coil-core-aspect ratio optimization for noise reduction and SNR enhancement in search coil magnetometers at low frequencies. IEEE Sens. J. 2015, 15, 6454–6459. [Google Scholar]
- How to Increase the Analog-to-Digital Converter Accuracy in an Application; Freescale Semiconductor, Inc.: Austin, TX, USA, 2016.
- Large, D.; James, F. The HFC Plant. In Broadband Cable Access Networks; Elsevier Inc.: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Alink, M.; Oude, S. Spurious-free dynamic range of a uniform quantizer. IEEE Trans. Circuits Syst. Express Briefs 2009, 56, 434–438. [Google Scholar] [CrossRef]
- Johns, D.A.; Ken, M. Analog Integrated Circuit Design; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Murmann, B. ADC Performance Survey 1997–2019. Available online: http://web.stanford.edu/~murmann/adcsurvey.html (accessed on 8 June 2019).
- Timothy, H.W. The hitchhiker’s guide to successful residential sensing deployments. In Proceedings of the 9th ACM Conference on Embedded Networked Sensor Systems, Seattle, WA, USA, 1–4 November 2011. [Google Scholar]
| Algorithm | Train/Test Sample Size | Test Accuracy without PCA | Test Accuracy with PCA |
|---|---|---|---|
| Deep Neural Network (DNN) | 8208/912 | 99.26% | 97.87% |
| K-Nearest Neighbors (KNN) | 8208/912 | 78.34% | 98.12% |
| Decision Tree Classifier (DTC) | 8208/912 | 90.30% | 90.72% |
| Random Forest Classifier (RFC) | 8208/912 | 98.96% | 98.65% |
| Gaussian Naïve Bayes (GNB) | 8208/912 | 93.49% | 78.55% |
| SNR | Machine Learning Model | ||||||
|---|---|---|---|---|---|---|---|
| DNN | KNN + PCA | DTC | DTC + PCA | RFC | RFC + PCA | GNB | |
| Baseline | 99.26% | 98.12% | 90.30% | 90.72% | 98.96% | 98.65% | 93.49% |
| 40 dB | 99.28% | 98.11% | 89.62% | 90.54% | 98.93% | 98.59% | 93.34% |
| 35 dB | 99.25% | 97.97% | 88.30% | 90.47% | 98.84% | 98.51% | 93.28% |
| 30 dB | 99.25% | 97.98% | 85.70% | 89.89% | 98.35% | 98.44% | 93.03% |
| 25 dB | 99.27% | 98.02% | 81.69% | 88.90% | 97.08% | 98.24% | 85.06% |
| 20 dB | 99.24% | 98.03% | 76.28% | 87.53% | 94.88% | 97.60% | 69.61% |
| 15 dB | 99.25% | 98.01% | 68.33% | 84.79% | 91.51% | 95.74% | 69.60% |
| 10 dB | 99.24% | 97.82% | 55.65% | 80.77% | 85.55% | 92.35% | 68.81% |
| 5 dB | 99.11% | 97.73% | 40.13% | 74.56% | 69.12% | 86.90% | 46.82% |
| 0 dB | 98.43% | 96.37% | 25.46% | 63.98% | 45.40% | 77.61% | 17.07% |
| Resolution | Machine Learning Model | ||||||
|---|---|---|---|---|---|---|---|
| DNN | KNN + PCA | DTC | DTC + PCA | RFC | RFC + PCA | GNB | |
| 16 bits[baseline] | 99.26% | 98.12% | 90.30% | 90.72% | 98.96% | 98.65% | 93.49% |
| 14 bits | 99.25% | 97.95% | 90.28% | 90.68% | 98.95% | 98.61% | 93.40% |
| 12 bits | 99.25% | 98.02% | 90.23% | 90.64% | 98.93% | 98.61% | 93.47% |
| 10 bits | 99.25% | 97.99% | 89.62% | 90.31% | 98.89% | 98.56% | 93.44% |
| 8 bits | 99.20% | 97.93% | 88.80% | 87.30% | 98.33% | 97.50% | 93.72% |
| 7 bits | 99.20% | 97.74% | 85.33% | 83.68% | 96.94% | 94.53% | 93.74% |
| 6 bits | 98.90% | 95.48% | 78.63% | 76.33% | 94.89% | 88.11% | 90.65% |
| 5 bits | 98.11% | 89.12% | 71.01% | 63.81% | 90.51% | 76.29% | 86.69% |
| 4 bits | 89.74% | 60.91% | 58.62% | 38.89% | 82.71% | 54.52% | 82.26% |
| Model | Simulated ADC Bits | ||||
|---|---|---|---|---|---|
| 8 bits | 7 bits | 6 bits | 5 bits | 4 bits | |
| DNN | 99.19% | 98.72% | 98.54% | 89.29% | 81.87% |
| KNN + PCA | 98.03% | 95.29% | 91.56% | 72.48% | 51.65% |
| DTC | 89.06% | 86.32% | 87.41% | 79.96% | 75.35% |
| DTC + PCA | 86.29% | 81.91% | 79.17% | 50.88% | 36.73% |
| RFC | 98.80% | 97.48% | 97.70% | 92.77% | 89.81% |
| RFC + PCA | 96.24% | 94.59% | 87.91% | 67.73% | 41.31% |
| GNB | 85.62% | 82.55% | 81.67% | 54.04% | 32.11% |
| Model | Failed Device | ||
|---|---|---|---|
| Accelerometer | Gyroscope | Magnetometer | |
| DNN | 93.75% | 98.81% | 83.92% |
| KNN + PCA | 64.42% | 94.77% | 94.74% |
| DTC | 63.98% | 90.28% | 66.26% |
| DTC + PCA | 30.46% | 90.72% | 90.48% |
| RFC | 87.55% | 98.82% | 82.58% |
| RFC + PCA | 41.38% | 98.26% | 96.26% |
| GNB | 76.87% | 92.79% | 86.08% |
| Model | Failed Tracker | ||||
|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | |
| DNN | 74.29% | 86.15% | 72.59% | 74.69% | 68.65% |
| KNN + PCA | 78.08% | 48.69% | 51.07% | 71.53% | 72.16% |
| DTC | 38.6% | 66.89% | 55.27% | 64.37% | 16.15% |
| DTC + PCA | 27.89% | 33.43% | 30.63% | 31.56% | 28.9% |
| RFC | 57.73% | 82.69% | 73.26% | 88.59% | 39.62% |
| RFC + PCA | 42.98% | 40.48% | 38.88% | 43.84% | 40.25% |
| GNB | 57.21% | 83% | 67.55% | 63.45% | 64.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammad, I.; El-Sankary, K. Practical Considerations for Accuracy Evaluation in Sensor-Based Machine Learning and Deep Learning. Sensors 2019, 19, 3491. https://doi.org/10.3390/s19163491
Hammad I, El-Sankary K. Practical Considerations for Accuracy Evaluation in Sensor-Based Machine Learning and Deep Learning. Sensors. 2019; 19(16):3491. https://doi.org/10.3390/s19163491
Chicago/Turabian StyleHammad, Issam, and Kamal El-Sankary. 2019. "Practical Considerations for Accuracy Evaluation in Sensor-Based Machine Learning and Deep Learning" Sensors 19, no. 16: 3491. https://doi.org/10.3390/s19163491
APA StyleHammad, I., & El-Sankary, K. (2019). Practical Considerations for Accuracy Evaluation in Sensor-Based Machine Learning and Deep Learning. Sensors, 19(16), 3491. https://doi.org/10.3390/s19163491






